統計検定2級に満点で合格するために必要な全知識を紹介します。試験範囲に含まれているようで実際には出題されていないものはバッサリとカットしています。
受検前の知識の確認に使ってください!
1変数,2変数の記述統計の分野
代表値
ヒストグラム…データをいくつかの階級に分けて,縦の長さが度数,横の長さが階級の幅に等しい長方形で表したグラフ
データの範囲…最大値ー最小値
中央値…データを大きさの順に並べたときの中央の値です。データが偶数個のときは,中央に並ぶ2つの値の平均です。
四分位数…データを大きさの順に並べて中央値(第2四分位数)で2つに分けるとき,第1四分位数は値の小さいグループの中央値,第3四分位数は値の大きいグループの中央値
四分位範囲…第3四分位数ー第1四分位数
箱ひげ図…データの散らばりを,第1四分位数と第3四分位数を両端とする箱と,最大値,最小値を端とするひげで表した図
相対度数…当該の階級の度数÷全度数
累積相対度数…当該の階級までの相対度数の合計
ローレンツ曲線…不均衡の度合いを示すのに使われる下の図のような折れ線グラフです。統計検定2級では,横軸に人口の累積相対度数,縦軸に所得の累積相対度数をとり,人口の累積相対度数20%ごとに点をとってつくった折れ線グラフが出題されています。
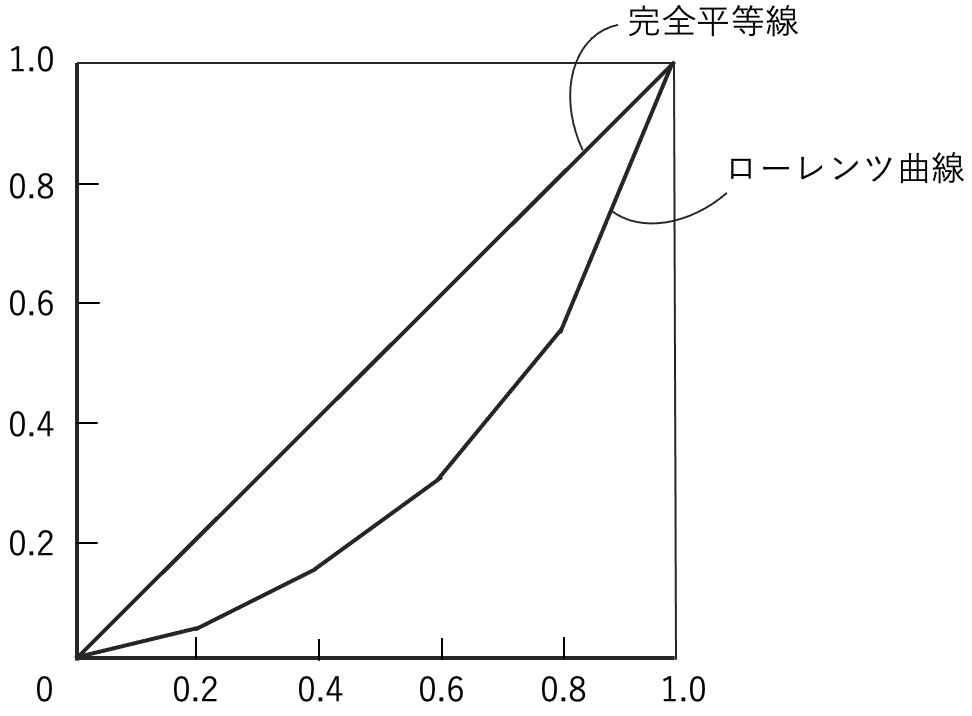
ジニ係数…(0,0)と(1,1)を結ぶ線分(完全平等線)とローレンツ曲線で囲まれた部分の面積の2倍の値
・データx1,x2,x3,…,xnの平均は次の式で求めます。
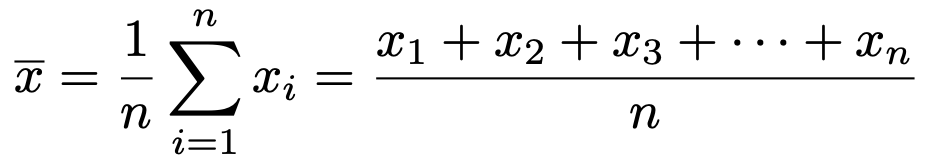
・データx1,x2,x3,…,xnの分散は次の式で求めます。
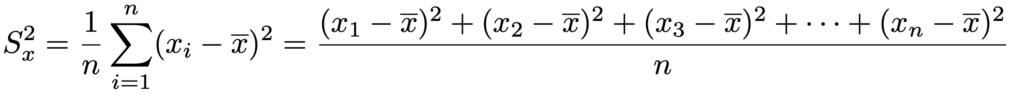
データの平均から分散を求める次の公式があります。
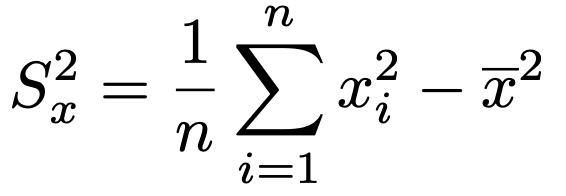
・データの標準偏差Sxは,分散の正の平方根です。
・データの変動係数は次の式で求めます。
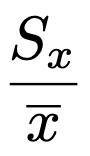
・データxiの標準化得点は次の式で求めます。
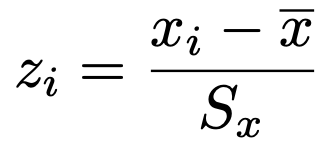
標準化得点の平均は0,分散は1であり,平均や分散が異なるデータどうしを比べることが可能になります。ただし,分母の標準偏差として不偏分散の正の平方根を使う場合がありますので,問題の指示に従ってください。
・データ(x1,y1),(x2,y2),(x3,y3),…,(xn,yn)の共分散は次の式で求めます。
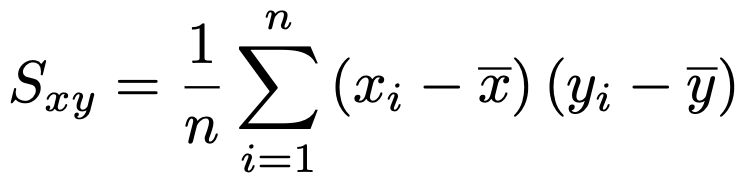
共分散について次の公式が成り立ちます。
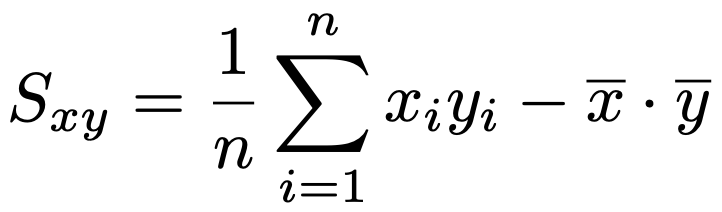
・データ(x1,y1),(x2,y2),(x3,y3),…,(xn,yn)の相関係数は次の式で求めます。
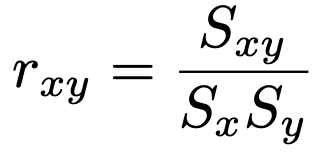
相関係数はー1以上1以下の値をとります。
・散布図…データ(x1,y1),(x2,y2),(x3,y3),…,(xn,yn)を座標とみなして平面上に表した図です。散布図上でデータを表す点は,相関係数が1に近い正の値をとるときには右上がりの直線に近い形で並び,相関係数がー1に近い負の値をとるときには右下がりの直線に近い形で並びます。
・擬相関…xとzの間に相関があり,yとzの間に相関があるとき,xとyの相関が大きくなる見かけ上の相関
・偏相関係数…zが,xとyの両方に相関があるとき,xからzの影響を除いた変量とyからzの影響を除いた変量の間の相関係数
・データx1,x2,x3,…,xnの歪度は次の式で求めます。
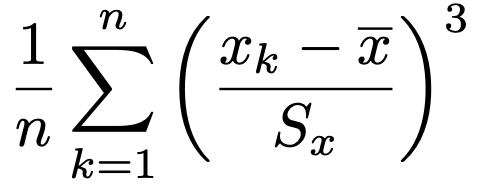
標準化得点の3乗の平均ですが,式は覚えなくていいです。この式を使った計算は統計検定では出題されませんし,歪度を計算するのに,この式にさらに係数をつけた式を使う場合もありますので,「標準化得点の3乗が関わるんだな」くらいに思ってください。
大事なのは,「標準化得点の3乗の平均」であることから「データの分布が右に長い裾を持つときには正の値,左に長い裾を持つときには負の値をとりやすく,左右対称ならば0になる」という事実が成り立つということです。
・データx1,x2,x3,…,xnの尖度は次の式で求めます。
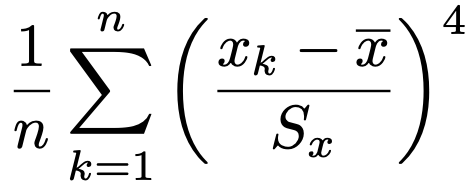
標準化得点の4乗の平均ですが,歪度と同じ理由で,この式は覚えなくていいです。データの分布に山が1つあり,その山が尖っているほど尖度は大きな値をとる傾向があります。正規分布の尖度を上の式と同様に計算すると3になるので,上の式から3をひいた式を尖度とする場合があります。
時系列データ
例えば,ある小売店の各月の売上データのように,時期とひもづいているデータのことです。時系列データの変動は,次の3つに分けられます。
傾向変動…長期にわたる動きを表す変動
季節変動…1年を周期として循環する変動
不規則変動…傾向変動や季節変動以外の変動(予測が困難な偶然の変動)
移動平均
時系列データに対して,3期の平均や4期の平均などが1期ごとにどのように変動するかを調べ,長期的な傾向を捉えやすくする手法です。
例えば,3項移動平均は,3月を中心とする3か月(2〜4月)のデータの平均を3月の値,4月を中心とする3か月(3〜5月)のデータの平均を4月の値,…のように計算します。
4項移動平均の場合には4つの月に真ん中の月がないため工夫が必要になります。例えば3月の値を求めるならば,3月を中心とする5か月のデータをもとに,次の式のように最初と最後の月のデータを半分だけ計算に入れた実質4か月の平均で計算します。

コレログラム
例えば,毎月の時系列データがあるとき,1か月だけずらしたデータ(ラグ1),2か月だけずらしたデータ(ラグ2),…のようにして,元のデータと時期をずらしたデータとの相関(自己相関係数(ACF)と言います)をグラフにしたものです。アイスクリームや灯油の販売量などは,1年前の同じ時期のデータと強い正の相関をもちやすいため,下の図のようにラグ12と強い正の相関があり,ラグ6と強い負の相関があります。
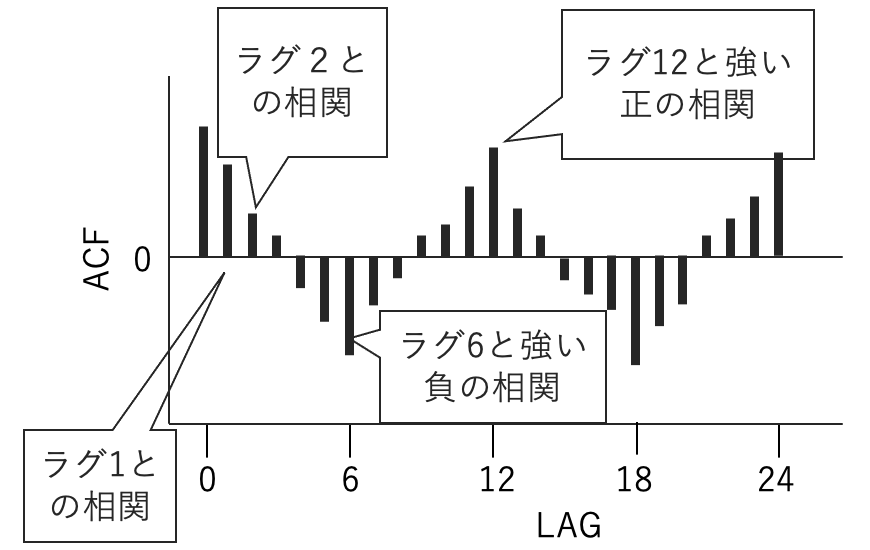
変化率
物価上昇率などの変化率は,基準となる時期の値(物価等)に対して比較対象の時期の値がどれだけ増えたかを表し,次の式で計算します。

また,基準となる時期の値がaで,そのn期後の比較対象の時期の値がbであるとき,次の式を満たすr(または100r)を平均変化率と言います。
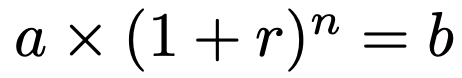
ラスパイレス指数とパーシェ指数
例として,市場にXとYの2つの財だけがある場合,数量と価格がそれぞれ次の表のようだったとします。
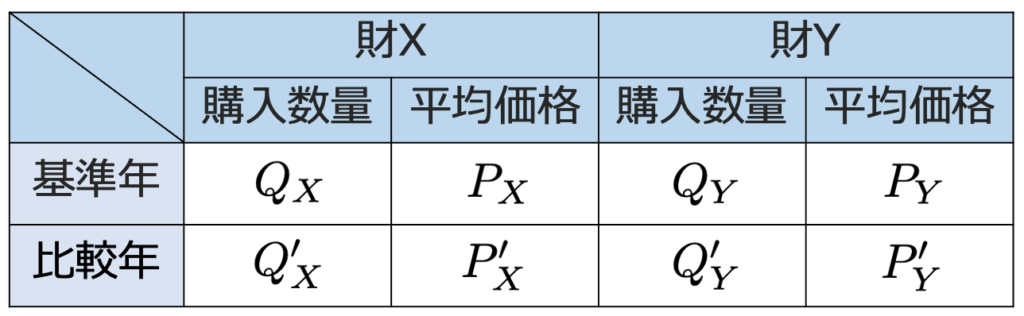
物価の上昇率を調べるには,基準とする時期と比較したい時期の購入数量を固定する必要があります。
ラスパイレス指数は,基準年の購入数量に固定した物価上昇率で,次のように計算されます。
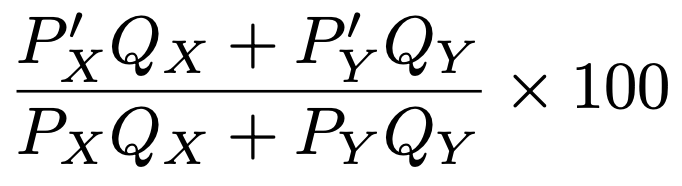
ラスパイレス指数は,最新(比較年)の数量を調べるコストがかからないため,消費者物価指数として主に使われています。
パーシェ指数は,比較年の購入数量に固定した物価上昇率で,次の式で計算されます。
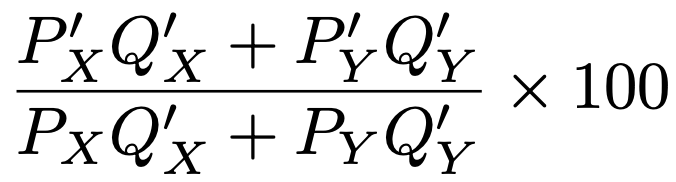
データ収集,確率,分布の分野
標本抽出法
単純無作為抽出以外で問われやすいのが次の4つです。
系統抽出法…母集団の要素すべてに番号をつけ,1つ目に抽出するデータの番号をランダムに決めた後,そこから等間隔で番号をたどってデータを抽出していく方法です。これにより,抽出の手間を削減しつつ,偏りない抽出が可能になります。
層化抽出法…企業を大企業,中小企業,零細企業の3つに分けるように,基準を決めていくつかの層に分けた後,それぞれの層から無作為抽出する方法です。事前に層化しない場合よりも精度の高い結果を得やすくなります。
集落(クラスター)抽出法…母集団をグループ分けした後,いくつかのグループを無作為に選び,選ばれたグループ内の標本を全数調査するものです。例えば,全国の高校生全員の名簿を得ることは困難ですが,高校の名簿ならば簡単に手に入るので,高校を無作為に選び,選ばれた各高校で全数調査する方法がこれにあたります。
二段抽出法…多段抽出法の一種で,無作為抽出を2回行います。例えば,全国の中から無作為にいくつかの県を抽出し,選ばれた県で無作為にいくつかの市町村を抽出する方法がこれにあたります。段数が増えるほど,選ばれる標本の数は減っていきますので,「二段抽出より三段抽出のほうが精度が高い」という選択肢は正しくないので,選ばないようにしましょう。
フィッシャーの3原則
局所管理…ブロック(狭い範囲)内で均一な条件を実現する
無作為化…処理をランダムに割り付ける
繰り返し…同じ処理を何度も行う
確率
事象Aが起こる確率をP(A)と表します。
試行…確率的な実験(例)サイコロを投げる
事象…確率的に起きた事がら(例)1の目が出る
排反…一方の事象が起これば,もう一方の事象は起こらない関係のこと
事象Aと事象Bが互いに排反であるときには次の式が成り立ちます。
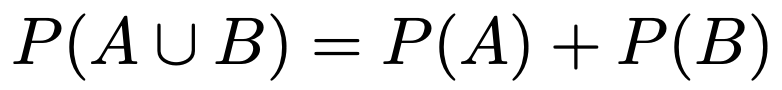
また,次の式が成り立つことを,2つの事象A,Bは独立であると言います。
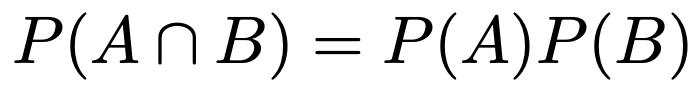
詳しくは【中学の数学からはじめる統計検定2級講座第1回】をご覧ください。
条件付き確率…事象Bが起きたという条件のもとでの事象Aの起きる確率であり,次の式で求めます。
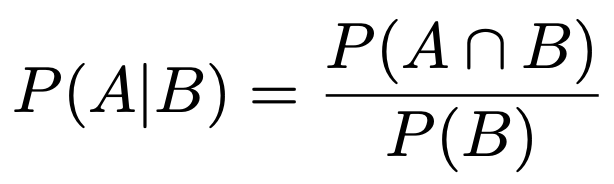
ベイズの定理…
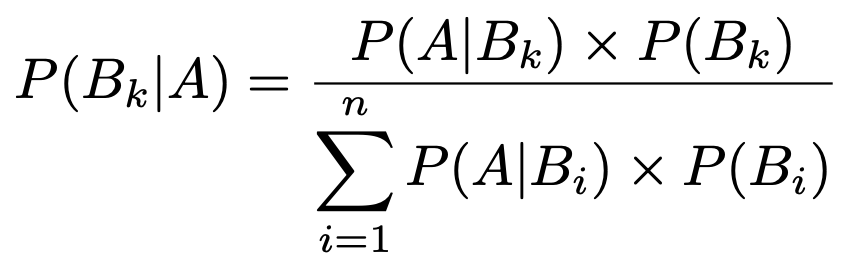
詳しくは【中学の数学からはじめる統計検定2級講座第2回】をご覧ください。
確率変数
変数であって,それぞれの値をとる確率が決まっているものです。とびとびの値をとる確率変数を離散型,連続的な値をとる確率変数を連続型と言います。確率変数はXやYなどの大文字で表し,X=3となる確率が2分の1であるとき,次のような記号で表します。
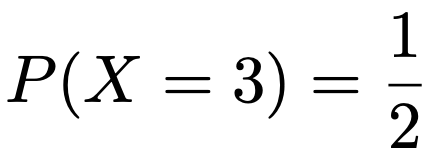
確率変数のとる値とその確率を一覧にして示したものを確率分布と言います。また,複数の確率変数の値に対して1つの確率が決まるような確率分布を同時確率分布と言います。
次の式で表されるような確率変数Xがある値x以下の値をとる確率のことをXの累積分布関数と言います。
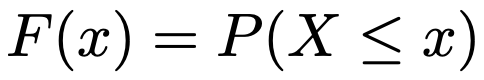
離散型の確率変数X,Yが独立であるとは,すべてのa,bについて次の式が成り立つことです。
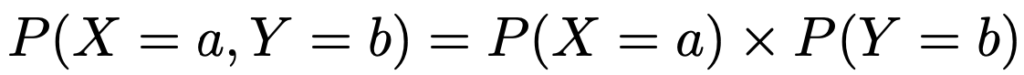
詳しくは【中学の数学からはじめる統計検定2級講座第3回】をご覧ください。
期待値と分散
・期待値…サイコロを投げ続ければ出た目の平均が3.5に近づくように,多数回の試行の結果として期待できる値のこと
離散型の確率変数Xの期待値は次の式で求めます。
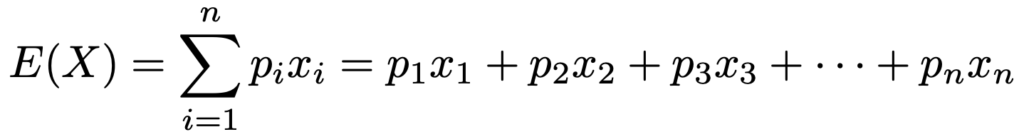
確率変数X,Yの期待値について,次の公式が成り立ちます。
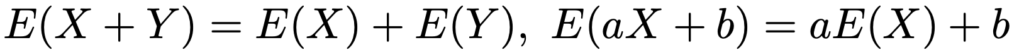
確率変数XとYが独立ならば,期待値について次の公式が成り立ちます。
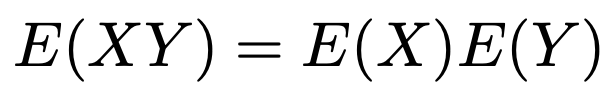
・分散…確率変数の値の期待値のまわりのバラツキの大きさ
離散型の確率変数Xの分散は次の式で求めます。
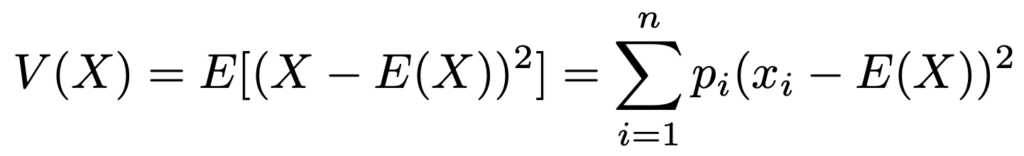
確率変数Xの分散について,次の公式が成り立ちます。
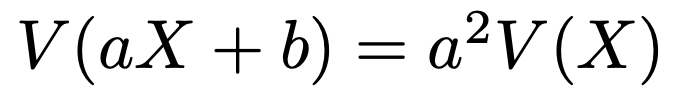
確率変数XとYが独立ならば,分散について次の公式が成り立ちます。
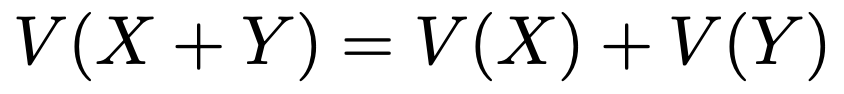
確率変数Xの期待値と分散について次の公式が成り立ちます。
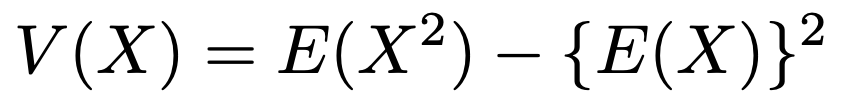
詳しくは【中学の数学からはじめる統計検定2級講座第4回】をご覧ください。
共分散と相関係数
・確率変数X,Yの共分散は次の式で求めます。
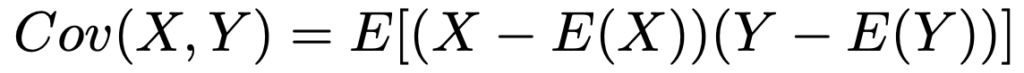
共分散について次の公式が成り立ちます。

したがって,確率変数XとYが独立ならば共分散は0になります。
また,分散のところで紹介した公式は,共分散を使うと次のように一般化できます。
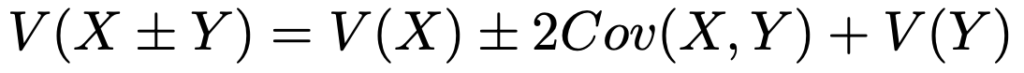
共分散について,次の公式も覚えておきましょう。
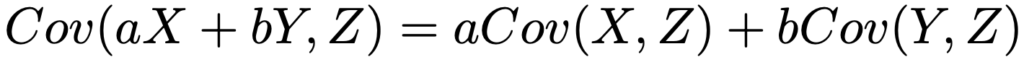
上の公式をさらに一般的に表すと,次の式になります。
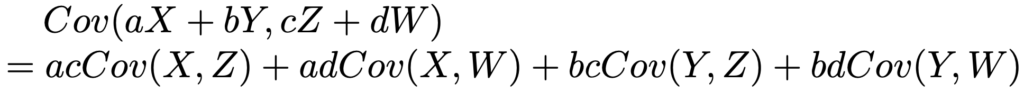
・確率変数X,Yの相関係数は次の式で求めます。
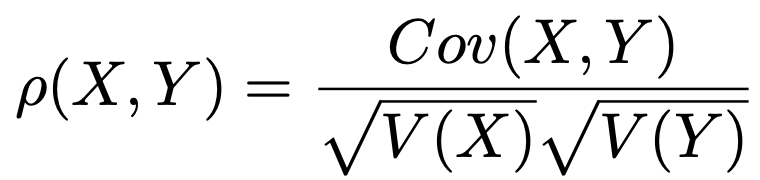
この場合の相関係数もー1以上1以下の値をとります。
確率変数の組(X,Y)を次のように(S,T)におきかえる一次変換
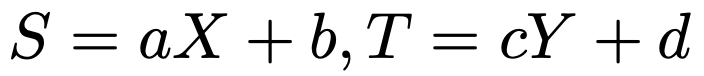
を考えると,S,Tの共分散とX,Yの共分散の間には次の式が成り立ちます。

また,S,Tの相関係数とX,Yの相関係数の関係は,ac>0ならば,
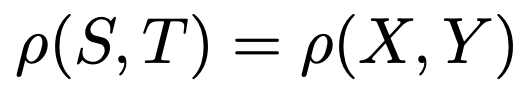
ac<0ならば,
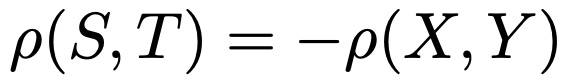
詳しくは【中学の数学からはじめる統計検定2級講座第5回】をご覧ください。
連続型確率変数
連続型の確率変数Xについて,次の式を満たすf(x)を確率密度関数と言います。
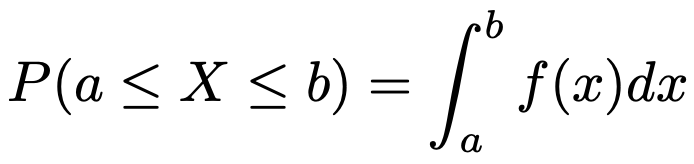
連続型の確率変数Xの期待値は次の式で求めます。
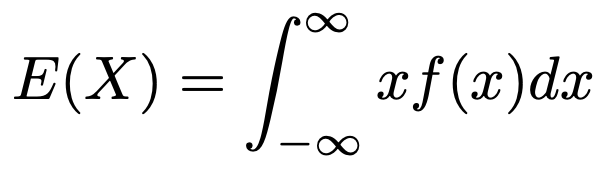
連続型の確率変数Xの分散は次の式で求めます。
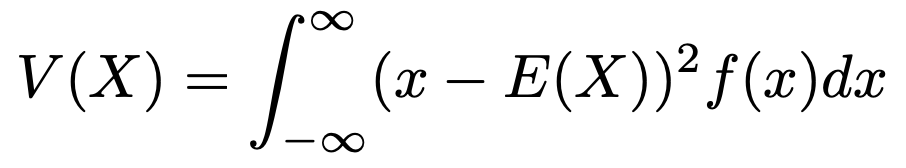
確率変数Xに対し,次の式で定まるF(x)を累積分布関数(または分布関数)と言います。

Xが連続型の確率変数の場合には,累積分布関数を微分すると確率密度関数が得られます。
詳しくは【中学の数学からはじめる統計検定2級講座第6回】をご覧ください。
正規分布
「18歳の日本人男性の身長」など,多くの分布が近似的に従う確率分布で,確率密度関数のグラフは左右対称で山が1つになります。
期待値がμ,分散がσ2である正規分布をN(μ,σ2)と表します。特に,期待値が0,分散が1である正規分布を標準正規分布と言い,N(0,1)と表します。
XがN(μ,σ2)に従うとき,次の式で定まるZはN(0,1)に従います。この操作を標準化と言います。

また,確率変数X,Yが独立で,それぞれ次の正規分布に従っているものとします。
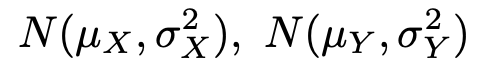
このとき,確率変数X+Yは次の正規分布に従います。
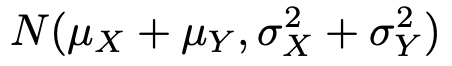
これを正規分布の再生性と言います。
詳しくは【中学の数学からはじめる統計検定2級講座第7回】をご覧ください。
t分布
標準正規分布と同じように,期待値が0(自由度が2以上のとき)で確率密度関数のグラフは左右対称で山が1つですが,自由度によってグラフの形が変わる確率分布です。自由度をどんどん大きくすると標準正規分布に近づいていきます。分散は覚えなくていいです。
母集団が正規分布に従っていて,その分散がわからないとき,標本平均を標準化して正規分布表を使うことができなくなるので,代わりにt分布を使います。
詳しくは【中学の数学からはじめる統計検定2級講座第8回】をご覧ください。
カイ2乗分布
次の式のような標準正規分布に従う独立なn個の確率変数の2乗の和で表される確率変数χ2が従う確率分布が自由度nのカイ2乗分布です。
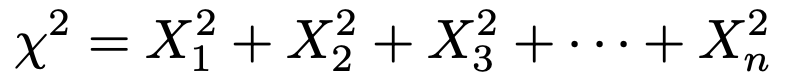
正規母集団の期待値をμ,分散をσ2とすると,大きさnの標本からつくられる次の確率変数は自由度nのカイ2乗分布に従います。
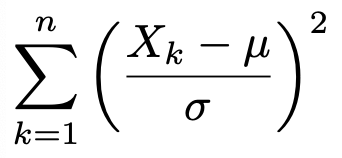
また,上の確率変数において,母平均μを標本平均で置き換えた次の確率変数は自由度nー1のカイ2乗分布に従います。
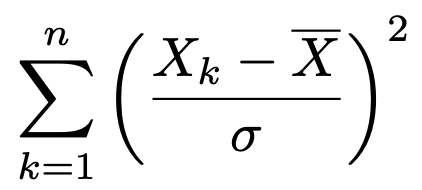
t分布のように,カイ2乗分布の確率密度関数のグラフの形は自由度とともに変わり,左右非対称です。期待値と分散は覚えなくていいです。
詳しくは【中学の数学からはじめる統計検定2級講座第13回】をご覧ください。
F分布
次のように,確率変数X1,X2がそれぞれ自由度n1,n2のカイ2乗分布に従っていて,独立であるものとします。
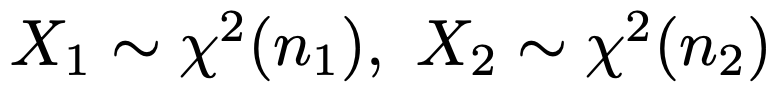
このとき,次の確率変数Fは自由度(n1,n2)のF分布に従います。
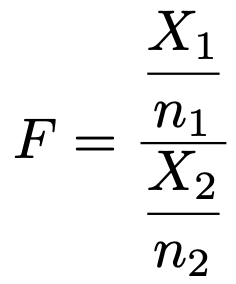
また,上のFの逆数で表される確率変数は,次のように自由度(n2,n1)のF分布に従います。
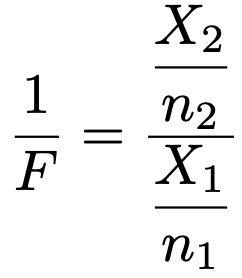
t分布やカイ2乗分布のように,F分布の確率密度関数のグラフの形は自由度とともに変わり,左右非対称です。期待値と分散は覚えなくていいです。
詳しくは【中学の数学からはじめる統計検定2級講座第14回】をご覧ください。
一様分布
離散一様分布は確率変数Xがとりうるどの値についても,その確率が等しい確率分布です。
(例)1個のサイコロを1回投げるときに出る目の数の確率分布
連続一様分布は次のような確率密度関数をもつ確率分布です。
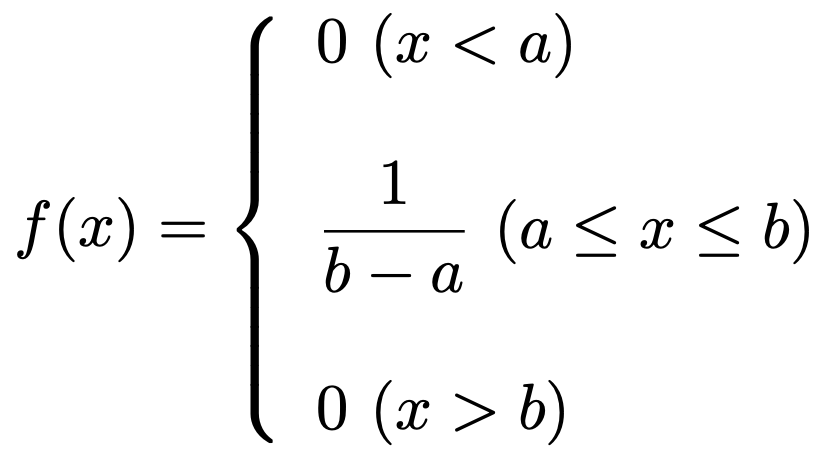
連続一様分布に従う確率変数の期待値はaとbの中点のa+b/2です。分散は覚えなくていいです。
ベルヌーイ分布
確率変数Xが0と1の2つの値をとる確率分布です。X=1となる確率をpとすると,X=0となる確率は1ーpとなり,期待値と分散は次のようになります。
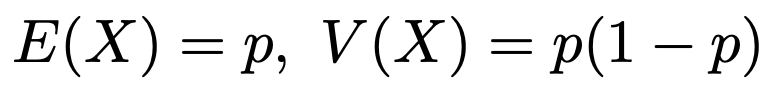
二項分布
独立に成功確率(X=1となる確率)pのベルヌーイ分布に従うn個の確率変数の和で表される確率分布で,B(n,p)と表します。
確率関数は次の式です。
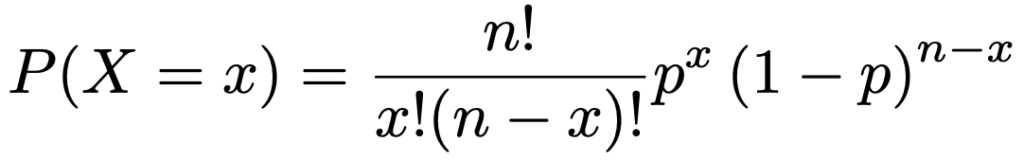
Xが二項分布に従うとき,その期待値と分散は次のようになります。
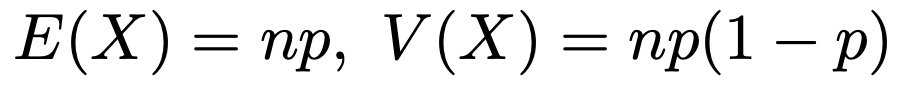
nが大きいときには,次のように正規分布で近似することができます。
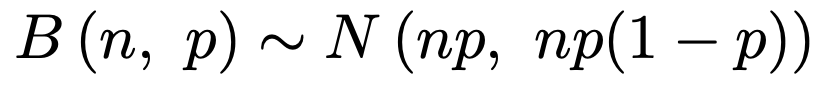
詳しくは【中学の数学からはじめる統計検定2級講座第10回】をご覧ください。
ポアソン分布
ある出来事が一定時間内に一定のλ回起こるときの確率分布です。二項分布でnが非常に大きく,pが非常に小さく,npが一定(=λ)であるときにはポアソン分布とみなすことができます。
λ>0として,確率関数は次の式です。
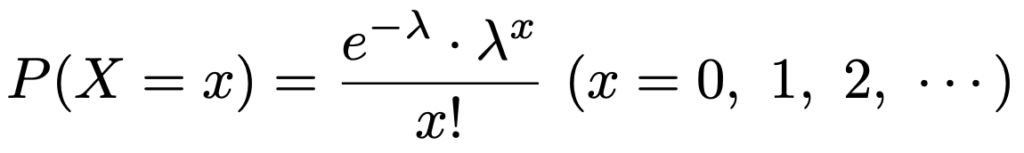
Xがポアソン分布に従うとき,E(X)=V(X)=λ
幾何分布
例えば,1個のサイコロをくり返し投げて,はじめて1の目が出るまでに投げた回数をXとすると,Xが従う確率分布が幾何分布です。1回あたりの成功確率をpとすると,確率関数は次の式で表せます。
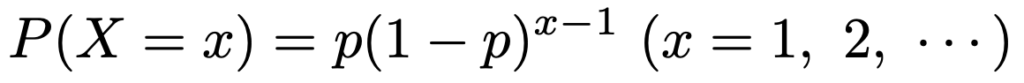
Xが幾何分布に従うとき,その期待値と分散は次のようになります。
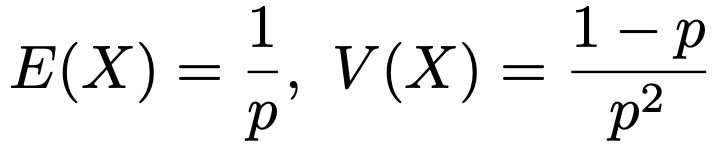
推定,検定,線形モデルの分野
母数…母集団を特徴づける値(母平均,母分散,母標準偏差など)
統計的推測…標本の性質をもとに,母集団の性質を調べること
推定…標本を調べることで母数を推測すること
検定…標本を調べてわかることが仮説と矛盾しないかを検証すること
統計量…標本のみの関数
推定統計量(推定量)…推定のために用いる統計量
検定統計量(検定量)…検定のために用いる統計量
標準誤差…推定量の標準偏差
不偏推定量…期待値が母数に等しくなる推定量
一致推定量…極限が母数に等しくなる推定量
標本平均…同じ母集団からの無作為標本X1,X2,X3,…,Xn(このnを標本の大きさと言う)に対して次のように定める統計量

不偏分散…同じ母集団からの無作為標本X1,X2,X3,…,Xnに対して次のように定める統計量

標本平均は母平均の,不偏分散は母分散の不偏推定量かつ一致推定量です。
中心極限定理…母集団分布の平均と分散が有限であるとき,大きさnの標本から計算した標本平均を標準化した確率変数は,nが大きいとき近似的に標準正規分布N(0,1)に従う
大数の法則…母集団分布の平均がμ,分散が有限であるとき,どんな正の数εについても,標本平均に関して次の式が成り立つ(要するに,標本の大きさnを大きくしていくと,標本平均は母平均μにいくらでも近づく)

チェビシェフの不等式…どんな正の数εについても成立する次の不等式のこと

区間推定
母集団分布がN(μ,σ2)であるとき,標本の大きさnの標本平均は次の正規分布に従います。
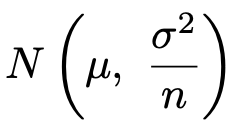
母平均の推定(母分散既知)の場合
母集団分布がN(μ,σ2)で標本の大きさがnのとき,信頼度95%の信頼区間は次の式から計算できます。
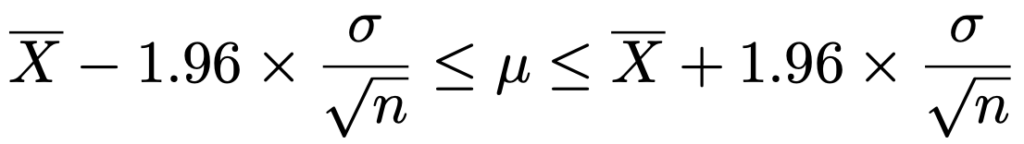
母平均の推定(母分散未知,小標本)の場合
母集団分布が正規分布で標本の大きさがnのとき,信頼度95%の信頼区間は次の式から計算できます。
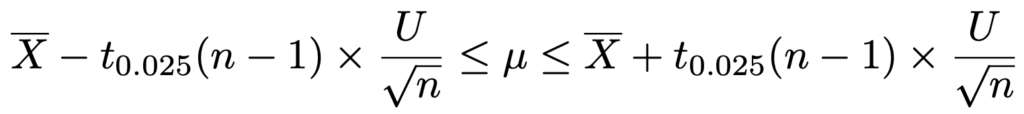
ただし,上の不等式に出てくる次の記号は,自由度nー1のt分布の上側2.5%点を表しています。
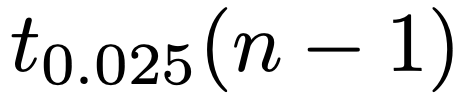
母平均の推定(母分散未知,大標本)の場合
標本の大きさがnのとき,信頼度95%の信頼区間は次の式から計算できます。
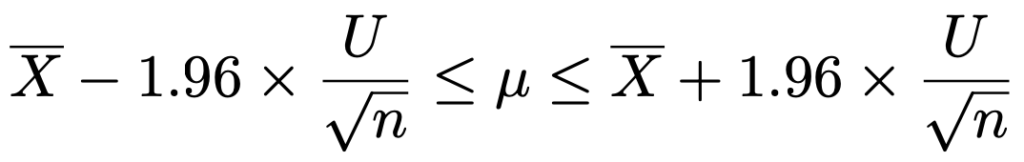
この場合,中心極限定理により,母集団分布はどんなものでもかまいません。
詳しくは【中学の数学からはじめる統計検定2級講座第9回】をご覧ください。
母分散の推定(母平均未知)の場合
母集団分布が正規分布で標本の大きさがnのとき,信頼度95%の信頼区間は次の式から計算できます。

ただし,上の不等式に出てくる次の記号は,自由度nー1のカイ2乗分布のそれぞれ上側2.5%点,上側97.5%点を表しています。
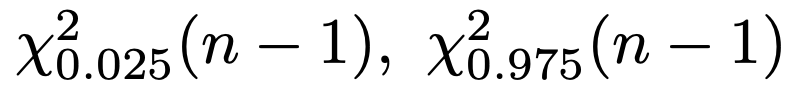
詳しくは【中学の数学からはじめる統計検定2級講座第13回】をご覧ください。
母比率の推定(大標本)の場合
標本の大きさがnのとき,信頼度95%の信頼区間は次の式から計算できます。
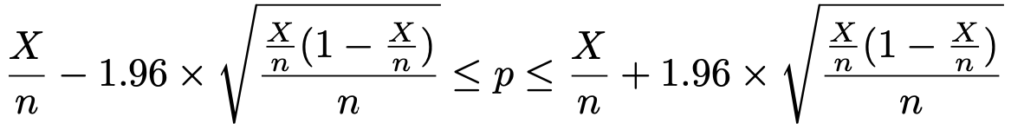
詳しくは【中学の数学からはじめる統計検定2級講座第10回】をご覧ください。
仮説検定
帰無仮説…否定したいほうの仮説
対立仮説…正しいことが期待されるほうの仮説
有意水準(危険率)…滅多に起こらないと言えるかどうかの判断基準となる非常に低い確率(通例は5%)
棄却域…帰無仮説が否定される値の集合
片側検定…棄却域を確率分布の片側だけに設定した検定
両側検定…棄却域を確率分布の両側に設定した検定
第一種の誤り(第一種の過誤)…帰無仮説が正しいとき,正しいはずの帰無仮説を棄却してしまう誤り
第二種の誤り(第二種の過誤)…対立仮説が正しいとき,正しくないはずの帰無仮説を受容してしまう誤り
検出力…対立仮説が正しいとき,帰無仮説を棄却できる確率
P値…帰無仮説のもとで検定統計量の値よりも極端な値をとる確率
母平均の検定
母平均の検定(母分散既知)の場合
母集団分布が母分散σ2が既知の正規分布で標本の大きさがnのとき,母平均がμに等しいという帰無仮説のもとで,次の検定統計量が標準正規分布に従うことを利用します。
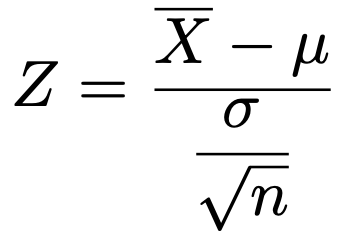
母平均の検定(母分散未知,小標本)の場合
母集団分布が正規分布で標本の大きさがnのとき,母平均がμに等しいという帰無仮説のもとで,次の検定統計量が自由度nー1のt分布に従うことを利用します。
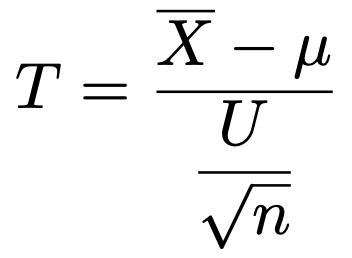
母平均の検定(母分散未知,大標本)の場合
標本の大きさをnとして,母平均がμに等しいという帰無仮説のもとで次の検定統計量が近似的に標準正規分布に従うことを利用します。この場合,中心極限定理により,母集団分布はどんなものでもかまいません。
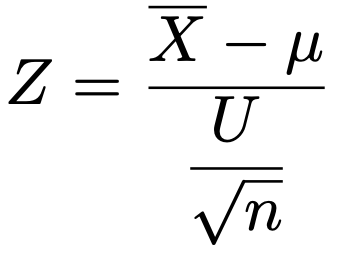
詳しくは【中学の数学からはじめる統計検定2級講座第11回】をご覧ください。
母分散の検定
母集団分布が平均が未知の正規分布で標本の大きさがnのとき,母分散がσ2に等しいという帰無仮説のもとで,次の検定統計量が自由度nー1のカイ2乗分布に従うことを利用します。
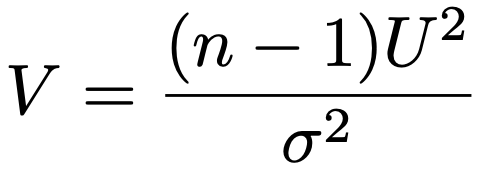
詳しくは【中学の数学からはじめる統計検定2級講座第13回】をご覧ください。
母比率の検定と母比率の差の検定
母比率の検定(大標本)の場合
母比率がpであるという帰無仮説のもとで,標本の大きさがnのとき,標本比率をX/nとして,次の検定統計量が近似的に標準正規分布に従うことを利用します。

母比率の差の検定(大標本)の場合
2群の母比率に差がないという帰無仮説のもとで,標本の大きさをそれぞれn1,n2,標本比率をそれぞれX1/n1,X2/n2とすると,次の検定統計量が近似的に標準正規分布に従うことを利用します。
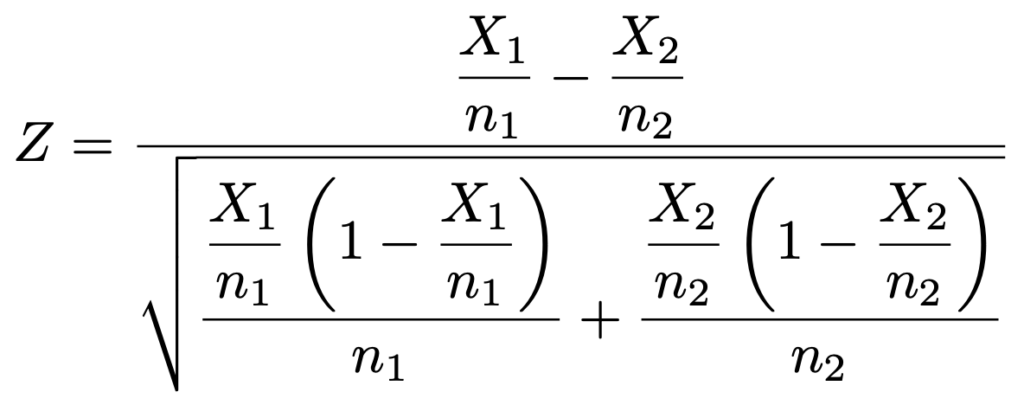
※分母のルートの中の標本比率は,プールした比率を使っても構いません。プールした比率を使うと次のようになります。
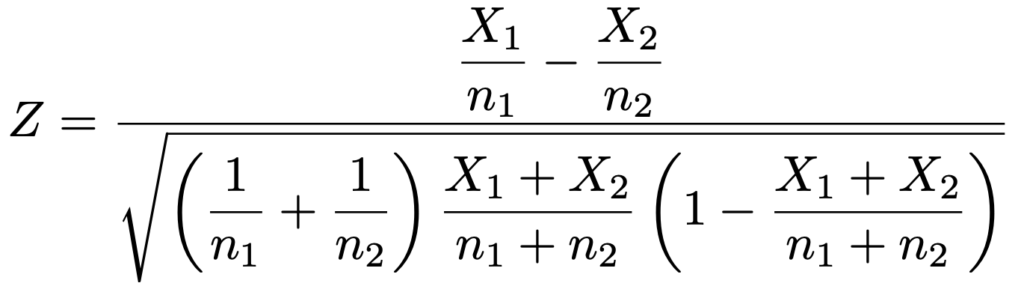
詳しくは【中学の数学からはじめる統計検定2級講座第12回】をご覧ください。
母平均の差の検定
2群の母平均に差がないという帰無仮説のもとで,それぞれ以下のように計算します。
対応のある2群の場合
母集団分布が正規分布で標本の大きさがn(対応するデータがn組)のとき,差の標本平均をX,差の不偏分散をU2とするとき,次の検定統計量が自由度nー1のt分布に従うことを利用します。
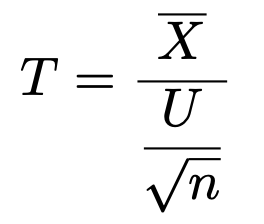
対応のない2群で,母分散既知の場合
母集団分布がそれぞれ正規分布で,母分散がσ12,σ22,標本の大きさがn1,n2のとき,次の検定統計量が標準正規分布に従うことを利用します。
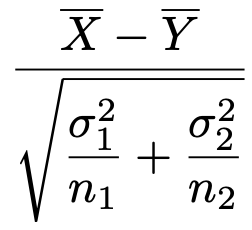
対応のない2群で,母分散未知(大標本)の場合
大標本であれば,不偏分散をU1,U2,標本の大きさをそれぞれn1,n2とすると,次の検定統計量が標準正規分布に従うことを利用します。
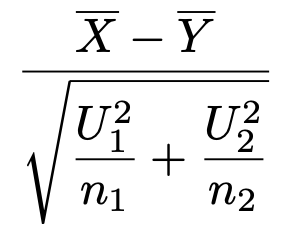
対応のない2群で,母分散未知(小標本,等分散)の場合
母集団分布がそれぞれ正規分布で,2つの母分散が等しいとき,標本の大きさをそれぞれn1,n2とすると,次の検定統計量が自由度n1+n2ー2のt分布に従うことを利用します。
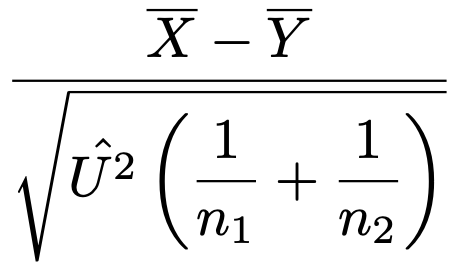
ただし,分母には次の式で求められるプールした分散を用いています。
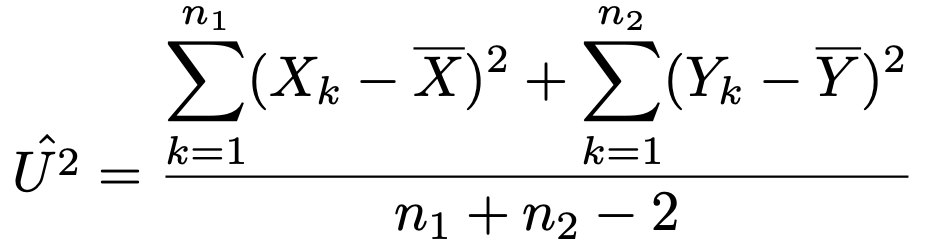
詳しくは【中学の数学からはじめる統計検定2級講座第15回】をご覧ください。
等分散仮説の検定
2つの正規母集団の無作為標本(標本の大きさはそれぞれnA,nB)から求められる不偏分散をそれぞれUA2,UB2とし,これらが独立であるものとします。2群の母分散が等しいという帰無仮説のもとで,次の検定統計量がF(nBー1,nAー1)に従うことを利用します。
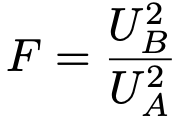
詳しくは【中学の数学からはじめる統計検定2級講座第14回】をご覧ください。
適合度検定
データの分布が特定の理論に合っていないことを示すために用います。帰無仮説と対立仮説は次の通りです。
- 帰無仮説:実験結果が仮定した理論に適合する
- 対立仮説:実験結果が仮定した理論に適合しない
とりうる値がk個のカテゴリーに分割されているものとして,観測度数をそれぞれ次のようにおきます。

全度数をnとして,各カテゴリーの期待度数をそれぞれ次のようにおきます。
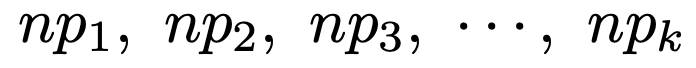
nが十分に大きいとき,次の統計量が近似的に自由度kー1のカイ2乗分布に従います。右片側検定です。
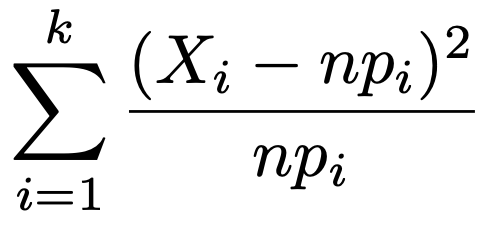
詳しくは【中学の数学からはじめる統計検定2級講座第13回】をご覧ください。
独立性の検定
k行ℓ列のクロス集計表において,2つの要因が独立ではないことを示すために用います。帰無仮説と対立仮説は次の通りです。
- 帰無仮説:行と列の要因は独立である
- 対立仮説:行と列の要因は独立でない
帰無仮説を仮定し,行と列の要因は独立であるとすると,期待度数は周辺度数の積を全度数でわって求められます。
観測度数をそれぞれ次のようにおきます。
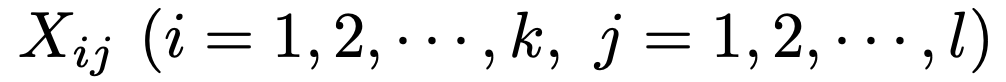
また,周辺度数をそれぞれ次のようにおきます。
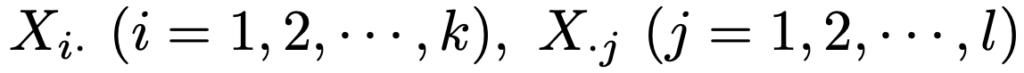
全度数をnとして,nが十分に大きいとき,次の統計量が近似的に自由度(kー1)(ℓー1)のカイ2乗分布に従います。右片側検定です。
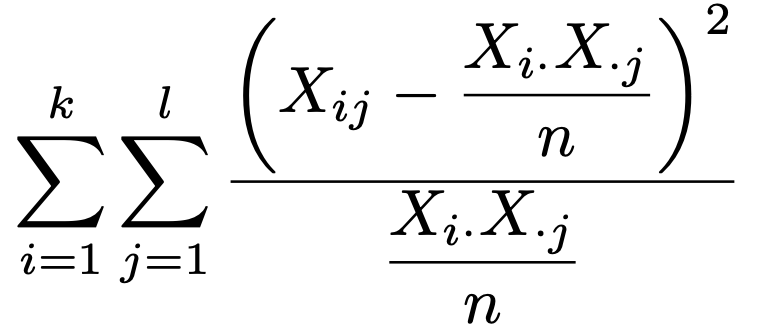
分散分析
3群以上(2群でも可)について,母平均に差があるかどうかを検定する手法です。
要因…観測データに影響を与える可能性のあるもの
水準…要因がとりうる一つひとつの条件のこと
一元配置分散分析…要因が1つの分散分析
水準間平均平方…水準間平方和÷自由度
残差平均平方…残差平方和÷自由度
F値…水準間平均平方÷残差平均平方
2群に対して,分散分析を行った結果とt検定を行った結果は一致します。
帰無仮説と対立仮説は次の通りです。
- 帰無仮説:すべての群の母平均が一致する
- 対立仮説:少なくとも1つの群の母平均が異なる
このときの検定統計量は,第1自由度が「水準の数ー1」,第2自由度が「すべての水準の標本の大きさの合計ー水準の数」のF分布に従います。右片側検定です。
詳しくは【中学の数学からはじめる統計検定2級講座第16回】をご覧ください。
回帰分析
単回帰分析
次の単回帰モデルで,yを被説明変数,xを説明変数,uを誤差項と言います。
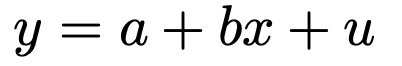
誤差項は独立に正規分布N(0,σ2)に従うものとし,説明変数は確率変数ではないものとします。
・予測値…最小二乗法によって推定される係数をaハット,bハットとしたとき,次の式のyハット
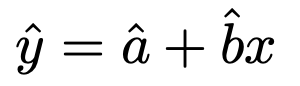
・最小二乗法によって推定される回帰直線は点(x,y)を通ります。つまり,次の式が成り立ちます。
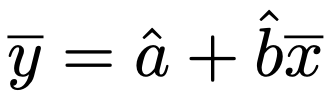
・回帰係数のt検定…帰無仮説:b=0,対立仮説:b≠0
このときの検定統計量は自由度nー2のt分布に従い,その実現値をt値と言います。
t値は回帰係数÷標準誤差で求めることができます。
・残差平方和…各標本について,予測値と観測値(x座標は等しい)の差の2乗の和
残差平方和を自由度のnー2でわったものが誤差項の分散の不偏推定量になります。
詳しくは【中学の数学からはじめる統計検定2級講座第17回】をご覧ください。
重回帰分析
説明変数が複数ある場合の回帰分析です。
重回帰モデルは次の式のように表され,yは被説明変数,x1,x2,…,xpは説明変数,uは誤差項です。
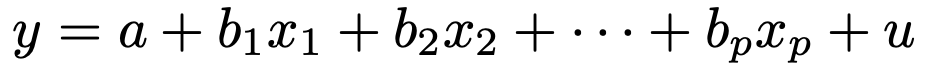
誤差項は独立に正規分布N(0,σ2)に従うものとし,説明変数が確率変数ではないのは単回帰モデルと同じです。
重回帰モデルにおける回帰係数は,他の説明変数が一定である条件のもとで,1つの説明変数が1単位増えたときにyがどれくらい増えるかを表しています。
・回帰係数のt検定…帰無仮説:bi=0,対立仮説:bi≠0(i=1,2,…,p)
このときの検定統計量は自由度nーpー1のt分布に従います。
・回帰係数のF検定…帰無仮説は次の式で表されます。
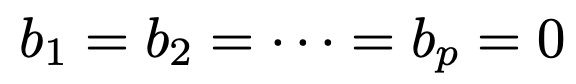
この検定で有意であることが示せると,回帰係数の中に0でないものが1つ以上あることになり,重回帰モデルに意味があることになります。
・ダミー変数…質的データを0と1の2つの値をとる変数として回帰モデルの説明変数にしたもの
・多重共線性…説明変数どうしの相関が高いと,回帰係数の誤差が大きくなって重回帰モデルが不安定になってしまうなどの問題が起きている状態
個別に単回帰分析をすると有意な説明変数であっても,相関が高い複数の説明変数を同時に使うことは避けたほうが良いです。
・決定係数…回帰モデルのデータへのあてはまりの良さを数値化したもので,R2と表されます。
意味のない説明変数であっても,説明変数の数を増やすと決定係数は大きくなるので,その分の調整を加えたものが自由度調整済み決定係数です。
R2=1の場合を除いて,単回帰モデルでも重回帰モデルでも自由度調整済み決定係数は決定係数より小さい値をとります。
モデルを選択するときには,決定係数ではなく自由度調整済み決定係数をもとに判断します。
・外挿…データが得られた範囲の外側でも予測式が成り立つと仮定して被説明変数を予測すること
詳しくは【中学の数学からはじめる統計検定2級講座第18回】をご覧ください。
以上です。本試験でもがんばってください!
なお,「統計検定CBTの楽な申込方法を知りたい」「統計検定CBTの点数を引き上げたい」という人は次の記事も参考にしてみてください。
参考図書
本稿を執筆するにあたり,次の書籍を参考にしました。
①統計検定2級公式問題集2017〜2019年(実務教育出版)
言わずと知れた公式の過去問集です。2016年以前に遡ると傾向が変わるので,2017年以降の出題内容をベースに2級合格に必要な知識を拾い上げました。
②入門統計解析(倉田博史・星野崇宏,新世社)
ローレンツ曲線・ジニ係数,標準化得点(本書では基準化変量と呼ばれている),歪度と尖度について参考にしました。
③統計学[改訂版](森棟公夫・他,有斐閣)
移動平均について参考にしました。
④概説 標本調査法(土屋隆裕,朝倉書店)
標本抽出法について参考にしました。
⑤入門統計学 第2版(栗原伸一,オーム社)
フィッシャーの3原則についてはこの本が詳しいです。








コメント
先週、統計検定2級に合格することができました。
私は大学は私立文系で大学受験では数ⅡBまでしかやっておらず、統計学は未履修でした。受験するにあたって、公式テキストで学習をすすめていたのですが、なにがポイントなのか分からなくなってしまい混乱していたところ、とけたろうさんの動画とブログを発見しました。
とけたろうさんのおかげで統計学の全体的なイメージと2級合格に必要な細部を自分のなかで繋げることができました。ありがとうございました!
コメント、ありがとうございます❗
そして、合格おめでとうございます🥳🎉🥳🎉🥳🎉
お役に立てたようで、私もうれしいです✨
こんにちは、本日統計検定2級合格できました。
試験直前のチェックを網羅的にできて大変助かりました。
また、各回の内容も丁寧で分かりやすかったです!
ありがとうございました。
本日,合格❗
すばらしい〜✨
おめでとうございます🎉🎉🎉
役立ててもらえて
うれしい限りです❗
はじめまして!
本日統計検定2級に合格した者です。
とけたろうさんのYouTubeとブログを目から血が出る思いで見倒した結果だと思っています!
すばらしいコンテンツの作成&共有を本当に本当にありがとうございます!!
合格おめでとうございます🥳🎉🎉🎉
目から血が出る…というのは痛そうですが、真剣にご覧いただいたということですね、ありがとうございます❗
感謝の言葉をいただけて、励みになります✨
はじめまして。
とけたろうさんのブログとYouTubeで統計学を基本から学び、昨日、統計検定2 級に合格できました。
本で学ぶより、動画で噛み砕いた説明のほうがとっつきやすく、非常に助かりました。
私もブログを運営しておりますので、僭越ながら紹介させていただきました。
この度はありがとうございました。
おめでとうございます🥳🎉🎉🎉
ブログも拝読しました❗
大々的にご紹介いただき
ありがとうございます❗
うれしいです✨
とけたろう先生のコンテンツのおかげで、先日2級に合格できました。
素晴らしいブログと動画を、本当にありがとうございます。
引き続き学び続けたいと思います!がんばります。
おめでとうございます🥳🎉🥳🎉🥳🎉
統計学を学ぶきっかけとなることは
私の目指すところでもあり
とてもうれしいです✨
ぜひ,これからもがんばってください❗
つい先ほど統計検定二級合格しました。
文系で知識ゼロ、勉強期間2週間で合格の要因はやはり、とけたろう先生の動画とブログだと思いました。
正直最初は、定理や公式が何故そうなるのかについての解説が多く、文系の私からすると「本当にこれで受かるのか?」と思っていました。
しかし、過去問を解いた人や試験を受けた人なら分かると思いますが、実際に問題に出てくるのはその理屈の部分で、本当に役立ちました。ありがとうございました。
とけたろうさんの専門分野にもよりますが、今後は機械学習などより実践的な内容も拝見出来たらと思っております。
改めて誠にありがとうございました。
おめでとうございます🥳🎉
知識ゼロから2週間での合格はスゴすぎです✨
私もブログや動画をさらに発展させていく予定なので、引き続きご注目いただければ幸いです
この動画を2周、公式テキスト2周して統計検定2級合格できました!
おめでとうございます🥳🎉🎉
統計検定2級に合格することができました。
中学までは数学が得意だったものの高校で挫折して文系に行った身としては、最初動画を見ても何を言っているのかさっぱりわかりませんでした。
動画を視聴後にキーワードをノートにまとめる、演習問題を解くを繰り返し、問題を暗記するくらいやりこみました。その後、2014~2018の過去問を3周する中で分からない問題をとけたろう先生のブログで調べていくうちにようやく意味が分かるようになり、合格にたどり着きました。
とけたろう先生のおかげです。ほんとうにありがとうございます。
合格おめでとうございます🥳🎉🎉
あきらめずに食らいついて勉強に励まれた様子が伝わってきました!
他の方にも参考になると思います!
コメントありがとうございます✨
このブログとYouTube動画を見て合格することができました🌟ありがとうございました。
文系&仕事で統計を使うことはない私でも理解ができたのは、とけたろう先生のおかげです。
先に●demyの教材を使って学んでいたのですが、全体像が示されておらず、また、「ハット」などの説明がほとんどされないまま解説が進み、初学者にとってはずいぶんしんどい教材でした。そんなときにとけたろう先生の動画に出会い、1つ1つの位置付けや重要度のメリハリが明確なことでいっきに学習が進みました。
やはり勉強は、教える人によって理解度が大きく左右されることを実感しました。改めてありがとうございました。
参考までに、これから統計検定2級を受ける人に私の状況です。↓↓↓
○社会人 40代 女性 文系
〇学習期間 1.5ヶ月
〇学習方法 動画教材(とけたろうblogと●demy)、過去問約10年分(21年6月過去問は直前に実施して65%程度で撃沈)、不明点はひたすらインターネットで調べまくる、過去問以外の本は使っていない
〇困ったこと 過去問の解説が私には不親切すぎた。わからないときに質問する環境を作れなかった。知恵袋などを見ても、かゆいところに手が届かないカンジ。
〇受検を終えて 過去問はめちゃくちゃ大事。似た問題も数問確認できた。100点を取る必要はない(偏微分、logなどはなんとなくだった)。
以上、長文失礼しました。
統計検定2級の合格おめでとうございます🥳🎉🎉
お役に立てて,良かったです✨
また,これから2級を受ける人に役立ちそうな情報をいただき,
ありがとうございます❗
こちらのサイトを参考にさせていただき統計検定2級合格しました。数ある統計学解説サイトの中で抜群にわかりやすいです。参考文献も初学者にぴったりの本を紹介いただいており助かりました。現在準1級を勉強中です。他力本願で本当に恐縮ですが準1級用のコンテンツ追加も楽しみにしております。
すいません、準1級対策のメインはnoteの方で公開されていたんですね。購入させていただきます。
統計検定2級の合格おめでとうございます🥳🎉🎉
このサイトが「抜群にわかりやすかった」との評価をいただけたのはうれしいです✨
準1級も合格目指して,がんばっていきましょう❗
はじめまして。
本日、統計検定2級を受験し、合格することができました。統計検定2級の資格が急遽必要になり二週間ほど前から焦って勉強していたところ、過去の受験者の体験談からとけたろうさんの統計検定2級チートシートの存在を知り、毎日読んでいました。
何度も読み返すことでなんとなく理解していた内容がさらに深まり、問題を読んだときに瞬時に必要な情報を取り出せるようになりました。チートシートの存在を知らずに過去問と公式テキストを取り組んでいたら十分に理解できなかったと思うので、非常に助かりました。
本当にありがとうございました。