テレビの視聴率は,1〜2万世帯に1世帯程度の割合で機械を設置して,そのデータをもとに算出しています。母比率の区間推定の原理を理解すれば,どうしてそんなに少ない標本で精度の高い調査ができるのかがわかります。
この記事では,組合せと呼ばれる場合の数の説明からはじめ,それを用いて二項分布を理解し,さらにそれを用いて母比率の区間推定を解説していきます。
なお,組合せの理解のためには第1回の確率の内容,二項分布の理解のためには第3回の確率変数と第4回の期待値と分散の内容,母比率の区間推定の理解のためには第9回の母平均の区間推定の内容が必須となりますので,必要に応じて先にそちらの記事を読んでください。
では,はじめていきましょう!
組合せ
まず,5人が5つのイスに座るとき,座り方が何通りあるかを考えてみましょう。

Aさん,Bさん,Cさん,Dさん,Eさんの順に座るイスを決めていくと,それぞれ5通り,4通り,3通り,2通り,1通りになりますので,全部で,次のように120通りになります。
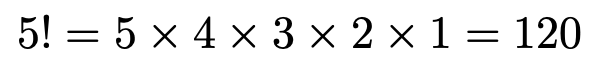
ここで5!という記号は5の階乗と読み,1から5までの自然数の積を表しています。(第1回の記事の演習2も参考にしてください)
一般的に言えば,異なるn個のものを横1列に並べる場合の数は次のようにn!通りになります。
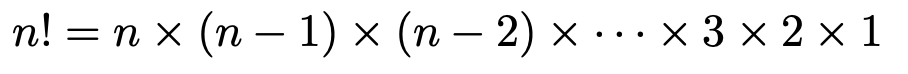
次に,5つのイスから2つを選ぶとき,選び方の総数を考えてみます。上の図のように,いちばん右のイスにはCが,右から2番目のイスにはAが座ることにして,B,D,Eが残りのどのイスに座ろうとも区別しないことにします。B,D,Eの3人の座り方は3!通りありますので,5!を3!でわることで,上の図のような,いちばん右のイスにC,右から2番目のイスにAが座る座り方を全部ひっくるめて1通りとみなしたことになります。さらに,AとCが左右のどちらに座るかを区別しないことにしましょう。AとCの並び方は2!通りありますので,5!を3!でわったものを,さらに2!でわると,5人の並び方は全く考えずに,5つのイスから2つを選ぶだけの選び方の数になります。それが次の数です。
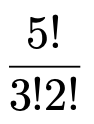
一般的に,異なるn個のものからr個を選ぶ選び方の総数は次の式で表せます。
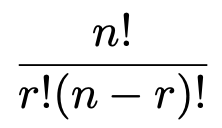
例えば,10色から3色を選ぶ選び方の総数は次のようになります。
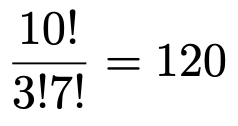
10色から3色を選ぶと,選ばない7色が自動的に決まるので,10色から3色を選ぶ選び方の総数は10色から7色を選ぶ選び方の総数と一致します。このような場合の数を組合せと言います。
二項分布
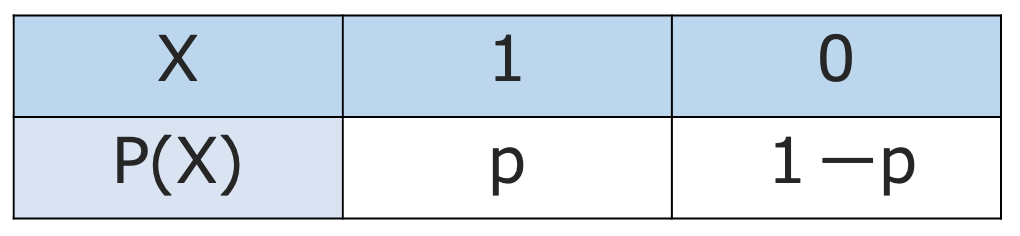
1枚のコインを1回投げるとき,表が出るか,裏が出るかの2通りしかありませんよね。ベルヌーイ分布というのは,こういう2択の確率分布です。より一般的に表現すると,次の確率変数Xが従う確率分布をベルヌーイ分布と言います。
ちなみに,ベルヌーイという名前は,はじめてこの確率分布を論じたとされる数学者ヤコブ・ベルヌーイに由来します。
次のような例もベルヌーイ分布に従う確率変数ですね。
(例)1個のサイコロを1回投げて,1の目が出たら1,それ以外の目が出たら0という値をとる確率変数
便宜上,ベルヌーイ分布において,X=1となることを成功,X=0となることを失敗と呼ぶことにします。したがって,以下では,X=1となる確率を成功確率と表現しています。
確率変数Xが成功確率pのベルヌーイ分布に従うとき,その期待値と分散は次の式のように計算できます。
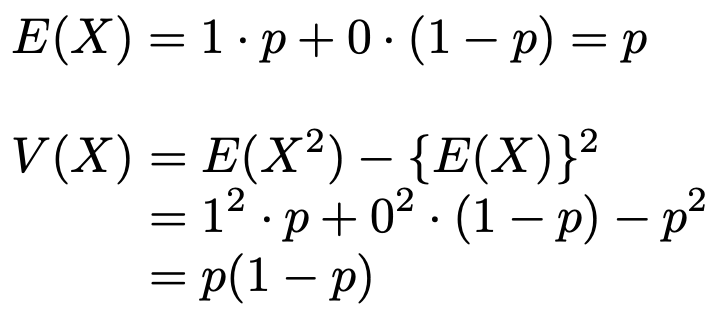
次のn個の確率変数が独立に成功確率pのベルヌーイ分布に従っているとします。
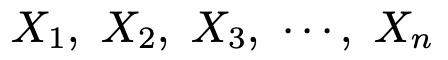
このとき,次の式で定められる確率変数Xが従う確率分布を二項分布と言い,B(n,p)と表します。
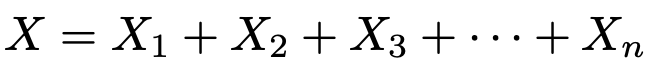
例えば,1枚のコインをn回投げるとき,表が出たコインの枚数が従う確率分布は二項分布です。
二項分布は,nとpを決めれば確率分布が確定します。B(n,p)のBは,二項分布を英語でbinomial distributionと呼ぶことに由来します。二項分布の確率は次の式で表されます。
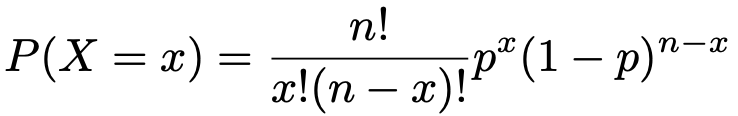
確率がこの式で求められることを具体例で確認してみましょう。例えば,サイコロを5回投げたとき,1の目が出る回数をXとすると,Xは次の二項分布に従います。
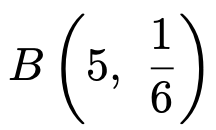
では,1の目が2回出る確率を求めてみましょう。5回のうち,はじめの2回は続けて1の目が出て,残りの3回は続けて1以外の目が出る確率は次のようになります。
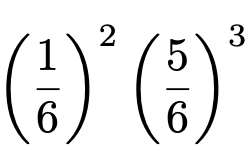
1の目が2回目と3回目に出て,残りの3回は1以外の目が出る確率なども同じですね。このような場合が全部で何通りあるかというと,「5回のうち1の目が出る2回の決め方」の数だけあることがわかるので,次の式で求められます。
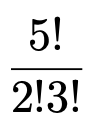
よって,1の目が2回出る確率は次のように計算できます。
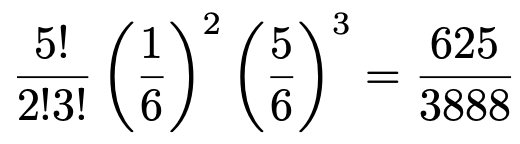
次に,二項分布B(n,p)の期待値と分散を確認しておきます。期待値は次のように計算できます。
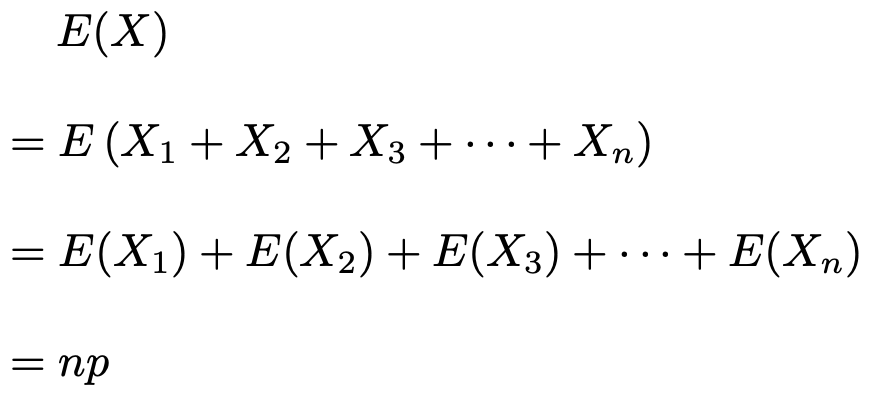
同じように,二項分布B(n,p)の分散は次のように計算できます。
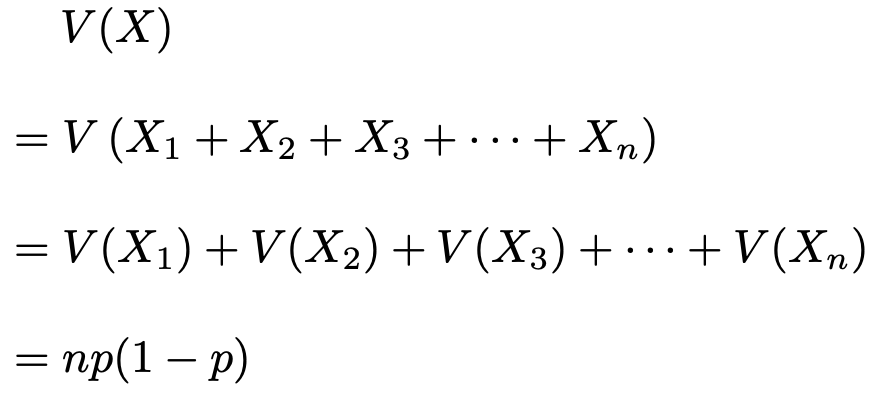
二項分布B(n,p)は,nを十分に大きくすると,正規分布に近づきます。これをド・モアブルーラプラスの定理と言います。ド・モアブルもラプラスもこの確率分布を研究した数学者の名前です。
確率変数Xが二項分布B(n,p)に従うとき,次の式で定まる確率変数Zは,n→∞において,標準正規分布に従う。
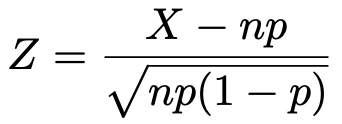
ド・モアブルーラプラスの定理は,中心極限定理の特別な場合と考えることができます。次のセクションでは,これと同じことが中心極限定理から導かれることを確認していきます。
母比率の区間推定
母集団の一部がある性質を持っている場合,この性質を持っているものの割合を母比率と言います。例えば,有権者全体という母集団における政党Aの支持率などのことです。この母比率を区間推定する方法を解説します。
いま,ある母集団から次の大きさnの標本を無作為に抽出することを考えます。
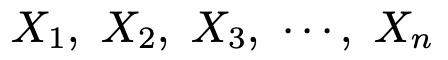
この母集団の中で,ある性質を持っているものの比率(母比率)がpであるものとします。このとき,上のn個の確率変数は「この性質を持っている→1,この性質を持っていない→0」という値をとるものとすると,それぞれ成功確率pのベルヌーイ分布に従います。
このとき,次の確率変数を標本比率と言い,Xは二項分布B(n,p)に従います。

標本比率の期待値は,Xの期待値を利用して,次のように計算できます。
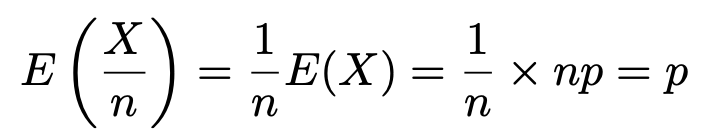
また,標本比率の分散は,Xの分散を利用して,次のように計算できます。
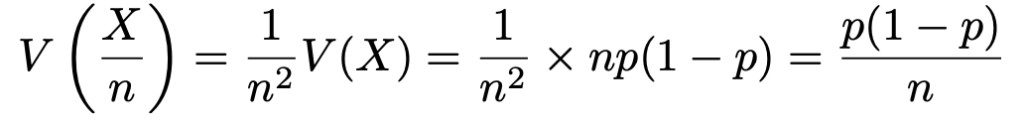
標本の大きさnが十分に大きいとき,中心極限定理から,標本比率は次の正規分布に従います。
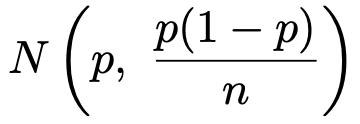
よって,次の式で定まる確率変数Zは標準正規分布に従います。
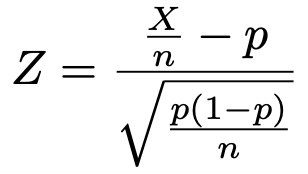
したがって,次の式が成り立ちます。
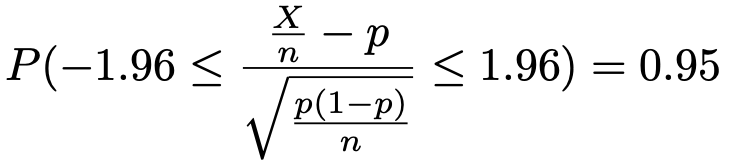
かっこ内の不等式の分母を払って,各辺にpを加えると,次のようになります。
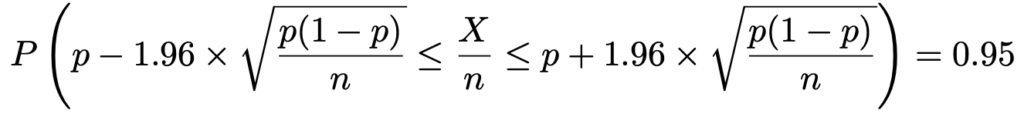
第9回でもやったように,不等式の真ん中にpがくるように変形すると,次のようになります。
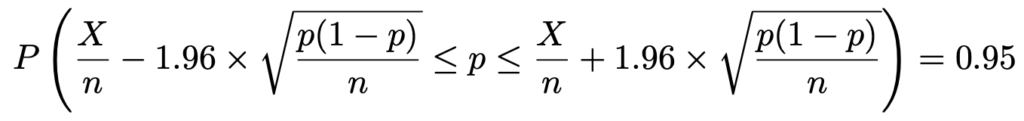
標本比率は,確率的にいろいろな値をとりますが,そのうち95%の場合でかっこ内の不等式が成り立ちます。かっこ内の不等式が,母比率pの信頼度95%の信頼区間を求める式だと言いたいのですが,このままだと不等式の最左辺と最右辺の計算ができませんね。母比率pは知りたい対象なので,代入する値を決められません。そこで,第8回で登場した大数の弱法則を思い出すと,次の式が成り立つことがわかります。
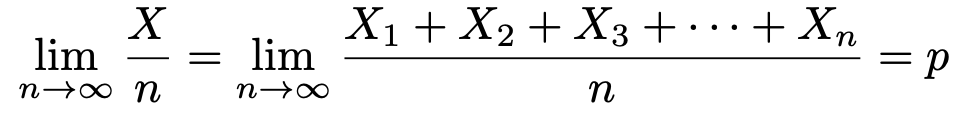
nをどんどん大きくすれば,標本比率は母比率に近づいていくわけです。nは標本の大きさなので,無限には程遠く,数百から数千くらいですが,おおむね母比率に近いものとして,さきほどの不等式の最左辺と最右辺の母比率pを標本比率でおきかえると,95%の確率で次の不等式が成り立つことになります。
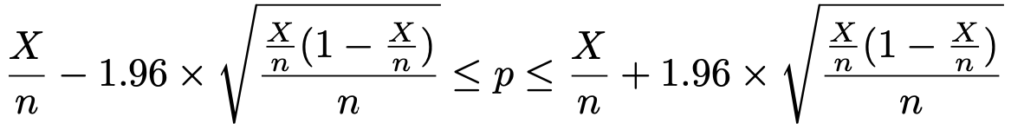
できました! この不等式にnの値と標本比率の実現値を代入すれば,母比率pの信頼度95%の信頼区間が求められます。では,この式を使って問題を解いてみましょう。
【問題】あるテレビ番組の視聴率を関東の2100世帯を対象に調査したところ,16.0%だった。この調査結果は,母集団をテレビを持つ関東の全世帯とし,標本サイズ2100の単純無作為抽出に基づくとみなす。この番組の視聴率の信頼度95%の信頼区間を求めなさい。
【解答】テレビを持つ関東の全世帯からなる母集団は十分に大きいので,このテレビ番組を視聴している世帯数Xは二項分布に従うと考えていいです。また,標本の大きさが2100と大きいので,二項分布を正規分布で近似して考えることができます。
よって,Xが二項分布B(n,p)に従うとき,母比率pの信頼度95%の信頼区間を求める式は次の通りです。
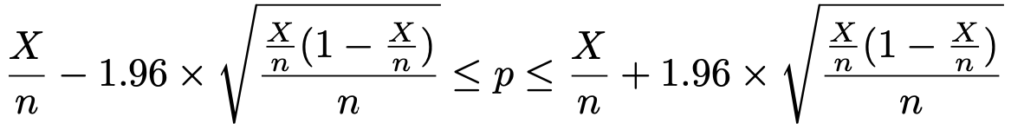
この不等式に,n=2100と標本比率0.16をそれぞれ代入すると,次のようになります。
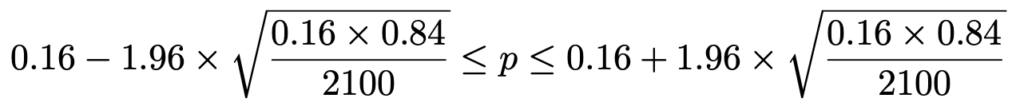
最左辺と最右辺をそれぞれ小数第3位まで求めると,母比率pの信頼度95%の信頼区間は次のようになります。
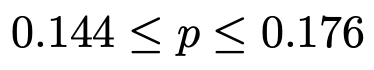
視聴率は14.4%以上17.6%以下ということになります。
(解答終わり)
【二項分布の正規近似についての補足】
二項分布B(n,p)のnが十分に大きいときには正規分布N(np,np(1ーp))に近づくことを紹介しましたが,「nをどれくらい大きくすれば正規分布とみなせるか」については,ケースバイケースです。例えば,次の図は,n=100,p=0.1の場合の二項分布の確率(青丸)と,同じ期待値,分散の正規分布の確率密度関数のグラフ(赤い曲線)です。
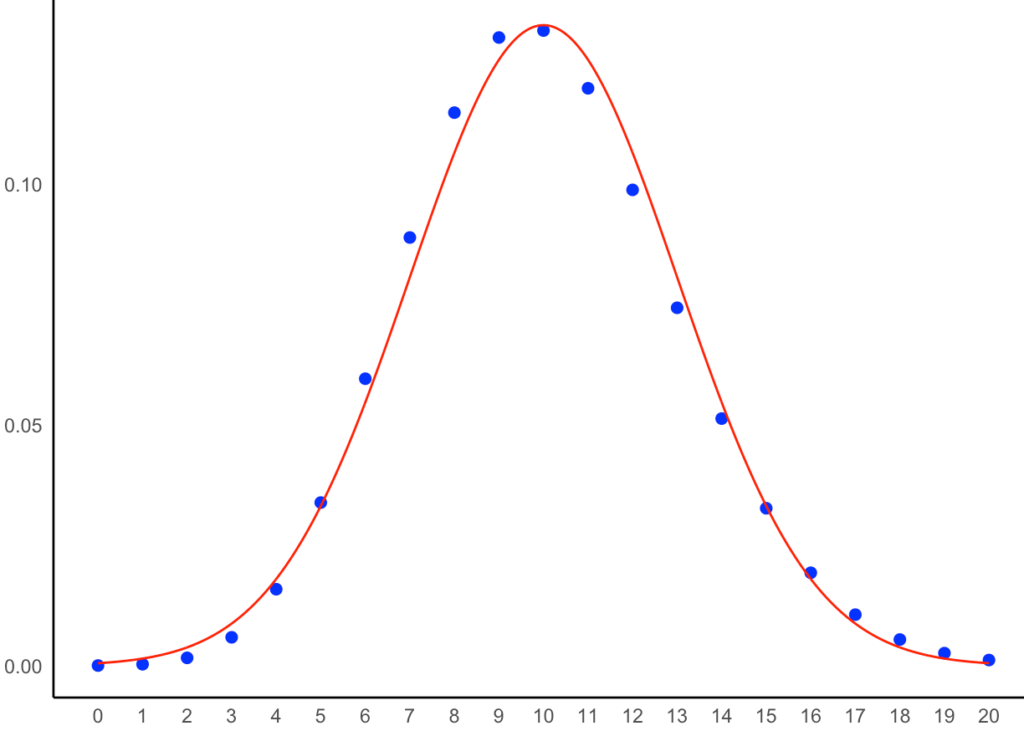
上の図ならば,二項分布がほぼ正規分布で近似できると言って良いでしょう。では,次のn=100,p=0.06の場合はどうでしょうか。
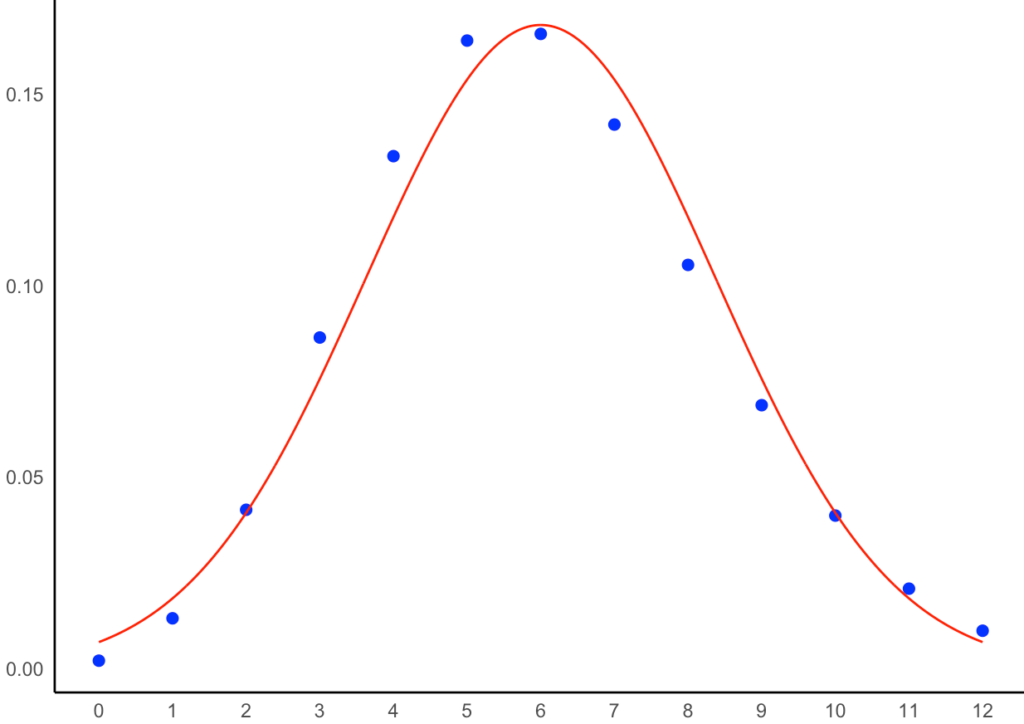
上の図では,青丸と赤い曲線はややズレています。また,次のn=100,p=0.03の場合はどうでしょうか。
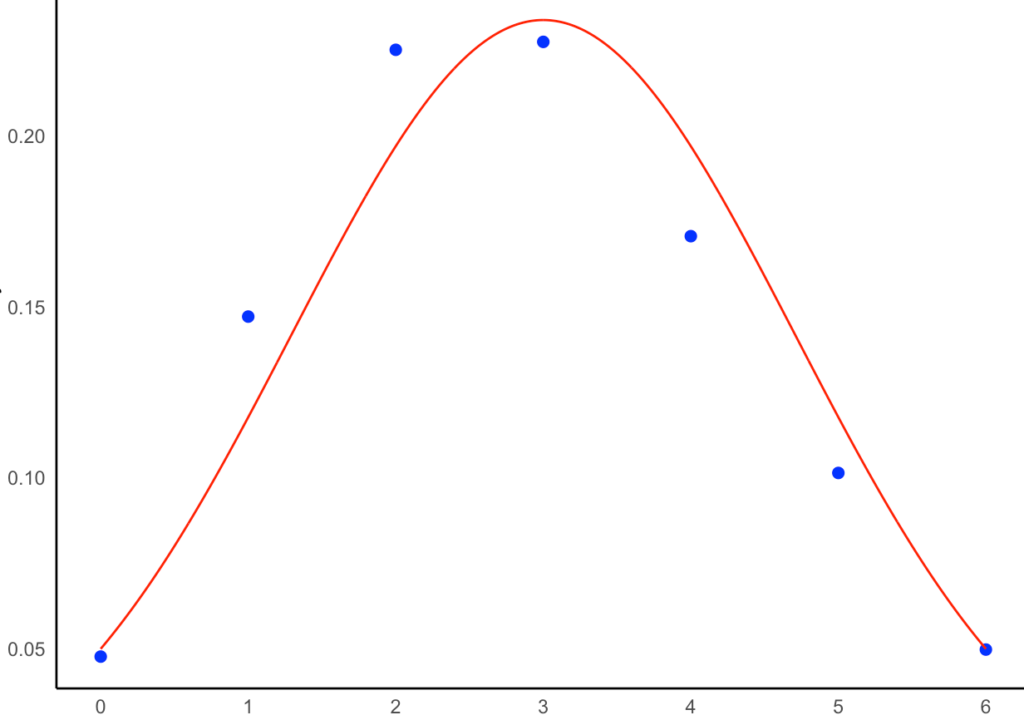
上の図は,青丸と赤い曲線のズレがかなり顕著です。このようにnpやn(1ーp)の値が極端に小さい場合,二項分布と正規分布のズレが目立つようになりますので,pが0や1に近いときに正規分布とみなすには,nの値をかなり大きくする必要があります。
(補足終わり)
母比率の区間推定についての基本的な説明は以上になります。ここからは,さらに理解を深めるための演習問題ですので,余力があればぜひチャレンジしてみてください。
演習1〜確率の最大値〜
【問題】赤玉が5個,白玉が3個入った袋がある。この袋から1個の玉を無作為に取り出し,玉の色を確認した後,袋に戻すことを8回繰り返す。このとき,赤玉が取り出される回数をXとする。
(1)次の式のa,bにあてはまる数を求めなさい。(ただし,x=0,1,2,3,…,7)
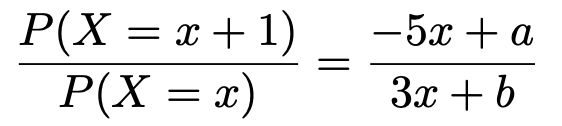
(2)P(X=x)が最大になるx(ただし,x=0,1,2,3,…,8)の値を求めなさい。
【解答】
(1)
玉を1個取り出すとき,それが赤玉である確率は8分の5,白玉である確率は8分の3なので,Xは次の二項分布に従います。

よって,赤玉を8回のうちx回取り出す確率は,次のようになります。
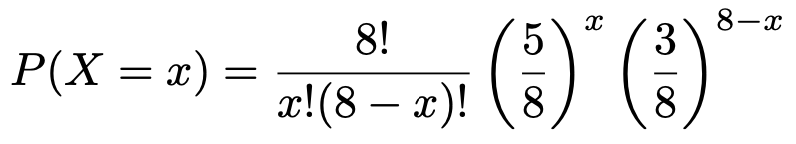
上の式のxをx+1でおきかえることで,赤玉を8回のうち(x+1)回取り出す確率は,次のようになります。
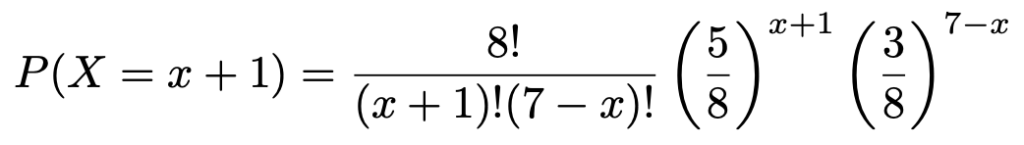
よって,求める確率の比を,(x+1)!=(x+1)・x!や(8ーx)!=(8ーx)・(7ーx)!であることに注意しつつ,分母と分子で約分して計算すると,次のようになります。
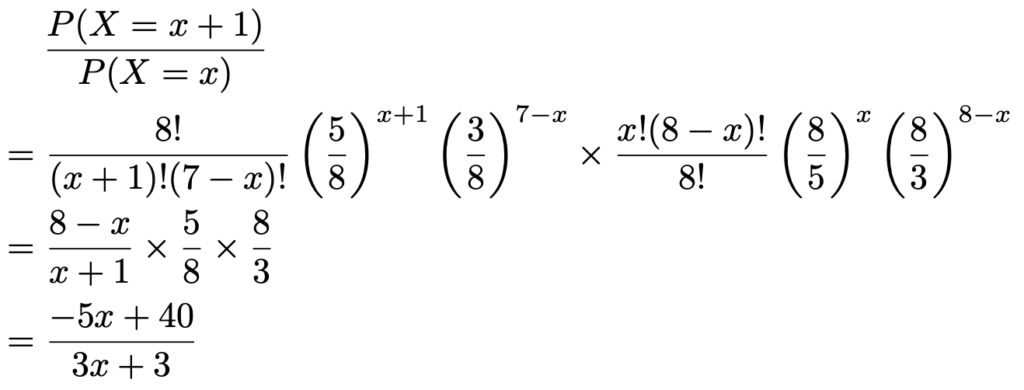
つまり,答えは次のようになります。
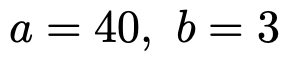
(2)
(1)で求めた確率の比を次のように変形してみましょう。

上の式の右辺の第1項は定数で,第2項は,x=0のときに最大値の15になり,xの値が大きくなるほど小さくなっていきますよね。右辺全体としても,x=0のときに最大値の3分の40になり,x=7のときに最小値の24分の5になります。
よって,(1)で求めた確率の比は,xの値が小さいときには1より大きく,xの値がある値を超えると1より小さくなるはずです。
このようなxの値を求めるため,次のように「(1)で求めた確率の比=1」という式を解きます。
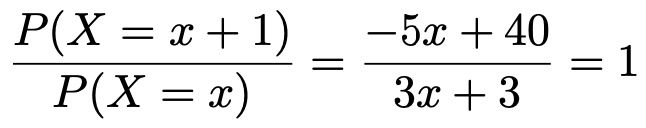
分母をはらって1次方程式を解くと,次のようになります。
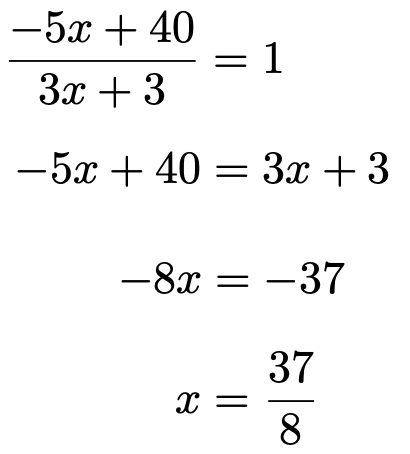
37÷8=4.625だから,(1)で求めた確率の比は,xが4以下ならば分子のほうが大きく,xが5以上ならば分母のほうが大きくなります。つまり,xが4以下ならば次の不等式が成り立ちます。
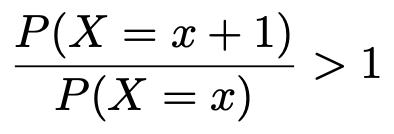
言い換えると,xが4以下ならば次の不等式が成り立ちます。
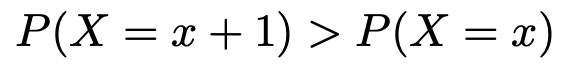
一方,xが5以上ならば次の不等式が成り立ちます。
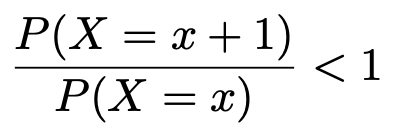
言い換えると,xが5以上ならば次の不等式が成り立ちます。
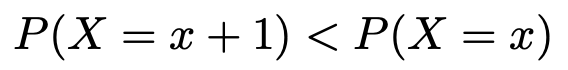
これらの不等式に,xの値を1つずつ代入して大小関係を確認すれば,次の式が成り立つことがわかります。
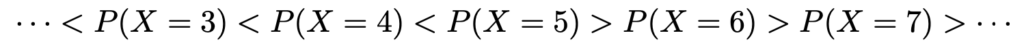
つまり,P(X=x)が最大になるxの値は5です。
(解答終わり)
演習2〜二項分布の正規近似〜
【問題】日本全国の小学校6年生のスマホ所有率は28%であるとする。この母集団から,大きさ1000の標本を無作為抽出したとき,スマホを所有している小学校6年生が250人以下となる確率を求めなさい。
【解答】日本全国の小学校6年生の母集団は十分に大きいので,スマホを所有している小学校6年生の人数Xは二項分布B(1000,0.28)に従うと考えていいです。よって,期待値と分散は次のように求められます。
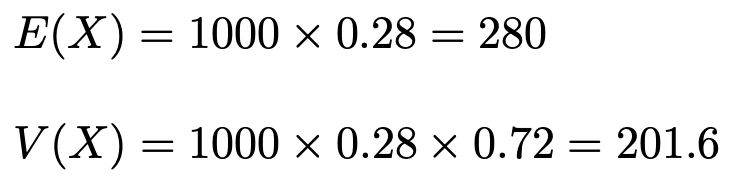
また,標本の大きさは十分に大きいので,Xの従う二項分布は正規分布N(280,201.6)で近似できると考えます。このとき,次の式で定まるZは標準正規分布に従います。
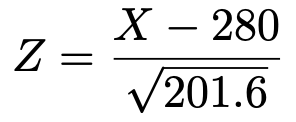
よって,求める確率を次のようにおきかえることができます。
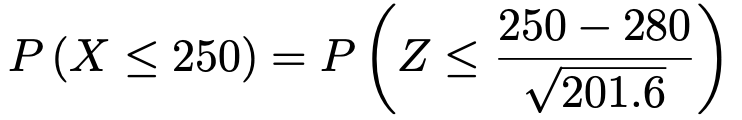
ここで,次のように近似的に計算します。
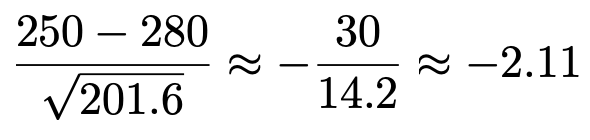
正規分布表で,2.11における上側確率を調べると,次のように0.0174であるとわかります。
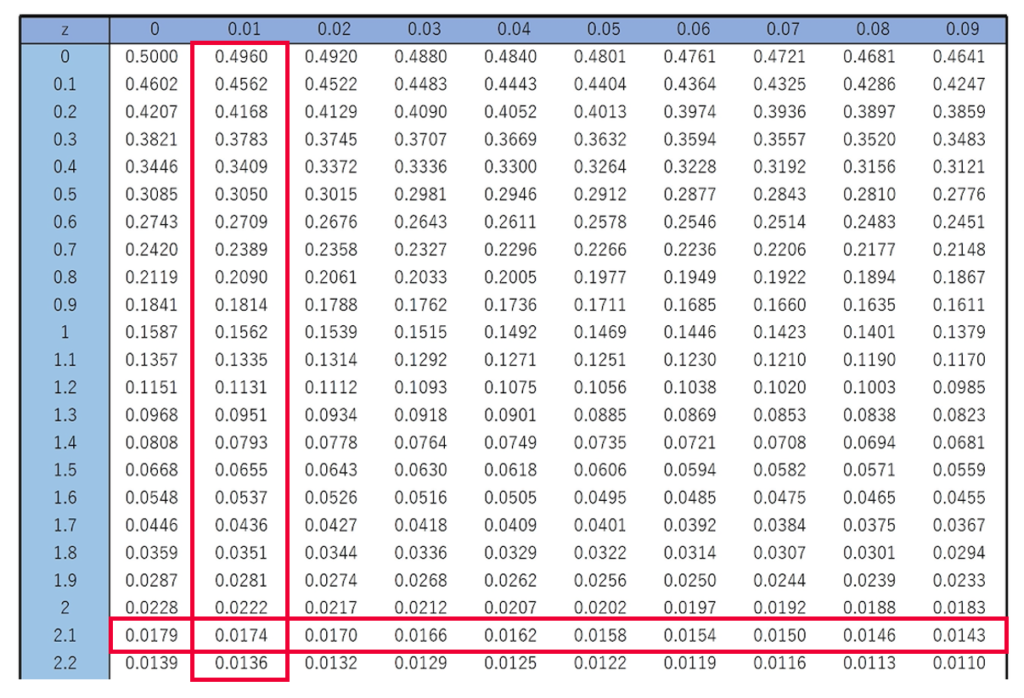
したがって,求める確率は次のようになります。
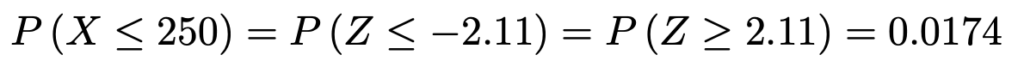
(解答終わり)
なお,二項分布を正規分布で近似するときには,近似の精度を上げるために半整数補正(統計検定2級の問題文では「連続修正」と表現されます)がよく用いられます。統計検定2級では出題されていないため,この記事では半整数補正を扱いませんでしたが,詳しく知りたい人は,その説明が詳しく書かれている「基本統計学(宮川公男,有斐閣)」を読んでみてください。
演習3〜母比率の推定〜
【問題】20歳〜29歳までの男性会社員300人にアンケートをとったところ,毎朝入浴する人は45人いた。この調査結果は,母集団を20歳〜29歳までの男性会社員全体とし,標本サイズ300の単純無作為抽出に基づくとみなす。20歳〜29歳までの男性会社員全体における毎朝入浴する人の割合(母比率)pの信頼度90%の信頼区間を求めなさい。
【解答】20歳台の男性会社員からなる母集団は十分に大きいので,毎朝入浴する人数Xは二項分布に従うと考えていいです。
Xが二項分布B(n,p)に従うとき,母比率pの信頼度95%の信頼区間を求める式は次のようになりましたね。
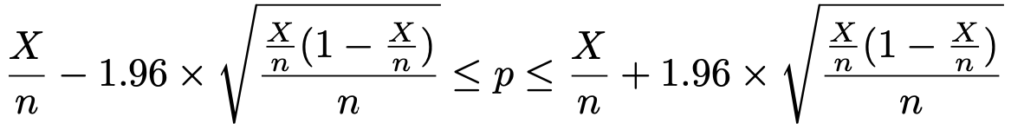
信頼度90%の信頼区間は1.96を1.64でおきかえて,次のようになります。
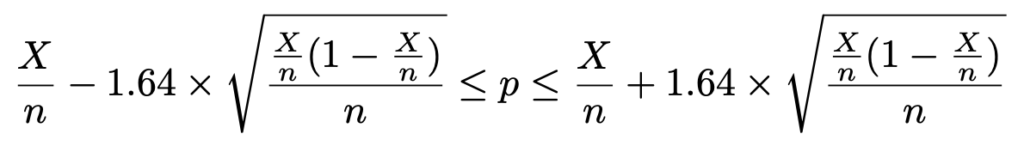
いま,標本比率は次のように与えられています。
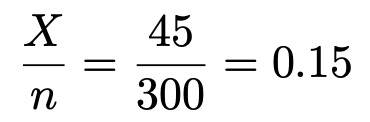
上の不等式に,標本比率とnの値をそれぞれ代入すると,次のようになります。
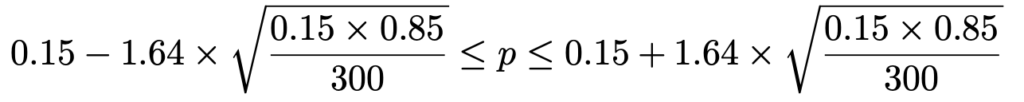
最左辺と最右辺をそれぞれ小数第3位まで求めると,母比率pの信頼度90%の信頼区間は次のようになります。
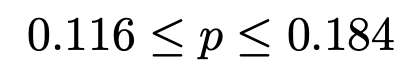
(解答終わり)
第10回は以上となります。最後までお付き合いいただき,ありがとうございました!
引き続き,第11回以降の記事へ進んでいきましょう!
2023年1月に「統計検定2級公式問題集[CBT対応版](実務教育出版)」が発売されました!(CBTが何かわからない人はこちら)
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが,本書は分野ごとにその形式の問題を並べた構成になっていて,最後に模擬テストがついています。CBT対策の新たな心強い味方ですね!
さらに実戦に向けた演習を積みたい人は,「統計検定2級公式問題集2018〜2021年(実務教育出版)」を手に取ってみてください!
また,もっと別の問題を解いてみたい人は,さらにさかのぼって「統計検定2級公式問題集2016〜2017年(実務教育出版)」を解いて実力に磨きをかけましょう!



![統計検定2級公式問題集[CBT対応版]](https://m.media-amazon.com/images/I/51q3GfZId3L._SL500_.jpg)




コメント
勉強不足で大変申し訳ないのですが、演習1の(2)の最初の式変形がわからないのですが、どうすれば記載の式変形ができますか?
分子を分母でわりたいので,
分母が3(x+1)と表せることに着目して,
分子にも-5(x+1)をつくり出すと,
-5x+40=-5(x+1)+45
となります。これで,分子を
-5(x+1)と45に分けられたので,
この分子をもつ2つの分数に分けて
約分すると,最初の式変形が完了します。
こんにちは!
演習2の二項分布の正規近似で
Zを定めるところがありますが、
ここの分母が√201.6となっていますが、
√201.6/√1000にならないのはなぜでしょうか?
標本を使うときは√nを使うと理解していたのですが、
√nするときとしないときの違いがわからなくなってしまいました。
標本平均のときには√nを使いますね。
母集団をN(μ,σ^2)とすれば,
サンプルサイズnの標本平均はN(μ,σ^2/n)に従うので,
標準化するときにσ/√nでわります。
この問題では,Xは二項分布B(n,p)に従い,nが大きいことから
この二項分布をN(np,np(1-p))とみなして計算しています。
「標本は√nでわる」という覚え方は勘違いしやすいので,
どの確率変数がどんな確率分布に従うのかを正確に捉えましょう。
ありがとうございます!
区別がしっかりついてなかったということですね!
解ける問題は増えてきましたが、理解もできるようにしていきたいです!
二項分布の正規分布に近似する条件について質問があります。
調べる中で二項分布の正規分布への近似条件として下記を見つけました。
“np > 5″ かつ “n(1-p) > 5″ を満たす事」※実用上との記載あり
これまでの理解としては、nがある程度大きい(n>=30)場合、正規分布に近似できるものと
思っていたのですが、”np > 5″ かつ “n(1-p) > 5” 」を満たしていない場合は、
二項分布は正規分布に近似できないのでしょうか
参考サイト(https://data-everyday.com/stat_ml/post-248/)
コメントを拝見し,本文の演習問題の直前に,【二項分布の正規近似についての補足】を追記しましたので,ご確認ください。
そこには,np=3,6,10の3つの場合について,グラフを示しました。
ご覧いただくと,np=6の場合でも,そこそこズレていることがわかると思います。
つまり,np=5はダメで,np=6ならOKという明確な基準ではありません。
あくまで,ケースバイケースで,
「npやn(1-p)が小さい場合にはズレが顕著になりやすいので要注意」
と認識しておいてもらえば良いと思います。