はじめて「t分布」と聞くと,「tって何?」と思いますよね。そんなt分布の歴史的な事情も含めて,区間推定や仮説検定で大活躍するこの確率分布をわかりやすく解説していきます。
t分布は正規分布の兄弟のようなものです。似ている部分もあれば,「自由度」のような違いもありますので,第6回の連続型確率変数や第7回の正規分布の記事の内容を踏まえた上で,正規分布と関連させてt分布を理解していきましょう。本当は,この2つの分布とカイ二乗分布も含めて3兄弟なのですが,このあたりの話は第15回の記事に譲ります。
また,次回以降の「推定と検定」の記事につながる内容として,「不偏推定量」なども紹介していきます。なじみのない言葉がいろいろと登場しますが,一つずつ説明していくので,ゆっくりと理解していきましょう。なお,母集団や標本といった用語は,第3回の記事で説明していますので,ご存じない方は先にそちらをご覧ください。では,はじめていきましょう!
統計的推測
母集団の期待値のことを母平均,母集団の分散のことを母分散,母集団の標準偏差のことを母標準偏差と言います。母平均や母分散のように,母集団を特徴づける値を母数(パラメータ)と言います。
標本の性質をもとに,母集団の性質を調べることを統計的推測と言います。統計的推測には推定と検定の2種類があります。推定は,標本を調べることで母数を推測することです。検定は,標本を調べてわかることが仮説と矛盾しないかを検証することです。推定には点推定と区間推定があり,点推定は今回の記事で説明し,区間推定は次回以降解説します。検定は推定の後の記事で扱います。標本から求められるものを統計量と言います。推定のために用いる統計量を推定統計量(推定量),検定のために用いる統計量を検定統計量(検定量)と言います。
いろいろと単語を並べましたが,これらの単語は誰でもはじめのうちは覚えにくいものです。これ以降,あえてこれらの単語をガンガン使いますので,言葉がわからなくなったら,ここに戻ってくることを繰り返しながら覚えていきましょう。
不偏推定量と一致推定量
推定量の期待値が母数に等しくなるとき,この推定量を不偏推定量と言います。以下で,これについて解説します。次の大きさnの標本を考えます。
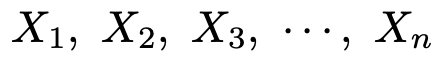
これらは独立で,同一の確率分布に従い,母平均をμ,母標準偏差をσとします。
標本平均とは,次の式で定まるようなものだったことを思い出しましょう。

このとき,次の式のように,標本平均の期待値は,母平均に一致します。(第7回でもやりましたね)

したがって,標本平均は母平均の不偏推定量です。
次に,母分散の不偏推定量を考えます。最初に思いつくのは,次の式だと思います。
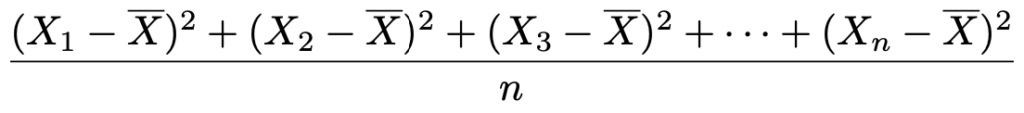
しかし,実はこれは不偏推定量ではありません。次の式で表されるものが母分散の不偏推定量です。

この統計量を不偏分散と言います。不偏分散は英語でunbiased varianceと言うので,U2で表しています。単に標本分散と言った場合,上の2つのどちらを指すのかが曖昧であるため,これ以降,標本分散という言葉は使わず,U2の式を不偏分散と呼ぶことにします。
この統計量が母分散の不偏推定量であることを次に示します。最初の式は唐突ですが,次のように式変形を行います。
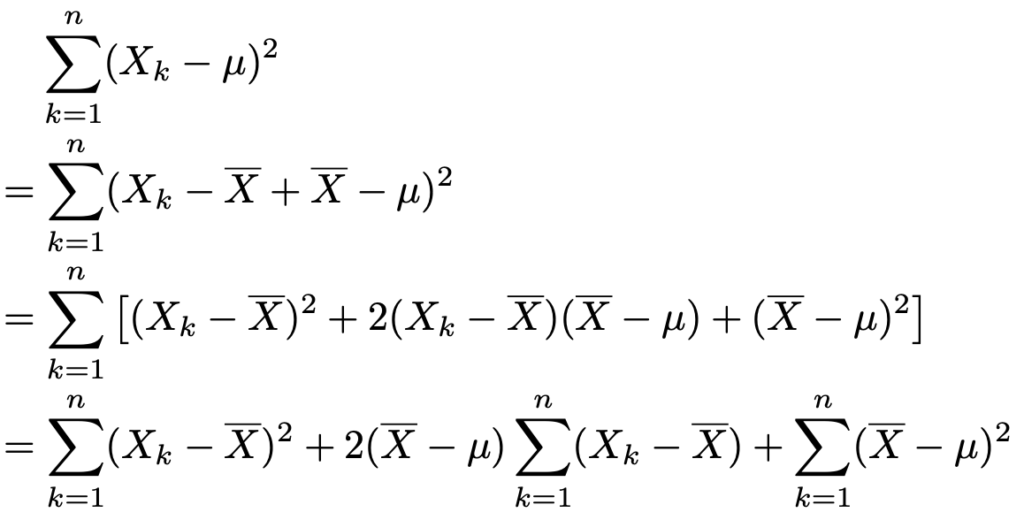
最後の式の第2項が0であることは次のようにわかります。
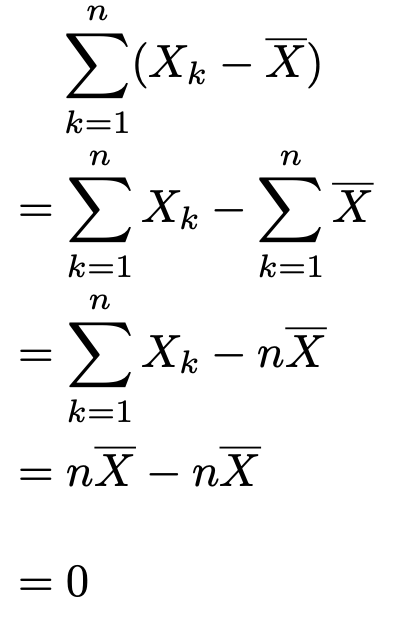
よって,次の式が成り立ちます。
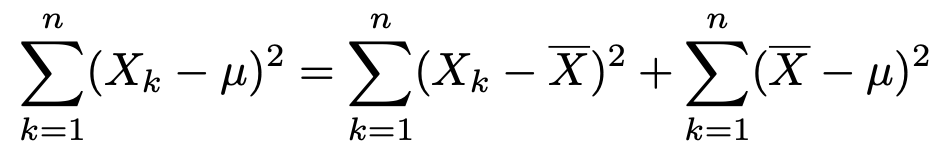
この式の両辺の期待値をとると,和の期待値は期待値の和に等しいので,次のようになります。

「和の期待値が期待値の和に等しい」ことをさらに使うと,次のようになります。
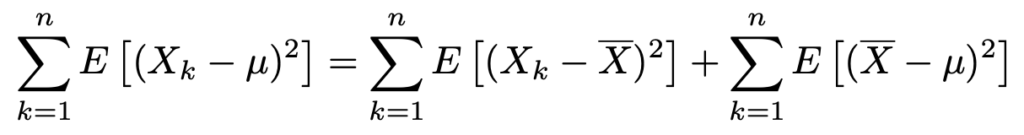
左辺の項と右辺の第2項は既知の分散であることをはっきりさせると次のようになります。
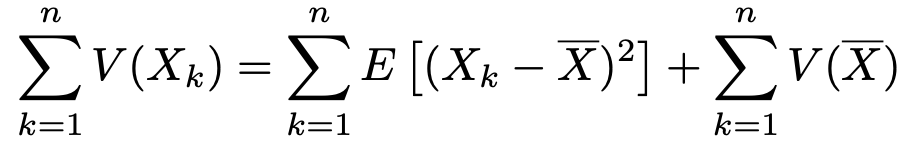
分散の値を代入すると,次のようになります。
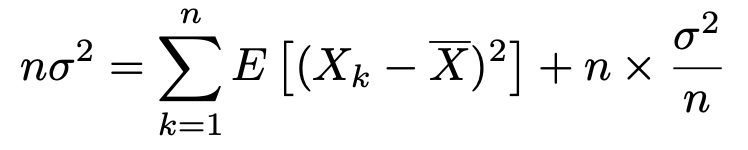
したがって,次のようになります。

これで,不偏分散が母分散の不偏推定量であることがわかりました。
次に,推定量の極限が母数に等しくなるとき,この推定量を一致推定量と言います。例えば,標本の大きさを大きくしていけば,標本平均はどんどん母平均に近づいていきますので,標本平均は一致推定量です。また,不偏分散は母分散の一致推定量になります。
また,標本の大きさが大きくなるにつれて標本平均が母平均に近づくことは,一般的には大数の弱法則(たいすうのじゃくほうそく)と呼ばれます。コインを多数回投げたときに,表が出た割合と裏が出た割合はどちらも0.5に近づくことも同じです。
さて,このセクションでは,これ以降,記事の後半にある「演習2」を解くために必要な式を使った説明をします。この問題は,統計検定の2019年,2021年の類題なので,チャレンジできることが望ましいのですが,やや難度が高いので,無理にはおすすめしません。難しい話を避けて効率良く合格点を取りたい人は,「演習2」とそのための次の説明をすべて読み飛ばしていただいても結構です。
Xを,母平均がμ,母分散がσ2である母集団から無作為抽出された大きさnの標本から求めた標本平均であるとします。大数の弱法則を式で表すと,任意のε>0に対して,

という式が成り立つことであると言えます。この式は,εをどんなに小さな数(例えば,0.0001とかを想像してください)にしても,標本の大きさのnをどんどん大きくすれば,標本平均とμの差がε以上となる確率を0にできると主張しています。はじめて聞くとちょっとわかりにくいですが,要するに,標本の大きさが大きくなれば,標本平均が母平均に限りなく近づくということを小難しく表現しただけです。この大数の弱法則は,チェビシェフの不等式と呼ばれる次の式から導かれます。

この不等式のXが大きさnの標本平均の場合を考えてみましょう。期待値と分散は次のようになりますね。
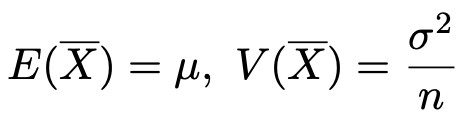
よって,この場合のチェビシェフの不等式は次のようになります。
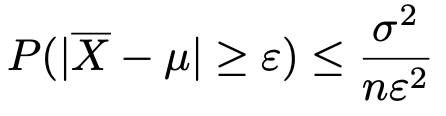
上の不等式で,nの値を十分に大きくとれば,右辺の値はいくらでも小さくできるので,左辺の確率は0に近づかなければなりません。これで大数の弱法則が成り立つことがわかりました。
点推定
1つの値によって母数を推測する推定のことを点推定と言います。例えば,母平均を知りたいときに,多少の誤差があることを覚悟して,標本平均の値をそのまま採用することが点推定にあたります。
母数の推定量としては,不偏性を持つものが良いとされますので,母平均の点推定には標本平均が,母分散の点推定には不偏分散がそれぞれ使われます。それ以外に,点推定に適した性質を持つ統計量を見つけるための代表的な方法として,最尤法というものがありますが,統計検定2級で出題されていないため,割愛します。
t分布
確率密度関数が次の式で表されるような確率分布を自由度nのt分布(Studentのt分布)と言います。
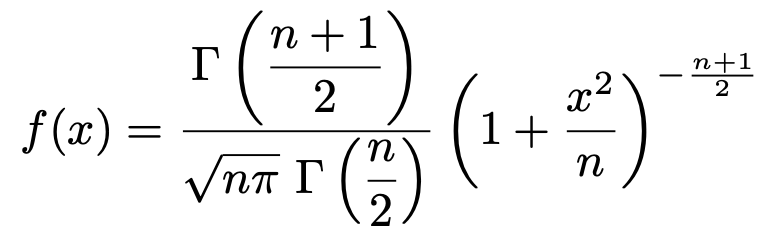
正規分布の確率密度関数は,μやσを決めることでただ1つのxの関数が定まりました。一方,t分布の確率密度関数は,nを決めることでただ1つのxの関数が定まります。このnのことを自由度と呼びます。Γ(s)はガンマ関数ですが,ここで説明することは避けたいと思います。なぜなら,正規分布の場合と同様に,t分布の確率も表にまとまっていて,確率を求めるのにこの式は使わないからです。この式は参考までに記載しただけです。
ちなみに,Studentというのは,この確率分布の発見者とされる英国人のゴセット(1876〜1937)が論文に使用したペンネームです。彼は,当時勤務していたギネス社(ギネス記録で有名な会社)に配慮して,本名をふせて論文を書いていたそうです。また,t分布のtという文字は,ゴセットの発見を高く評価した著名な統計学者のフィッシャー(1890〜1962)が,「z=〜」と論文で書かれていた式を修正したときにたまたま「t=〜」とおきなおした変数であり,この文字に特に意味はないようです。
t分布のグラフ
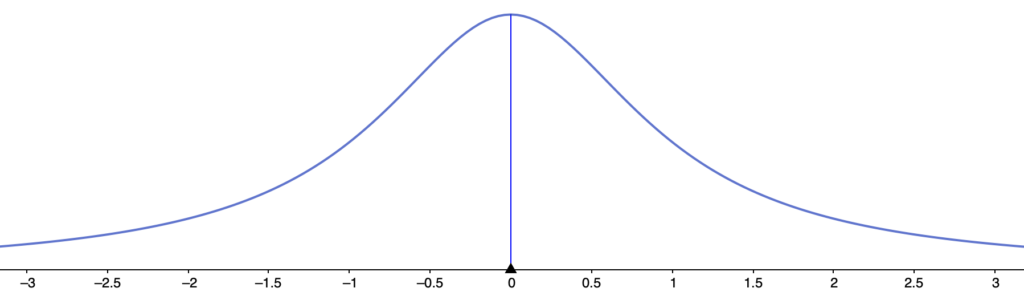
t分布のグラフは山が1つで,山の頂点が縦軸上にあり,左右対称なので標準正規分布のグラフに似ています。自由度を変えるとグラフの形が変わり,自由度→∞の極限で,標準正規分布のグラフに一致します。以下では,自由度の違いによるグラフの形の違いを確認していきます。
自由度1のt分布のグラフは次のようになります。このグラフは標準正規分布のグラフとの違いがはっきり見てとれます。
自由度3のt分布のグラフは次のようになります。
自由度30のt分布のグラフは次のようになります。ここまで自由度を上げると,標準正規分布のグラフにそっくりです。

繰り返しになりますが,「t分布のグラフは標準正規分布のグラフに似ていて,自由度を上げるほど標準正規分布のグラフに近づく」ということを覚えてもらえれば大丈夫です。
t分布の確率
t分布に従う確率変数の確率は,正規分布の場合と同じように,表を使って求めます。すべての統計学のテキストに,次のようなt分布表が載っています。ただし,正規分布表と同じように,t分布表にも複数のパターンがありますので,注意してください。ここでは,上側確率がそれぞれ,0.1,0.05,0.025,0.01,0.005に一致するようなTの値(順に,上側10%点,上側5%点,上側2.5%点,上側1%点,上側0.5%点と言います)をまとめた次の表を使います。
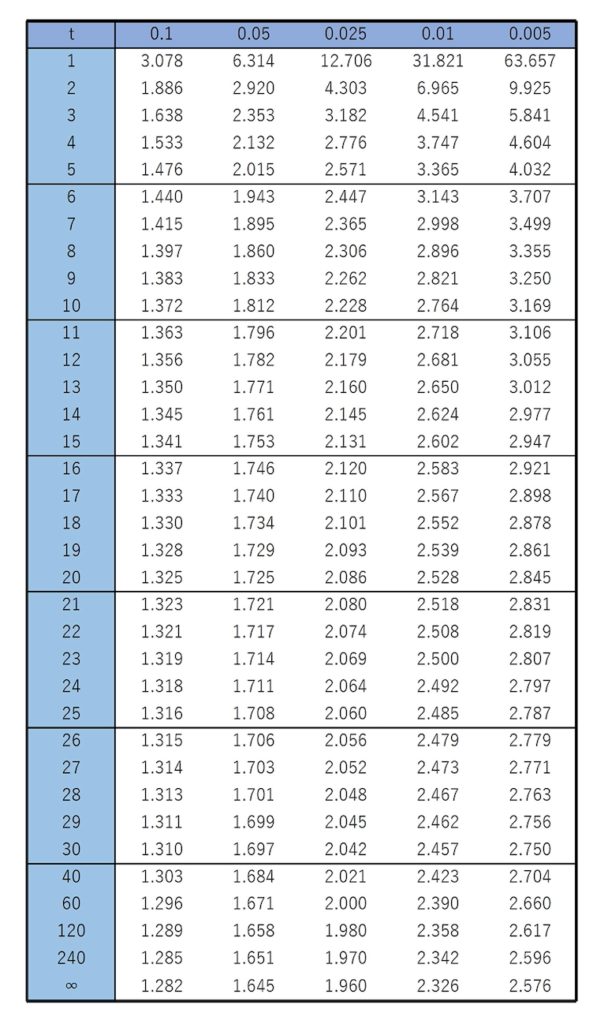
この表の見方としては,はじめに,いちばん左の縦1列で自由度を指定して,その行を横に見ていきます。次に,いちばん上の行で上側確率を指定して,その列を縦に見ていき,これらが交差したところに書かれている数が,下の図のtの値になります。
では,実際にt分布表を使う問題を解いてみましょう。
【問題】自由度23のt分布の上側5%点を求めなさい。
【解答】求めるパーセント点を次のように表す場合があります。

上側5%点を図で表すと,次のようになります。
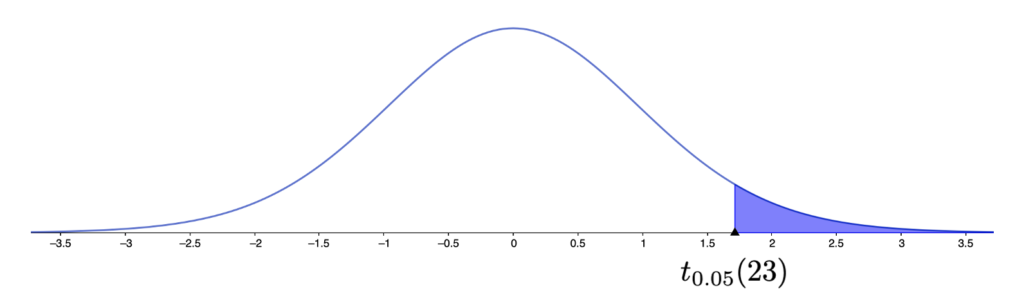
t分布表で,いちばん左の縦1列が自由度を表していますので,この中から23の行を見つけます。次に,いちばん上の行で,上側確率0.05の列を見つけます。これらが交差したところに書かれている数が求める値です。図にすれば,次のようになりますね。
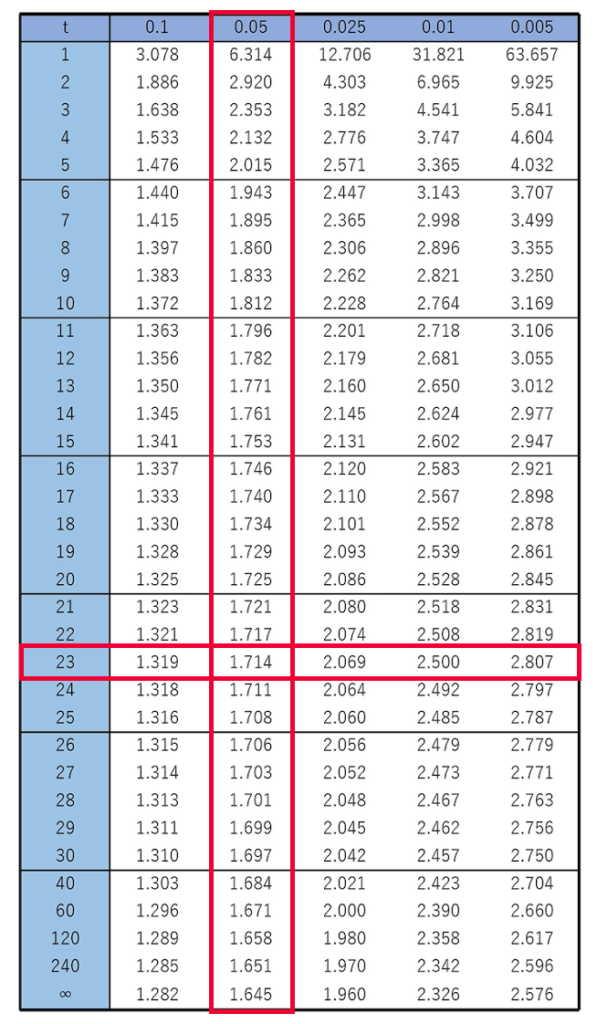
したがって,求める上側5%点は1.714です。
(解答終わり)
不偏分散とt分布
次のn個の標本を考えます。
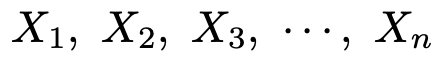
これらの確率変数は独立で,次の正規分布に従うものとします。

このとき,第7回の記事で説明したように,次の式で表される標本平均は下の正規分布に従います。
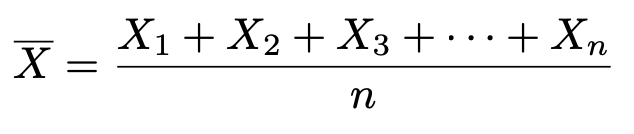
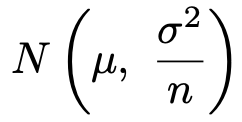
このことから,次の確率変数Zは標準正規分布に従うのでしたね。
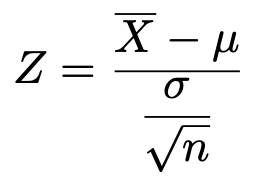
母平均を推定したいとき,このようにせめて母分散がわかっていると,上のおきかえによって正規分布の性質を利用できるのですが,母平均がわからないときには母分散もわからない場合が多いです。よって,母分散の代わりになるものが必要になります。それが不偏分散です。なぜなら,上で説明したように,不偏分散は一致性と不偏性を持っているからです。上の変数変換の式のσを不偏分散の正の平方根におきかえると次のようになります。

この式で定まる確率変数Tは自由度n−1のt分布に従います。自由度はnではなく,nー1であることに注意してください。不偏分散を求めるときにわる数がn−1だったので,自由度はこの数と一致しています。
Tを定める上の式とt分布の確率密度関数を関係づける数学的な議論はできなくても問題ありませんが,興味のある人は,例えば,「データ解析のための数理統計入門(久保川達也著,共立出版)」を参照してください。
上の式で定まるTが自由度n−1のt分布に従うという事実は,第9回の記事で扱う区間推定で活躍することになりますので,結果は覚えておきましょう。
【問題】次の大きさ4の無作為標本
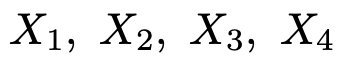
の母集団は期待値μの正規分布に従っているものとする。また,これらの標本平均と不偏分散を次のようにおく。
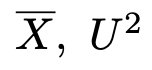
このとき,次の確率を求めなさい。
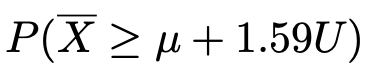
【解答】上で説明したように,標本平均も期待値μの正規分布に従います。このとき,次の式で定まる確率変数Tは,4−1=3より,自由度3のt分布に従います。
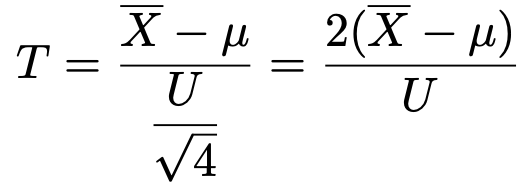
ここで,求める確率は,次のように変形できます。
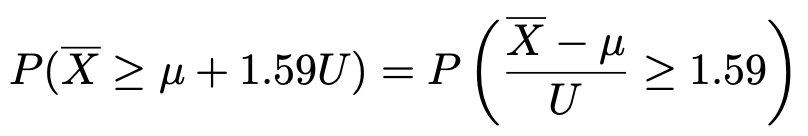
この確率をTを使って表現すると,次のようになります。
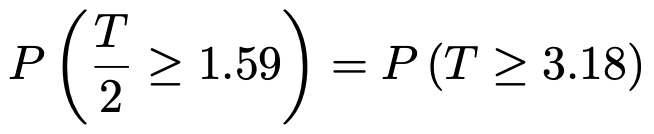
自由度3のt分布表で,Tの値が3.18となるのは,次のところです。

つまり,3.182における上側確率が0.025だとわかりますので,求める確率は0.025です。
(解答終わり)
t分布についての基本的な説明は以上になります。この後は,参考図書の紹介に続けて,さらに理解を深めるための演習問題ですので,余力があればぜひチャレンジしてみてください。
参考図書
本稿を執筆するにあたり,次の書籍を参考にしました。
基本統計学 第5版(宮川公男,有斐閣)
統計的推測のセクションで定義した用語や,不偏分散の期待値の計算,t分布のグラフの特徴などが詳しく解説されています。
演習1〜t分布のパーセント点〜
【問題】自由度6のt分布で,上側1%点を求めなさい。なお,必要があれば,上のt分布表を使いなさい。
【解答】t分布表のいちばん左の縦1列で,6の行を見つけます。次に,いちばん上の行で,上側確率0.01の列を縦に見ていき,これらが交差したところに書かれている数は,次の図のように3.143です。
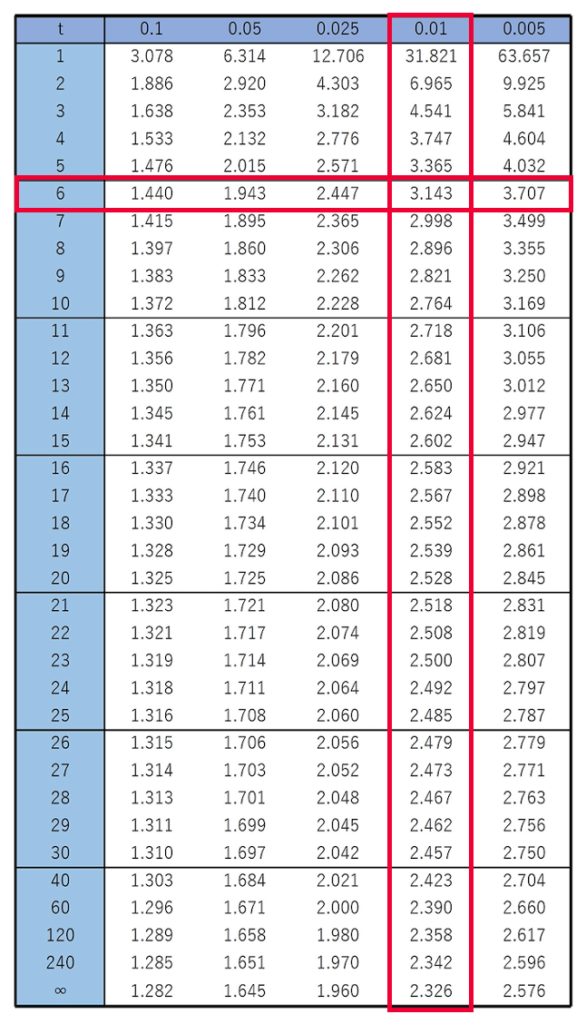
(解答終わり)
演習2〜不偏推定量〜
【問題】次の大きさnの無作為標本
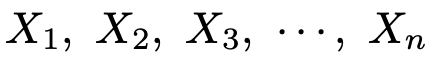
の母集団の期待値はμ,標準偏差はσであるものとする。母平均μの推定量として,
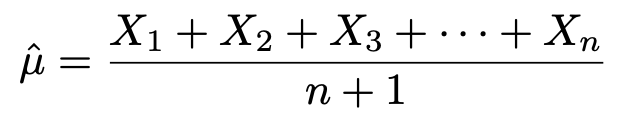
を考えると,これは,不偏推定量であると言えるか。また,一致推定量であると言えるか。
【解答】不偏推定量であるかどうかは,次のように期待値を計算すればいいですね。
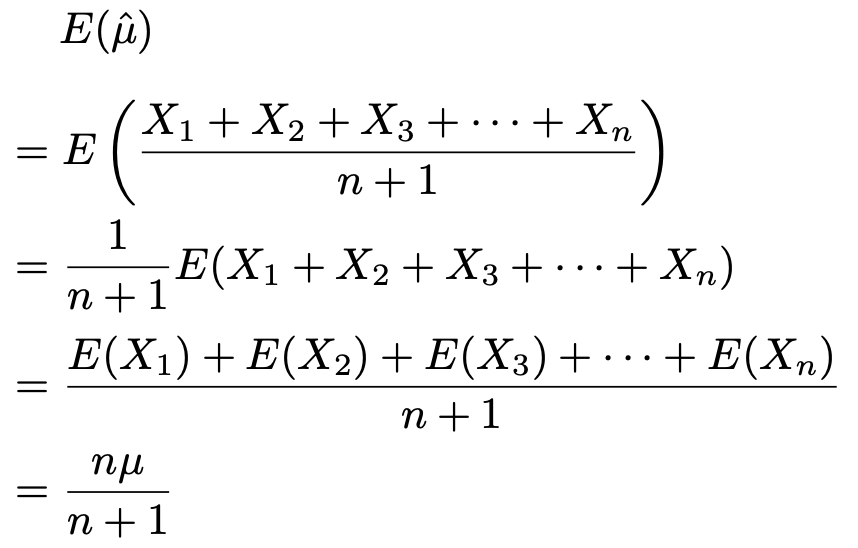
期待値が母平均に一致しないので,母平均の不偏推定量ではありません。
次に,一致推定量であるかどうかを確認します。一致推定量であるためには推定量の分散のn→∞の極限が0である必要があるので,分散を求めてみます。
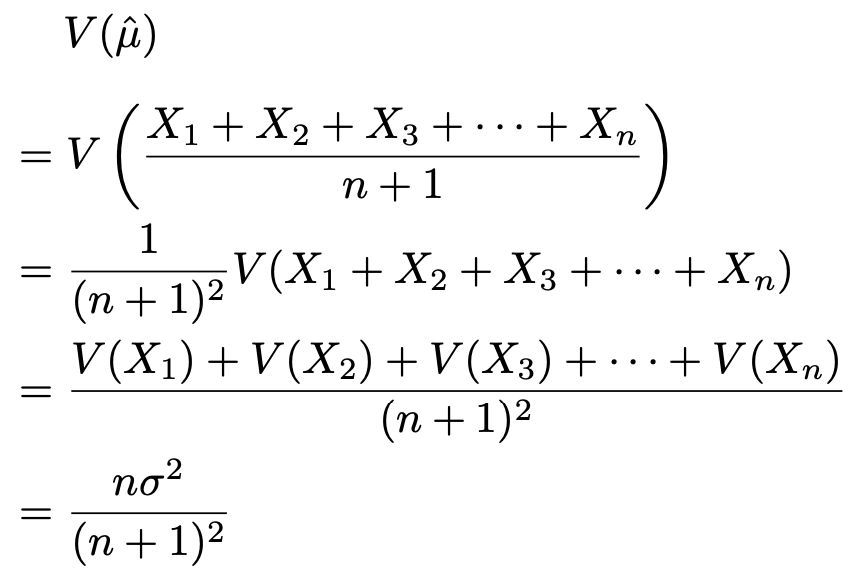
この分散は,分子より分母のほうがnの次数が大きいので,n→∞の極限が0になります。
さて,ここまでのことから,この推定量は一致推定量であると言えます。そのことを明らかにするにはチェビシェフの不等式を使いますが,以下の議論はやや複雑なので,式を追える人だけ追ってください。まず,ε>0に対して,次の確率を考えます。
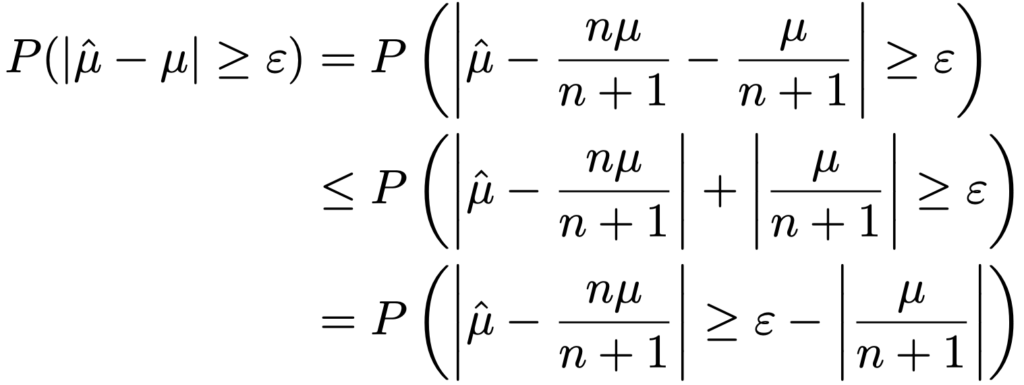
ここで,上の確率のかっこ内の不等式の右辺を次のようにε’とおきます。
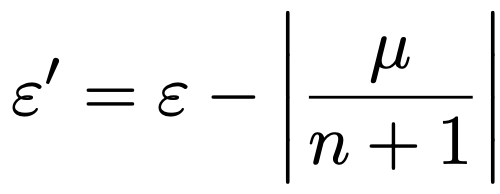
このε’に対して,チェビシェフの不等式より,次の不等式が成り立ちます。
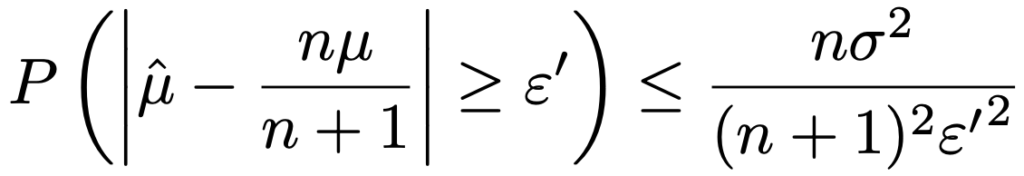
すぐ上の不等式の右辺はnをどんどん大きくすると0に近づいていくので,出発点となった確率について次の式が成り立ちます。
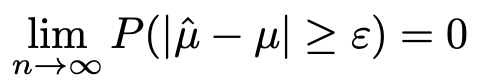
逆に表現すれば,次のようになります。

つまり,この推定量は,nを大きくすればμにどこまでも近づくので,一致推定量であると言えます。
(解答終わり)
演習3〜t分布の確率と不偏分散〜
【問題】次の大きさ16の無作為標本

の母集団は期待値μの正規分布に従っているものとする。また,これらの標本平均と不偏分散を次のようにおく。
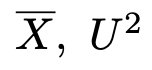
このとき,次の確率を求めなさい。なお,必要があれば,上のt分布表を使いなさい。
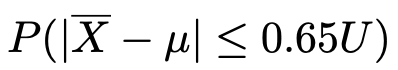
【解答】まず,記号の確認をします。例えば,|−1|という記号の意味を知っているでしょうか。縦棒は絶対値を表しますので,|−1|=1です。よって,求める確率を絶対値を使わずに表すと,次のようになります。
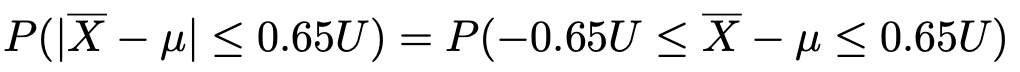
さて,16ー1=15より,次の式で定まる確率変数Tは自由度15のt分布に従うのでしたね。
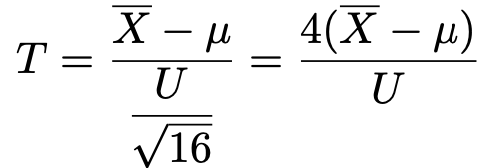
よって,求める確率をTを使って表すと,次のようになります。
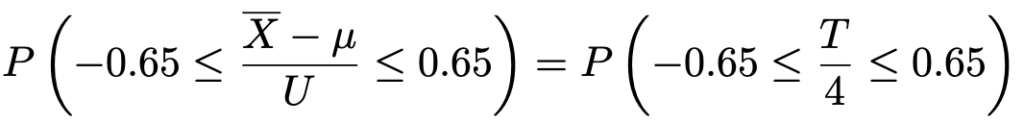
つまり,次の確率です。
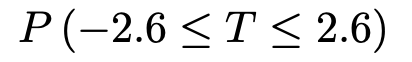
t分布表で自由度15の確率を見ると,次のことがわかります。
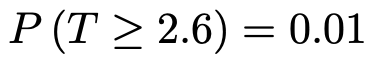
t分布表では上側確率が0.01になるtの値は2.602となっていますが,小数第4位は切り捨てました。また,t分布の確率密度関数のグラフが左右対称であることから,次のこともわかりますね。
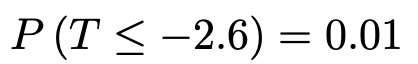
よって,求める確率は次のようになります。
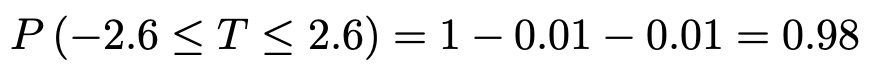
(解答終わり)
第8回は以上となります。最後までお付き合いいただき,ありがとうございました!
引き続き,第9回以降の記事へ進んでいきましょう!
2023年1月に「統計検定2級公式問題集[CBT対応版](実務教育出版)」が発売されました!(CBTが何かわからない人はこちら)
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが,本書は分野ごとにその形式の問題を並べた構成になっていて,最後に模擬テストがついています。CBT対策の新たな心強い味方ですね!
さらに実戦に向けた演習を積みたい人は,「統計検定2級公式問題集2018〜2021年(実務教育出版)」を手に取ってみてください!
また,もっと別の問題を解いてみたい人は,さらにさかのぼって「統計検定2級公式問題集2016〜2017年(実務教育出版)」を解いて実力に磨きをかけましょう!




![統計検定2級公式問題集[CBT対応版]](https://m.media-amazon.com/images/I/51q3GfZId3L._SL500_.jpg)



コメント
コメント失礼します。
演習2の不偏推定量に関する問題についてですが、V(μ^)がnσ²/(n+1)²になっていますが、分子はσ²ではないのでしょうか?自分は標本Xの分散がσ²/nだと思ったのでこう考えたのですが、これはXの分散がσ²ということでしょうか?
σ^2/nは標本平均の分散ですね。
μ^は標本平均の分母のnをn+1に変えたものですが,
もし,分母をnにすれば標本平均に一致し,
分散はnσ^2/(n+1)^2→σ^2/nとなります。
母集団からXiを取り出したとき,その分散がσ^2なので,
V(Xi)=σ^2となります。
返信ありがとうございます!
あくまで標本の一つ一つの分散はσ²ということですね わかりました!
追伸
いつも動画とブログで勉強させてもらってます!ありがとうございます!
演習2について質問です。
一致推定量は推定量に極限をとった時に母平均に一致するかどうかということならば、(n/n+1)μをn→∞で極限取って一致を示すだけではダメなのでしょうか?
とても良い着眼点の質問だと思います。
確かに,この推定量はn→∞で期待値がμに近づきますが,
「期待値」がμに近づくだけで,
推定量の値自体がμに近づく保証がありません。
推定量の値が平均的にμに近いだけだと,
例えばμ+1とμー1をそれぞれ0.5の確率でとるような推定量を考えればわかるように,
期待値はμでも一致推定量ではありません。
nが十分に大きければほとんどμに等しい値にならないといけないのです。
つまり,一致推定量であるためには分散が0に近づいていく必要があります。