まず,期待値の意味と計算方法を理解していきましょう。期待値と言えば,宝くじです。宝くじの公式サイトが公表している令和元年度のデータによると,宝くじの収益金のうち,当選金として支払われた金額は46.5%だそうです。これは期待値の計算から求められる理論値に近いので,期待値という統計学の指標の信頼性を実証してくれているような結果です。このように,宝くじの期待値は50%未満なので,宝くじは,買った直後に買った値段の半分未満の価値に暴落します。期待値を勉強する意義の1つは,このことを自分の頭で理解できるようになることです。
今回の記事のもう1つの柱は分散です。「分散って何の役に立つの?」という疑問を持つ人もきっといることでしょう。確率変数を特徴づける代表的な2つの指標である期待値と分散に不安のある人には最後までぜひ読んでみてほしいと思います。
なお,確率,確率変数の知識は既知として,話を進めます。これらの知識に自信のない方は,【中学の数学からはじめる統計検定2級講座】の第1回と第3回の記事を先にご覧ください。また,今回の記事は離散型の確率変数にしぼって解説しますので,連続型確率変数の期待値と分散については第6回を参照してください。
では,はじめていきましょう!
期待値とは
期待値とは,確率変数の値として平均的に期待できる値のことです。期待値のことを平均ともいいます。後で,具体例を見ながら,この意味を確認しましょう。離散的な確率変数の期待値の定義は次のような式になります。期待を英語で”expectation“というので,確率変数Xの期待値のことを,E(X)と表すのが通例です。
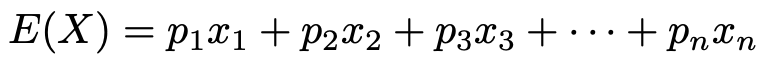
このように,確率変数のすべての実現値について,実現値とその確率の積をたし合わせたものです。また,シグマを使って表すと,次のような式になります。
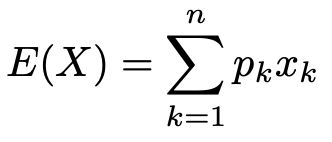
シグマについては第5回で説明していますので,「よくわからない」という人はシグマの式を読み飛ばしてもらっても大丈夫です。
【問題】サイコロを1回投げて出た目の数をXとするとき,E(X)を求めなさい。
【解答】定義の通りに式を作ると,次のようになります。
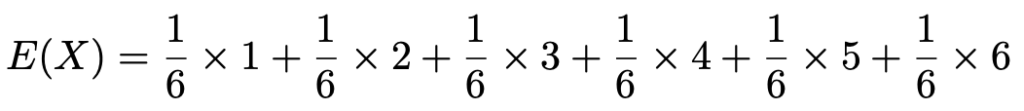
これを計算すれば終わりなのですが,式を少し変形して,分母が6の1つの分数にまとめると次のようになります。
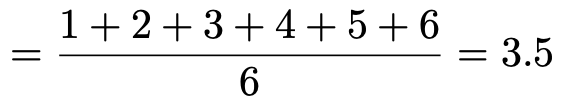
この式は,目の数の合計÷個数となっているので,小学校で習った平均を求める式ですよね。サイコロの目は平均して3.5くらいの値が期待できるのです。(解答終わり)
ちなみに,平均のことを英語で”mean”といいます。ギリシア文字でアルファベットのmに相当するのがμなので,期待値の値のことをμと書くことが多いです。今の場合ならば,
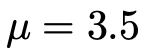
では,別の例を見てみましょう。
【問題】100が書かれた玉1個と,10が書かれた玉2個が袋の中に入っている。この中から1個の玉を取り出し,取り出した玉に書かれた数をXとするとき,E(X)を求めなさい。
【解答】定義の通りに式を作ると,次のようになります。
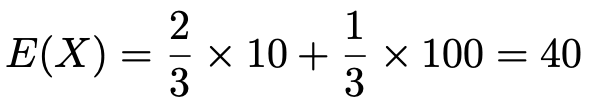
(解答終わり)
この場合でも,次のように少し式を変形することで,平均を求めていることがわかると思います。この3個の玉ならば,平均して40くらいの値が期待できるということです。
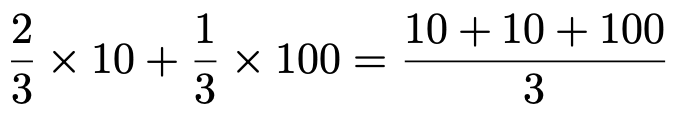
期待値の公式
【第3回】の記事で,すでにわかっている確率変数から新しい確率変数をつくることを学びました。この新しい確率変数の期待値をもとの確率変数の期待値から求める公式を2つ紹介します。いずれも,証明はできなくても大丈夫ですが,結果は必ず覚えてください。
確率変数Xの1次関数で表される確率変数aX+bの期待値について,次の式が成り立ちます。
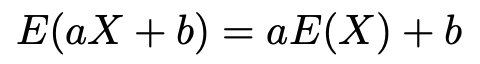
Xの期待値を右辺に代入することで,1次関数の形の確率変数aX+bの期待値を求めることができます。この式を証明しておきます。証明といっても,少し式を変形するだけなので,はじめて見ると,あっけにとられるかもしれません。
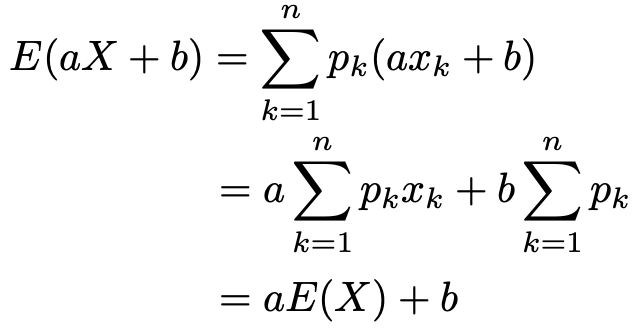
これで証明できました。もし,この式変形を見て,何をやっているかがわからないという人は,シグマを使わずに,具体的に書き出してみることをおすすめします。やっていることは,たし算の順序を変えて,分配法則を使っているだけです。
2つ目の公式として,確率変数XとYの和で表される確率変数の期待値は,次のような式で表されます。
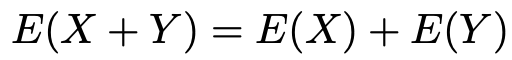
Xの期待値とYの期待値を右辺に代入することで,X+Yという新しい確率変数の期待値を求めることができます。この式を証明しておきます。まず,XとYの同時確率分布を次のように表すことにします。
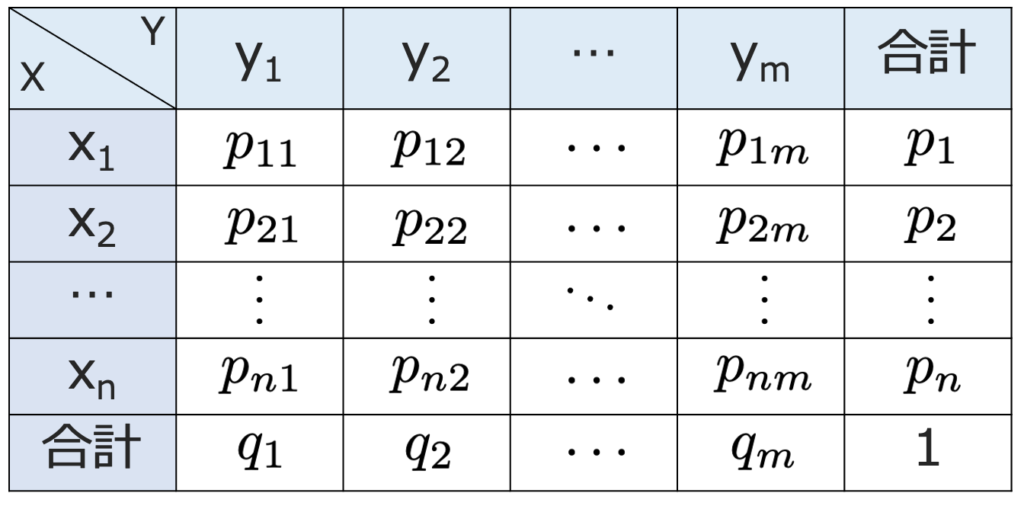
上記の文字を使って,確率変数の和の期待値の公式は次のように証明できます。
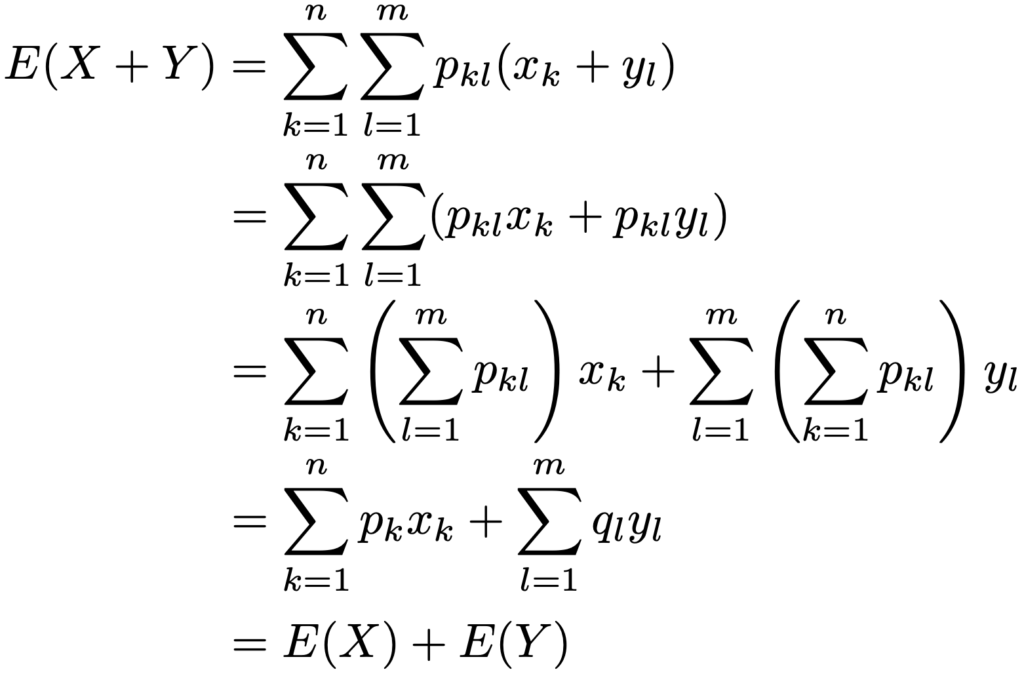
シグマが2つありますので,慣れないと難しく感じると思いますが,この式変形も,分配法則を使いつつ,たし算の順序を変えているだけです。わかりにくい場合は,具体的に書き出してみましょう。なお,第5回の記事でシグマが2つ並ぶ場合も解説しますので,そちらを見た後でもう一度見直してみてください。
さて,期待値についての公式2つを紹介し終わったところですが,次の式を追加で紹介します。
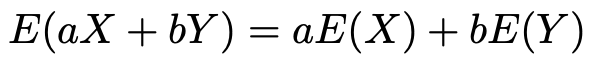
「また,覚えることが増えた!」と思うでしょうか。この式は上に紹介した2つの公式から明らかに成り立つことがわかります。念のため,確認しておきましょう。まず,上に紹介した公式の2つ目「和の期待値は期待値の和に等しい」という式を,確率変数aXとbYに使うと次のようになります。
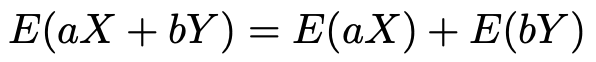
上に紹介した公式の1つ目で,b=0とすると,次の式が成り立ちます。

つまり,確率変数の係数を「外に出す」ことができるわけです。よって,
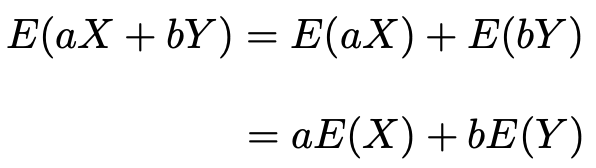
という感じで示すことができました。この3つ目の公式は,先の2つの公式からこのように導けることがパッとわかれば,覚える必要はありません。
分散,標準偏差とは
分散とは,データの値のばらつきの大きさを表す値です。離散的な確率変数の分散の定義は次のような式になります。分散を英語でvarianceというので,確率変数Xの分散のことを,V(X)と表すのが通例です。
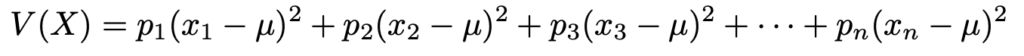
ここで使われているμは,次のことを表しています。

はじめの式をシグマを使って表すと,次のようになります。
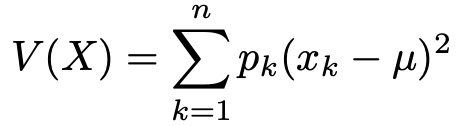
期待値の式と似ていますね。上に紹介した分散を定義する式は,期待値の式において,次の変換を行ったものです。
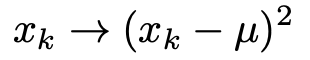
つまり,分散は,期待値の一種とみなすことができます。具体的には,確率変数の実現値と平均との差の2乗の期待値です。式で表すと,次のようになります。
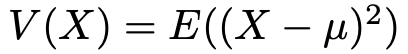
ここまで,分散を定義する式を3つ書きましたが,表現が異なるだけですべて同じ式です。では,分散の具体例を見ていきましょう。
【問題】サイコロを1回投げて出た目の数をXとするとき,V(X)を求めなさい。
【解答】サイコロの目の期待値は,E(X)=3.5でしたから,定義の通りに式を作ると,次のようになります。
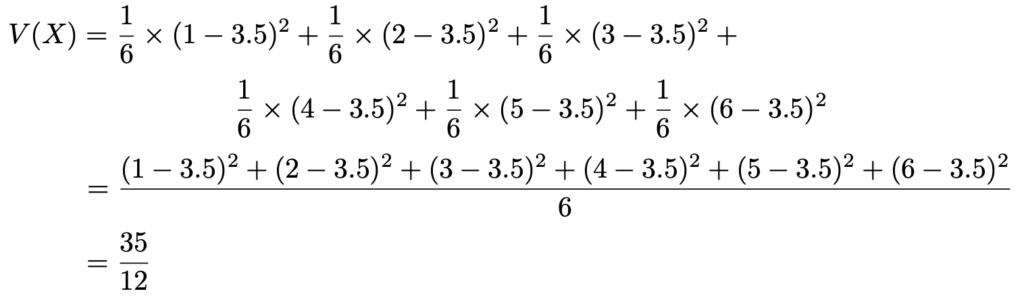
(解答終わり)
答えの1つ手前の式は,確率変数の実現値と期待値との差の2乗の平均といえますね。サイコロの目の平均の3.5からのズレの2乗の平均が12分の35くらいなのです。では,別の例を見てみましょう。
【問題】100が書かれた玉1個と,10が書かれた玉2個が袋の中に入っている。この中から1個の玉を取り出し,取り出した玉に書かれた数をXとするとき,V(X)を求めなさい。
【解答】期待値はすでに計算済みで,E(X)=40でした。定義の通りに式を作ると,次のようになります。
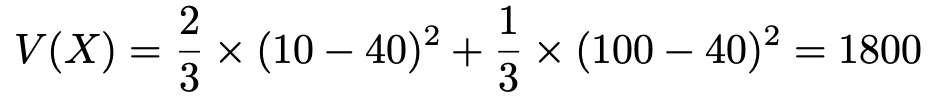
(解答終わり)
玉に書かれた数が10と100で,平均が40なのに,データのばらつきを表す値が1800って大きすぎますよね。ズレを平均する前に2乗しているので,大きくなってしまうのです。そこで,次のσを考えます。

分散の正の平方根をσで表し,これを確率変数Xの標準偏差といいます。標準偏差は英語でStandard deviationです。ギリシア文字でアルファベットのsに相当するのがσなので,標準偏差の値のことをσと書くことが多いです。先ほどの問題に戻って,標準偏差を計算すると,次のようになります。
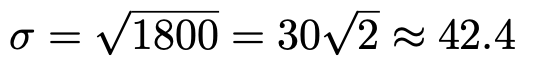
約42.4です。データの値のばらつきを表す値なので,このくらいの方が自然ですね。分散よりも標準偏差の値のほうが実感に近いのです。
分散の公式
期待値と同じように,分散についても,既知の確率変数X,Yの分散から新しい確率変数の分散を求める公式を2つ紹介します。いずれも,証明はできなくても大丈夫ですが,結果は覚えてください。1つ目は次の式です。
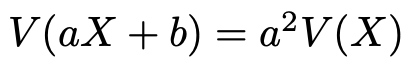
この式を証明しておきます。まず,

とすると,期待値の公式から,
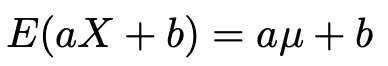
次に,分散の定義から,
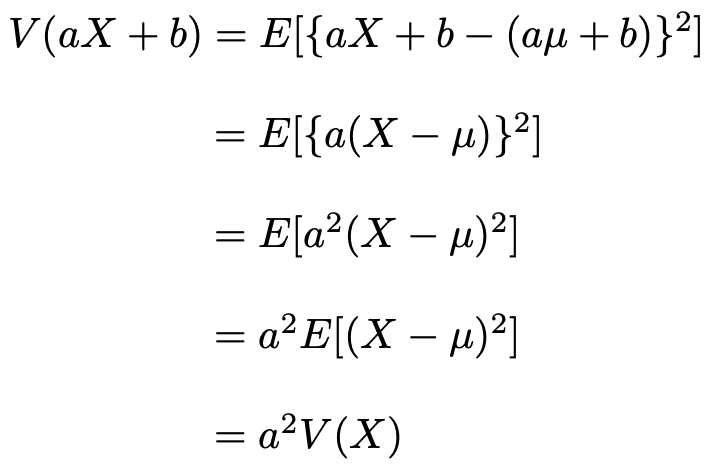
これで証明できました。Σを使って証明しても良いのですが,使わない方がスマートな印象ですね。
2つ目の公式として,確率変数XとYが独立であるとき,次の式が成り立ちます。

この式を証明しましょう。まず,
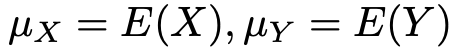
とすると,分散の定義から,
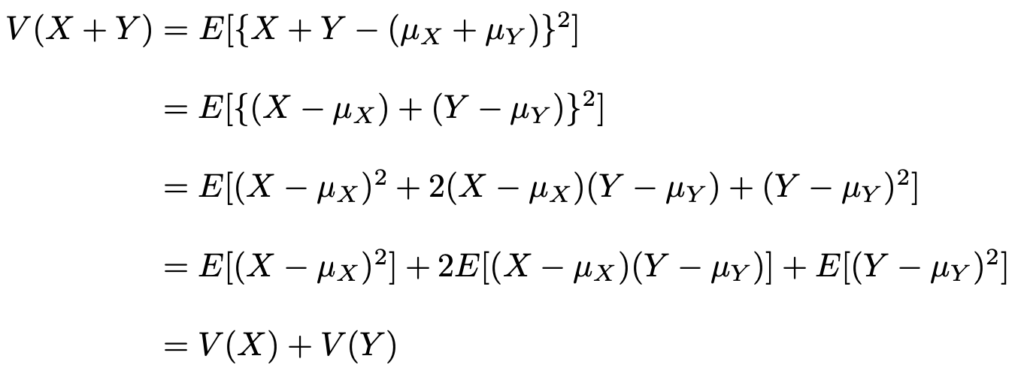
最後の変形では,XとYが独立であるときに成り立つ次の式を使いました。
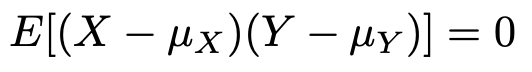
この式の左辺を確率変数X,Yの共分散といいます。XとYが独立であるときに共分散が0になることは,第5回の記事で改めて説明しますので,この証明はいったん完成したことにしておきます。
さて,分散の2つの公式を紹介しましたが,期待値のときと同じように,この2つの式からすぐに示せる式がありますね。XとYが独立であるとき,次の式が成り立ちます。
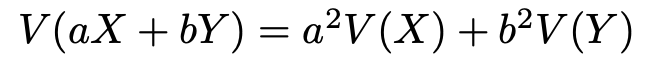
この式も示しておきましょう。まず,aXとbYが独立であるから,「和の分散が分散の和に等しい」という分散の公式として2つ目に紹介した式が成り立ちますね。よって,
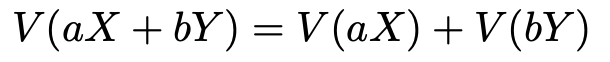
次に,1つ目に紹介した分散の公式で,b=0とすると,次の式が成り立ちます。
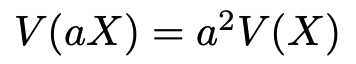
確率変数の係数は2乗して「外に出す」ことができるわけです。よって,
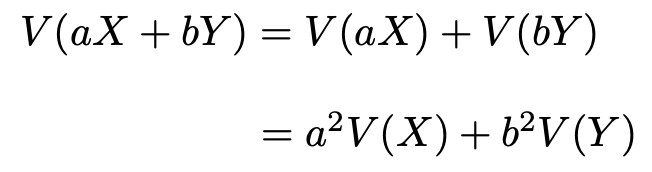
ということで証明完了です。3つ目の公式は,期待値の3つ目の公式と同様に,成り立つことがパッとわかれば覚えなくていいです。
期待値から分散を求める公式
分散の求め方は主に2つあります。1つは,すでに紹介した分散の定義式を用いる方法です。もう1つは,次の式を用いる方法です。

この式を証明しておきましょう。E(X)=μとします。

E(X)=μだったので,最後の式は示したかった式と一致していますね。
では,この式を使って分散を求めてみましょう。
【問題】1が書かれたカードが200枚,10が書かれたカードが80枚,100が書かれたカードが16枚,1000が書かれたカードが4枚で,合計300枚のカードが入った袋がある。この中から1枚を取り出し,取り出したカードに書かれた数をXとするとき,V(X)を求めなさい。
【解答】確率分布は次のようになります。
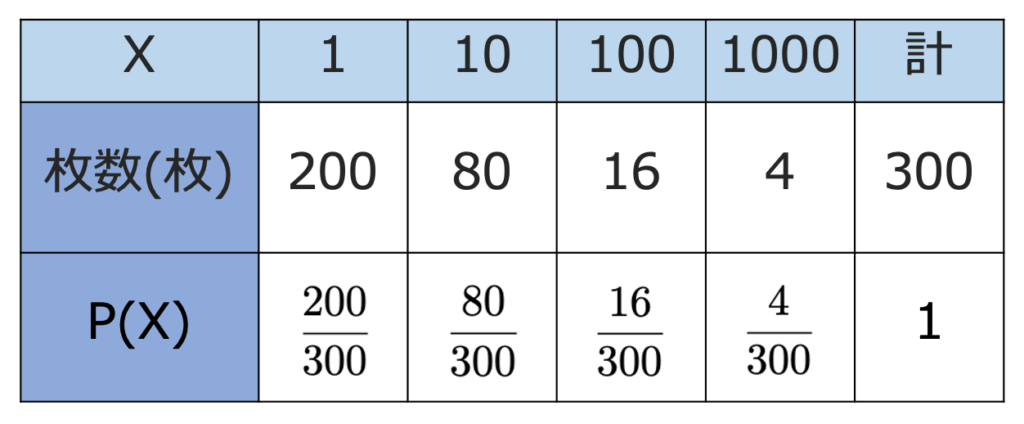
期待値を定義から計算すると,次のようになります。
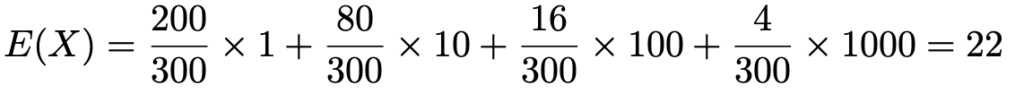
分散を定義から計算しようとすると,
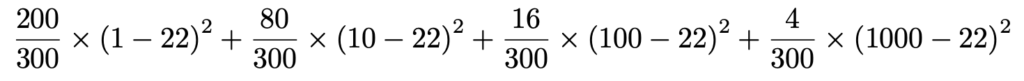
となり,カッコの2乗の計算がめんどうな感じがします。そこで,先ほど紹介した式を使ってみることにします。この公式の右辺第1項にあたるものを計算すると,次のようになります。
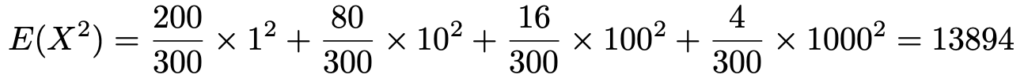
こちらのほうが2乗の計算が楽です。先ほどの公式に代入して,分散を求めると,
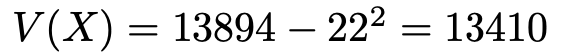
となります。
(解答終わり)
分散を求めるときには,問題に応じて,計算しやすいほうの式を選んで使いましょう。
期待値と分散の方程式
【問題】独立な2つの確率変数XとYが次の式を満たすとする。
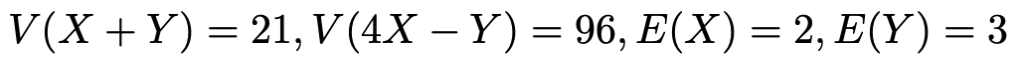
このとき,次の式を満たすa,bの値を求めなさい。
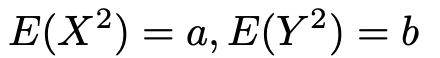
【解答】XとYが独立であるという条件があるので,次の公式が使えます。
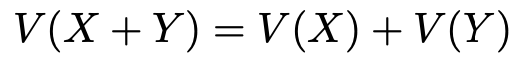
これによって,問題の条件式の1つ目は次のように書きかえられます。

XとYが独立ならば,4XとーYも独立なので,同じようにして,条件式の2つ目は次のように書きかえられます。
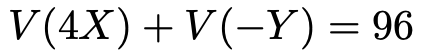
この式に対して,次の公式を使いましょう。
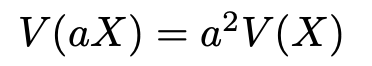
確率変数X,Yの係数を2乗して外に出すと,次の式が得られます。
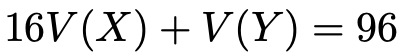
ここまでで,V(X)とV(Y)の2元1次方程式が2つできましたので,これらを連立方程式として解きましょう。解は次のようになります。
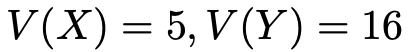
さて,XとYの分散がわかりましたが,求めるものは,Xの2乗の期待値とYの2乗の期待値ですね。これらを結びつける公式はすでに紹介済みです。パッと思い出せるでしょうか。次の式です。

先ほど求めたV(X),V(Y)と問題で与えられているE(X),E(Y)の値を代入すると,次のようになります。
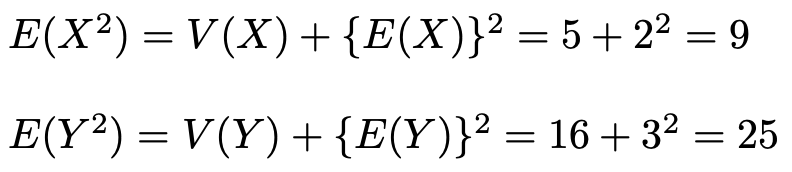
つまり,解答は次のようになります。
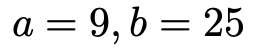
(解答終わり)
離散的な確率変数の期待値と分散についての説明は以上になります。ここからは,さらに理解を深めるための演習問題ですので,余力があればぜひチャレンジしてみてください。
演習1〜データの分散の計算の工夫〜
【問題】次の表は,受験生であるAさんとBさんの2人が受けた4回の模試の数学の得点をまとめたものである。2人の数学の得点の分散を求めなさい。
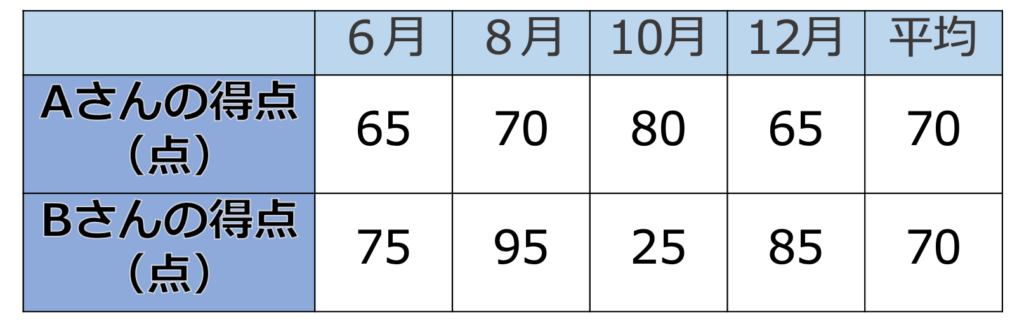
【解答】データの分散は次の式で求められます。
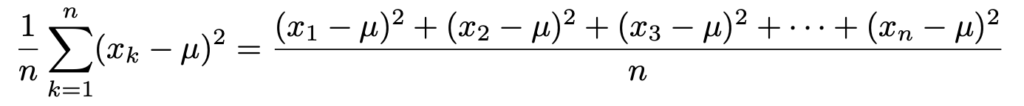
μはデータの平均です。分散の説明の中で例示した1個のサイコロの目の分散の式もこの形でしたね。ちなみに,データの平均は次の式で求められます。
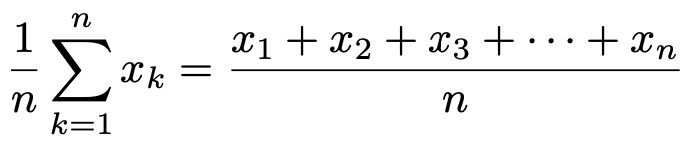
つまり,データの平均や分散は,等確率でそのデータの値をとる確率変数の期待値と分散に一致します。
上の分散の公式に代入すれば答えは求められますが,ここでは少し工夫して求めてみましょう。
得点をXとするとき,平均が70なので,Xー70という量は「70からのズレ」を表していると言えます。
また,Xー70を計算してみると,すべての数値が5の倍数なので,5でわったほうが簡単な数値になります。
そこで,次の式のようにXー70を5でわったものをYとします。
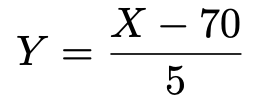
2人の得点をもとに,Yの値を求めると,次の表のようになります。
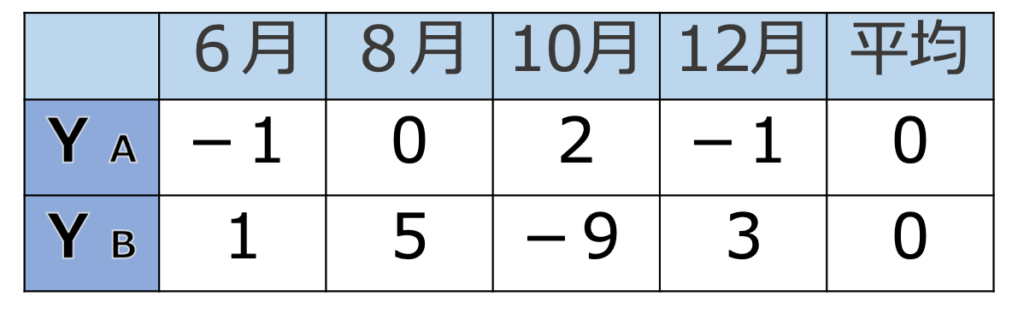
上段がAの得点から求めたYの値で,下段がBの得点から求めたYの値です。
では,これらの数値をもとにして,Yの分散を計算してみましょう。上段の数値の分散は,次のように求められます。
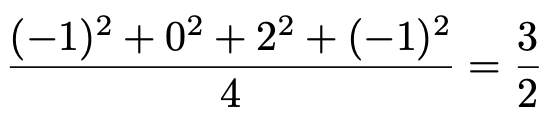
同じように,下段の数値の分散は,次のように求められます。
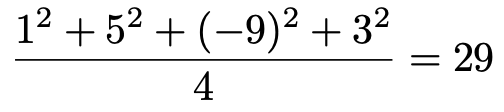
さて,これらは得点自体の分散ではないので,得点の分散に変換する必要があります。そのために,次の公式を使います。
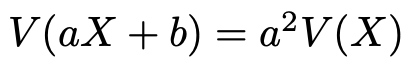
また,上述の「Y=…」の式をXについて解くと,次の式になります。
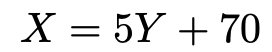
この2つの式から,
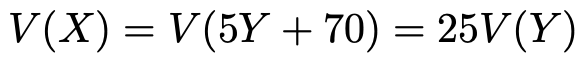
Yの分散は,Aが2分の3,Bが29だったので,それぞれこの式に代入すると,得点の分散は,A,Bの順に次のようになります。
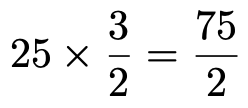
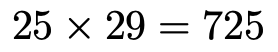
(解答終わり)
分散の公式に2人の得点を代入して,ふつうに計算してみてください。Aさんの得点の分散を求めるにはさほど苦労はないと思いますが,Bさんの得点の分散を求めるのは少し計算が大変ですよね。この例よりもさらにデータの数が多い場合などには,このような置き換えが効果を発揮しますので,覚えておきましょう。
ちなみに,この問題のAさんとBさんはどちらのほうが入試本番で良い得点が取れそうでしょうか。
平均は2人とも70点ですが,Aさんの得点は分散が小さいので,本番でも70点前後の点数が取れそうなのに対して,Bさんは得点の分散が大きいので,本番で70点が取れるかどうか,あまり信頼できないと思います。つまり,過去の結果から未来を予測する上で,平均だけでなく,値のばらつき具合を表す分散も重要だと言えます。
演習2〜確率変数の期待値と分散〜
【問題】袋の中に赤玉2個と白玉3個が入っている。この中から1個ずつ玉を取り出す試行を袋の中の赤玉がなくなるまで続けるとき,玉を取り出す試行の回数の期待値と分散を求めなさい。ただし,取り出した玉はもとに戻さないものとする。
【解答】玉を取り出す試行の回数をXとします。Xは2以上5以下の整数の値をとりますね。まずは,それぞれの場合の確率を求めて,確率分布を把握します。
X=2となるのは,2回続けて赤玉を取り出す場合ですね。1回目に赤玉を取り出す確率は,5個の中の2個だから5分の2です。1回目に赤玉を取り出した後,袋の中には赤玉1個と白玉3個が入っているから,2回目に赤玉を取り出す確率は,4個の中の1個だから4分の1です。第1回〜第2回で学習した確率の積の法則から,X=2となる確率は次のようになります。

X=3となるのは,赤玉を2回,白玉を1回取り出す場合ですね。ただし,3回目は赤玉ですから,白玉を取り出すのは1回目か2回目です。この2つの場合は互いに排反なので,次の式のように,それぞれの確率をたせばX=3となる確率が求められます。
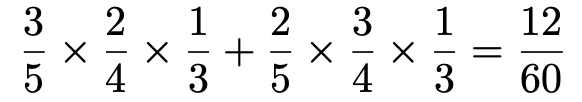
X=4となるのは,赤玉を2回,白玉を2回取り出す場合ですね。ただし,4回目は赤玉ですから,白玉を取り出すのは1回目から3回目の中のいずれか2回です。X=3となる場合と同じように,互いに排反な3つの場合があります。白玉を取り出すのが,(1回目,2回目),(1回目,3回目),(2回目,3回目)の3つの場合について,この順に確率をたし合わせると,次のようになります。
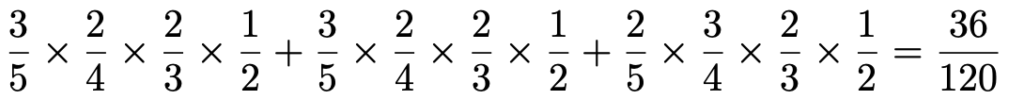
X=5となるのは,赤玉を2回,白玉を3回取り出す場合です。ただし,5回目は赤玉ですから,白玉を取り出すのは1回目から4回目の中のいずれか3回です。白玉を取り出すのが,(1回目,2回目,3回目),(1回目,2回目,4回目),(1回目,3回目,4回目),(2回目,3回目,4回目)の4つの場合について,この順に確率をたし合わせると,次のようになります。
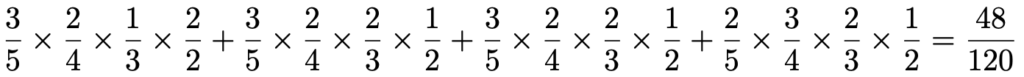
X=5の4つの場合の最後に,すべて「×1分の1」が省略されています。これらから,期待値は,

また,分散を定義通りに計算すると,次のようになります。
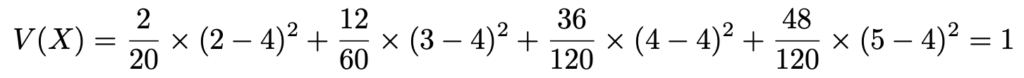
(解答終わり)
この問題の場合には,分散の求め方として紹介した2通りのうちのどちらでも計算量はほとんど変わりませんが,どちらかと言えば定義通りのほうが計算が楽でしょうか。どちらを使うかはケースバイケースです。
演習3〜確率変数の係数の決定〜
【問題】1枚のコインを3回投げて,表の出た回数をXとする。Y=aX+bによって定まる確率変数Yについて,次の式が成り立つとする。
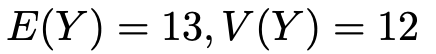
このとき,a,bの値を求めなさい。ただし,a>0とする。
【解答】E(Y),V(Y)の式のYに,Y=aX+bを代入して,期待値や分散の公式を使う方針が立ちますね。その先の計算をするのに,E(X),V(X)の値が必要になりますので,まずはこれらを求めておきましょう。
コインを3回投げたときの表の出た回数Xは,0〜3の整数の値をとります。
X=0となるのは,3回続けて裏が出る場合です。1回目の結果と2回目の結果と3回目の結果は独立だから,確率の積の法則から,次のようになります。
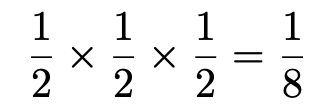
X=3となるのは,3回続けて表が出る場合だから,X=0のときと全く同じ確率になりますね。
X=1となるのは,表が1回出て,裏が2回出る場合です。(1回目,2回目,3回目)=(表,裏,裏)となる確率は,やはり2分の1を3回かければ良いので,8分の1です。(裏,表,裏)や(裏,裏,表)となる確率も同じように8分の1ですから,X=1となる確率は8分の3になります。
X=2となるのは,表が2回出て,裏が1回出る場合です。X=1の場合と比べて,表と裏が入れ替わっただけなので,確率は同じで,8分の3ですね。
これで,Xの確率分布が把握できましたので,期待値を計算します。次のようになります。

次に,Xの分散を計算するために,Xの2乗の期待値を計算しましょう。次のようになります。

これらから,Xの分散は次のように求められます。
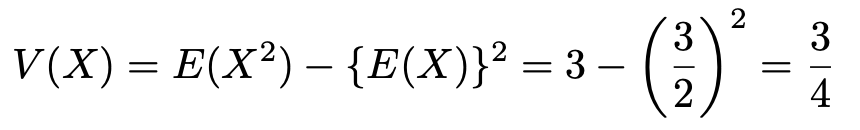
はじめに立てた方針にしたがって,E(Y)を計算すると,次のようになります。

同じように,V(Y)を計算すると,次のようになります。
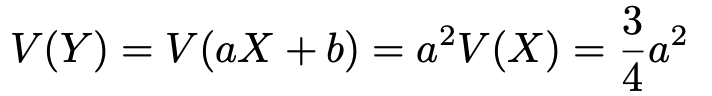
問題の条件から,E(Y)=13,V(Y)=12なので,次の2つの式ができます。
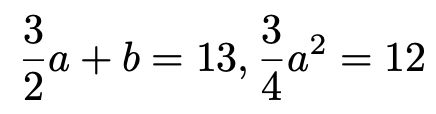
この2つ目の式から,aの2乗が16となります。aは正の数という条件がありますので,a=4
このaの値を1つ目の式に代入して,b=7
まとめると,解答は次のようになります。
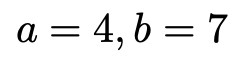
(解答終わり)
演習4〜連立方程式で求める期待値と分散〜
【問題】独立な2つの確率変数X,Yをもとにして,新しい確率変数S,Tを次の式で定める。
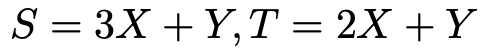
S,Tの期待値と分散は次の通りである。
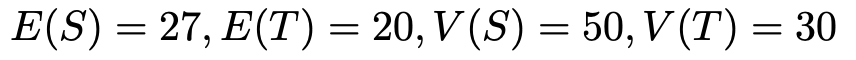
このとき,次の式のa,b,c,dの値をそれぞれ求めなさい。

【解答】「S=…」,「T=…」という式を期待値と分散についての条件式に代入してみると,次のようになります。
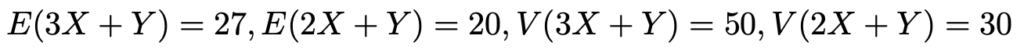
この左辺を見たら,期待値と分散の公式が使いたくなりますよね。まず,期待値については次の公式を使います。
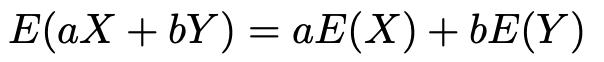
これを使うと,条件式のうち,期待値に関する2つは次のように書き直すことができます。

E(X)とE(Y)の連立方程式として解くと,次のように求められます。
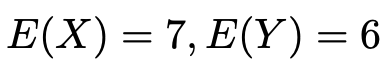
次に分散です。XとYが独立であるという条件があるので,次の公式が使えます。
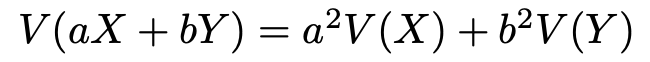
これを使って,問題で与えられた条件式のうち,分散に関する2つは次のように書き直すことができます。
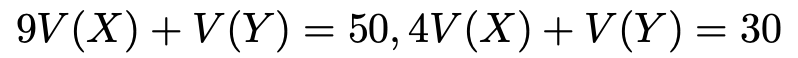
V(X)とV(Y)の連立方程式として解くと,次のように求められます。
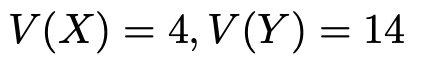
つまり,解答をまとめると次のようになります。
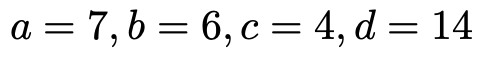
(解答終わり)
第4回は以上となります。最後までお付き合いいただき,ありがとうございました!
引き続き,第5回以降の記事へ進んでいきましょう!
2023年1月に「統計検定2級公式問題集[CBT対応版](実務教育出版)」が発売されました!(CBTが何かわからない人はこちら)
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが,本書は分野ごとにその形式の問題を並べた構成になっていて,最後に模擬テストがついています。CBT対策の新たな心強い味方ですね!
さらに実戦に向けた演習を積みたい人は,「統計検定2級公式問題集2018〜2021年(実務教育出版)」を手に取ってみてください!
また,もっと別の問題を解いてみたい人は,さらにさかのぼって「統計検定2級公式問題集2016〜2017年(実務教育出版)」を解いて実力に磨きをかけましょう!


![統計検定2級公式問題集[CBT対応版]](https://m.media-amazon.com/images/I/51q3GfZId3L._SL500_.jpg)




コメント
初めまして、演習1について質問なのですが [Y=(X – 70)/5]の5は何の数字でしょうか?良くわからず、、教えていただければ幸いです。
ご質問ありがとうございます。
ご指摘のように,解説にわかりにくい部分がございましたので,
修正を加えました。
改めて,ご確認ください。
なお,5は恣意的に決めた数で,
5でわったほうが計算が簡単になりそうだな
という程度のものです。