シグマ・共分散・相関係数【中学の数学からはじめる統計検定２級講座第５回】

「共分散や相関係数を理解したいのに，Σ（シグマ）がわからないせいで先に進めない！」なんて人はいませんか。この記事では，シグマをゼロから解説していきますので，「高校のとき，シグマがよくわからなかった」という人でも，離散型の確率変数の共分散や相関係数まで無理なくたどり着くことができます。

また，「大学の授業で出てきたΣΣ（シグマが２つ続く）がさっぱりわからない」という人にもこの記事を読んでほしいです。統計検定２級でも，問題文に「ΣΣ」が登場したことがありますので，２級を受検するならこのシグマの使い方も理解しておきたいところです。

なお，この記事では，第１回，第３回，第４回の内容の理解を前提として解説しますので，これらに自信のない人は先にそちらをご覧ください。

では，はじめていきましょう！

シグマ・共分散・相関係数【中学の数学からはじめる統計検定２級講座第５回】

シグマΣ

シグマとは，和を表すための記号です。まずは，次の和を見てください。

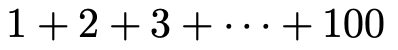
これを見て，多くの人は「１から１００までの自然数の和」を意味しているだろうと予想しますよね。でも，それはあくまで「予想」です。なぜなら，「…」の部分を，「きっと，この規則で続くのだろう」と頭の中で補っているからです。

シグマを使うメリットの１つは，この曖昧さをなくすことができる点にあります。先ほどの式をシグマを使って表すと次のようになります。

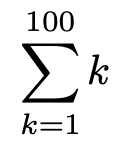
Σはギリシャ文字の大文字で，アルファベットのsに対応しています。なぜsに対応する記号を使うかと言えば，英語で和を”sum”と言うからです。ちなみに，統計学ではσ（小文字のシグマ）をよく使いますが，今回の主役の大文字のシグマとは使われ方が全く異なります。

シグマ記号の右には，代入される式が置かれます。今の場合はkです。シグマ記号の下にあるk＝１は「kという文字を１から始めますよ」という意味です。シグマ記号の上にある100は「kという文字は100まで続けますよ」という意味です。そして，シグマ記号自体は和を表すので，全体としては「シグマ記号の右にあるkという文字に，１から始まる自然数を１ずつ大きくしながら100まであてはめていって和をとる」という意味になります。つまり，１から100までの自然数の和を表すことになります。

基本となるシグマのルールをもう一度くり返すと，シグマの右に代入される式，下に代入する最初の数，上に代入する最後の数を書くわけです。

別の例を見てみましょう。

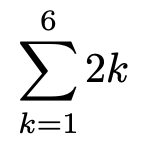
代入される式が２kです。kに１から６までの自然数を代入して和をとりますので，２＋４＋６＋８＋10＋12という和になりますね。このくらいならば，まだシグマを使わずに和を書くのも簡単ですが，項の数が多くなると和を書き下すのが大変になるので，シグマという記号のありがたみを感じられるようになります。

おまけにもう１つ別の例を見てみましょう。

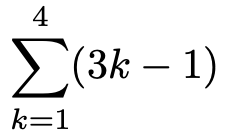
代入される式が３kー１です。kに１から４までの自然数を代入して和をとりますので，２＋５＋８＋11という和になりますね。感覚はつかめたでしょうか。

ここで，シグマ記号を使うメリットをまとめておくと，次のようになります。

• 曖昧さがなくなる
• 書く手間を減らせる
• 思考を節約できる

３つ目は伝わりにくいかもしれませんが，第４回の記事で紹介した期待値や分散の公式の証明を，シグマを使わずにやってみてください。シンプルに表現できることで，理解できる幅が広がることがきっとわかると思います。

次に，シグマを２つ並べたものについて説明していきます。次の式を見てください。

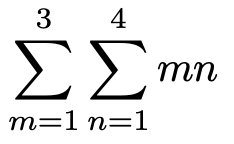
はじめて見る人は，この式が何を表しているか，わからないと思いますので，順を追って考えてみましょう。まず，この式には，mについての和とnについての和という２つのシグマがありますよね。これらをいっぺんに相手にするのをやめて，nについての和としてのみ，考えてみることにします。それはちょうど，次の式のかっこの中を考えることに相当します。

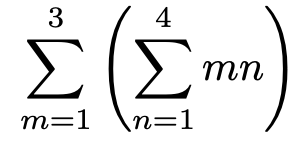
かっこの中の式をシグマを使わずに書いてみます。nに１，２，３，４を代入してできる４つの項の和は次のようになりますね。

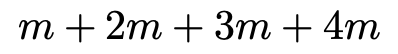
この時点で，シグマの数は１つ減り，次のような和になりました。

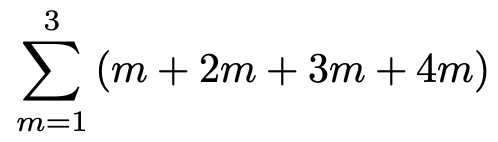
この式をシグマを使わない形で表すとしたらどうなるか考えてみましょう。まず，mに１を代入すると，次のようになります。

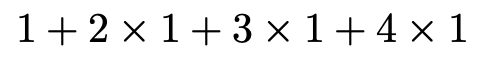
今度は，mに２を代入すると，次のようになります。

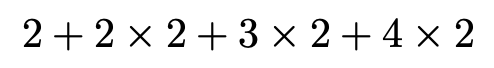
最後に，mに３を代入すると，次のようになります。

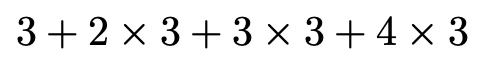
ここまで，和の式を３つ書きましたが，この３つの式をすべて加えて，１つの式に直したものが，はじめに考えようとしていたシグマが２つある式の正体です。

では，上の３つの式を縦に加えてみましょう。３つの式には，２がかかっている項，３がかかっている項，４がかかっている項，何もかかっていない（１がかかっている）項がそれぞれありますので，この種類ごとに縦に加えてまとめると，次のようになります。

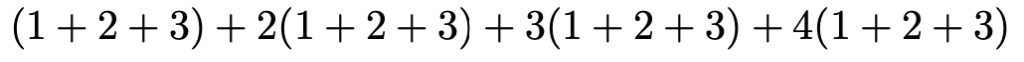
この式の４つの項では（１＋２＋３）が共通因数になっているので，これをくくり出すと，次のようになります。

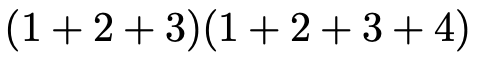
かなりスッキリしましたね。この式をシグマを使って書き直すと，次のようになります。

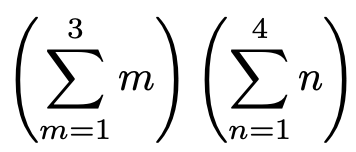
さて，何が起きたのかを振り返りましょう。最初の式と最後の式を等号で結ぶと，次のようになります。

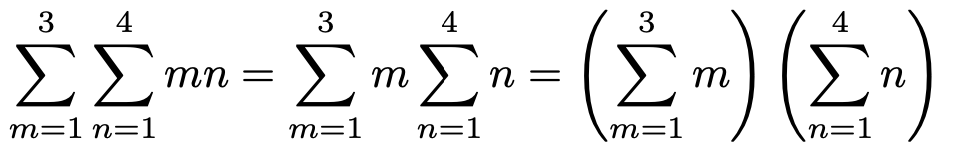
この式を見てわかるように，「nについてのシグマ」と「m」の前後を入れ替える変形をしたのです。慣れるまでは，この並べ替えができることがしっくりこないでしょうから，ここまでの説明のようにシグマを使わない式で丁寧に書き出してその都度，意味を考えてみましょう。

さて，次のセクションでは，いま説明したような「ΣΣの扱い方」を踏まえて，確率変数X，Yが独立のときに成り立つ次の式を証明していきます。

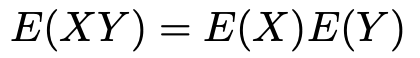
離散型の確率変数の共分散

確率変数X，Yの期待値をそれぞれ次のように表します。

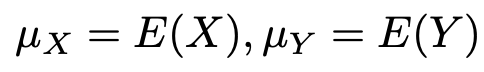
このとき，X，Yの共分散とは，次の式で表されるものです。

念のため補足しておくと，この式の右辺によって左辺を定義するということです。右辺は，第４回の記事の中で，分散の公式を導く途中に登場しました。一目見て，「期待値の一種だな」とわかりますね。Xの値の平均からのズレとYの値の平均からのズレの積の期待値です。これに，左辺の新しい記号を割り当てるわけです。この記号は，共分散を英語で”covariance“と呼ぶことに由来します。さて，上の式の右辺で，X＝Yとすると，

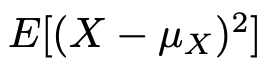
となり，Xの分散V(X)そのものになります。つまり，共分散という名前は，XとYの両方にまたがる分散というニュアンスです。ちなみに，確率変数の共分散以外にも，データの共分散というものがあります。これは散布図とともに理解していくべきものですが，確率変数の本論から脱線してしまうので，これについては別の記事で改めて説明します。

次に，共分散の公式を紹介します。

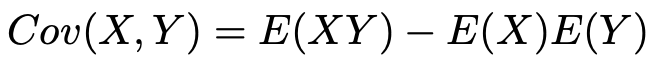
この式を証明します。

この式も証明はできなくても良いですが，結果は覚えましょう。

次に，確率変数X，Yが独立であるとき，共分散は０であることを示しましょう。次の式を示せば良いですね。

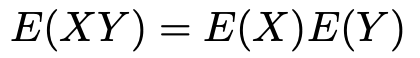
証明には，確率変数X，Yが独立であるという条件を使わなければなりません。第３回で紹介したように，確率変数X，Yが独立であるとは，X，Yのすべての実現値a，bに対して次の式が成り立つことでした。

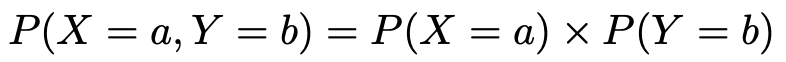
では，これを使って証明してみましょう。

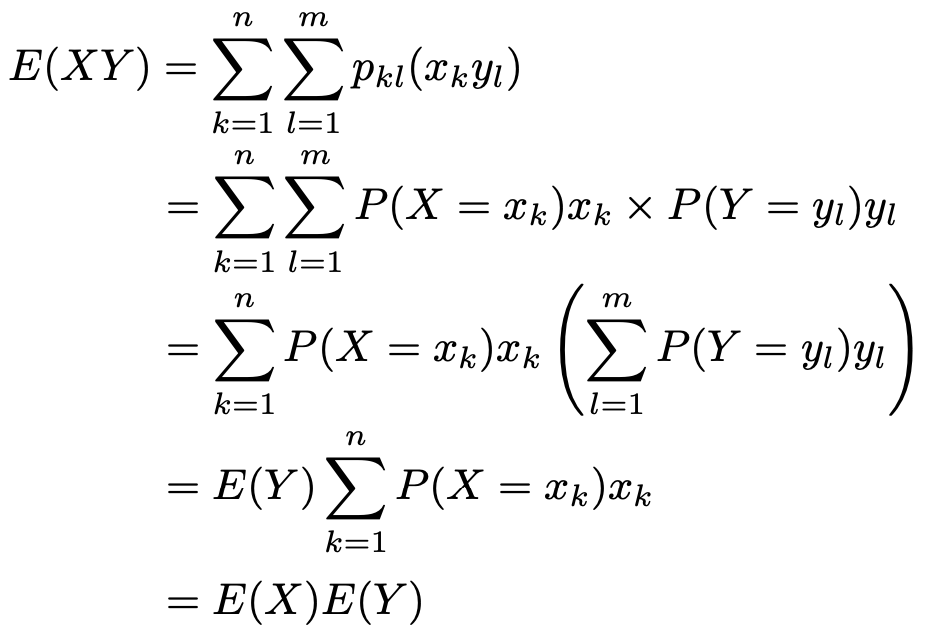
これで証明終わりです。「独立ならば共分散が０である」ことが証明できましたが，その逆の「共分散が０ならば独立である」は一般的には成り立ちません。確率変数が独立であるという条件は，共分散が０であるという条件よりも強いということです。

また，共分散については次の公式も大切です。

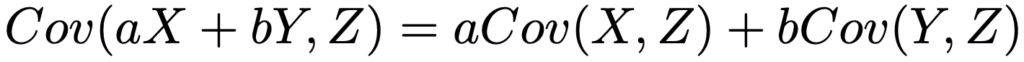
これも証明しておきましょう。３つの確率変数の期待値を次のようにおくことにします。

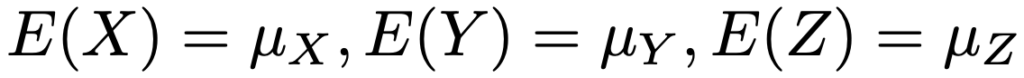
このとき，aX＋bYの期待値は次のように計算できます。

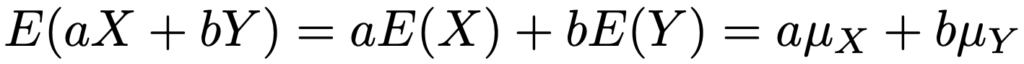
このことを使って，aX＋bYとZの共分散は，定義から次のように計算できます。

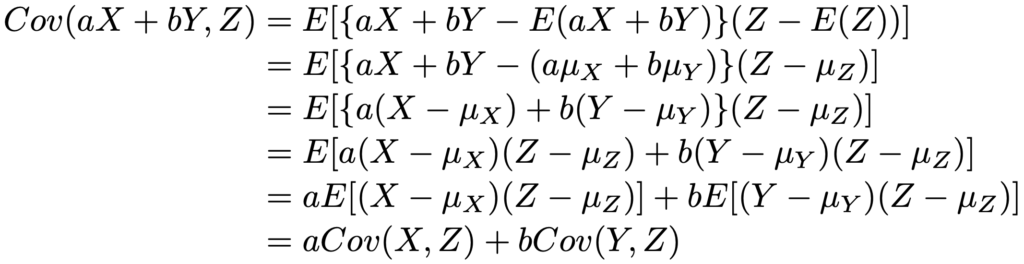
また，上の共分散の公式の証明と同じようにして，さらに一般的な次の式も証明できます。

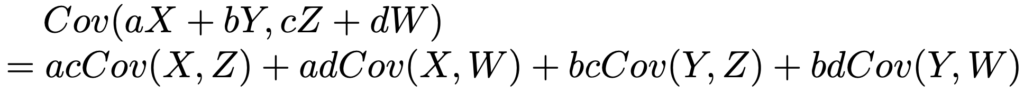
ここでは証明は省略しますが，余力のある人は，自分で証明してみてください。

共分散の計算例

共分散の式がわかっただけでは，実感がイマイチわかないと思います。そこで，次の問題を通して，共分散の計算をやってみましょう。

【問題】袋の中に200が書かれた玉が６個，50が書かれた玉が９個，20が書かれた玉が10個の合計25個の玉が入っている。この中から続けて２個の玉を取り出し，玉に書かれた数の最大値をX，最小値をYとする。このとき，X とYの共分散を求めなさい。

【解答】XもYも20，50，200の３つの値をとり，X≧Yなので，次のように６通りの場合があります。

①X＝200，Y＝200の場合，１回目に200が書かれた玉を取り出す確率は25分の６，１回目に200が書かれた玉を取り出した上で，２回目も200が書かれた玉を取り出す確率は24分の５だから，

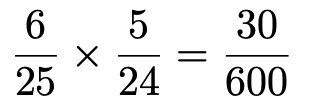
②X＝200，Y＝50の場合，１回目に200が書かれた玉を取り出す確率は25分の６，１回目に200が書かれた玉を取り出した上で，２回目に50が書かれた玉を取り出す確率は24分の９です。１回目に取り出す玉と２回目に取り出す玉が逆の場合もあるから，

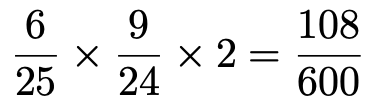
③X＝200，Y＝20の場合，１回目に200が書かれた玉を取り出す確率は25分の６，１回目に200が書かれた玉を取り出した上で，２回目に20が書かれた玉を取り出す確率は24分の10です。１回目に取り出す玉と２回目に取り出す玉が逆の場合もあるから，

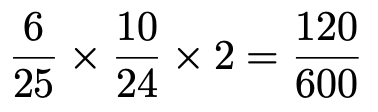
④X＝50，Y＝50の場合，１回目に50が書かれた玉を取り出す確率は25分の９，１回目に50が書かれた玉を取り出した上で，２回目も50が書かれた玉を取り出す確率は24分の８だから，

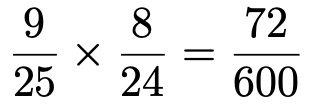
⑤X＝50，Y＝20の場合，１回目に50が書かれた玉を取り出す確率は25分の９，１回目に50が書かれた玉を取り出した上で，２回目に20が書かれた玉を取り出す確率は24分の10です。１回目に取り出す玉と２回目に取り出す玉が逆の場合もあるから，

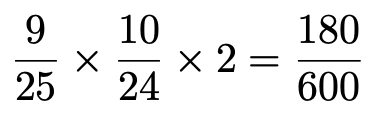
⑥X＝20，Y＝20の場合，１回目に20が書かれた玉を取り出す確率は25分の10，１回目に20が書かれた玉を取り出した上で，２回目も20が書かれた玉を取り出す確率は24分の9だから，

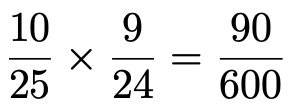
これらをもとに，XとYの期待値をそれぞれ計算すると，次のようになります。

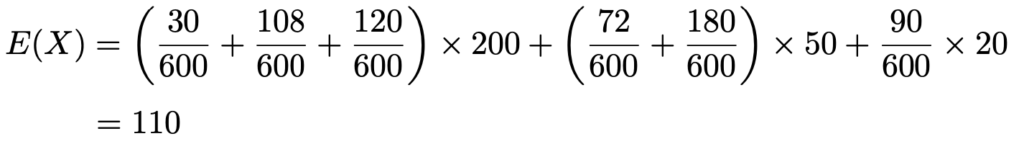
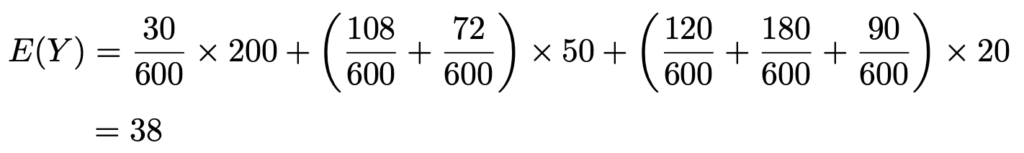
共分散を求めるために，E(XY)を計算すると，

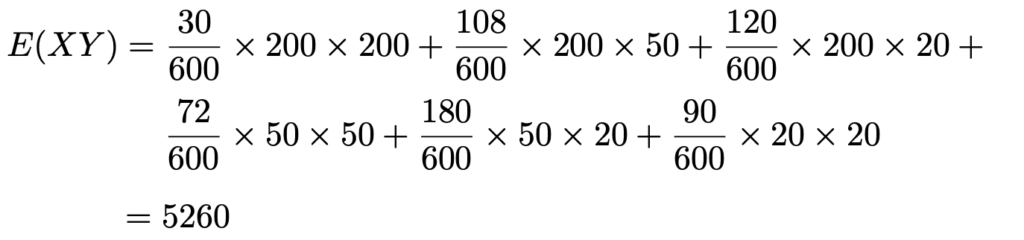
したがって，共分散は次のように求められます。

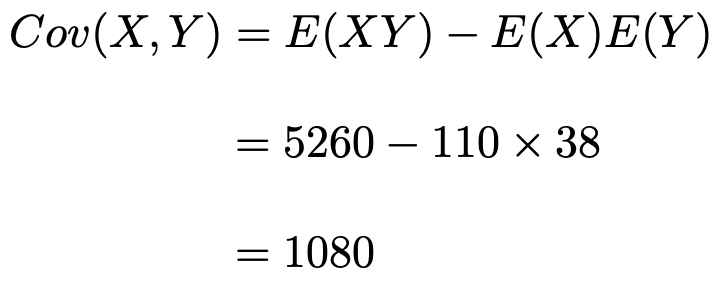
（解答終わり）

分散もそうでしたが，共分散の値も，200，50，20というX，Yのとりうる値の大きさに影響されているのがわかると思います。共分散はXとYの関係性の強さを測る１つの指標ですが，共分散を求めたところで，「1080という値は大きいの？　それとも小さいの？」という疑問が発生してしまうのです。その点を補うには，相関係数に登場してもらう必要があります。

共分散から相関係数へ

さて，第４回で証明した分散の公式を改めて確認しておきましょう。次の式でした。

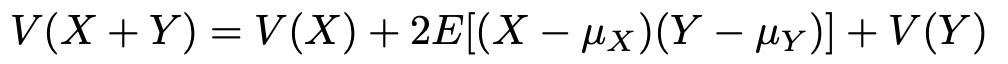
右辺の第２項はX，Yの共分散ですから，次のように書き直すことができます。

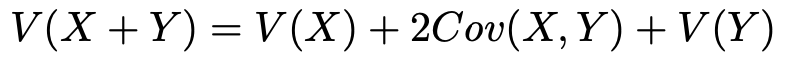
XとYが独立であるとき，共分散は０なので，第４回で学習した次の式が成立するわけですね。

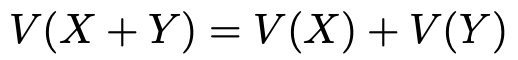
さて，XとYが独立とは限らないときの分散の公式で，tを実数として，XをtXとおきかえてみると，次の式になります。

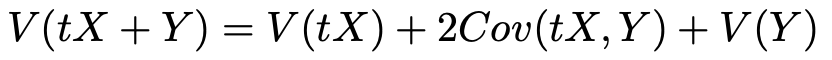
まず，右辺第１項は，分散の別の公式によって，次のように書き直すことができます。

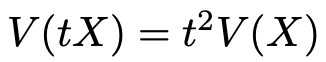
次に，右辺第２項について，

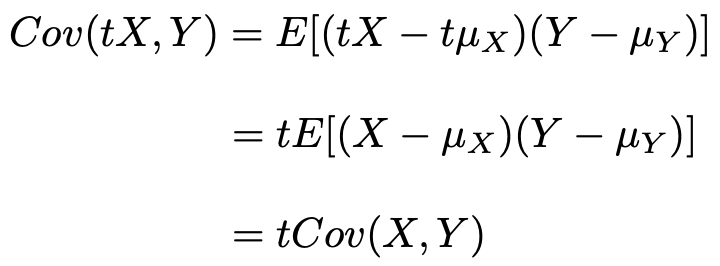
これらを使って，もとの分散の式を書き直すと次のようになります。

さて，証明したいことがらまであと少しです。上の式の右辺はtの２次式です。ここで，２次関数の平方完成を復習しておきましょう。次のような変形ができるのでした。

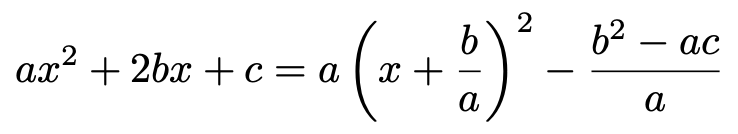
この変形が正しいことは，右辺を展開して整理すれば左辺に一致することからわかります。この変形と同じことを，上の分散についてのtの２次式に適用すると，次のようになります。

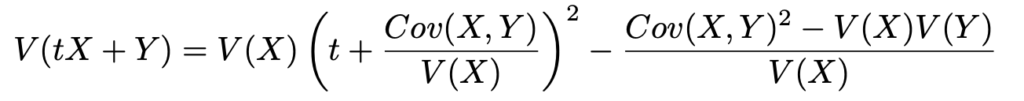
分散は０以上なので，tがどんな値であろうとも左辺は０以上です。ということは，tの値に関係なく右辺も０以上でなければなりません。右辺の第１項は０以上の値をとりますが，tの値によっては０になりうるので，右辺の第２項は０以上でないといけません。よって，次の不等式が成り立ちます。

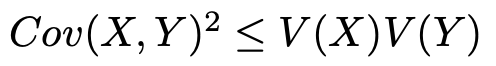
右辺の分散の積は０以上です。分散が０である場合を除いて考えると，右辺の式で両辺をわって次の式が得られます。

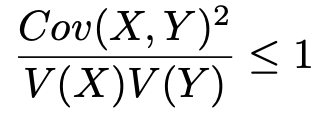
つまり，次の式が成り立ちます。

この真ん中の式がX，Yの相関係数です。

離散型の確率変数の相関係数

確率変数X，Yの相関係数とは，次の式で表されるものです。

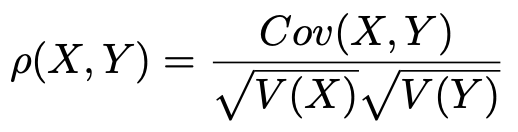
先ほど証明したように，相関係数はー１以上１以下の値をとります。この値が１やー１のときにはXとYの間にY＝aX＋bという直線的な関係が成り立ちます。また，この値が０のときは無相関であるといいます。相関係数を表すのにρ（ロー）という記号を用いることが多いです。これは，相関係数が英語で”correlation coefficient“であり，”relation”のrに対応するギリシア文字がρだからです。なお，統計検定の本試験ではr(X,Y)と表記されています。

相関係数に慣れるためにも，計算してみるのが近道です。共分散の計算で例として挙げた問題を使って，相関係数も計算してみましょう。

【問題】袋の中に200が書かれた玉が６個，50が書かれた玉が９個，20が書かれた玉が10個の合計25個の玉が入っている。この中から続けて２個の玉を取り出し，玉に書かれた数の最大値をX，最小値をYとする。このとき，X とYの相関係数を求めなさい。

【解答】共分散はすでに計算してあるので，分散を求めましょう。Xの２乗の期待値とYの２乗の期待値をそれぞれ計算すると，次のようになります。

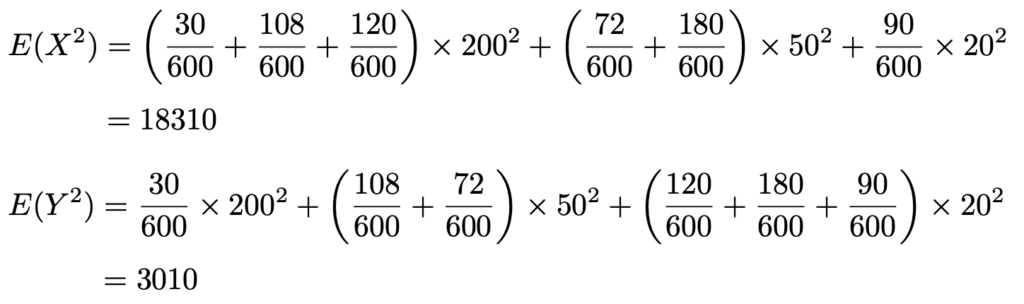
この結果とすでに計算済みの期待値から，XとYの分散はそれぞれ次のようになります。

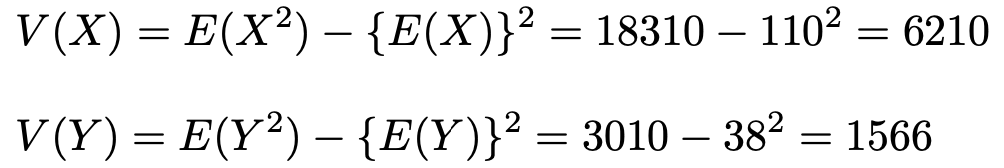
この値と，すでに計算済みの共分散の値から，相関係数を計算すると次のようになります。

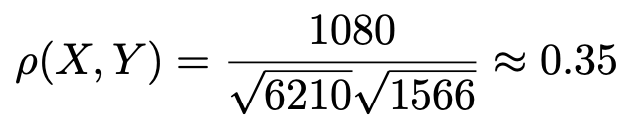
（解答終わり）

一次変換と共分散・相関係数

次の式で，a，b，c，dは整数や分数などの数だと思ってください。このとき，この式は，（X，Y）と（S，T）の対応関係を与えています。

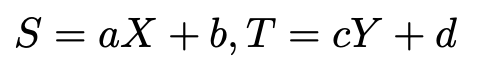
このような対応関係を一次変換といいます。X，Yの共分散とS，Tの共分散の関係を求めてみましょう。まず，表記の簡略化のため，次のように文字をおきます。

S，Tの共分散の定義式から計算していくと，次のようになります。

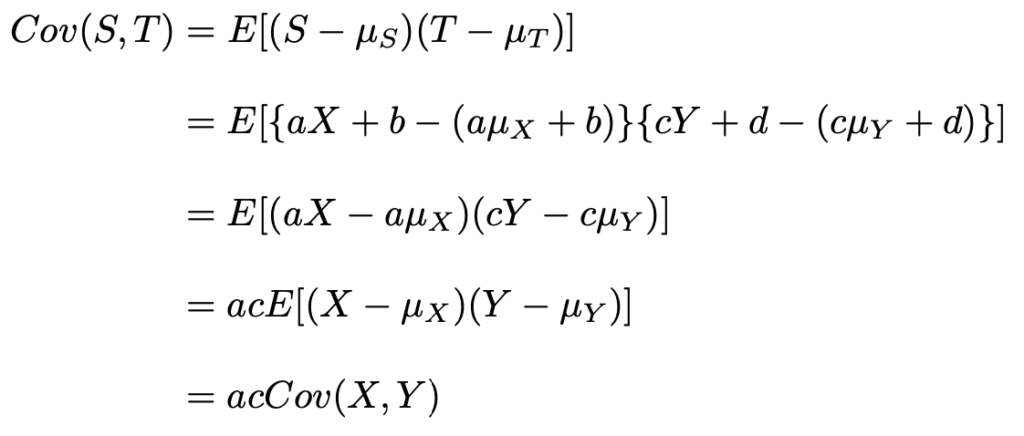
これが，一次変換に伴う共分散の変換公式です。次に相関係数を計算していきます。第４回で学習した分散についての次の公式を思い出しておきましょう。

先ほどの設定を引き継いで，S，Tの相関係数とX，Yの相関係数の関係を求めます。共分散はすでに計算した結果があるので，代入すると次のようになります。

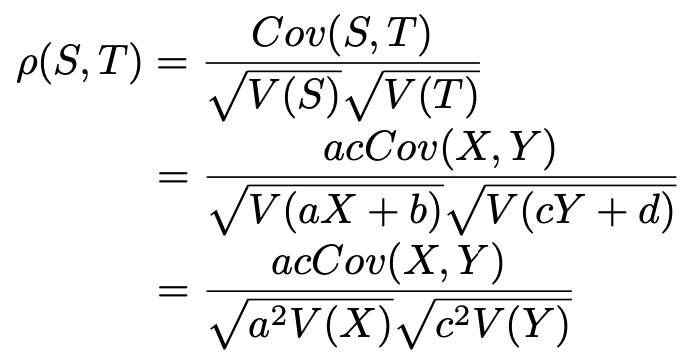
まだ計算の途中です。分母のaとcをルートの外に出したいのですが，aとcの符号によって結果が変わります。aとcが同符号のとき，この続きは次のようになります。

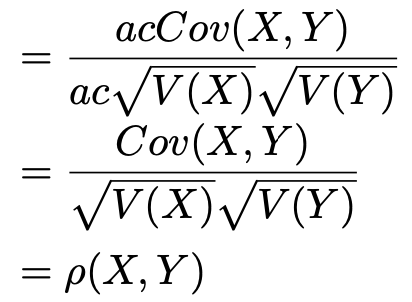
また，aとcが異符号のとき，先ほどの続きは次のようになります。

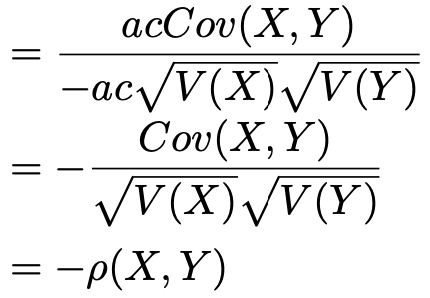
結局のところ，この変換で相関係数の絶対値は変わりません。相関係数の符号は，XとYの係数の符号によって決まります。

では，これらを用いて，問題を解いてみましょう。

【問題】２つの確率変数X，Yの期待値や分散について，次の式が成り立っている。

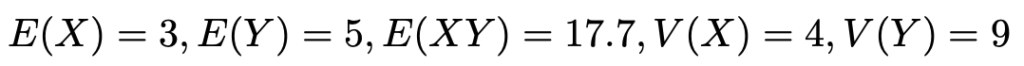
XとYに，それぞれ次のような一次変換を施して，新しい確率変数SとTをつくる。

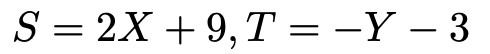
このとき，S，Tの共分散と相関係数を求めなさい。

【解答】まず，X，Yの共分散は次のようになります。

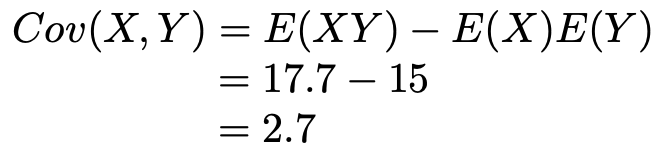
次に，X，Yの相関係数は次のようになります。

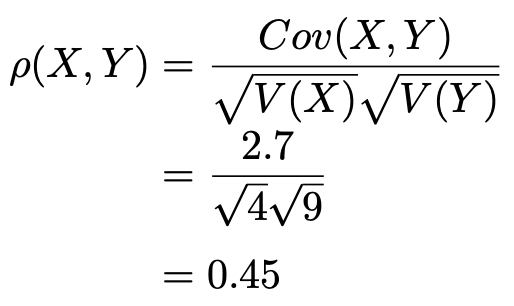
さらに，一次変換による共分散の変換公式によって，S，Tの共分散と，X，Yの共分散の関係は次のようになります。

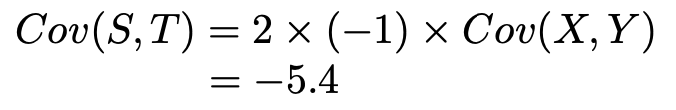
最後に，S，Tの相関係数は，X，Yの相関係数と絶対値が同じで符号が異なる（X，Yの係数の２と−１の符号が異なることに由来する）ので，

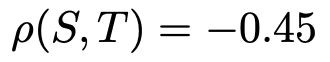
（解答終わり）

離散的な確率変数の共分散と相関係数についての説明は以上になります。ここからは，さらに理解を深めるための演習問題ですので，余力があればぜひチャレンジしてみてください。

演習１〜シグマの計算〜

【問題】次の問いに答えなさい。なお，必要ならば，次の式を用いなさい。

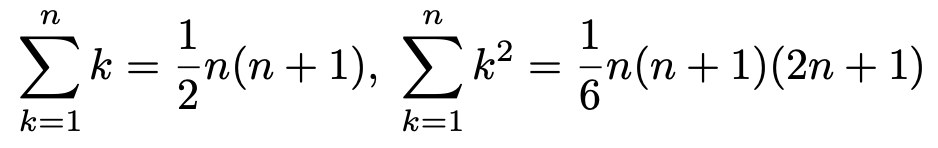
（１）次の和を求めなさい。

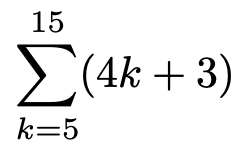
（２）次の和を，nを用いた式で表しなさい。

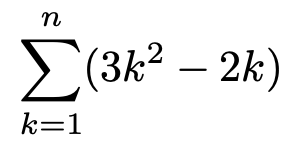
（３）次の和を，nを用いた式で表しなさい。

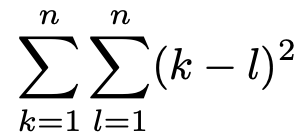
【解答】

（１）この式が表している和をはっきりさせましょう。シグマを使わずに書くと，次の式の右辺のようになります。

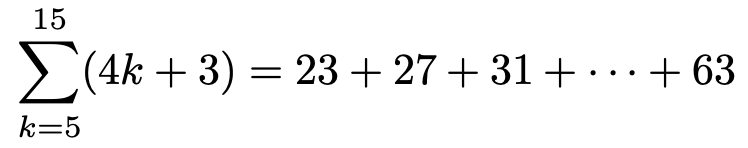
４k＋３に，k＝５を代入すると23，k＝６を代入すると27，k＝７を代入すると31，…，k＝15を代入すると63となるので，これらの和です。この和の項の数は，15ー５＋１＝11です。このように代入してみれば，４ずつ増える数の和であることがわかると思います。このように，23から始まり，４ずつ増える数列を初項23，公差４の等差数列といいます。等差数列の和の求め方は高校で学習します。次のように，１段目に23から63までを左から右へ並べ，２段目には，逆に23から63までを右から左へ並べて，上下の数をそれぞれ加えると，すべて86になります。

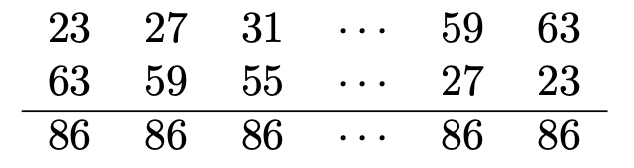
この和の項の数は11でしたから，86が11個できているわけです。つまり，23から63までの和の２倍は，86×11に等しいので，求める和は，

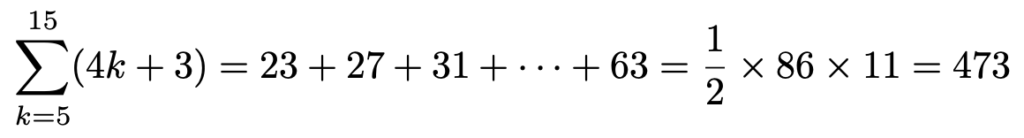
（２）（１）とは異なり，シグマを使わずに和を書き表してみても，うまく求められそうにありません。このタイプでは，次のようなシグマの計算方法を使いこなす必要があります。

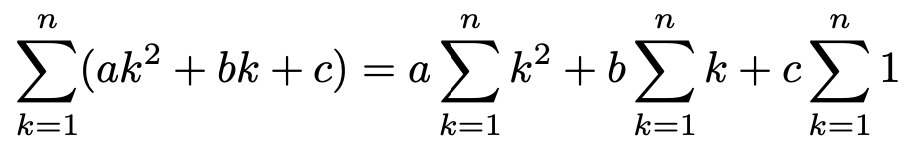
「係数をシグマの外に出す」操作は，シグマを使わない式で言えば，共通因数をくくり出すことに相当します。この形をつくると，問題で与えられたシグマの公式（高校数学ではこの式の暗記は必須）を代入できるようになります。よって，次のように計算できます。

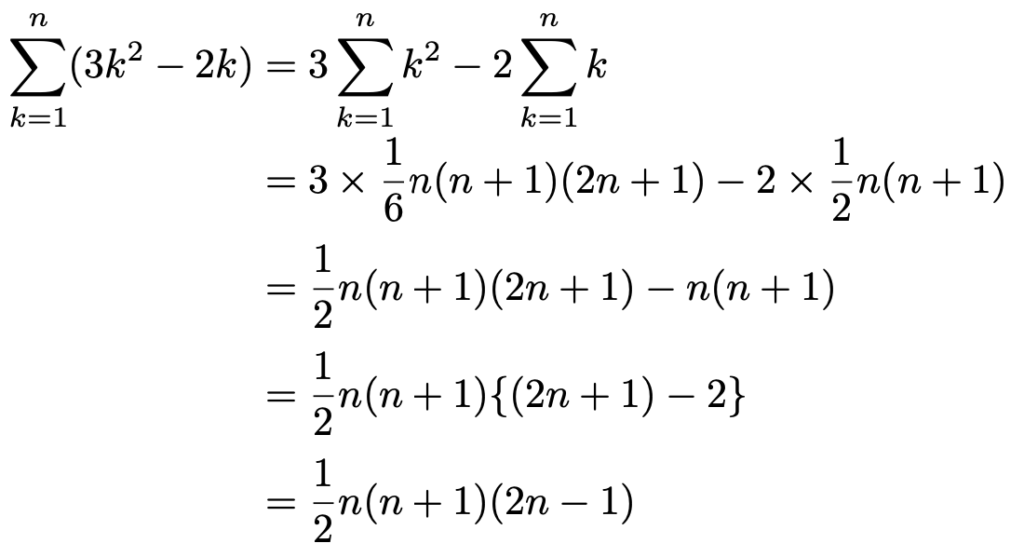
このように，因数分解した式を答えたほうが計算が楽ですが，展開した式を答えても正解です。

（３）シグマ２つの計算です。シグマや文字を計算しやすいように入れ替えましょう。

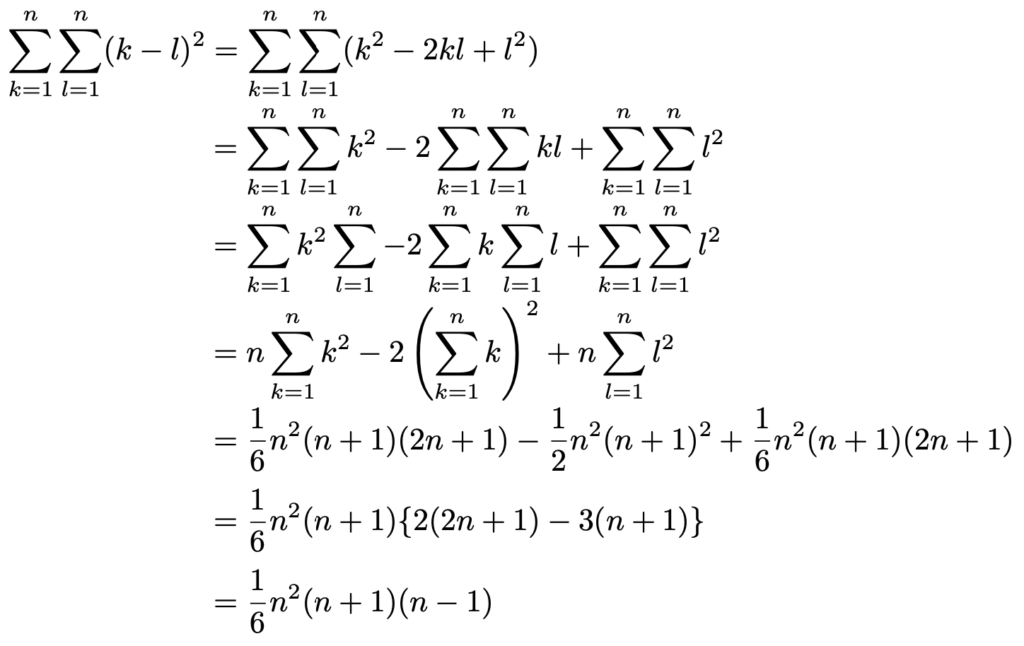
ちなみに，上から３行目から４行目にかけての変形では，次の性質を使っています。

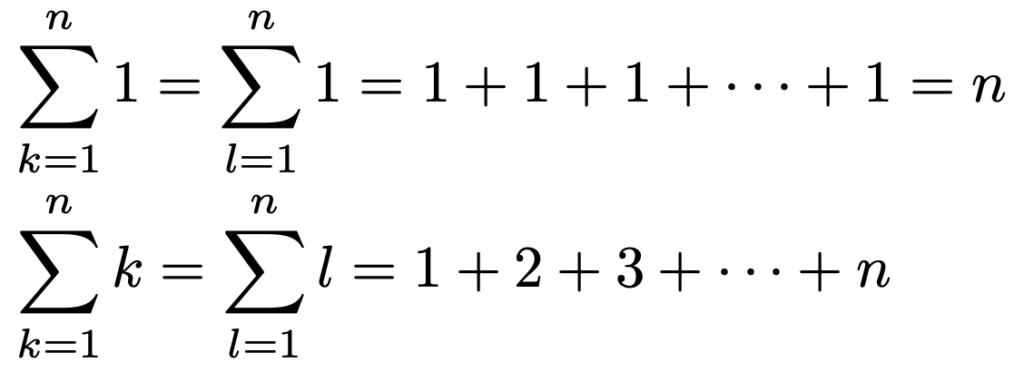
（解答終わり）

演習２〜共分散と相関係数の計算〜

【問題】XとYの同時確率分布が次の表で与えられているとき，あとの問いに答えなさい。

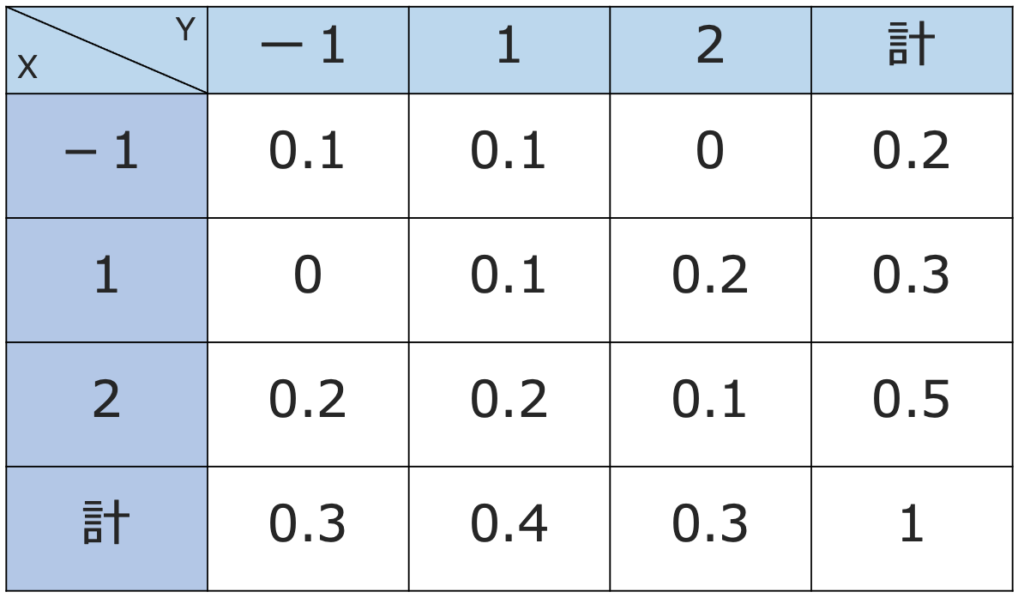
（１）X，Yの共分散を求めなさい。
（２）X，Yの相関係数を求めなさい。

【解答】

（１）まず，Xの期待値から求めていきましょう。Xの周辺分布は次のようになっていますよね。

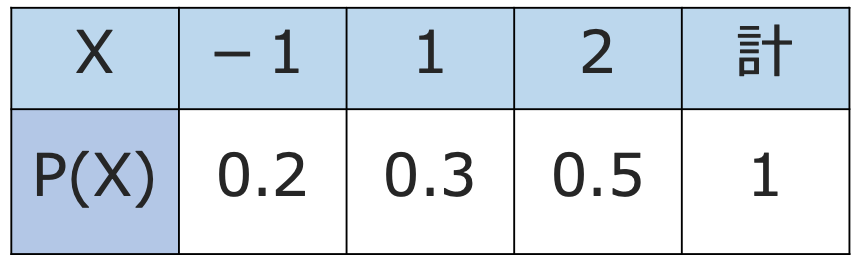
よって，Xの期待値は次のように計算できます。

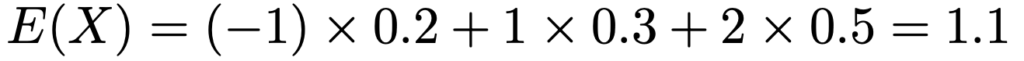
次に，Yの期待値を求めます。Yの周辺分布は次のようになっていますよね。

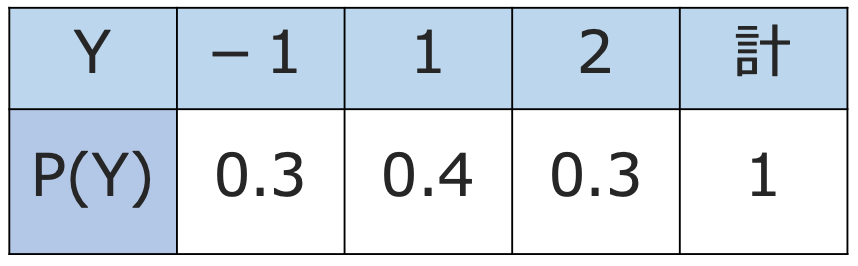
よって，Yの期待値は次のように計算できます。

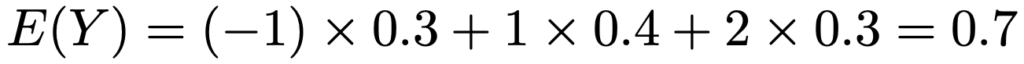
次に，E(XY)は次のように計算できます。確率が０の項は省略しています。

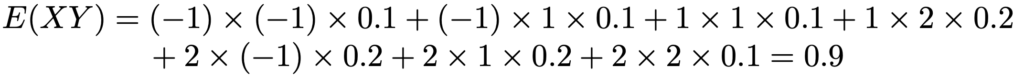
したがって，X，Yの共分散は次のようになります。

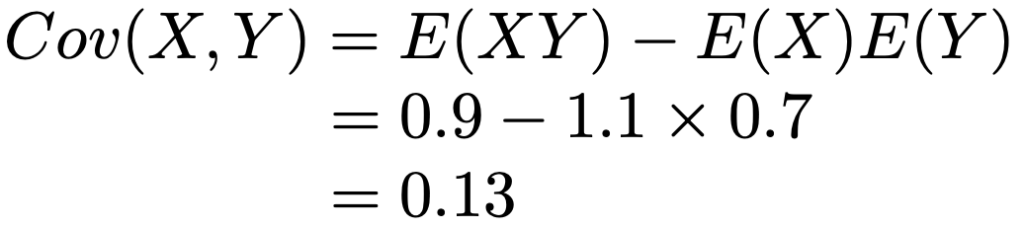
（２）相関係数は，（１）で求めた共分散をXの標準偏差とYの標準偏差でわって求められるので，まずはXの分散を求めるため，X²の期待値を計算します。X²の確率分布は次のようになっていますよね。

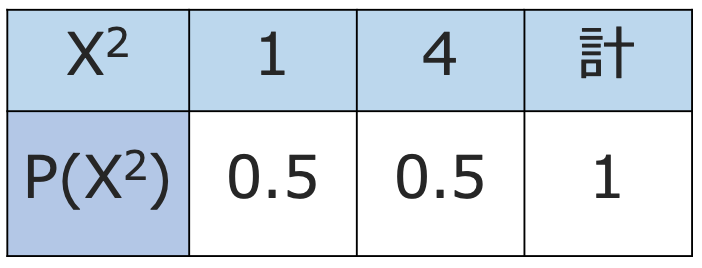
よって，X²の期待値は次のように計算できます。

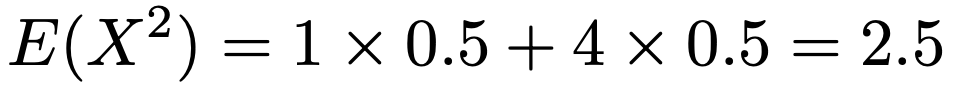
したがって，Xの分散は次のように計算できます。

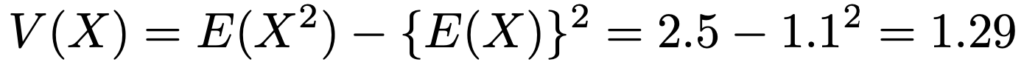
次に，Yの分散を求めるため，Y²の確率分布を確認しましょう。

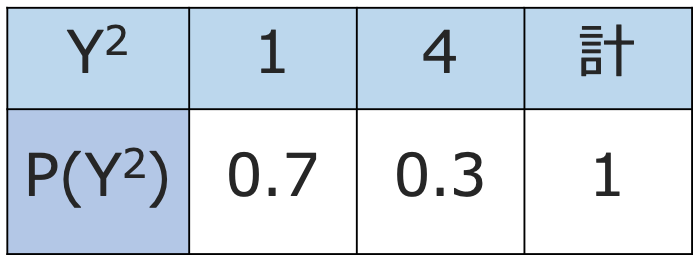
よって，Y²の期待値は次のように計算できます。

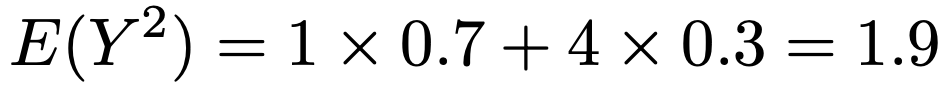
したがって，Yの分散は次のように計算できます。

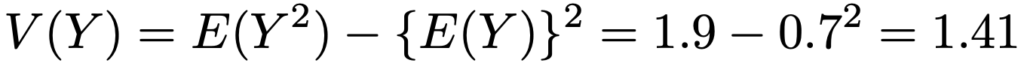
最後に，これらの結果を使って相関係数を計算すると，次のようになります。

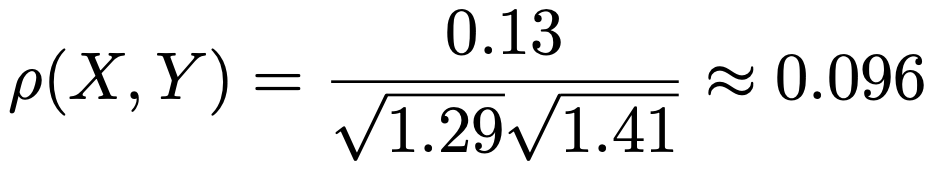
（解答終わり）

演習３〜一次変換と共分散・相関係数〜

【問題】２つの確率変数X，Yの期待値や分散について，次の式が成り立っている。

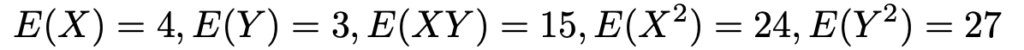
XとYに，それぞれ次のような一次変換を施して，新しい確率変数SとTをつくる。

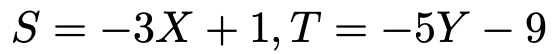
このとき，S，Tの共分散と相関係数を求めなさい。

【解答】まず，X，Yの共分散は次のようになります。

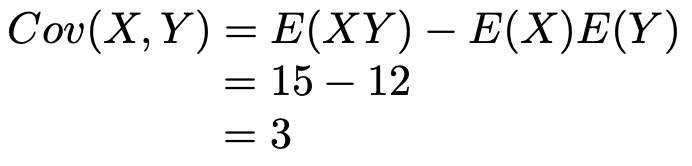
次に，X，Yの分散は次のようになります。

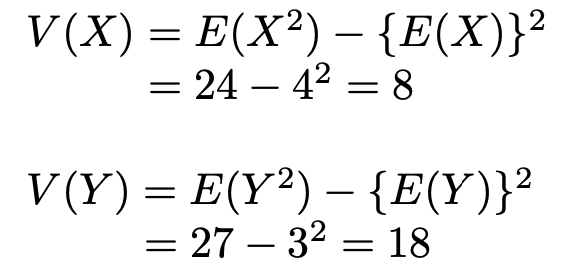
したがって，X，Yの相関係数は次のようになります。

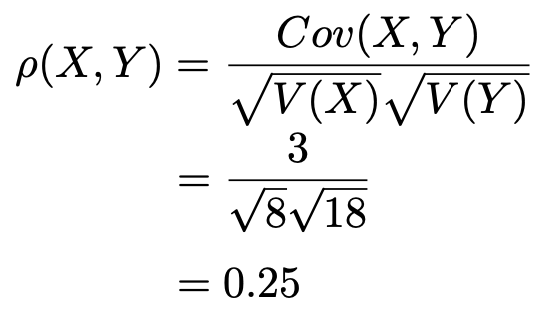
さらに，一次変換による共分散の変換公式によって，S，Tの共分散と，X，Yの共分散の関係は次のようになります。

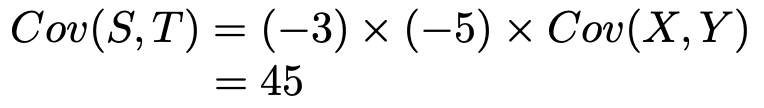
最後に，S，Tの相関係数は，一次変換の式のX，Yの係数が同符号であることから，X，Yの相関係数に等しいので，

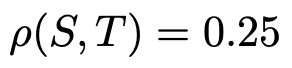
（解答終わり）

第5回は以上となります。最後までお付き合いいただき，ありがとうございました！
引き続き，第6回以降の記事へ進んでいきましょう！

2023年1月に「統計検定２級公式問題集[CBT対応版]（実務教育出版）」が発売されました！（CBTが何かわからない人はこちら）
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが，本書は分野ごとにその形式の問題を並べた構成になっていて，最後に模擬テストがついています。CBT対策の新たな心強い味方ですね！

さらに実戦に向けた演習を積みたい人は，「統計検定２級公式問題集2018〜2021年（実務教育出版）」を手に取ってみてください。

また，もっと別の問題を解いてみたい人は，さらにさかのぼって「統計検定２級公式問題集2016〜2017年（実務教育出版）」を解いて実力に磨きをかけましょう！