【完全網羅】統計検定準１級チートシート

統計検定準１級のCBTでは，統計学実践ワークブック（以下，ワークブック）の各章末の例題と同様の出題が多く，その内容を徹底的に学習することが合格のために有効です。準１級の合格を目指す人で，まだ購入していない人は（PBTの過去問集より優先して）即購入しましょう。

しかし，ワークブックの解説には難解な表現が見られ，合格には不要な内容も含まれています。そこで，ワークブックの構成を尊重しつつも，本稿では全体をスッキリと読みやすいものに再構成し，次のような工夫を取り入れて，試験前に準１級で必須の知識を短時間で確認できるようにしています。

• 文章や数式は理解しやすいものに書き直した
• オリジナルの例や図を追加して，イメージしやすいようにした
• 試験対策としては明らかに不要と思われる内容はカットした
• ワークブックの正誤表にも載っていない誤りを訂正した
• ワークブックに記載がなくても，PBTで出題実績がある項目など，必要な内容を追加した

なお，説明が詳しい項目とそうでない項目がありますが，統計検定準１級講座（リンクはこちら）を利用している人にとって使いやすいように配慮して，説明の仕方を決めています。

また，本稿を執筆する上で，ワークブック以外に30冊以上の書籍を参考にしましたが，これらは改めて別の記事にて紹介します。

第１章　事象と確率

事象Aが起きる確率をP(A)と表します。
・包除原理…事象A，Bについて，AまたはBが起きる（和事象）確率は一般に次の式の右辺のように求められます。

上の式の右辺第３項は，AとBがどちらも起きる（積事象）確率を表しています。
事象AとBが排反（同時には起きない）ならば，上の式は次のようになります。

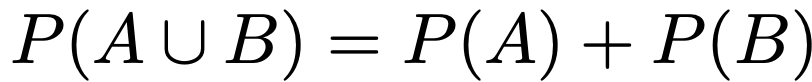
・事象の独立…事象AとBについて，次の式が成り立つこと。

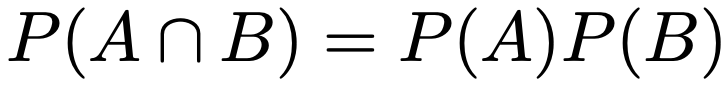
・条件付き確率…Aが起きたもとでBが起きる確率を次の式の右辺で定義します。

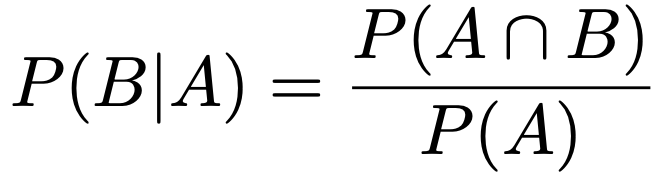
上の式の両辺にP(A)をかけると，次の式が成り立ちます。（AとBが独立の場合との違いに注意）

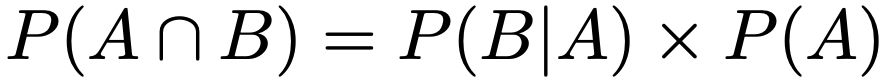
事象AとBが同時に起こる確率について，P(B|A)×P(A)＝P(A|B)×P(B)が成り立つことから，両辺をP(B)でわって次の式が得られます。

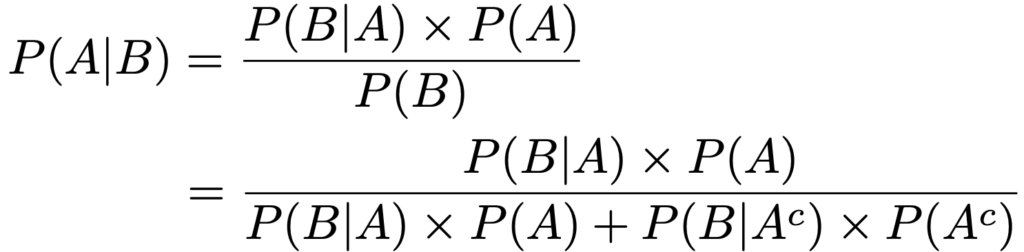
上の式はベイズの定理と呼ばれ，２行目の分母では，P(B)をAが起きたもとでBが起きる場合とAが起きなかったもとでBが起きる場合に分けています。ここで，A^cはAの余事象（A以外のすべて）を表しています。例えば，ある病気に罹患している確率をP(A)とすると，罹患していない確率がP(A^c)です。このとき，P(B)を検査で陽性となる確率とすると，P(A|B)は陽性であったときにこの病気に罹患している確率であり，P(A)は事前確率，P(A|B)は陽性という情報を得た上での条件付き確率ということで事後確率と呼ばれます。

・条件付き独立…事象A，B，Cについて，Cを与えたもとでAとBが条件付き独立であるとは，次の式が成り立つこと。

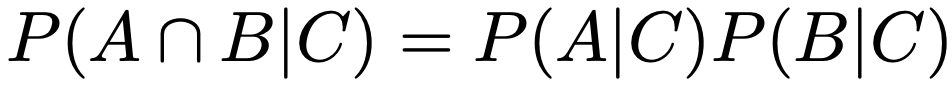
・確率変数…事象に対して実数を対応させる関数。
確率変数には離散型と連続型がありましたね（２級講座参照）。
・確率関数…離散型確率変数Xがとりうるすべての値について，次の２つの式を満たすような関数p(x)のこと。

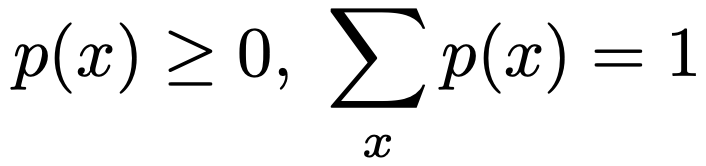
・確率密度関数…連続型確率変数Xの定義域全体について，次の２つの式を満たすような関数f(x)のこと。

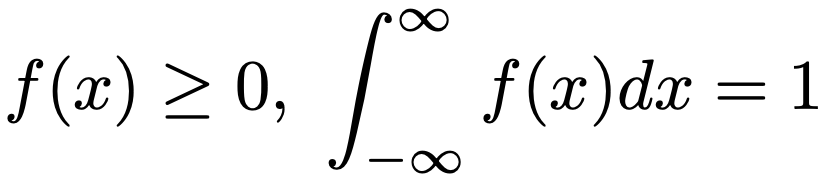
・期待値（平均）…確率変数がとりうる値の起きやすさを加味した平均。
離散型確率変数Xの確率関数をp(x)とするとき，Xの期待値はかっこ内の条件のもとで次の式で定めます。

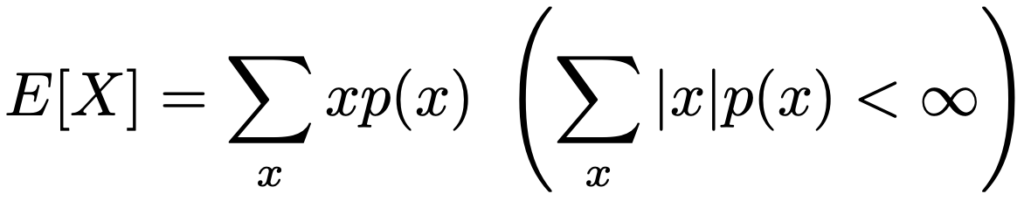
より一般に，離散型確率変数Xの関数g(X)の期待値は，かっこ内の条件のもとで次の式で定めます。

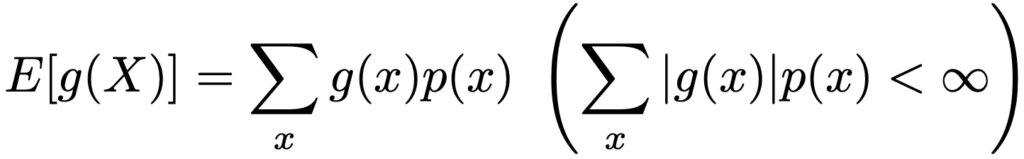
連続型確率変数Xの確率密度関数をf(x)とするとき，Xの期待値は，かっこ内の条件のもとで次の式で定めます。

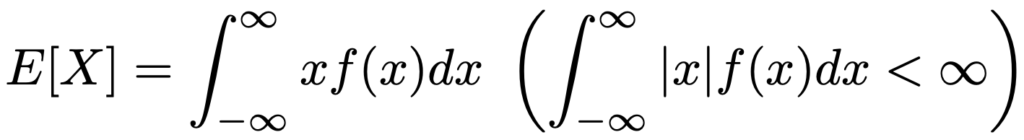
より一般に，連続型確率変数Xの関数g(X)の期待値は，かっこ内の条件のもとで次の式で定めます。

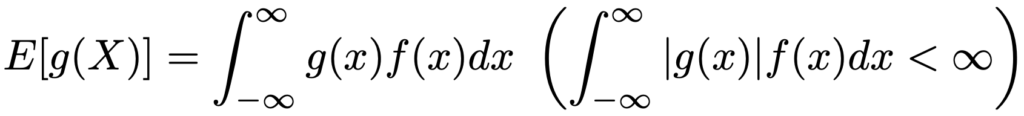
確率変数X，Yが離散型の場合でも連続型の場合でも，a，b，cを定数として，期待値について次の式が成り立ちます。

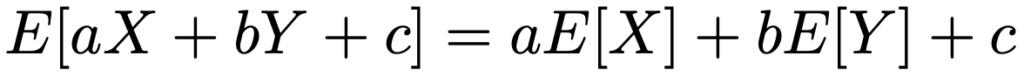
・分散…確率変数がとりうる値の期待値からのばらつき具合の平均。
離散型確率変数Xの確率関数をp(x)，E[X]=μとするとき，Xの分散はかっこ内の条件のもとで次の式で定めます。

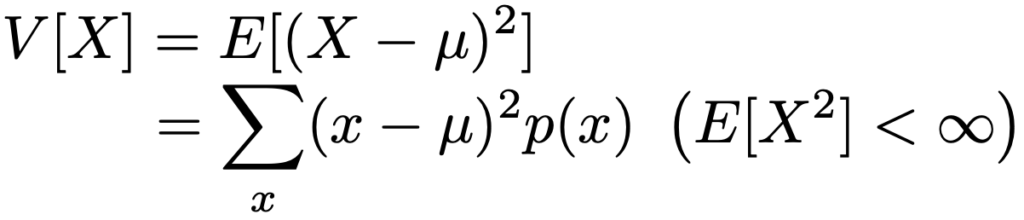
連続型確率変数Xの確率密度関数をf(x)，E[X]=μとするとき，Xの分散は，かっこ内の条件のもとで次の式で定めます。

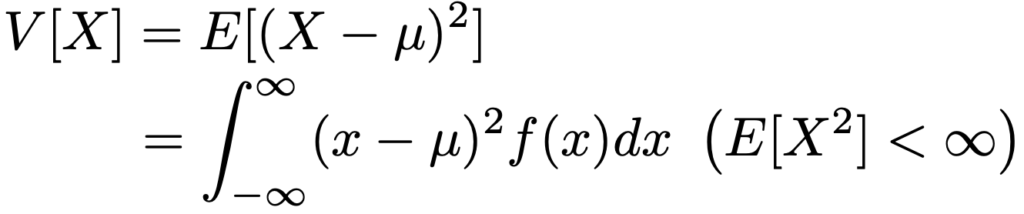
確率変数Xが離散型の場合でも連続型の場合でも，a，bを定数として，分散について次の式が成り立ちます。

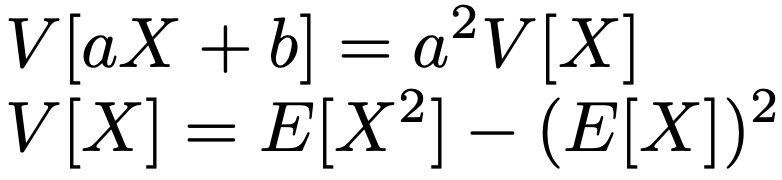
分散の正の平方根を標準偏差と言います。

第２章　確率分布と母関数

・累積分布関数…確率変数Xに対し，F(x)＝P(X≦x)のこと。非減少関数で，分布関数とも言います。Xが連続型確率変数で，その累積分布関数が微分可能で，その確率密度関数が連続である場合，累積分布関数を微分すると確率密度関数が得られます。
※生存関数，ハザード関数は第19章を参照
・同時累積分布関数…確率変数X，Yに対し，F(x，y)＝P(X≦x，Y≦y)のこと。
・同時確率関数…離散型確率変数X，Yに対し，p(x，y)＝P(X＝x，Y＝y)のこと。次の式のように，同時確率関数を１つの確率変数のとりうるすべての値についてたし上げたものを周辺確率関数と言います。

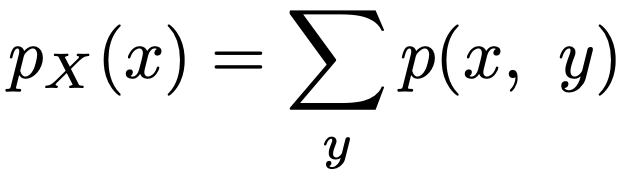
・条件付き確率関数…Xの周辺確率関数p_X(x)≠０となるxに対して，同時確率関数をp_X(x)でわった次の関数を，Xを与えたときのYの条件付き確率関数と言います。Yを与えたときのXの条件付き確率関数も同様。

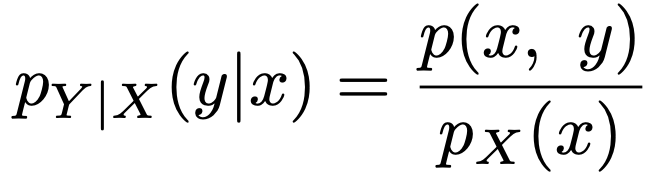
・同時確率密度関数…連続型確率変数X，Yの同時累積分布関数F(x，y)が２回連続微分可能であるとき，次の式を満たすf(x，y)のこと。

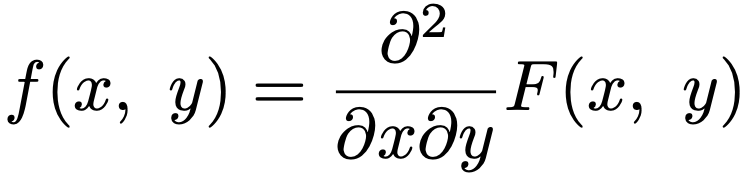
f(x，y)はつねに０以上の値をとり，全体で積分すれば１になります。
また，次の式は，XとYの同時確率密度関数をyについて積分したものであり，Xの周辺確率密度関数と言います。

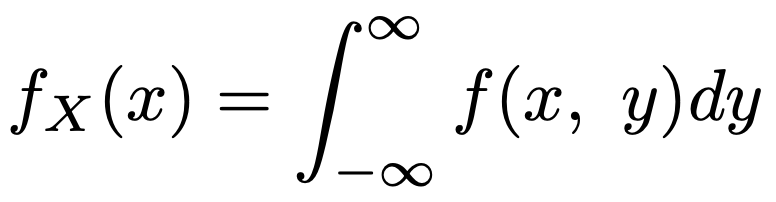
・条件付き確率密度関数…Xの周辺確率密度関数f_X(x)≠０となるxに対して，同時確率密度関数をf_X(x)でわった次の関数を，Xを与えたときのYの条件付き確率密度関数と言います。Yを与えたときのXの条件付き確率密度関数も同様。

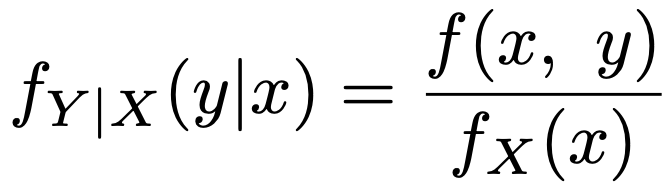
・条件付き期待値…Xを与えたときのYの条件付き期待値は，次の式のように条件付き確率密度関数を使って定めます。

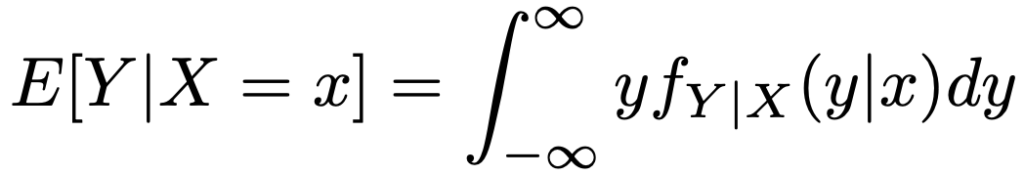
離散型の確率変数に対しても，条件付き確率関数を使って，同じように条件付き期待値を定めることができます。
条件付き期待値については，くり返しの法則と呼ばれる次の式が成り立ちます。

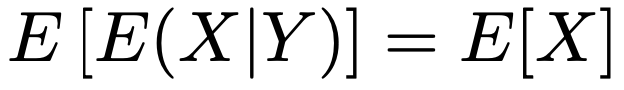
※条件付き分散は出題されないと考えられるので省略。

・確率変数の独立…次のようにXとYの同時確率(密度)関数がXの周辺確率(密度)関数とYの周辺確率(密度)関数の積に一致すること。

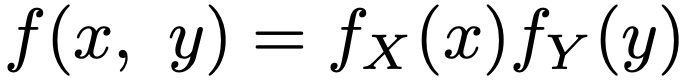
・条件付き独立…Zを与えたときのX，Yの条件付き確率密度関数が，次の式のように，Zを与えたときのXの条件付き確率密度関数とZを与えたときのYの条件付き確率密度関数の積に等しいとき，Z＝zを与えたときにXとYは条件付き独立であると言います。

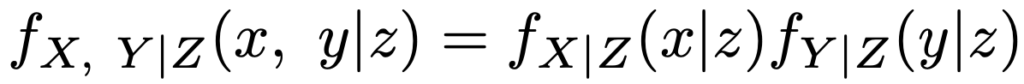
・確率母関数…離散型確率変数Xの確率関数をp(x)とするとき，１に十分に近いすべてのsに対して，次のべき級数が収束するときのG_X(s)のこと。

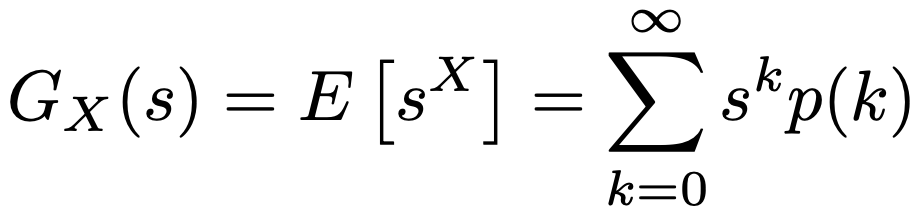
確率母関数を微分してs＝１を代入することで，次のようなXの階乗モーメントを求めることができるので，これを利用してXの期待値や分散などがわかります。

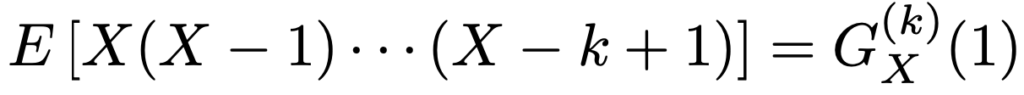
・モーメント（積率）母関数…０に十分に近いすべてのtに対して，次の期待値が存在するときのM_X(t)のこと。

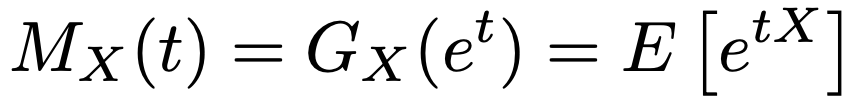
モーメント母関数を微分してt＝０を代入することで，次のような原点まわりのモーメントを求めることができます。

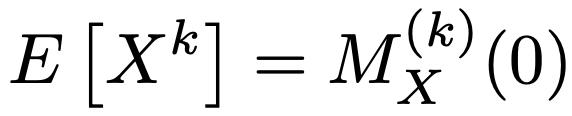
また，XとYが独立なとき，X＋Yのモーメント母関数は次の式のようにXのモーメント母関数とYのモーメント母関数の積で求めることができます。

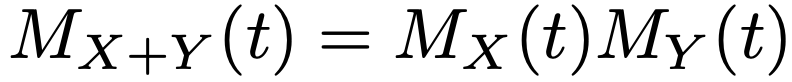
※特性関数は出題されないと考えられるので省略。

第３章　分布の特性値

・分位点…Xが連続型の確率変数で，累積分布関数F(x)が増加関数のとき，F(x_0.25)＝0.25となるx_0.25を第１四分位数，F(x_0.5)＝0.5となるx_0.5を中央値，F(x_0.75)＝0.75となるx_0.75を第３四分位数，x_0.75ーx_0.25を四分位範囲と言います。
・最頻値（モード）…確率密度関数f(x)（または確率関数p(x)）を最大にするx
・変動係数…非負値の確率変数Xのばらつきが期待値に対してどれくらいかを示す次の指標。

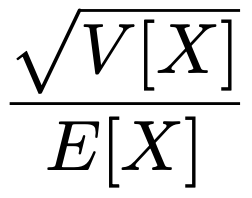
・歪度…確率変数Xの期待値をμ，分散をσ²とするとき，次のようにXを標準化した確率変数の３乗の期待値。

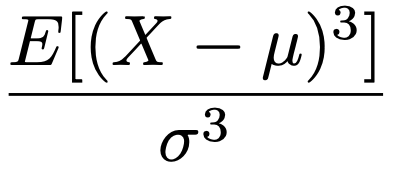
分布が，右に長い裾を持つときには正の値，左に長い裾を持つときには負の値をとりやすく，左右対称ならば０になります。
・尖度…確率変数Xの期待値をμ，分散をσ²とするとき，次のようにXを標準化した確率変数の４乗の期待値。

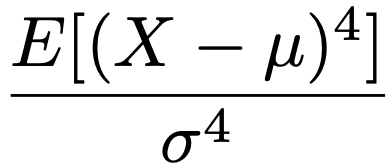
確率密度関数のグラフに山が１つあり，その山が尖っているほど尖度は大きな値をとる傾向があります。この期待値を正規分布で計算すると３になるので，上の式から３をひいた値が正か負かによって分布の形状を正規分布と比べることがあります。
・共分散…確率変数X，Yの関連性を表す量であり，E[X]=μ_X，E[Y]=μ_Yとして，次の式で表せます。

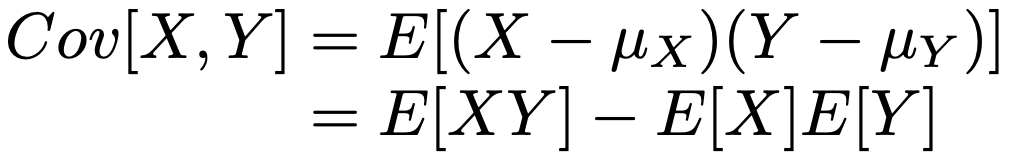
XとYが独立ならば共分散は０であり，そのとき次の式が成り立ちます。

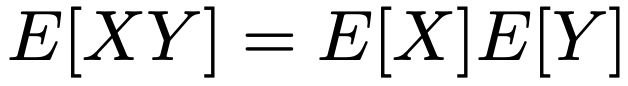
X，Yを確率変数，a，b，c，dを定数として，共分散について次の式が成り立ちます。

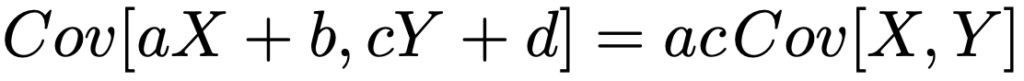
分散について，共分散を使った次の式が成り立ちます。

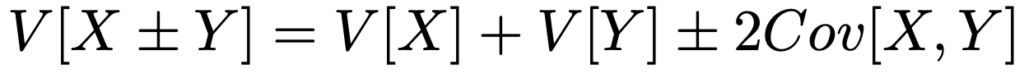
特に，XとYが独立ならば，次の式が成り立ちます。

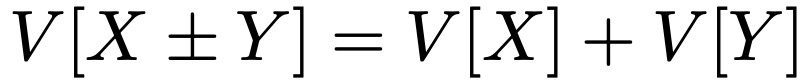
・相関係数…確率変数を基準化し，ー１以上１以下の値をとるようにして確率変数X，Yの関連性を表した次の量。

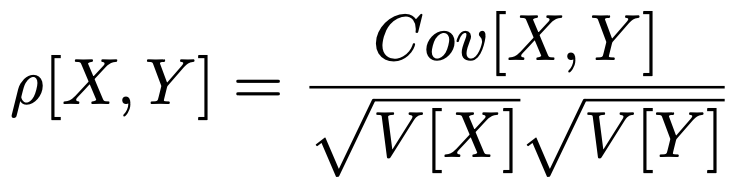
・偏相関係数…Zが，XとYの両方に相関があるとき，XとYの間に直接的な相関がなくてもZを介して相関が発生します（擬似相関）。偏相関係数は，Zの影響を除いた場合のXとYの相関係数で，次の式で計算できます。

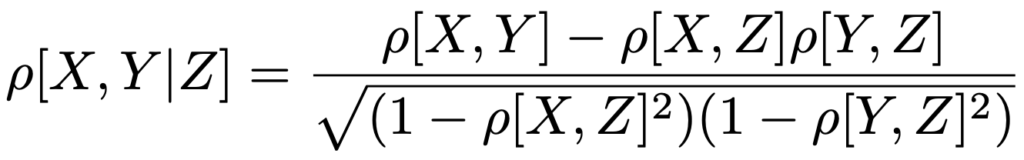
・加重平均…データx₁，…，x_nに対して，w₁，…，w_nを重みとして次の式で定めます。

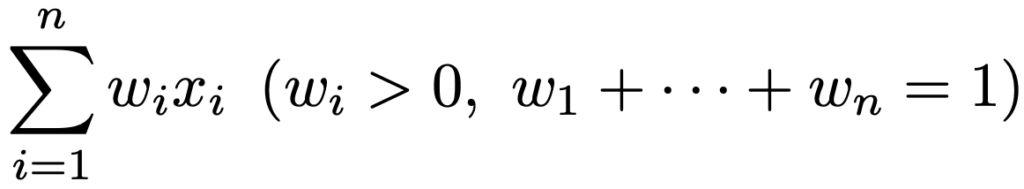
特に，w₁＝…＝w_n＝1/nのとき，算術平均に一致します。
・幾何平均…正の値をとるデータx₁，…，x_nに対して，次の式で定めます。

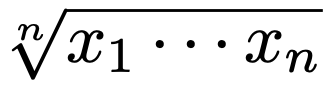
・調和平均…正の値をとるデータx₁，…，x_nに対して，次の式で定めます。

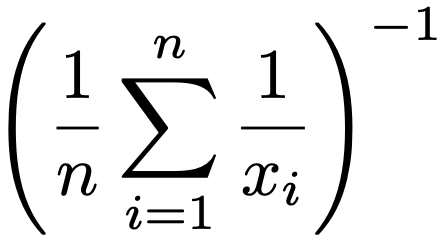
・確率変数ベクトル…確率変数x₁，…，x_pに対して，x＝(x₁，…，x_p)^Tをp次元確率変数ベクトルと言います。
・平均ベクトル…確率変数x₁，…，x_pに対して，E[x]＝(E[x₁]，…，E[x_p])^Tをp次元平均ベクトルまたは期待値ベクトルと言います。平均ベクトルについて，Aをr×p定数行列，bをr次元定数ベクトルとして，次の式が成り立ちます。

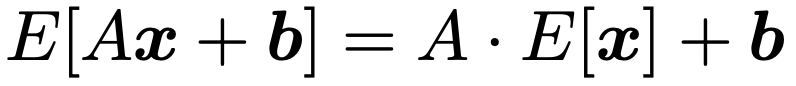
・分散共分散行列…p次元確率変数ベクトルx＝(x₁，…，x_p)^Tに対して，Cov[x_i，x_j]を(i，j)成分とする次のような半正定値対称行列。

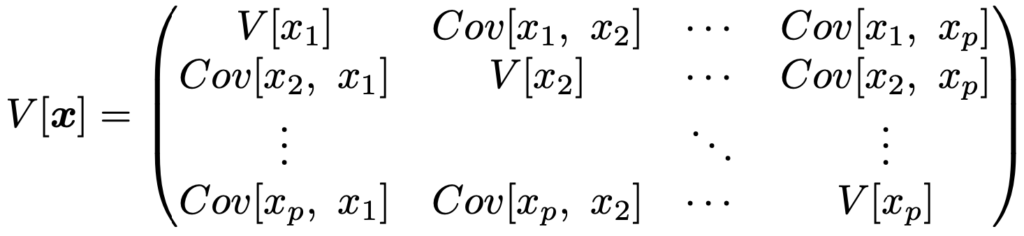
・標本分散共分散行列…p変数(x₁，…，x_p)のサイズnの標本(x₁₁，…，x_1p)，…，(x_n1，…，x_np)に対して，次のようなx_iとx_jの共分散を(i，j)成分とするp次正方行列。

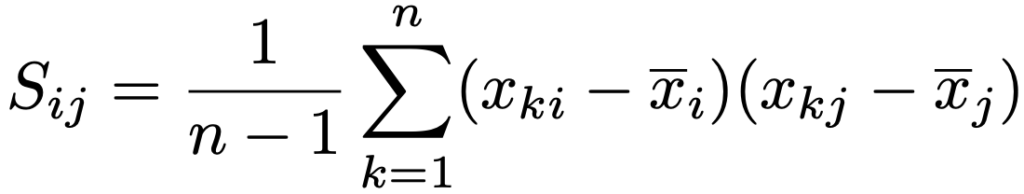
・相関行列…p次元確率変数ベクトルx＝(x₁，…，x_p)^Tに対して，ρ[x_i，x_j]を(i，j)成分とする半正定値対称行列。
・標本相関行列…p変数(x₁，…，x_p)のサイズnの標本(x₁₁，…，x_1p)，…，(x_n1，…，x_np)に対して，x_iとx_jの相関係数を(i，j)成分とするp次正方行列。

第４章　変数変換

・Y＝g(X)の確率密度関数…X，Yを連続型確率変数，Xの確率密度関数をf_X(x)，Yの確率密度関数をf_Y(y)として，y＝g(x)が単調増加または単調減少の関数のとき，逆関数x＝g^ー1(y)が存在します。g^ー1(y)が微分可能ならば，f_X(x)からf_Y(y)が次のように求められます。

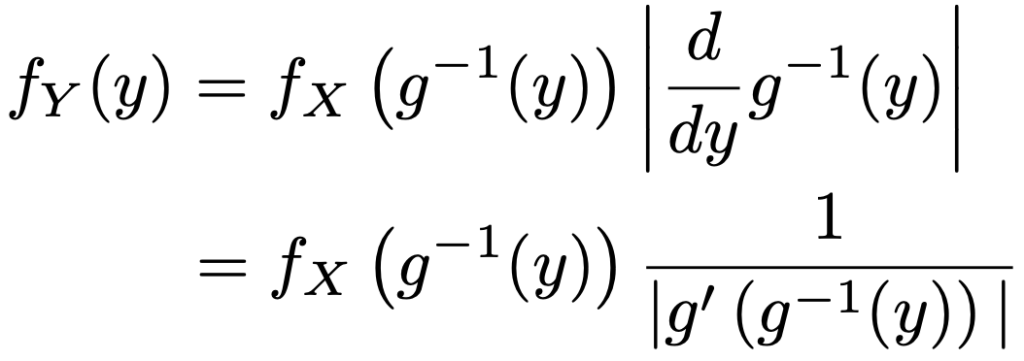
（例）f_X(x)＝λe^ーλx（x＞０，λ＞０），y＝g(x)＝１ーe^ーxとすると，0＜y＜1です。x＝g^ー1(y)＝ーlog(1ーy)だから，上の公式にあてはめると，f_Y(y)は次のようになります。

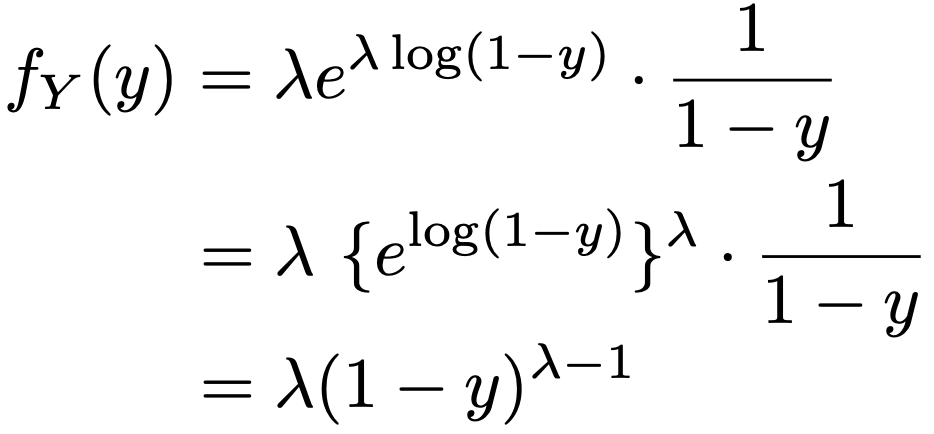
・X＋Yの確率密度関数…X，Yを連続型確率変数，Xの確率密度関数をf_X(x)，Yの確率密度関数をf_Y(y)として，X，Yが独立だとすると，X，Yの同時確率密度関数はf_X(x)f_Y(y)です。Z＝X＋Y，T＝Yという変数変換を考えると，その逆変換はX＝ZーT，Y＝Tであるから，Z，Tの同時確率密度関数はf_X(zーt)f_Y(t)となり，周辺分布を求めてZの確率密度関数は次のようになります。

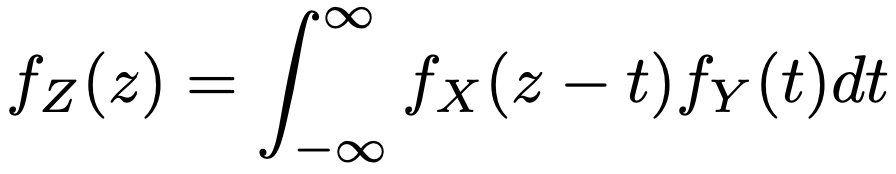
ここで，(x，y)→(z，t)の変換にともなって登場する次の行列式（ヤコビアン）が１になっていることに注意します。

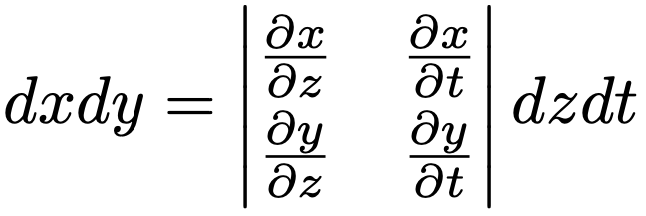
（例）Xの確率密度関数f_X(x)（x＞０）とYの確率密度関数f_Y(y)（y＞０）を，m＞０，n＞０のもとで次の式で定義します。

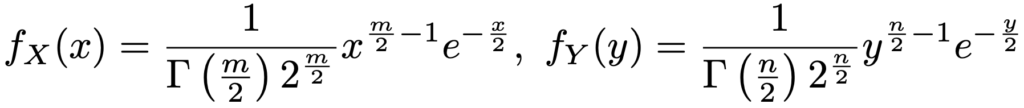
X＝ZーT＞０，Y＝T＞０より，0＜t＜zであるから，Zの確率密度関数f_Z(z)は次のように計算できます。

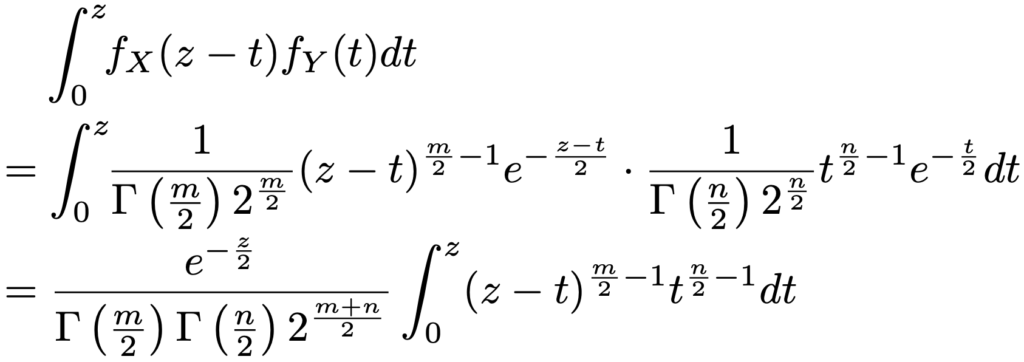
ここで，t＝zxと置換すると，次のようになります。

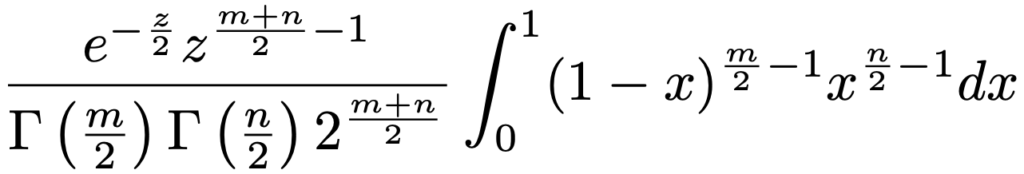
上の積分は，次のようなベータ関数になっています。

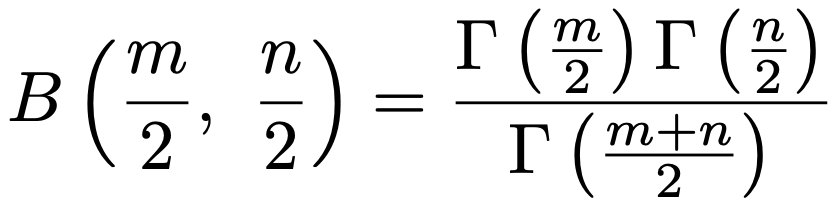
よって，積分をガンマ関数を用いて書き直すと，Z＝X＋Yの確率密度関数が次のように求められます。

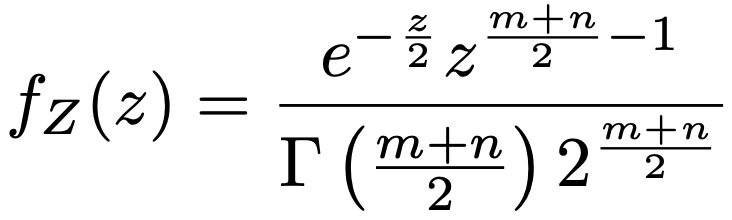
・Box-Cox変換…非対称であるなど，正規分布からずれている非負のデータxを正規分布に近づける次の変換のこと。

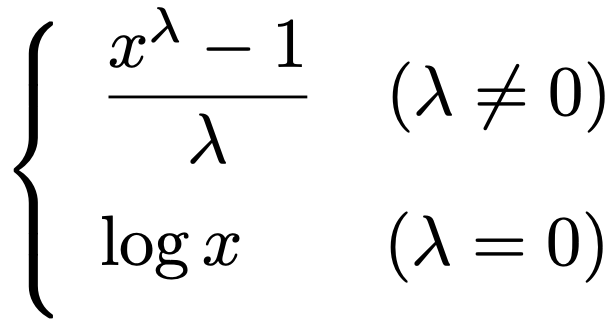
λの値を変化させることでべき乗変換や対数変換など，様々な変換が可能であり，その中で変換後のデータが正規分布に近づくものを選択します。

※ロジット変換，ロジスティック変換，プロビット変換については第18章を参照。

第５章　離散型分布

・離散一様分布…サイコロを１回投げたときに出る目の分布のように，有限個の事象が等確率で起きる場合の確率分布。Xが{1，2，…，k}上の離散一様分布にしたがうとは，Xがこれらのk通りの値を等確率でとることであり，次のように表せます。

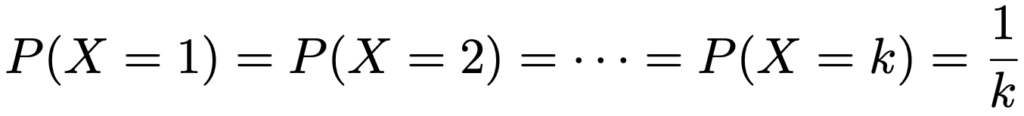
Xが{1，2，…，k}上の離散一様分布にしたがうとき，期待値，分散，確率母関数は次の通りです。

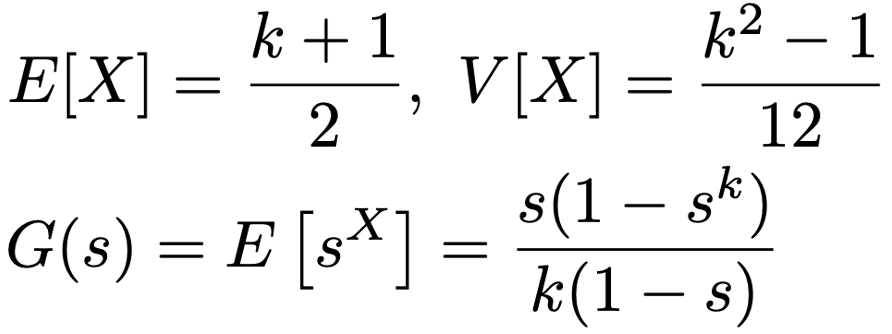
・ベルヌーイ分布…コイン投げのように，結果が２通り（一方を成功，他方を失敗と呼ぶ）の試行をベルヌーイ試行と言い，ベルヌーイ試行を１回行ったときの成功回数がしたがう確率分布。ベルヌーイ試行の成功確率をpとして，ベルヌーイ分布をBin(１，p)と表します。確率関数は次の通りです。

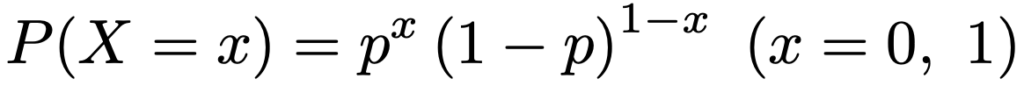
X〜Bin(１，p)のとき，期待値，分散，確率母関数は次の通りです。

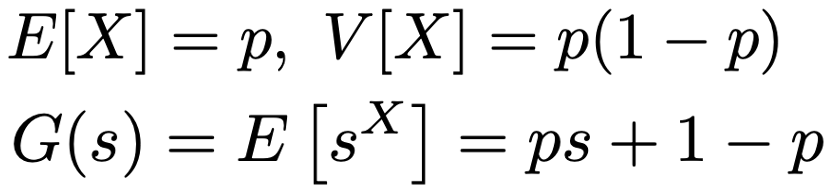
・二項分布…成功確率pの独立なベルヌーイ試行をn回行ったときの成功回数がしたがう確率分布で，Bin(n，p)と表します。確率関数は次の通りです。

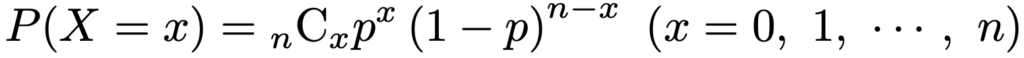
X〜Bin(n，p)のとき，期待値，分散，確率母関数は次の通りです。

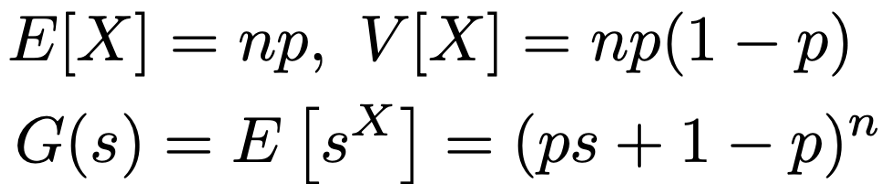
二項分布には再生性があり，X₁〜Bin(n₁，p)，X₂〜Bin(n₂，p)が独立であるとき，X₁＋X₂〜Bin(n₁＋n₂，p)が成り立ちます。

・超幾何分布…N本のくじの中にM本の当たりがあり，n本のくじを非復元抽出するとき，ひいた当たりの本数がしたがう確率分布で，HG(N，M，n)と表します。確率関数は次の通りです。

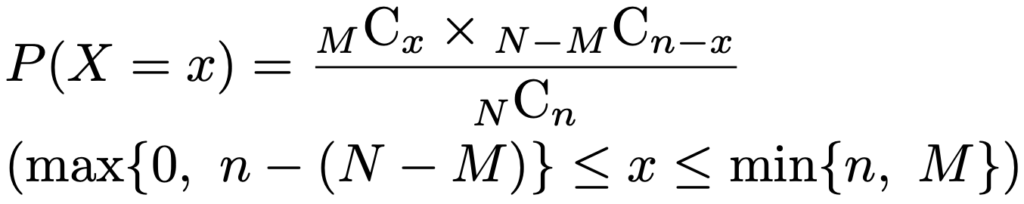
X〜HG(N，M，n)のとき，期待値，分散は次の通りです。

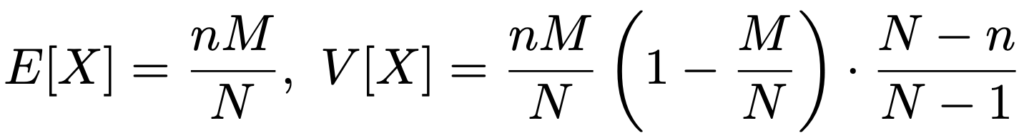
nとM/Nを一定にしたまま，N→∞とすると，二項分布Bin(n，M/N)に収束します。

・ポアソン分布…λ＞０を平均発生率とするとき，特定の時間（空間）内に事象がx回発生する確率のモデル化に用いられる確率分布で，Po(λ)と表します。確率関数は次の通りです。

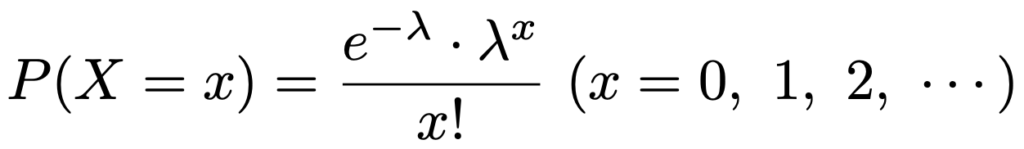
X〜Po(λ)のとき，期待値，分散，確率母関数は次の通りです。

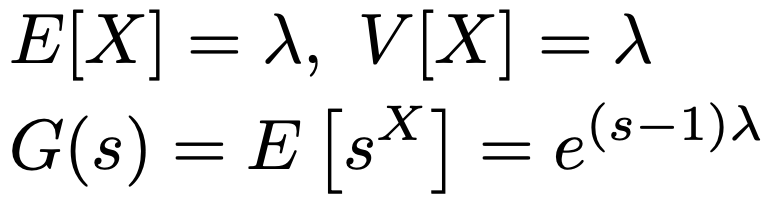
ポアソン分布には再生性があり，X₁〜Po(λ₁)，X₂〜Po(λ₂)が独立であるとき，X₁＋X₂〜Po(λ₁＋λ₂)が成り立ちます。

二項分布Bin(n，p)で，np＝λ，n→∞とすると，Po(λ)に分布収束します。（少数の法則）

・幾何分布…独立な成功確率pのベルヌーイ試行をくり返すとき，はじめての成功が起きるまでの失敗の回数Xがしたがう分布で，Geo(p)と表します。確率関数は次の通りです。

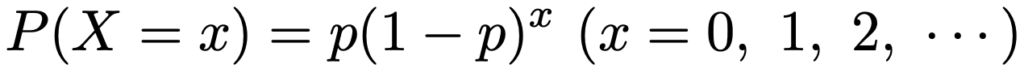
はじめての成功が起きるまでの試行の回数Yがしたがう分布を幾何分布と呼ぶ場合もあり，そのときの確率関数は次の通りです。

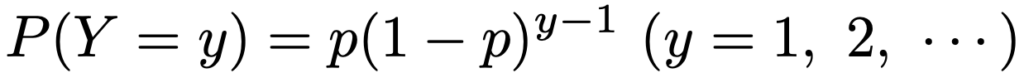
X〜Geo(p)のとき，期待値，分散，確率母関数は次の通りです。

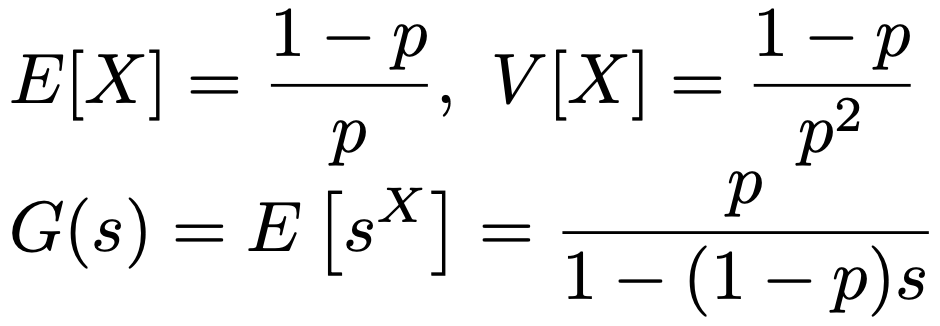
Y＝X＋１であることを利用して，Yの期待値，分散，確率母関数も求められます。
幾何分布については，どんな０以上の整数m，nに対しても次の式が成り立ちます。これを無記憶性と言います。

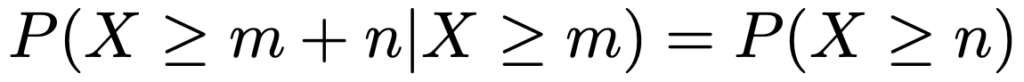
・負の二項分布…成功確率pのベルヌーイ試行をくり返すとき，r回目の成功が起きるまでの失敗の回数がしたがう分布で，NB(r，p)と表します。r＝１のときには幾何分布に一致します。確率関数は次の通りです。

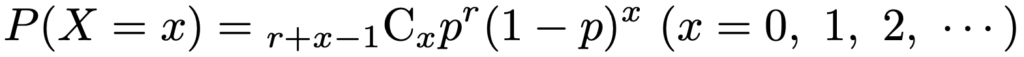
X〜NB(r，p)のとき，期待値，分散，確率母関数は次の通りです。

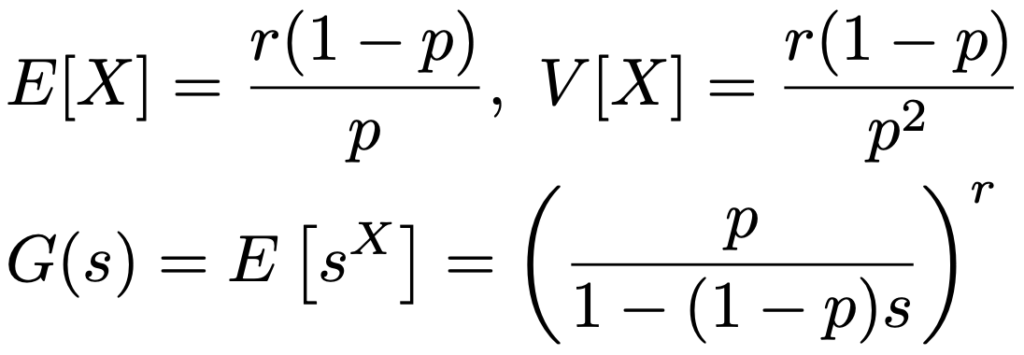
負の二項分布には再生性があり，X₁〜NB(r₁，p)，X₂〜NB(r₂，p)が独立であるとき，X₁＋X₂〜NB(r₁＋r₂，p)が成り立ちます。

・多項分布…ベルヌーイ試行は結果が２通りですが，より一般的に結果がk通りで，それぞれが起こる確率がp₁，p₂，…，p_k（p₁＋p₂＋…＋p_k＝１）で一定の場合を多項試行と呼ぶことにします。独立な多項試行をn回行ったとき，k通りの結果が起きる回数がしたがう確率分布が多項分布で，M(n；p₁，p₂，…，p_k)と表します。k＝２のときには二項分布に一致します。同時確率関数は次の通りです。

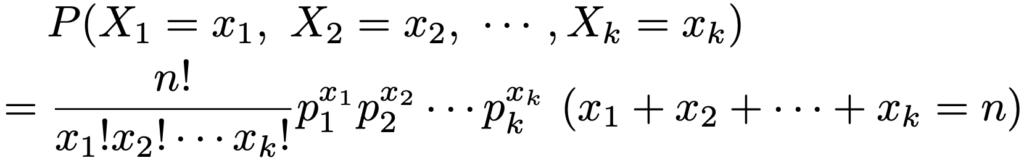
(X₁，…，X_k)〜M(n；p₁，p₂，…，p_k)のとき，X_i〜Bin(n，p_i)であり，X_iとX_j（i≠j）の共分散と相関係数は次の通りです。

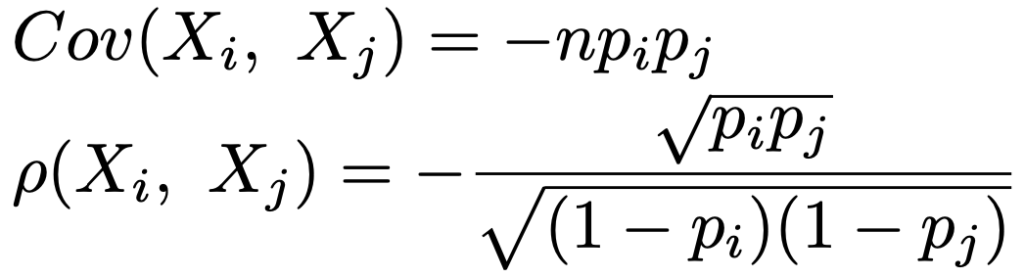
※多変数の確率母関数は出題されないと考えられるので省略。

第６章　連続型分布と標本分布

・連続一様分布…区間[a，b]で一定の確率密度をもつ確率分布で，a＜bとして，U(a，b)と表します。確率密度関数は次の通りです。

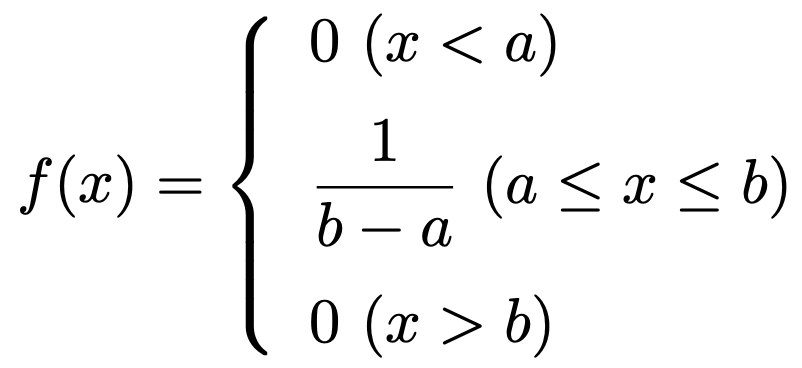
X〜U(a，b)のとき，平均，分散，モーメント母関数は次の通りです。

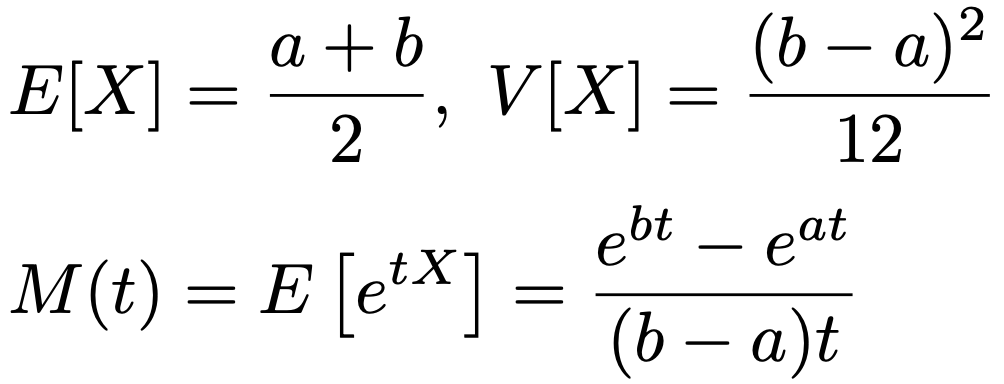
・正規分布…偶然誤差に見られるように，平均μを中心とする対称な確率分布で，σ＞０として，N(μ，σ²)と表します。確率密度関数は次の通りです。

特に，μ＝０，σ²＝１の場合を標準正規分布と言います。
X〜N(μ，σ²)のとき，平均，分散，モーメント母関数は次の通りです。

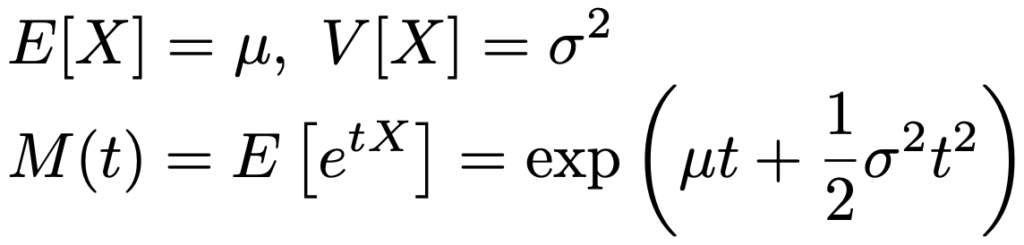
正規分布には再生性があり，X₁〜N(μ₁，σ₁²)，X₂〜N(μ₂，σ₂²)が独立であるとき，X₁＋X₂〜N(μ₁＋μ₂，σ₁²＋σ₂²)が成り立ちます。より一般的に，aX₁＋bX₂〜N(aμ₁＋bμ₂，a²σ₁²＋b²σ₂²)も成り立ちます。

・指数分布…機械が故障するまでの時間などを表すのにも使われる確率分布で，λ＞０として，Exp(λ)と表します。確率密度関数は次の通りです。

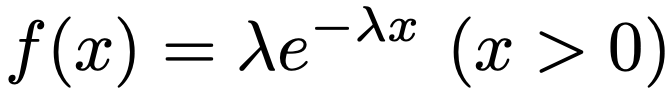
X〜Exp(λ)のとき，平均，分散，モーメント母関数は次の通りです。

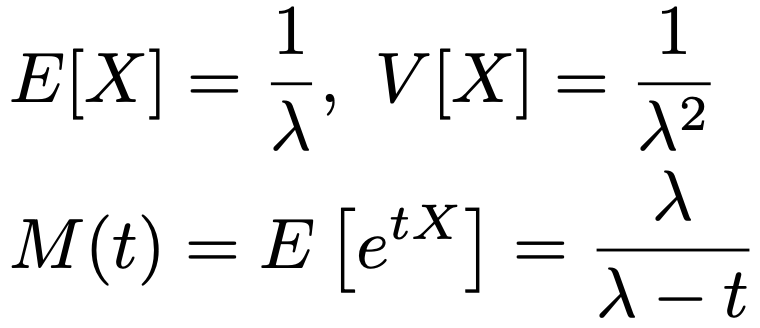
指数分布については，どんな正の数a，bに対しても次の式が成り立ちます。これを無記憶性と言います。

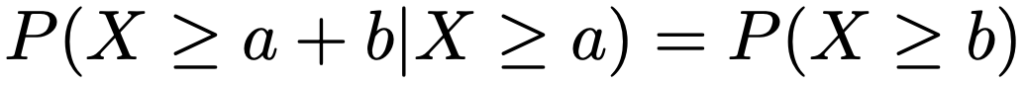
・ガンマ分布…x＞０で定義される確率分布で，a＞０，b＞０として，Ga(a，b)と表します。確率密度関数は次の通りです。

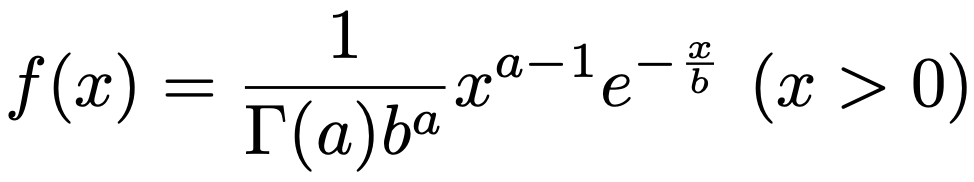
aを形状母数，bを尺度母数と言い，上の式のΓ(a)はガンマ関数です。a＝１のときには，指数分布Exp(1/b)に一致します。
X〜Ga(a，b)のとき，平均，分散，モーメント母関数は次の通りです。

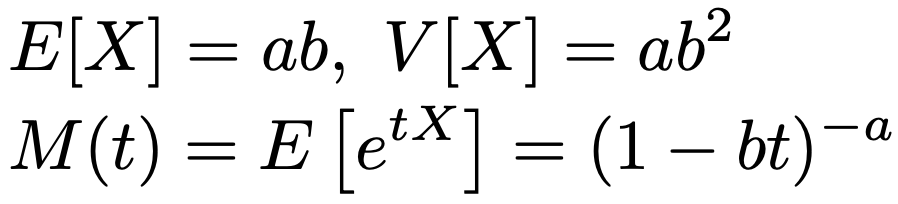
ガンマ分布には再生性があり，X₁〜Ga(a₁，b)，X₂〜Ga(a₂，b)が独立であるとき，X₁＋X₂〜Ga(a₁＋a₂，b)が成り立ちます。

・ベータ分布…０＜x＜１で定義される確率分布で，a＞０，b＞０として，Be(a，b)と表します。確率密度関数は次の通りです。

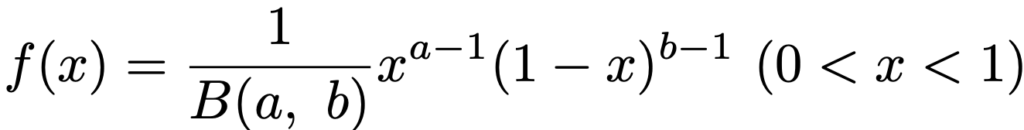
上の式のB(a，b)はベータ関数です。
X〜Be(a，b)のとき，平均，分散は次の通りです。

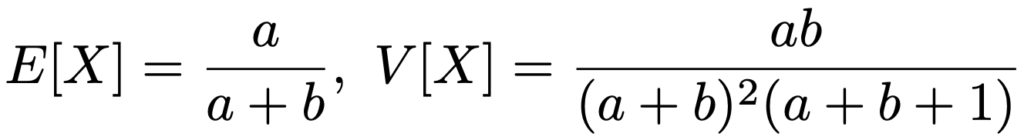
※コーシー分布，対数正規分布は省略

・多変量正規分布…x＝(x₁，…，x_k)^T，その平均ベクトルをμ＝(μ₁，…，μ_k)^T，分散共分散行列をΣとするk変量正規分布をN(μ，Σ)と表します。同時確率密度関数は次の通りです。

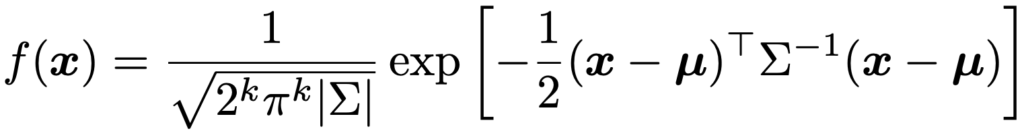
２変量の場合には次のように表せます。

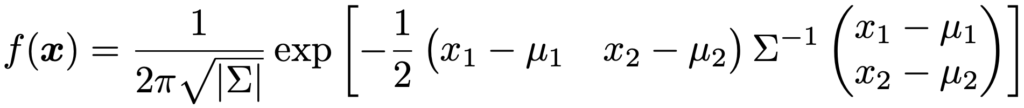
また，X₁とX₂の相関係数をρとして，(X₁，X₂)^Tが次の２変量正規分布にしたがうとき，X₁〜N(μ₁，σ₁²)，X₂〜N(μ₂，σ₂²)が成り立ちます。

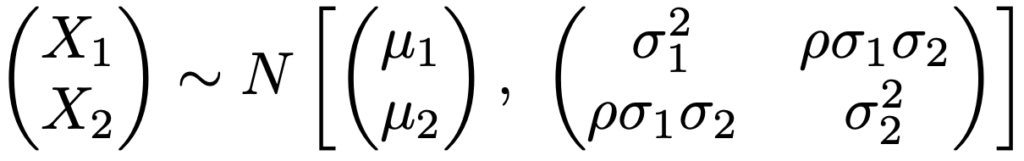
このとき，aX₁＋bX₂は次の正規分布にしたがいます。

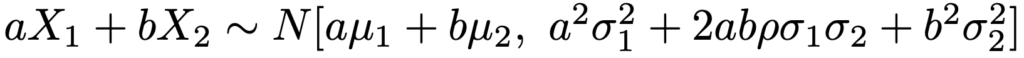
X₁＝x₁が与えられたときのX₂の条件付き分布は次の期待値，分散をもつ正規分布です。

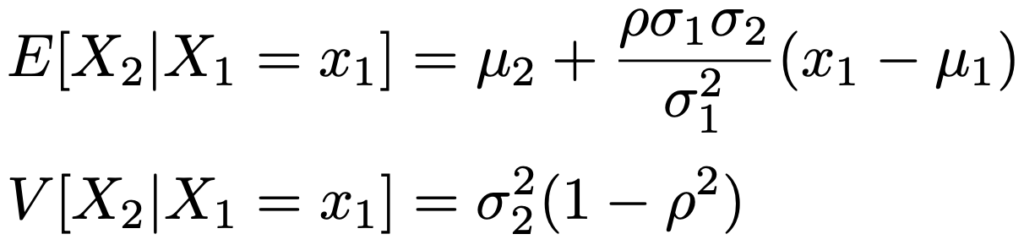
※多変数のモーメント母関数は出題されないと考えられるので省略。

・混合正規分布…複数の正規分布を合成してできる確率分布。例えば，N(０，１)の確率密度関数をφ₁(x)，N(４，１)の確率密度関数をφ₂(x)として，f(x)＝0.3φ₁(x)＋0.7φ₂(x)は２成分混合正規分布の確率密度関数であり，そのグラフは次の図のようになります。

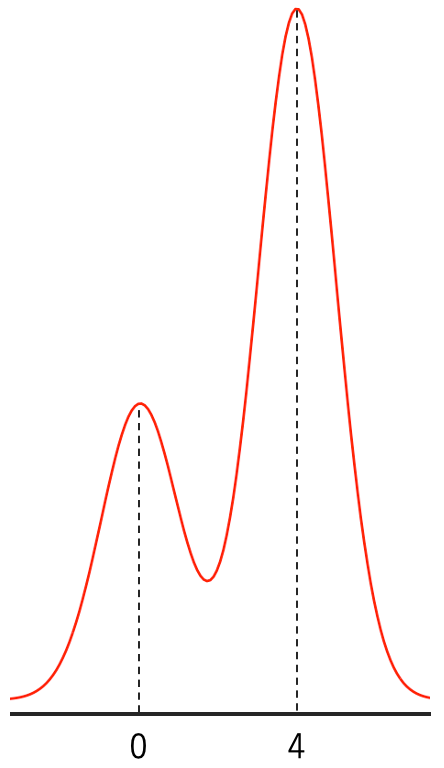
より一般に，π₁＋π₂＋…＋π_k＝１を満たす正の数をπ₁，π₂，…，π_k，正規分布の確率密度関数をφ₁，φ₂，…，φ_kとして，k成分混合正規分布の確率密度関数はf＝π₁φ₁＋π₂φ₂＋…＋π_kφ_kのように定めます。
いま，２成分混合正規分布の確率密度関数をf＝πφ₁＋(１ーπ)φ₂とし，π，φ₁，φ₂が未知のとき，そのパラメータθ＝(μ₁，σ₁²，μ₂，σ₂²，π)は，データから次の手順で推定します。これをEMアルゴリズムと言います。
① パラメータの初期値θ⁽⁰⁾を決める
②【Eステップ】観測値x_iがN(μ₁，σ₁²)から得られる確率をγ_iとして，パラメータのk回目の更新値θ^(k)を使い，次の式でγ_i^(k+1)を求める

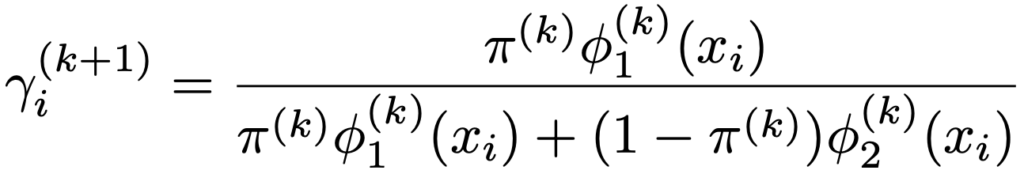
③ 【Mステップ】γ_i^(k+1)を使って，パラメータのk＋１回目の更新値を次の式で求める

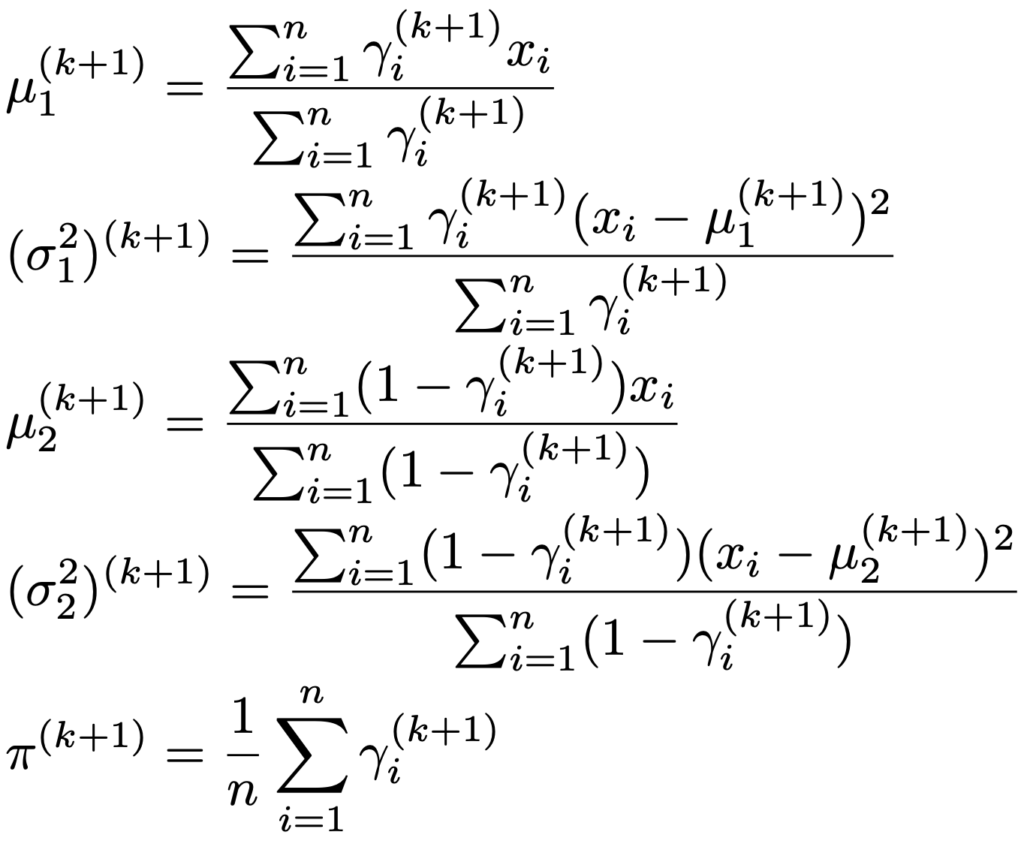
④ ②と③を収束するまでくり返す

・カイ２乗分布…nを自然数として，Ga(n/2，2)を自由度nのカイ２乗分布と言って，χ²(n)と表します。確率密度関数は，ガンマ分布の確率密度関数から導けるので，覚える必要はありません。
【特徴①】Z〜N(０，１)のとき，Z²〜χ²(１)であり，Z₁，Z₂，…，Z_nが独立でそれぞれ標準正規分布にしたがうとき，Z₁²＋Z₂²＋…＋Z_n²〜χ²(n)
【特徴②】ガンマ分布の再生性から，X〜χ²(m)，Y〜χ²(n)でXとYが独立のとき，X＋Y〜χ²(m＋n)
【特徴③】X〜χ²(n)のとき，E[X]＝n，V[X]＝2nであり，モーメント母関数はガンマ分布のモーメント母関数から導けるので，覚える必要はありません。

また，Z₁，Z₂，…，Z_nが独立に標準正規分布にしたがい，λ＝μ₁²＋μ₂²＋…＋μ_n²＞０のとき，(Z₁＋μ₁)²＋(Z₂＋μ₂)²＋…＋(Z_n＋μ_n)²は，自由度n，非心度λの非心カイ２乗分布にしたがうと言って，χ²(n，λ)と表します。カイ２乗分布の再生性は非心カイ２乗分布の再生性として一般化でき，X₁，X₂，…，X_nが独立に（非心）カイ２乗分布にしたがい，X_i〜χ²(n_i，λ_i)であるとき，これらの和は次の（非心）カイ２乗分布にしたがいます。

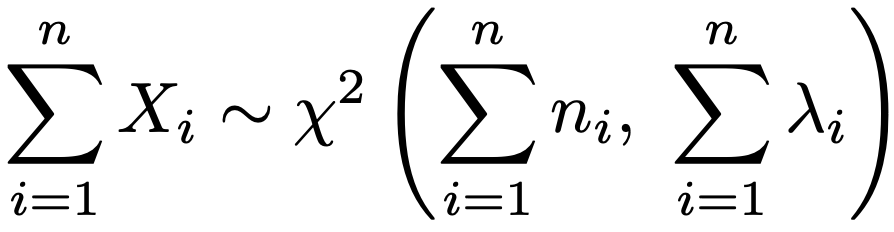
・t分布…Z〜N(０，１)，Y〜χ²(n)でZとYが独立のとき，次のTがしたがう確率分布を自由度nのt分布と言って，t(n)と表します。

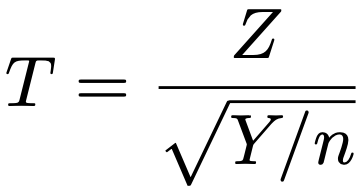
確率密度関数は覚えなくていいので省略します。
t(１)はコーシー分布に一致し，n→∞でt(n)は標準正規分布に分布収束します。また，X〜t(n)ならば，n＞１のときE[X]＝０で，n＞２のときV[X]＝n/(nー2)です。
上のTの式で，Z〜N(λ，１)のとき，Tがしたがう確率分布を自由度n，非心度λの非心t分布と言います。

・F分布…X₁〜χ²(n₁)，X₂〜χ²(n₂)でX₁とX₂が独立のとき，次のFがしたがう確率分布を自由度(n₁，n₂)のF分布と言って，F(n₁，n₂)と表します。

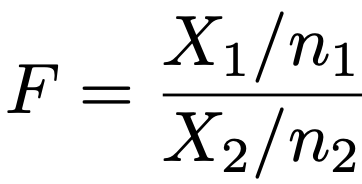
確率密度関数，期待値，分散は覚えなくていいので省略します。
T〜t(n)のとき，Z〜N(０，１)，Y〜χ²(n)として，T²は次のように表せて，Z²〜χ²(１)であるから，自由度(1，n)のF分布にしたがいます。

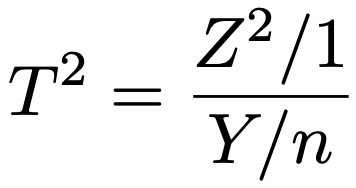
X₁〜χ²(n₁，λ)，X₂〜χ²(n₂)でX₁とX₂が独立のとき，上のFがしたがう確率分布を自由度(n₁，n₂)，非心度λの非心F分布と言います。

第７章　極限定理，漸近理論

確率変数の列X₁，X₂，…の収束は，条件の強いものから順に次のように分類できます。
・X_nが確率変数Yに概収束するとは次が成り立つことです。（例）大数の強法則

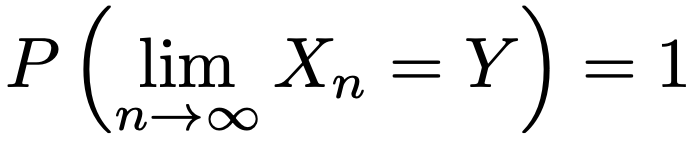
・X_nが確率変数Yに平均二乗収束するとは，次が成り立つことです。（例）大数の弱法則（確率収束の例でもある）

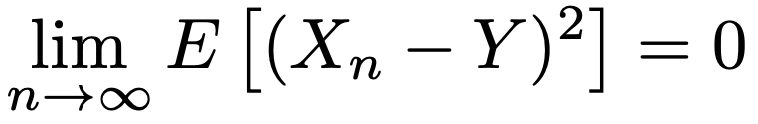
・X_nが確率変数Yに確率収束するとは，任意のε＞０に対して次が成り立つことであり，「X_n→_p Y」と表します。

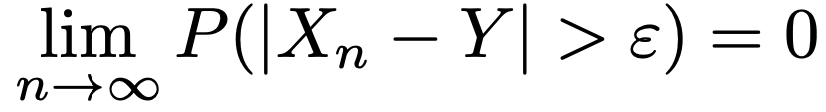
・F_nが確率分布Gに分布収束（法則収束）するとは，X_nの分布関数をF_n(x)として，Gのすべての連続点xにおいて次が成り立つことであり，「F_n→_d G」と表します。

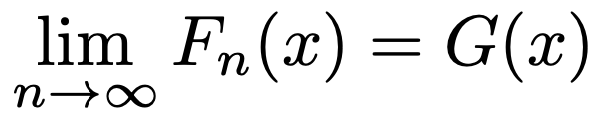
・大数の弱法則…確率変数の列X₁，X₂，…が平均μ，分散σ²の同一の分布に独立にしたがうとき，その標本平均はμに平均二乗収束します。
・中心極限定理…確率変数の列X₁，X₂，…が平均μ，分散σ²の同一の分布に独立にしたがうとき，その標本平均について，次の分布収束が成り立ちます。

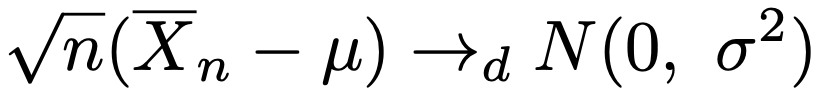
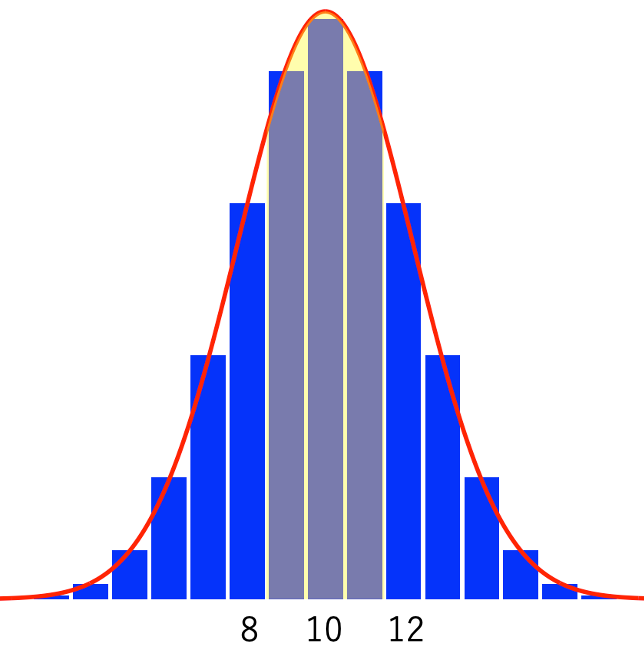
・連続修正…離散分布を中心極限定理によって正規分布で近似するとき，区間幅を0.5だけずらして近似の精度を上げる方法。例えば，X〜Bin(n，p)，Y〜N[np，np(1ーp)]として，P(a≦X≦b)はP(aー0.5≦Y≦b＋0.5)でよく近似できます。次の図で，黄色いアミかけ部分（8.5≦Y≦11.5）と二項分布のP(9≦X≦11)を比べてみてください。

※極値分布は出題されないと考えられるので省略。
・連続写像定理…X_n→_d Xで，関数hが連続であるとき，h(X_n)→_d h(X)が成り立ちます。
（例）{X_n}が平均μ，分散σ²の同一の分布に独立にしたがうとき，その標本平均について，中心極限定理によって次の分布収束が成り立ちます。

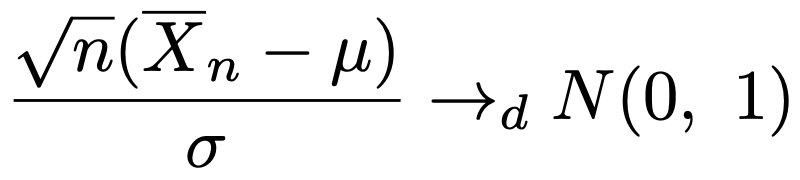
f(x)＝x²が連続関数であることから，連続写像定理により，次の分布収束が成り立ちます。

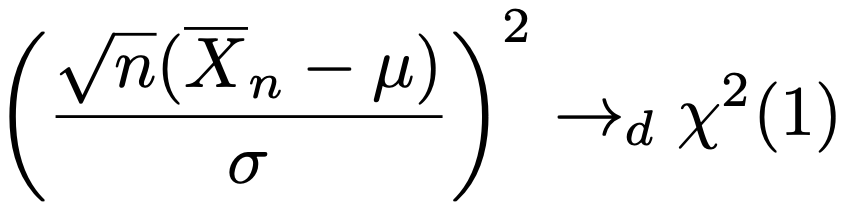
・スルツキーの補題…U_n→_d U，V_n→_p aであるとき，U_n＋V_n→_d U＋a，U_nV_n→_d aUが成り立ちます。
・デルタ法…次のように正規分布に分布収束する確率変数列U_n（サンプルサイズnの標本平均X___nなど）を考えます。

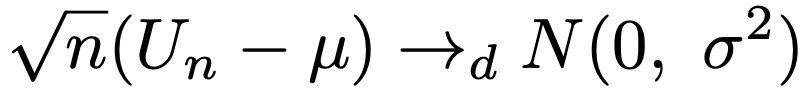
このとき，導関数が連続でh(μ)≠０を満たす関数hに対して次の分布収束が成り立ちます。

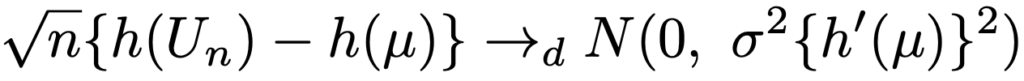
※多次元の分布収束は出題されないと考えられるので省略。

第８章　統計的推定の基礎

・統計的推定…次のような独立に同一の分布f(x；θ)にしたがう標本X₁，…，X_nの観測値をもとに，その分布のパラメータθを推測すること。標本の関数h(X₁，…，X_n)を用いて，パラメータの値を推定することを点推定，関数h(X₁，…，X_n)を推定量，観測値を代入したh(x₁，…，x_n)を推定値と言い，推定量のように標本のみの関数を統計量と言います。推定量の具体例としては標本平均や標本分散がありますが，これらは最尤法の説明の中で紹介します。
・順序統計量…同一の分布からの標本の観測値を次のように大きさの順に並べかえたもの。

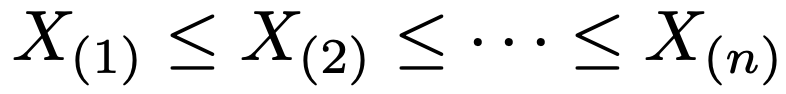
・モーメント…平均μの確率変数Xに対し，E[X]，E[X²]，…などのように，E[X^k]を原点まわりのk次のモーメントと言い，E[Xーμ]，E[(Xーμ)²]，…などのように，E[(Xーμ)^k]を平均まわりのk次のモーメントと言います。
・モーメント法…θ＝(θ₁，…，θ_k)とし，確率変数Xが確率密度関数f(x；θ)をもつ分布にしたがうとき，次のようにk次までのモーメントがθの関数として表されている場合を考えます。

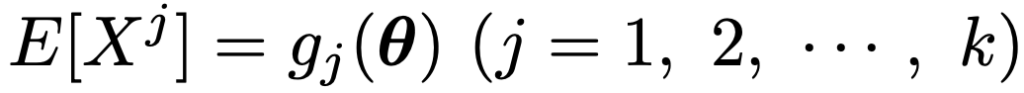
このとき，j次のモーメントを次のように(1/n)ΣX^jでおきかえ，これを母数について解くことで母数の推定量を得る方法をモーメント法と言います。

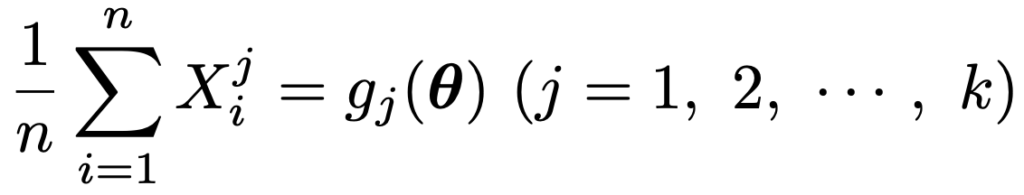
・最尤法…尤度が最大になるようにパラメータの推定値を決める方法。まず，確率密度関数f(x；θ)をもつ同一の分布に独立にしたがう標本の観測値をx₁，…，x_nとして，次の式をθの関数と見たものを尤度関数と言います。

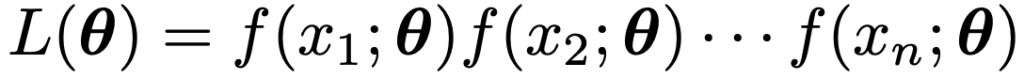
尤度関数L(θ)が微分可能であるとき，L(θ)が最大になるようなθを求めるためには，L(θ)を微分するか，対数をとったlogL(θ)（対数尤度関数）を微分して，導関数が０になるようなθの値を求めます。L(θ)が最大になるようなθは最尤推定値と呼ばれ，それを確率変数として表したものを最尤推定量と言います。母数θの関数g(θ)の最尤推定量はθの最尤推定量を関数gで変換したものに等しく，これを不変性と言います。
（例）期待値μと分散σ²が未知の正規分布に独立にしたがう標本をX₁，…，X_nとして，μの最尤推定量は次の標本平均です。

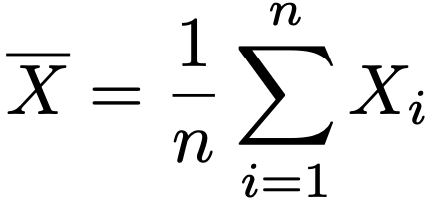
また，σ²の最尤推定量は次の標本分散です。

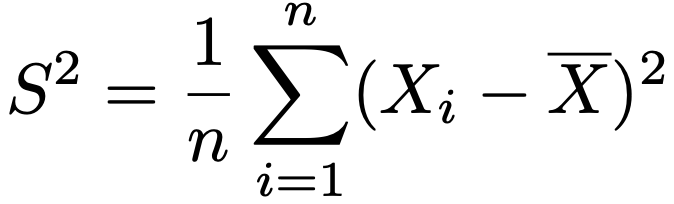
標本平均と標本分散は一致性をもちます。つまり，n→∞のとき，母数の真値に確率収束します。
・漸近正規性…確率密度関数f(x；θ)をもつ同一の分布に独立にしたがう確率変数をX₁，…，X_nとし，θの最尤推定量をハットをつけて表すと，n→∞のとき，適当な正則条件のもとで次の分布収束が成り立ちます。

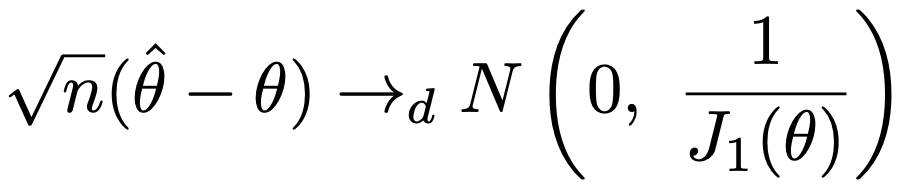
上のJ₁(θ)は，次のフィッシャー情報量でn＝１としたものです。

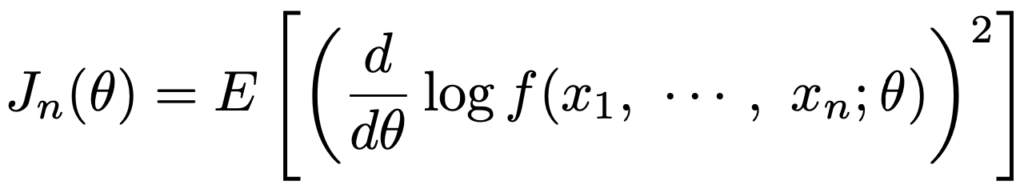
フィッシャー情報量は，ある条件のもとで次のようにも表せます。

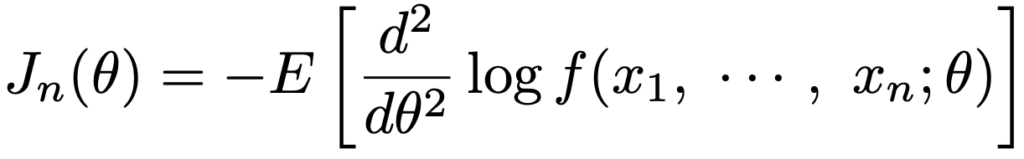
・バイアス・バリアンス分解…確率密度関数f(x；θ)をもつ分布について，θの推定量をハットをつけて表すと，次の式の左辺が平均２乗誤差で，右辺第１項のθハットの分散（バリアンス）と，第２項のバイアスの２乗の和に一致します。

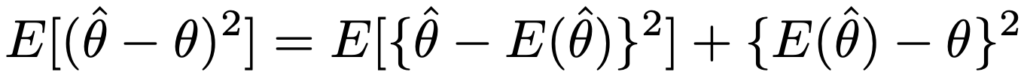
・不偏推定量…母数θに対して，バイアスが０である推定量（期待値が母数の真値に一致する推定量）。例えば，最尤法の説明の中で紹介した標本分散は母分散の不偏推定量ではありませんが，次の不偏分散は母分散の不偏推定量です。

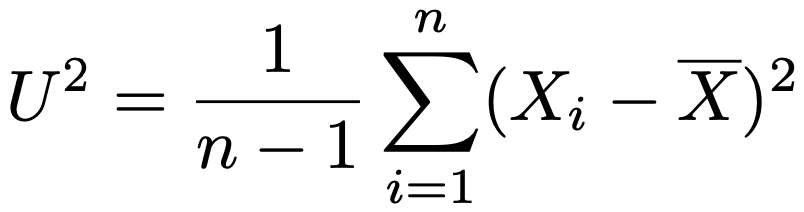
・ジャックナイフ推定量…バイアスのある推定量について，次の方法でバイアスを補正したもの。
①標本X₁，…，X_nから求められるθの推定量（バイアスあり）を考える
②X₁を取り除き，X₂，…，X_nから①と同じように求めたθの推定量をθ₍₁₎，X₂を取り除き，X₁，X₃，…，X_nから①と同じように求めたθの推定量をθ₍₂₎，…とし，θ₍₁₎，θ₍₂₎，…，θ_(n)の平均を求める
③新しい推定量をn×①ー(nー1)×②とする
・一様最小分散不偏推定量（UMVUE）…不偏推定量の中で，分散が最小であるもの。
※最小２乗法，ガウス・マルコフの定理，BLUEについては，第16章で紹介します。
・クラメール・ラオの不等式…不偏推定量の分散の下限を与える次の不等式のこと。（ワークブックでは「クラーメル」と書かれているが誤植）

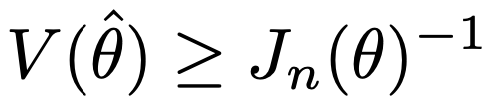
・漸近有効推定量…n→∞のとき，分散がクラメール・ラオの下限を達成する一致推定量。
・有効推定量…不偏推定量の中で，クラメール・ラオの下限を達成するもの。有効推定量はUMVUEです。
・十分統計量…確率（密度）関数f(x；θ)をもつ同一の分布に独立にしたがう確率変数をX₁，…，X_nとし，X＝(X₁，…，X_n)の実現値をx＝(x₁，…，x_n)とするとき，統計量T(X)がθに関する十分統計量であるとは，T(X)＝tを与えたときのX＝xの条件付き確率がθに依存しないことを言います。そして，T(X)がθに関する十分統計量であることは，Xの同時密度関数f(x；θ)が次の式の右辺のように分解できることと同値です。

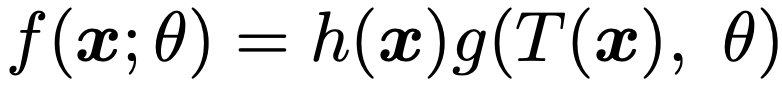
つまり，θに依存する部分は，T(x)の関数として表せるということで，これをフィッシャー・ネイマンの分解定理と言います。
（例）互いに独立にパラメータλのポアソン分布にしたがう確率変数をX₁，…，X_nとすると，同時確率関数は次のようになります。

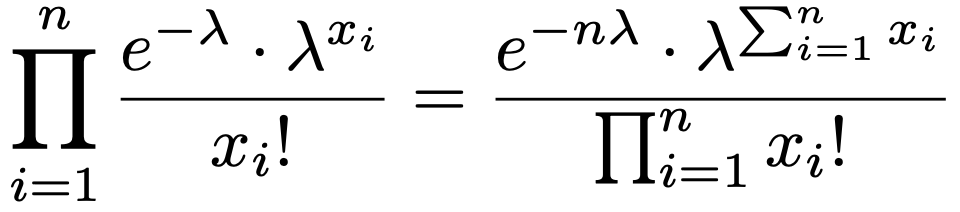
パラメータλに依存する部分はΣx_iの関数として表せるので，Σx_iがλの十分統計量です。

第９章　区間推定

母集団分布が正規分布である場合の母平均の区間推定と母分散の区間推定はいずれも２級内容のため，統計検定２級のチートシートを参照してください。また，多項分布の信頼区間は，実質的に母比率の区間推定と同じなので，これも統計検定２級のチートシートを参照してください。
・分散の比の区間推定…２つの正規母集団の無作為標本（標本の大きさはそれぞれn_A，n_B）から求められる不偏分散をそれぞれU_A²，U_B²とし，これらが独立であるものとします。２つの正規母集団の母分散をσ_A²，σ_B²とおくとき，信頼度95％の信頼区間は次の不等式で計算します。

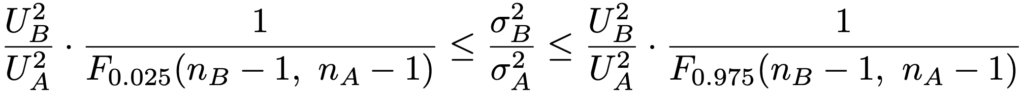
ただし，上の不等式に出てくるF_0.025(n_Bー１，n_Aー１)とF_0.975(n_Bー１，n_Aー１)は，それぞれ自由度(n_Bー１，n_Aー１)のF分布の上側2.5％点と上側97.5％点を表しています。
・多項分布の差の信頼区間…(X₁，X₂，…，X_k)〜M(n，p₁，p₂，…，p_k)のとき，p₁ーp₂の信頼度95％の信頼区間は次の不等式で計算します。

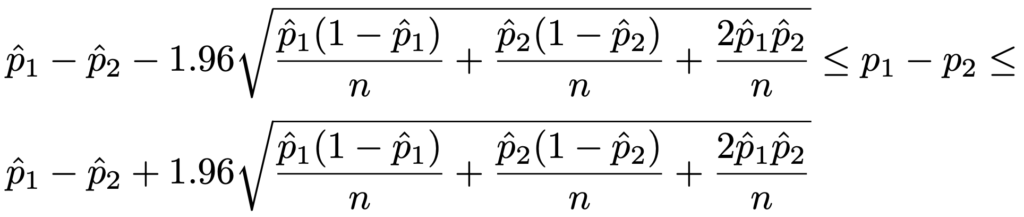
ただし，上の不等式でp₁，p₂にハットをつけた記号は，X₁，X₂の実現値をx₁，x₂として，次の標本比率を表しています。

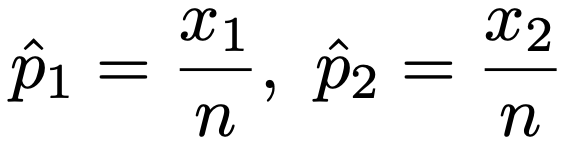
第10章　検定の基礎と検定法の導出

次の手順により，母数に関する２つの仮説のうち，データによって支持されるものを選ぶ手法。（２級内容のため，用語については統計検定２級のチートシートを参照）

1. 母数に関して，帰無仮説（否定したい仮説）と対立仮説（正しいことが期待される仮説）を設定する。
2. 帰無仮説を仮定したもとでの検定統計量の確率分布を求め，有意水準と棄却域を決める。
3. 検定統計量の実現値が棄却域に落ちれば帰無仮説を棄却（否定すること）し，そうでなければ帰無仮説を受容する。

・検出力とサンプルサイズ…母比率pに関する有意水準2.5％の片側検定で，帰無仮説をp＝p₀，対立仮説をp＝p₁(p₁＞p₀)として，サンプルサイズnが十分に大きいとき，標本比率は近似的に正規分布にしたがい，それぞれの仮説のもとでの分布は次の図のように表せます。

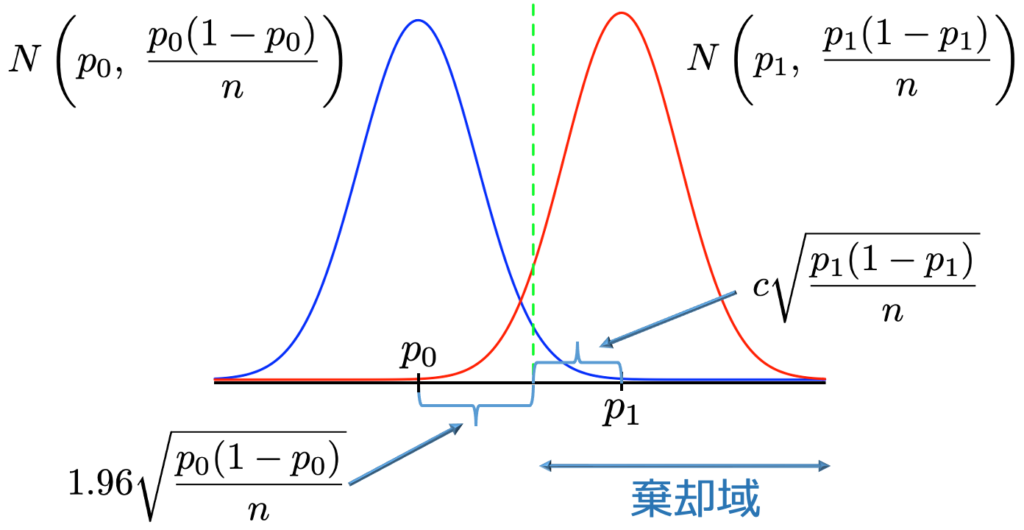
このときの棄却限界値は次の値です。

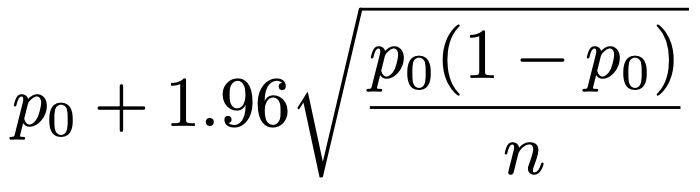
対立仮説のもとでの正規分布の曲線下面積のうち，上の棄却限界値を超える部分が検出力になるので，棄却限界値がp₁から標準偏差の何倍離れているか（上の図のc）がわかれば，検出力が計算できます。p₁ーp₀は帰無仮説のもとでの標準偏差の1.96倍と，対立仮説のもとでの標準偏差のc倍の和に等しいという次の関係式が成り立つので，p₀，p₁に加えて，サンプルサイズnが与えられれば検出力が求められ，逆に検出力が与えられればサンプルサイズnが求められます。

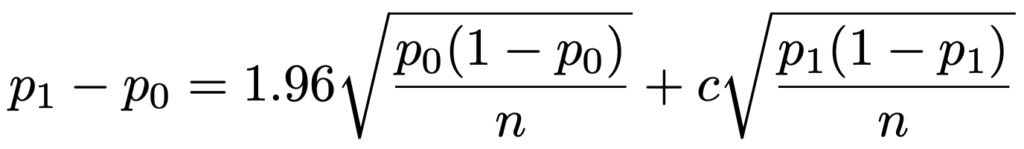
・生産者危険…帰無仮説が正しいときに，誤って帰無仮説を棄却してしまう誤りが第一種の過誤ですが，これを生産者危険とも言います。なぜなら，生産者が正しく管理できている状態を帰無仮説とすると，正しく管理できているのに，抜取検査でたまたま不良品が多く観測されて出荷できなくなった場合，生産者が損失を被るからです。帰無仮説のもとでの不良品率をp₀，サンプルサイズをnとすると，不良品数が合格規準値のcを超えてしまう確率は次のように計算できます。

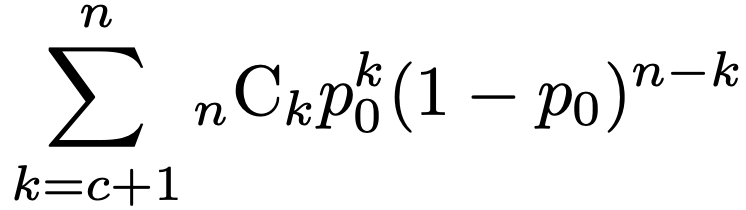
・消費者危険…対立仮説が正しいときに，誤って帰無仮説を受容してしまう誤りが第二種の過誤ですが，これを消費者危険とも言います。なぜなら，生産者が正しく管理できていない状態を対立仮説とすると，正しく管理できていないのに，抜取検査でたまたま不良品が少なく観測されて出荷してしまった場合，消費者が損失を被るからです。対立仮説のもとでの不良品率をp₁，サンプルサイズをnとすると，不良品数が合格規準値のc以内となる確率は次のように計算できます。

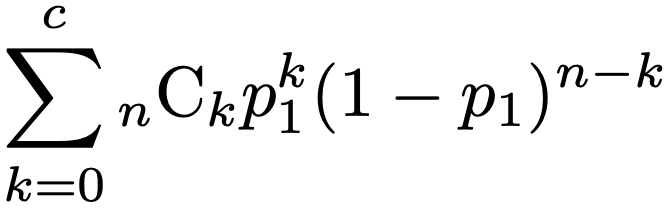
第11章　正規分布に関する検定

母集団分布が正規分布であることを仮定する検定。１標本の平均の検定（母分散が既知・未知），２標本の平均の検定（母分散が既知・未知で等しい），１標本の分散の検定，２標本の等分散の検定はいずれも２級内容のため，統計検定２級のチートシートを参照してください。

第12章　一般の分布に関する検定法

母比率の検定と母比率の差の検定は２級内容のため，統計検定２級のチートシートを参照してください。
・ポアソン分布に関する検定…λが大きいとき，Po(λ)はN(λ，λ)で近似できるため，λ＝λ₀を帰無仮説として，次の統計量が近似的に標準正規分布にしたがうと考えて検定することが可能。

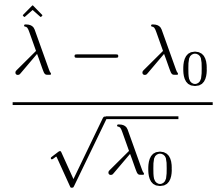
・無相関の検定…(X，Y)が２変量正規分布にしたがうとき，帰無仮説を「母相関係数＝０」，対立仮説を「母相関係数≠０」，サンプルサイズをn，ピアソンの相関係数(２級で学習する相関係数)をRとして，次の検定統計量が帰無仮説のもとで自由度nー２のt分布にしたがうことを利用します。

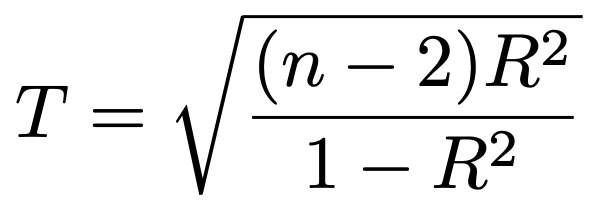
・適合度検定…(X₁，…，X_k)〜M(n，p₁，…，p_k)（X₁＋…＋X_k＝n，p₁＋…＋p_k＝１）のとき，帰無仮説p₁＝p₁₀，…，p_k＝p_k0のもとでの期待度数はnp₁₀，…，np_k0となります。nが大きいとき，実現値をx₁，…，x_kとして，次の検定統計量が帰無仮説のもとで近似的に自由度kー１のカイ２乗分布にしたがうことを利用して検定します。

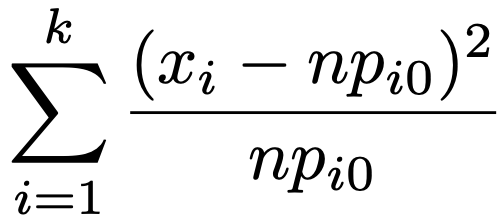
また，帰無仮説にℓ個のパラメータが含まれる場合，パラメータに最尤推定値をあてはめて期待度数を計算し，上の検定統計量が帰無仮説のもとで近似的に自由度kーℓー１のカイ２乗分布にしたがうことを利用します。
また，度数が極端に小さいカテゴリーがある場合には，検定統計量の分子を(|x_iーnp_i0|ー0.5)²とおきかえることがあり，これをイエーツの補正と言います。これによって，検定統計量の実現値は小さくなり，第一種の過誤を犯しにくく（第二種の過誤は犯しやすく）なります。

・尤度比検定…確率（密度）関数f(x；θ)に対して，最尤推定値を代入した尤度を分子，帰無仮説のもとでの最尤推定値を代入した尤度を分母とする次のような尤度比λを考えます。

ただし，帰無仮説は次のようにパラメータベクトルθの一部分θ₁を定数に固定するものとします。

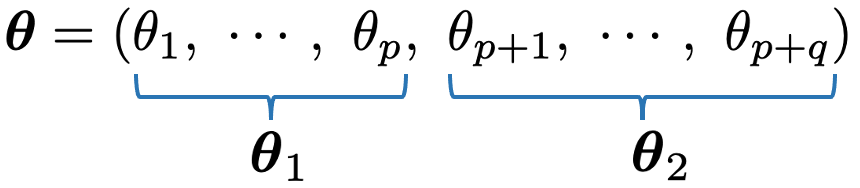
このとき，帰無仮説のもとで，サンプルサイズが大きいときに近似的に，2logλは自由度pのカイ２乗分布にしたがうことを利用して検定を行うことができます。
※尤度比検定の例は第28章を参照。

第13章　ノンパラメトリック法

母集団が特定の確率分布にしたがうことを仮定しない仮説検定。母集団が特定の確率分布にしたがうことを仮定するパラメトリック法との対応関係は次の通りです。

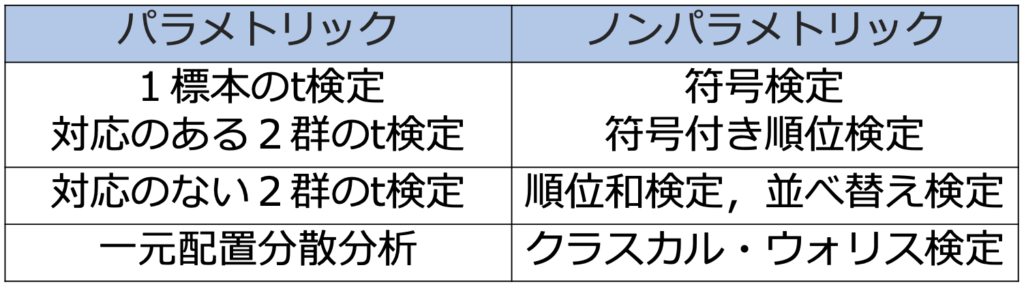
・符号検定…１群の検定または対応のある２群の差の検定。対応のある２群（XとY）の場合には，Z＝XーYとおきます。
帰無仮説：Zの中央値＝０，対立仮説：Zの中央値＞０など
（手順１）Zの符号が「＋のデータ」と「ーのデータ」に分ける。０のデータは除く。
（手順２）＋であるZの個数Tを検定統計量，サンプルサイズをnとして，帰無仮説のもとでTはBin(n，1/2)にしたがうことを利用してP値を計算。または，サンプルサイズnが大きいときには，Bin(n，1/2)がN(n/2，n/4)で近似できることを使う。

・符号付き順位検定…１群の検定または対応のある２群の差の検定。対応のある２群（XとY）の場合には，Z＝XーYとおきます。
帰無仮説：Zの中央値＝０，対立仮説：Zの中央値＞０など
（手順１）Zの符号が「＋のデータ」と「ーのデータ」に分ける。０のデータは除く。
（手順２）|Z|に小さい順に１からはじまる順位をつける。
（手順３）「＋のデータ」（または「ーのデータ」）の順位の合計を検定統計量とする。
（手順４）サンプルサイズnが大きく，タイ（同順位）がなければ，検定統計量が近似的に次の正規分布にしたがうことを利用して検定を行う。

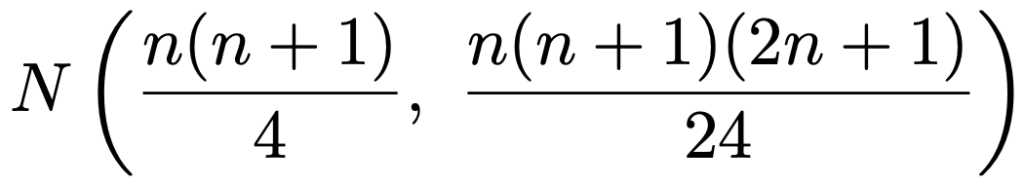
・ウィルコクソンの順位和検定…対応のない２群の差の検定。２群の分布形が似ていることを仮定。
帰無仮説：２群の分布にズレがない，対立仮説：２群の分布にズレがあるなど
（手順１）２群のデータをひとまとめにして，値が小さい順に順位をつける。
（手順２）一方の群の順位和を計算し，検定統計量とする。
（手順３）２群のサンプルサイズm，nが大きく，タイ（同順位）がなければ，検定統計量が近似的に次の正規分布にしたがうことを利用して検定を行う。

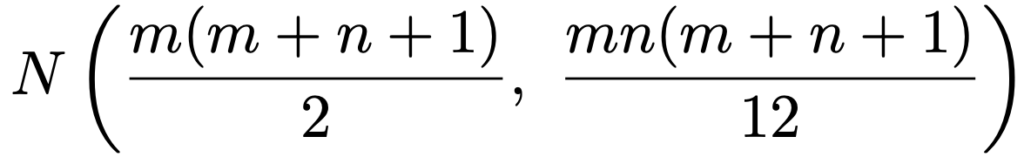
サンプルサイズが極めて小さい場合には，次の並べ替え検定と同じ方法でP値を直接求めることも可能です。

・並べ替え検定…対応のない２群の差の検定。
帰無仮説：２群の母集団は共通である，対立仮説：２群の母集団は異なる
（手順１）一方の群（サイズをmとする）のデータの平均を計算し，検定統計量とする。
（手順２）標本からサイズmのデータを抽出して得られる平均の分布をつくり，P値を求める。

・クラスカル・ウォリス検定…３群以上の差の検定。分散分析とは異なり，母集団分布が正規分布であることを仮定することなく，データを順位におきかえて，群ごとに違いがあるかどうかを検定します。帰無仮説は「すべての群の分布が等しい」，対立仮説は「少なくとも１つの群の分布が異なる」であり，群の数をk，群ごとのサンプルサイズをn₁，…，n_k(n₁＋…＋n_k＝N)，群ごとの順位の合計をR₁，…，R_k，群ごとの順位の平均をR__₁，…，R___kとして，タイ（同順位）がなければ検定統計量は次のようになります。

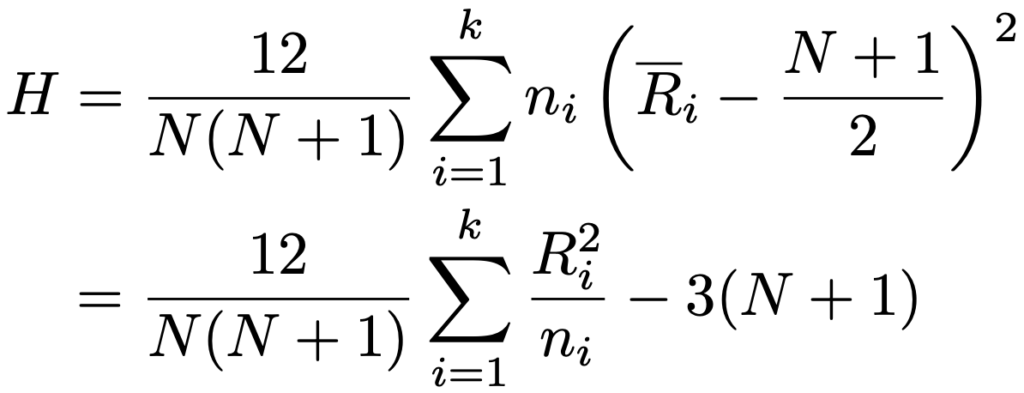
この検定統計量が，サンプルサイズが大きいときに近似的に自由度kー１のカイ２乗分布にしたがうことを利用して検定を行います。

・順位相関係数…２変量データを順位におきかえて計算した相関係数であり，外れ値の影響を受けにくいという特徴があります。サイズnの２変量データを順位におきかえたものを(x₁，y₁)，…，(x_n，y_n)とすると，タイ（同順位）がなければ，x₁〜x_nの平均と，y₁〜y_nの平均が(n+1)/2であることから，xとyの相関係数は次のように計算できます。

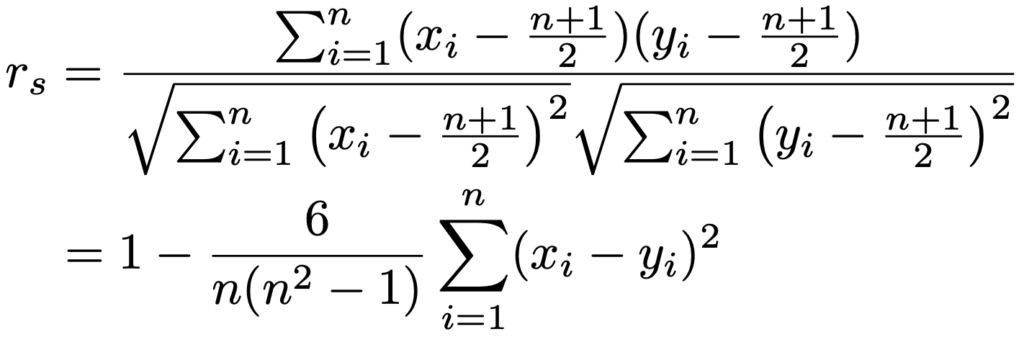
上のr_sをスピアマンの順位相関係数と言います。

一方で，(x_i，y_i)と(x_j，y_j)（i≠j）の２組の順位データについて，(x_iーx_j)(y_iーy_j)が正ならば＋１，(x_iーx_j)(y_iーy_j)が負ならばー１として，n(n-1)/2組の平均を計算したものがケンドールの順位相関係数であり，(x_iーx_j)(y_iーy_j)が正になる組の数をP，負になる組の数をNとして，次の式で表せます。

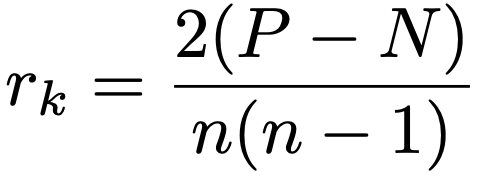
第14章　マルコフ連鎖

{1，2，…，N}のいずれかの値をとる確率変数X_nを，時点n＝0，1，2，…の順に並べた確率変数列X₀，X₁，X₂，…が，次の式を満たすとき，この確率変数列をマルコフ連鎖と言います。

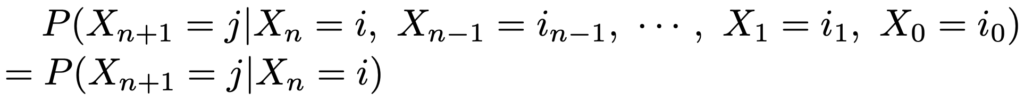
とりうる状態の全体{1，2，…，N}を状態空間と言い，iやjは{1，2，…，N}のいずれかを表します。このような条件付き確率がnによらずにiとjだけで決まる場合を斉時的と言い，その場合だけを考えれば十分です。
・状態確率ベクトル…時点nでそれぞれの状態にある確率を並べたベクトルπ_n＝(p_n(1)，…，p_n(N))のこと。特に，π₀を初期分布と言います。
・推移確率行列…π_n+1＝π_nQを満たし，時点nの各状態から時点n＋１の各状態へ移る確率をまとめたN次正方行列Q。
・定常分布…π＝πQを満たす状態確率ベクトルπのこと。ある条件のもとで，マルコフ連鎖はただ１つの定常分布をもちます。
・パラメータの推定…推移確率行列がパラメータθを含むとき，観測データX₀＝x₀，X₁＝x₁，…，X_n＝x_nを用いてθを最尤推定するには，次の変形を利用します。

初期分布P(X₀＝x₀)が定数として与えられれば，同時確率P(X₀＝x₀，X₁＝x₁，…，X_n＝x_n)は推移確率行列の成分の積で表せ，θの関数になります。これを尤度関数として，最尤推定値を求めます。

第15章　確率過程の基礎

・確率過程…X₁，X₂，…のような確率変数列X＝(X_t)を離散時間の確率過程，tが０以上のすべての実数をとるとき，X＝(X_t)を連続時間の確率過程と言います。
・ブラウン運動…離散時間の確率過程であるランダムウォークの時間間隔を短くした極限として得られる連続時間の確率過程で，次の条件を満たすB＝(B_t)のこと。
① B₀＝０でBのパスは連続
②【独立増分性】任意の時間分割０＝t₀＜t₁＜…＜t_nに対して，次のようなn個の増分は互いに独立

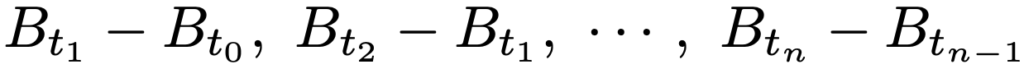
③【定常増分性】任意のt＞s≧０に対して，増分は，次のような正規分布にしたがう

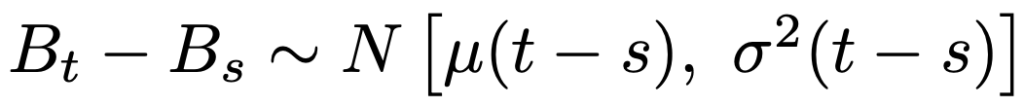
ブラウン運動のパラメータμ，σは，一定の時間間隔Δで観測したときの増分Z_kがN(μΔ，σ²Δ)にしたがうことを利用して，次の式によって推定します。

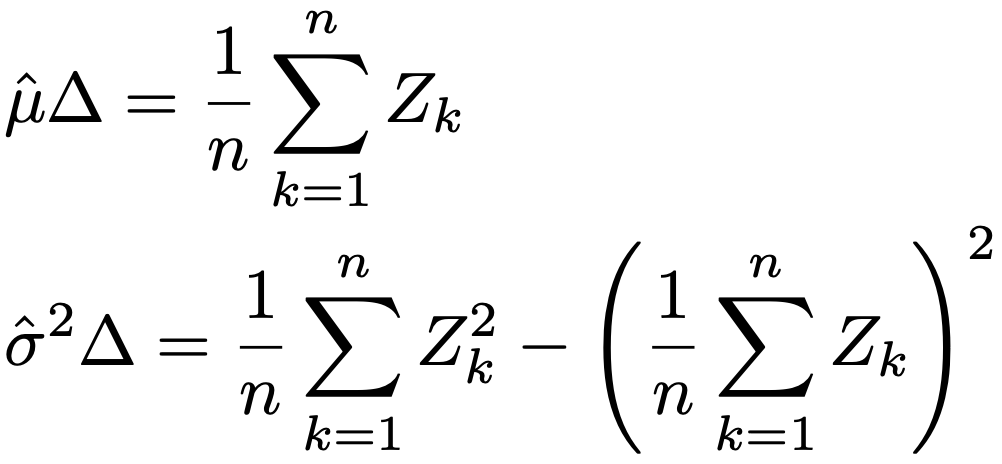
・ポアソン過程…店に訪れる客の数のように，０以上の整数値をとる連続時間の確率過程で，次の条件を満たすN＝(N_t)が強度λのポアソン過程です。
① N₀＝０
②【独立増分性】任意の時間分割０＝t₀＜t₁＜…＜t_nに対して，次のようなn個の増分は互いに独立

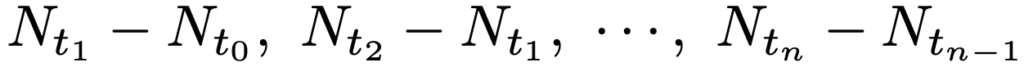
③【定常増分性】任意のt＞0，s≧０に対して，

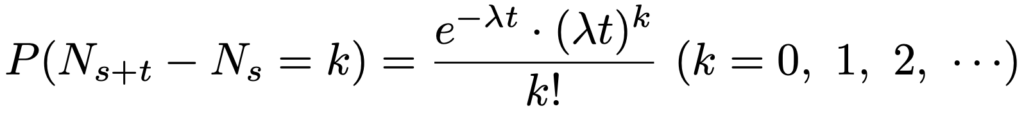
強度λのポアソン過程で，n番目のイベントの発生時刻をT_nとして，発生時間間隔W_n＝T_nーT_n-1はパラメータλの指数分布にしたがうことから，ポアソン過程のパラメータλは，観測されたイベントの総回数を観測時間でわった値によって推定できることがわかります。
・複合ポアソン過程…あとの①，②の条件のもとで，次の式で定まる確率過程X＝(X_t)

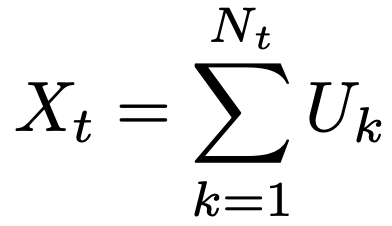
① N＝(N_t)はポアソン過程
② (U_k)は独立に同じ分布にしたがう確率変数列で，Nとも独立

複合ポアソン過程X＝(X_t)について，E[N_t]＝λt，E[U_k]＝μ，V[U_k]＝σ²のとき，E[X_t]＝λμt，V[X_t]＝λt(μ²＋σ²)が成り立ちます。

第16章　重回帰分析

観測値ベクトルy＝(y₁，…，y_n)^T，説明変数行列X＝(x_ij)，回帰係数ベクトルβ＝(β₀，…，β_d)^T，誤差ベクトルε＝(ε₁，…，ε_n)^Tに対し，y＝Xβ＋εは，次のようにn本の式をまとめたものです。

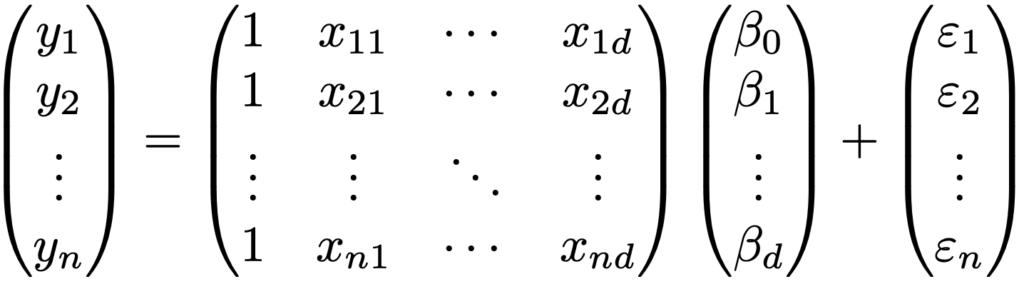
・最小２乗法…Xを定数行列とみなし，X^TXが正則であるならば，誤差平方和ε^Tεが最小になるようなβは次の式のように求められます。

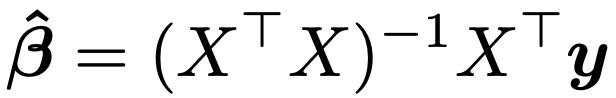
これを最小２乗推定量と言います。E[ε]＝０であるとき，最小２乗推定量はβの不偏推定量です。また，誤差ベクトルεの分散共分散行列がV[ε]＝E[ε^Tε]＝σ²Iと表されるとき，最小２乗推定量の分散共分散行列はσ²(X^TX)^ー1となります。最小２乗推定量はβの最良線形不偏推定量（BLUE）であり，これをガウス・マルコフの定理と言います。
最小２乗推定量を用いてつくった回帰式から予測される値を並べて，次のように予測値ベクトルを定めます。

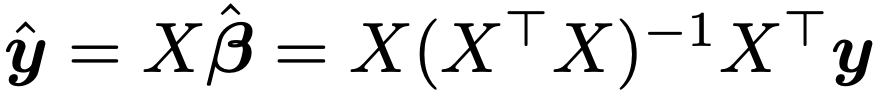
また，残差ベクトルは，観測値ベクトルと予測値ベクトルの差として，次のように定めます。

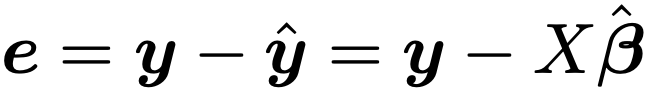
残差の自由度はnーdー1であり，残差平方和e^Teをその自由度でわったものが誤差分散σ²の不偏推定量になります。
・決定係数…次の式のような総変動に対する回帰変動の割合のこと。０以上１以下の値をとり，１に近いほど回帰式のデータへのあてはまりが良いと解釈できますが，モデルの予測性能を表すものではありません。また，説明変数を増やすだけで値が大きくなってしまうという欠点があります。

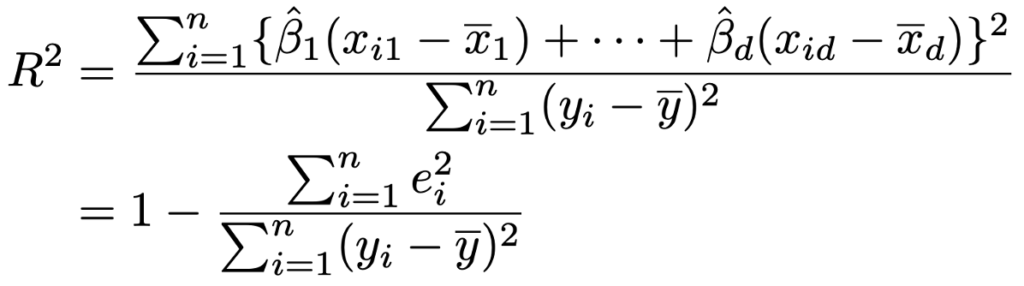
・自由度調整済み決定係数…次の式のように，決定係数に自由度による調整を加えたもので，説明変数を増やしただけでは必ずしも値が大きくはなりません。

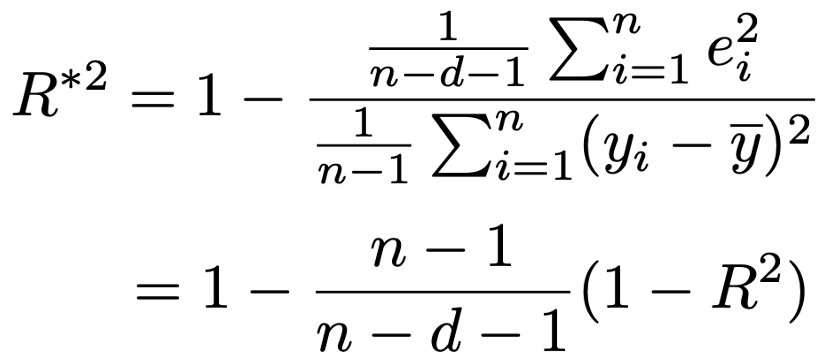
・回帰係数の推定と検定…誤差ベクトルεがn変量正規分布N(０，σ²I)にしたがうことを仮定すると，最小２乗推定量は(d＋1)変量正規分布N(β，σ²(X^TX)^ー1)にしたがうことを利用して，回帰係数の推定や検定を行うことができます。例えば，β_i＝０を帰無仮説とするとき，（β_iの推定量）/（β_iの標準誤差）は自由度nーdー1のt分布にしたがい，β₁＝β₂＝…＝β_d＝０を帰無仮説とするとき，次の統計量が自由度(d，nーdー1)のF分布にしたがうことを利用します。

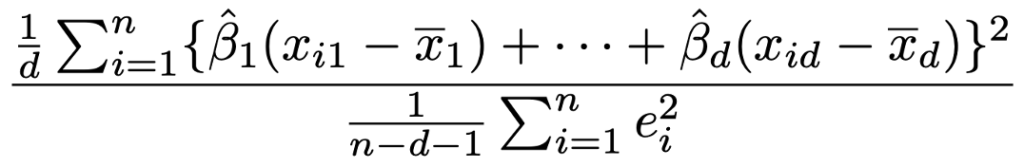
・一般化最小２乗法…回帰モデルの誤差項が不均一分散であったり，相関がある場合には，通常の最小２乗推定量はBLUEではなくなり，適切な変換を組み込んだ一般化最小２乗推定量がBLUEになります。
・正則化…例えば，多項式回帰モデルy＝β₀＋β₁x＋…＋β_dx^dの次数を十分に大きくすると，誤差２乗和を０にすることができますが，非常に大きな絶対値の回帰係数を用いて学習データに無理やり合わせたモデルとなってしまいます（過学習）。これでは予測性能の面で使いものにならないので，正則化項を追加することで回帰係数の絶対値を制御し，モデルが複雑になりすぎないようにします。
・L₂正則化（リッジ回帰）…定数項を除くパラメータの２乗和を正則化項として，次の式全体が最小になるようにパラメータを推定します。

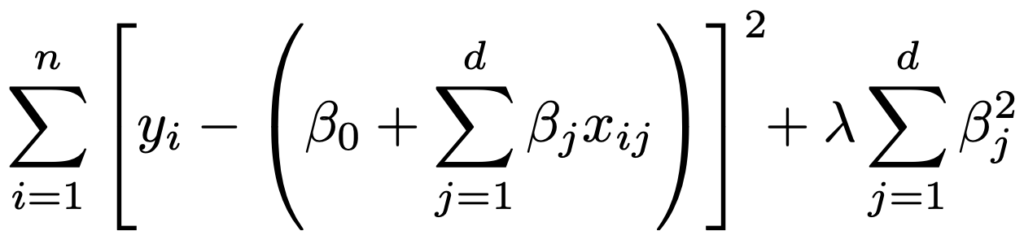
λは正則化パラメータと呼ばれ，λ＝０ならば通常の最小２乗法と一致します。λを大きくすると，正則化項の影響が大きくなり，回帰係数は０に近い値をとるようになります。
・L₁正則化（Lasso回帰）…定数項を除くパラメータの絶対値の和を正則化項として，次の式全体が最小になるようにパラメータを推定します。

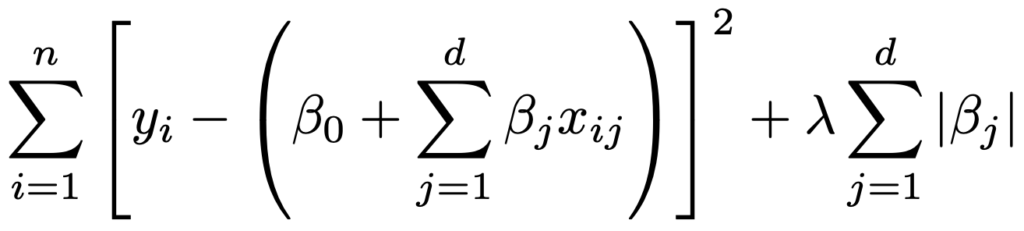
回帰係数の値の多くを，０に近い値ではなく，０と推定する傾向（スパース性）があるため，パラメータの推定とモデル選択を同時に行うことができます。なお，正則化パラメータλの適切な値を決める方法としては，第30章で説明する交差検証法があります。
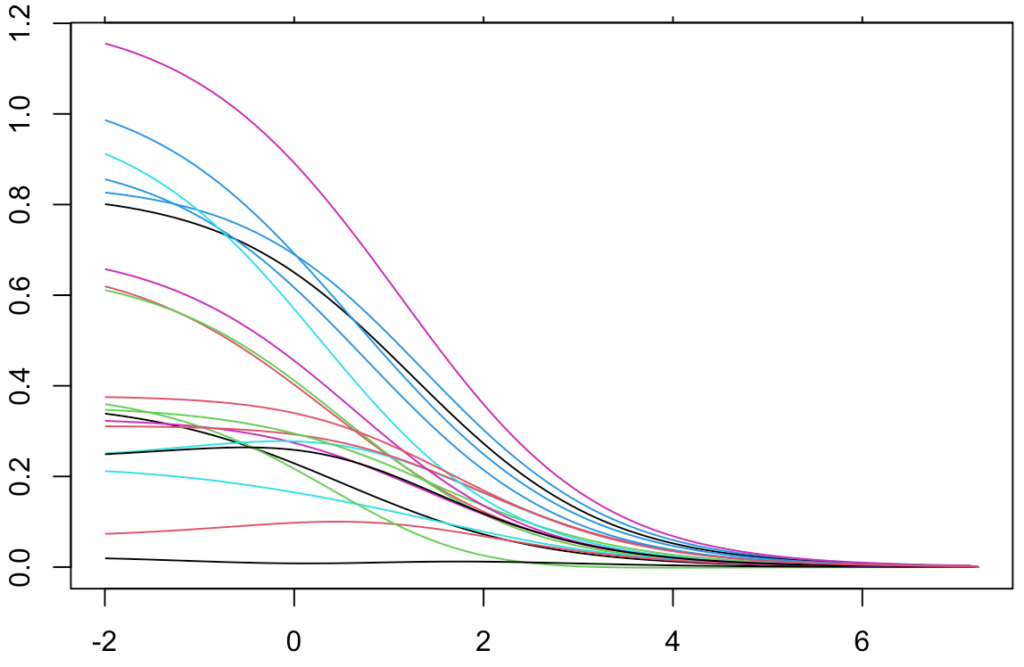
・正則化パス…横軸にlogλ，縦軸に回帰係数の値をとり，正則化パラメータの値の変化に対して，それぞれの回帰係数の値の変化をグラフにしたものです。次のグラフはリッジ回帰における正則化パスの例です。logλが大きくなると，回帰係数が０に近い値になっていくことが見てとれます。

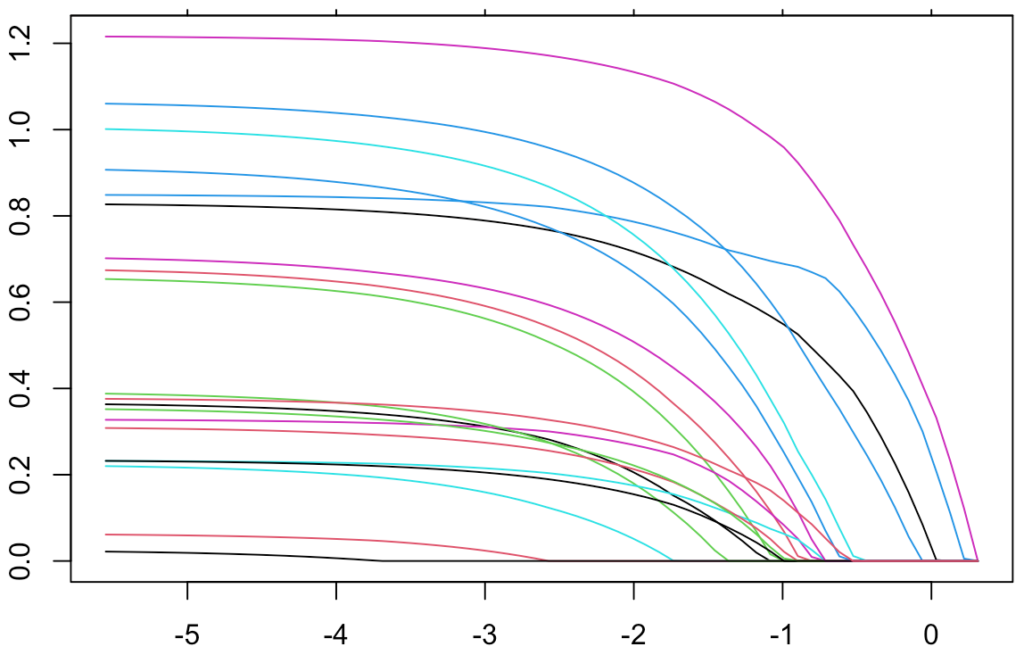
次のグラフはLasso回帰における正則化パスの例です。logλが大きくなるにつれて，回帰係数が真に０になるものが増えていくことが見てとれます。

・Elastic Net…L₁正則化とL₂正則化を混ぜたもので，変数選択と係数の縮小を同時に行います。変数間の相関が高い場合などに有効です。
・Fused lasso…隣接する回帰係数の差に罰則を課すL₁正則化で，隣接する回帰係数が同じ値になりやすくなります。時系列データなどに適用すると，時間的に滑らかな変化を示すモデルを構築できます。

※Mallows’C_p規準は出題されないと考えられるので省略。

第17章　回帰診断法

・残差プロット…単回帰モデルの誤差項u_i＝y_iー(α＋βx_i)は，y_iの変動をα＋βx_iで説明した後の残りを表していて，残差は０を中心としてランダムに散らばる必要があります。この前提が満たされているかどうかを確認するために利用するのが次の図のような残差プロットで，横軸にx_iやy_i，縦軸に残差（を標準偏差でわったもの）をとります。

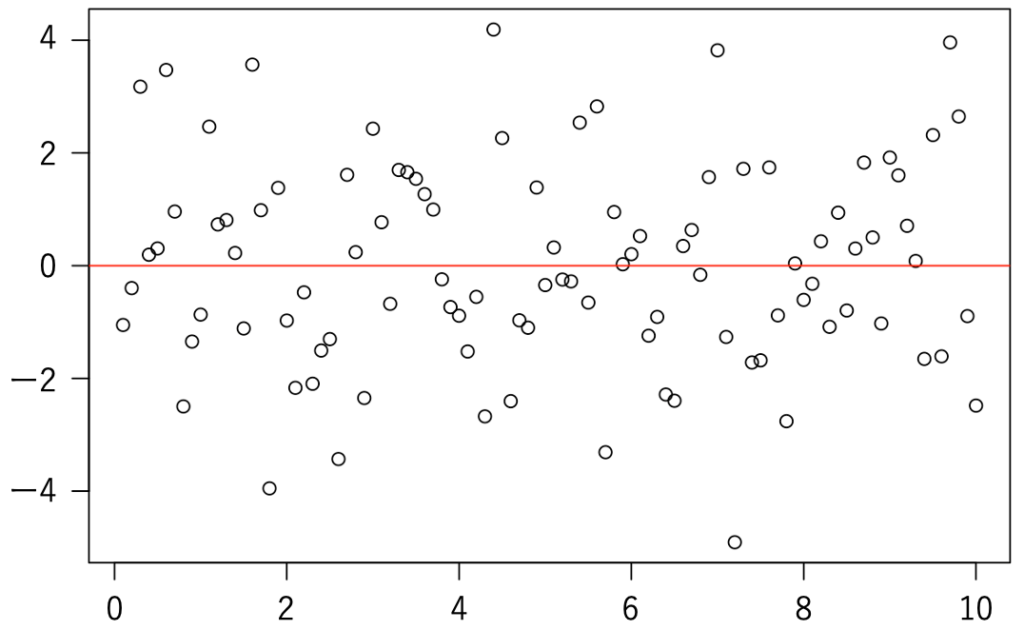
・正規Q-Qプロット…標準化した残差の分位点を縦軸（y），正規分布の理論的分位点を横軸（x）とした次のような図で，残差に正規性があれば，プロットはy＝xに沿って並びます。

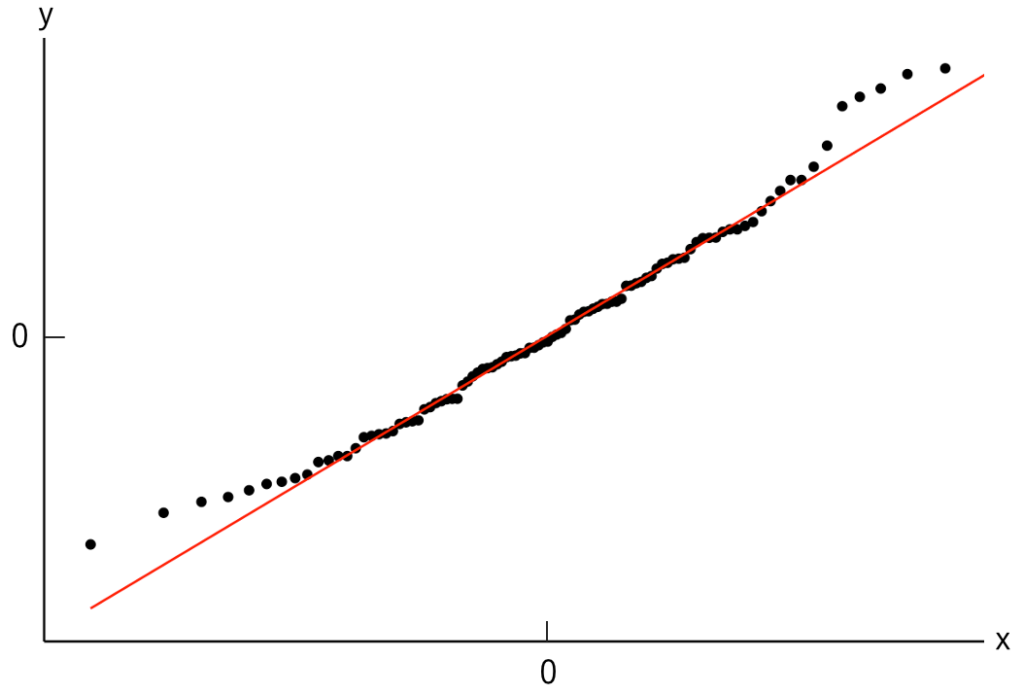
・leverage(てこ比)…最小２乗法による予測値X(X^TX)^ー1X^Tyにおける行列X(X^TX)^ー1X^Tの対角成分h_iiのことで，h_iiの値が大きいときにはy_iの回帰係数への影響が大きいことから，外れ値の候補になります。
・Cookの距離…サイズnの全サンプルから特定のデータ(x_i，y_i)を除いたサイズnー1のデータから推定したときに回帰係数が大きく変化するのかを調べるもので，標準化された残差の２乗とh_ii/(1ーh_ii)に比例します。Cookの距離が大きい観測値は，モデルへの影響が大きく，外れ値であることが疑われます。
※系列相関とDW比は第27章を参照。

第18章　質的回帰

・一般化線形モデル…次の式のように，X₁，…，X_kを与えたもとでのYの条件付き期待値が，１対１の関数gを用いてX₁，…，X_kの一次結合になるようなモデル。gはYの条件付き期待値を右辺の線形予測子と結びつける役割を果たしており，リンク関数と呼ばれます。また，期待値を計算するもとになる確率分布を誤差構造と呼びます。

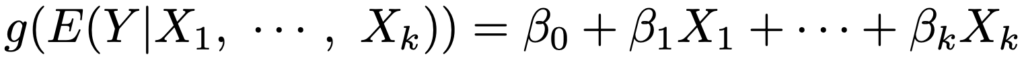
一般化線形モデルの代表的なものは次の表の通りです。

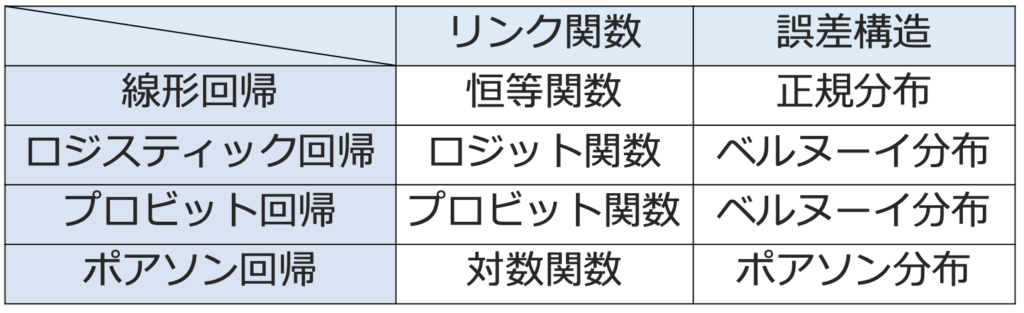
線形回帰の目的変数（応答変数）は量的変数ですが，応答変数が２値の質的変数の場合の代表的なモデルには，次のロジスティック回帰モデルとプロビット回帰モデルがあります。
・ロジスティック回帰モデル…β^Tx＝β₀＋β₁x₁＋…＋β_kx_kとして，応答変数yが２値（０と１）をとる確率を，次のようにモデル化します。

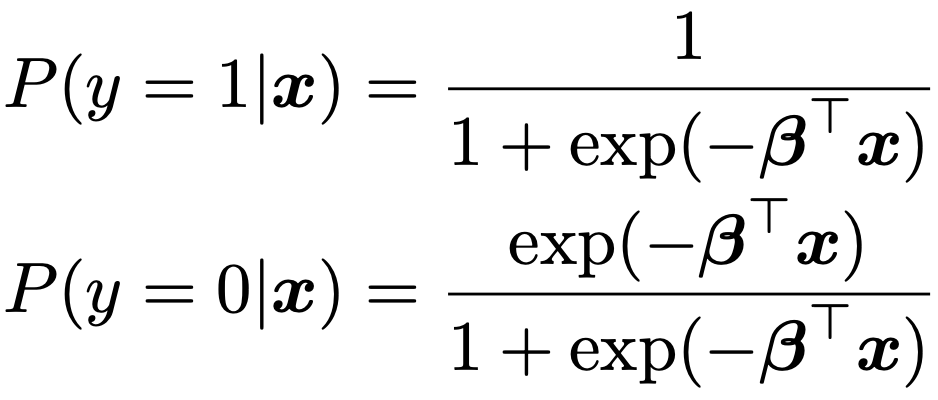
このモデルは，x_iが与えられたもとで応答変数y_iが１をとる確率（条件付き期待値）をπ_iとして次のようにも表せます。

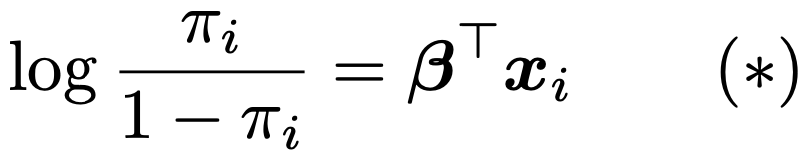
上の式の左辺はπ_iの対数オッズです。左辺の関数はロジット関数と呼ばれ，π_i→(π_iの対数オッズ)の変換をロジット変換と言います。ロジスティック回帰モデルはロジット関数をリンク関数とする一般化線形モデルです。この式から，他の説明変数の値を固定したまま，j番目の説明変数x_ijの値を１増加させると，π_iの対数オッズはβ_j増加することがわかります。
また，対数の定義から，上のモデルは次のようにも表せます。

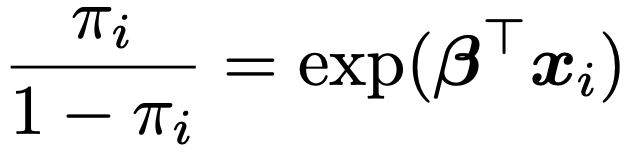
上の式から，他の説明変数の値を固定したまま，説明変数x_ijの値を１増加させると，π_iのオッズがexp(β_j)倍されることがわかります。
さらに，上の式をπ_iについて解くと，次のようにも表せます。

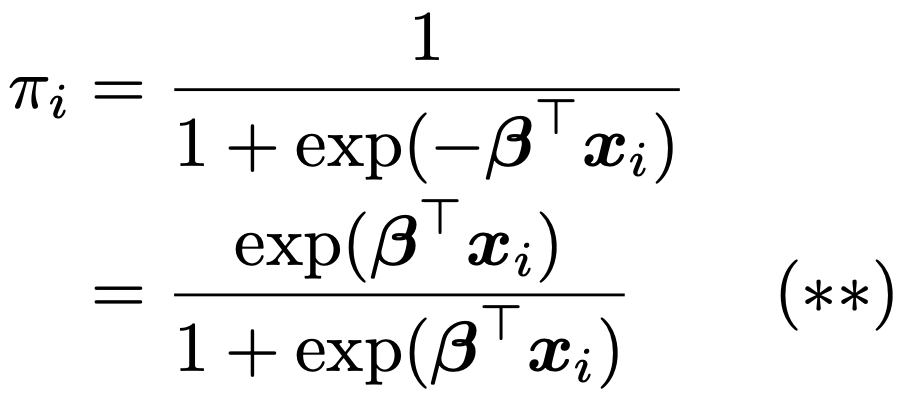
上の式のx→exp(x)/(1＋exp(x))という変換をロジスティック変換と呼びます。これはロジット変換の逆変換です。
ロジスティック回帰モデルのパラメータの推定には最尤法が用いられます。i番目の観測値をy_i(＝０ or １)，y_iがしたがうベルヌーイ分布をBin(１，π_i)とすると，その確率は次のように表せます。

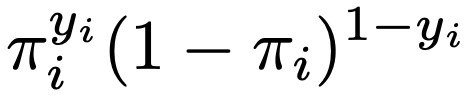
尤度関数はこれらの積なので，サンプルサイズをnとして，対数尤度関数は次のように表せます。

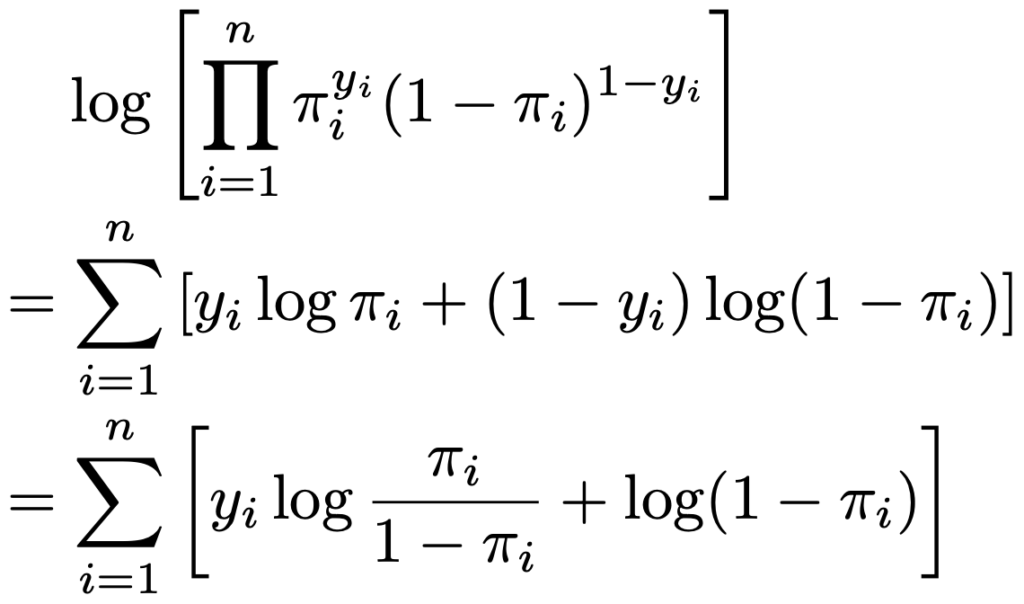
(＊)および(＊＊)を代入すると，対数尤度関数は次のように表せます。

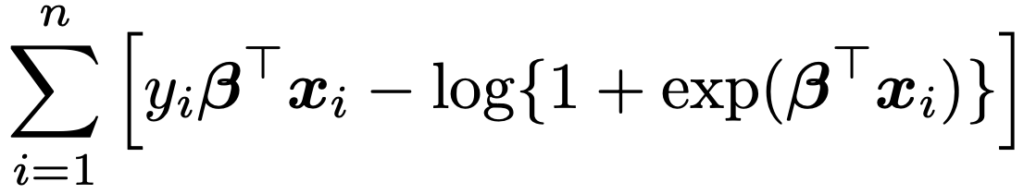
・プロビット回帰モデル…応答変数が２値の場合，応答変数yが１をとる確率（条件付き期待値）pを，標準正規分布の累積分布関数Φを用いて次のようにモデル化したもの。

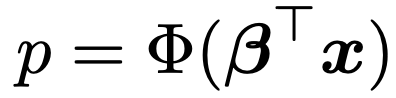
上の式は次のようにも表せます。

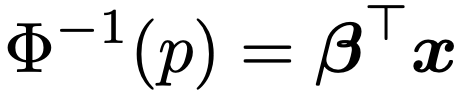
上の式の左辺のp→Φ^ー1(p)の変換をプロビット変換と言います。プロビット回帰モデルはプロビット関数をリンク関数とする一般化線形モデルで，パラメータの推定には最尤法を使います。
説明変数の値を増加させたときのpの変化については，上のpの式を説明変数x_iで偏微分した式を用いて知ることができます。これを限界効果と言って，標準正規分布の確率密度関数をφとして，次の式で表せます。

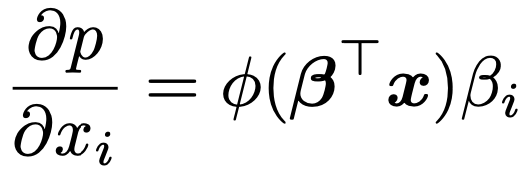
・ポアソン回帰モデル…一定期間の１店舗の来客数などの０以上のカウントデータの平均πと，いくつかの説明変数との関係を次のようにモデル化したもの。

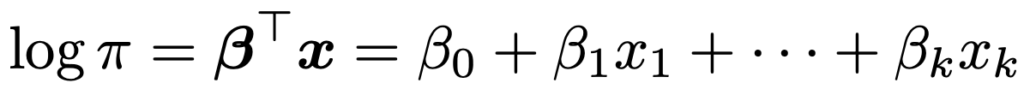
上の式は，π＝exp(β₀＋β₁x₁＋…＋β_kx_k)と書き直せるので，説明変数x_iの値が１増えると，平均πはexp(β_i)倍になります。
ポアソン回帰モデルのパラメータの推定も最尤法によって行うことができます。

・指数型分布族…一般化線形モデルにおける応答変数Yは，正規分布，二項分布，ポアソン分布など，理論上の性質が良い確率分布にしたがうことを仮定します。この確率分布のファミリーを指数型分布族と呼び，その確率（密度）関数は次のように表せます。

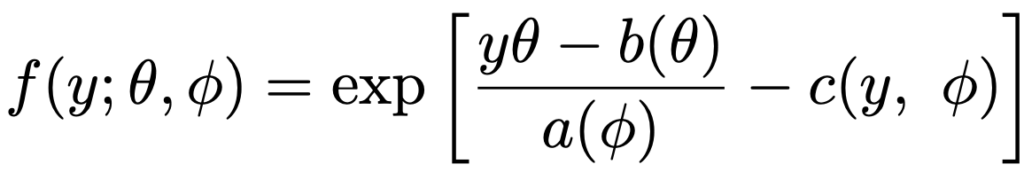
ここで，a(・)，b(・)，c(・)は既知の関数で，θは正準母数，φは散らばり母数と呼ばれます。例えば，正規分布の確率密度関数は次のように変形できます。

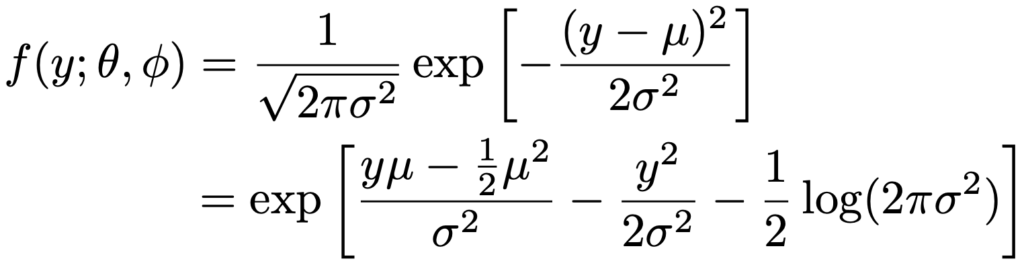
正規分布の確率密度関数は，指数型分布族の確率密度関数の一般式において，次のようにおいたものになっています。

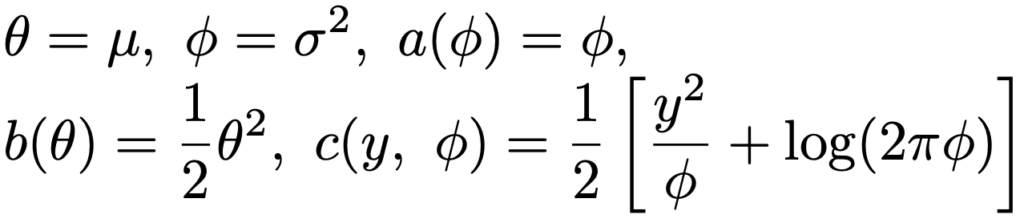
また，指数型分布族の確率分布にしたがう確率変数Yの期待値，分散は次のように計算できます。

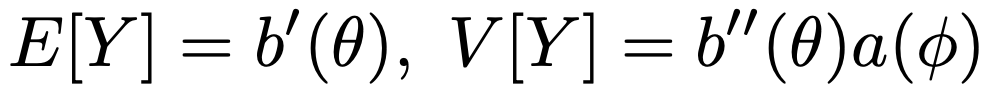
実際に，正規分布にしたがう確率変数Yについて，E[Y]＝μ，V[Y]＝σ²となることが確認できます。

第19章　回帰分析その他

・トービットモデル…Yを目的変数とした回帰モデルをつくりたいが，Yが０以上の値しかとらないというケースがよくあります。このような場合に，Y*＝β₀＋β₁X₁＋β₂X₂＋εなどの回帰モデルで表せ

る潜在変数Y*を考え，Y*が０以下の場合にはY＝０，Y*が０より大きい場合にはY＝Y*とするのがトービットモデルの例です。
では，データ(x₁，y₁)…，(x_n，y_n)に対して，次のトービットモデルを考え，尤度関数を構成します。

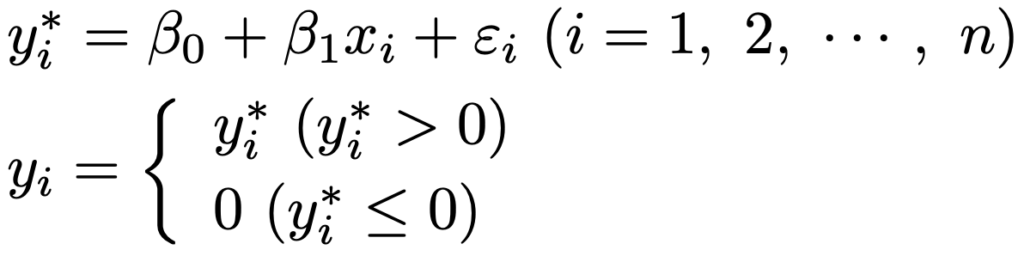
ここで，ε_iは互いに独立に正規分布N(０，σ²)にしたがう誤差項であるとすると，x_iを与えたもとで，y_i*は次の正規分布にしたがいます。

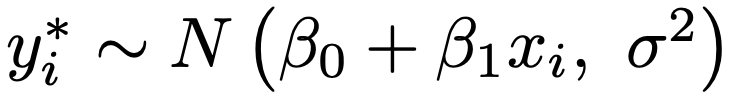
つまり，y_i*＞０のとき，y_i（＝y_i*）の確率密度関数は次の式になります。

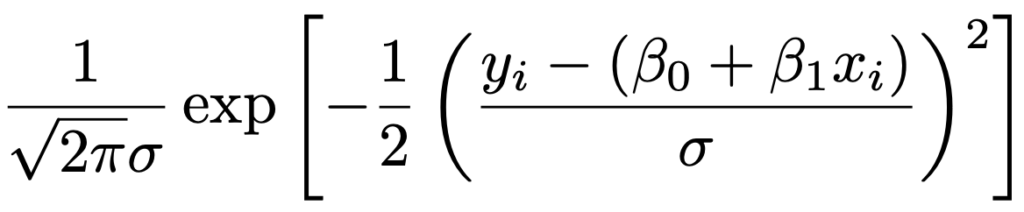
標準正規分布の確率密度関数をφ(x)とすると，上のy_iの確率密度関数は次のように表せます。

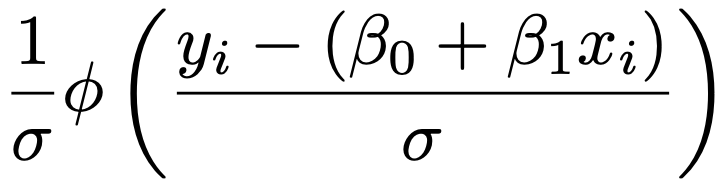
次に，y_i*≦０となる確率は，y_i*の確率密度関数を使って次のように表せます。

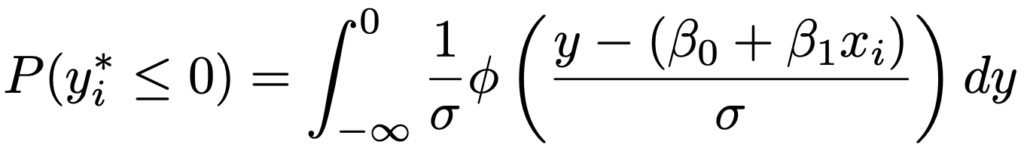
上の被積分関数φ(・)のかっこ内をzと置換すると，次のようになります。

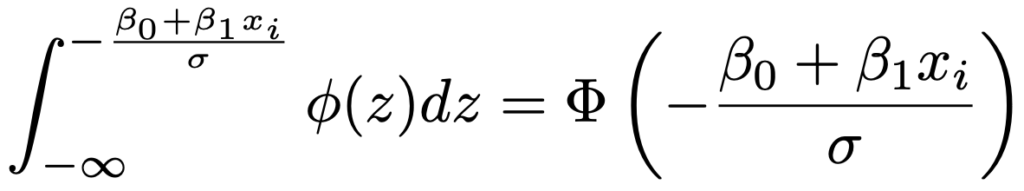
ここで，上の式の右辺のΦ(・)は，標準正規分布の累積分布関数です。よって，尤度関数は，y_i*＞０となるiに関する確率密度関数の積とy_i*≦０となるiに関する累積分布関数の積を合わせて，次のようになります。

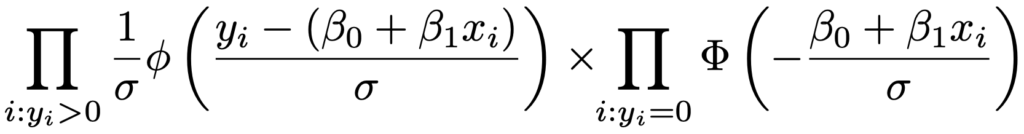
・生存時間…入院してから退院するまでの時間や就職してから退職するまでの時間など，基準となる時点からイベントが発生するまでの時間。
・生存関数…生存時間がt以上である確率のことであり，生存時間を表す確率変数Tの確率密度関数をf(x)として，次の式で表されるようなS(t)です。

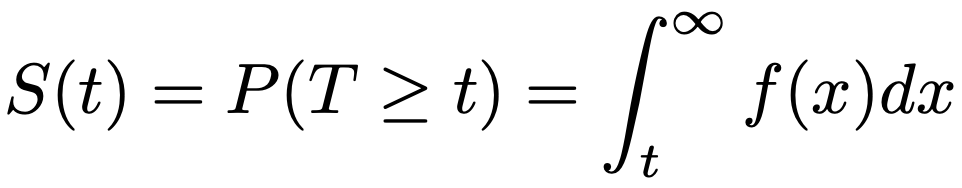
累積分布関数をF(t)として，S(t)＝１ーF(t)の関係があり，S(t)をtで微分すると，次のようになります。

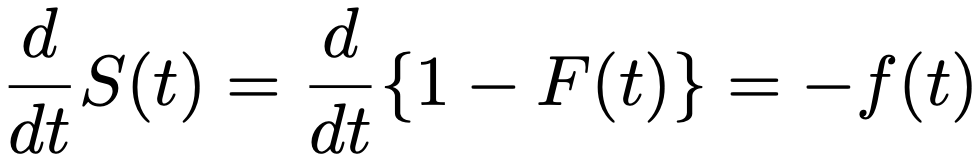
・ハザード関数…時刻tにおける瞬間イベント発生率（時刻tまでイベントが発生していない条件のもとで直後にイベントが発生する条件付き確率）を表す関数で，次のように確率密度関数と生存関数を用いて表せるh(t)です。

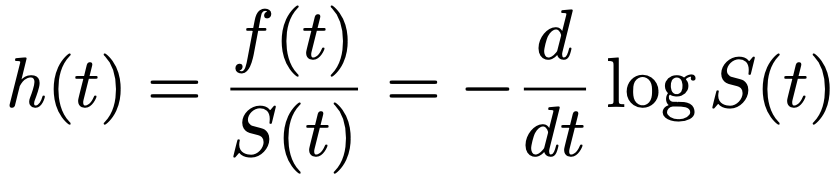
・累積ハザード関数…次のようにハザード関数を積分したものであり，最右辺のように生存関数を用いて表せます。

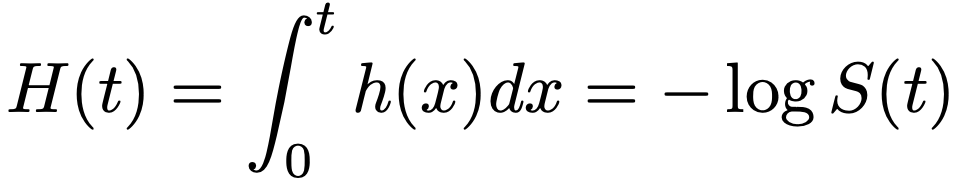
確率密度関数は，ハザード関数と累積ハザード関数を用いて次のように表せます。

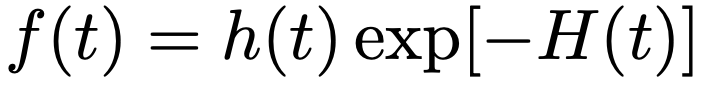
・カプラン・マイヤー法…生存時間に特定の確率分布を仮定することなく，生存関数を推定する方法。例えば，時点tまでに，次の表のようなk時点でイベントが発生した場合を考えます。

このとき，時点tにおける生存率を次の式で計算します。

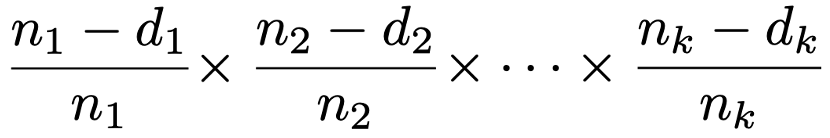
このような計算を観察期間全体について行い，その結果をプロットしてできる階段状のグラフをカプラン・マイヤー曲線と言います。
・Cox比例ハザードモデル…イベントの発生に影響を与えることが想定される共変量をx₁，…，x_nとして，次のようにハザード関数を表すモデル。

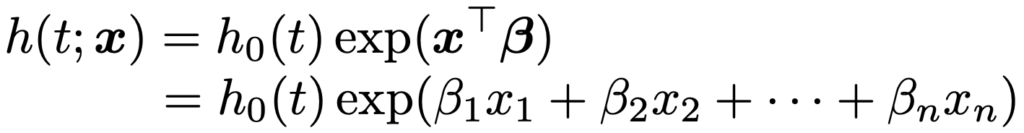
h₀(t)は基準ハザード（ベースラインハザード）と呼ばれる正の値をとるtの関数で，特定の分布形を仮定しません。Cox比例ハザードモデルをあてはめる場合には，比例ハザード性（ハザード比が時間によって変化しない）を確認する必要があります。
・ニューラルネットワークモデル…d個の入力x₁，x₂，…，x_dにそれぞれの重みw₁，w₂，…，w_dをかけ，これらの積の合計にバイアスbを加えたw^Tx＋b＝b＋w₁x₁＋…＋w_dx_dの入力を受けた1つのユニットは，活性化関数fを施してf(w^Tx＋b)を出力します。このようなユニットを層状に並べ，層自体も複数並べたものがニューラルネットワークモデルです。各ユニットに非線形活性化関数を使用することで，複雑な非線形関係をモデル化することが可能になります。

第20章　分散分析と実験計画法

２級で学習した１元配置分散分析は３群以上の母平均の差の検定でした。まず，基本となる用語を確認しておくと，観測データに影響を与える可能性のあるもののうち，実験で取り上げるものを因子，因子がとりうる一つひとつの条件を水準，複数の因子の水準の組み合わせを処理と言います。因子が２つ以上の場合も含めて，一般的に分散分析は，複数の因子の主効果とそれらの交互作用効果の有無を評価する検定といえます。
・フィッシャーの３原則
①無作為化…処理をランダムに割り当てる
②反復…同じ処理を複数回行う
③局所管理…ブロック内で均一な条件を実現
上の①と②を満たすものを完全無作為化法，①〜③のすべてを満たすものを乱塊法と言います。
・１元配置完全無作為化法…応答変数Yに関して１つの因子を取り上げ，A₁，…，A_aの水準ごとの母平均をμ₁，…，μ_a，水準の効果をα₁，…，α_aとすると，構造モデルは次の式です。

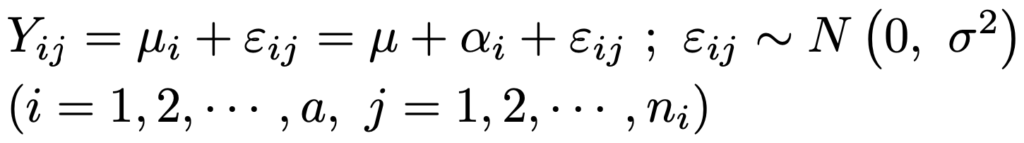
ただし，水準ごとのくり返し数をn₁，…，n_a（n₁＋…＋n_a＝n）として，n₁α₁＋…＋n_aα_a＝０が成り立つものとし，μは次の式で定まる一般平均です。

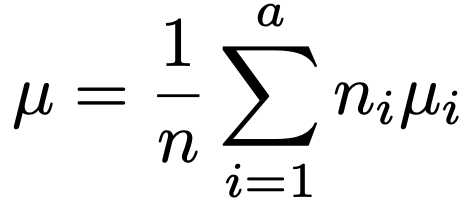
平方和の分解は次の式です。

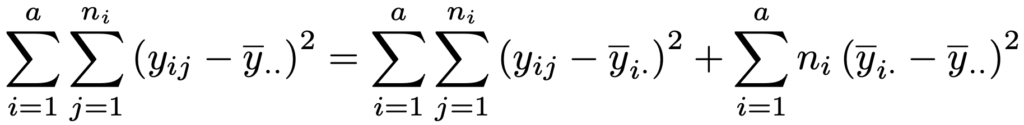
上の式の左辺を総平方和，右辺第１項を誤差（残差）平方和，右辺第２項を水準間平方和と呼び，それぞれS_T，S_E，S_Aと表します。これらの平方和を自由度でわったものを平均平方（分散）と呼び，次のような分散分析表にまとめます。

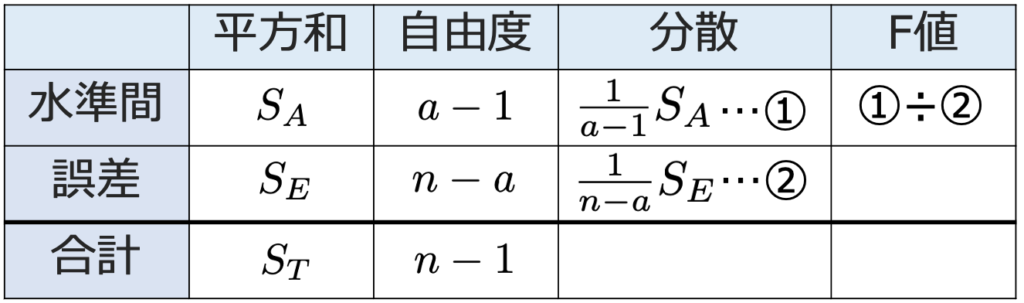
帰無仮説を「すべての水準の母平均は等しい」，対立仮説は「少なくとも１つの水準の母平均が異なる」として，①÷②の統計量がF(aー1，nーa)にしたがうことを利用して検定します。
水準の母平均の区間推定を行うには，上の表の②が誤差分散σ²の推定値であることを使います。この推定値をσ²ハットと表すと，i番目の水準の母平均の信頼度95％の信頼区間は次の通りです。

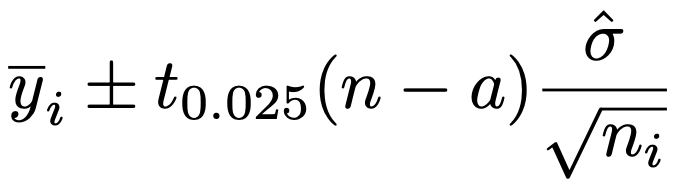
・１元配置乱塊法…１元配置完全無作為化法にブロックR₁，…，R_rを取り入れたもので，ブロック因子をγ_jとして，構造モデルは次の式です。

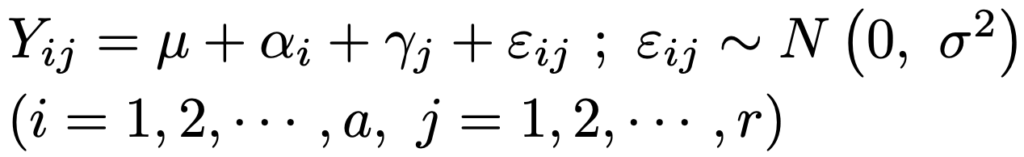
ただし，α₁＋…＋α_a＝０，γ₁＋…＋γ_r＝０が成り立つものとします。平方和の分解は次の式です。

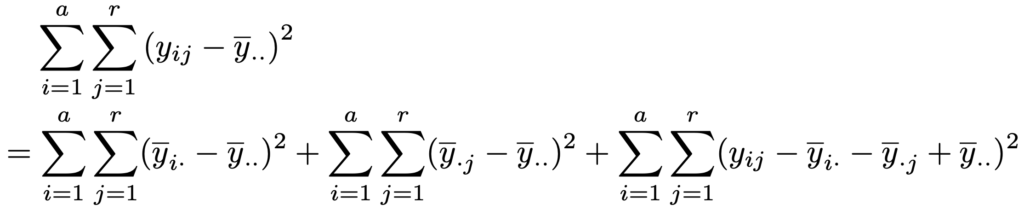
上の式の右辺第１項は水準間平方和，第２項はブロック平方和，第３項は誤差平方和であり，ブロック平方和をS_Rと表すと，分散分析表は次のようになります。

因子の効果については，①÷③の統計量がF[aー1，(aー1)(rー1)]にしたがうことを利用し，ブロックの効果については，②÷③の統計量がF[rー1，(aー1)(rー1)]にしたがうことを利用して検定します。
・２元配置完全無作為化法…２つの因子を考えるのが２元配置法で，それぞれの因子の効果（主効果）だけでなく，２つの因子の組み合わせ効果（交互作用）まで調べることができます。２つの因子をA，Bとし，A₁，…，A_aの水準の効果をα₁，…，α_a，B₁，…，B_bの水準の効果をβ₁，…，β_bとし，交互作用があることを仮定するとき，構造モデルは次の式です。

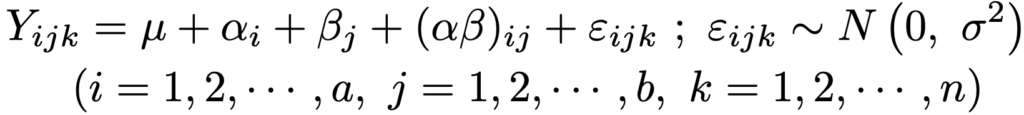
ただし，α₁＋…＋α_a＝０，β₁＋…＋β_b＝０が成り立つものとし，交互作用項については次の式が成り立つものとします。

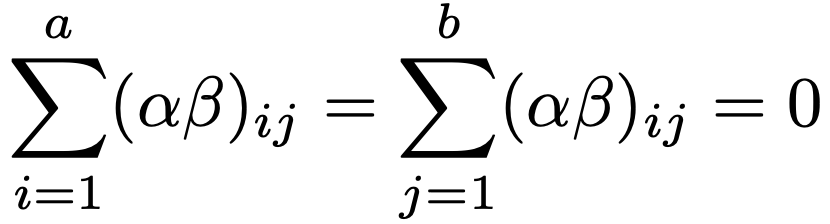
平方和の分解は次の式です。

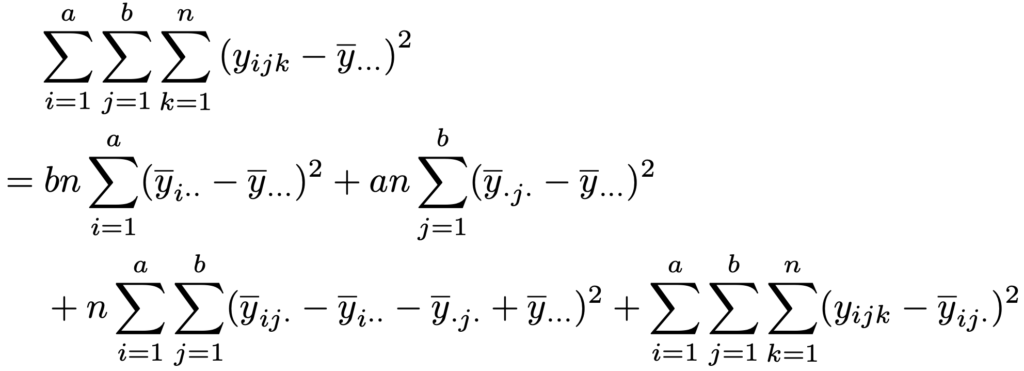
上の式の右辺第１項はAの水準間平方和，第２項はBの水準間平方和，第３項は交互作用平方和，第４項は誤差平方和であり，それぞれS_A，S_B，S_A×B，S_Eと表すと，分散分析表は次のようになります。

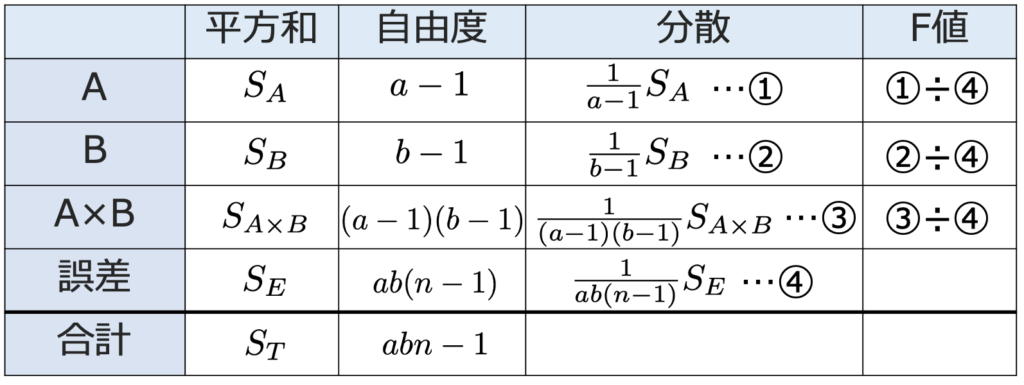
①÷④の統計量はF[aー1，ab(nー1)]，②÷④の統計量はF[bー1，ab(nー1)]，③÷④の統計量はF[(aー1)(bー1)，ab(nー1)]にしたがうことを利用して検定します。
・２元配置乱塊法…２元配置完全無作為化法にブロックR₁，…，R_rを取り入れたもので，ブロック因子をγ_kとして，構造モデルは次の式です。

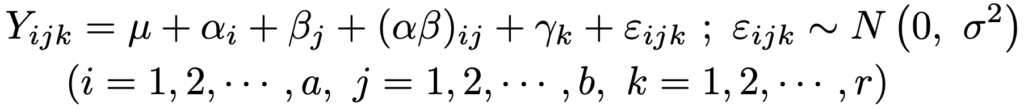
ただし，２元配置完全無作為化法におけるα_i，β_j，(αβ)_ijの制約に加え，γ₁＋…＋γ_r＝０が成り立つものとします。平方和の分解は次の式です。

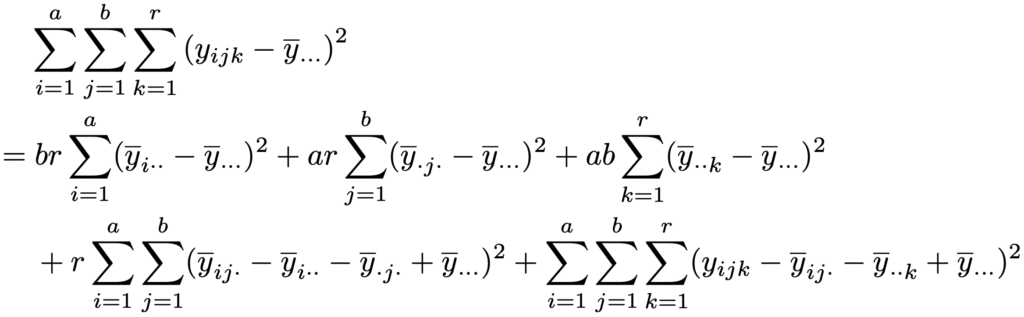
上の式の右辺第１項はAの水準間平方和，第２項はBの水準間平方和，第３項はブロック平方和，第４項は交互作用平方和，第５項は誤差平方和であり，それぞれS_A，S_B，S_R，S_A×B，S_Eと表すと，分散分析表は次のようになります。

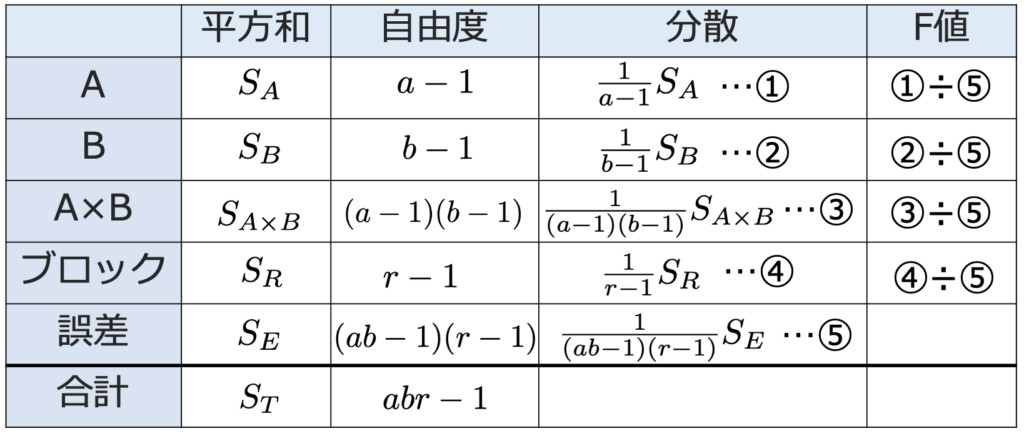
・直交表…因子の数や水準の数が増えるにしたがい，すべての水準組み合わせの実験を実施するのはコストが大きくなるため，一部の交互作用のみを取り上げることで実験の回数を減らしたものが一部実施要因計画です。そのために用いるのが直交表です。例えば，次の直交表は水準の数が２つの因子を割り付けるために使われるものです。

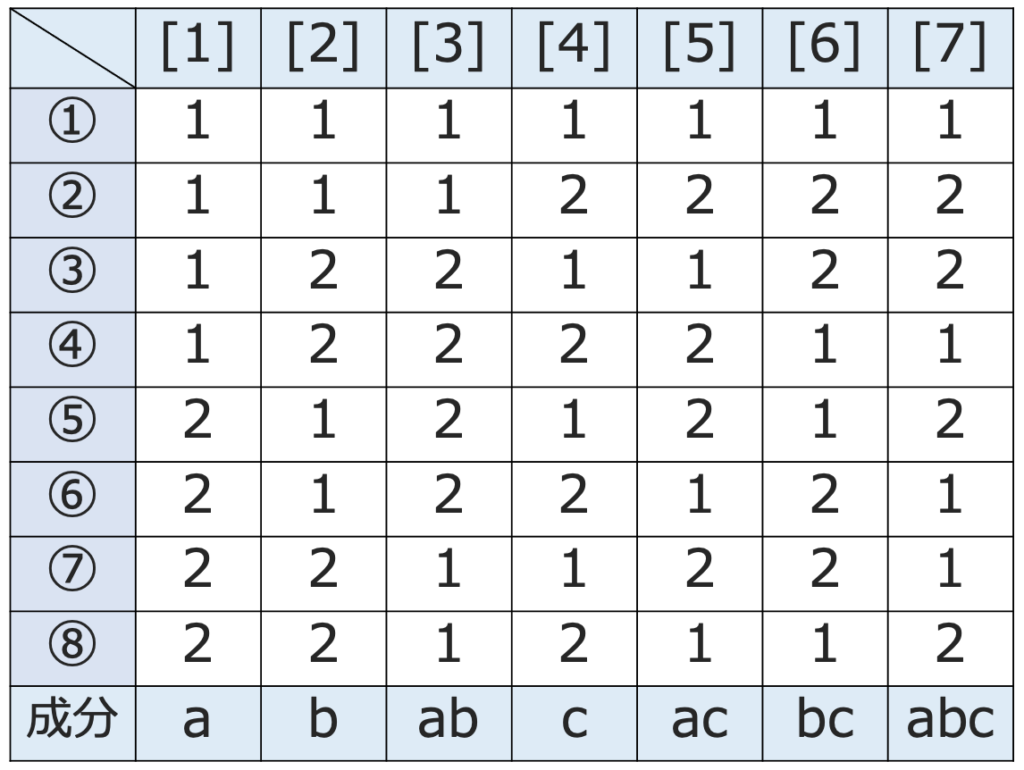
上の表の①〜⑧の行は実験を表していて，いくつかの列には因子を対応（割り付けと言う）させます。例えば，[3]の列に因子A，[6]の列に因子Bを割り付ければ，①はA₁B₁での実験，②はA₁B₂での実験，…という感じで，⑧までで４つの水準組み合わせの実験を２回ずつ行う計画になります。上の表のいちばん下の行の成分は列の性質を表していて，[3]の成分の”ab”と[6]の成分の”bc”の積は，b²＝１より，ab×bc＝acとなります。これは，[3]に割り付けた因子Aと[6]に割り付けた因子Bの交互作用が[5]に現れることを意味します。したがって，３つの２水準因子A，B，Cの主効果と交互作用A×Bについて調べる場合に，Aを[3]，Bを[6]に割り付け，Cを[5]に割り付けたら，Cの主効果と交互作用A×Bが区別できなくなります。このことを交絡と言います。
なお，上の直交表はL₈(2⁷)と呼ばれるもので，２が水準の数，７が列の数，８は実験の数を表しています。

第21章　標本調査法

調査単位と抽出単位が一致していて，各標本を抽出する確率が等しい抽出法が単純無作為抽出で，それ以外の抽出法としては，調査者が決めた基準にしたがって標本を抽出する有意抽出法などがあります。以下では，単純無作為抽出かつ非復元抽出（同じ対象を２回以上抽出しない）の場合を考えます。
・標本平均の期待値と分散…大きさNの母集団（母平均μ，母分散σ²）から大きさnの標本を非復元単純無作為抽出するとき，母平均の推定量として標本平均X__を用いると，その期待値，分散は次のようになります。

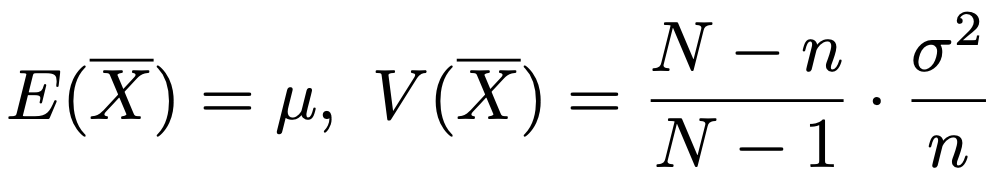
無限母集団の場合や復元抽出の場合と比べて，標本平均の分散には(Nーn)/(Nー１)がかけられており，これを有限修正項と言います。標本平均の分散を一定値以下におさえるにはサンプルサイズnをある程度大きくすればよく，V(X__)≦cという不等式を解けば，nは次の不等式の右辺以上でなければならないことがわかります。

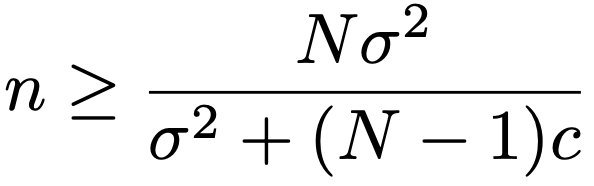
・層化抽出法…企業を大企業，中小企業，零細企業の３つに分けるように，基準を決めていくつかの層に分けた後，それぞれの層から無作為抽出する方法です。できるだけ層内を均質に，層間を異質に層化すれば，事前に層化しない場合よりも精度の高い結果を得やすくなります。
・標本配分法…層化抽出法での各層（層の数をkとする）からの標本の大きさn₁，…，n_k（n₁＋…＋n_k＝n）の決め方として，代表的なものを３つ紹介します。次の式のように，層の大きさをN₁，…，N_k（N₁＋…＋N_k＝N）として，層の大きさの比で標本の配分を決めるのが比例配分法です。

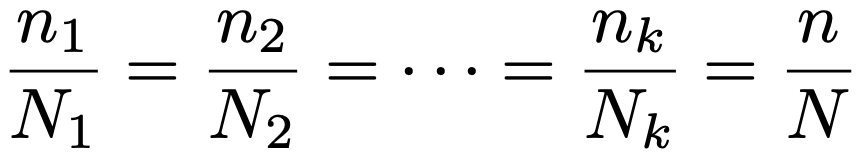
比例配分法のもとでの標本平均の分散は，単純無作為抽出の場合の標本平均の分散を超えないことを示すことができます。
次の式のように，それぞれの層からの標本の大きさがすべて等しいような決め方が等配分法です。

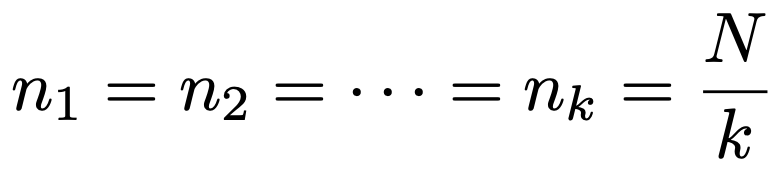
推定量の分散が最小になるような決め方がネイマン配分法で，j番目の層の母標準偏差をσ_jとして，標本の大きさは次の式で決めます。

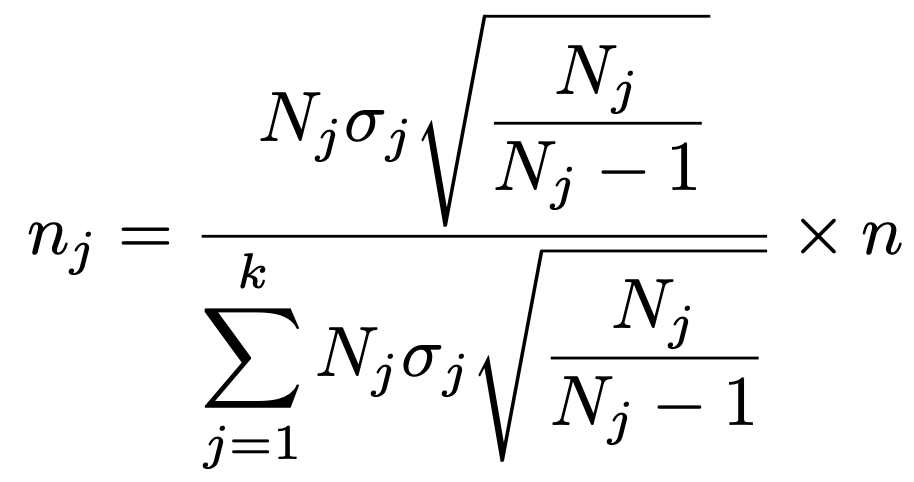
層の大きさが十分に大きい場合には，ルートの部分を１とみなして，次の式で表せます。つまり，層の大きさ×層内標準偏差の比で配分することになります。

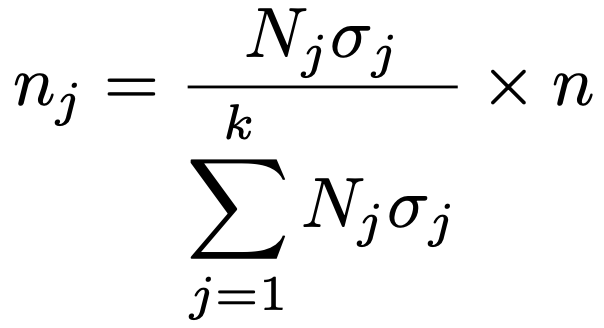
※集落抽出法，二段抽出法，系統抽出法は，２級内容のため，統計検定２級のチートシートを参照してください。

第22章　主成分分析

相関を利用して，多変数のデータをより少ない変数に縮約する手法。p次元データの標本分散共分散行列（または標本相関行列）の固有値がλ₁，λ₂，…，λ_p（λ₁≧λ₂≧…≧λ_p），対応するノルム１の固有ベクトルがw₁，w₂，…，w_pだとすると，中心化したp次元データをw₁方向の直線上に射影したときの分散が最大であり，その分散はλ₁に等しくなります。このw₁と直交し，射影したデータの分散が次に大きくなる方向がw₂であり，その分散はλ₂に等しくなります。このようにして，w₁，w₂，…，w_p方向の軸を順につくり，新しい軸上でデータを表示し直します。このとき，添字の数字が大きいほど分散が小さくなるので，分散の小さい主成分を使わないようにすれば，もとのデータを少ない変数で表すことができます。
・主成分…もとの変数をx₁，x₂，…，x_p，w₁＝(w₁₁，…，w_1p)とするとき，z₁＝w₁₁x₁＋…＋w_1px_pを第１主成分と言い，同じようにw₂，…，w_pから第２主成分，…，第p主成分がつくれます。
・寄与率…データの分散の合計のうち，ある主成分の分散が占める割合。例えば，第１主成分の寄与率は，λ₁/(λ₁＋λ₂＋…＋λ_p)
・累積寄与率…寄与率を大きいほうから合計したもので，例えば，第２主成分までの累積寄与率は，(λ₁＋λ₂)/(λ₁＋λ₂＋…＋λ_p)です。次元削減を目的とする場合には，「累積寄与率が80％を超えるまでの主成分だけを使う」といった目安として使われます。
・主成分得点…もとのデータの主成分軸上での値。例えば，w₁＝(w₁₁，…，w_1p)とするとき，i番目のデータx_i＝(x_i1，x_i2，…，x_ip)の第１主成分得点は，w₁₁x_i1＋w₁₂x_i2＋…＋w_1px_ipで計算できます。
・主成分負荷量…もとの変数と合成された主成分との相関係数。例えば，第１主成分z₁＝w₁₁x₁＋w₁₂x₂＋…＋w_1px_pとx₂との相関係数（主成分負荷量）は，x₂の分散をs₂₂と表して，次の式で計算できます。

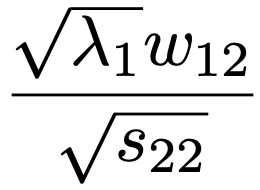
標準化されたデータであれば，上の主成分負荷量の式の分母は１になってなくなります。
・自己符号化器…ニューラルネットワークモデル（第19章参照）の一種で，入力xを低次元の表現に変換（符号化）した後，この低次元表現から元の入力に近いデータを再構築（復号化）することを目的としており，主成分分析と同じように，データの圧縮や特徴抽出に利用されます。自己符号化器は２つの主要な部分から構成され，入力xに変換y=f(w^Tx＋b)を適用する符号化器と，このyに次の変換を適用する復号化器です。

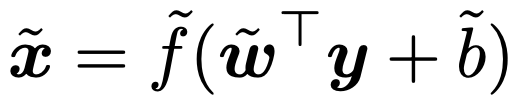
元の入力xにできるだけ近い出力が得られるように，符号化器と復号化器の重みとバイアスを調整します。

第23章　判別分析

あらかじめグループ分けが判明しているデータを学習して，新たに得られたデータが属するグループを特徴量に基づいて判定する手法。分類規則の与え方には様々なものがあります。
・フィッシャーの線形判別分析…２変数(x₁，x₂)の場合を例とし，Y＝w₁x₁＋w₂x₂という１次式で，Yの値によって属するグループをより良く判別できるようにw＝(w₁，w₂)^Tを決めます。そのために，群間変動w^TS_Bwを群内変動w^TS_Wwでわった比が最大になるようにすればいいと考えます。ここで，２群の学習データの標本平均ベクトルをx__⁽¹⁾，x__⁽²⁾とするとき，S_B＝(x__⁽¹⁾ーx__⁽²⁾)(x__⁽¹⁾ーx__⁽²⁾)^Tであり，S_Wは２群のプールされた標本分散共分散行列です。この最適化問題の解wは次の式で与えられます。

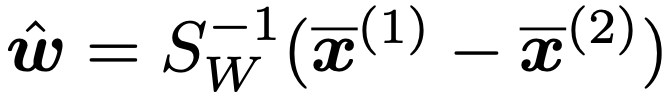
よって，２群の標本平均ベクトルの中点を基準として，次の関数が正になるか，負になるかによって，新たなデータの属する群を判定します。

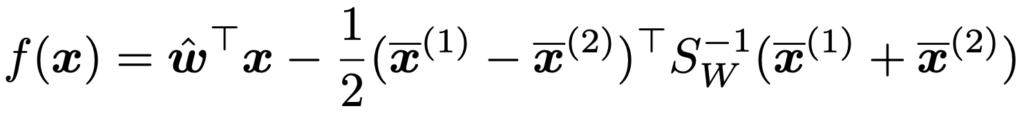
この関数f(x)をフィッシャーの線形判別関数と言います。
・マハラノビス距離による判別…データの標本平均ベクトルをx__，標本分散共分散行列をSとするとき，次のD²(x)をxとx__のマハラノビス平方距離と言います。

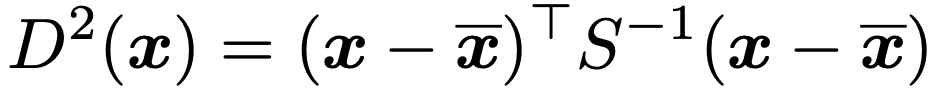
xと２群の標本平均ベクトルx__⁽¹⁾，x__⁽²⁾とのマハラノビス平方距離を比べて，小さいほうの群にxが属すると判別するとき，２群のプールされた標本分散共分散行列S_Wを使った次の関数が正ならばxは群２，負ならば群１と考えることができます。

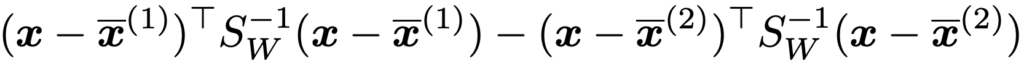
上の関数はフィッシャーの線形判別関数のー２倍に等しくなり，２種類の判別は一致します。
また，群１の標本分散共分散行列をS₁，群２の標本分散共分散行列をS₂として，次の関数により群の判別を行うことを２次判別分析と言います。

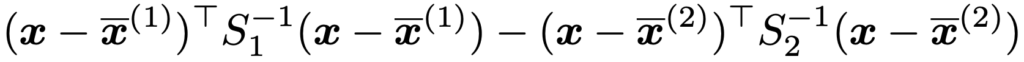
・ベイズ判別…データxを与えたもとで，群１に属する事後確率P(G₁|x)の群２に属する事後確率P(G₂|x)に対する比の対数は，ベイズの定理を用いて次の式の右辺のように表せます。

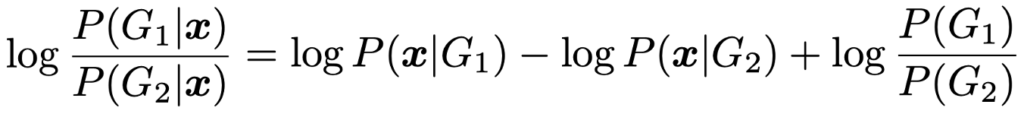
上の式のP(G₁)，P(G₂)は事前確率であり，各群に属する事前確率を分類規則に反映できるのがベイズ判別です。P(G₁)＝P(G₂)と２群のデータが同一の分散共分散行列をもつ多変量正規分布にしたがうことを仮定すれば，マハラノビス距離による判別と一致します。
・正準判別分析…p変数(x₁，…，x_p)のg個の群G₁，…，G_gを２次元や３次元などの低次元への射影を利用する判別分析。g個の群をできるだけよく分離できるような射影軸y＝w₁x₁＋…＋w_px_p＝w^Txの係数ベクトルwは，フィッシャーの線形判別分析と同じように，群間変動w^TS_Bwを群内変動w^TS_Wwでわった比の最大化を通して，S_W^ー１S_Bの最大の固有値に対する固有ベクトルとして求められます。なお，S_BとS_Wは，第i群について，標本平均ベクトルをx__⁽ⁱ⁾，サンプルサイズをn_i，標本分散共分散行列をS_i，学習データ全体の標本平均ベクトルをx__として，次のように定義します。

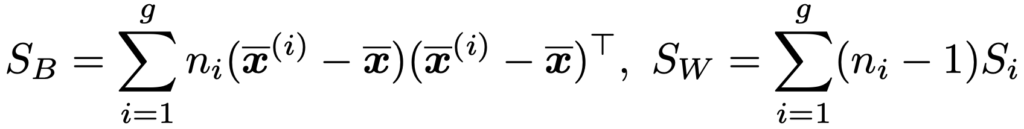
同じように，次に最適な射影軸の係数ベクトルは，S_W^ー１S_Bの２番目に大きな固有値に対する固有ベクトルとして求められます。
・ハードマージンSVM…超平面によって線形分離可能な場合のSVM（サポートベクターマシン）。超平面w^Tx＋b＝０によって２群に分けるとき，その超平面に最も近い学習データをサポートベクターと言い，マージン（サポートベクターから超平面までの距離）を最大にするようにw_，bを決定します。具体的には，データx_iのクラスラベルを表す変数をy_iとして，y_i(w^Tx_i＋b)≧１（i＝１，２，…，n）のもとで，0.5||w||²を最小化することで，次のように求められます。

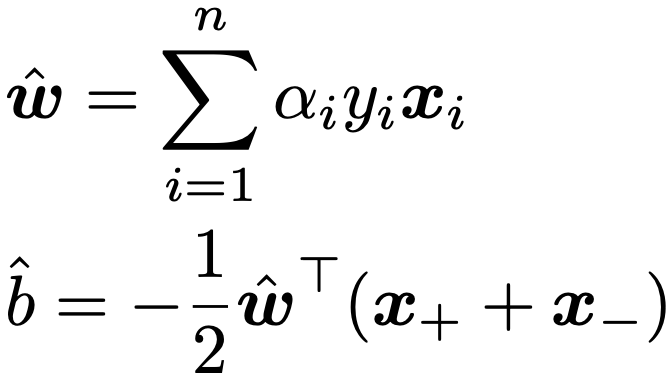
ただし，ラグランジュ乗数のα_iには最適化問題の解を代入し，x₊はy_i＝１を満たすサポートベクター，x₋はy_i＝ー１を満たすサポートベクターです。
・ソフトマージンSVM…線形分離可能でない場合に，はみ出したデータに罰則を課す線形SVM。はみ出しを表すスラック変数をξ_i≧０として，y_i(w^Tx_i＋b)≧１ーξ_iのもとで，次の和が最小になるwとξ_iを求めます。

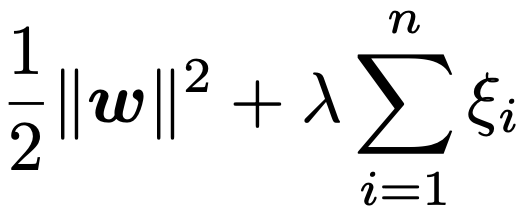
λははみ出しに対する罰則の強さを決めるパラメータで，λが大きいと罰則が強く，ξ_iの和はあまり大きな値をとれません。
・混同行列…判別器による判別結果を次の表の形式でまとめたもの。

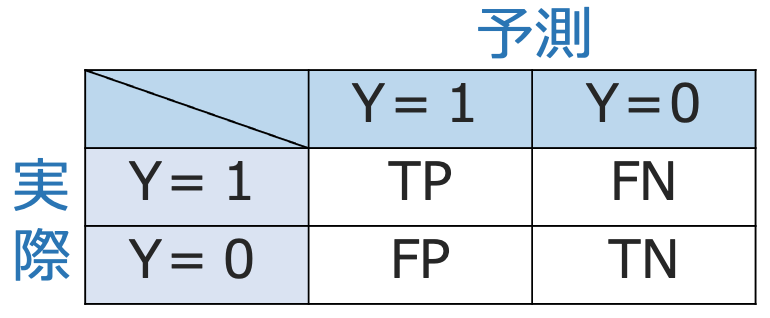
上の表のPは予測結果が陽性（positive），Nは予測結果が陰性（negative）であることを示しています。TPR＝TP/(TP＋FN)は，実際にY＝１であるもののうち，正しくY＝１と予測できた割合で，真陽性率と言います。また，FPR＝FP/(FP＋TN)は，実際にY＝０であるもののうち，誤ってY＝１と予測した割合で，偽陽性率と言います。例えば，次の図の青の点は合格者の偏差値，黄色の点は不合格者の偏差値で，緑の破線の右側を合格，左側を不合格と判別するとしましょう。

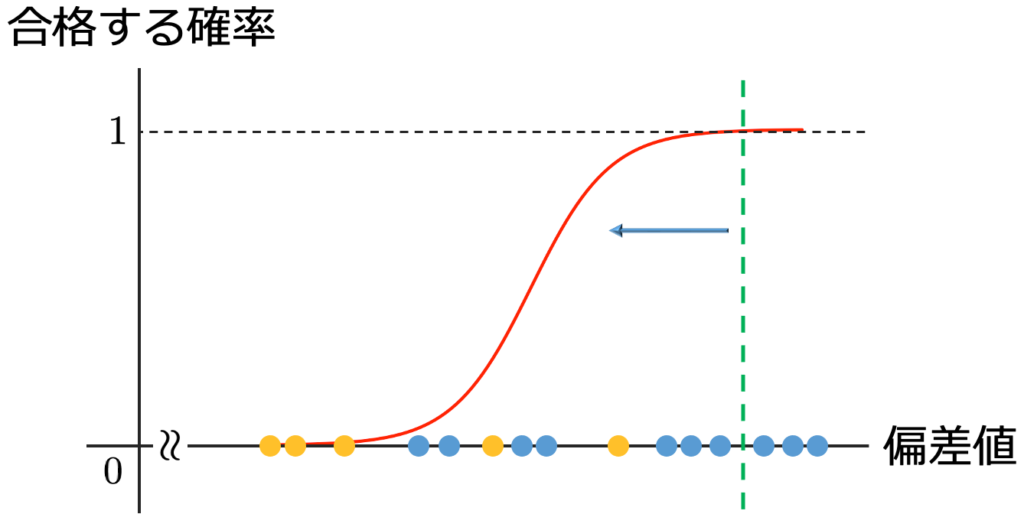
緑の破線を右端から左へ移動させると，合格者６人のデータを合格と判定した後，１人の不合格者のデータを合格と判定し，最終的には全員を合格と判定するようになります。このように，TP＝FP＝０の状態から，FN＝TN＝０の状態へ移る過程を，横軸にFPR，縦軸にTPRをとって，グラフにしたもの（下の図の赤い線）がROC曲線で，ROC曲線と横軸で囲まれた部分の面積がAUC（曲線下面積）です。

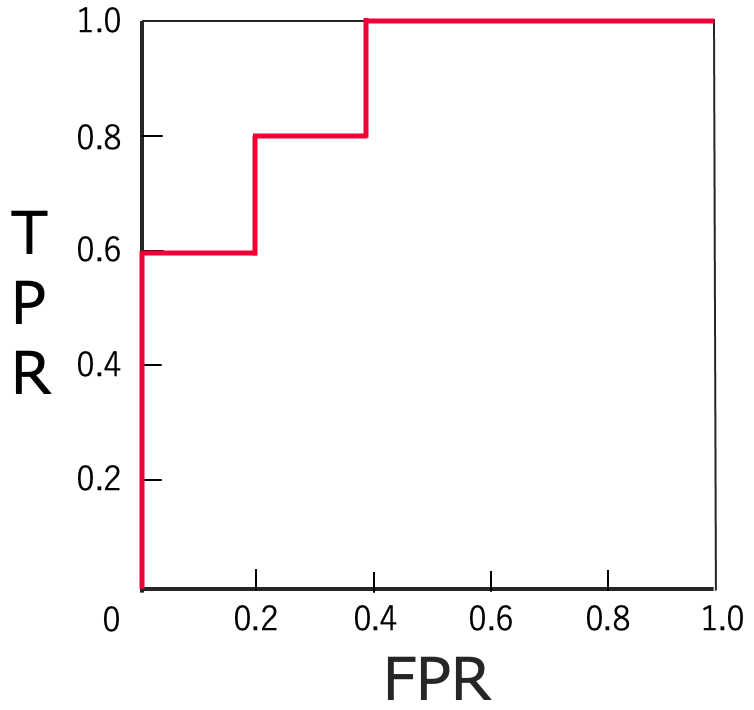
上の図では，AUC＝0.88であり，AUCが１に近いほど，判別器の性能が良いと言えます。なお，TPRを感度（再現率），１ーFPRを特異度とも言います。病気の判別では，感度は病気にかかっている人を漏らさずに陽性と判定する割合を意味するので，高いことが重要です。また，全サンプルを健康と予測するモデルだと特異度が１になります。

第24章　クラスター分析

分類の手本がない状態で，近さを測る指標（距離など）を定めて，データをグループ分け（クラスタリング）する手法。x＝(x₁，…，x_p)とy＝(y₁，…，y_p)の距離として，最も問われやすいのは次のユークリッド距離です。

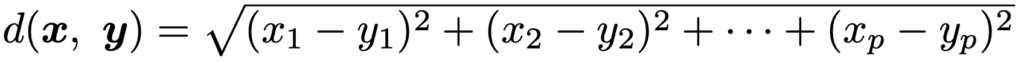
・階層的クラスタリング…１つのデータ（個体）を１つのクラスターとみなし，距離の近いクラスターを順次融合していくクラスタリング。融合の過程を表した図をデンドログラムと言います。データ間の距離をユークリッド距離などによって定め，それをもとにクラスター間の距離を次の最短距離法，最長距離法，群平均法，重心法，ウォード法などによって定めます。
・最短距離法（最近隣法）…２つのクラスターから１個体ずつ選んで求めた距離のうち，最も短い距離をクラスター間の距離とする方法。鎖効果を起こしやすく，クラスター構造が捉えにくい場合があります。
・最長距離法（最遠隣法）…２つのクラスターから１個体ずつ選んで求めた距離のうち，最も長い距離をクラスター間の距離とする方法。
・群平均法…２つのクラスターから１個体ずつ選んで求めた距離の平均をクラスター間の距離とする方法。
・重心法…クラスター内の重心どうしの距離をクラスター間の距離とする方法。
・ウォード法…クラスター内のデータの重心からの距離の２乗和の増分が最小となるクラスターを順に合併していく方法。
・K-means法…非階層的クラスタリングの代表例であり，クラスタリングの手順の一例は次の通りです。
① クラスターの数を決める
② クラスター中心をランダムに決める
③ 全データと各クラスター中心との距離を計算する
④ 中心との距離が最も近いクラスターにデータを振り分ける
⑤ クラスターの重心を計算して中心を更新する
⑥ ③〜⑤をくり返してデータのクラスター間の移動がなくなったら終了
※混合分布とEMアルゴリズムについては第６章を参照。

第25章　因子分析・グラフィカルモデル

５教科の得点を総合的な学力と教科ごとの能力で捉えるように，多数の観測変数間の構造を明らかにする目的で，それらに影響を与える少数の共通因子と変数ごとの独自因子を想定した分析。例えば，３つの観測変数x₁，x₂，x₃を考えるとき，これらを平均０，分散１に標準化した上で，何個の共通因子によって説明するかを決めます。ここでは，２つの共通因子f₁，f₂を仮定するとして，２因子モデルは次のように表せます。

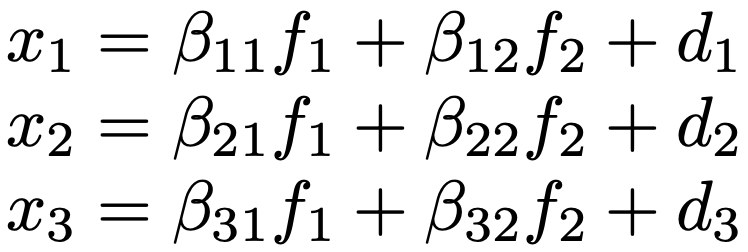
β_ijは因子負荷量と呼ばれる係数です。d₁，d₂，d₃は独自因子を表していて，f₁，f₂，d₁，d₂，d₃はすべて互いに独立で，E[f₁]＝E[f₂]＝０，V[f₁]＝V[f₂]＝１，E[d₁]＝E[d₂]＝E[d₃]＝０を仮定します。d₁の分散をσ₁²とすると，観測変数x₁の分散について，β₁₁²＋β₁₂²＋σ₁²＝１が成り立ちます。このとき，β₁₁²＋β₁₂²を共通性，σ₁²を独自性と言います。観測変数の変動のうち，共通因子で説明できる部分が共通性，説明できない部分が独自性だと解釈します。
・寄与率…すべての観測変数の変動を，それぞれの共通因子がどれだけ説明できているかを表すもので，上の例のf₁の寄与率は次の式で計算できます。

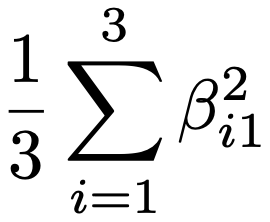
・因子軸の回転…回転によって因子負荷量を解釈しやすいものにとり直すことが可能です。因子軸が直交した状態での回転（直交回転）の代表例がバリマックス回転で，因子軸が必ずしも直交しない回転（斜交回転）の代表例がプロマックス回転です。
・操作変数法…次のような図をパス図と呼び，ここに示される因果関係をZ＝aX＋bY＋u，Y＝cX＋vという式（構造方程式）で表すことができます。

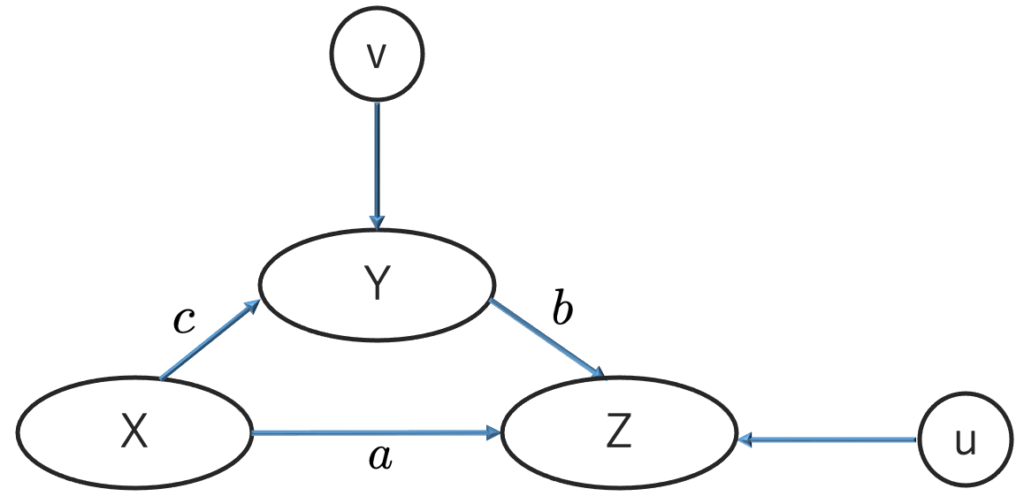
a，b，cはパス係数と呼ばれます。E[X]＝E[Y]＝E[Z]＝０，V[X]＝V[Y]＝V[Z]＝１，誤差項uはX，Yと，vはXとそれぞれ無相関であることを仮定した上で，構造方程式に変数（操作変数と言う）をかけて期待値をとることで，次の例のようにパス係数を相関係数を用いて表すことができます。（例）Y＝cX＋v→E[XY]＝cE[X²]＋E[vX]→c＝r_XY
Z＝aX＋bY＋uで同じように計算すると，r_XZ＝a＋bcが得られます。このとき，aはX→Zの直接効果，bcはX→Y→ZのようにYを介した間接効果であり，両者を合わせて総合効果と呼ばれます。
・グラフィカルモデル…確率変数ベクトル(X₁，…，X_d)がd変量正規分布にしたがっているとき，グラフィカルモデルでは，これらの変数を頂点に対応させ，変数間の条件付き独立性を辺の有無で表現します。例えば，分散共分散行列の逆行列の(1，2)成分が０ならば，X₁とX₂が他の変数を与えたもとで条件付き独立だと言えます。このように間接的な関係しかない変数どうしには辺をひかず，直接的な関係にある変数どうしを辺で結んでできるのが無向独立グラフです。

第26章　その他の多変量解析手法

・多次元尺度構成法…個体間の距離が与えられたときに，その距離関係を保つような個体の座標を求める手法。特に，２〜３次元の座標で表すことで個体間の位置関係を視覚化できます。計算方法は次の通り。
① 与えられたn次距離行列Dに対して，n次単位行列をI_n，すべての成分が１のn次正方行列をJ_nとして，次の行列Bを計算

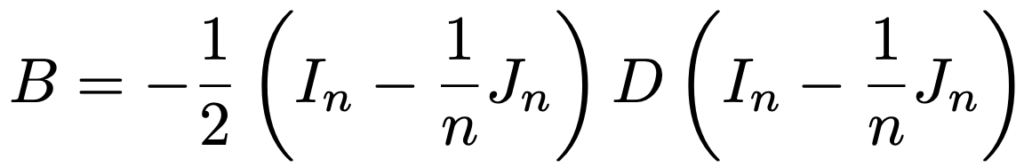
② Bの固有値，互いに直交するノルム１の固有ベクトルを求める。正の固有値を対角成分に並べた行列をΛ，固有ベクトルを並べた行列をUとして，B＝UΛU^Tと表せることに注意
③ XX^T＝Bを満たす行列Xとして，X＝UΛ^0.5（Λ^0.5は対角成分に固有値の正の平方根を並べたもの）がとれる。例えば，２次元座標で表すには，並べる固有ベクトル，固有値を２つずつにする
・正準相関分析…x＝(x₁，x₂，…，x_p)^Tとy＝(y₁，y₂，…，y_q)^Tの変数間の相関係数はpq通りあるため，p，qが大きいときには相関関係の把握が煩雑になりやすいです。そこで，u＝a₁x₁＋a₂x₂＋…＋a_px_pとv＝b₁y₁＋b₂y₂＋…＋b_qy_qの相関係数が最大になるようにa＝(a₁，a₂，…，a_p)とb＝(b₁，b₂，…，b_q)を決めて，xとyの関係を理解しようとするのが正準相関分析です。このような相関係数の最大化は，行列の固有値問題に帰着し，最大の固有値に対する固有ベクトルとして１組のaとbが得られます。この固有ベクトルをa₁，b₁としてできるu₁＝a₁^Txとv₁＝b₁^Tyの組を第１正準変数と呼び，同じように２番目に大きい固有値に対する固有ベクトルa₂，b₂からu₁，v₁と無相関であるようなu₂，v₂が得られ，第２正準変数と呼びます。（以下同様）
・数量化法…質的データなどを「数量化」して多変量解析の枠組みで分析する手法です。下の表などを通して数量化Ⅰ〜Ⅲ類の区別を覚え，理論の概要を知っておきましょう。

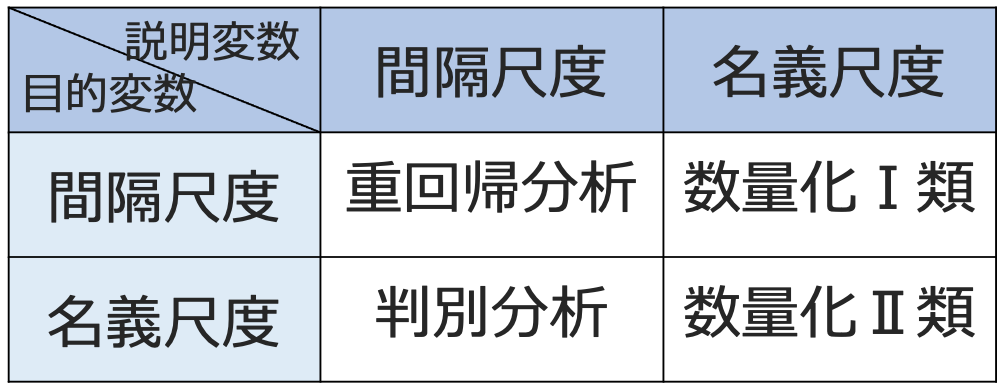
また，数量化Ⅲ類は，いわば主成分分析の名義尺度版であり，アンケートデータのような○と×のデータから得られる相関をもとに固有値を計算してデータを縮約します。
数量化Ⅰ類や数量化Ⅱ類では，変数が説明変数と目的変数に二分されていて，この場合に目的変数を説明変数に関する外的基準と呼びます。一方で，数量化Ⅲ類では変数どうしの関係は対等であり，内部構造に基づく分析であるため，外的基準のない手法と言えます。

第27章　時系列解析

月や年など，時間軸にそって観測されるのが時系列データであり，確率変数Y_t（t＝１，２，…）で表します。
・弱定常過程（共分散定常過程）…平均と分散が一定であり，自己共分散が時点によらずラグのみによって決まる時系列。h次の自己共分散をCov[Y_t，Y_t-h]＝γ_hと表すと，V[Y_t]＝V[Y_t-h]＝γ₀であり，h次の自己相関係数はγ_h/γ₀です。
・ホワイトノイズ…平均が０，分散が一定で，０でないラグに対する自己共分散がすべて０である時系列で，弱定常過程の一種。以下では，U_tは分散σ²のホワイトノイズを表すものとします。
・p次自己回帰過程[AR(p)]…現在の値が過去p時点の値の影響と現在の偶然変動により決まるモデルで，次の式で表せます。

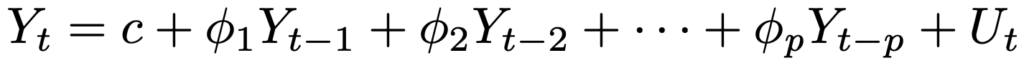
１次の自己回帰過程ならば，|φ₁|＜１のときに弱定常になります。AR(1)モデルY_t＝c＋φ₁Y_t-1＋U_tのとき，期待値，分散，自己共分散，自己相関係数は次のようにまとめることができます。

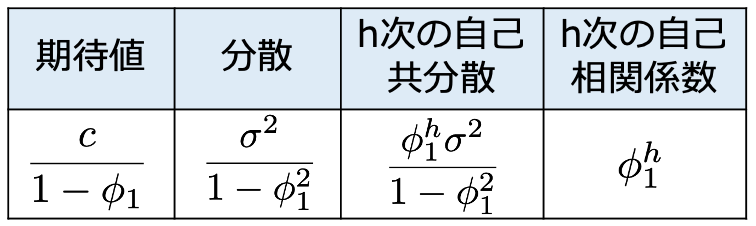
・q次移動平均過程[MA(q)]…現在の値が過去q時点の偶然変動の影響と現在の偶然変動により決まるモデルで，次の式で表せます。

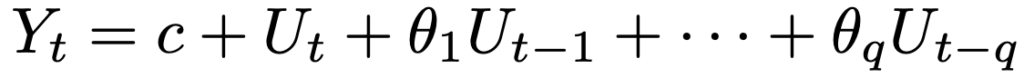
移動平均過程は弱定常です。MA(1)モデルY_t＝c＋U_t＋θ₁U_t-1のとき，期待値，分散，自己共分散，自己相関係数は次のようにまとめることができます。

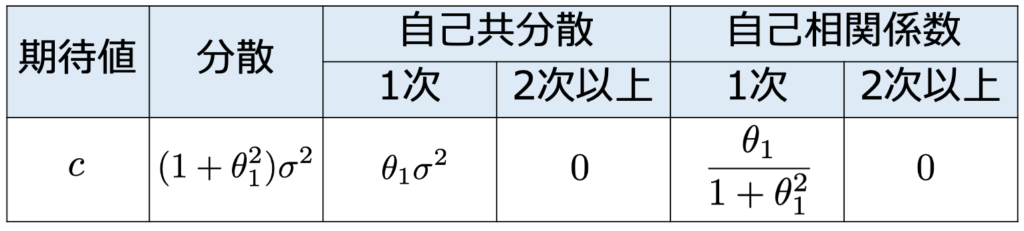
・(p,q)次自己回帰移動平均過程[ARMA(p,q)]…AR過程とMA過程の両方の性質をもつ次のようなモデルで，AR過程の部分が定常ならば，全体として定常になります。

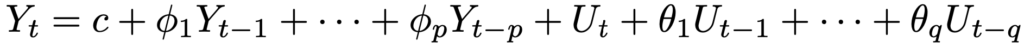
ただし，p＝０の場合はMA過程，q＝０の場合はAR過程，p＝q＝０の場合はホワイトノイズとします。
・ディッキー・フラー検定…AR(1)モデルY_t＝φY_t-1＋U_tの両辺からY_t-1をひき，ΔY_t＝Y_tーY_t-1，β＝φー１とおいたΔY_t＝βY_t-1＋U_tにおいて，帰無仮説をβ＝０，対立仮説をβ＜０とする検定。β＝０ならばφ＝１であり，このとき，AR(1)モデルは単位根を持つと言います。また，時系列Y_tが非定常過程であり，その差分系列ΔY_t＝Y_tーY_t-1が定常過程である場合，Y_tを単位根過程と言います。さらに，この差分系列が定常かつ反転可能なARMA(p，q)過程で表される場合，Y_tは自己回帰和分移動平均（ARIMA）過程と言います。
・状態空間モデル…通常は観測できない状態の変化を記述する状態方程式と，その状態から観測値が得られる過程を記述する観測方程式を組み合わせたものです。このモデルは，ARMAモデルを含む様々な時系列データを表現できます。状態方程式は，時点tー１での状態に時点tでの誤差を加えた形で表され，観測方程式は，時点tでの状態に時点tでの観測誤差を加えた形ですが，ARMAモデルのような特定の一般式をもつわけではなく，モデルの形は扱う時系列データの特性に応じて変化します。
・ACFとPACF…AR(1)モデル，MA(1)モデルのACF（自己相関関数）とPACF（偏自己相関関数）のグラフは次のような特徴をもちます。

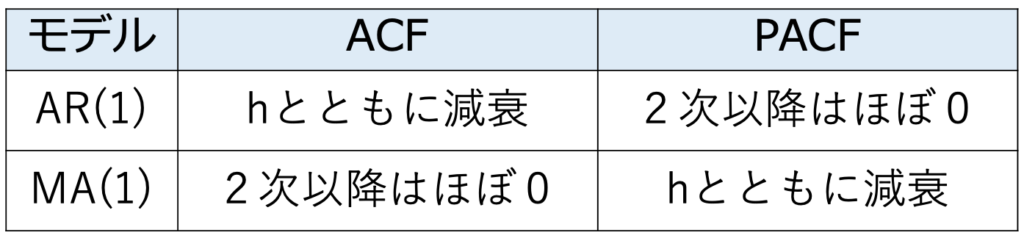
なお，（標本）自己相関関数のグラフはコレログラムと呼ばれます。
・ダービン・ワトソン検定…時系列データに回帰モデルをあてはめたときに，残差に自己相関（系列相関）が見られる場合があり，そのような系列相関の有無を判定するための検定。誤差項u_tにAR(1)モデルu_t＝ρu_t-1＋U_tを仮定し，帰無仮説をρ＝０とします。検定統計量は，最小２乗法で推定したときの残差をe_tとして，次の式で表せます。

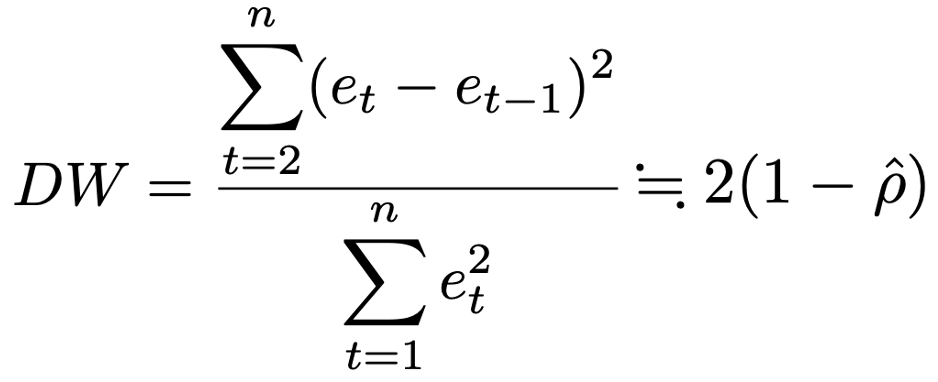
上の式のρハットは１次の自己相関係数の推定値で，この値が０に近ければDWの値は２に近くなりますから，DWの値が２から離れて０や４に近くなるときに帰無仮説を棄却することになります。
・スペクトル密度関数(スペクトラム)…時系列の変動を様々な周期成分によって表し，その特徴を分析します。
（例１）AR(1)モデルY_t＝c＋φY_t-1＋U_t（ー１＜φ＜１）のスペクトル密度関数は次のf(λ)になるので，φ＞０ならば低周波で大きな値，φ＜０ならば高周波で大きな値をとり，φの絶対値が大きいほど周波数による違いが顕著になります。

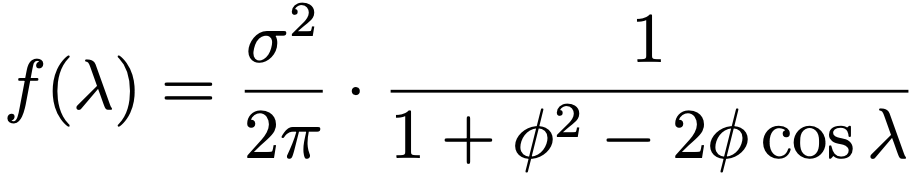
（例２）MA(1)モデルY_t＝c＋U_t＋θU_t-1のスペクトル密度関数は次のf(λ)になるので，θ＞０ならば低周波で大きな値，θ＜０ならば高周波で大きな値をとり，θの絶対値が大きいほど周波数による違いが顕著になります。

真のスペクトラムを推定するために標本から求められる推定値を与えるのがペリオドグラムです。

第28章　分割表

a個のカテゴリーをもつ変数Xとb個のカテゴリーをもつ変数Yのab通りのカテゴリーの組み合わせについて，カウントされたデータを表にまとめたものがa×b分割表です。このとき，変数を因子，各カテゴリーを水準と呼び，２因子の分割表を２元分割表と言います。因子の数が３，４，…ならば，３元分割表，４元分割表，…と言います。
・相対リスク…例えば，ある疾患の発症率を，喫煙群と非喫煙群で比べる場合，発症率の差ではなく，発症率の比をとることがあり，これを相対リスクと言います。例えば，喫煙群の発症率が0.15，非喫煙群の発症率が0.03ならば，相対リスクは，0.15÷0.03＝５
・前向き研究…研究開始以降に被験者の状態の変化を記録する研究。
・後向き研究…研究開始以前のデータをもとに行う研究。
・コホート研究…特定の集団（コホート）を追跡し，処置とアウトカム（病気など）の関連を調べる研究。
・ケースコントロール研究…特定のアウトカムをもつ被験者ともたない被験者を比較し，過去のリスク要因を調べる研究。
・オッズ…失敗の確率に対する成功の確率の比。例えば，ある疾患から５年以内に回復する確率が0.8ならば，回復しない確率は0.2なので，オッズは，0.8÷0.2＝4
・オッズ比…オッズの比。例えば，疾患Aから５年以内に回復するオッズが６，疾患Bから５年以内に回復するオッズが２ならば，オッズ比は，６÷２＝３
ここで，次の２元分割表を考えます。ある手術を受けた患者が退院までにかかった日数が10日以上かどうかを年齢別に集計したものです。

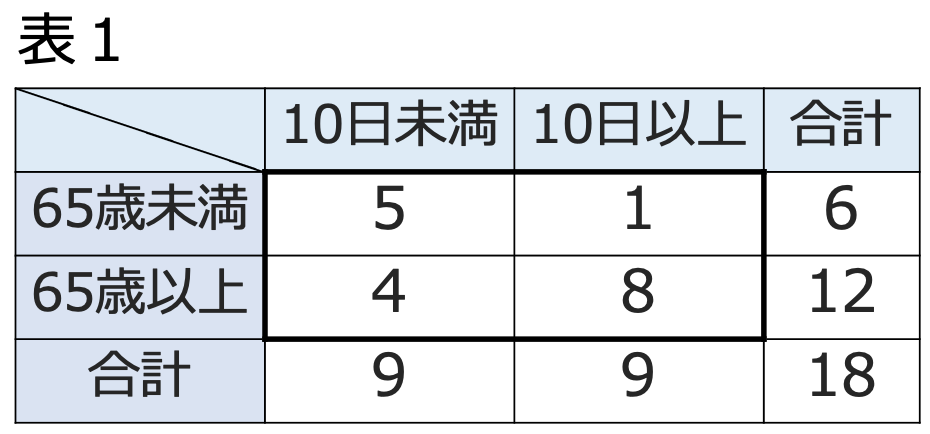
・標本オッズ…分割表の度数から求められる母オッズの推定値。例えば，上の表１で，年齢別に10日未満で退院した人数を10日以上で退院した人数でわった値が標本オッズであり，65歳未満なら，５÷１＝５，65歳以上なら，４÷８＝0.5となります。
・標本オッズ比…標本オッズの比であり，母オッズ比の推定値。例えば，上の表１で標本オッズ比は，５÷0.5＝10となります。また，表１の対数標本オッズの標準誤差の推定値は次のように求められます。

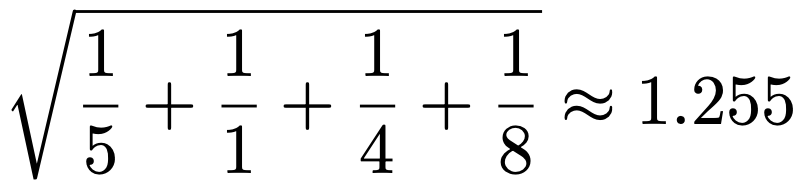
・フィッシャーの正確検定…２元分割表で，２つの変数が独立であるかどうかをP値を直接計算することによって検定する手法。次の表２は，表１と同じ設定で，年齢と退院までの日数が独立だとしたときの２元分割表です。

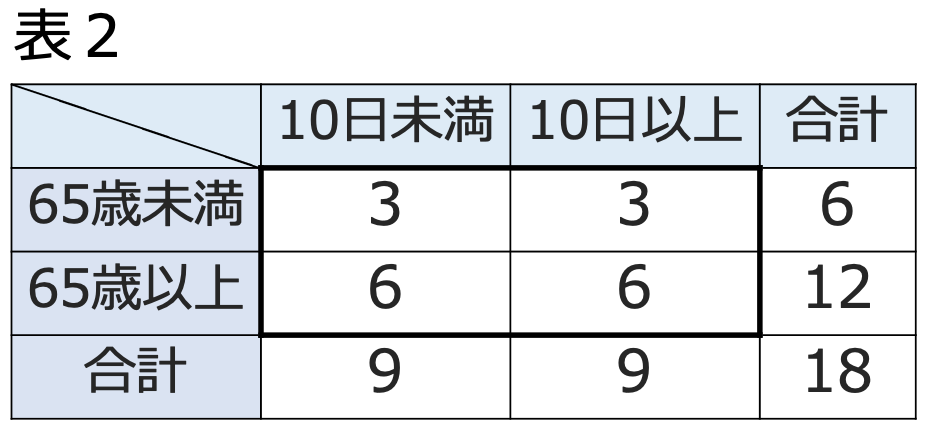
表２で，年齢ごとの標本オッズを計算すると，65歳未満も65歳以上も１なので，標本オッズ比は１となります。このように，独立ならば標本オッズはほぼ同じ値になると考えられるので，標本オッズ比が１に近ければ独立である可能性が高く，１から離れた値ならば独立ではない可能性が高くなります。「年齢と退院までの日数が独立＝オッズ比が１」という帰無仮説を仮定し，「65歳未満のほうが10日未満の退院が多い＝オッズ比が１より大きい」を対立仮説とすると，実際に観測された表１以上に極端な結果となる場合として，次の表３が考えられます。

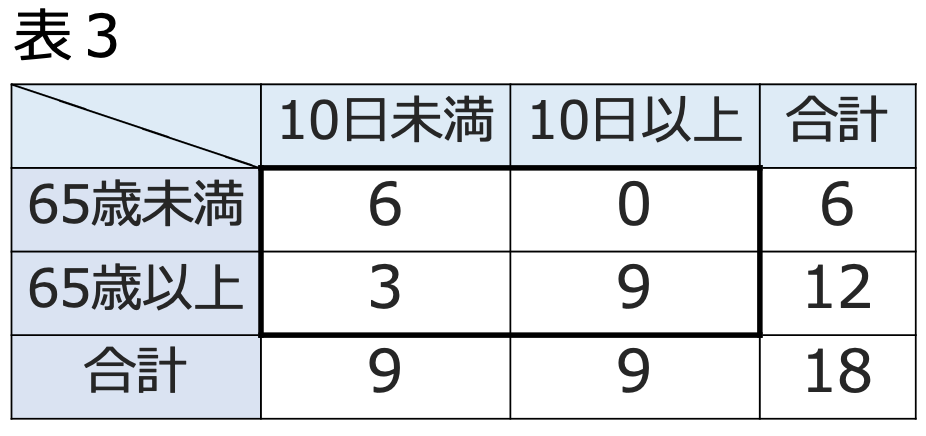
各行の合計と各列の合計を固定した上で，65歳未満で10日以内に退院した人数は帰無仮説のもとで超幾何分布にしたがうので，独立なのに偶然に表１の度数になる確率と偶然に表３の度数になる確率は次のように計算できます。

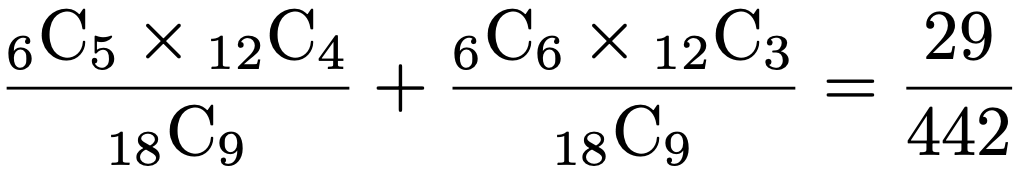
片側P値は約0.0656なので，有意水準を５％とすれば有意ではありません。つまり，年齢と退院までの日数が独立なのに，度数がたまたま表１のようになったという可能性を否定できないことになります。
・独立性の検定…フィッシャーの正確検定と同じように，２元分割表の２つの変数が独立であるかどうかを検定する手法として，分割表の度数が十分に大きい場合にカイ２乗分布を用いる手法があります。a×b分割表において，全体の度数の合計をn，i行目j列目のセルの度数をn_ij，i行目の度数の合計をn_i・，j列目の度数の合計をn_・jと表すと，検定統計量は次の式で計算できます。

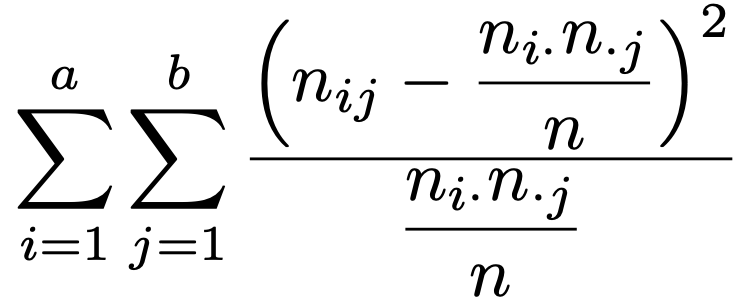
nが大きいとき，この検定統計量は，「２つの変数が独立」という帰無仮説のもとで近似的に自由度(aー1)(bー1)のカイ２乗分布にしたがうことを利用して検定します。
特に，２×２分割表では，n₁₁，n₁₂，n₂₁，n₂₂をそれぞれa，b，c，dとすると，上の検定統計量は次の式で表せます。

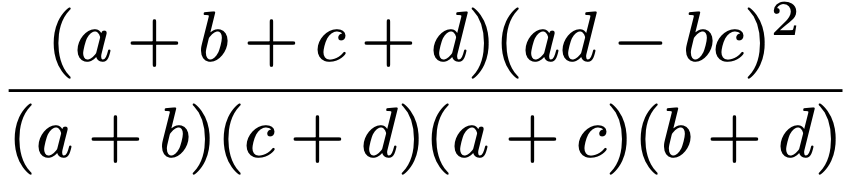
この２×２分割表における検定統計量に第12章で紹介したイエーツの補正を施すと，a＋b＋c＋d＝nとして，次の式になります。

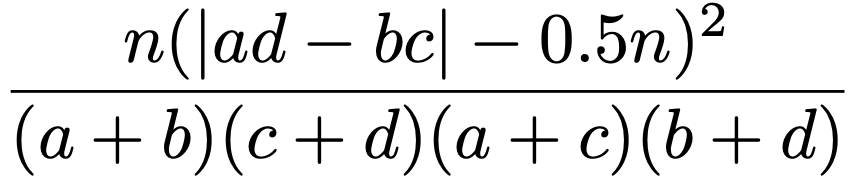
なお，分割表のすべての度数をa倍すると，カイ２乗統計量もa倍になります。分割表の行と列の数が変わらなければ自由度は変化しないので，独立性の検定はサンプルサイズを増やすだけで有意になりやすくなります。そこで，分割表のすべての度数をa倍しても変化しない指標として，次のようなクラメールの連関係数Vを用いることがあります。

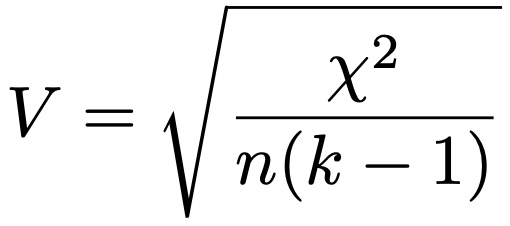
ただし，上の式でχ²はカイ２乗統計量，nはサンプルサイズ，kは分割表の行の数と列の数のうちの大きくないほうの数を表しています。クラメールの連関係数Vは０以上１以下の値をとり，１に近いほど２元分割表の２つの変数に関連があることを示唆します。
・尤度比検定…a×b分割表で特定の統計モデルを仮定するとき，i行j列の観測度数をx_ij，モデルのもとでの期待度数をm_ijとして，統計モデルのデータへのあてはまりを次の統計量（逸脱度と呼ぶ）によって検定します。（λは尤度比）

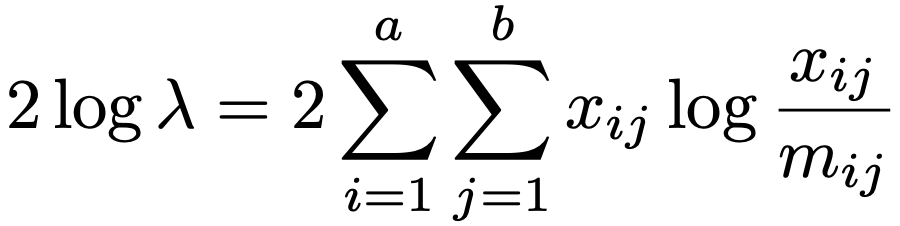
サンプルサイズnが十分に大きいとき，この統計量は近似的にカイ２乗分布にしたがい，その自由度は，帰無仮説のもとでの自由に値を決められるパラメータ数と対立仮説のもとでの自由に値を決められるパラメータ数の差になります。これを逸脱度の自由度と言います。
・対数線形モデル…分割表の因子間の独立性や条件付き独立性を解析するために使われるモデル。例えば，３元分割表におけるフルモデルは，３因子A_iB_jC_kに属する同時確率をp_ijkとして，次の式の右辺のように，主効果項α_i，β_j，γ_k，交互作用項(αβ)_ij，(αγ)_ik，(βγ)_jk，(αβγ)_ijkを用いて表せます。

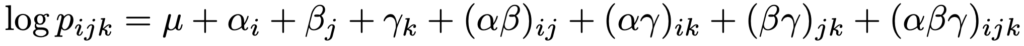
ただし，a×b×c分割表ならば，i＝１，…，a，j＝１，…，b，k＝１，…，cであり，次の制約を課します。

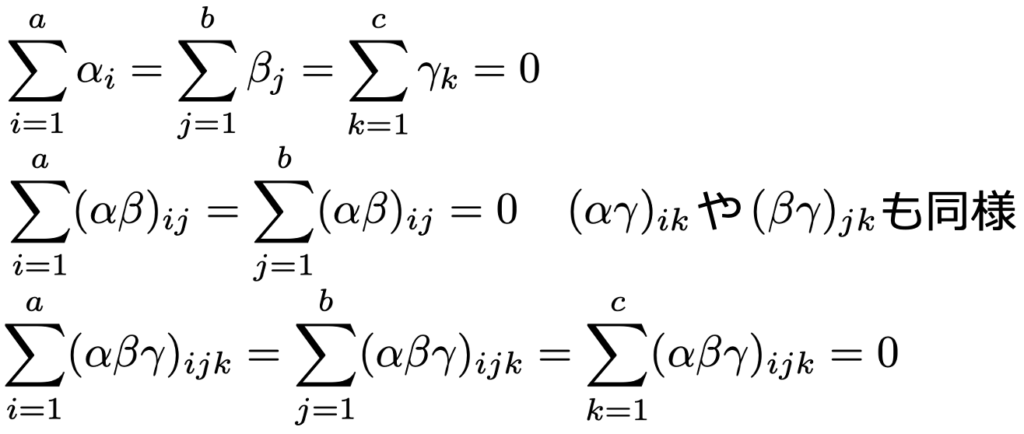
交互作用項がある場合，それに含まれる低次の交互作用項と主効果項をすべて含むものを階層的対数線形モデルと言います。また，主効果項からはじめて，より高次の交互作用項をたどることで，極大項が見つけられます。これを生成集合と言います。
３因子の階層的対数線形モデルのうち，フルモデル以外は大きく分けて次の３通りに分類できます。

・グラフィカルモデル…与えられた無向グラフのクリーク（極大な完全部分グラフをなす頂点集合）が生成集合となる階層的対数線形モデル。無向グラフに対して，ただ１つ定まります。
・分解可能モデル…対応する無向グラフが長さ４以上の弦のない閉路を持たないグラフィカルモデル。このモデルのもとでは，分割表の周辺度数を使って，特定の水準組み合わせの同時確率や期待度数が計算できます。

第29章　不完全データの統計処理

欠測（データの一部が観測されない）の例として，次のような場合などが考えられます。
・打ち切り…あらかじめ期間が決められている製品の寿命検査のように，ある値以上（または以下）であることはわかるが，その値自体は得られないタイプの欠測。
・トランケーション…特定の幅の値しか観測できず，この幅に入っていないデータの個数もわからないタイプの欠測。
欠測メカニズムは，大きく分けて次の３つに分類されます。

欠測に対する主な対応として，次のCC解析，単一代入法，多重代入法があります。
・CC(complete case)解析…少なくとも１つの変量に欠測が生じた個体を除いた解析。サンプルサイズが小さくなるため，推定精度や検出力が下がり，MCAR以外の場合にはバイアスが生じます。
・単一値代入法…欠測値に適切な値を埋め込み，擬似的な完全データを作成する方法。代表的なものは次の通り。

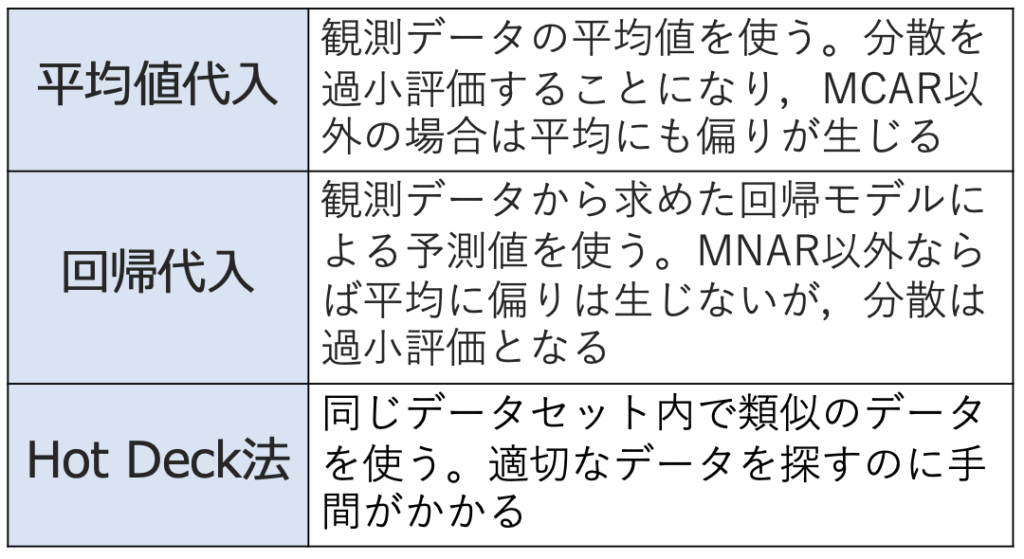
・多重代入法…欠測値に適切な値を埋め込んだ複数組の擬似的な完全データを作成し，独立に推定値を計算し，最後にそれらの結果を統合する手法。不確実性をつくり出し，単一代入法で起こりがちな誤差の過小評価を補正します。
・１変量正規分布における推測…X〜N(μ，σ²)であり，標準正規分布の確率密度関数をφ(x)，累積分布関数をΦ(x)，a＝(cーμ)/σとして，X≧cのもとでのXの条件付き期待値は，次のように表せます。

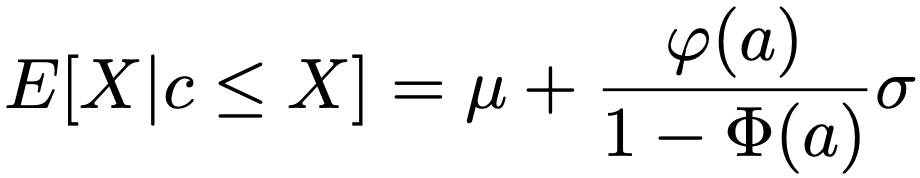
c以上の値が観測されない打ち切りのケースで，母平均μが未知，母分散σ²が既知であるとき，上の条件付き期待値を用いて，母平均μの最尤推定値を求める手順は，サンプルサイズをn，観測されたデータのサイズをm（m＜n）として，次の①〜④です。
① μ⁽⁰⁾を観測されたサイズmのデータの平均とする
② t＝０，１，２，…に対し，μ^(t)をもとに次の式でa^(t)を計算

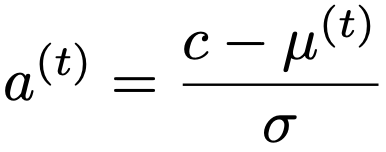
③ a^(t)，μ^(t)をもとにμ^(t+1)を次の式で計算

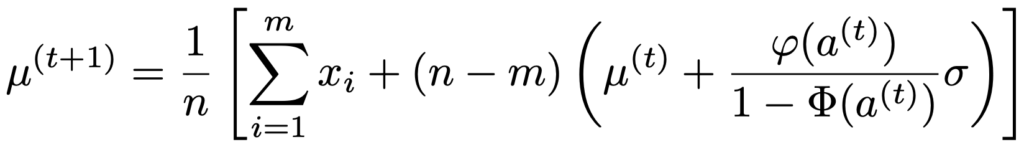
④ μ^(t)が収束するまで②と③をくり返す
同じ設定でトランケーションの場合，母平均μの最尤推定値は次の①〜④の手順で求めます。
① μ⁽⁰⁾を観測されたサイズmのデータの平均とする
② t＝０，１，２，…に対し，μ^(t)をもとに次の式でa^(t)を計算

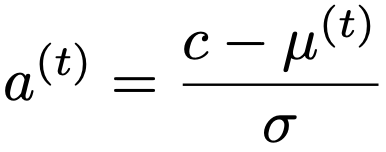
③ a^(t)をもとに次の式でμ^(t+1)を計算

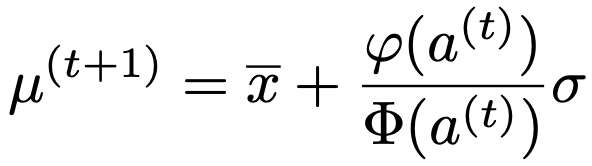
④ μ^(t)が収束するまで②と③をくり返す
・２変量正規分布における推測…(X，Y)^Tが次の２変量正規分布にしたがうものとします。

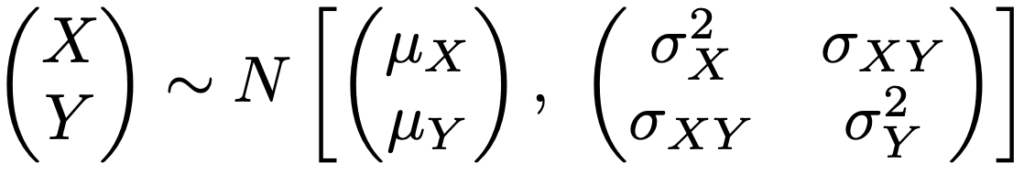
欠測はYのみに生じて，観測されたデータを(x₁，y₁)，…，(x_m，y_m)，x_m+1，…，x_n（m＜n）とし，欠測メカニズムがMARだとするとき，パラメータの推定値は次の手順で求めます。
① μ_X，σ_X²の最尤推定値をサイズnのデータを使って，次の式で計算

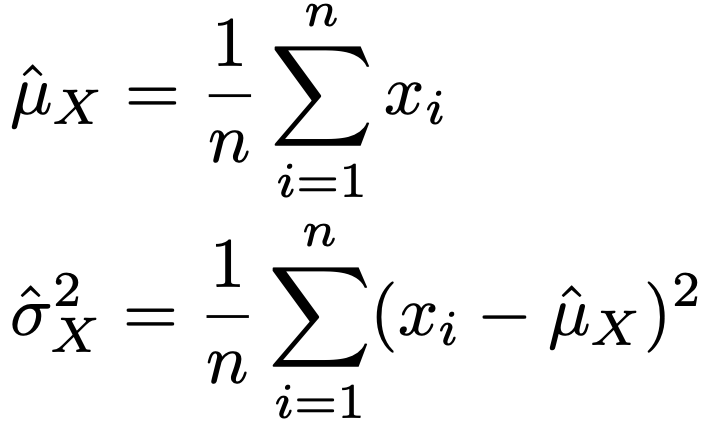
② サイズmのデータを使って，x__，S_X²，y__，S_Y²，S_XYを次の式で計算

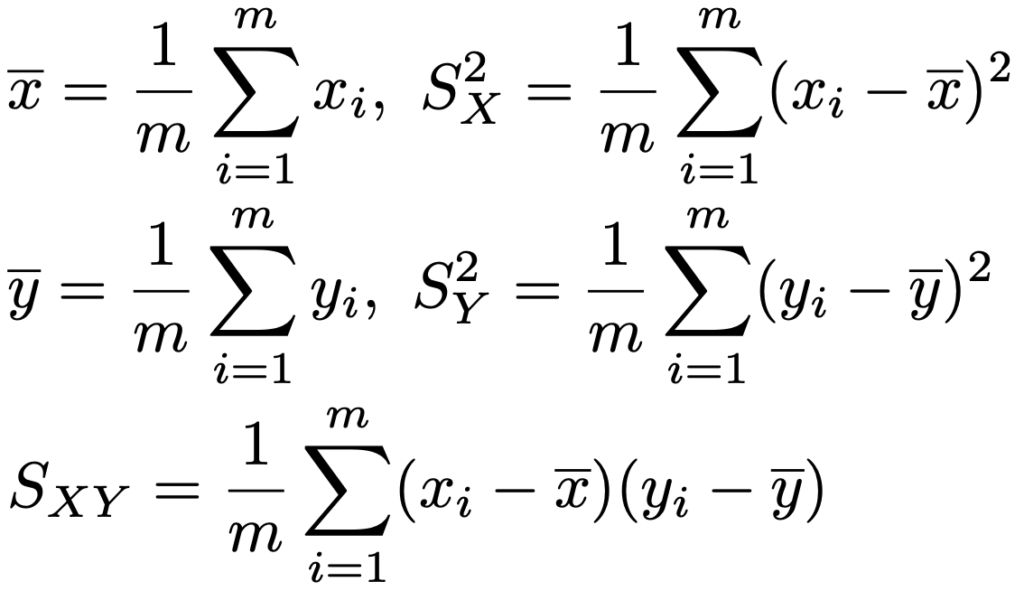
③ ②で求めた統計量をもとに，Xを与えたもとでのYの条件付き分布をN(α＋βx，τ²)と表したときのα，β，τ²を計算
④ α，β，τ²を使って，次の式でμ_Y，σ_Y²，σ_XYの最尤推定値を計算

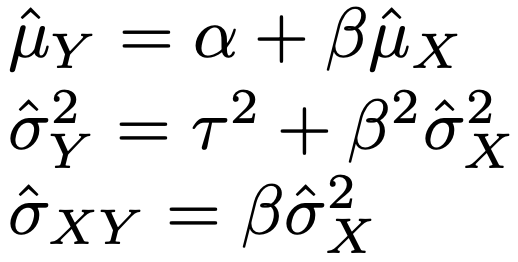
なお，MCARの場合には，単純に観測されている(x₁，y₁)，…，(x_m，y_m)のみを用いてMARの②のように計算するだけでよく，x_m+1，…，x_nからy＝α＋βxによって求めたyの値を使うこともXとYに相関がある場合には効果的です。

第30章　モデル選択

・AIC（赤池情報量規準）…ー２×（最大対数尤度）＋２×（推定するパラメータ数）
・BIC（ベイズ情報量規準）…ー２×（最大対数尤度）＋log(n)×（推定するパラメータ数）
どちらの情報量規準も，候補となる統計モデルの中から，相対的に数値が小さいものを最適なモデルとして選びます。
例えば，説明変数がp個の次の重回帰モデルを考え，サンプルサイズをnとし，誤差項が独立に同一の正規分布にしたがうことを仮定します。

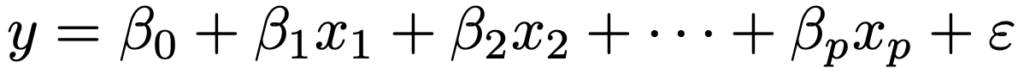
上の重回帰モデルに対して，誤差分散の最尤推定量をσハット２乗として，AICは次のように表せます。

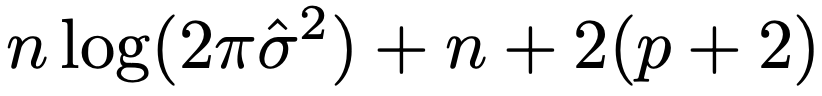
ここで，推定するパラメータ数は，説明変数の数＋切片＋誤差分散＝p＋2であることに注意します。上の重回帰モデルに対するBICは，AICの第３項の先頭の２をlog(n)でおきかえて，次のようになります。

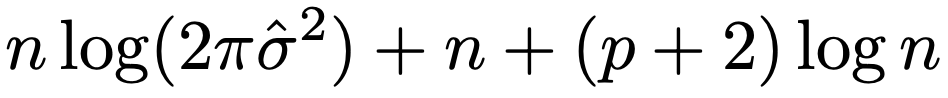
log(n)＞２を満たすサンプルサイズである場合がほとんどなので，BICのほうがAICよりモデルのパラメータ数に対する罰則が強く，よりパラメータ数の少ないモデルを選ぶ傾向があります。また，BICにはモデル選択の一致性があり，候補となる統計モデルの中に真のモデルがあるとき，n→∞で真のモデルを選ぶ確率が１に収束します。
・交差検証法（クロスバリデーション）…データを訓練用とテスト用に分け，訓練用データによるパラメータの推定とテスト用データによる予測誤差の検証をくり返し，予測誤差が最小となるモデルを見つけ出す方法。
・Leave-one-out法…サンプルサイズをnとして，次の手順でモデルを選択する交差検証法。
① i番目のデータを取り除き，それ以外のnー１個を訓練用としてモデルを推定する
② 推定したモデルを用いて，i番目のデータに対する予測誤差を求める
③ すべてのi（i＝1，2，…，n）についての予測誤差の平均によってモデルを評価する
・k分割交差検証法…データをほぼ同じサイズのk個のグループに分割して，そのうちの１個のグループをテスト用，それ以外のkー１個のグループを訓練用とし，予測誤差をk回求めることをくり返す交差検証法。k＝nの場合がLeave-one-out法。

第31章　ベイズ法

・共役事前分布…事前分布と事後分布が同じタイプの確率分布になるような事前分布。次の表の３種類は覚えておきましょう。

・ベータ・二項モデル…２値の確率変数Yを考え，サンプルサイズnのデータのうち成功がy回だとするとき，事前分布と事後分布は次の通り。

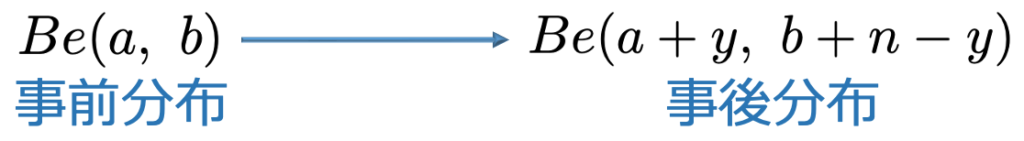
・ガンマ・ポアソンモデル…非負値の確率変数Yを考え，サンプルサイズnのデータの合計がΣyだとするとき，事前分布と事後分布は次の通り。

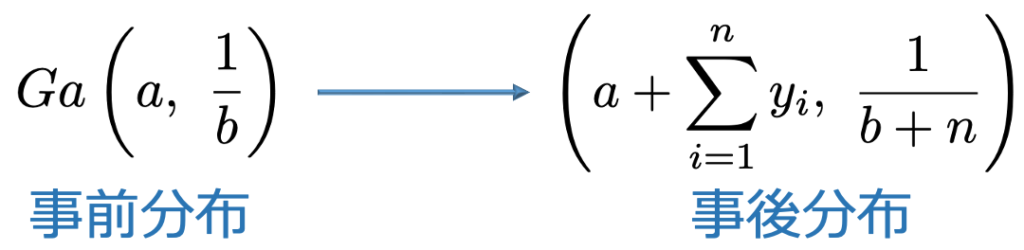
・正規・正規モデル…事前分布N(μ₀，σ₀²)と標本y₁，…，y_n〜N(θ，σ²)に対して，事後分布は次の通り。

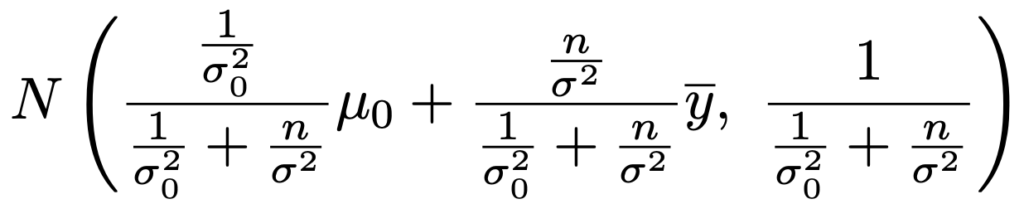
・ベイズ推定量…事後分布の期待値。ガンマ分布Ga(a，b)の期待値はab，ベータ分布Be(a，b)の期待値はa/(a+b)
・MAP推定量…事後分布のモード。ガンマ分布Ga(a，b)のモードはa＞1のとき(aー1)b，ベータ分布Be(a，b)のモードはa＞1，b＞1のとき(aー１)/(a+bー2)
・ベイズ予測分布…データxを与えたもとでの事後分布π(θ|x)を用いた，新たなデータに対する予測分布。
・MCMC法…事前分布が共役事前分布以外のときには事後分布の計算が困難になることが多いため，その代わりに事後分布からの多数の独立なサンプルを得ることで事後分布を近似する手法。パラメータベクトルをθ＝(θ₁，θ₂，…，θ_p)とし，θ⁽⁰⁾→θ⁽¹⁾→…のように，あるルールでパラメータの更新をくり返すと，十分な回数の更新後には事後分布π(θ|x)からのサンプルを得ることができます。MCMC法の代表的なものには，次のメトロポリス法，メトロポリス・ヘイスティングス法，ギブスサンプリングなどがあります。
・メトロポリス法…次の①〜④の手順で事後分布π(θ|x)からのサンプルを得る手法。
① 初期値θ⁽⁰⁾を決める
② θ⁽⁰⁾の近くのθ’をθ’＝θ⁽⁰⁾＋u（uは正規分布などの対称な分布）によって発生させる

③ 次のrを計算し，r＞１ならばθ⁽¹⁾＝θ’として採用し，r＜１ならば確率rでθ⁽¹⁾＝θ’，確率１ーrでθ⁽¹⁾＝θ⁽⁰⁾とする

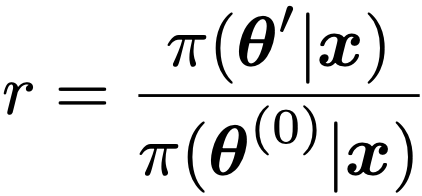
④ ②と③をくり返す
・メトロポリス・ヘイスティングス法…メトロポリス法の③で非対称な確率分布q(θ|θ’)を用いて，次のrに取り替えた手法。

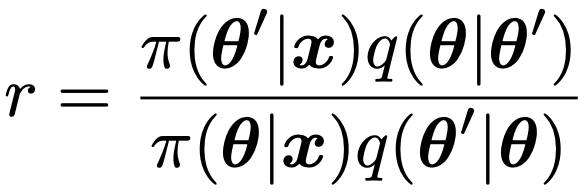
・ギブスサンプリング…n変量でかまいませんが，ここでは２変量の例を挙げます。(X，Y)の同時分布f(x，y)からの抽出は難しいものの，条件付き分布f(x|y)，f(y|x)からの抽出は可能であるものとして，次の①〜④の手順で行います。
① 初期値(x⁽⁰⁾，y⁽⁰⁾)を決める
② (x^(j)，y^(j))が与えられたとき，y^(j+1)を次のように得る

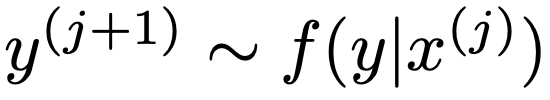
③ y^(j+1)から次のようにx^(j+1)を得る

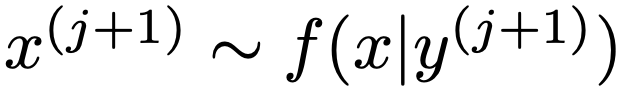
④ ②と③をくり返す

第32章　シミュレーション

・擬似乱数…再現不可能な本来の乱数に対し，計算機によって生成される乱数のように，一定の条件のもとで再現できてしまう乱数。
・逆関数法…一様分布にしたがう乱数をもとに，特定の確率分布にしたがう乱数を得る方法。一様分布U(0，1)にしたがう乱数をu，確率変数Xの累積分布関数をF_X(x)として，x=F_X^ー1(u)とすればXの確率分布にしたがう乱数を得ることができます。
・採択・棄却法…確率密度関数f(x)をもつ分布にしたがう乱数を得たいとき，別の確率密度関数g(x)と定数Cが存在して，すべてのxに対して，f(x)/g(x)≦Cが成り立つものとし，確率密度関数g(x)をもつ分布にしたがう乱数は容易に得られるものとします。このとき，次の①②の手順で確率密度関数f(x)をもつ分布にしたがう乱数を得ることができます。
① y〜g(x)，u〜U(0，1)を独立に生成する
② 次の不等式が成り立てばyを出力し，そうでなければ①に戻る

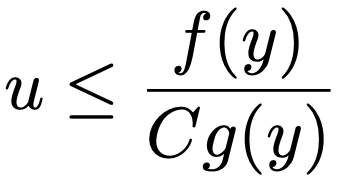
このときのCはできるだけ小さくとったほうが良いことが知られています。
・モンテカルロ法…正方形領域(0，1)×(0，1)内の図形Aの面積Sの近似値を乱数を使って求めるには，一様分布U(0，1)にしたがう乱数(u，v)をn組発生させて，そのうちA内に入ったものの個数がX組ならば，S≒X/nと推定できます。X〜Bin(n，S)であることから，V[X]＝nS(１ーS)です。
・モンテカルロ積分…積分を直接的に求めることが難しいとき，乱数を発生させて近似的に積分値を求める方法。X〜U(0，1)のとき，期待値の定義から，次の式が成り立ちます。

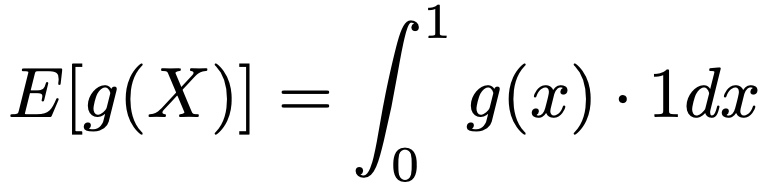
よって，上の式の右辺の積分の近似値を求めるには，X₁，…，X_n〜U(0，1)として，g(X₁)，…，g(X_n)の平均を計算すれば，大数の法則によりnが十分に大きければ，E[g(X)]に近づきます。より一般に，X〜U(a，b)のとき，期待値の定義から，次の式が成り立ちます。

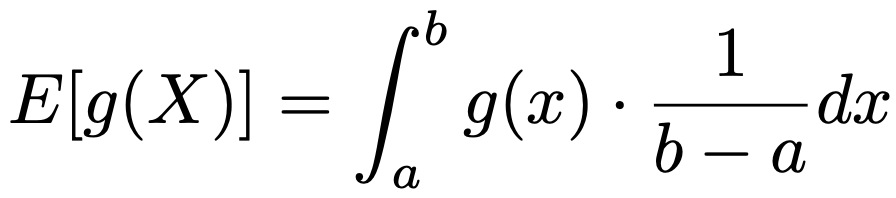
よって，g(x)の[a，b]上での積分の近似値を求めるには，X₁，…，X_n〜U(a，b)として，g(X₁)，…，g(X_n)の平均を計算し，(bーa)をかけます。さらに一般に，[a，b]上で定義された確率密度関数f(x)をもつ分布からの乱数が容易に得られるならば，X₁，…，X_n〜f(x)として，g(X₁)，…，g(X_n)の平均を計算すれば，次の積分の近似値を求めることができます。

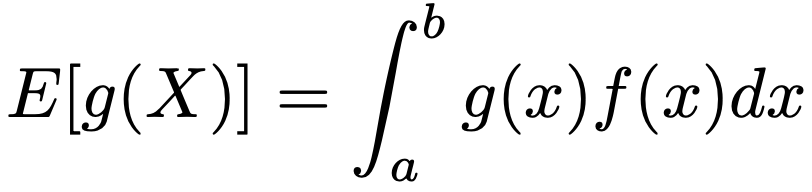
この積分値をθとおき，次の推定量の精度について考えます。

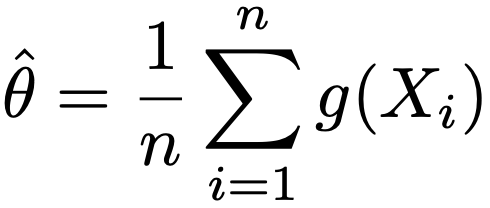
この推定量の分散は，V[g(X)]＝σ²として，次のようになります。

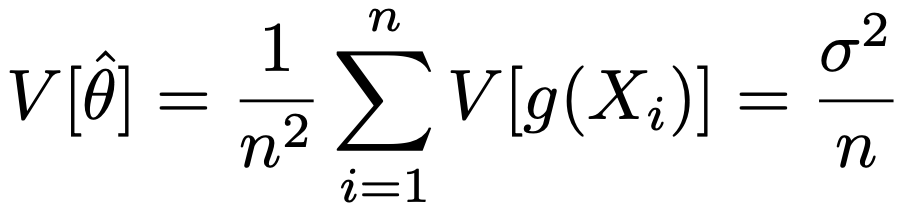
σ²＝E[{g(X)ーθ}²]なので，次のようなσ²の推定量を考えます。

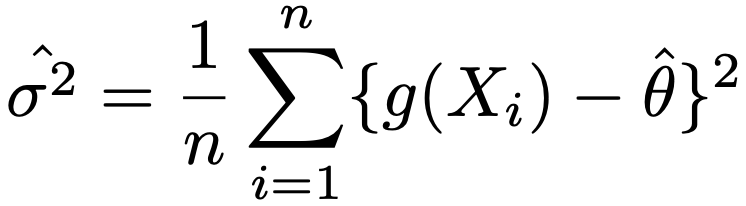
よって，θハットの標準誤差は次のように表せます。

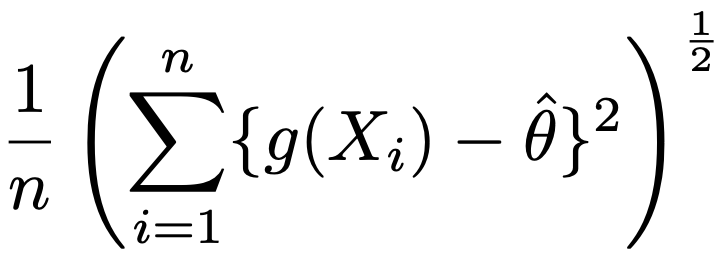
・ブートストラップ法…標本から重複を許してランダムに抽出をくり返すことにより，標本平均やその他の統計量の分布を推定する手法。特に，サンプルサイズが小さい場合に，標本統計量の母数からのバイアスを推定するのに役立ちます。「ブートストラップ法によるバイアス＝ブートストラップ推定量の平均ー標本統計量」としてバイアスを求め，標本統計量からこのバイアスをひくことで，バイアス修正後の推定値が求められます。
※ジャックナイフ法については，第８章を参照。