二項分布と関係が深い3つの確率分布について,具体例を通して性質を理解しつつ,期待値や分散の求め方なども説明していきます。負の二項分布や超幾何分布は,難しそうな名前とは裏腹に,その確率分布自体はシンプルです。多項分布は,離散型の同時分布の代表例であり,複数の確率変数の組を同時に扱いますが,サイコロの目の出方だと考えればそれほど難しくは感じないでしょう。統計検定準1級で必須となるこれらの確率分布について,本稿を通して恐怖心をなくすことを目指していきましょう。
本稿の目的は,多項分布・負の二項分布・超幾何分布を解説すること以外にもう1つあり,それはこれらの確率分布を理解するために必要な数学を解説することです。【統計検定準1級のための数学】と題した記事では,統計検定2級からスムーズに準1級に進めるように,ギャップをうめるために必要な数学も解説していきます。本稿では,負の二項分布に関連して,テイラー展開を解説します。
この記事で前提とする知識は,【中学の数学からはじめる統計検定2級講座】の第1回の確率の和と積,第3回の確率変数,第4回の期待値と分散,第5回の共分散と相関係数,第10回の二項分布,【統計検定準1級のための数学】の①(幾何分布),②(ポアソン分布)の内容になります。これらの内容に不安がある人は,先にそちらの記事を読んでください。
では,はじめていきましょう!
多項分布
結果が2通りで,各回の成功確率が一定の試行のことをベルヌーイ試行と言いましたね。コイン投げならば,結果は表か裏かの2通りなので,ベルヌーイ試行で用がたりるのですが,サイコロ投げならば,結果は6通りあります。サイコロ投げも含めて,結果が3通り,4通り,…などの場合も考えられると,より多くの確率現象を記述できそうです。このようなことを踏まえて,結果がk(k≧2)通りで,それぞれが起こる確率が一定の試行を多項試行と呼ぶことにします。k=2のときにはベルヌーイ試行そのものになります。
次に,ベルヌーイ試行から二項分布を定めたのと同じように,多項試行から確率分布を定めましょう。例えば,次のような例を考えてみます。
(例)箱の中に,赤玉が10個,青玉が8個,白玉が2個の合計20個の玉が入っています。この中から1個の玉を取り出し,色を確認した後で箱の中に戻すという試行を6回くり返します。このとき,赤玉を3回,青玉を2回,白玉を1回取り出す確率は?
毎回の試行は,起こりうる結果が3通りで,取り出した玉をもとに戻すので,それぞれが起こる確率は毎回一定になっています。つまり,赤玉を取り出す確率が2分の1,青玉を取り出す確率が5分の2,白玉を取り出す確率が10分の1の多項試行です。まず,1〜3回目に赤玉,4〜5回目に青玉,6回目に白玉を取り出す確率は,次のように求められます。
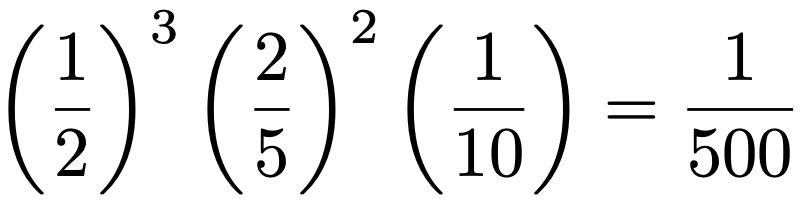
他にも,赤玉が3回,青玉が2回,白玉が1回取り出される取り出し方は,次のようにいろいろな場合が考えられますが,そのどれも起こる確率は500分の1です。
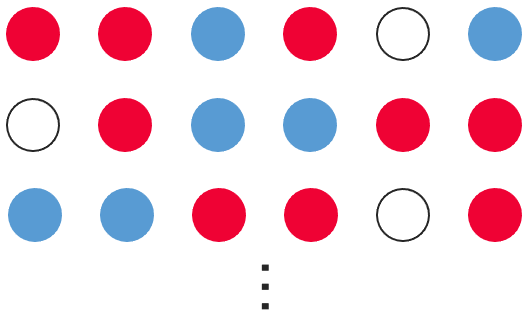
求める確率が,確率500分の1の何個分になるかを知りたいので,横に並んだ6個の玉を並べるとき,上のような赤3個,青2個,白1個の並び方が何通りあるかを考えてみます。ここで,区別できるもののほうが並べ方の数を数えやすいことから,赤玉どうし,青玉どうしが区別できるように,次のような数字を玉に書いてみます。

これで異なる6個の玉を並べることになるので,並べ方は,6!=720(通り)です。しかし,実際には数字の区別はしないので,並んでいる色の順番という意味では次の2通りは同じ並び方だと言えます。

また,次の6通りの並び方も並んでいる色の順番という意味では同じですよね。

つまり,6!=720(通り)の中には,並んでいる色の順番が同じものが,3!×2!=12(通り)ずつ含まれているということです。よって,色の並びが同じで数字の並びだけが異なるものを1通りと数えるためには,次のように計算すればいいことになります。
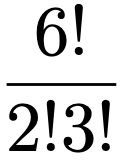
これが赤3個,青2個,白1個の並べ方の数です。よって,赤玉を3回,青玉を2回,白玉を1回取り出す確率は次のようになります。
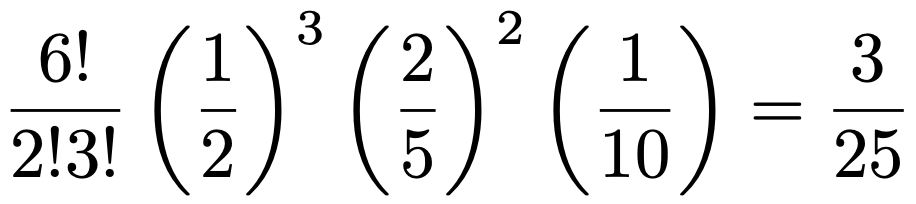
この例を踏まえて,多項分布の確率関数を書いてみましょう。1回の試行でk通りの事象が起こりうるとして,それぞれが起こる確率をp1,p2,p3,…,pk,n回の試行でそれぞれが起こる回数をX1,X2,X3,…,Xkとします。このとき,X1=n1,X2=n2,…,Xk=nk(n1+n2+…+nk=n)となる確率は,次のように求められます。
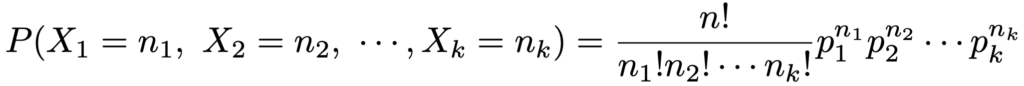
これが多項分布の同時確率関数です。このときの多項分布(multinomial distribution)を次のように表すことにします。
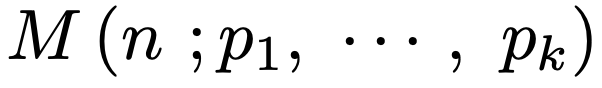
さて,同時確率関数であると言うためには,すべてのn1,n2,n3,…,nkの組み合わせについて確率を合計したときに1にならなければいけないので,このことを示しておきましょう。まず,1回の試行でk個の選択肢のうちのどれか1つが起きるので,p1+p2+p3+…+pk=1が成り立ちます。実は,この式の両辺をn乗するだけで多項分布の確率の和が1であることがわかるのですが,そのことを納得するには次の多項定理を知っておく必要があります。
nを自然数,n1,n2,…,nkを0以上の整数,p1,p2,p3,…,pkを実数とするとき,次の式が成り立つ。
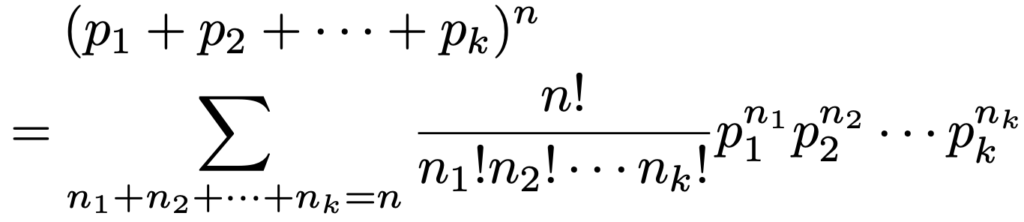
上の定理のΣで表される和では,n1,n2,…,nkはn1+n2+n3+…+nk=nを満たすすべての0以上の整数をとります。例えば,k=2の場合には(n1,n2)=(0,n),(1,nー1),…,(n,0)になります。k=2の場合の多項定理は,次の式になります。
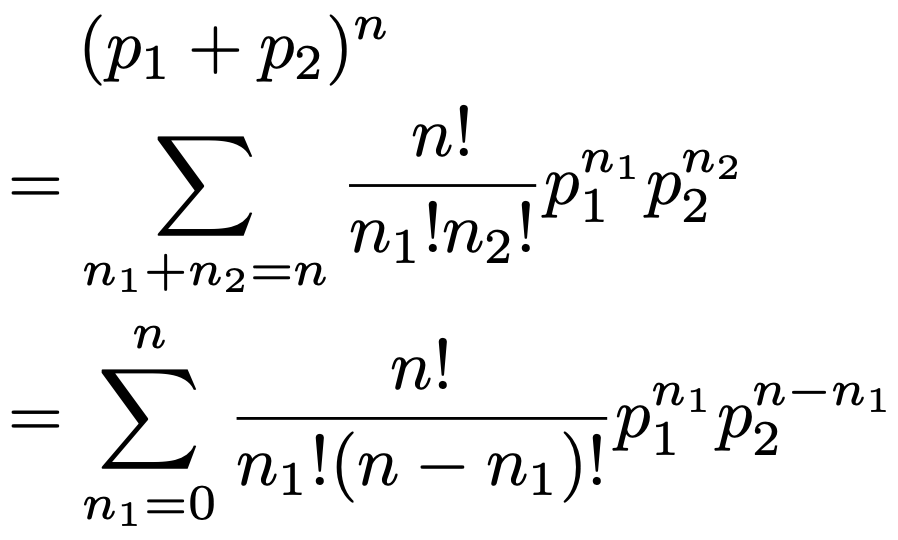
これはポアソン分布の記事(リンクはこちら)で扱った二項定理ですね。多項定理は二項定理を一般化したものです。多項定理がk=3の場合に成り立つことを示すと次のようになります。
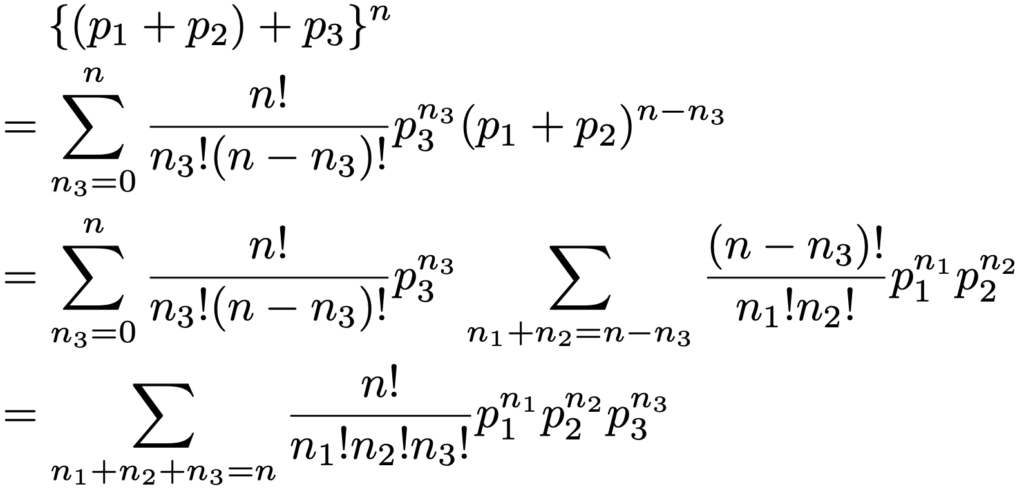
上の変形の1行目から2行目,2行目から3行目では二項定理を使っています。同じ手続きをくり返すこと(正確には,あとで紹介する数学的帰納法)で,kが4以上の場合にも示すことができます。
多項定理を使うと,多項分布のすべての確率の和は1になることが次のようにわかります。
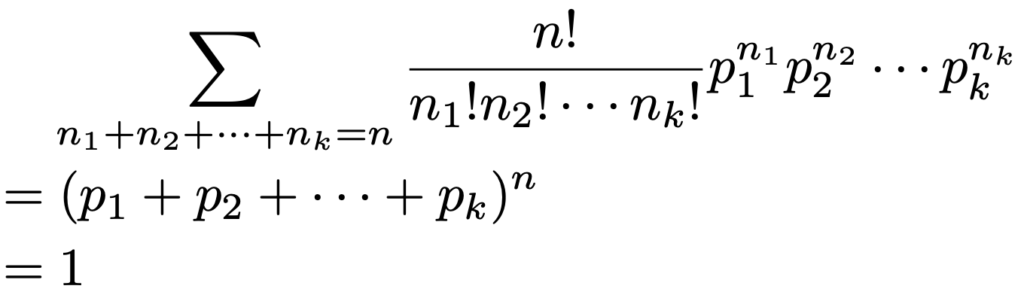
次に,X1の周辺分布を求めてみましょう。
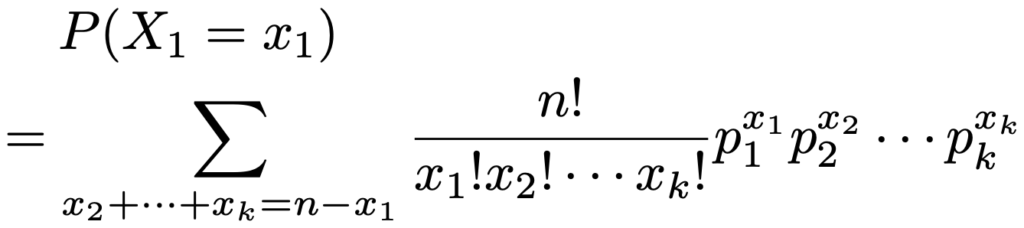
0≦x1≦nとなるx1を固定して,x2,x3,…,xkは和がnーx1に一致するような0以上のすべての整数値をとります。Σはx2,x3,…,xkに関するものなので,それらに関係しないものをΣの外に出すと次のようになります。
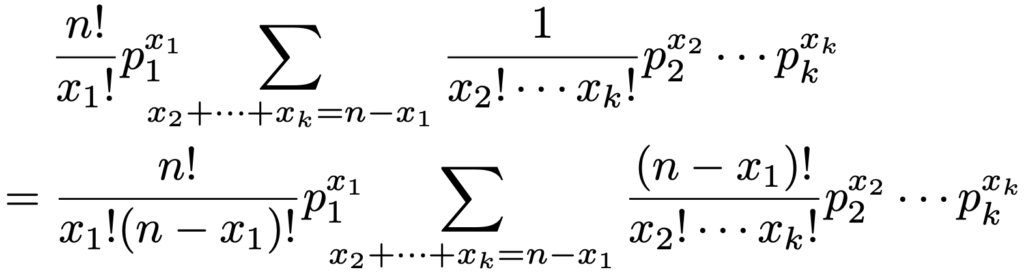
上の2行目では,分母と分子に(nーx1)!をわざとつくっています。約分すれば1行目の式に戻ります。さらに,Σの部分に多項定理を使うと,次のようになります。
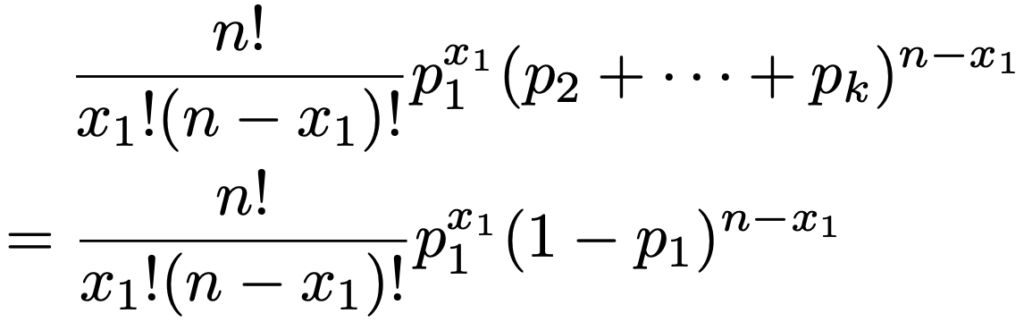
これは,X1の周辺分布が二項分布Bin(n,p1)であることを示しています。このように,(X1,X2,X3,…,Xk)がM(n;p1,p2,p3,…,pk)にしたがうとき,X1〜Xkの周辺分布は二項分布になります。
次にX1とX2の共分散を求めるため,積X1X2の期待値を計算します。定義から次の式の右辺を計算していきます。
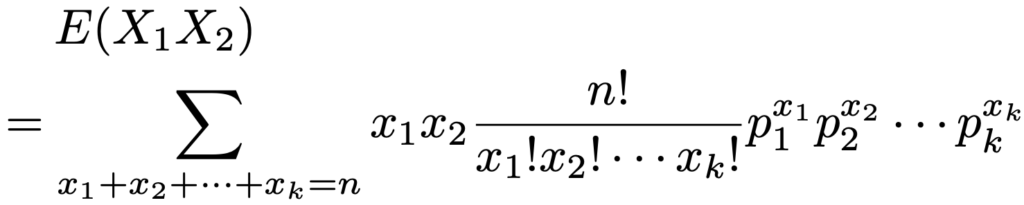
上のΣで,x1,x2,…,xkはx1+x2+…+xk=nを満たす0以上のすべての整数値をとります。x1とx2で約分したいのですが,x1=0やx2=0のときには約分できません。しかし,上の和では,x1=0の項はそもそも0になるので,x1≧1として構いません。x2についても同様なので,約分すると次の式になります。
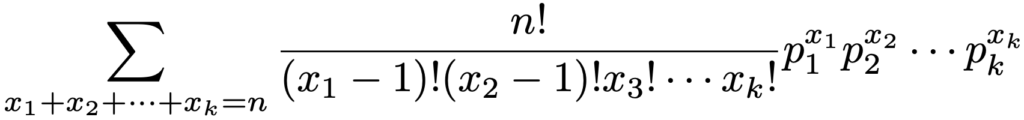
ここで,分子とp1,p2の指数部分を,分母のx1ー1,x2ー1に合わせて,不要なものをΣの外に移動すると,次のようになります。
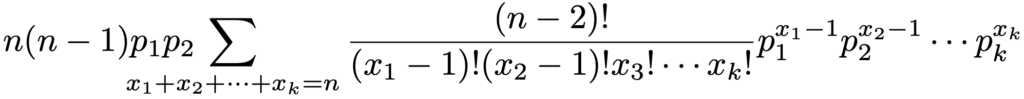
式を見やすくするため,x1ー1=y1,x2ー1=y2,x3=y3,…,xk=ykとおくと,y1≧0,y2≧0,y3≧0,…,yk≧0であり,これらの和はnー2になるので,次のように積X1X2の期待値を求めることができます。
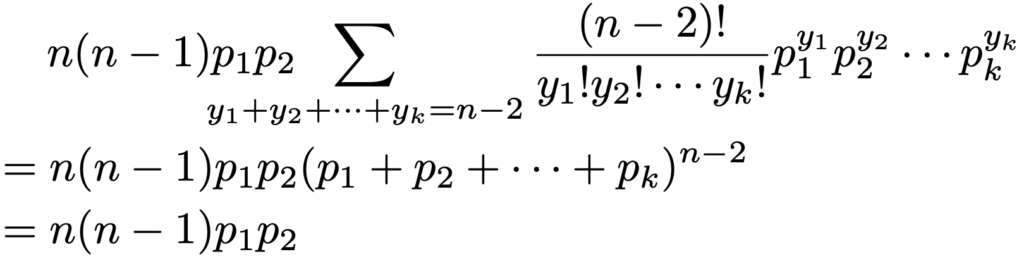
上の計算の1行目から2行目では多項定理,2行目から3行目ではp1+p2+p3+…+pk=1であることを使っています。よって,X1とX2の共分散は次のようになります。
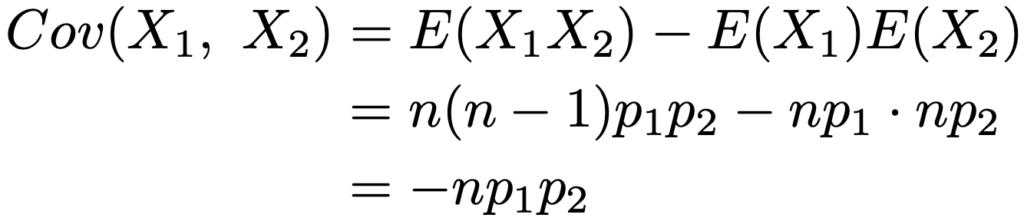
上の計算では,X1やX2が二項分布にしたがうことから,E(X1)=np1,E(X2)=np2となることを用いています。
また,X1とX2の相関係数は次のようになります。
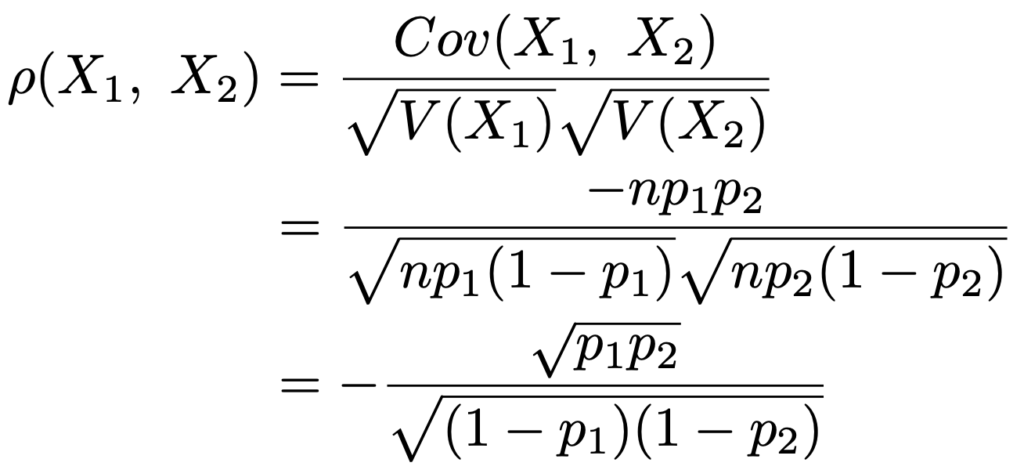
ここまで,X1とX2の共分散と相関係数を計算してきましたが,他のXi,Xj(i≠j)についても同様ですね。
最後に多項分布の例を挙げておきましょう。1個のサイコロをn回投げる試行を行うとき,1の目が出る回数をX1,2の目が出る回数をX2,…,6の目が出る回数をX6とすると,(X1,X2,X3,…,X6)は次の多項分布にしたがいます。
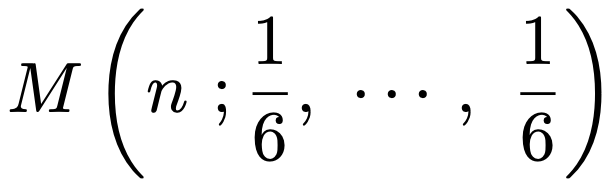
このとき,X1とX2の相関係数は次のようになります。
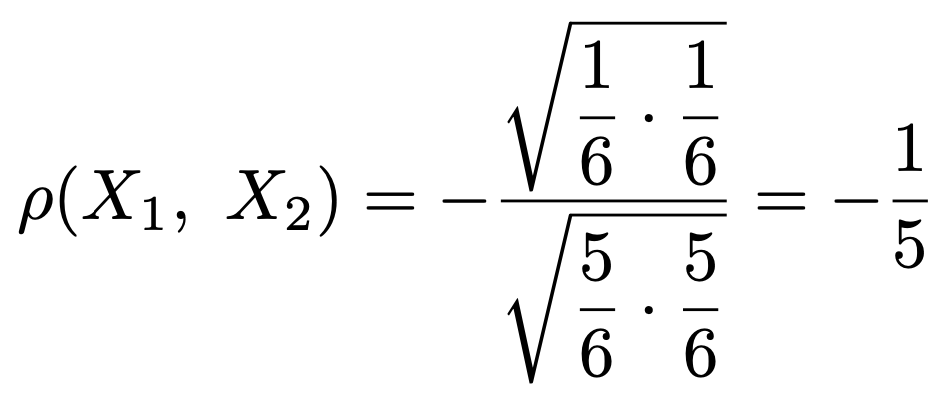
このように,1の目が出る回数と2の目が出る回数には負の相関があります。なぜなら,1の目が出る回数が多くなれば,それだけ2の目が出る回数は少なくなりやすいからです。
負の二項分布
成功確率p(0<p<1)の独立なベルヌーイ試行をくり返して,はじめて成功するまでに失敗した回数Xがしたがうのが幾何分布でしたね。同じように,成功確率pの独立なベルヌーイ試行をくり返して,r回成功するまでに失敗した回数Yがしたがうのが負の二項分布であり,r=1のときには幾何分布に一致します。Yは0以上の整数の値をとりますので,Y=0,1,2,…となる確率を考えてみましょう。まず,Y=0となるのは,r回連続して成功する場合なので,r回の試行が独立であることから,その確率は次のように表せます。
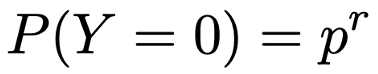
次に,Y=1となる確率を考えます。r回成功するまでに1回だけ失敗するので,試行の回数は(r+1)回です。最後は成功して終わるので,1回目の試行からr回目の試行までのどこかの1回で失敗します。
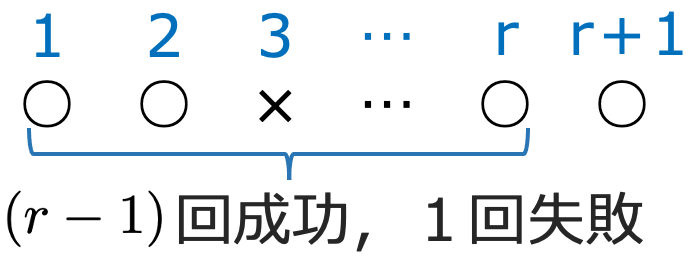
上の図は,3回目に失敗していることを表していますが,失敗が,1回目となる確率,2回目となる確率,…,r回目となる確率を合計して,Y=1となる確率は次のように表せます。
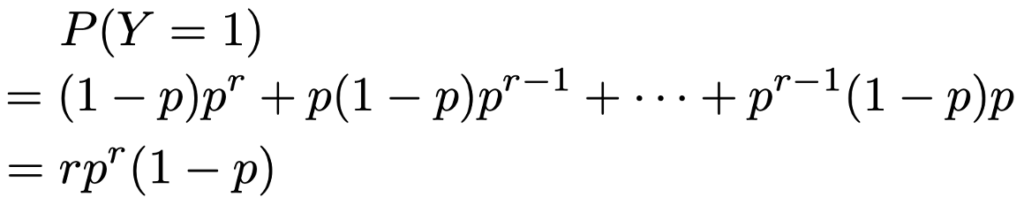
次に,Y=2となる確率を考えます。r回成功するまでに2回だけ失敗するので,試行の回数は(r+2)回です。最後は成功して終わるので,1回目から(r+1)回目までのどこかの2回で失敗します。

上の図は,2回目と(r+1)回目に失敗していることを表していますが,「1〜(r+1)回目までの何回目と何回目に失敗するか」の決め方は,(r+1)個のものから2個を選ぶ選び方の総数だけありますので,Y=2となる確率は次のようになります。
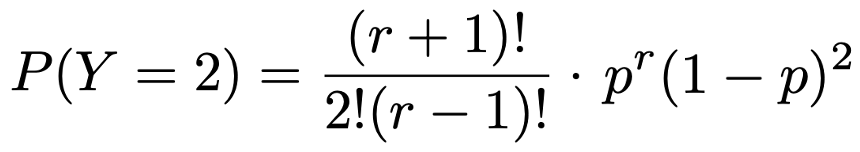
さらに一般的に,Y=y(y=0,1,2,…)となる確率を考えます。r回成功するまでにy回だけ失敗するので,試行の回数は(r+y)回です。最後は成功して終わるので,1回目から(r+yー1)回目までのどこかのy回で失敗します。失敗するy回の決め方は,(r+yー1)個のものからy個を選ぶ選び方の総数だけありますので,Y=yとなる確率は次のようになります。
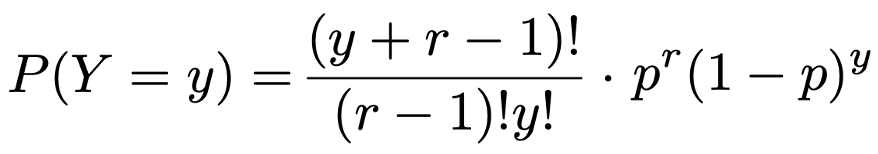
これが負の二項分布の確率関数です。パラメータがrとpの負の二項分布(negative binomial distribution)をNB(r,p)と表します。この確率関数を見たときに思うのは,「なぜ『負の』二項分布という名称なのか」ではないでしょうか。確率関数の係数に使われている階乗に負の整数が出てきていないので,「負の」という雰囲気が感じられないんですよね。そこで,その名の由来の紹介を兼ねて,二項係数と一般二項係数を説明します。
まず,二項係数というのは,ポアソン分布の記事(リンクはこちら)で紹介した二項定理に登場する係数のことであり,次のように表せます。
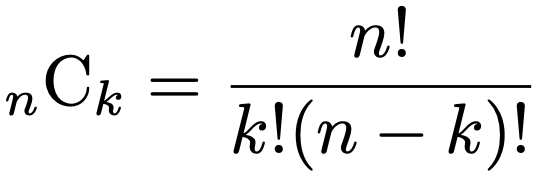
これは,二項分布の記事(リンクはこちら)で説明したように,異なるn個のものからk個を選ぶ組み合わせの総数であり,組み合わせを英語で”combination”と言うことから,上の式の左辺のように表します。この二項係数ではnは自然数ですが,これを任意の実数aに拡張したものが一般二項係数であり,次のように定義されます。
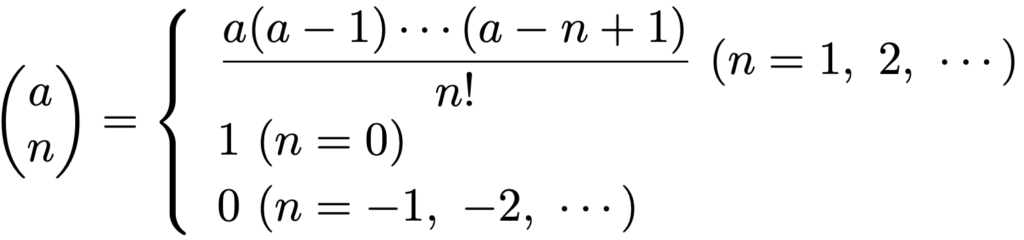
一般二項係数でaが自然数で,0≦n≦aのときには,通常の二項係数に一致します。負の二項分布の確率関数は,二項係数を使っても一般二項係数を使っても表すことができますが,一般二項係数を使うと,次のようになります。
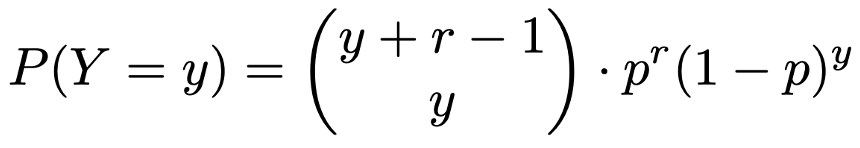
上の式は,次のように変形できます。
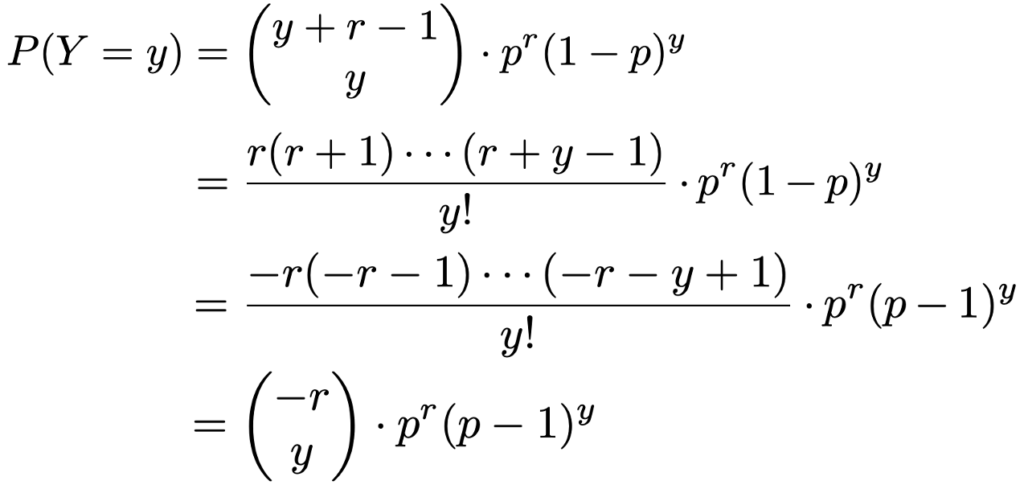
上の2行目から3行目の変形では,(1ーp)y=(ー1)y(pー1)yとして,y個のー1を分数の分子に1つずつかけています。このように変形して得られた最後の式は,二項分布の確率関数になんとなく似ていますが,一般二項係数に負の整数が現れています。負の二項分布の確率関数がこのように表せることが,その名の由来です。
さて,負の二項分布の確率関数として導出した式は,確率関数になっていると言えるでしょうか。つまり,0<p<1より,y=0,1,2,…という確率はすべて正であることがわかりますが,これらの確率の和は1になるでしょうか。自分で計算してみるとわかりますが,1になることを示すのは意外に手強いです。このことを示すために,負の二項定理と呼ばれる次の式を紹介します。
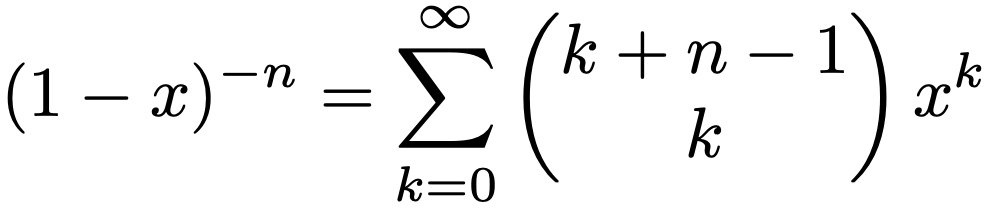
上の式が成り立つことは,すぐ後で紹介するテイラー(マクローリン)展開によってわかりますが,この式をいったん認めて負の二項分布の確率の和が1になることを示しておきましょう。負の二項定理にx=1ーp,n=rを代入すると,次の式になります。
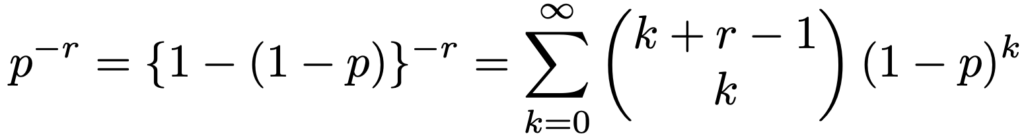
上の式の最左辺と最右辺にprをかけると,次の式になります。
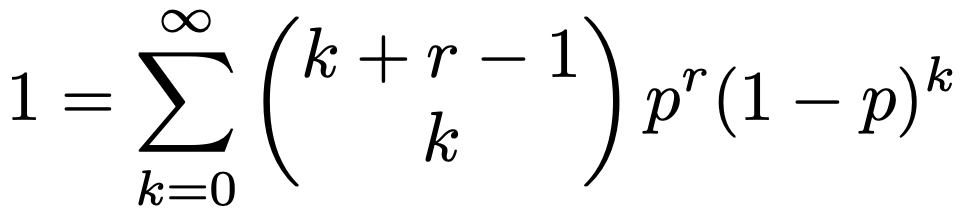
上の式は,負の二項分布NB(r,p)の確率の和が1になることを示していますね。
では,負の二項定理が成り立つことを確認していきます。関数f(x)がx=aで何回でも微分できて,f(x)が次の式の右辺のようなべき級数(f(k)(x)はk次導関数)で表せるとき,そのべき級数をf(x)のx=aにおけるテイラー展開と言います。
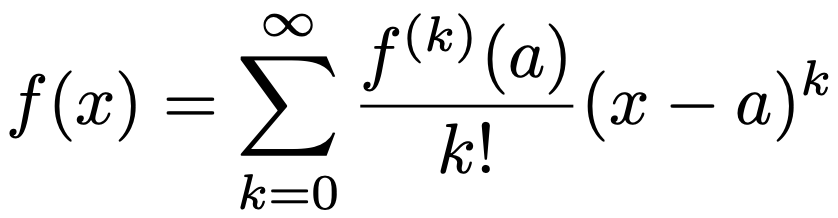
特に,a=0の場合のテイラー展開をマクローリン展開と言います。ポアソン分布の記事で,指数関数が次の式の右辺のべき級数で表せることを紹介しましたが,このべき級数が指数関数のマクローリン展開です。
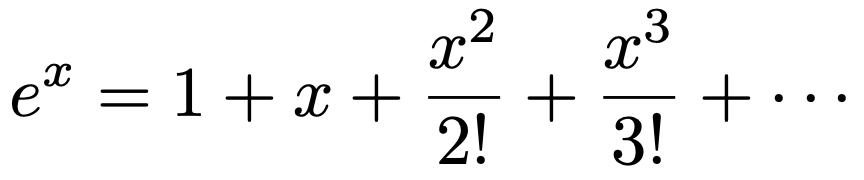
では,マクローリン展開の係数を求めるために,f(x)=(1ーx)ーnとおいて微分の計算をしていきましょう。まず,1次導関数は次のようになります。
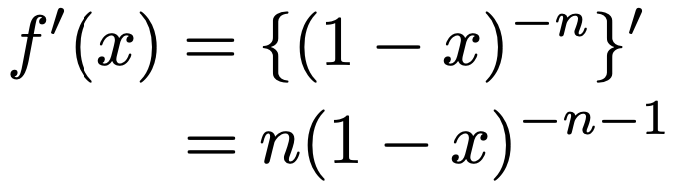
1次導関数にx=0を代入すると,f'(0)=nですね。次に,2次導関数は次のようになります。
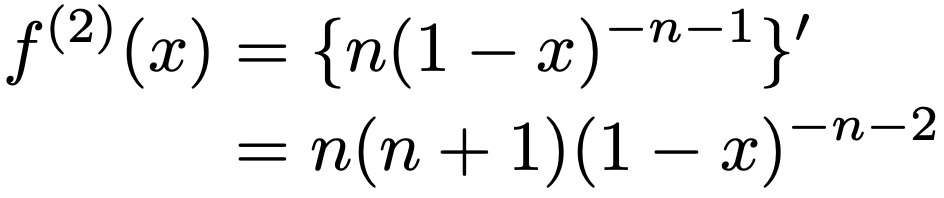
2次導関数にx=0を代入すると,f(2)(0)=n(n+1)ですね。同じように考えると,k次導関数は次のようになります。
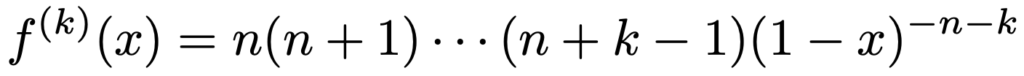
よって,f(x)=(1ーx)ーnのマクローリン展開は次の式になります。
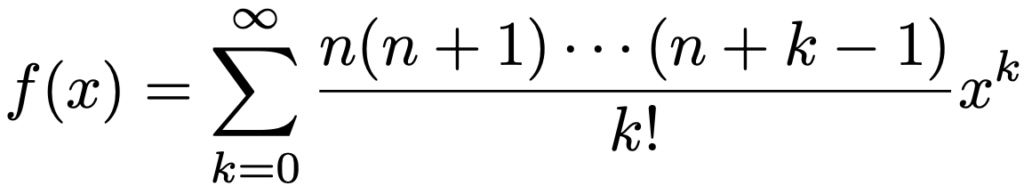
上の式の右辺のべき級数はー1<x<1の範囲で収束し(べき級数の収束について勉強したい人は,例えば,本稿下部で紹介している参考図書④を参照してください),f(x)=(1ーx)ーnと一致します。一般二項係数を使えば,次の式が成り立つことになります。
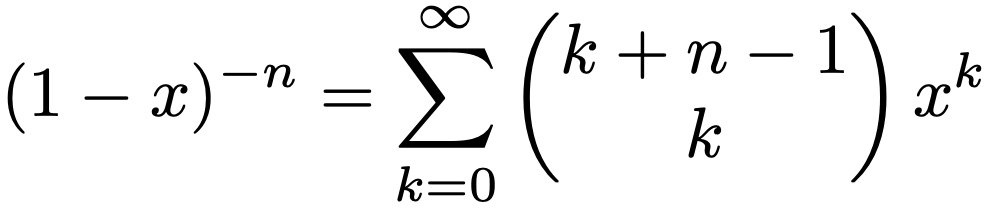
負の二項分布の確率の和を計算するときにxに代入するのはx=1ーp(0<1ーp<1)なので,ー1<x<1の範囲を満たしています。
さて,負の二項分布の期待値や分散の計算に進みますが,その前に次の命題を紹介しておきましょう。
X1,X2,X3,…,Xrが独立に幾何分布Geo(p)にしたがうとき,Yr=X1+X2+…+Xrは負の二項分布NB(r,p)にしたがう。
例えば,次の図で3回目に成功するまでに失敗した回数について考えてみましょう。

まず,はじめて成功するまでに失敗する回数は幾何分布にしたがいますよね。1回目の成功のことは忘れて,改めて次に成功するまでに失敗する回数は幾何分布にしたがいます。同じように,1,2回目の成功のことは忘れて,改めてその次に成功するまでに失敗する回数は幾何分布にしたがいます。そして,それらの失敗の回数の合計が3回目に成功するまでに失敗する回数ですよね。これが上の命題が主張していることです。この命題の証明は長くなるので,このセクションの最後に回して,先に負の二項分布の期待値と分散を求めます。上の命題のようにYr=X1+X2+…+Xrと表される確率変数Yrを考えます。まず,幾何分布Geo(p)の期待値と分散を思い出しておくと,次の通りでした。
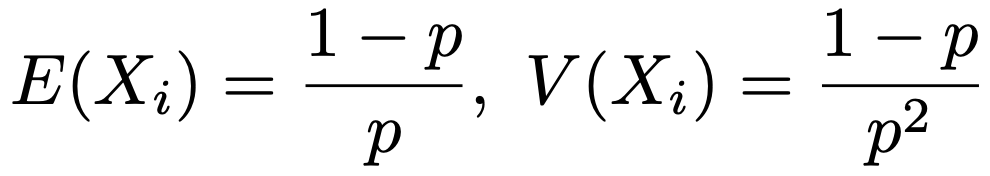
この幾何分布の期待値を使うと,負の二項分布NB(r,p)にしたがうYrの期待値は,次のようになります。
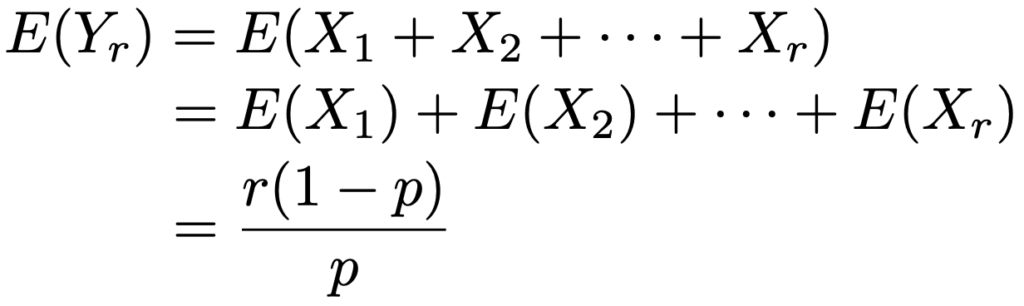
同じように,Yrの分散は,Xi(i=1,2,…,r)が独立であることから,次のようになります。
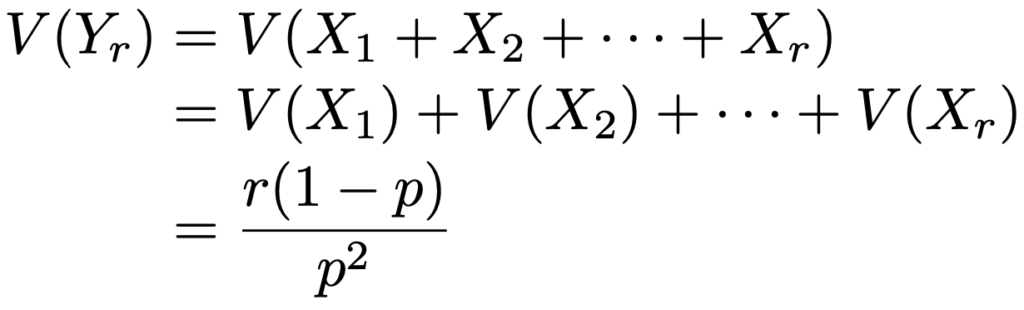
これで負の二項分布にしたがう確率変数Yrの期待値と分散がわかりました。E(Yr)<V(Yr)であることがポイントです。
では,最後に上の命題を証明します。まず,Yr=X1+X2+…+Xrの確率関数がNB(r,p)の確率関数であることを仮定して,Yr+1=X1+X2+…+Xr+Xr+1の確率関数がNB(r+1,p)の確率関数であることを示します。Yr+1=mとなるのは,「Yr=0,Xr+1=mの場合」,「Yr=1,Xr+1=mー1の場合」,…,「Yr=m,Xr+1=0の場合」のm+1通りあることから,Yr+1=mとなる確率は次のように表せます。
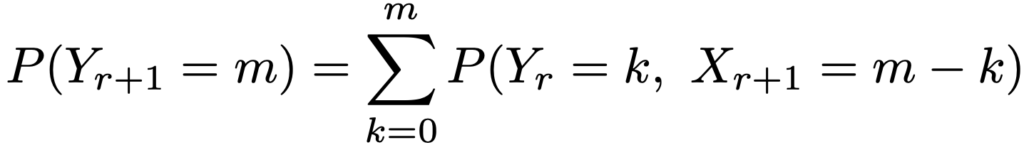
YrとXr+1が独立であることから,上の確率は次のように計算できます。
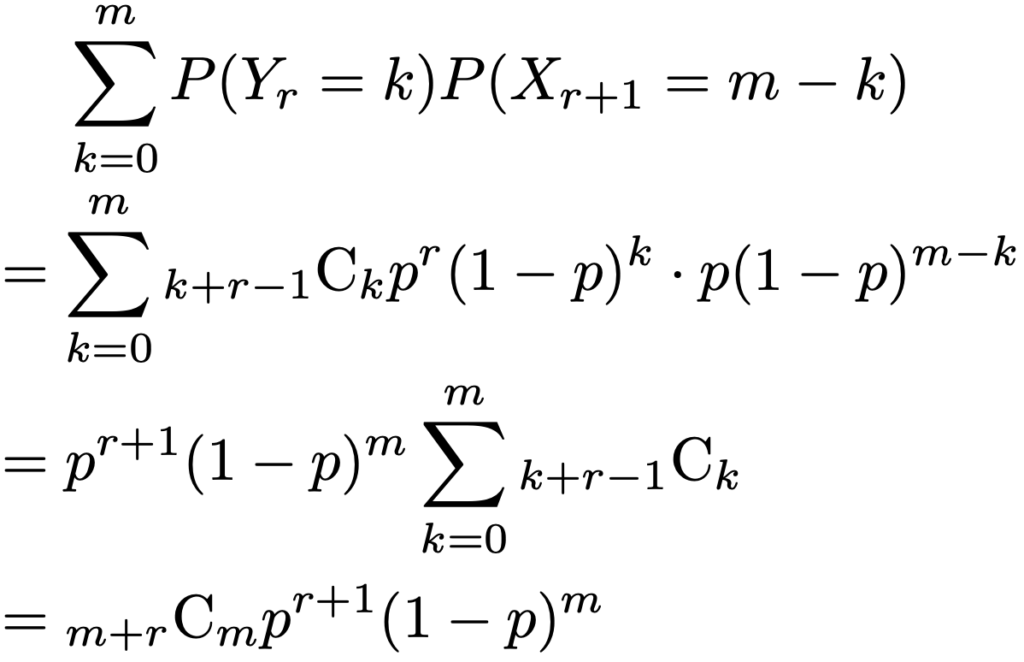
上の計算の3行目から4行目のところがわかりにくいと思いますが,いったん認めることにしましょう。そのとき,Yrの確率関数がNB(r,p)の確率関数であることを仮定すれば,Yr+1の確率関数がNB(r+1,p)の確率関数に一致していることがわかりました。そして,Y1=X1の確率関数はNB(1,p)の確率関数と一致しています。これらのことから,Y1〜NB(1,p)→Y2〜NB(2,p)→Y3〜NB(3,p)→…のように,すべての自然数rについて,Yr〜NB(r,p)が成り立つことがわかります。この論法のことを数学的帰納法と言います。
さて,上の命題の証明の途中で,次の式が成り立つことを使いました。
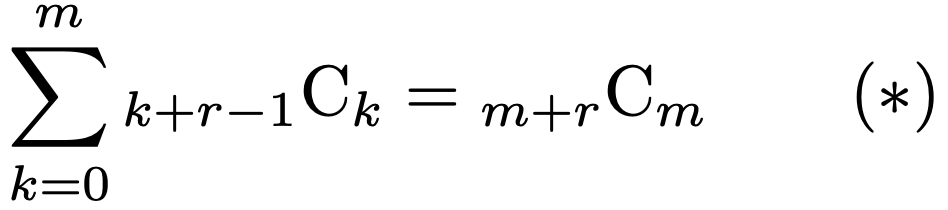
これが成り立つことを,自然数rは固定されているとして,mについての数学的帰納法によって示しましょう。まず,m=1のとき,上の式は次の式になります。
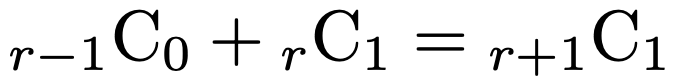
上の式は両辺ともr+1なので,m=1のときには成り立っています。次に,(*)が成り立つことを仮定して,(*)のmをm+1でおきかえた式が成り立つことを示します。次の式が,示すべき式の左辺を表しています。
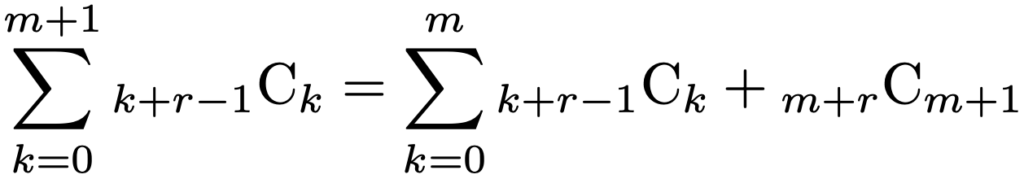
上の式の右辺に,仮定した(*)の式を代入すると,次のようになります。
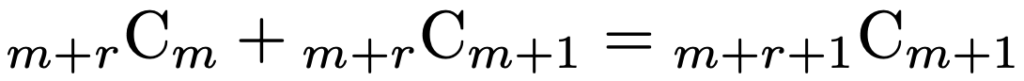
上の式の等号は左辺を階乗で表してから通分すれば示すことができますが,ポアソン分布の記事で紹介したパスカルの三角形で「となり合う2つの数をたすと真下の数になる」という性質そのものです。これで(*)のmをm+1でおきかえた式が成り立つことが示せましたので,数学的帰納法により,(*)がすべての自然数について成り立つことがわかりました。
以上で,独立に同一の幾何分布にしたがう確率変数の和が負の二項分布にしたがうことが示せたことになります。
超幾何分布
まず,次のようなよくあるくじ引きの例を考えてみましょう。
(例)50本のくじの中に当たりが3本入っている。この中から,くじを1本ずつ合計3回引くとき,x回当たる確率はいくらか。
では,x回当たる確率をxで表せるでしょうか? 答えは”No”です。くじを引いた後に,引いたくじをもとに戻すのかどうかが書かれていません。もし,くじを引くたびにもとに戻すのならば,1回の試行で当たりを引く確率は0.06で一定ですね。こういう取り出し方を復元抽出と言って,くじを3回引くときに当たる回数は,二項分布Bin(3,0.06)にしたがいます。
一方で,引いたくじをもとに戻さないときには,当たりを引く確率は一定ではなく,3回引いてx回当たる確率は二項分布では求められなくなります。と言うのも,1回目に当たりを引く確率は0.06ですが,1回目にはずれを引くと2回目に当たりを引く確率は49分の3に変わります。また,1回目に当たりを引くと2回目に当たりを引く確率は49分の2となってしまいます。このように,引いたくじをもとに戻さないような取り出し方を非復元抽出と言って,この確率を計算するときに役に立つのが超幾何分布です。
「1本ずつ3回引く」ときの被復元抽出は,「3本まとめて1回引く」と考えても確率は変わりませんよね。次の例では,まとめて引くと考えて確率を考えてみます。
(例)14本のくじの中に当たりが4本入っている。この中から3本のくじを同時に引くとき,2本当たる確率はいくらか。
まず,確率を考えるときには,次の図のように当たりくじ4本とハズレくじ10本にそれぞれ番号をつけて,14本を異なるものとして区別するようにしましょう。
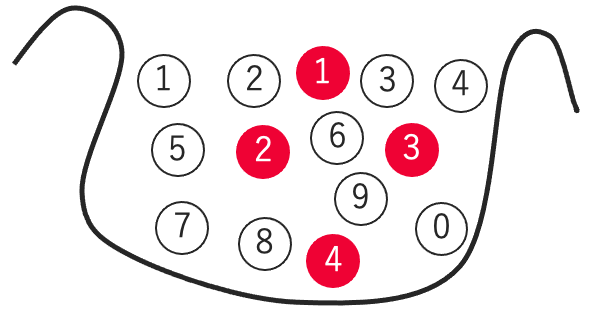
3本のくじの取り出し方の総数は,異なる14個のものから3個を選ぶ選び方の数なので,14C3です。次に,当たりくじ2本とハズレくじ1本の選び方の総数を考えます。当たりくじの選び方は異なる4個から2個を選ぶので,4C2=6(通り)です。ハズレくじは異なる10個のものから1個を選ぶので10通りです。当たりくじを6通りの中の1つに決めると,それに対してハズレくじの決め方が10通りあるので,当たりくじ2本とハズレくじ1本の組は全部で,6×10=60(通り)あります。よって,3本のくじを引くとき,2本当たる確率は次のように求めることができます。
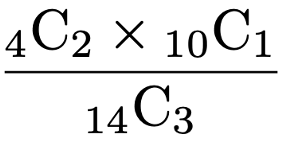
次に,問題の設定を一般的に文字で表して考えてみましょう。
(例)N本のくじの中に当たりがM本入っている。この中からn本のくじを同時に引くとき,k本当たる確率はいくらか。
当たりの本数,ハズレの本数,選び方の数を表にまとめると,次のようになります。
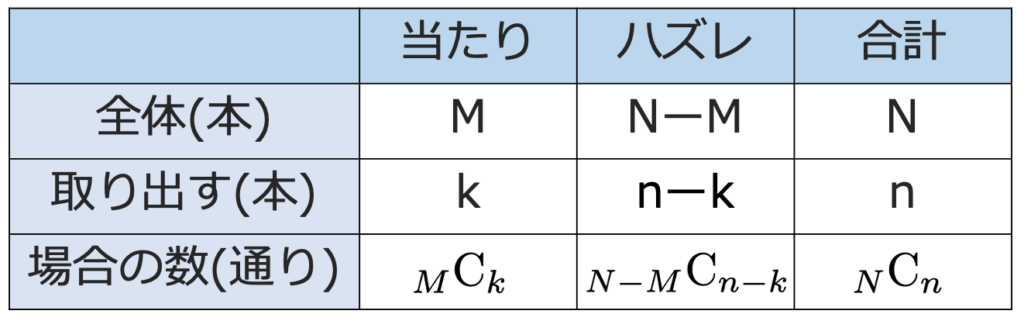
ただし,当たりくじは全部でM本しかないので,kはMを上回ることはできないことに注意してください。同じように,ハズレくじは全部で(NーM)本しかないので,(nーk)は(NーM)を上回ることはできません。kがその範囲の整数だとすると,n本のうちk本当たる確率は,前の例と同じように,次のように求められます。
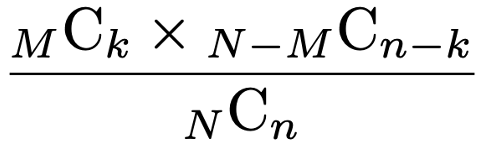
上の例で,当たりくじの本数がしたがう確率分布が超幾何分布であり,その確率関数は次の式になります。
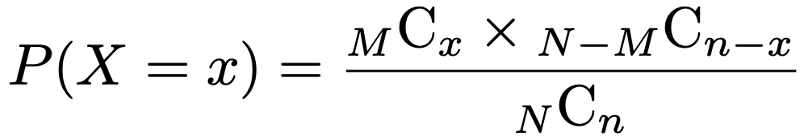
上の式にはN,M,nというパラメータが使われているので,この場合の超幾何分布(hypergeometric distribution)をH(N,M,n)で表します。ただし,上の確率関数では,xがとりうる値の範囲に注意が必要です。MCxやNーMCnーxの右下の数は0以上なので0≦x≦nです。また,MCxやNーMCnーxの左下の数は右下の数以上なので,M≧x,NーM≧nーxが成り立ちます。よって,xはnとMの一方でも上回ることはできませんし,0とnー(NーM)の一方でも下回ることはできませんから,範囲をまとめて表すと,次のようになります。
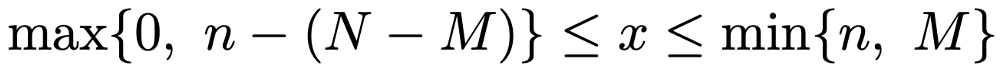
max{A,B}は「AとBの大きいほう」,min{A,B}は「AとBの小さいほう」という意味です。このように,xの範囲はちょっと面倒ですが,一般二項係数を使うと,この煩雑さは解消します。上の確率関数を一般二項係数を使って表すと,次の式になります。
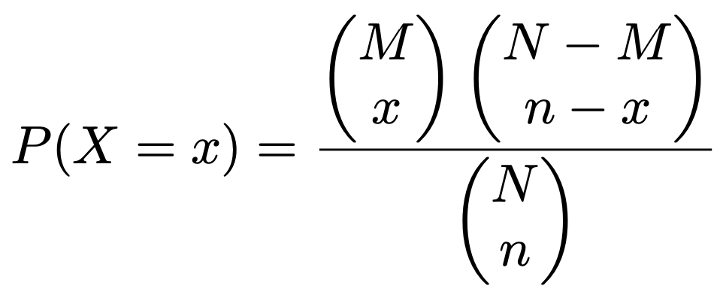
一般二項係数の定義により,分子のxやnーxが負のときには上の確率は0になります。また,M<xやNーM<nーxのときにも上の確率は0になります。よって,一般二項係数を使う場合には,xは0以上の整数としておくだけで問題はありません。ですが,これ以降はわかりやすさを優先して,xの定義域が0以上n以下の整数となる場合だけを考えて二項係数で式を表すことにします。
では,超幾何分布H(N,M,n)の確率の和が1になることを確認していきます。そのためには次の式を使います。
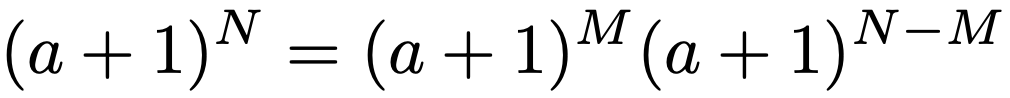
指数法則によって,上の式が成り立ちます。この両辺を,二項定理を使って展開すると,次のようになります。
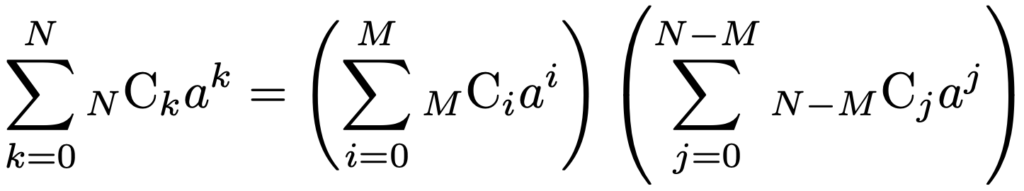
上の式で,anの係数について両辺を比較すると,次の式が成り立ちます。
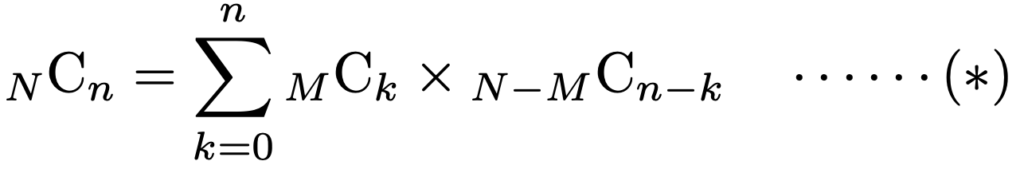
(*)の式の両辺を,左辺でわれば,次のように超幾何分布H(N,M,n)の確率の和が1であることがわかります。
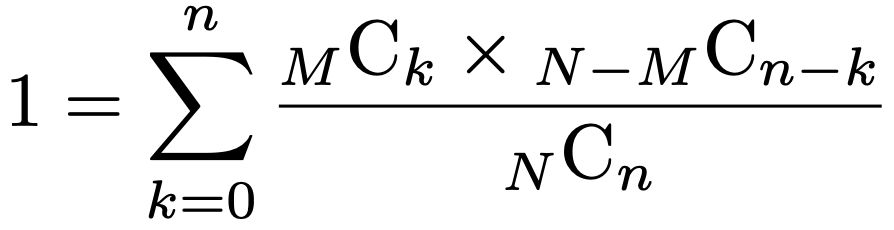
では,超幾何分布H(N,M,n)の期待値と分散を計算してみましょう。期待値の定義は次の式の1行目ですが,k=0の項は0になるので,k≧1について和をとったものと等しくなります。
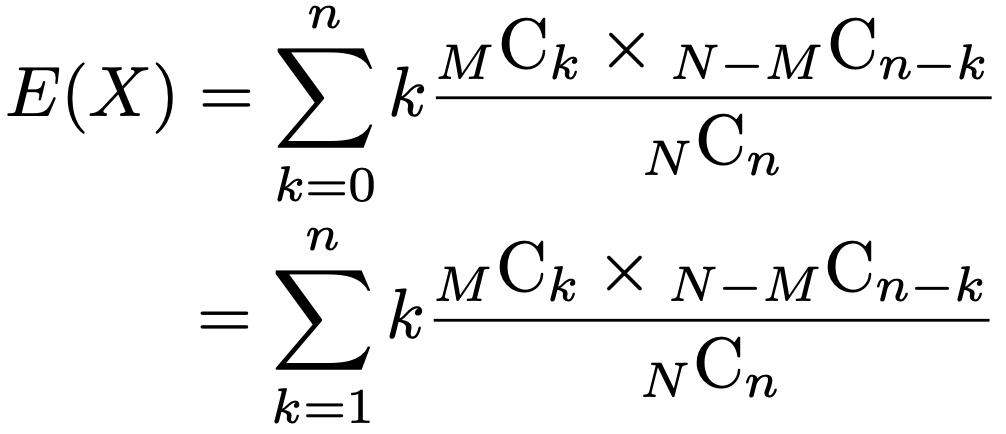
kを約分して,さらに計算を進めると,次のようになります。
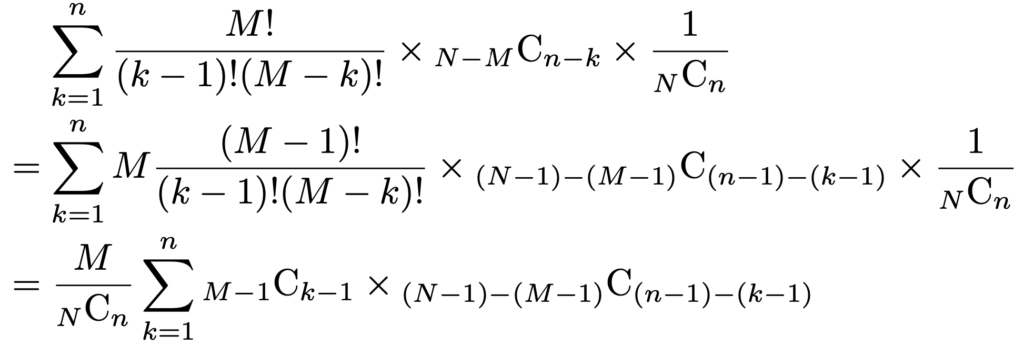
すぐ上の式のΣの部分は,(*)の式でM→Mー1,k→kー1,N→Nー1,n→nー1とおきかえた形になっているので,次のように書き直すことができます。
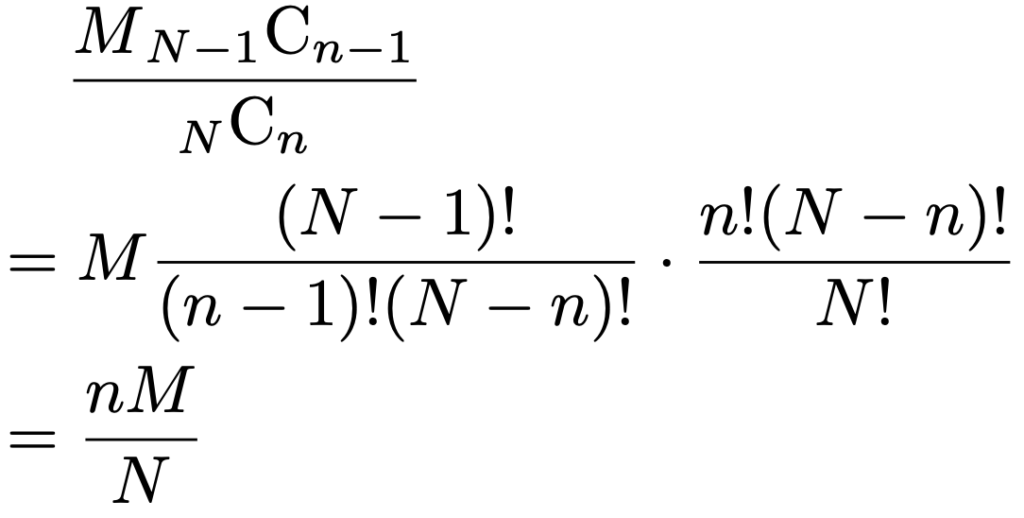
これで期待値が求められました。復元抽出の二項分布の場合には,1回あたり当たる確率はM/Nなので,当たりの本数の期待値は超幾何分布の場合と一致します。
次に,分散を計算するために,n≧2としてE[X(Xー1)]を計算します。E(X)の計算と同じように,次の式でk=0,1の項は0になるので,k≧2について和をとったものと等しくなります。
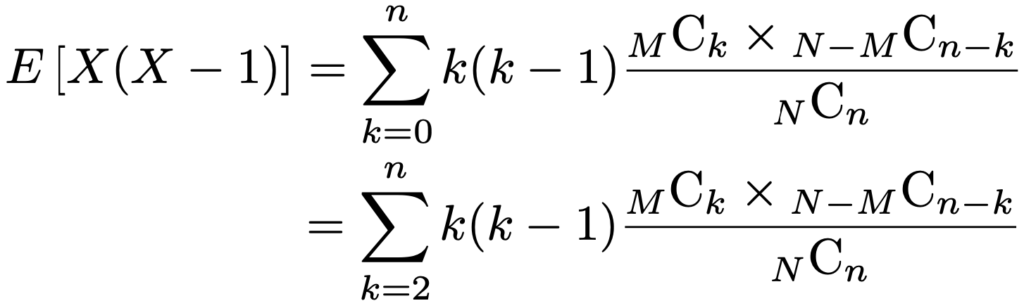
k(kー1)を約分して,さらに計算を進めると,次のようになります。
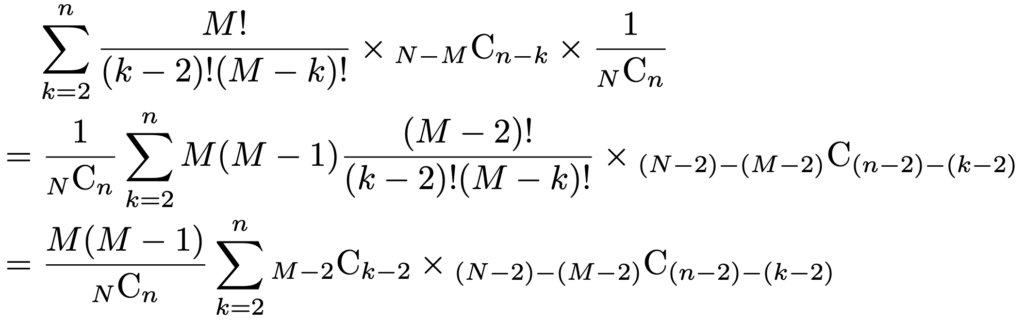
すぐ上の式のΣの部分は,(*)の式でM→Mー2,k→kー2,N→Nー2,n→nー2とおきかえた形になっているので,次のように書き直すことができます。
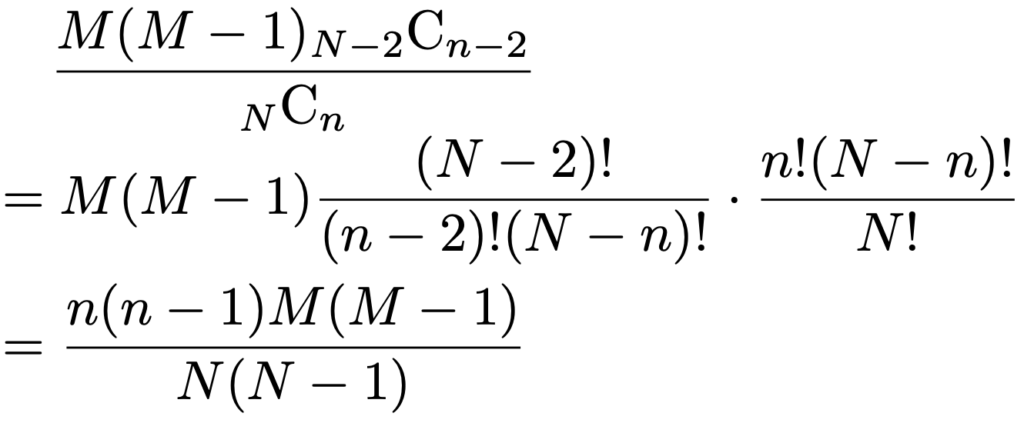
この結果を使うと,分散は次のように計算できます。
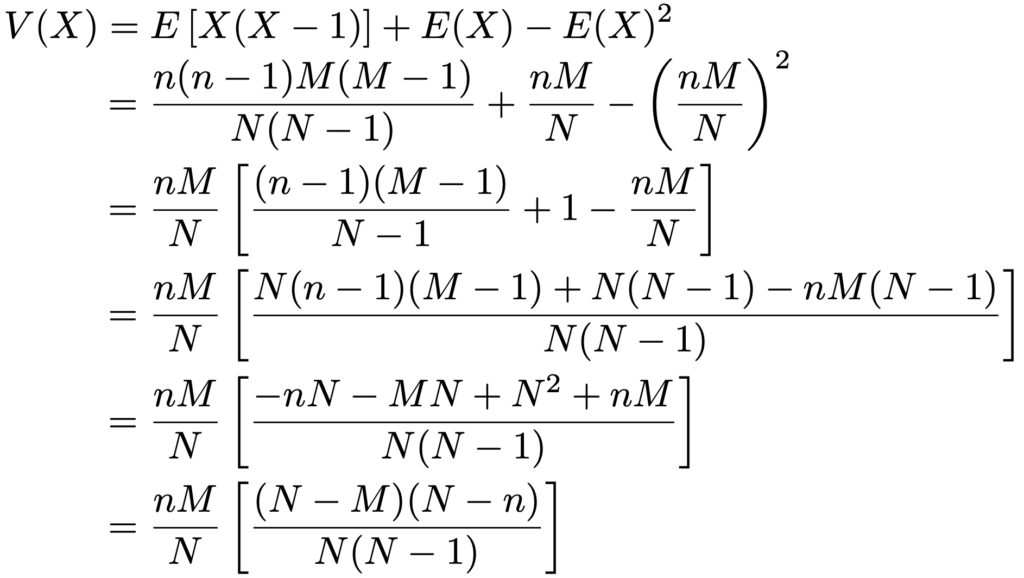
いま求めた分散は次の式のように表すこともできます。
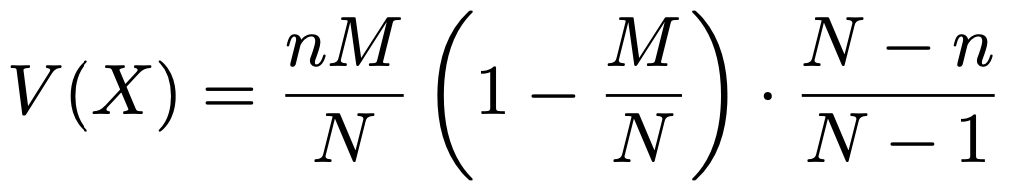
ここで,次のようにおいてみます。
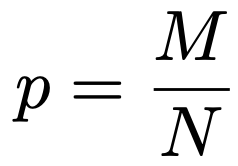
pを使うと,上で求めた分散は次のように表せます。
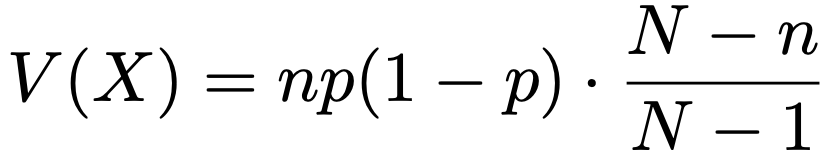
復元抽出の二項分布の場合の分散に(Nーn)/(Nー1)をかけた結果になっています。n≧2なので(Nーn)/(Nー1)は1より小さく,二項分布の場合よりも分散が小さくなります。この分数を有限母集団修正と言います。N→∞のとき,(Nーn)/(Nー1)の極限は1なので,そのときには期待値も分散も二項分布のそれらと一致します。ということは,「2つの確率分布自体が一致するのでは?」と考えられますね。このことを確かめてみましょう。まず,次のように,確率関数を階乗を使って表して,かけ算の順番を変えます。
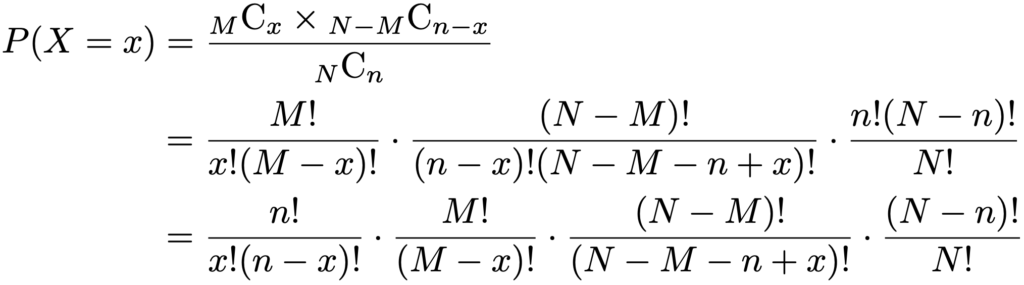
先頭の分数はnCxですが,それを除いた2〜4番目の分数を,それぞれ約分してまとめると,次のようになります。
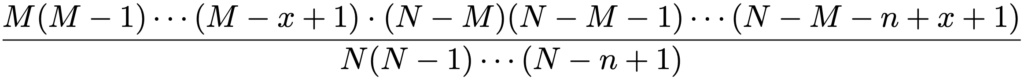
上の分数の分子は,前半のx個と後半のnーx個に分けることができるので,次のように分母もx個とnーx個に分けることにします。
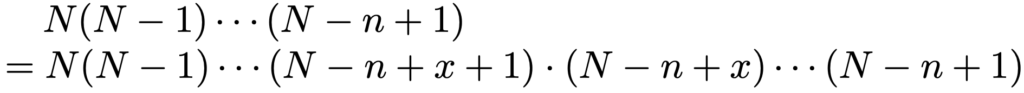
次に,分母,分子ともにnーx個の積になっている分数を次のように変形します。
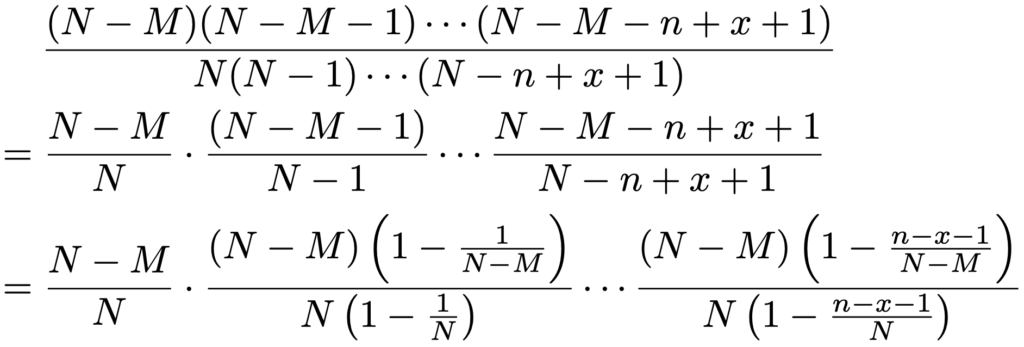
p=M/Nとおくと,次のようになります。
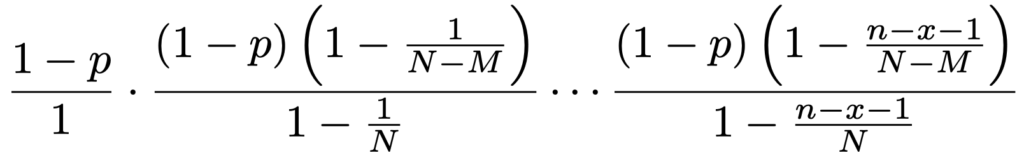
pを一定にしたまま,上の分数の積のN→∞の極限を考えると,NーM→∞でもあるので,(1ーp)nーxになります。次に,分母,分子ともにx個の積になっている分数を次のように変形します。
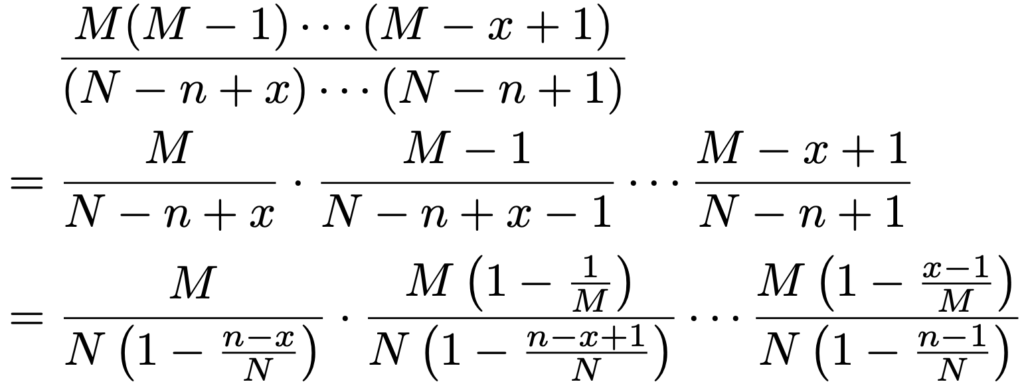
p=M/Nとおくと,次のようになります。
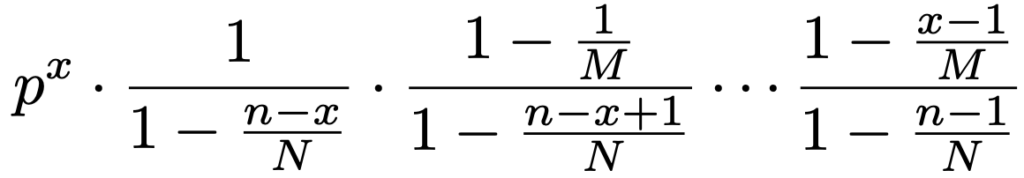
pを一定にしたまま,上の積のN→∞の極限を考えると,M→∞でもあるので,pxになります。よって,超幾何分布の確率関数が,この極限のもとでnCxpx(1ーp)nーxになることが示せました。
参考図書
本稿を執筆するにあたり,次の書籍を参考にしました。
①数理統計学の基礎(尾畑伸明著,共立出版)
多項分布や超幾何分布について詳しく書かれています。また,一般二項係数についても触れられています。
②これからはじめる統計学(蓑谷千凰彦,東京図書)
負の二項分布についてはこの書籍が詳しく,本稿では扱わなかった負の二項分布とポアソン分布の関係にも触れられています。
③ガイダンス確率統計(石谷謙介,サイエンス社)
独立に同一の幾何分布にしたがう確率変数の和が負の二項分布にしたがうことの証明について参考にさせてもらいました。
④手を動かしてまなぶ微分積分(藤岡敦,裳華房)
べき級数の収束など,大学1年の微分積分を学びたい人にオススメです。
本稿はここまでとなります。最後までお読みいただき,ありがとうございました!
引き続き,勉強をがんばっていきましょう!







コメント