指数分布【統計検定準１級のための数学③】

「指数分布がなんとなくしっくりこない…」と感じていませんか。教科書を見れば確率密度関数とグラフの形はわかりますが，それらと有機的に結びつくイメージが大切です。そのために，本稿では「指数分布がどこから生まれるか」に着目し，指数分布の源流としてイメージがしやすいと思われる幾何分布との関係を説明します。最後まで読み終える頃には，指数分布と仲良くなれているはずです。

本稿の目的は，指数分布を解説すること以外にもう１つあり，それは指数分布を理解するために必要な数学を解説することです。【統計検定準１級のための数学】と題した記事では，統計検定２級からスムーズに準１級に進めるように，ギャップをうめるために必要な数学も解説していきます。本稿では，指数分布に関連して合成関数の微分と部分積分を解説します。

この記事で前提とする知識は，【中学の数学からはじめる統計検定２級講座】の第１回の確率，第２回の条件付き確率，第３回の確率変数，第４回の期待値と分散，第６回の微分積分，第７回の広義積分，【統計検定準１級のための数学】の①（幾何分布）と②（指数関数）の内容になります。これらの内容に不安がある人は，先にそちらの記事を読んでください。

では，はじめていきましょう！

合成関数の微分

では，指数分布の話に入る前に数学的な準備からはじめます。
合成関数というのは，例えば，次のような関数のことです。

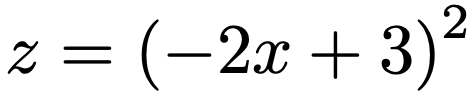
上の式の「どこが合成なのか」がわからない人もいるかもしれませんが，次の図のように関数y＝ー2x＋3と関数z＝y²を合成したものとみなすことができます。

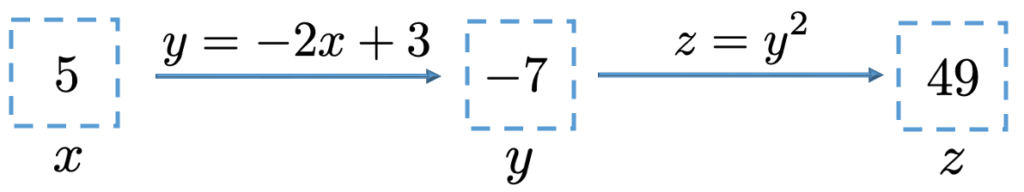
上の図の左端の枠の中には例として５を入れていますが，どんな数でもかまいません。その数にー２倍して３を加えた数が真ん中の枠に入り，さらにその数を２乗して得られる数が右端の枠に入るという関係を表しています。

では，合成関数の微分について成り立つ規則を紹介しましょう。

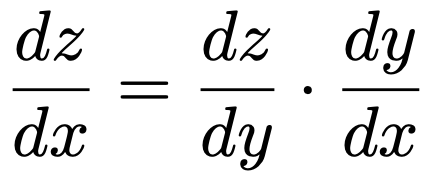
左辺はzをxの関数と見たときの微分であり，それは右辺のように計算できると上の式は言っています。実際に，上の例を使って計算してみましょう。zをyの関数として微分すると，次のように2yになりますよね。

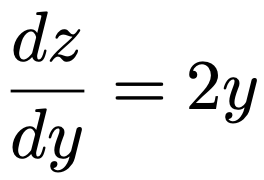
また，yをxの関数として微分すると，次のようにー2になりますよね。

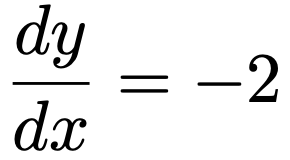
よって，上の合成関数の微分の公式により，zをxの関数として微分した結果は次のようになります。

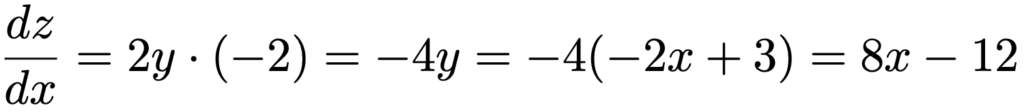
さて，この例では，合成関数の微分の公式を使わなくても微分が直接できるので，試しにやってみましょう。zを定義する式の右辺を展開すると，次のようになります。

最右辺をxで微分すれば，確かに8xー12となって，合成関数の微分の公式を使った結果と一致します。どちらでも計算できるなら合成関数の微分は不必要に思えるかもしれませんが，ここではあえて２つの方法で計算できる多項式を例として取り上げました。指数関数と多項式の合成関数などでは，合成関数の微分は威力を発揮しますので，覚えておきましょう。

積の微分と部分積分

このセクションでは，関数f(x)とg(x)は[a，b]でC¹級（微分可能で導関数が連続）であるものとします。積f(x)g(x)の微分について，次の公式が成り立ちます。

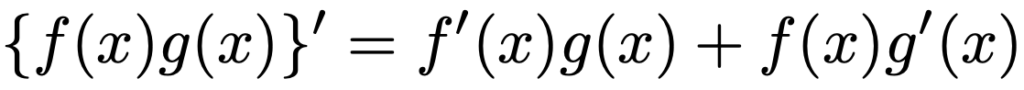
左辺の微分は，右辺のように，f(x)とg(x)の片方だけを微分したものの和に等しいわけです。これを積の微分公式と呼ぶことにします。例えば，関数y＝(2x＋3)(3xー5)をf(x)＝2x＋3とg(x)＝3xー5の積と考えて，積の微分公式を使うと，次のように計算できます。

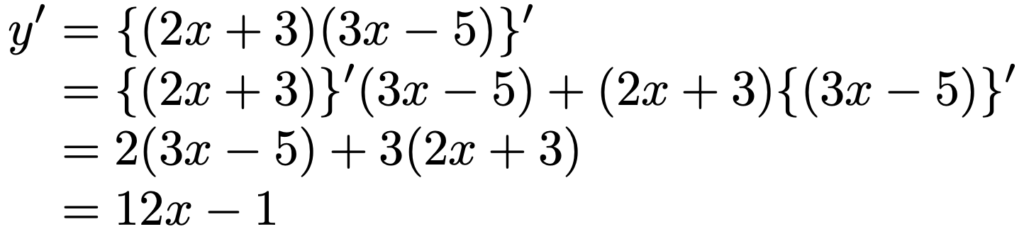
同じ関数y＝(2x＋3)(3xー5)を，積の微分公式を使わずに展開してから微分すると，次のようになります。

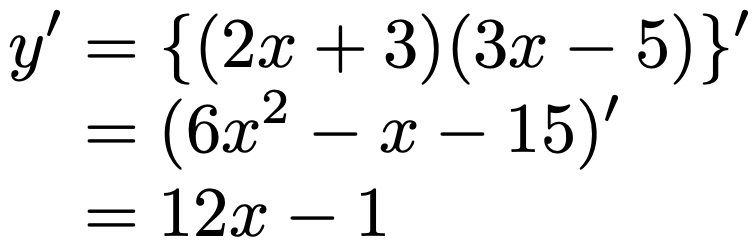
２つの結果が一致したことから，積の微分公式は正しそうだとわかりますね。この場合にはどちらの方法でも大差はありませんが，積の微分公式を使わなければ微分の計算が困難な場合は無数にありますので，覚えておいてください。

次に，積の微分公式の両辺を積分すると，次のようになります。

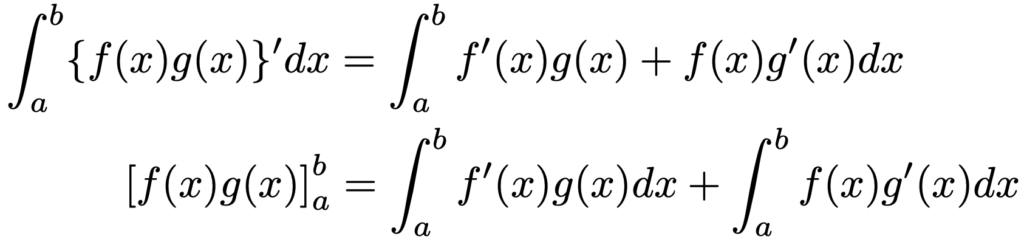
移項すると，次の式になります。

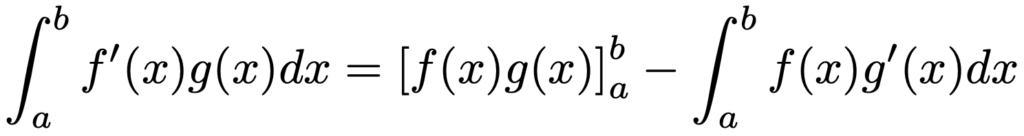
この左辺から右辺への変形を部分積分と言います。左辺の積分よりも右辺の積分のほうが計算しやすい場合には，この公式が役に立ちます。次のセクションでは，実際に部分積分を使っていきます。

指数分布

指数分布を理解するために，魚釣りをしている一人の少年を想像しましょう。次の図１は，釣りをはじめてからの経過時間を数直線で，魚が釣れた時刻を緑の丸で表したものです。

時間を30分単位に区切り，魚が釣れた区間に◯，釣れなかった区間に×をつけると，次の図２になりますね。

ここで，次の条件を仮定しましょう。

• 魚が釣れる確率はつねに一定
• 魚が釣れる事象は互いに独立
• 同時に２匹以上の魚が釣れることはない

上の図２では，１つの区間で釣れた魚の数は多くても１匹ですが，もし別の日の釣果を30分単位で表すと，１つの区間で２匹以上釣れることもあるかもしれません。でも１分単位に区切れば，１つの区間で釣れる魚の数は高々１匹だと考えてよいでしょう。そのくらい細かく時間を区切ったとき，一定の数の区間のうちの◯がつく区間の数は二項分布にしたがいます。そして「１つの区間に◯がついた後，次に◯がつくまでに並ぶ×の数」は幾何分布にしたがいますよね。図２を，左から３マス，５マス，２マス，４マスの順に区切ると，幾何分布にしたがう確率変数が並んだものだと考えることができるわけです。

次に，図２から図１に移行していきましょう。そのためには，区間の幅をどこまでも細かくしていく極限を考える必要があります。後で数式で示すように，幾何分布の時間の幅を無限に小さくした極限が指数分布になるので，幾何分布にしたがう確率変数が並んだ図２は，時間の幅が短くなるにつれて指数分布にしたがう確率変数が並んだ図１へと近づいていきます。つまり，図１で，１つの◯がついた直後から次に◯がつくまでの時間がしたがう確率分布が指数分布です。

では，指数分布を数式でとらえていきましょう。パラメータλ（λ＞０）の指数分布の確率密度関数は次の式で表せます。

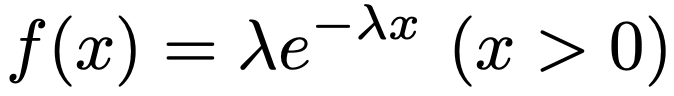
後で示すように，パラメータのλは「単位時間にイベントが平均して起きる回数」を表しています。ということは，λが大きいほどイベントが起こりやすいので，ランダムなイベントが次に起こるまでの時間は平均的に短くなりそうです。そのことを図で確認してみましょう。次の図は，指数分布の確率密度関数のグラフで，λ＝１の場合が青のグラフ，λ＝２の場合が赤のグラフになります。

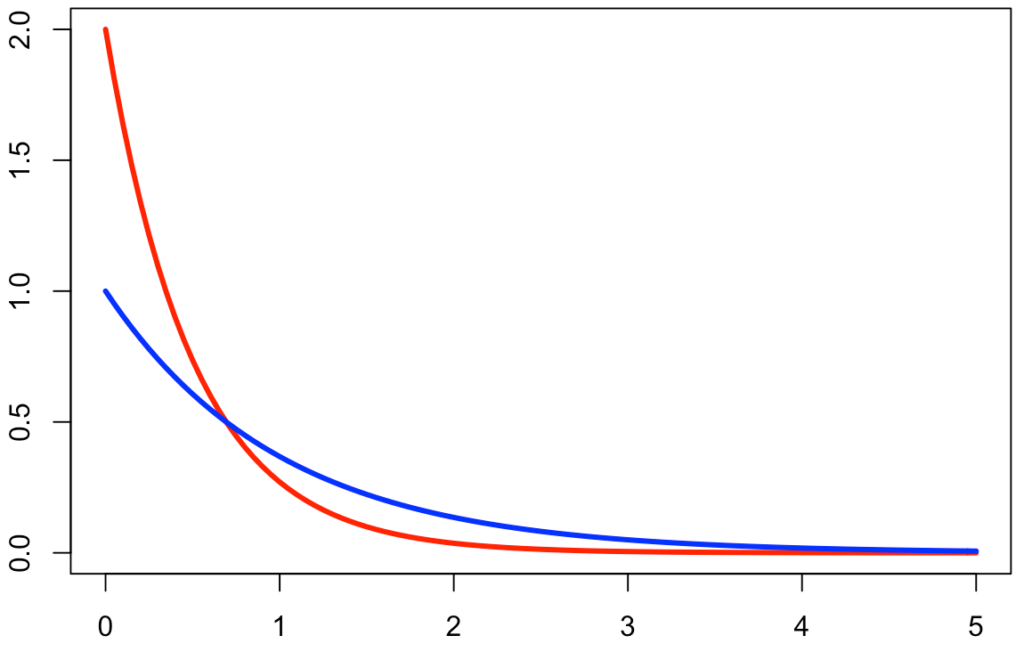
上の図を見れば，λが大きいほうが急速に確率密度が０に近づいていくのがわかりますね。

では，f(x)が確率密度関数の条件を満たしているかどうかを確認してみましょう。λ＞０，e^ーλx＞０より，確率密度関数はx＞０でつねに正の値をとることはわかるので，f(x)を（０，∞）で積分した結果が１であることを示せればいいですね。そのために，合成関数の微分の知識が必要になります。まず，次の関数zをxで微分してみましょう。

この関数を，y＝ーλxと指数関数z＝e^yの合成関数と考えます。zをyの関数として微分すると，指数関数は微分しても形が変わらないので，e^yのままです。また，yをxの関数として微分するとーλになるので，zをxで微分した結果は次のようになります。

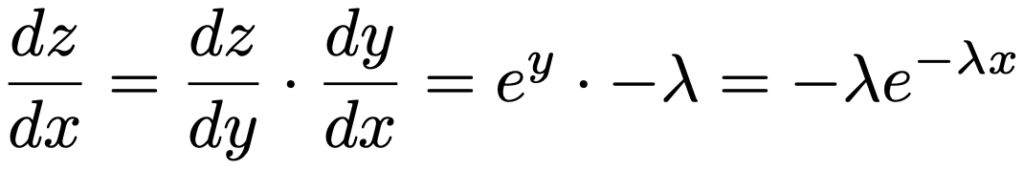
これで，次のことがわかりました。

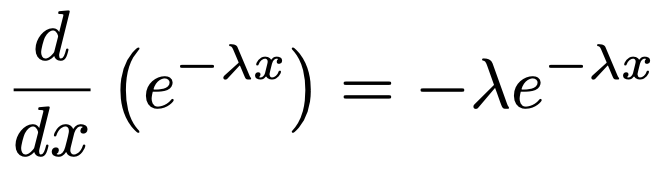
よって，指数分布の確率密度関数を（０，∞）で積分すると，次のようになります。

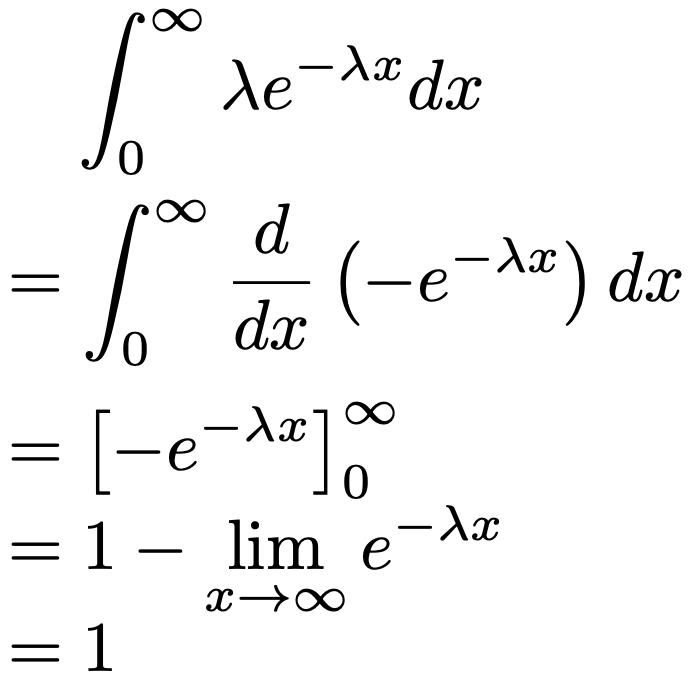
上の計算では，次の極限を使っています。

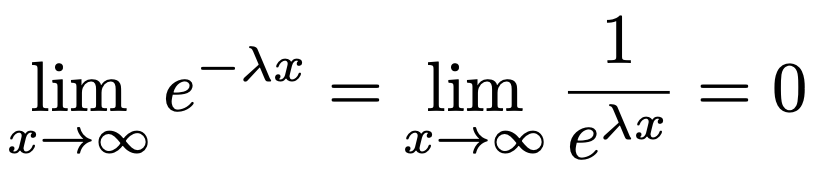
これで，f(x)が確率密度関数であることがわかりました。次に，x＞０として累積分布関数を求めてみると，次のようになります。

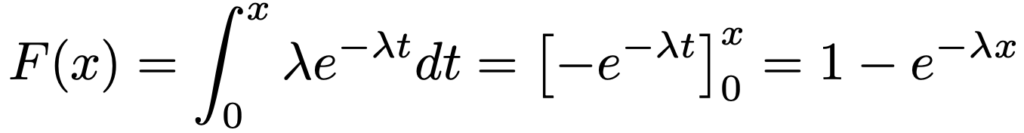
累積分布関数の計算結果は，Xを指数分布にしたがう確率変数として，次のように言い換えることができます。

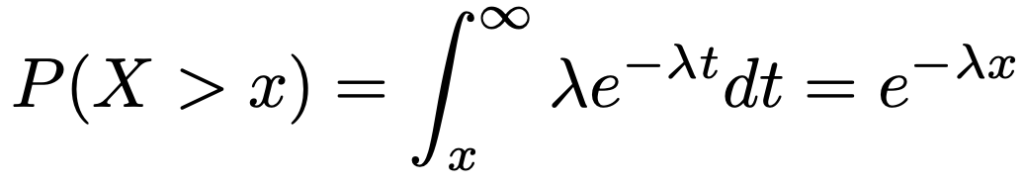
指数分布は機械の故障のようなイベントが起こるまでの時間を表すのに使われることが多いので，上の確率はxの時点で機械が故障していない確率だと言えます。

次に，指数分布の期待値を計算します。部分積分を使うために，期待値を定義する式を次のように読み替えます。

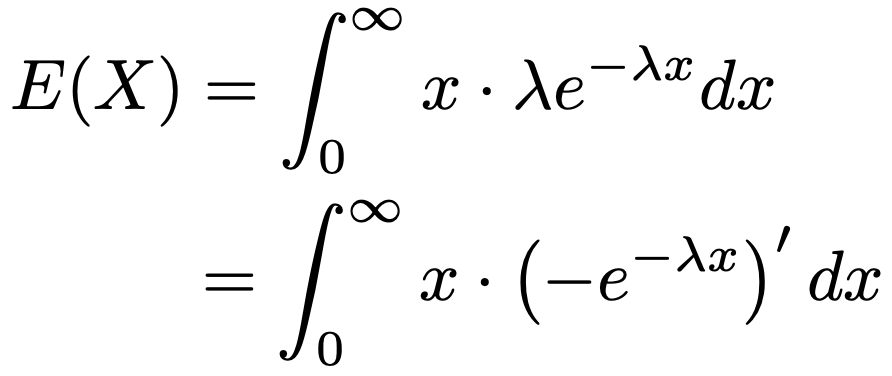
ここで部分積分を行うと，次のようにxが微分されて１になることで，被積分関数が積の形ではなくなります。

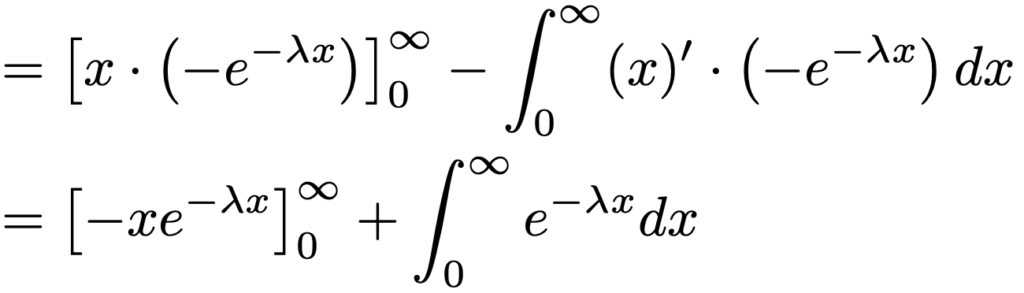
上の計算を続けるには，次の極限に注意しましょう。

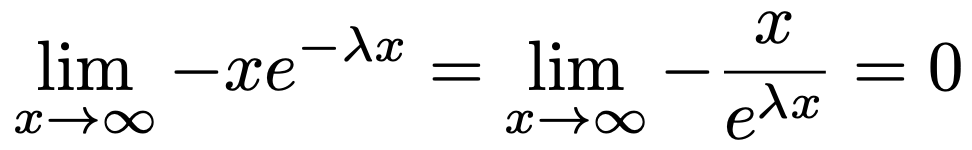
上の極限が０であることを計算で示すには，ロピタルの定理を用いる方法がありますが，ここでは「x→∞のとき，xよりも指数関数のほうが無限大に発散するスピードが速いため」のように直感的に理解しておくことにします。このことを踏まえると，先ほどの期待値の計算の続きは次のようになります。

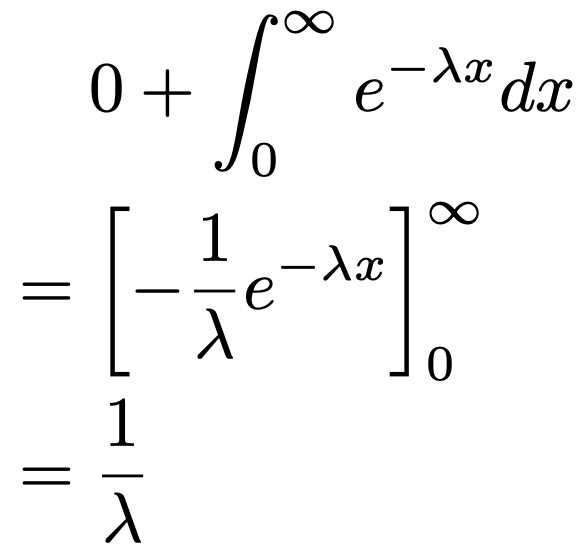
期待値はλの逆数になりました。λが大きいほどイベントが起こりやすく，ランダムなイベントが次に起こるまでの時間は平均的に短くなるということを反映していますね。

では，分散を計算していきます。そのために，次のように２乗の期待値を計算します。

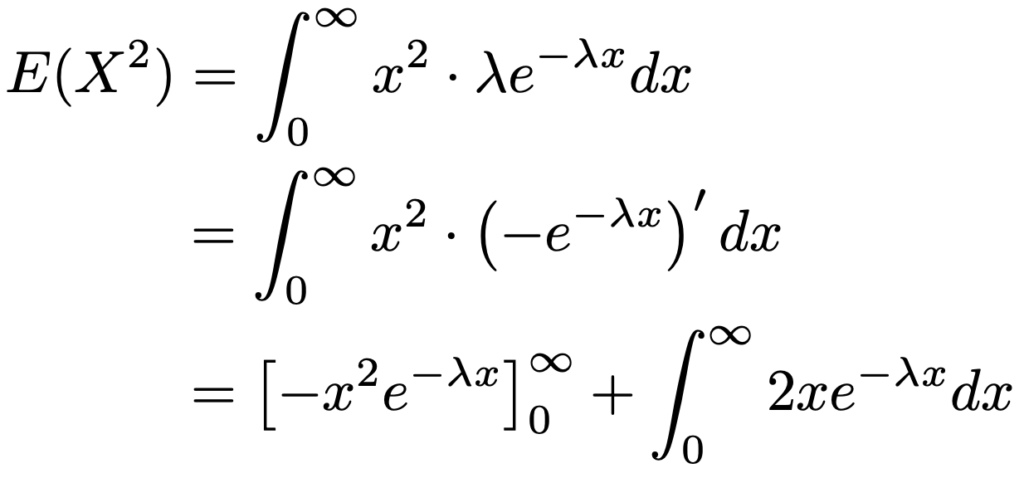
上の計算を続けるには，次の極限に注意します。

xの２乗でも指数関数が無限大に発散するスピードにはかなわないということですね。よって，２乗の期待値の計算は積分を残すのみですが，ほとんど同じ積分をすでに計算しているので，その結果を利用すると，次のようになります。

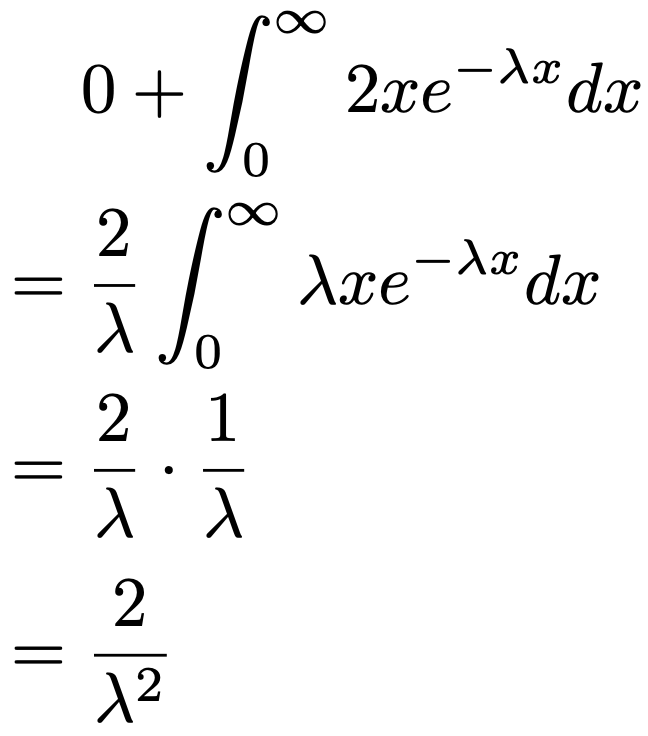
これで２乗の期待値が求められたので，分散は次のようになります。

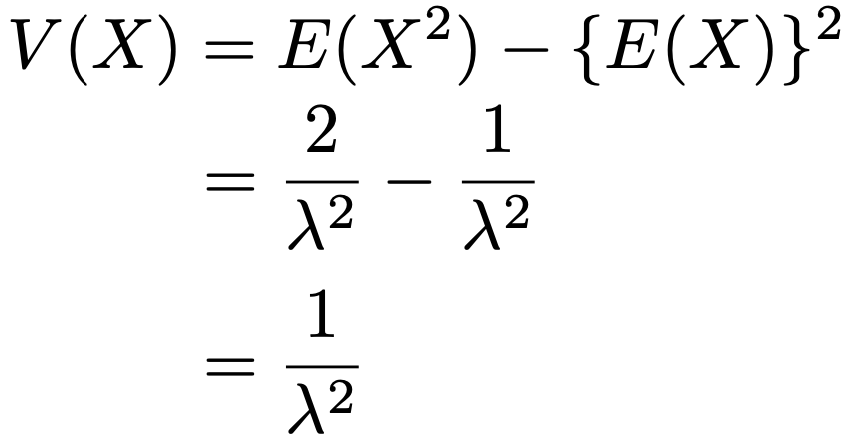
つまり，指数分布の期待値と標準偏差はどちらもλ分の１で等しくなるわけです。

では，ここまでの内容を踏まえて，次の問題を解いてみましょう。

【問題】ある電子機器の寿命は平均２年の指数分布にしたがうものとする。この電子機器が２年以内に壊れる確率を求めなさい。

【解答】時間の単位を年だとして，指数分布の確率密度関数を次のように表すときのλを求めましょう。

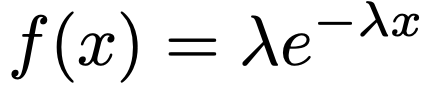
上の確率密度関数から求めた期待値（＝平均）はλ分の１でしたね。平均が２年なので，λ分の１＝２を解いて，λは２分の１だとわかります。よって，この電子機器の寿命がしたがう指数分布の確率密度関数は次の式になります。

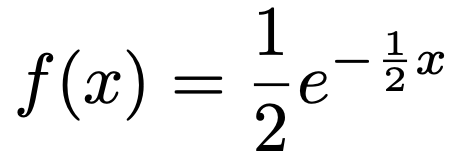
次の図は，この確率密度関数を表していて，グラフと軸で囲まれる部分のうち，２年以内に対応するのは緑の破線の左側になります。

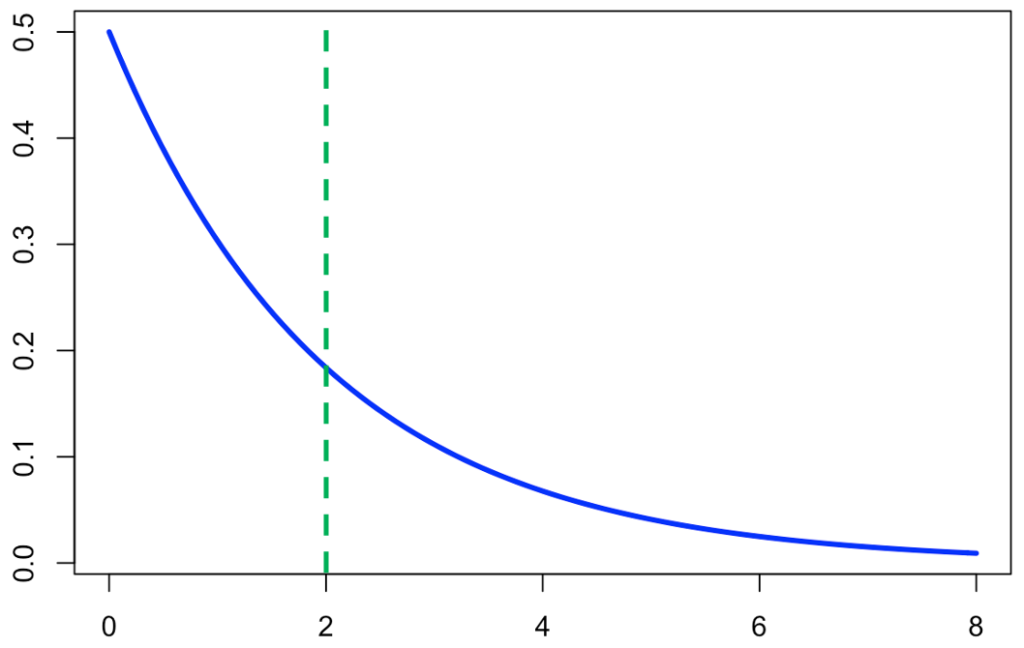
よって，２年以内に壊れる確率は次の積分を計算することで求めることができます。

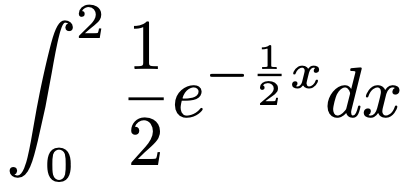
積分をそのまま計算してもよいですが，すでに求めてある累積分布関数を使うと，次のようになります。

（解答終わり）

幾何分布との関係と無記憶性

幾何分布は，離散型確率分布の中で無記憶性を持つただ一つの確率分布でした。そして，指数分布は，連続型確率分布の中で無記憶性を持つただ一つの確率分布です。このセクションでは，指数分布が無記憶性を持つことを確認し，幾何分布の極限として指数分布が得られることを示します。

まず，無記憶性についてです。Xが指数分布にしたがうとき，どんな正の数a，bに対しても次の式が成り立ちます。

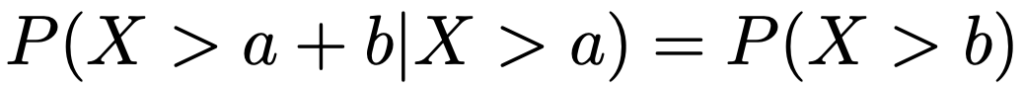
この性質が無記憶性です。この式の解釈については後で補足するとして，パラメータλの指数分布についてこの式が成り立つことを示しましょう。a＞０とすると，X＞aとなる確率は次のように表せることを思い出しましょう。

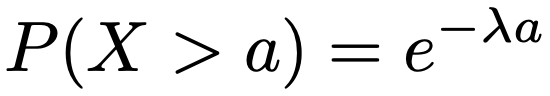
このことを使うと，無記憶性が成り立つことは次のように示せます。

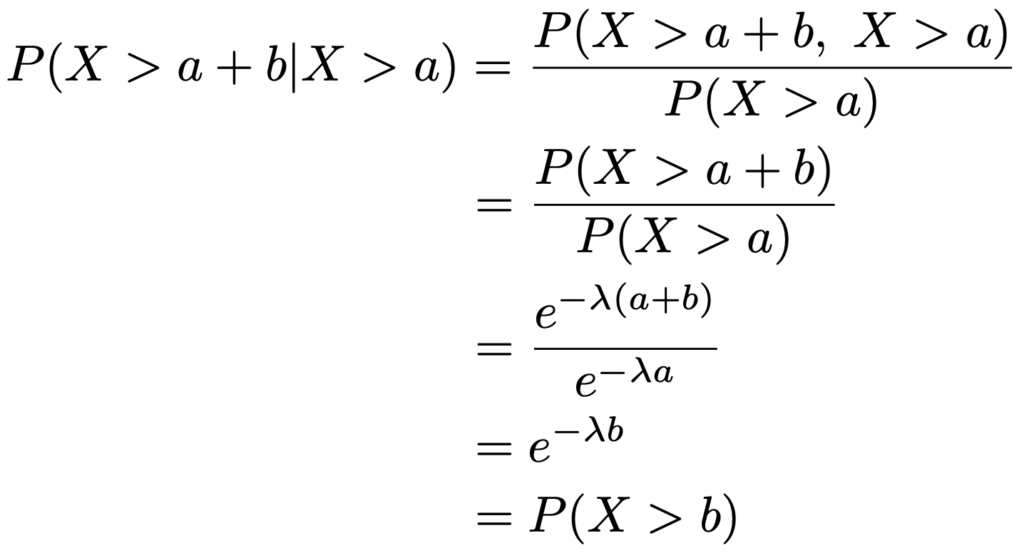
では，無記憶性の解釈について補足します。前のセクションで解いた問題を次のように書き直してみましょう。

（例）ある電子機器の寿命は平均２年の指数分布にしたがうものとする。この電子機器が１年経過しても壊れなかったという条件のもとで，３年以内に壊れない確率を求めなさい。

電子機器の寿命を表す確率変数をX（年）とすると，無記憶性は次の式で表すことができます。

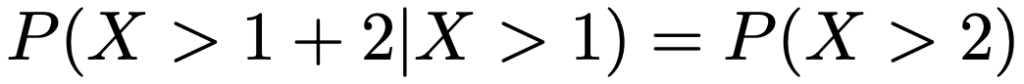
つまり，１年経過しても壊れなかったという条件のもとで３年以内に壊れない確率は，２年以内に壊れない確率と等しいのです。上の式の左辺は１年が経過していますが，「何年経っているかは関係なく，つねにゼロからのスタートと同じ」というのが無記憶性の意味するところです。経年劣化などはなく，故障は偶然に起こるということです。

ここで，ふたたび，次の図をイメージしましょう。

無記憶性の帰結として「ランダムなイベントが１回起きた後に試行を何回くり返せば次のイベントが起こるかわからない」ということになり，上の図のように離散的に考えると幾何分布，Δt→０として連続的に考えると指数分布になります。

では，指数分布を幾何分布から導出していきます。非常に短い時間Δtごとにベルヌーイ試行を行い，その成功確率pは時間幅に比例する（p＝λΔt）ものとします。単位時間あたりの試行回数は１÷Δtなので，単位時間あたりの成功回数は平均λ（＝p÷Δt）回であるということになります。はじめて成功するまでにかかる時間をXとすると，その確率は次の式で表せます。

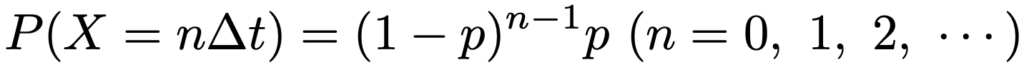
正の数xに対して，nΔt≦x＜(n＋１)Δtとなるnをとると，X＞xとなる確率は次のように表せます。

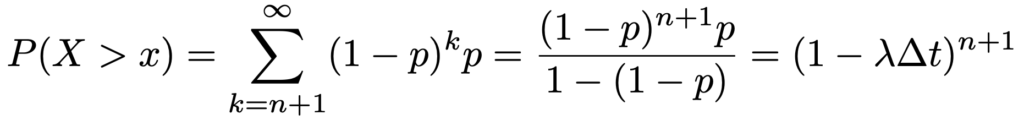
ここで，nΔt≦x＜(n＋１)Δtを変形すると，次の不等式が得られます。

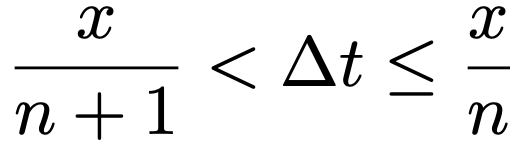
Δtの範囲がこのようになることを使うと，P(X＞x)について次の不等式が得られます。

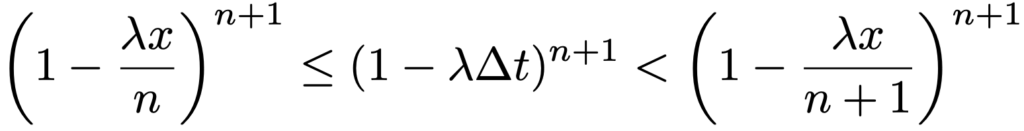
ここで，xを固定し，nΔt≦x＜(n＋１)Δtの関係を保った上で，n→∞，Δt→０の極限を考えると，ポアソン分布の記事（リンクはこちら）で学習したように，上の不等式の最右辺と最左辺はどちらも次の式のように同じ極限に収束します。

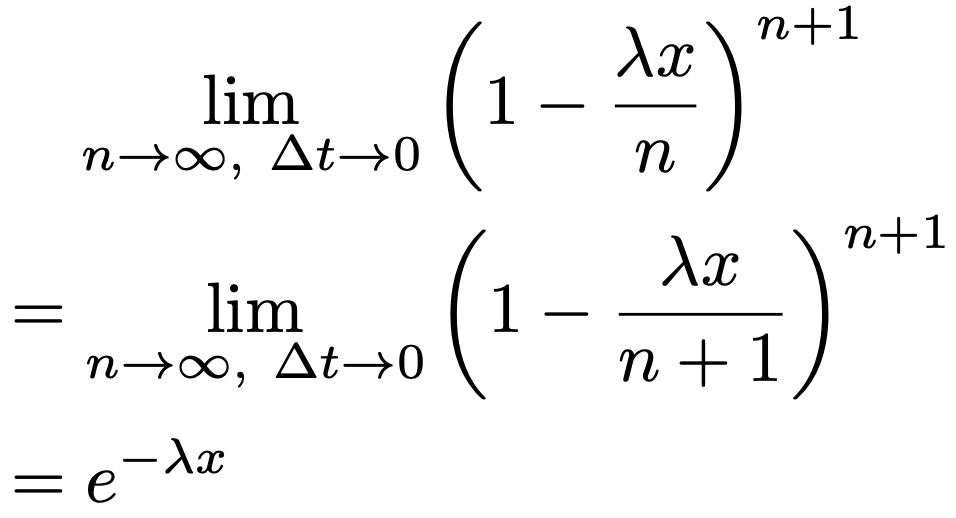
よって，はさみうちの原理から，次の結果が得られます。

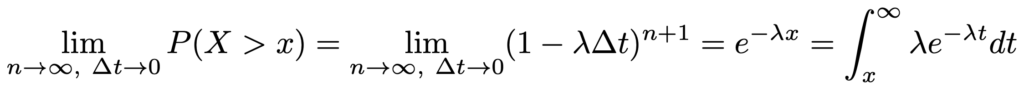
最後の積分の被積分関数は指数分布の確率密度関数ですね。つまり，単位時間あたりの成功回数がλであるようなベルヌーイ試行をΔtの間隔でくり返すと，はじめて成功するまでの待ち時間の分布はΔt→０の極限でλをパラメータとする指数分布に一致します。

中央値

このセクションでは，指数分布の中央値を扱います。まずは，その準備として，対数の説明からはじめます。ポアソン分布の記事（リンクはこちら）では，指数関数を説明しましたが，対数は指数と密接に関連しています。例えば，次の図は，y＝2^xという指数関数のグラフです。

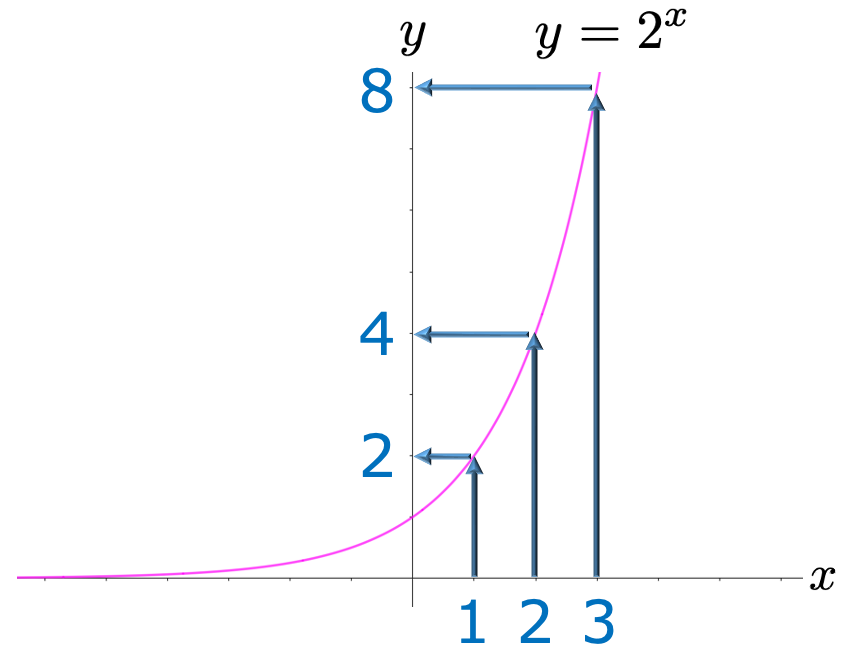
この指数関数によるxとyの対応関係の一部を示すと，次のようになります。

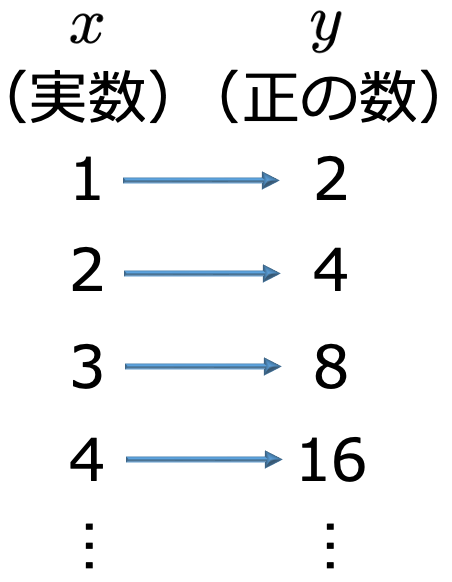
xは横軸全体，つまり実数全体の値をとるのに対して，yは正の数全体（縦軸のおよそ上半分）の値をとることに注意しましょう。そして，この逆の対応を与えるのが対数です。つまり，底を２とする対数であれば，次のような対応になります。

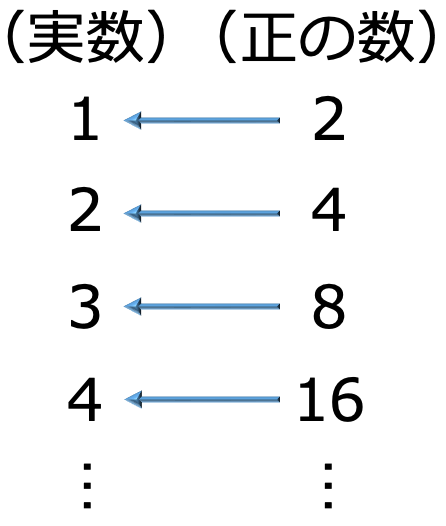
つまり，「2を何乗すれば右の数になるか」を与えてくれるのが２を底とする対数です。指数関数のグラフをもとにすれば，次の図のように，どんな正の数aを縦軸上にとったとしても，２を何乗かすればaになるような横軸上の実数がただ１つ存在するはずです。それを２を底とするaの対数と呼び，log₂aと表します。

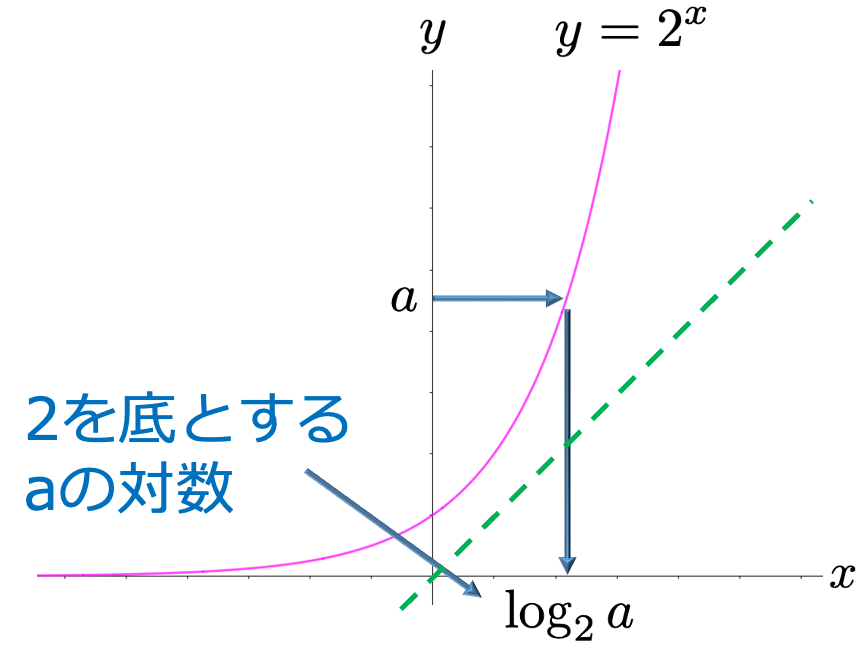
log₂aは，慣れないうちは違和感のある記号だとは思いますが，すぐに慣れます。log₂aは「2を何乗すればaになるか」を表しているので，定義から次の式が成り立ちます。

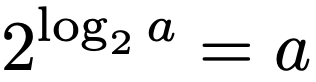
log₂aとは，２の右肩の指数部分に乗っかるべき数なのです。ちなみに，logという記号は”logarithm”の略です。

さて，上の図では，縦軸上の数aを決めて，それに対応する横軸上の数を考えましたが，関数のグラフを表すときには横軸上に先に数をとりますよね。そこで，上のグラフを直線y＝x（緑の直線）に関して対称移動すると，次の図になります。

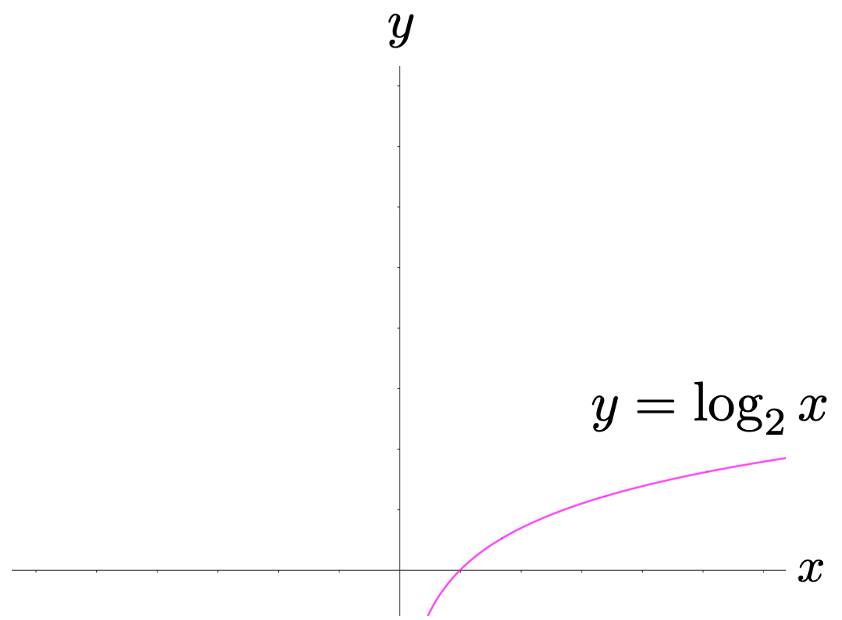
これが対数関数y＝log₂xのグラフです。定義域はx＞０の範囲です。xが大きくなるとyは緩やかに＋∞に向かって大きくなり，xが０に近づくとyは急速にー∞に向かいます。

では，いくつかの対数の性質を紹介します。log₂2は「２を何乗すれば２になるか」を表す数なので１，log₂1は「２を何乗すれば１になるか」を表す数なので０，log₂2ⁿは「２を何乗すれば２ⁿになるか」を表す数なのでnですよね。これらの性質は，底が２以外の場合にも成り立つので，一般的にまとめると次のようになります。

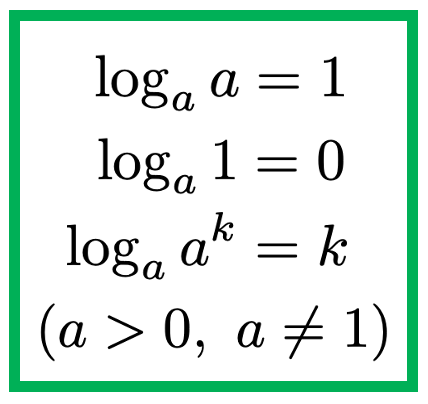
次に，対数の計算規則として重要な２つを紹介します。

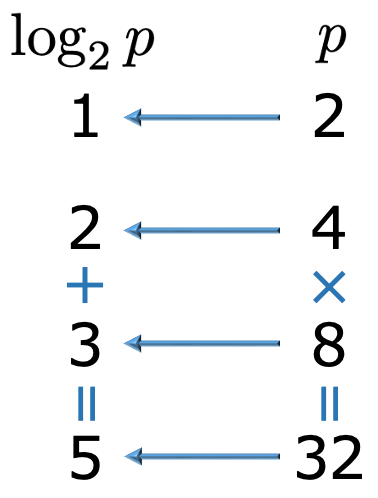
上のように，２つの真数４と８の積を計算した後に２を底とする対数をとっても，４と８の２を底とする対数を先にとってから加えても，結果は同じ５になります。これは指数法則により，2²・2³＝2⁵が成り立つことから，もとの数のかけ算は指数部分のたし算になることからわかります。この計算規則を一般的に表すと，次のようになります。

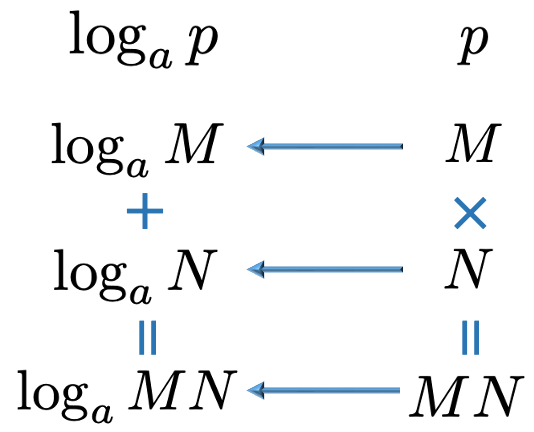
つまり，次の式が成り立ちます。

対数の計算規則の２つ目は，次の式です。

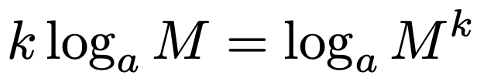
「右辺の真数の右肩にのっているkを対数の前に移動できる」と形式的に覚えてもらえれば十分ですが，これが成り立つ理由を述べておきましょう。x＝log_aMとおくと，対数の定義からa^x＝Mです。両辺をk乗するとa^kx＝M^kとなります。これはkx＝log_aM^kを表しているので，xを再びlog_aMと書き直せば，klog_aM＝log_aM^kになります。

さて，この後の問題で登場する対数では，底が明示されていません。このような表し方は，底がネイピア数のときによく使われます。なぜなら，統計学や数学で最もよく使われるのがその場合だからです。底がネイピア数の対数を自然対数と呼びます。真数がMの自然対数は，底を省略してlogMと表したり，底を明示してlog_eMとしたり，テキストによってはlnM（”n”はnaturalに由来）と表す場合もあります。

【問題】ある製品の使用開始から故障するまでの時間TがExp(λ)にしたがうと仮定する。50個の製品について故障するまでの時間を調べ，確率変数Tの標本平均を求めたところ3.0年となった。Tの中央値の推定値を求めなさい。ただし，必要に応じて，log2≒0.7を用いてよい。

【解答】求めるものは，確率変数の中央値の推定値です。はじめに，連続型確率変数の中央値について確認しておきましょう。

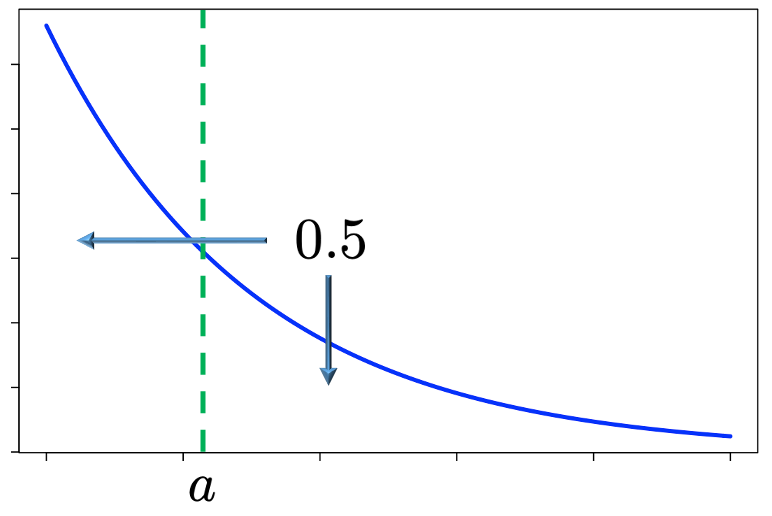
上の図の青い曲線は指数分布の確率密度関数のグラフです。この曲線と２本の軸で囲まれた三角形に近い形の領域の面積は１になりますよね。連続型確率変数の中央値は，上の図のように，その面積を0.5ずつに分けるようなaのことです。P(T＞a)＝0.5となるようなaを求めることになります。ところで，指数分布Exp(λ)について，P(T＞a)＝e^ーλaと表せることはすでに計算してありますので，次の式を満たすようなaを求めることになります。

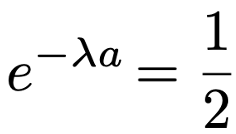
上の式の両辺をそれぞれ真数とする自然対数をとると，次の式になります。

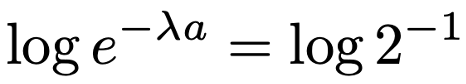
対数の計算規則の２つ目より，上の式の真数の右肩にのっているものを対数の前に移動すると，次の式になります。

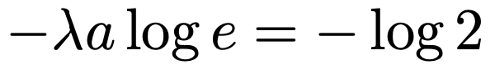
loge＝１であることから，aについて解くと，次のようになります。

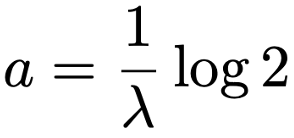
さて，問題で与えられた条件のうち，まだ使っていなかった「Tの標本平均が３年」というものをここで使います。標本平均はnが十分に大きければ，真の平均（期待値）に近づくのでしたね。そこで，指数分布Exp(λ)の期待値が1/λであることから，1/λ＝３と推定します。また，log2≒0.7を用いると，a＝３×0.7＝2.1となります。つまり，Tの中央値の推定値は2.1年です。

（解答終わり）

参考図書

本稿を執筆するにあたり，次の書籍を参考にしました。

①確率過程の基礎（R.デュレット著，丸善出版）
本稿でも扱っていない指数分布の基本的な性質が網羅的に説明されているので，さらに進んだ勉強をしたい人にオススメです。

②数理統計学の基礎（尾畑伸明著，共立出版）
指数分布が幾何分布の極限であることの証明について参考にさせてもらいました。

本稿はここまでとなります。最後までお読みいただき，ありがとうございました！
引き続き，勉強をがんばっていきましょう！