「正規分布とは何か」と問われたら,あなたは何と答えるでしょうか。「左右対称で山が1つのグラフが正規分布だ!」と答えたとしたら正しくありません。「正規分布」という言葉自体はよく知られているものの,正確な定義を知らない人が多いので,この記事を通して正しく理解していきましょう。
正規分布は統計学の根幹となる確率分布で,区間推定や仮説検定などのさまざまな形で応用されますが,これらは改めて別の記事で説明します。まずは,正規分布表の見方を理解して,正規分布の確率の計算方法を理解することが第一歩です。さらに,正規分布の再生性を紹介し,その応用として,正規母集団の標本平均が正規分布に従うことを導出します。わかりやすく解説していくので,ぜひ最後まで読んでみてください。
なお,【中学の数学からはじめる統計検定2級講座】の第3回の確率変数と標本平均,第4回の期待値と分散,第6回の微分積分と連続型確率変数の知識は既知として,話を進めます。これらの理解に自信のない方は,先にそちらをご覧ください。
では,はじめていきましょう!
広義積分
正規分布の記事なのに,いきなり積分の話から入りますが,お許しください。正規分布を定義するのに広義積分というものが必要になります。
広義積分とは,読んで字のごとく,積分をより広い意味でとらえたものです。第6回の記事で扱った積分の考え方を少し広げていきましょう。次の積分は,広義積分の一例になります。
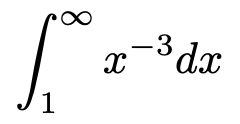
第6回の記事で扱った積分では,積分範囲の上端と下端には数が入るのですが,∞は数ではありません。その意味で,この積分はこれまでの積分の枠を超えるものであり,広義積分と呼ばれます。この積分は次の式の右辺のように解釈します。
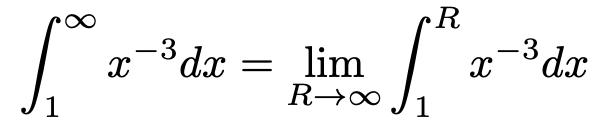
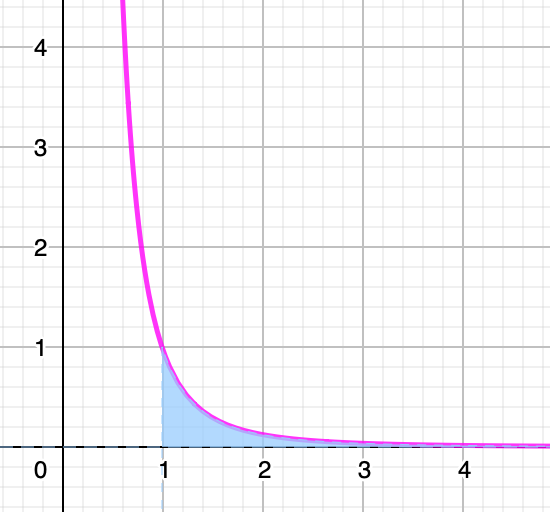
この右辺の式は,次の図の青い部分の面積に等しくなります。y=1/x3において,xの値をどれだけ大きくしてもyの値は0にはならないので,下の赤紫色のグラフはどこまで行ってもx軸と交わることはなく,青い部分は永遠に右に伸び続けています。
この広義積分の計算は次の2段階です。
- Rという非常に大きなx座標(例えば,1000などをイメージ)をとり,1以上R以下の範囲の積分をRの式で表す。
- R→∞の極限を求める。
1段階目として,積分をRの式で表してみると,次のようになります。
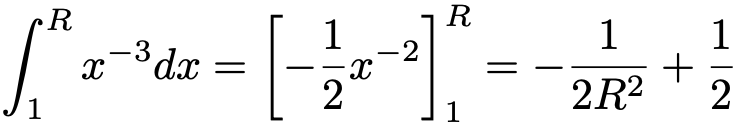
関数を積分するときの規則は,第6回の記事で紹介したものと同じです。xの右肩にのっている数が負の数でも,右肩の数を1だけ大きくして,その逆数をかけるというルールです。次に,2段階目として,R→∞の極限をとると,次のようになります。
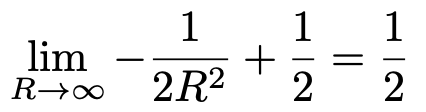
上の極限をとる前の式の第1項は,Rが分母にあるので,Rをどんどん大きくすれば,分数全体としては0に近づいていきますね。こんな感じで,広義積分の計算ができるわけです。広義積分って,なんとなくこんなものか…とイメージできたでしょうか。正規分布の確率や期待値,分散は広義積分で定義されますが,それくらいのイメージさえあれば十分理解できると思います。
正規分布
正規分布は,第6回で学習した連続型確率変数の代表格です。身近な例では,日本全国の同世代の人たちを集めて身長を集計すると,ほぼ正規分布に従うことは有名です。
さて,ここでいきなりですが,難しい式を紹介しますので,覚悟してください…。「左右対称で山が1つのグラフ」だったら何でも正規分布なわけではないので,正確に定義しなければなりません。そのために,確率密度関数を持ち出す必要があるのです。
期待値μ,標準偏差σの正規分布とは,確率密度関数が次の式で与えられるような確率分布のことです。
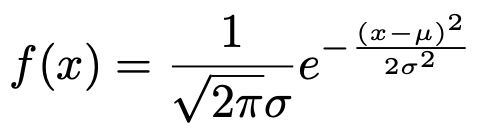
と言われても……と多くの人は思いますよね。わかります。ひとまず,定義はこれであることを了承していただければ,それで十分です。この式を覚えなくても問題は解けます。後で説明するように,正規分布の確率を求めるためにこの式を使うことはないからです。
期待値μ,標準偏差σの正規分布のことを,簡略化して次のように表すことが多いので,この表し方に慣れてください。

Nは,正規分布を英語で”normal distribution“と呼ぶことに由来します。Nの後は,(期待値,分散)の順なので,間違えないようにしましょう。
正規分布の確率密度関数の式f(x)について,少しだけ解説します。この式のπが円周率を表していることはわかってもらえるかなと思いますが,eを知らない人もいるかと思います。eはネイピア数と呼ばれる定数で,自然対数の底として高校数学で学習します。πと同じように無理数で,小数で表すと,e=2.71…と無限に続きます。
さて,正規分布の確率密度関数の式f(x)で,期待値μ,標準偏差σを決めてしまえば,変数のx以外はすべて定数になってしまいます。実際に,μ=0,σ=1を代入すると,次のようになります。
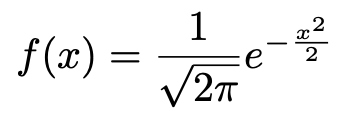
この場合が,正規分布の中で式が最もシンプルになります。このときの確率分布を,特に標準正規分布と言います。標準正規分布を簡略化して表すと,次のようになりますね。
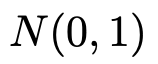
確率密度関数であるためには,全範囲での積分が1に等しくないといけませんね。もちろん,次の式が成り立ち,1になります。
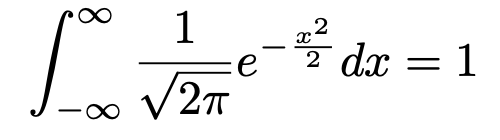
この計算は,統計検定2級の合格に関係ありませんので,ここでは省略しますが,証明のポイントはガウス積分と呼ばれる次の式です。
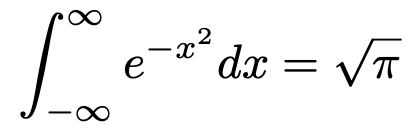
この式を変数変換すれば,上の式において確率が1に等しいことを示すことができます。ここでは,ガウス積分の証明は省略しますが,興味のある方は,「確率・統計入門(小針晛宏著,岩波書店)」を参照してください。
また,標準正規分布の期待値が0であることを式で表すと,次のようになります。
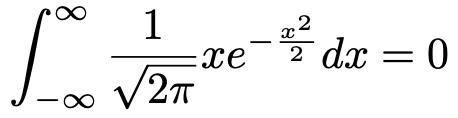
左辺の積分が0になることを確認するのはそれほど難しくありませんが,合成関数の微分が必要になりますので,ここでは割愛します。また,標準正規分布の分散が1であることを式で表すと,次のようになります。

この左辺の積分も,合成関数の微分と部分積分の知識があれば計算できますが,本題からかなりそれてしまうので,割愛します。
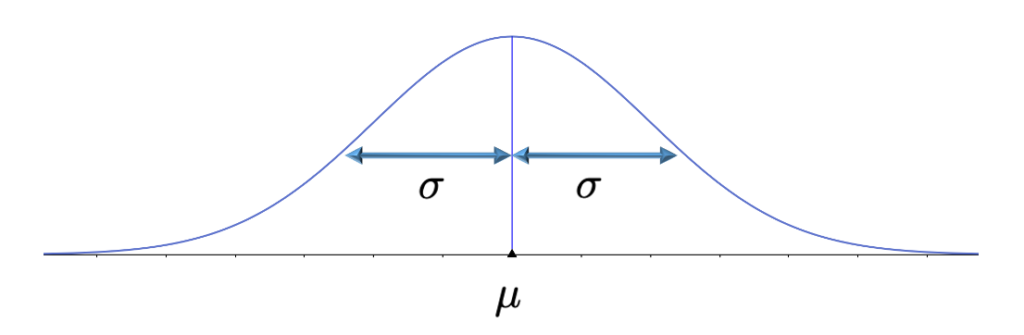
正規分布のグラフ
正規分布の確率密度関数のグラフは,連続型確率変数のグラフの代表例なので,何となく見たことがある人が多いのではないでしょうか。次の図のように左右対称なグラフで,μが対称の軸の位置,σが山の広がり具合を決めています。
標準正規分布N(0,1)の確率密度関数のグラフは次のようになります。

横軸の両端に近づくほど縦軸の確率密度の値は0に近づいていきますが,0になることはありません。別の例として,正規分布N(1,0.3)の確率密度関数のグラフは次のようになります。
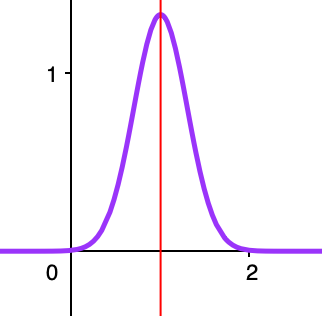
期待値を1にしたことで,対称の軸が右へ1だけ平行移動しました。また,標準偏差の値を小さくしたことで,対称の軸の近くの確率密度がグッと大きくなった感じになります。
第6回の記事の演習2で3次関数のグラフの概形の問題を掲載しましたが,同じように正規分布の確率密度関数を微分することで,概形が上の図のようになることを確認することができます。しかし,やはり合成関数の微分が必要になりますので,ここでは割愛します。
標準正規分布の確率の計算
確率変数XがN(0,1)に従うものとして,次の確率を求める問題を考えてみましょう。
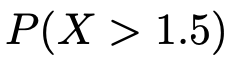
ひとまず,この確率をグラフ上の面積として表してみると次のようになります。
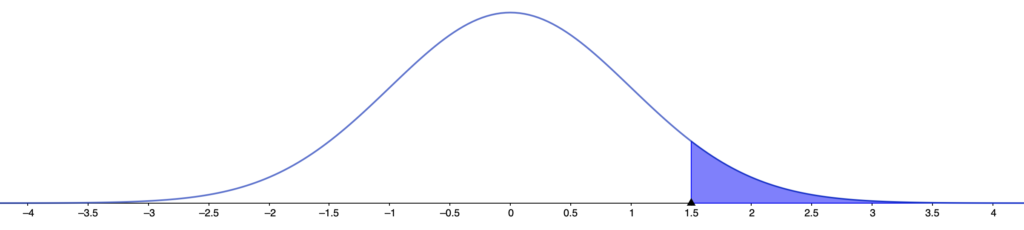
上の図の色のついた部分の面積を求める式は次のようになります。
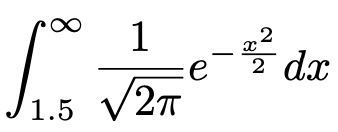
広義積分は解説済みではあるものの,「この積分を計算して確率を求めなさい」と言われたら,困り果てますよね。しかも,数値が変わるたびに計算し直さなければいけなくて,とてもやってられません。でも,大丈夫なんです。実は,標準正規分布については,確率が計算されつくしていて,上の確率も積分をせずに一瞬で求めることができます。それは次の正規分布表があるからです。
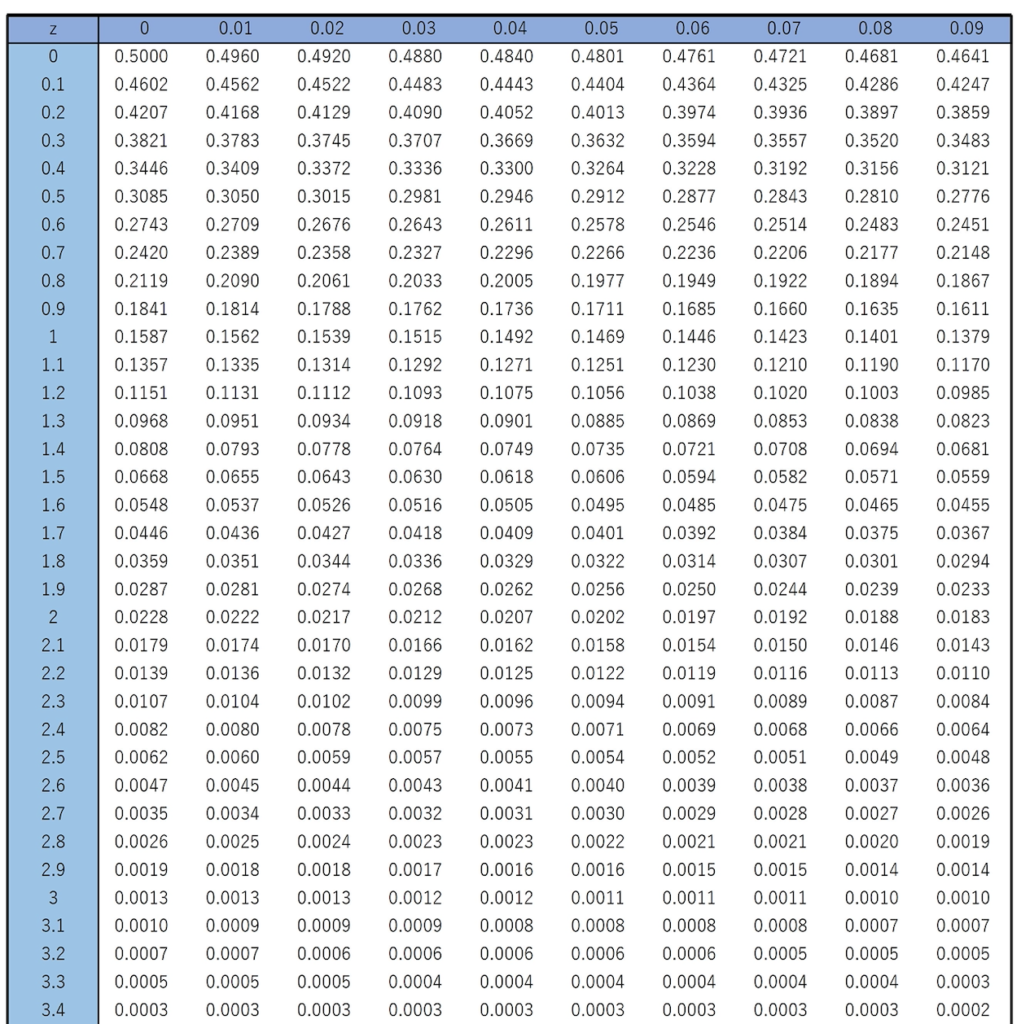
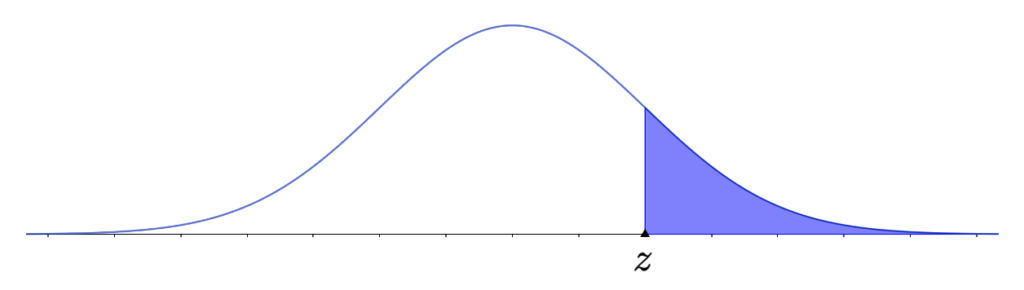
この表の見方は後で解説します。左端の1列といちばん上の1行は確率変数Zのとる値zであり,それ以外の数値は次の図の色のついた部分の面積(上側確率と言います)がzの値ごとに書かれています。
正規分布表はすべての統計学の教科書の巻末についていて,統計検定などのテストの際にも参照できるように問題の一部として与えられます。したがって,数値を覚える必要はありません。この記事内のこれ以降の問題では,上に示した標準正規分布表を使って答えを出してください。ただ,注意してほしいことが3つあります。
1つ目は,本によってこの表の表し方が異なる場合があることです。ここでは,上側確率の形の表を示しましたが,本によっては下側確率だったり,そのいずれでもない形で与えられることもあります。それでも,確率の求め方の根本は変わりませんので,上側確率の場合で十分に練習を積んでおけば,どんな与えられ方をしても対応できるはずです。
2つ目は,表に書かれている数値は近似値だということです。表の1つずつの確率は,本来は無限に続く小数になるものを,小数第4位まで表したものです。だから,多少のズレは許容して,「およそこれくらいの確率」くらいの認識で付き合いましょう。
3つ目は,求める確率について,確率変数の値の範囲が不等号を使って示されますが,このときの不等号に等号が入っているかどうかは気にしなくていいということです。これについては,次の問題の解答の中で,具体的に説明します。
【問題】確率変数ZがN(0,1)に従うとき,次の確率を求めなさい。

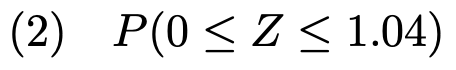
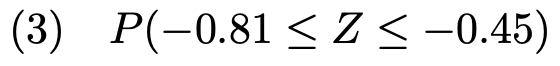
【解答】
(1)求める確率は次の図の色のついた部分の面積に等しくなります。
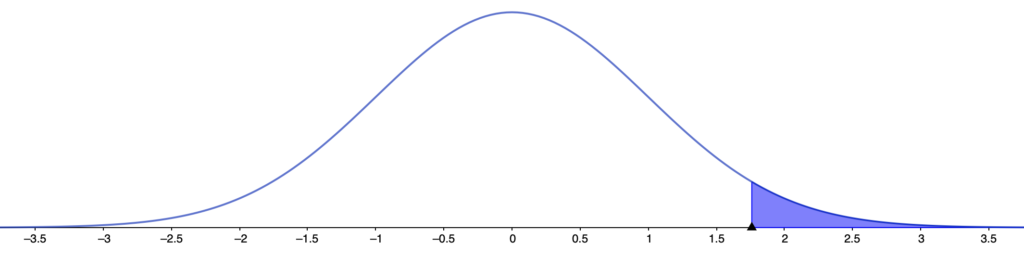
これは上側確率なので,正規分布表からそのまま答えを出せます。
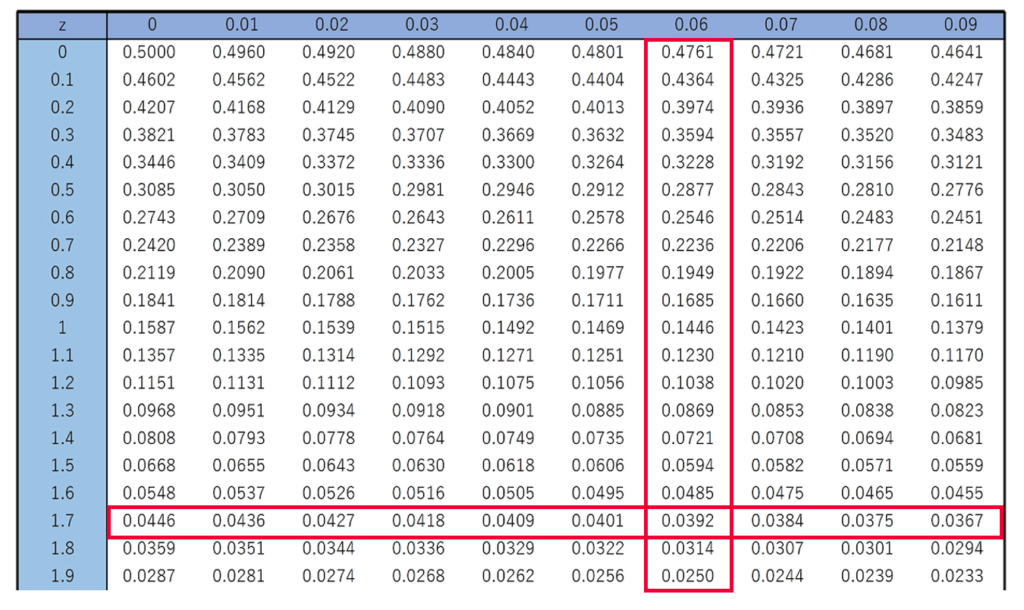
Z=1.76における上側確率なので,1.76の場所を探します。いちばん左の列でZの小数第1位までを指定して,いちばん上の行で小数第2位を指定します。つまり,上の図の赤い枠のように,1.76は,はじめにいちばん左の列の1.7のところを真横に見ていきます。次に,いちばん上の行の0.06のところを縦に見ていき,これらが交差したところに書かれている「0.0392」が求める確率になります。
(2)求める確率は次の図の色のついた部分の面積に等しくなります。
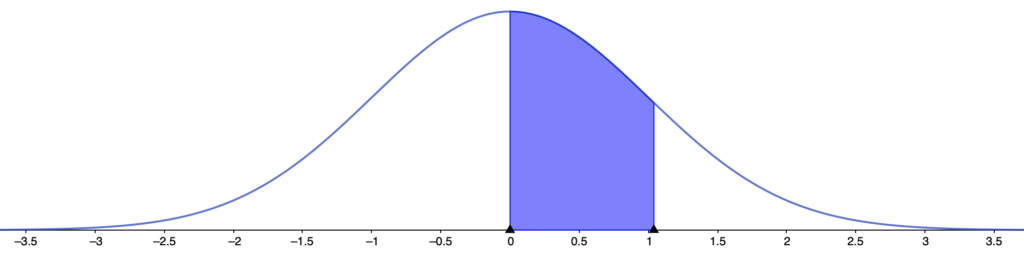
正規分布表に載っているのは上側確率なので,(1)とは異なり,色のついた部分の面積に相当する確率がそのまま載っているわけではありませんので,少し計算が必要です。上の図の右のほうの白い部分の面積ならば上側確率なので表から値が求められますね。つまり,次の確率です。
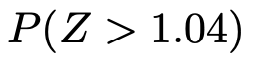
さて,グラフの右半分のうち,「0≦Z≦1.04」ではない部分ということで,等号を入れずに「Z>1.04」と表してみたのですが,等号が入っていてもいなくても確率は変わりません。なぜなら「Z=1.04」となる確率は0だからです。1点の確率が0だということに違和感を持つ人もいると思いますが,確率は確率密度関数のグラフ上の面積に等しいので,1点の確率は横の長さが0の長方形の面積が0であるのと同じく,0になるのです。さて,本題に戻ると,正規分布表の縦の目盛り1.0,横の目盛り0.04のところを見て,次のことがわかりますね。
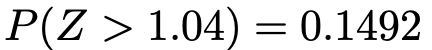
さて,あと一歩です。全体の確率が1なので,右半分の面積に相当する確率は0.5ですね。よって,求める確率は次のように計算できます。
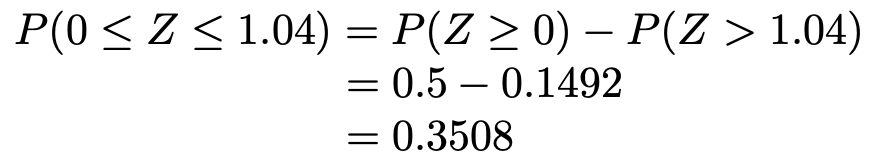
(3)求める確率は次の図の色のついた部分の面積に等しくなります。
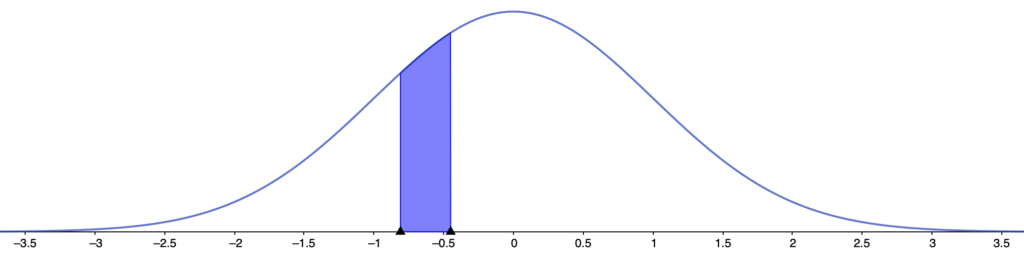
さて,グラフの対称性から,上の図の色のついた部分の面積は,次の図の色のついた部分の面積に等しいですね。
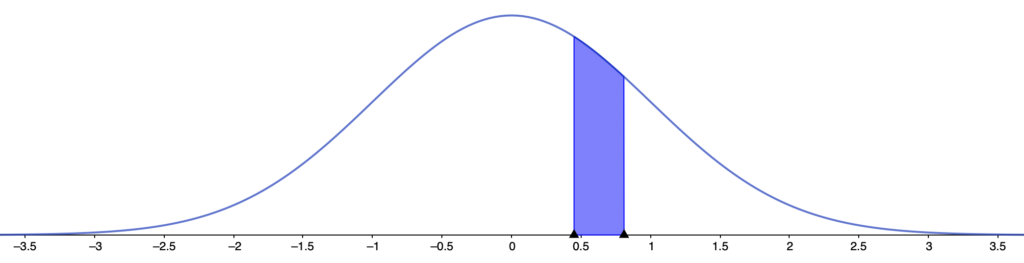
正規分布表に載っているのは,Zの値が正の場合のみなので,この図で考えていきましょう。こんなふうに,図をかくとイメージしやすくなりますので,図をかいて考える習慣をつけましょう。
正規分布表に書かれているのは上側確率なので,求める確率を上側確率を使って書き換えると,次のようになります。
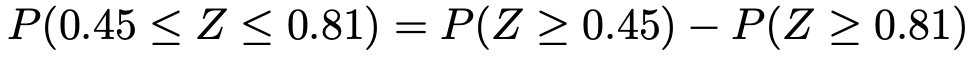
標準正規分布表から,右辺の確率を読み取って,求める確率は次のように計算できます。
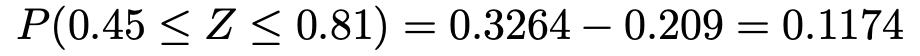
(解答終わり)
一般の正規分布の確率の計算
期待値μ,標準偏差σの正規分布の確率も,正規分布表を使って計算することができます。まず,その理由を示しておきます。
確率変数Xは次の正規分布に従うものとします。

このとき,Xの確率密度関数は次のようになります。
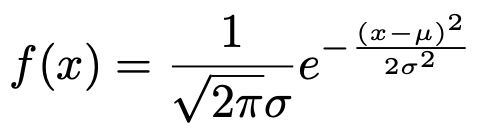
この式で,次の変数変換(ここでは,これを変換①と呼ぶことにしましょう)を行います。
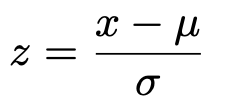
このとき,上のf(x)の式の右辺は次のようにzで表せます。
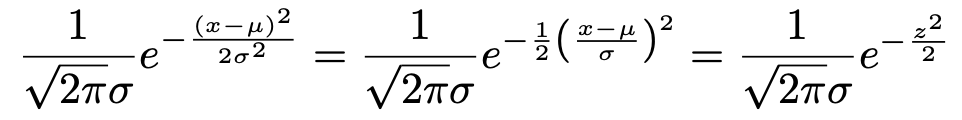
次に,確率を求める積分に現れるdxをdzに変換すると,次のようになります。この式が成り立つ理由は※印のところで説明します。

これらによって,次の等式が成り立ちます。
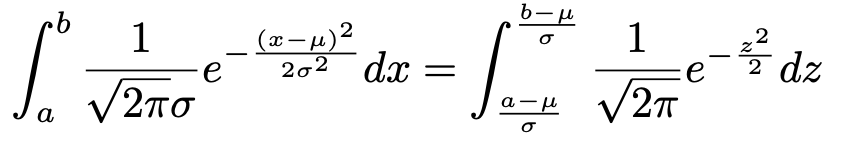
※(補足)第6回の記事で説明したように,dxというのは面積を求めるときの長方形の横幅でしたね。式で表すと,次の差で表される幅を無限に小さくした極限のことです。
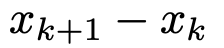
変換①の式から,確率変数Xについての横軸方向の分割点と確率変数Zについての横軸方向の分割点の間に次の式の対応関係が成り立ちます。
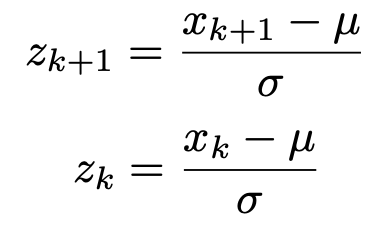
各辺をひき算することによって,次の式が得られます。
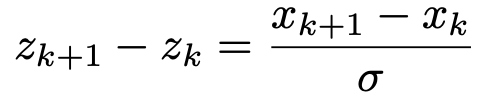
この式の両辺を無限に小さくした極限を表しているのが次の式です。
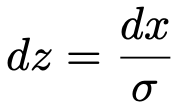
つまり,xの変化量のσ分の1がzの変化量になるということです。(補足終わり)
改めて,上の変換①を確率変数の対応関係として書き直すと,次のようになります。

この変換のことを,標準化と言う場合があります。標準化することで,期待値μ,標準偏差σの正規分布の確率がN(0,1)の確率におきかわったわけです。こうして,一般的な正規分布に従う確率変数Xの確率を正規分布表を使って求めることができるようになりました。では,実際に求めてみましょう。
【問題】確率変数Xが次の正規分布に従うものとする。
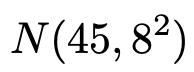
このとき,次の確率を求めなさい。
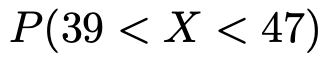
【解答】次の変数変換によって定まる確率変数Zは標準正規分布に従います。
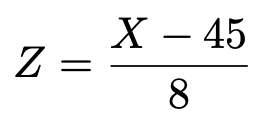
この式の右辺にX=39を代入すると,Z=ー0.75,X=47を代入すると,Z=0.25だから,求める確率について,次の言いかえが成り立ちます。

上の式の右辺の確率を求めていきます。正規分布表を使うために,求める確率を次のように読みかえます。
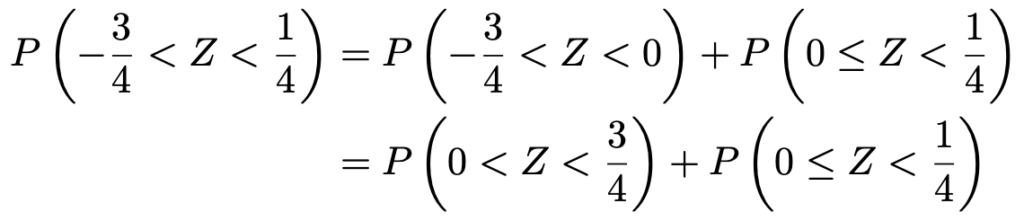
正規分布表で,Z=0.75のときの上側確率は0.2266,Z=0.25のときの上側確率は0.4013なので,求める確率は次のようになります。
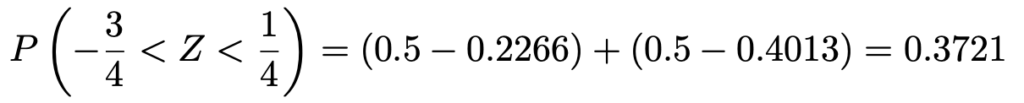
(解答終わり)
正規分布の一次結合
正規分布に従う確率変数から派生する確率変数も正規分布に従う場合があります。統計検定でも出題例がある大切な事実になります。一連の証明の中にはかなり骨の折れるものも含まれていますので,事実だけ覚えてもらえれば十分です。
次のn個の確率変数を考えます。
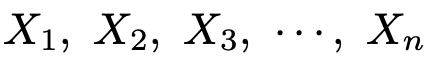
このとき,第3回で学習したように,次の式で標本平均が定義されます。
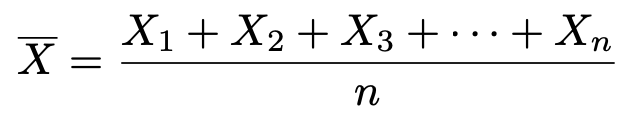
n個の確率変数の期待値がすべてμであるとすると,第4回や第5回の記事で説明した和の期待値の公式から,次の式が成り立ちます。
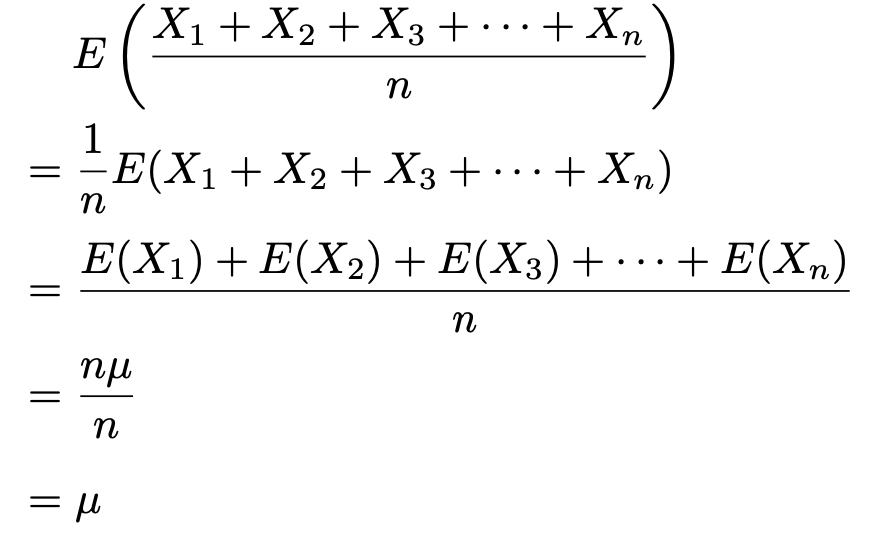
つまり,標本平均の期待値もμです。
次に,n個の確率変数がすべて独立であり,その標準偏差がすべてσであるとすると,第4回や第5回の記事で説明した和の分散の公式から,次の式が成り立ちます。
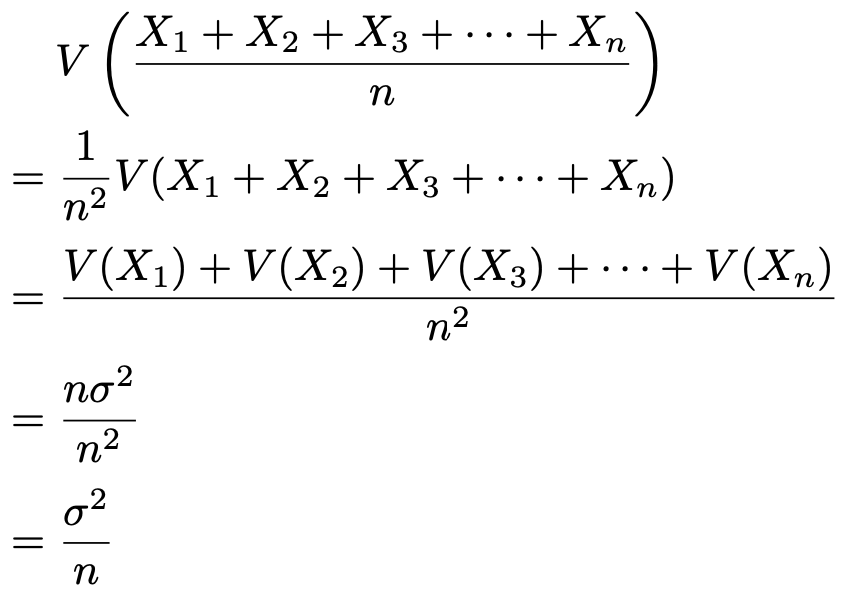
これが標本平均の分散です。
次に,正規分布の性質が受けつがれるのかを解説します。先ほどと同じように,次のn個の確率変数を考えます。
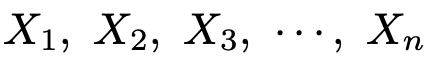
これらが独立で,次の正規分布に従っているものとします。
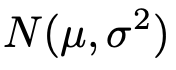
このとき,実は標本平均は次の正規分布に従います。
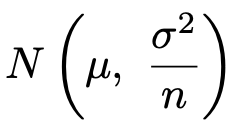
期待値と分散については,上で説明したのと同じ値ですから,「標本平均が正規分布に従う」という点が新しい情報です。さて,この事実について,以下で解説してみたいと思います。
確率変数Xが次の正規分布に従っているものとします。
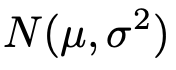
このとき,cを実数として,確率変数cXは次の正規分布に従います。
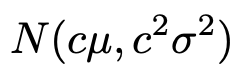
この理由を示しておきます。条件から,確率変数Xの確率密度関数は次のf(x)になります。
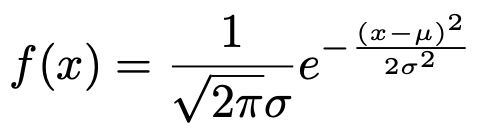
Y=cXとおくと,前のセクションで説明したのと同じように,次の式が成り立ちます。
よって,次の式が成り立ちます。
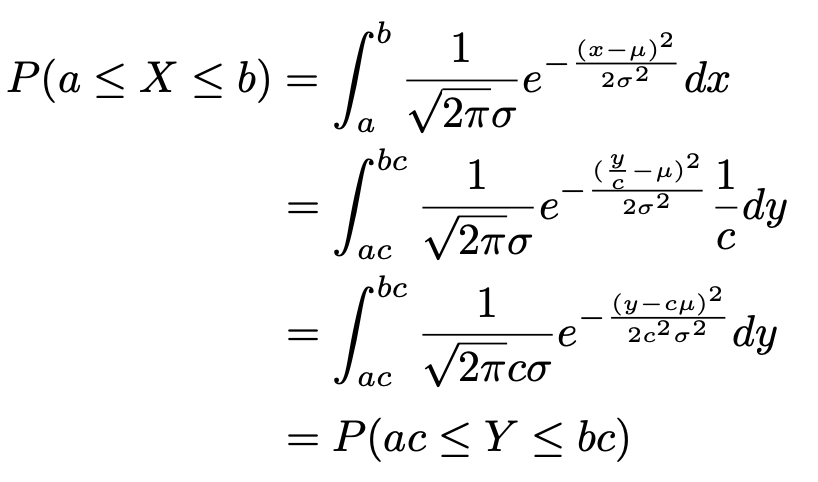
したがって,確率変数Y=cXが次の正規分布に従うことが示せました。
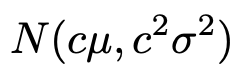
次に,確率変数X,Yが独立で,それぞれ次の正規分布に従っているものとします。
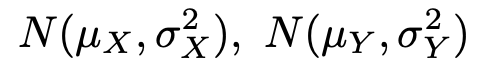
このとき,確率変数X+Yは次の正規分布に従います。
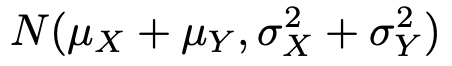
期待値と分散がこのようになることは,期待値と分散の公式から直ちに示すことができますが,この確率分布が正規分布であることの証明はかなりハードであり,ここでは割愛します。証明はさておき,結果として「正規分布に従う互いに独立な確率変数の和で表される確率変数も正規分布に従う」という性質は重要で,正規分布の再生性と呼ばれます。
これらのことを組み合わせると,次のことがわかります。
確率変数X,Yが独立で,それぞれ次の確率分布に従っているものとします。
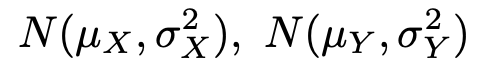
このとき,確率変数aX+bYは次の確率分布に従います。
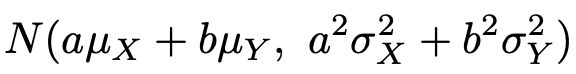
ここで,a=b=1とおいたり,a=1,b=−1とおいたりすることで,確率変数X,Yが正規分布に従うとき,X+YやXーYがそれぞれ次の正規分布に従うことがわかります。
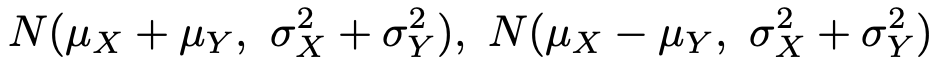
そして,2つの確率変数について成り立った上の事実は,確率変数が何個になっても成り立つので,n個の確率変数でも成り立ちます。それらを次のようにおきます。
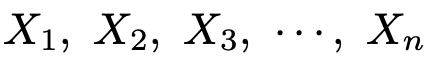
これらが独立で,次の正規分布に従っているものとします。
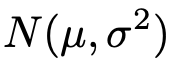
このとき,標本平均の確率分布が次の正規分布に従うことがわかるわけです。
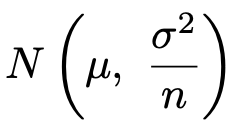
なお,正規分布の一次結合が正規分布に従うことのきちんとした証明は,「ガイダンス確率統計(石谷謙介著,サイエンス社)」に記載されています。易しくはないので,どうしても知りたい人はこちらをどうぞ。
正規分布と標本平均
【問題】製品Aを作る工場で,完成した製品の中から大きさ4の標本を取り出し,それぞれの重さを次のようにおく。
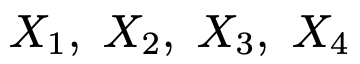
これらは独立で,期待値120,標準偏差8の正規分布に従っていると仮定する。このとき,次の式で表される4つの製品Aの重さの標本平均が115以下である確率を求めなさい。

【解答】前のセクションで学習したように,標本平均は,次の正規分布に従います。
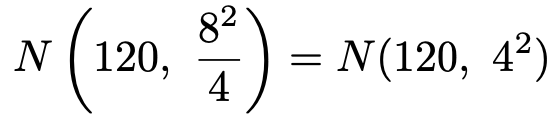
このとき,次の変数変換によって定まる確率変数Zは標準正規分布に従います。
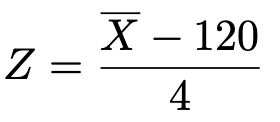
この式の右辺にX=115を代入すると,Z=ー1.25だから,求める確率について,次の言い換えが成り立ちます。
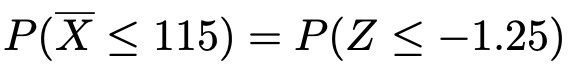
上の式の右辺の確率を求めていきます。正規分布表を使うために,求める確率を次のように読みかえます。
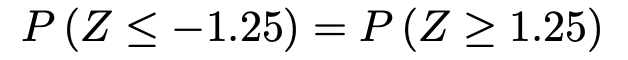
正規分布表で,Z=1.25のときの上側確率を調べて,答えは0.1056
(解答終わり)
正規分布についての基本的な説明は以上になります。ここからは,さらに理解を深めるための演習問題ですので,余力があればぜひチャレンジしてみてください。
演習1〜標準正規分布の確率の計算〜
【問題】確率変数ZがN(0,1)に従うとき,次の確率を求めなさい。
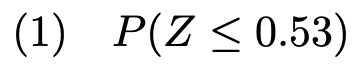
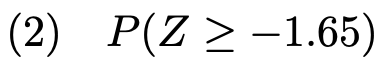
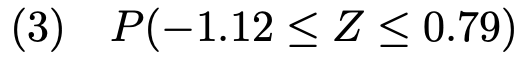
【解答】
(1)求める確率は次の図の色のついた部分の面積に等しくなります。
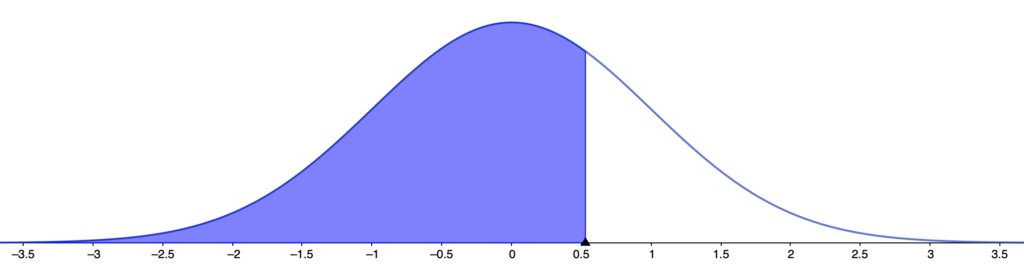
この場合,白い部分が上側確率なので,全体から上側確率をひいて確率を求めます。次の式のように計算できます。
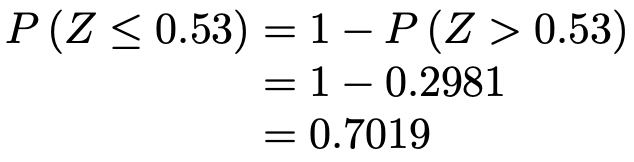
(2)求める確率は次の図の色のついた部分の面積に等しくなります。
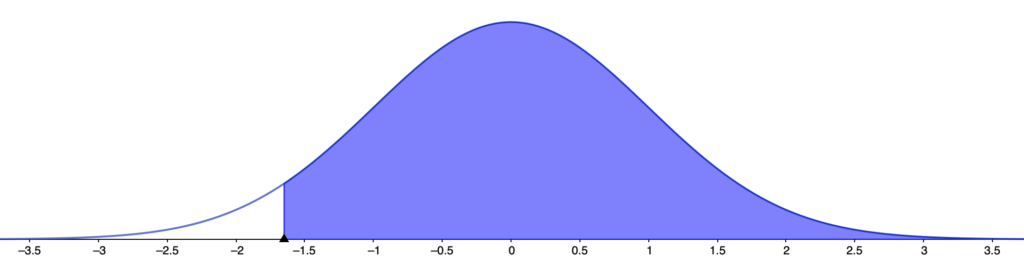
グラフの対称性から,上の図の色のついた部分の面積は,次の図の色のついた部分の面積に等しいですね。
正規分布表に書かれているのは上側確率なので,求める確率を上側確率を使う式に書きかえて計算すると,次の式のようになります。
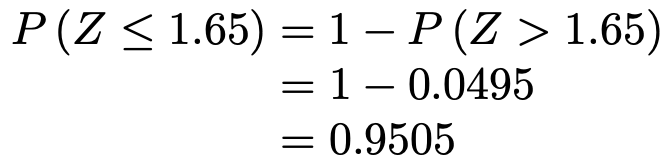
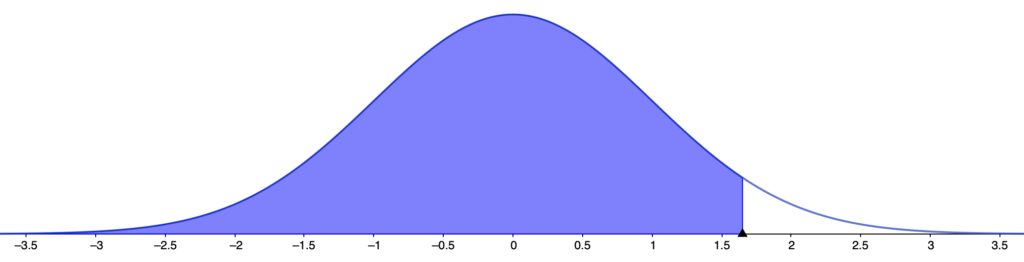
(3)求める確率は次の図の色のついた部分の面積に等しくなります。
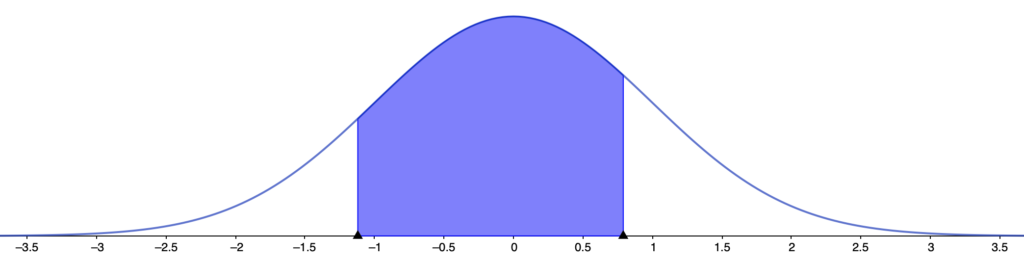
上の図で,全体の確率から,右側の白い部分と左側の白い部分の確率をひけばいいですね。右側の白い部分の確率は,次の上側確率です。
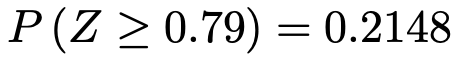
左側の白い部分は,左右反転して,上側確率として求めると,次のようになります。
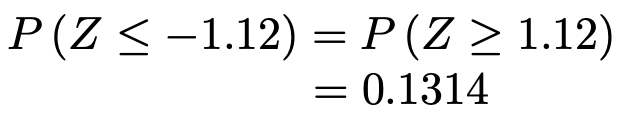
よって,確率は次のように計算できます。
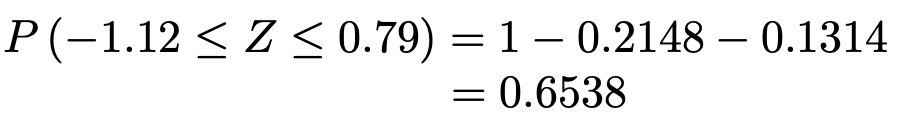
(解答終わり)
演習2〜正規分布の確率の計算〜
【問題】確率変数Xが次の正規分布に従うものとする。

このとき,次の確率を求めなさい。
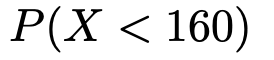
【解答】次の変数変換によって定まる確率変数Zは標準正規分布に従います。
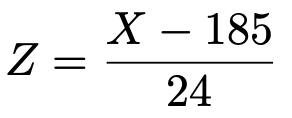
この式の右辺にX=160を代入すると,Z=ー1.041…だから,求める確率について,次の言いかえが成り立ちます。
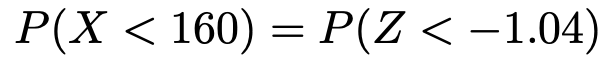
右辺の確率を,グラフの対称性から,次のように読みかえます。
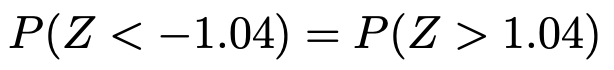
上の式の右辺は上側確率なので,正規分布表から,求める確率は0.1492
(解答終わり)
演習3〜正規分布の逆算〜
【問題】確率変数Xが次の正規分布に従うものとする。
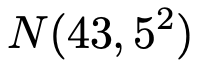
このとき,次の式を満たすようなaの値を求めなさい。
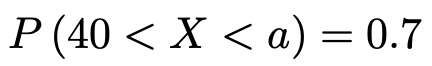
【解答】次の変数変換によって定まる確率変数Zは標準正規分布に従います。
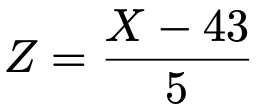
X=40のときZ=ー0.6だから,次のようにおきかえられます。
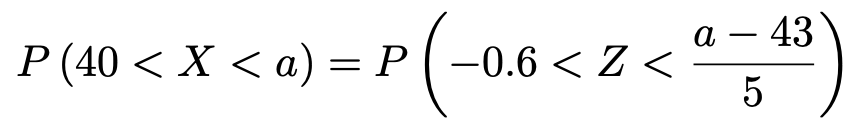
問題の条件からこの確率は0.7であるため,次の不等式が成り立たなければなりません。
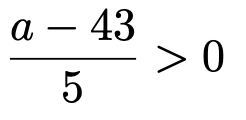
なぜなら,この分数が0以下ならば,P(Z<0)=0.5より確率が小さくなってしまうからです。したがって,上の確率を次のように2つに分けることができます。
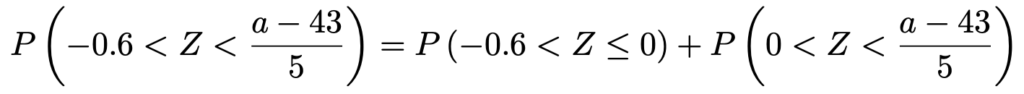
右辺の第1項は,グラフの対称性から,次のようにおきかえられます。
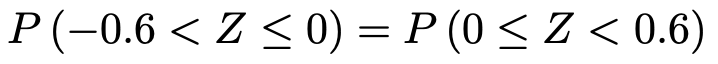
この確率は,グラフの右半分の確率から上側確率をひいて,次のように計算できます。
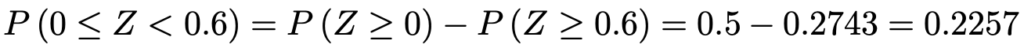
よって,未知数aを含む確率が次のように表せます。
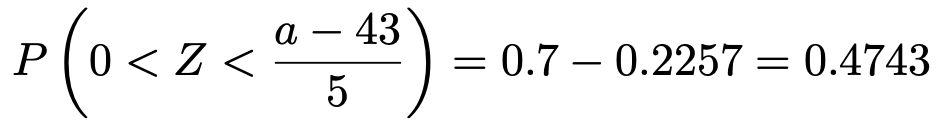
この確率を上側確率に書き換えると,次のようになります。
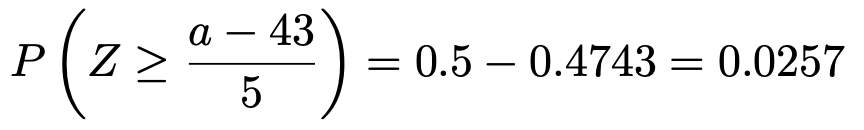
正規分布表から,上側確率がこの値に最も近いZの値をさがすと,次の式をつくれます。
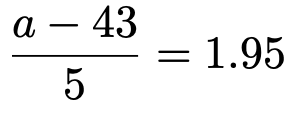
これを解いて,aは次のように求められます。
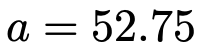
(解答終わり)
演習4〜正規分布の再生性〜
【問題】互いに独立な確率変数X,Yがそれぞれ次の正規分布に従うものとする。
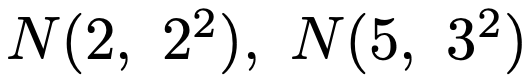
このとき,確率変数3X+2Yが従う確率分布を答えなさい。
【解答】少しずつ順番に考えていきましょう。
まず,正規分布N(μ,σ2)に従う確率変数Wを定数c倍してできる確率変数cWは次のような正規分布に従うんでしたね。
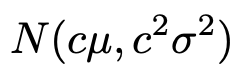
この性質を使うと,確率変数3Xが従う確率分布は次のようになります。
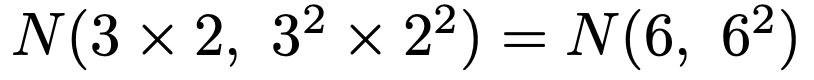
同じように,確率変数2Yが従う確率分布は次のようになります。
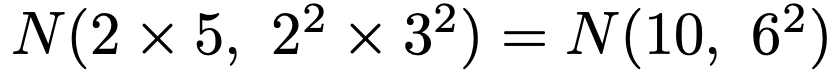
ここで,再生性と呼ばれる「正規分布に従う互いに独立な確率変数の和で表される確率変数も正規分布に従う」という性質を使うと,確率変数3X+2Yが従う確率分布は次のようになります。
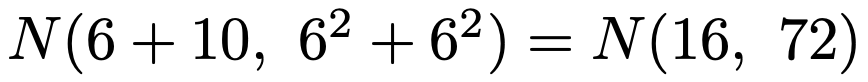
つまり,期待値16,分散72の正規分布になります。
(解答終わり)
演習5〜正規分布の文章題〜
【問題】ある地域における毎年5月の最高気温は,平均22.8℃,標準偏差6℃の独立で同一の正規分布で近似される。次の問いに答えなさい。
(1)ある年において,5月の最高気温が18℃以上となる確率を求めなさい。
(2)ある年において,5月の最高気温がその前年の5月の最高気温より12℃以上高くなる確率を求めなさい。
【解答】
(1)5月の最高気温をXとすると,Xは次の確率分布に従います。
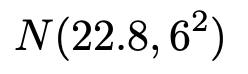
よって,次の変数変換によって定まる確率変数Zは標準正規分布に従います。
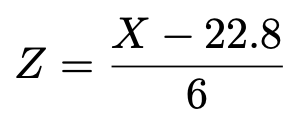
この式の右辺にX=18を代入すると,Z=ー0.8だから,求める確率について,次の言いかえが成り立ちます。
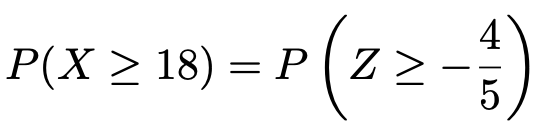
上の式の右辺の確率を求めます。正規分布表を使うために,求める確率を次のように読みかえます。
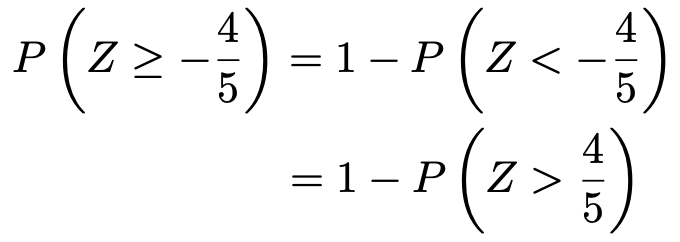
正規分布表でZ=0.8の確率を調べることで,求める確率は次のようになります。
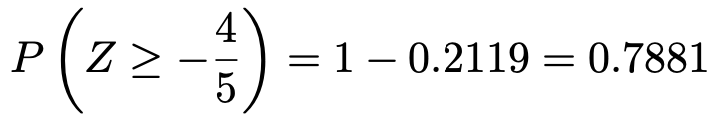
(2)ある年の5月の最高気温をX,その前年の5月の最高気温をYとすると,いずれも次の確率分布に従います。

このとき,この年と前年との最高気温の差を表す確率変数はXーYになります。正規分布の一次結合になるので,XーYは次の確率分布に従います。
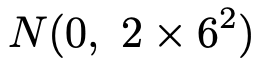
ここで,求める確率を確認しておくと,次のようになります。
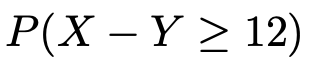
ここで,次の変数変換を行うと,確率変数Zは標準正規分布に従います。
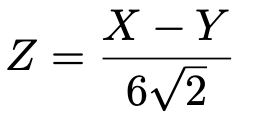
この式の右辺にXーY=12を代入して,このときのZの値を求めると次のようになります。
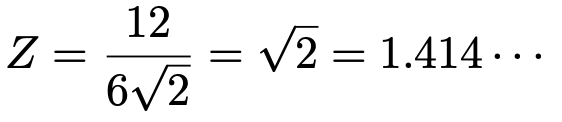
よって,求める確率は,正規分布表を読み取って次のようになります。
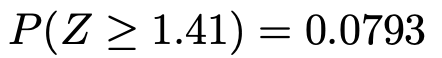
(解答終わり)
第7回は以上となります。最後までお付き合いいただき,ありがとうございました!
引き続き,第8回以降の記事へ進んでいきましょう!
2023年1月に「統計検定2級公式問題集[CBT対応版](実務教育出版)」が発売されました!(CBTが何かわからない人はこちら)
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが,本書は分野ごとにその形式の問題を並べた構成になっていて,最後に模擬テストがついています。CBT対策の新たな心強い味方ですね!
さらに実戦に向けた演習を積みたい人は,「統計検定2級公式問題集2018〜2021年(実務教育出版)」を手に取ってみてください!
また,もっと別の問題を解いてみたい人は,さらにさかのぼって「統計検定2級公式問題集2016〜2017年(実務教育出版)」を解いて実力に磨きをかけましょう!



![統計検定2級公式問題集[CBT対応版]](https://m.media-amazon.com/images/I/51q3GfZId3L._SL500_.jpg)



コメント
最近とけたろうさんのブログで統計学を勉強し始めました。素晴らしいコンテンツをありがとうございます。
演習問題5について、
「正規分布の一次結合になるので,XーYは次の確率分布に従います。」
→N(0,2×6^2)の0と2はどこから来たものなのでしょうか。
ご回答いただけると嬉しいです。よろしくお願いいたします。
正規分布の一次結合というセクションで,
X,Yが正規分布に独立に従うときに
XーYが従う正規分布が記載されているので,そちらをご確認ください。
結論から言えば,期待値は差で,分散は和で計算できます。
この問題では,XーYが従う正規分布の期待値は,22.8ー22.8=0,
分散は,36+36=72となります。