大学生の1か月の支出額の平均が知りたいとしましょう。でも,全数調査によってすべての大学生に聞き取り調査を行うには,多大なコストがかかってしまいますよね。そんなとき,正規分布やt分布を利用すると,一部の大学生の支出額を標本として「母平均は高確率でこの幅の中にある」といった推定ができるようになります。この記事では,そんな母平均の区間推定の理論的な背景を解説していきます。統計学の本領が発揮される分野ですので,これまでに学習したことをフル活用して,攻略しましょう!
もう1つのテーマは中心極限定理です。第7回の記事では,「正規分布がなぜ重要なのか」には触れませんでしたが,その謎が明かされます。
なお,母集団,標本,標本平均という用語は第3回の記事で説明しています。また,この記事を読み進めるには第7回の正規分布と第8回のt分布の内容の理解は必須となりますので,必要に応じて先にそちらの記事を読んでください。
では,はじめていきましょう!
信頼度95%の信頼区間
冒頭で紹介したように,母平均の区間推定とは,標本をもとに母平均を幅をもって推定することです。無作為に抽出されたある程度の大きさの標本があれば,標本平均を用いて母平均を推定することが可能です。そして,標本平均がどのような確率分布に従うのかを考慮すれば,「母平均は高確率でこの幅の中にある」といった幅を算出することもできます。
その幅の求め方は,「母集団についてわかっている情報」によって変わります。まずは,母分散がわかっている場合の考え方からはじめて,母分散がわかっていない場合の話へと進めていきます。
では,次の正規分布に従う母集団を想定し,その母平均μを推定することを考えましょう。
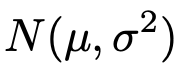
まずは,母分散は値がわかっているものとしてイメージしてください。この母集団から,大きさnの標本を無作為に抽出し,次の式のように標本平均を求めます。
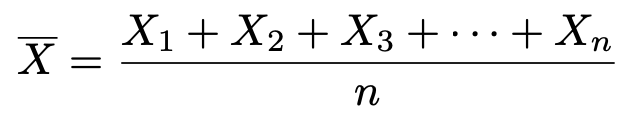
このとき,第7回で学習したように,標本平均は次の正規分布に従います。
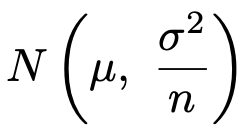
したがって,次の式によって定まるZは標準正規分布に従います。これを標準化と言いましたね。
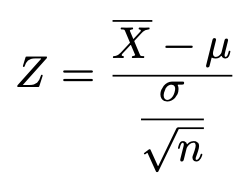
次のように正規分布表を見ると,標準正規分布の上側2.5%点は1.96であるとわかります。
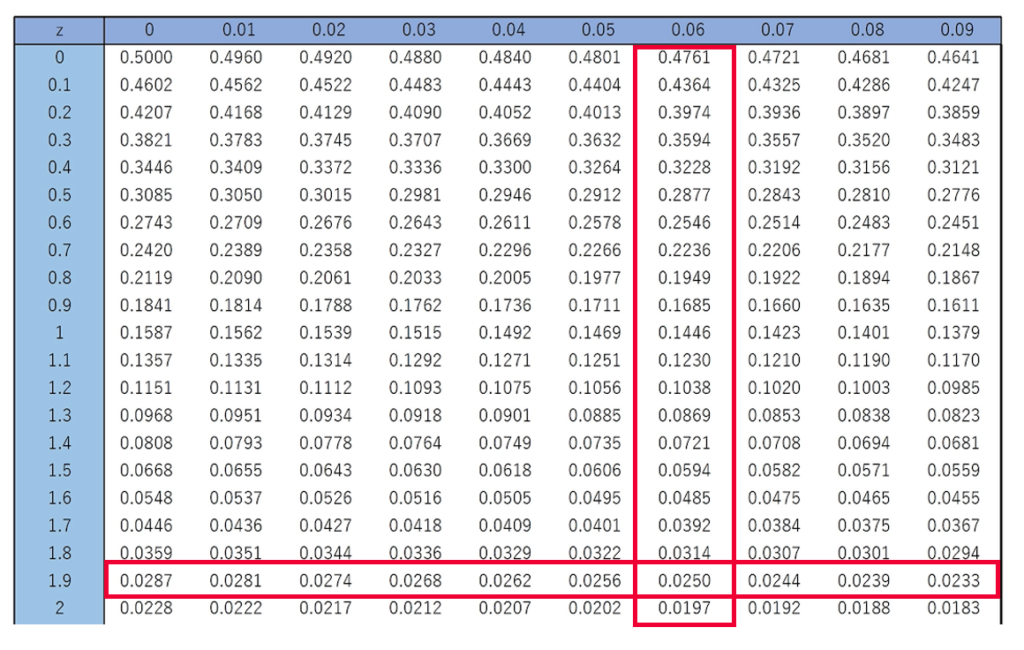
つまり,次の式のように,Zがー1.96以上1.96以下となる確率は95%だということです。
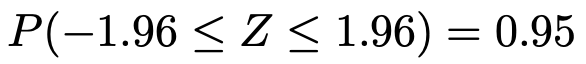
図で表すと,次の色のついた部分の確率が95%になります。
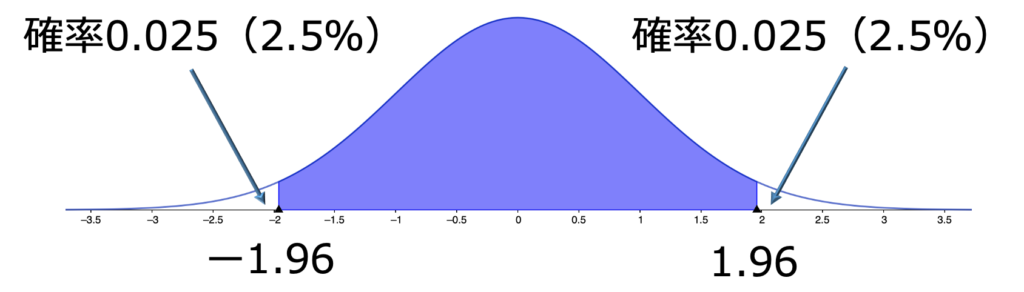
さて,P(ー1.96≦Z≦1.96)=0.95の左辺のZに上のZとXの関係式を代入すると,次のようになります。
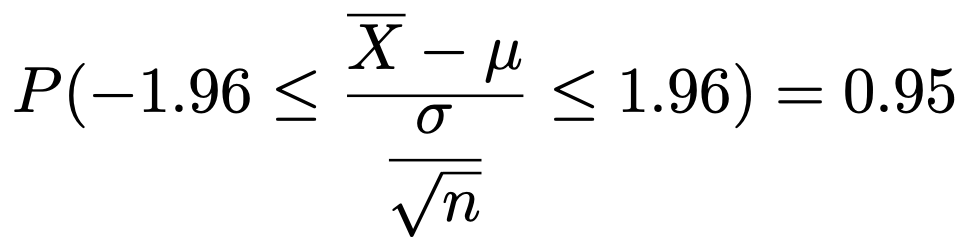
次に,左辺のかっこ内の分母をはらうと,次のようになります。

さらに,左辺のかっこ内のすべての辺にμを加えると,次のようになります。
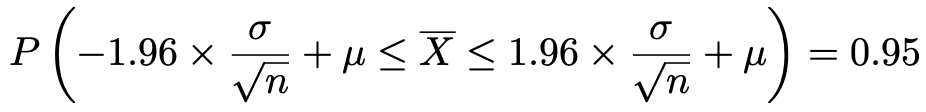
この式が意味しているのは,「標本平均は確率的にいろいろな値をとるけれども,左辺のかっこ内の不等式の範囲に入る確率が95%である」ということです。
次に,このかっこ内の不等式を2つに分けます。
左の不等号をはさむ部分を取り出して,移項すると2行目のようになります。これがμの上限を表しています。
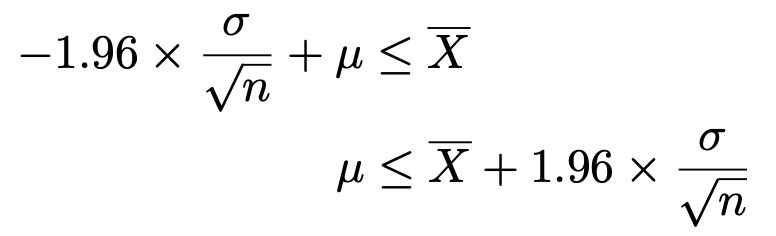
同じように,右の不等号をはさむ部分を取り出して,移項すると2行目のようになります。これがμの下限を表しています。
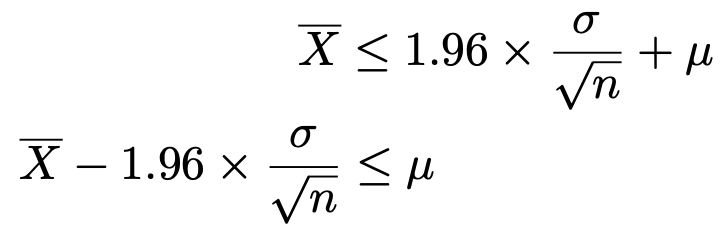
2つの不等式を合わせると,次のようになります。
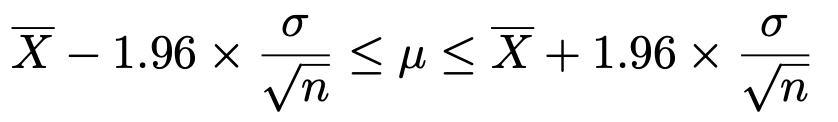
この不等式の最左辺や最右辺は,母分散がわかっていれば,数値で表すことができます。そうして得られる不等式が母平均μの信頼度(信頼係数)95%の信頼区間です。
95%だけではなく,99%や90%などを使う場合もあります。そのときには,1.96という数を,それぞれ標準正規分布の上側0.5%点,上側5%点に変える必要があります。その中でも,95%の信頼区間は頻出なので,1.96という数は覚えておきましょう。
さて,「信頼度95%の信頼区間」という言葉の意味を補足しておきます。上の不等式に母分散やn,標本平均の値をひとたび代入すると,その幅に母平均が見事に入っていることもあれば,残念ながら入っていないこともあります。でも,「この信頼区間を100回つくったならば,およそ95回は母平均が含まれる信頼区間が得られる」というのが,信頼度95%という意味になります。
では,次のセクションからは,実際に信頼区間を求めていきましょう。
区間推定(正規母集団で母分散既知の場合)
ここでは,母集団が正規分布に従っていて,母分散は事前にわかっている場合を扱います。母平均がわからない場合,現実的には母分散もわからないことが多いのですが,まずは第一段階として母分散がわかっている場合から考えていきましょう。
では,前のセクション内容を踏まえて,次の問題を解いていきます。
【問題】あるメーカーの電球Aの寿命を調べるため,次のように無作為に5つの標本を取り出した。
1134,1253,1078,1190,1045(時間)
この電球A全体の寿命の平均(母平均)をμとして,母集団は次の正規分布に従うものとする。
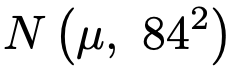
このとき,母平均μの信頼度95%の信頼区間を求めなさい。
【解答】与えられた大きさ5の標本から,標本平均の実現値は次のようになります。
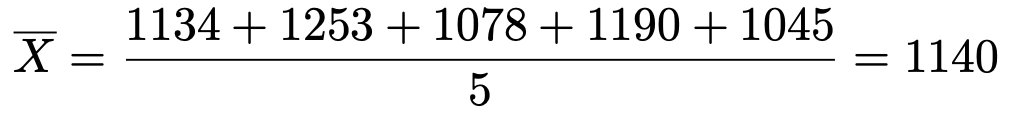
問題で与えられた母集団についての仮定と,標本の大きさが5であることから,標本平均は次の正規分布に従います。
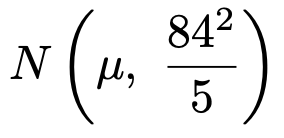
前のセクションで導いた母平均μの信頼度95%の信頼区間に,わかっている数値を代入すると,次のようになります。
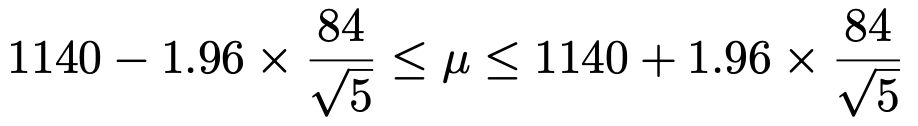
ルート5の近似値を2.236として,四捨五入して整数の範囲で最左辺と最右辺を計算すると,求める母平均μの信頼度95%の信頼区間は次のようになります。

(解答終わり)
区間推定(正規母集団で母分散未知の場合)
前のセクションで扱ったのは,母分散がわかっている問題でしたが,同じ問題を母分散がわかっていない条件のもとで解いてみましょう。
【問題】あるメーカーの電球Aの寿命を調べるため,次のように無作為に5つの標本を取り出した。
1134,1253,1078,1190,1045(時間)
この電球Aの寿命のデータ全体(母集団)は正規分布に従うものとするとき,母平均μの信頼度95%の信頼区間を求めなさい。
【解答】標本平均の実現値は,前問と同じく,次のようになります。
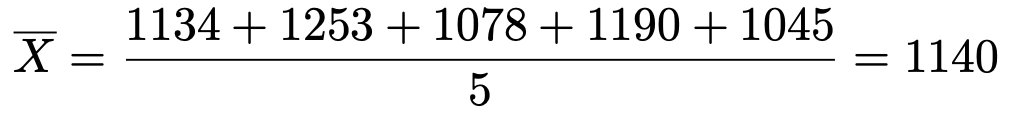
母標準偏差をσとすると,標本平均は次の正規分布に従います。

第8回の記事で学習した内容から,不偏分散をU2として,次の式によって定まるTは自由度4のt分布に従います。
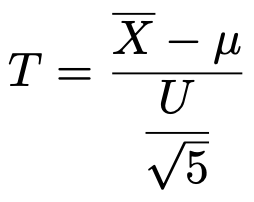
次のように,t分布表を見ると,自由度4のt分布の上側2.5%点は2.776であるとわかります。

つまり,次の式のように,Tがー2.776以上2.776以下となる確率は95%だということです。
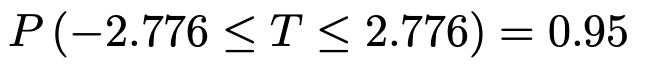
さて,P(ー2.776≦T≦2.776)=0.95の左辺のTに上のTとXの関係式を代入すると,次のようになります。
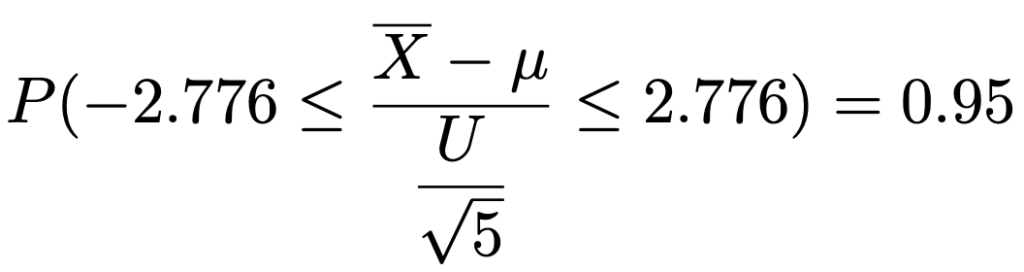
次に,左辺のかっこ内の分母をはらうと,次のようになります。
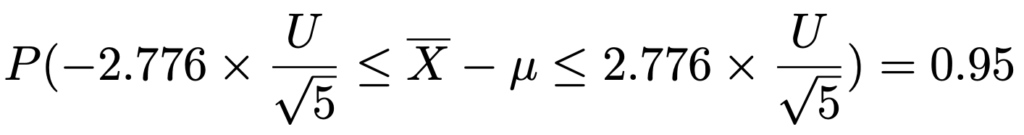
さらに,左辺のかっこ内のすべての辺にμを加えると,次のようになります。
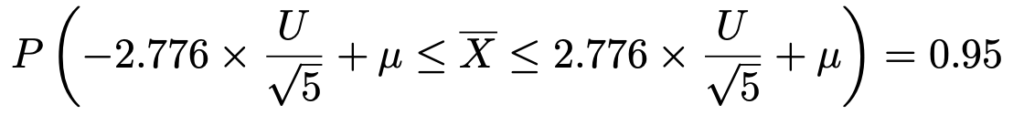
この式を母平均μが真ん中にくるように書きかえると,次のようになります。
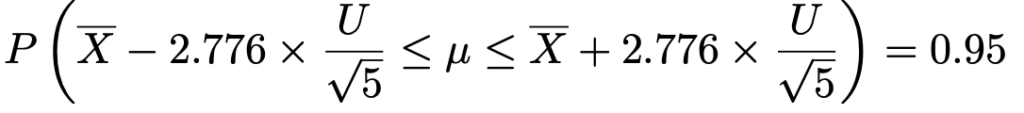
ここで,不偏分散の実現値は次のようになります。

よって,不偏分散の実現値の正の平方根は約83.9であるから,母平均μの信頼度95%の信頼区間を求める式は次のようになります。

最左辺と最右辺を整数で求めると,母平均μの信頼度95%の信頼区間は次のようになります。
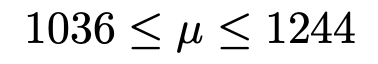
(解答終わり)
前問で,正規分布表から求めた場合の母平均μの信頼度95%の信頼区間と比べると,同じ95%信頼区間なのに幅が広くなっています。逆に言えば,同じ幅にしようとすると,信頼度を低くしないといけません。これは,t分布が標準正規分布よりも分散が大きく,確率密度関数のグラフのすそが左右に広がっていることに起因します。
中心極限定理
中心極限定理とは,母集団がどんな確率分布であっても,標本の大きさが十分に大きければ,その標本平均の確率分布は正規分布だとみなすことができる,というものです。より正確には,次のようになります。
次の大きさnの標本は,母平均μ,母分散σ2の母集団から無作為抽出されたものとする。
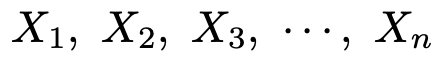
また,標本平均を次の式で定める。
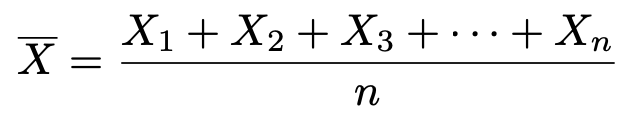
これらをもとに,次の式で確率変数Zを定める。
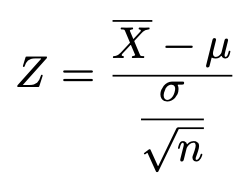
このとき,標本の大きさnが十分に大きければ,Zは近似的に標準正規分布に従う。
この定理は式を使って証明することが可能ですが,かなりの脱線になってしまいますので,ここでは割愛します。証明を知りたい人は,例えば,「データ解析のための数理統計入門(久保川達也著,共立出版)」を参照してください。
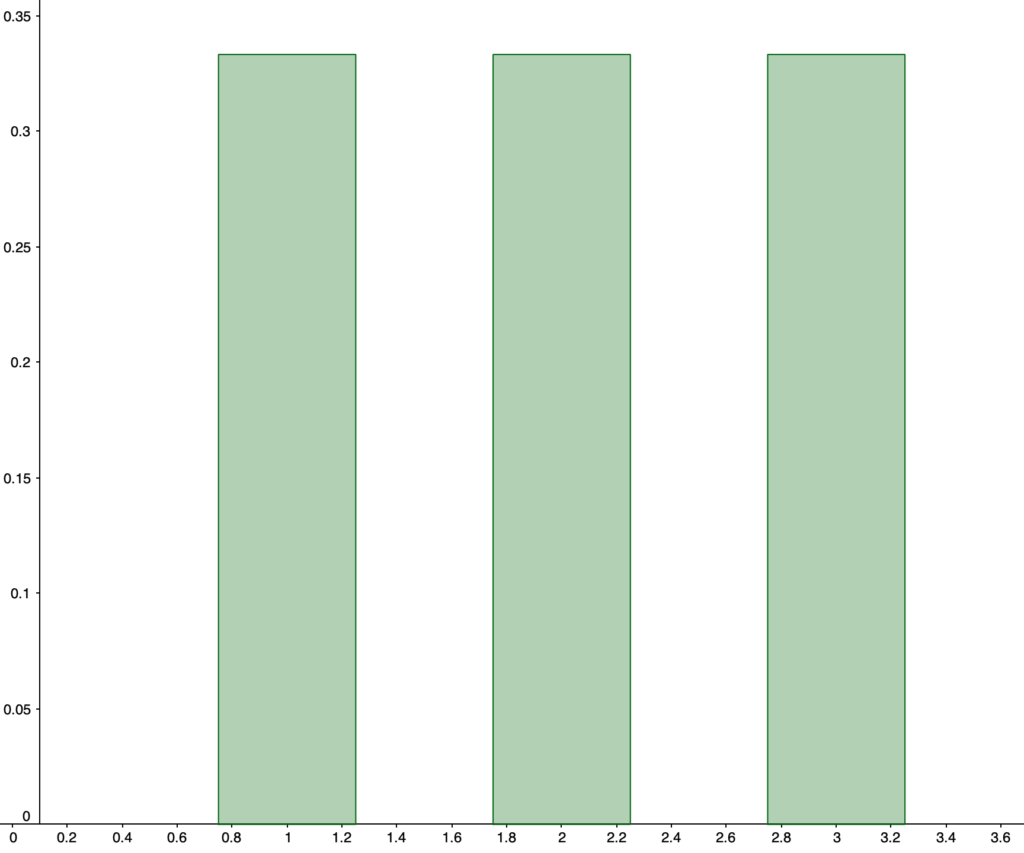
中心極限定理の意味を具体的に考えてみましょう。例えば,1,2,3の数字が1つずつ書かれた3枚のカードが入っている袋から,カードを1枚ずつ無作為復元抽出する試行を考えましょう。1枚だけ取り出すとき,取り出したカードに書かれた数をXとすると,P(X=1)=P(X=2)=P(X=3)=1/3ですよね。よって,この確率分布は次の図のようになります。
次に,1枚ずつ無作為復元抽出することを2回くり返して,1枚目のカードに書かれた数をX1,2枚目のカードに書かれた数をX2とするとき,標本平均は次の式で表されます。
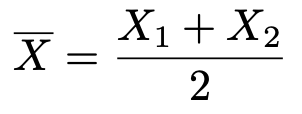
このとき,標本平均の確率分布は次の表のようになります。
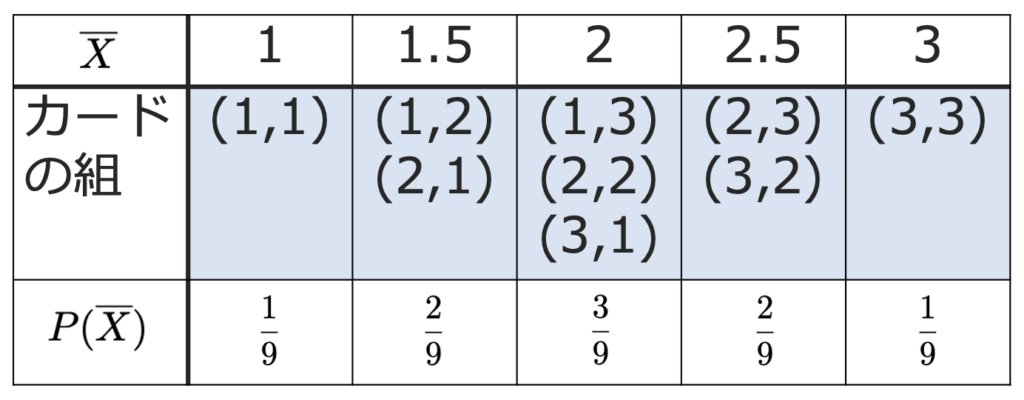
この確率分布を図に表すと,次のようになります。
次に,1枚ずつ無作為復元抽出することを3回くり返して,1枚目のカードに書かれた数をX1,2枚目のカードに書かれた数をX2,3枚目のカードに書かれた数をX3とするとき,標本平均は次の式で表されます。
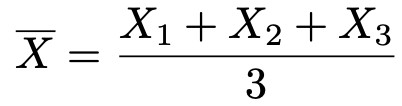
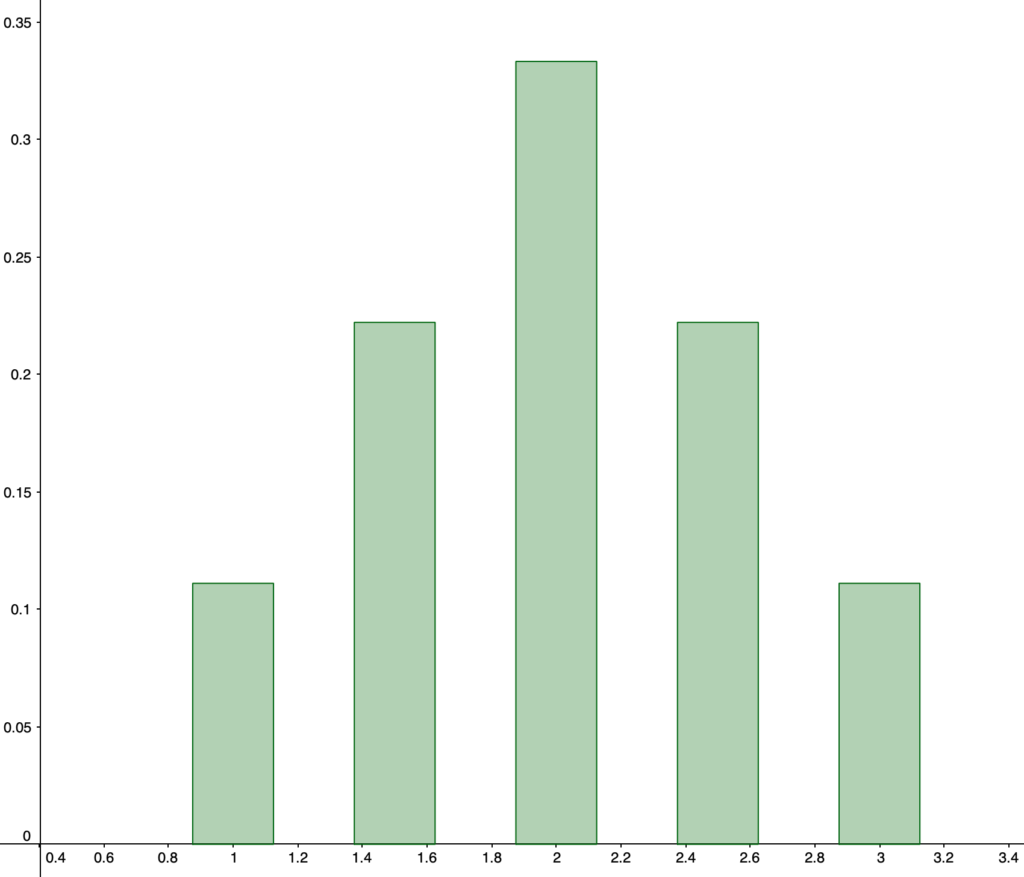
このとき,標本平均の確率分布は次の表のようになります。
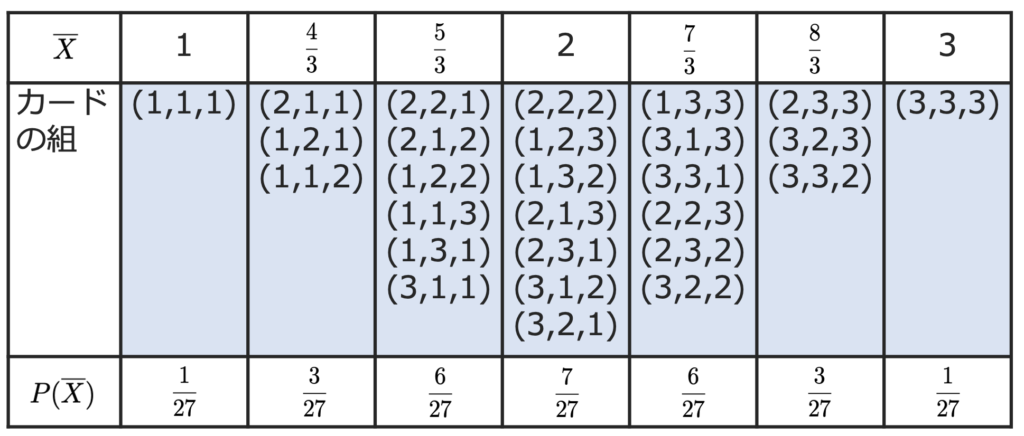
この確率分布を図に表すと,次のようになります。
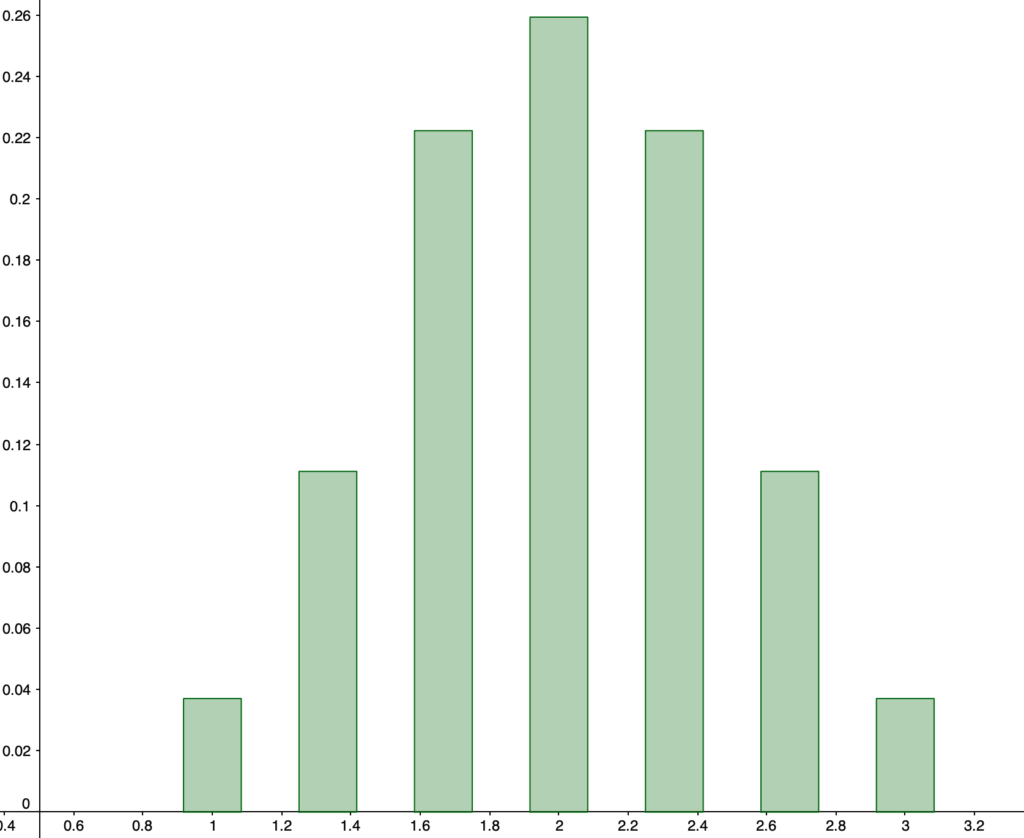
このように,取り出す枚数が1枚のときの確率分布は平らな形(一様分布)でも,2枚,3枚,…と取り出す枚数を増やしたときの標本平均の確率分布は,正規分布の確率密度関数のグラフの形に近づいていきます。
ちなみに,中心極限定理を適用して正規分布として考えていい標本の大きさの基準は,一般的には30以上とされています。
ここで,中心極限定理のポイントを改めて強調しておきます。次の2点に注意しましょう。
- 母集団の確率分布が何であるかによらない
- 標本平均の確率分布が正規分布に近づく
これで,正規分布がなぜ統計学の主役であるのか,はっきりしましたね。どんな分布でも標本平均をとれば,標本の大きさが十分に大きいときに正規分布に近づくからです。
区間推定(一般母集団で大標本の場合)
母集団の確率分布が正規分布とは限らない場合でも,標本の大きさが十分に大きければ,中心極限定理によって標本平均は近似的に正規分布に従うと考えて区間推定ができます。このことを利用して,問題を解いていきましょう。
【問題】ある森で生育している樹木Aの高さを調べたところ,無作為に抽出された50本の樹木Aの高さの平均は17.7m,標準偏差は6.2mであった。この森の樹木Aの平均的な高さ(母平均)をμとするとき,μの信頼度95%の信頼区間を求めなさい。ただし,標準偏差とは不偏分散の正の平方根のこととする。
【解答】問題文から,標本平均と不偏分散はそれぞれ次のようにわかります。
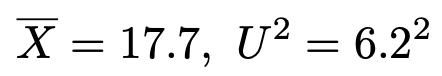
不偏分散を用いた区間推定なので,t分布を用いることも可能(この場合の自由度は49)ですが,ここでは標本の大きさが十分に大きいと考えて,中心極限定理から,標本平均は正規分布に従うとみなすことにします。つまり,次の式で定まるZが標準正規分布に従うものと考えます。
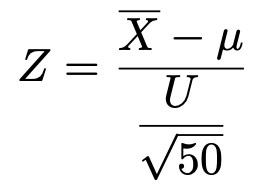
正規母集団で母分散既知の場合と同じように,標準正規分布ではー1.96以上1.96以下の値をとる確率が0.95なので,次の式が成り立ちます。

上の式のかっこ内の分母をはらって,不等式の各辺にμを加えると,次のようになります。
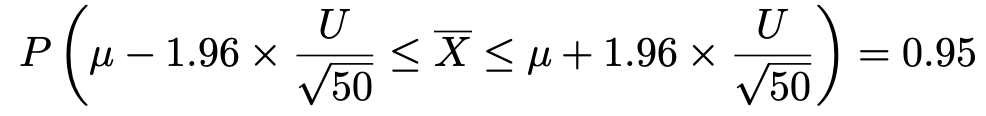
つまり,確率95%で標本平均が入る区間は次のようになります。
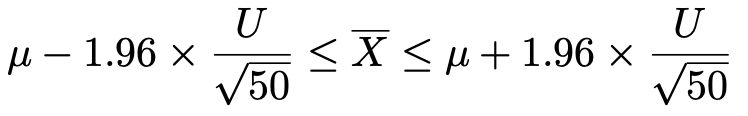
この式を母平均μが真ん中にくるように書きかえると,次のようになります。
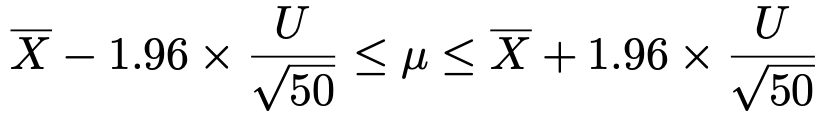
問題で与えられている標本平均と不偏分散の実現値を代入すると,次のようになります。
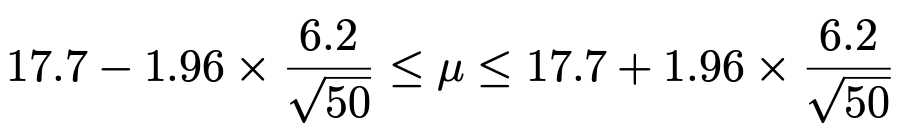
最左辺と最右辺を,四捨五入して小数第1位まで求めると,母平均μの信頼度95%の信頼区間は次のようになります。
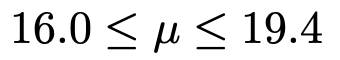
(解答終わり)
母平均の区間推定についての基本的な説明は以上になります。ここからは,さらに理解を深めるための演習問題ですので,余力があればぜひチャレンジしてみてください。
演習1〜信頼区間(正規母集団で母分散既知の場合)〜
【問題】ある果樹園で栽培しているイチゴの糖度について,大きさ4の標本を無作為抽出して調べたところ,次のような結果になった。
11.2,9.9,12.1,9.6(度)
この果樹園で栽培されたイチゴ全体の糖度の平均(母平均)をμとして,母集団は次の正規分布に従うものとする。
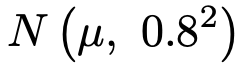
このとき,母平均μの信頼度99%の信頼区間を求めなさい。なお,必要があれば,次の正規分布表を使いなさい。
【解答】大きさ4の標本平均は次の正規分布に従います。
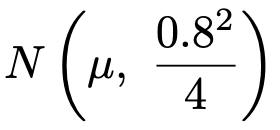
いま,標本平均の実現値は次のようになります。
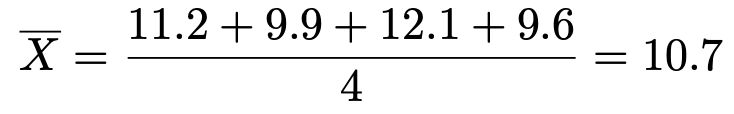
正規分布表を見ると,標準正規分布の上側0.5%点は約2.58であるとわかります。
さて,この記事の前半で導いた,正規母集団で母分散が既知の場合の母平均μの信頼度95%の信頼区間を求める式は次のように表せました。
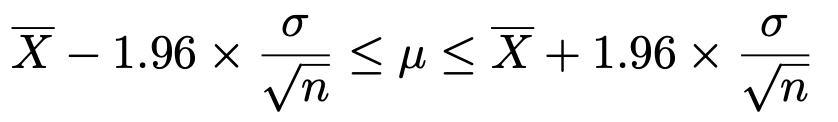
この式で,1.96を2.58でおきかえて,母平均μの信頼度99%の信頼区間を求める式は次のように表せます。
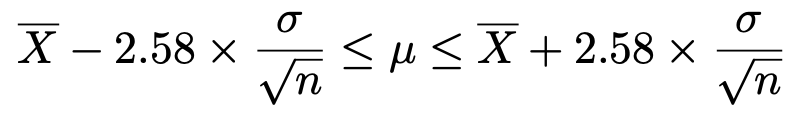
この式にわかっている数値を代入すると,次のようになります。
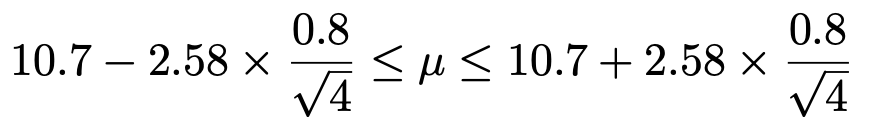
最左辺と最右辺を,四捨五入して小数第2位まで求めると,求める母平均μの信頼度99%の信頼区間は次のようになります。
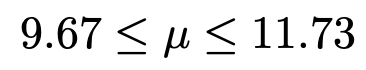
(解答終わり)
演習2〜信頼区間(正規母集団で母分散未知の場合)〜
【問題】正規母集団から,次の大きさ21の無作為標本を抽出する。
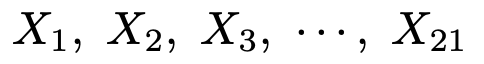
得られた標本から,標本平均と不偏分散の実現値はそれぞれ次の値であったとする。

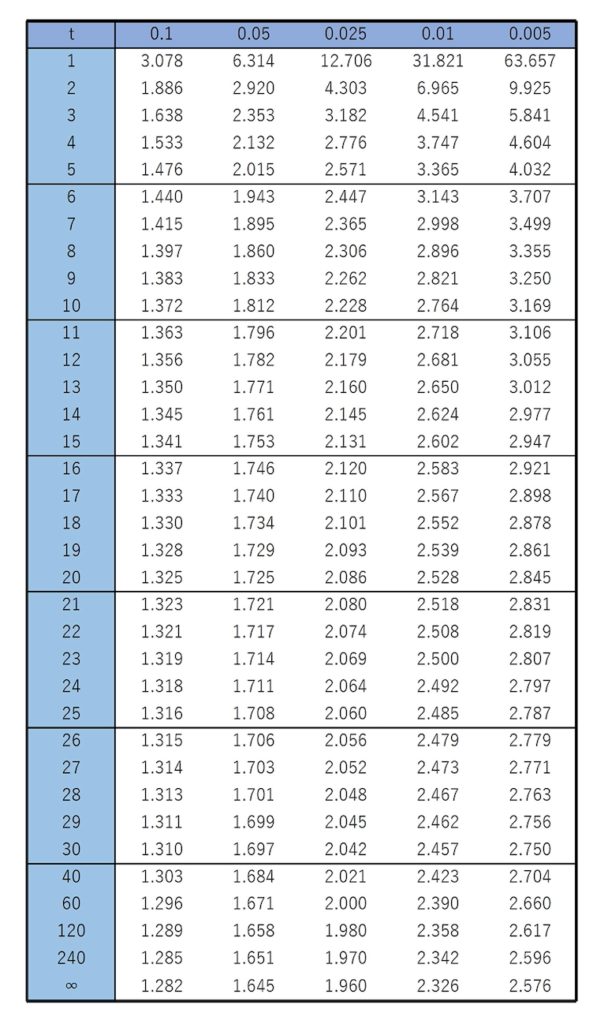
このとき,母平均μの信頼度95%の信頼区間を求めなさい。なお,必要があれば,次のt分布表を使いなさい。
【解答】母集団が正規分布に従うので,標本平均も正規分布に従います。このとき,次の変換によって定まるTは,21ー1=20より,自由度20のt分布に従います。
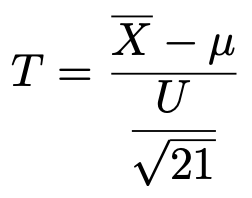
t分布表を見ると,自由度20のt分布の上側2.5%点は2.086であるとわかります。よって,次の式が成り立ちます。

上の式のかっこ内の分母をはらって,不等式の各辺にμを加えると,次のようになります。
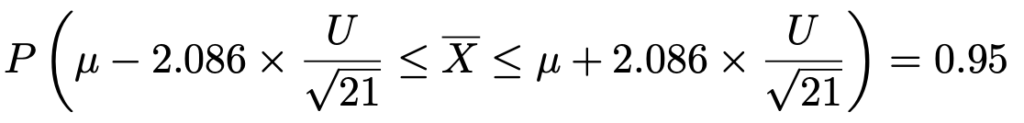
つまり,確率95%で標本平均が入る区間は次のようになります。
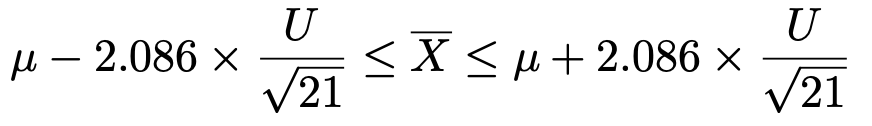
この式を母平均μが真ん中にくるように書きかえると,次のようになります。
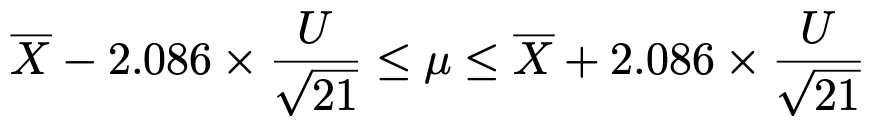
ここで,問題で与えられた標本平均と不偏分散の実現値を代入すると,次のようになります。
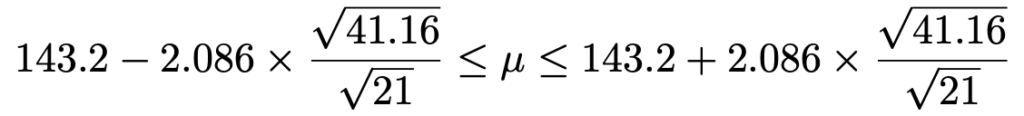
ここで,次のことに注意します。
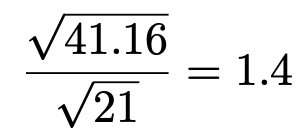
最左辺と最右辺を,四捨五入して小数第1位まで求めると,母平均μの信頼度95%の信頼区間は次のようになります。
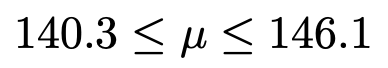
(解答終わり)
演習3〜信頼区間(一般母集団で大標本の場合)〜
【問題】ある農園で採れたリンゴから,無作為に抽出された100個のリンゴの重さの平均は294.5g,標準偏差は27.9gであった。このときに採れたリンゴの平均的な重さ(母平均)をμとするとき,μの信頼度90%の信頼区間を求めなさい。ただし,標準偏差とは不偏分散の正の平方根のこととする。
【解答】問題文から,標本平均と不偏分散は次のようにわかります。
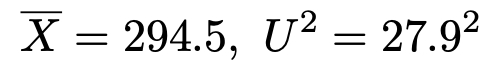
標本の大きさは十分に大きいので,中心極限定理から,標本平均は正規分布に従うとみなすことができます。つまり,次の式で定まるZが標準正規分布に従うものと考えます。
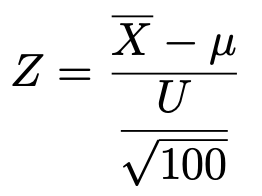
正規分布表を見ると,標準正規分布の上側5%点は約1.64であるとわかります。よって,次の式が成り立ちます。
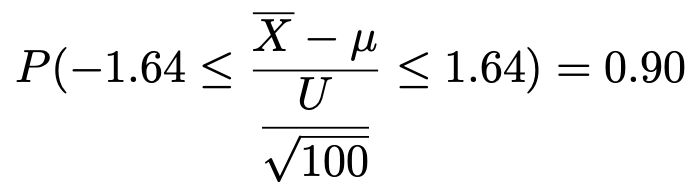
上の式のかっこ内の分母をはらって,不等式の各辺にμを加えると,次のようになります。
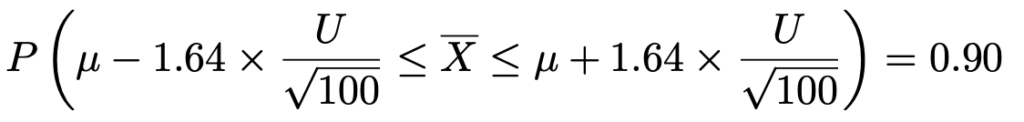
つまり,確率90%で標本平均が入る区間は次のようになります。
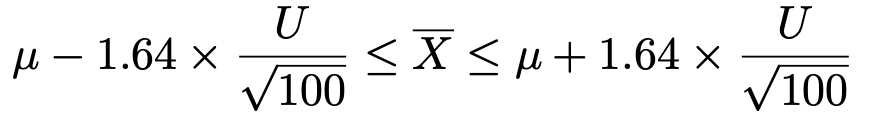
この式を母平均μが真ん中にくるように書きかえると,次のようになります。
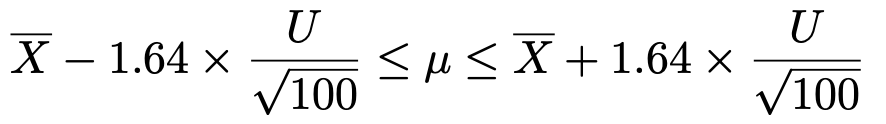
問題で与えられている標本平均と不偏分散の実現値を代入すると,次のようになります。
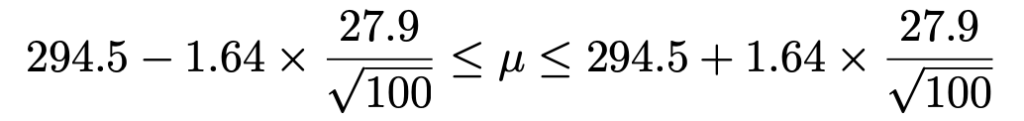
最左辺と最右辺を,四捨五入して小数第1位まで求めると,母平均μの信頼度90%の信頼区間は次のようになります。
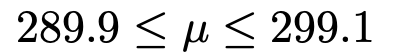
(解答終わり)
第9回は以上となります。最後までお付き合いいただき,ありがとうございました!
引き続き,第10回以降の記事へ進んでいきましょう!
2023年1月に「統計検定2級公式問題集[CBT対応版](実務教育出版)」が発売されました!(CBTが何かわからない人はこちら)
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが,本書は分野ごとにその形式の問題を並べた構成になっていて,最後に模擬テストがついています。CBT対策の新たな心強い味方ですね!
さらに実戦に向けた演習を積みたい人は,「統計検定2級公式問題集2018〜2021年(実務教育出版)」を手に取ってみてください!
また,もっと別の問題を解いてみたい人は,さらにさかのぼって「統計検定2級公式問題集2016〜2017年(実務教育出版)」を解いて実力に磨きをかけましょう!



![統計検定2級公式問題集[CBT対応版]](https://m.media-amazon.com/images/I/51q3GfZId3L._SL500_.jpg)




コメント