微分積分と連続型確率変数【中学の数学からはじめる統計検定２級講座第６回】

統計検定２級では，積分を使う問題も出題されます。「統計学を勉強してみたいけれど，積分がわからないから無理」という人も，この記事を読んでもらえば大丈夫です。今回は，微分積分の解説からはじめて，連続型の確率変数について，第３回の記事で紹介した内容よりも踏み込んで，積分を伴う確率や期待値などの計算をしていきます。第１回の確率の計算，第３回の確率変数，第４回の期待値と分散を理解した上で，以下の記事を読み進めてください。

なお，重積分（２変数以上の積分）を必要とする一部の式の証明は，重積分が統計検定２級で出題されていないため，省略いたします。また，連続型の確率変数の同時確率分布やそれを必要とする共分散なども，重積分が関わるため，本稿では扱いません。では，はじめていきましょう！

微分積分と連続型確率変数【中学の数学からはじめる統計検定２級講座第６回】

極限とは

微分積分という分野は極限を土台として成り立っているので，はじめに極限について説明します。まず，次のような数列（数を順番に並べたもの）を考えます。

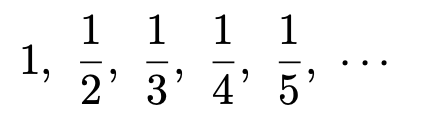
この数列は，nを自然数として次のようにも表せますね。

nの値をどんどん大きくしていくと，この分数は０に近い値になっていきます。nの値を十分に大きくすれば，いくらでも０に近づけることができることを次のように書き表します。

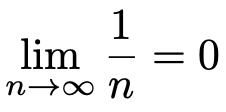
この”lim”が極限（limit）で，上の式を，「n分の１のn→∞での極限は０である」と表現します。「n→∞」というのは，「nの値を十分に大きくする」という意味です。別の例も見てみましょう。次の数列を見てください。

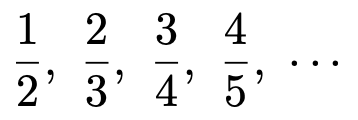
この数列は，nを自然数として次のように表せますね。

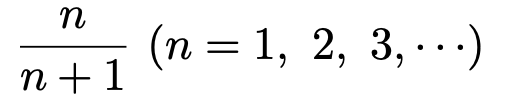
この分数のnの値をどんどん大きくしてみてください。n＝10000などを代入すればわかるように，ほぼ１になっていきますよね。nの値を十分に大きくすれば，いくらでも１に近づけることができるので，次のように表します。

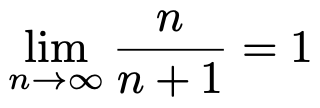
nをどれだけ大きくしても，１つ目の数列は０にはならないし，２つ目の数列は１になりませんが，どんどんそこへ向けて近づいていきます。この「ゴール」のことを極限と言うわけです。

極限の値は必ずしも定まるわけではありません。例えば，次の例では，nをどれだけ大きくしても，ある１つの値にいくらでも近づくということはないので，極限は存在しません。

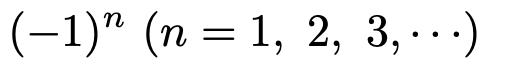
極限のイメージを何となくでも持ててもらえればOKです。今回は極限の話はここまでにしておきます。

関数の表し方

関数は，英語でfunctionですから，xを変数とする関数を表すのにf(x)という記号をよく用います。例えば，次のように使います。

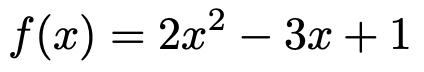
この式に，x＝４を代入すると，

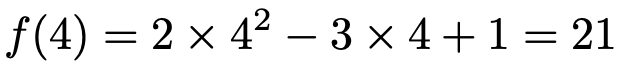
よって，y＝f(x)という関数のグラフは，点(4，21)を通ることがわかります。

微分とは

微分とは，平たく言えば，関数の傾きを求めること，または傾きの情報を持つ関数を求めることです。微分の計算の仕方はいたってシンプルです。関数の項ごとに次の操作を行います。

左辺の項の右上についた「’」という記号は，「微分しますよ」という意味です。つまり，上の式の左辺は，「xのn乗という関数をいまから微分しますよ」と言っています。右辺は微分した結果です。微分すると，xの右肩にのっている数が１だけ小さくなります。この場合のように，微分される項の右肩にのっている数がnであれば，微分した後には１だけ小さくなってnー１に変わります。そうしてできた「xのn−１乗」に，もともと右肩にのっていたnをかけたものが上の式の右辺ですね。これが微分の計算ルールです。では次に，微分の具体例を確認してみましょう。最も基本的な２次関数と言えば，

です。この関数を微分すると次のようになります。

つまり，微分して得られる関数は，

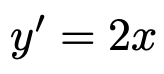
この例で微分をもう一度確認すると，微分する前と後では，xの右肩の数が２→１となって１だけ小さくなっています。さらに，もともと右肩にのっていた２をかけて，２xという関数になります。次に，もう少し複雑な次の関数を微分してみましょう。

この関数を先ほどと同じ方法で項ごとに微分すると，次の関数が得られます。

この微分では，次の置き換えを行なっています。

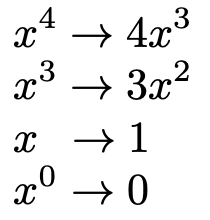
定数項はxの０乗の項と考えられるので，微分すると０をかけることになり，それ自体が０になってなくなってしまいます。

では次に，微分の図形的な意味を確認しましょう。次の図を見てください。

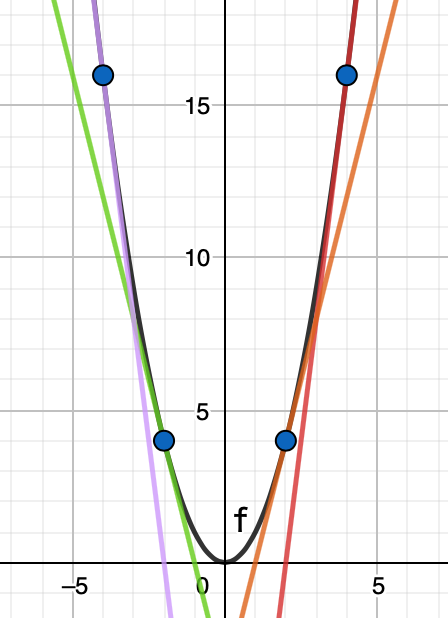
この図のもとになっているのは，先ほども登場した次の関数です。

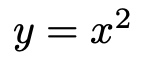
このグラフ上の４つの点を青く示してあります。左から(ー4，16)，(ー2，4)，(2，4)，(4，16)です。色のついた４本の直線は，この４つの点における接線です。また，x＝０における接線はx軸で，その傾きは０ですね。これらの点のx座標と接線の傾きを表にまとめると，次のようになります。

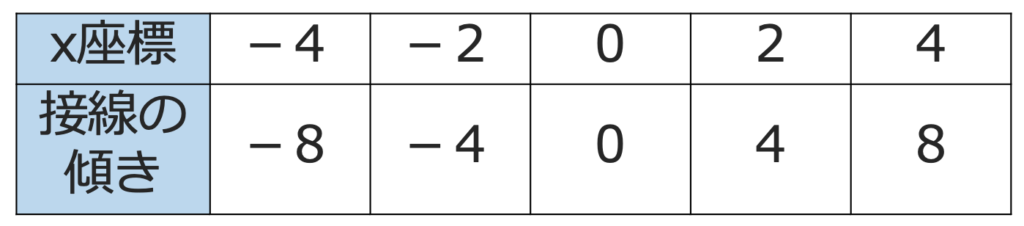
この表から，各点のx座標を２倍すると，接線の傾きに等しくなることがわかると思います。つまり，傾きをyとすると，次の関係が成り立っています。

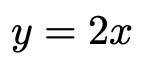
この関数は，関数y＝x²を微分することで得られたことを思い出してください。微分すると，それぞれのx座標に対して，その点の接線の傾きを教えてくれる関数が求められるということです。

積分とは

さて，いよいよ積分の話を始めます。積分とは，平たく言えば，関数のグラフで囲まれた図形の面積を求めること（定積分），または面積の情報を持つ関数を求めること（不定積分）です。微分と同じように，まずは計算方法から確認していきます。積分したい関数の式について，項ごとに次の操作を行います。

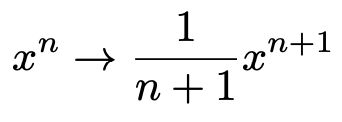
この積分の計算は微分の計算の真逆の操作です。例えば，微分のところで紹介した次の関数

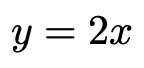
を積分（不定積分）してみましょう。積分では，xの右肩にのっている数が１だけ増えます。上の式では，xの右肩に１乗が省略されていますので，１を頭の中で補ってください。積分すると，xの右肩にのっている数が１だけ増えて，２になります。さらに，いま新しく右肩にのった数の逆数をかけます。この例では，２分の１をかけます。この計算をすると，

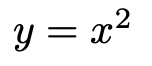
になります。この関数を微分すると，もとのy＝２xに戻りますよね。つまり，積分して得られた関数を微分するともとに戻るということです。ただし，厳密には，今の説明の中に積分定数と呼ばれる定数が入り込んでくるのですが，話を簡略化するために省略しました。積分定数は統計学であまり登場しないので，ここではさらっと流します。次に，もう少し複雑な次の関数を積分してみましょう。

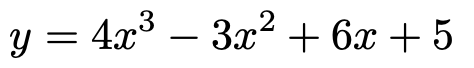
この関数を先ほどと同じ方法で項ごとに積分すると，次の関数が得られます。

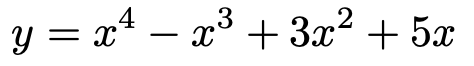
この積分では，次の置き換えを行っています。

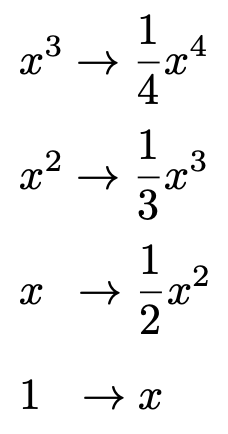
５＝５×１として，１をxの０乗と考えると，定数項も同じルールで積分ができます。

では次に，積分の図形的な意味を確認しましょう。次の図を見てください。

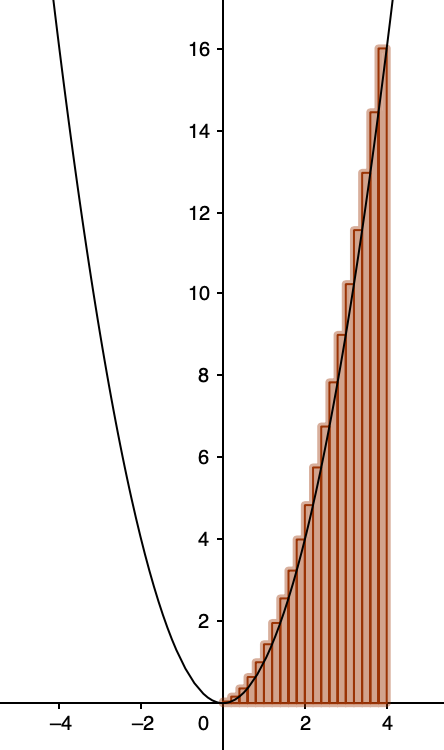
この図のもとになっているのは，何度も登場している次の関数です。

この関数のグラフと，x軸，直線x＝４で囲まれた部分の面積を求めてみましょう。この面積は，上の図の横幅の短い長方形の面積の和とほとんど同じだということがわかるでしょうか。この長方形の横幅をどんどん短くしていくと，求めたい面積に近づいていきます。横幅を無限に小さくしたときの極限の値を教えてくれるのが積分です。

では，この面積を積分を使って求めてみましょう。まず，一般的な関数y＝f(x)の積分は，次の式のように表されます。

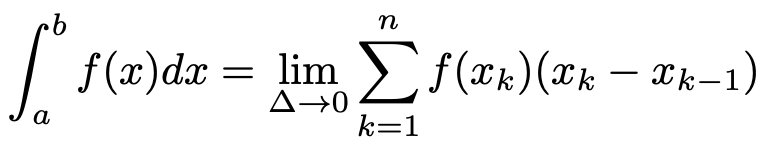
はじめて見ると，ギョッとするかも知れません。右辺のいちばん右のカッコの中は，上の図の１つ１つの長方形の横幅です。その左隣は長方形の縦の長さです。さらにその左隣のΣは，そういう長方形をn個（たくさん）たし合わせましょう，という意味です。そして，いちばん左側のlimは，長方形の横幅をどこまでも短くしていくときの極限を求めましょう，という意味です。

この右辺の式は複雑なので，左辺のようにシンプルな新しい記号を割り当てて，これが積分の記号になります。左辺の記号を「インテグラルエフエックスディーエックス」と読みます。「f(x)という関数をaからbまで積分しますよ」という意味です。ここで，aやbは積分範囲を表すx座標です。

左辺のいちばん左側の記号のインテグラルは，右辺と比べると，limとΣを合わせたものだと理解できます。「s」みたいな形をしていますが，和を英語で”sum“と言うので，「積分＝和の極限」の意味で，sをもじった記号が使われます。また，左辺のdxは，右辺でいちばん右にあるカッコに対応していて，長方形の微小な横幅を表しています。

では，上の式の左辺を計算する方法を紹介します。次の式を見てください。

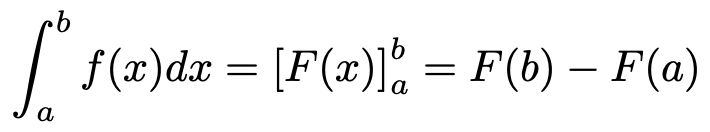
いちばん左の積分を「真ん中→いちばん右」の順に２段階で計算します。真ん中のF(x)は，f(x)を積分（不定積分）して得られる関数です。例えば，f(x)=2xならば，

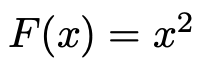
になります。この関数に積分の上端と下端の値を代入して，差をとったものが求めたい積分の値になります。したがって，上の図で求めたかった面積は，次のように計算できます。

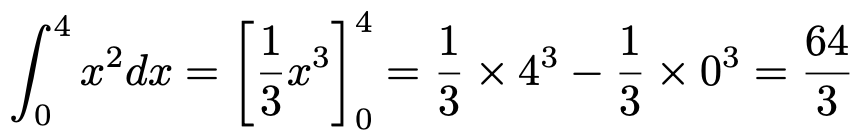
微分積分学の基本定理

何やら，いかめしいタイトルですが，そんなに身構えなくても大丈夫です。y＝f(x)を連続な関数とするとき，次の式が微分積分学の基本定理と呼ばれるものになります。

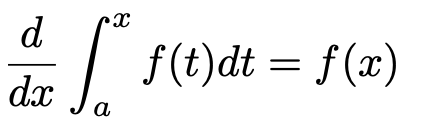
この式の左辺のいちばん左の記号は，「ディーディーエックス」と読み，「xで微分します」という意味です。この式を言葉で表現すると，「f(t)という関数を積分して微分するともとに戻る」となります。f(t)がf(x)に変わっていますが，テクニカルなことなのであまり気にせずに，同じだと思ってください。

この定理は，微分という関数の傾きを求める操作と，積分という面積を求める操作が，かけ算とわり算のような逆演算の関係になっているということを示していて，本稿の累積分布関数のセクションで利用します。

連続型確率変数の確率

第３回の記事で触れたように，連続型確率変数の確率は積分によって定義します。確率変数Xの値がa以上b以下となる確率が関数f(x)を使って次の式のように書けるとき，確率変数Xは連続型の確率分布をもつと言います。

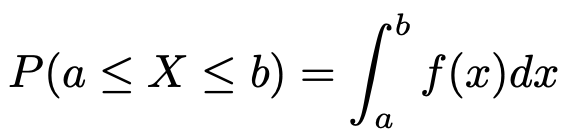
そして，f(x)を確率変数Xの確率密度関数と言います。ただし，確率は０以上なので，すべてのxについて，f(x)の値は０以上でなければなりません。また，全体の確率は１なので，次の式が成り立つ必要があります。

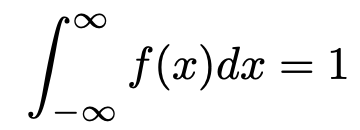
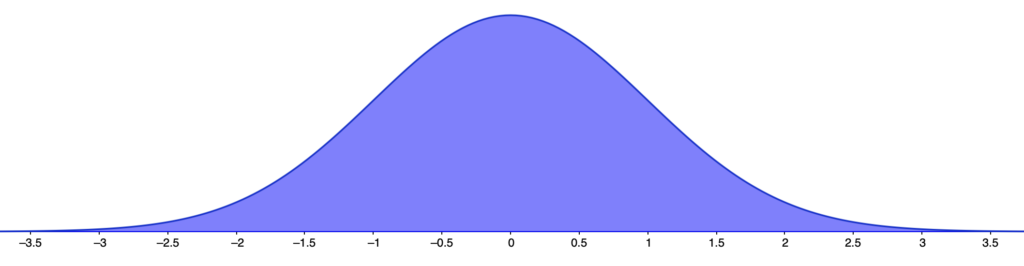
ただし，上の積分は，積分範囲に∞が入っているのが「？」ですよね。今回の記事では，∞が絡む計算はしませんので，「端から端まで」だと思ってもらえればそれでいいです。この積分は，一般的には広義積分と呼ばれるもので，第７回の記事で解説します。例えば，確率変数Xの確率密度関数f(x)のグラフが次の図のように表せるとき，色のついた部分全体の面積が１になるというのが，「端から端まで」という意味です。

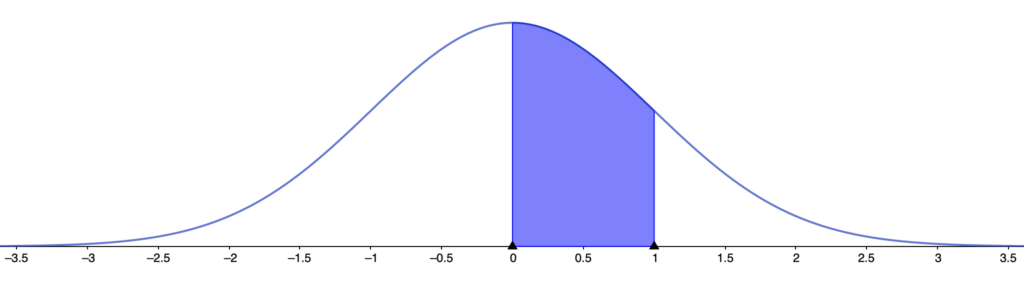
また，下の図の色のついた部分の面積はXの値が０以上１以下となる確率を表しています。

よって，この確率は，確率密度関数をf(x)として，次の式の右辺のように計算できます。

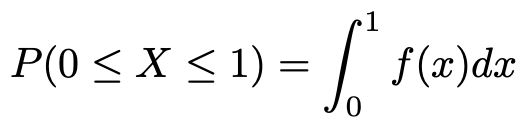
累積分布関数

確率変数Xに対し，次の式で累積分布関数（単に，分布関数とも言う）を定義します。

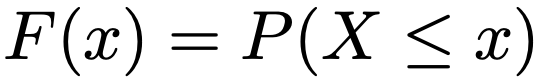
まずは，離散型の確率変数で考えてみましょう。例えば，サイコロを１回投げたときに出た目をXとすると，Xの累積分布関数のグラフは次の図のようになります。

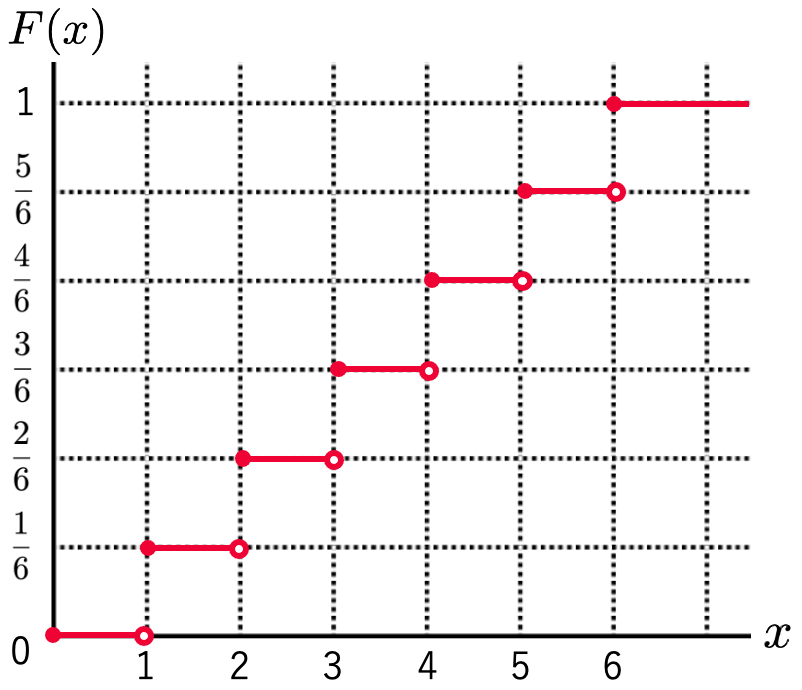
この場合には，x＜１の値をとることはないので，この範囲でF(x)＝０，１≦x＜２のときにはx以下の値をとる確率は６分の１なので，この範囲でF(x)の値は６分の１，…のようになります。このように，離散型の場合には，累積分布関数のグラフは階段状になります。

次に，連続型確率変数Xの累積分布関数F(x)を考えてみましょう。累積分布関数は，Xがあるxという数以下の値をとる確率なので，Xの確率密度関数をf(x)とすると，次の式のような積分で表すことができます。

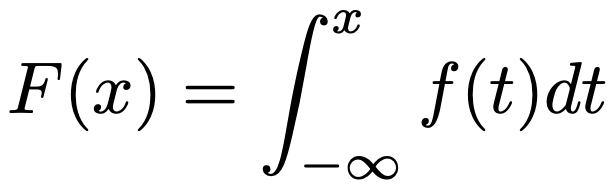
例えば，次の図は，第７回で学習する正規分布の確率密度関数のグラフです。

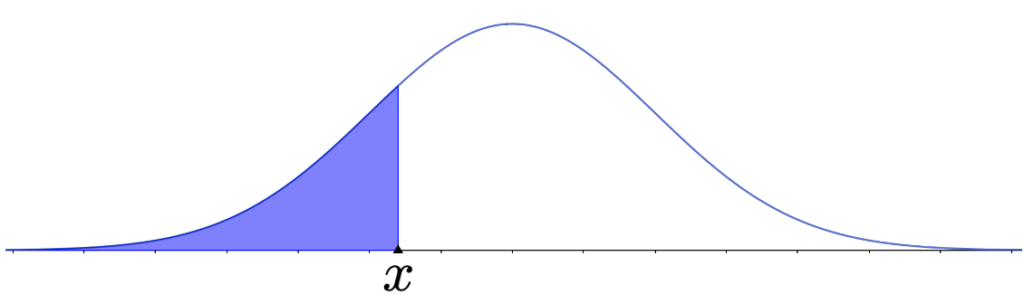
xという数以下の値をとる確率は，上の図の色のついた部分の面積になります。

また，ある連続型確率変数の累積分布関数が与えられると，その確率密度関数を求めることができます。累積分布関数は，確率密度関数を積分したものだったので，累積分布関数を微分すると，微分積分学の基本定理から，確率密度関数が得られます。

最後に，累積分布関数を使うと連続型確率変数の中央値が定義できることを紹介しておきましょう。累積分布関数をF(x)として，次の式を満たすcのことを，この確率分布の中央値と言います。

連続型確率変数の期待値，分散

連続型確率変数Xの確率密度関数をf(x)とするとき，Xの期待値は次の式で定義されます。

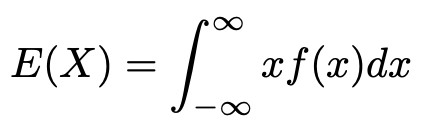
「また新しい公式を覚えるのか…」と思う人もいるかもしれませんが，第４回で紹介した離散型確率変数の期待値の公式を思い出してみましょう。次の式でしたね。

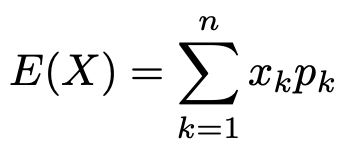
積分記号とシグマが対応し，f(x)dxが確率と対応しているので，式の構成は同じです。

第４回で学習した離散型の期待値について成り立つ公式は，連続型でも成り立ちます。まず，１つ目は次の式です。

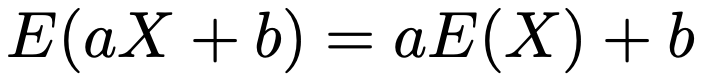
この式が成り立つことを理解するには，確率変数Xの関数g(X)の期待値についての次の式が必要になります。

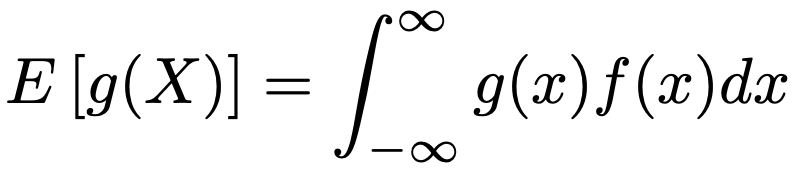
上の式の左辺を右辺のように定義するということです。この式を使うと，上の期待値の公式は，次のように示せます。

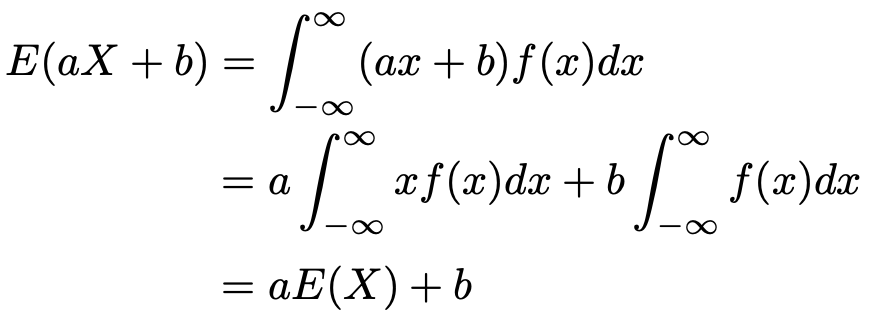
ただし，１行目から２行目の変形では，積分について次の式が成り立つことを使っています。

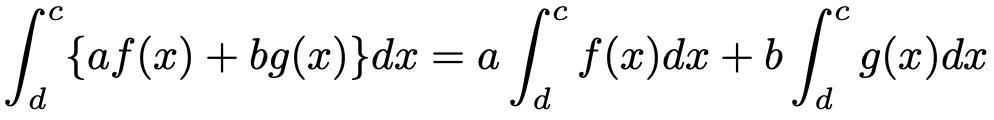
このインテグラルという記号は，「極限＋シグマ」でしたね。このような式変形ができるのは，シグマについて，次の変形ができるのとほとんど同じです。

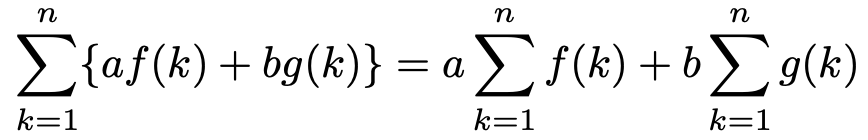
では，期待値の２つ目の公式に進みましょう。次の式です。

連続型のときのこの式の証明は重積分になってしまいますので，ここでは割愛します。なお，重積分を使った証明を知りたい人は，例えば，「データ解析のための数理統計入門（久保川達也著，共立出版）」を参照してください。

次に，分散です。連続型確率変数Xの確率密度関数をf(x)とするとき，Xの分散は次の式で定義されます。

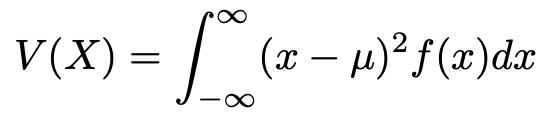
この式において，もちろん，μ＝E(X)です。期待値と同じように，離散型確率変数の分散と対応させて覚えるのが良いでしょう。次の式でしたね。

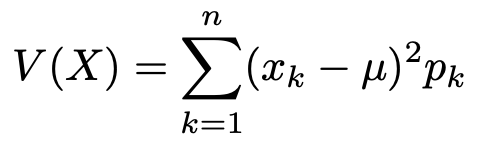
やはり，積分記号とシグマ，f(x)dxと確率がそれぞれ対応しているので，式の構成は同じです。

連続型確率変数の分散についても，離散型確率変数の分散について成り立った公式はそのまま成り立ちます。１つ目は次の式です。

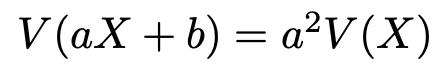
この式の証明は，第４回で紹介した離散型確率変数について成り立つ同じ形の公式と形式上同じように証明できるので，省略します。また，２つ目は次の式です。

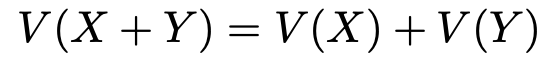
この式の証明は，期待値のときと同様に重積分になってしまいますので，ここでは割愛します。

さらに，期待値から分散を求める次の公式も成り立ちます。

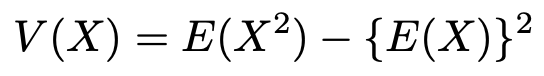
この式の証明も，第４回で紹介した離散型確率変数について成り立つ同じ形の公式と形式上同じように証明できるので，省略します。

次のセクションでは，実際にこれらの式を使って，連続型確率変数の期待値や分散を計算してみましょう。

連続型確率変数の総合問題

【問題】確率密度関数f(x)が次のような式で表される確率変数Xを考える。

ただし，aは定数であり，a＞0である。

（１）aの値を求めなさい。

（２）確率変数Xの期待値と分散を求めなさい。

【解答】

（１）a＝１の場合のf(x)のグラフをかくと，次の図のようになります。

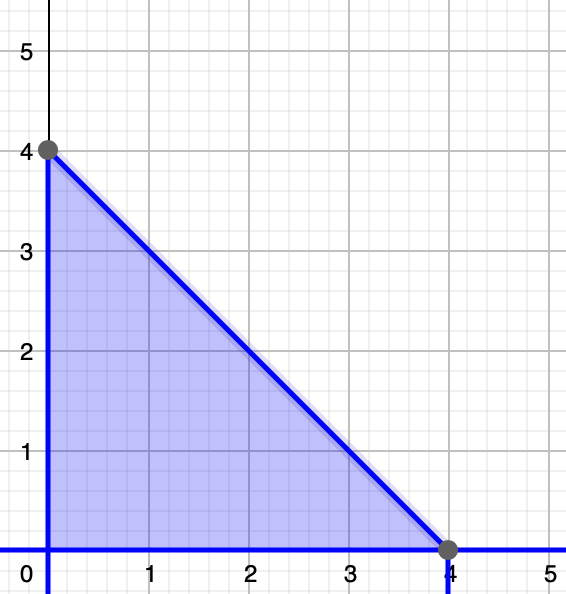
f(x)という関数は，０≦x≦４の範囲以外では０という値をとっているので，０≦x≦４に全確率が集まっていると言えます。上の図の三角形がその確率を表しているので，その面積が１になるように定数aの値を決めてあげればいいのです。

直線y＝ーax＋４aは，y軸との交点が（０，４a），x軸との交点が（４，０）だから，三角形の面積が１になるように式をたてると，次のようになります。

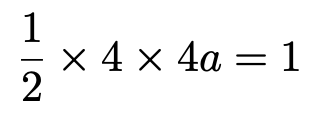
これを解いて，答えは次のようになります。

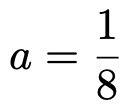
（２）（１）でaの値が８分の１だとわかったので，確率密度関数f(x)は次のようになります。

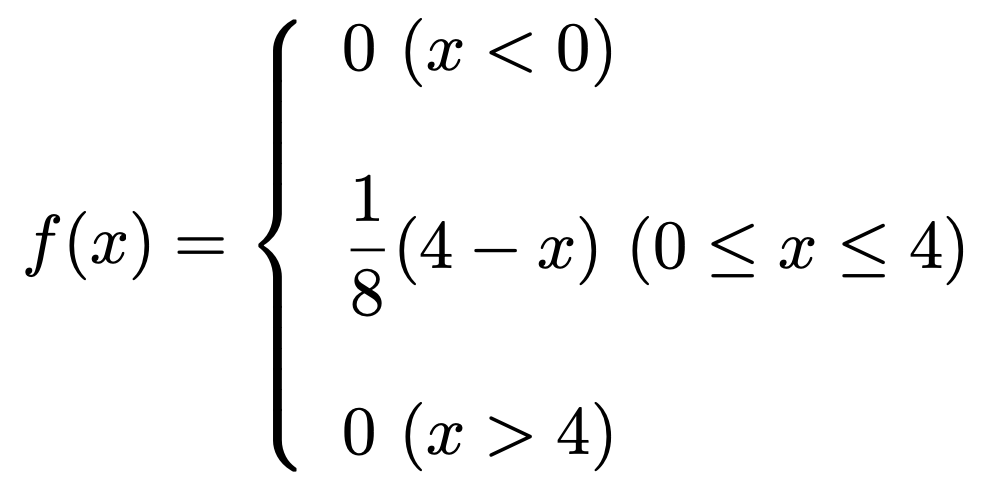
0を積分した値は０なので，期待値は０≦x≦４の積分だけを考えれば十分であることから，次のようになります。

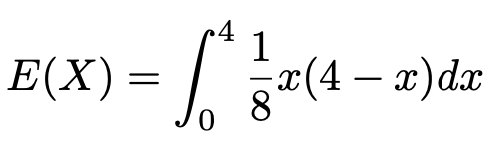
下の演習３で紹介している積分の公式を使うと計算量を減らすことができますが，ここでは，これまで説明してきたような正攻法で計算すると，次のようになります。

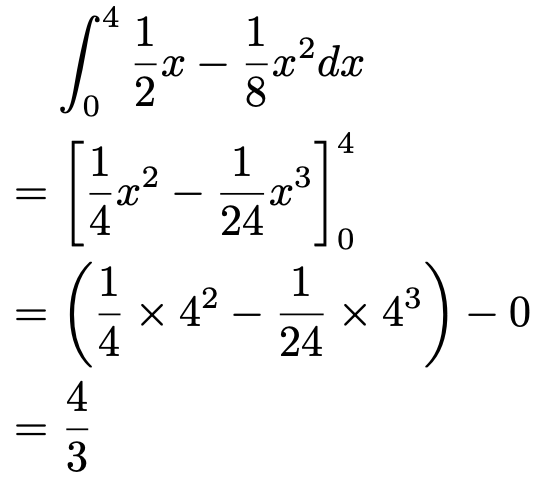
よって，期待値は３分の４です。次に分散を計算していきましょう。分散は，次の公式を使って計算します。

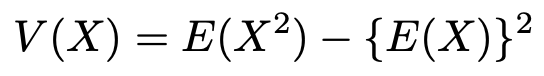
この式を使うには，Xの２乗の期待値を求める必要がありますね。次のようになります。

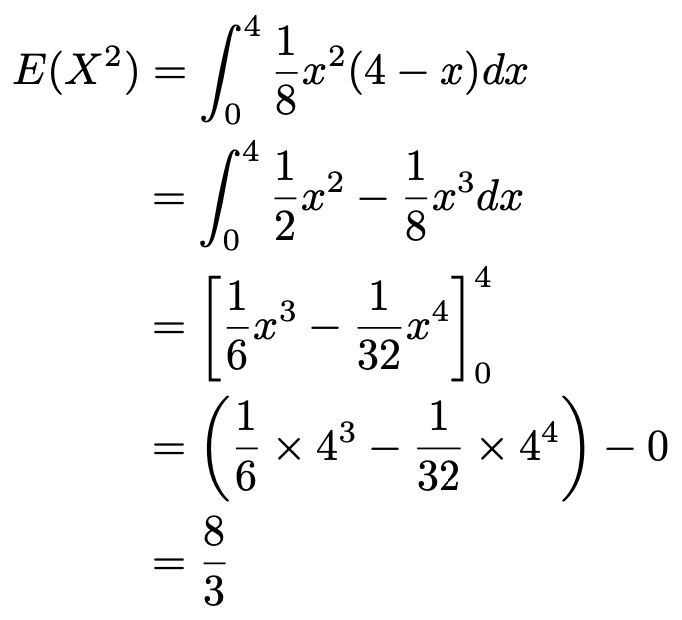
よって，分散は次のように求めることができます。

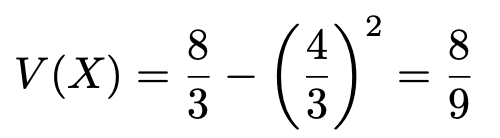
（解答終わり）

連続型確率変数についての基本的な説明は以上になります。ここからは，さらに理解を深めるための演習問題ですので，余力があればぜひチャレンジしてみてください。

演習１〜極限の計算〜

【問題】次の極限を求めなさい。

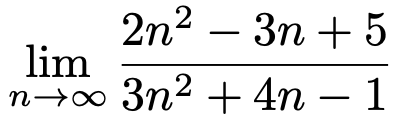
【解答】n＝10000など，大きな数をnに代入してみると，分母と分子の値はほとんど左端の２乗の項で決まるのがわかります。nが大きければ大きいほど，２乗の項の値がずばぬけて大きくなるからです。よって，分母のnの２乗の項と分子のnの２乗の項の係数の比に近づいていくので，次のようになります。

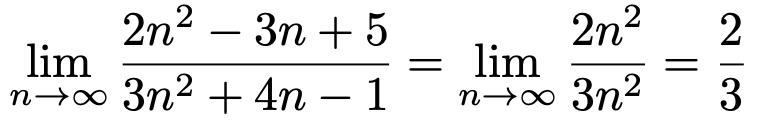
（解答終わり）

演習２〜３次関数のグラフの概形〜

【問題】次の関数のグラフの概形をかきなさい。

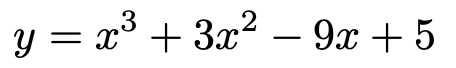
【解答】グラフの概形を知るには，微分を利用します。微分すると，関数の傾きがわかるんでしたね。傾きの符号の変化を追うと，グラフの大体の形が見えてきます。与えられた式を微分して因数分解すると，次のようになります。

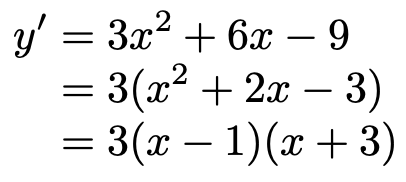
この式から，各点での傾きの値が求められますが，グラフの概形を知るには「y’」の符号がわかれば十分です。

まず，x＝１，ー３のとき，値が０になりますよね。傾きが０ということは，この２点での接線はx軸に平行になるわけです。

では，その前後ではどうでしょうか。

x＝ー４，０，２などを代入してみると，x座標の小さいほうから順に，「y’」の符号は正→負→正と変化しているのがわかります。傾きが正ということはグラフが右上がりだということ，負ということはグラフが右下がりだということです。x座標の小さいほうから，グラフはx＝ー３まで上がって，x＝１まで下がって，また上がる形だとわかりました。

また，この上昇，下降の分岐点（極値と言います）での座標が（１，０），（ー３，32）であることは，問題で与えられた式からわかります。

最後に，x座標をすごく大きくしたときにy座標もすごく大きくなり，x座標をすごく小さくしたときにy座標もすごく小さくなることも座標を代入してみればわかりますね。このときのy座標は，演習１で考えたのと同じように，ほぼxの３乗の値によって決まるわけです。このことを式で表すと，次のようになります。

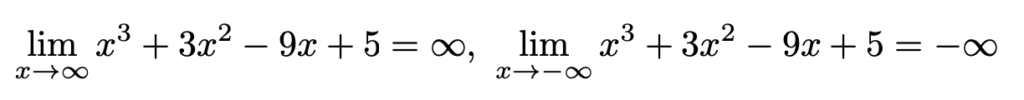
以上のことから，グラフの概形は次の図のようになります。

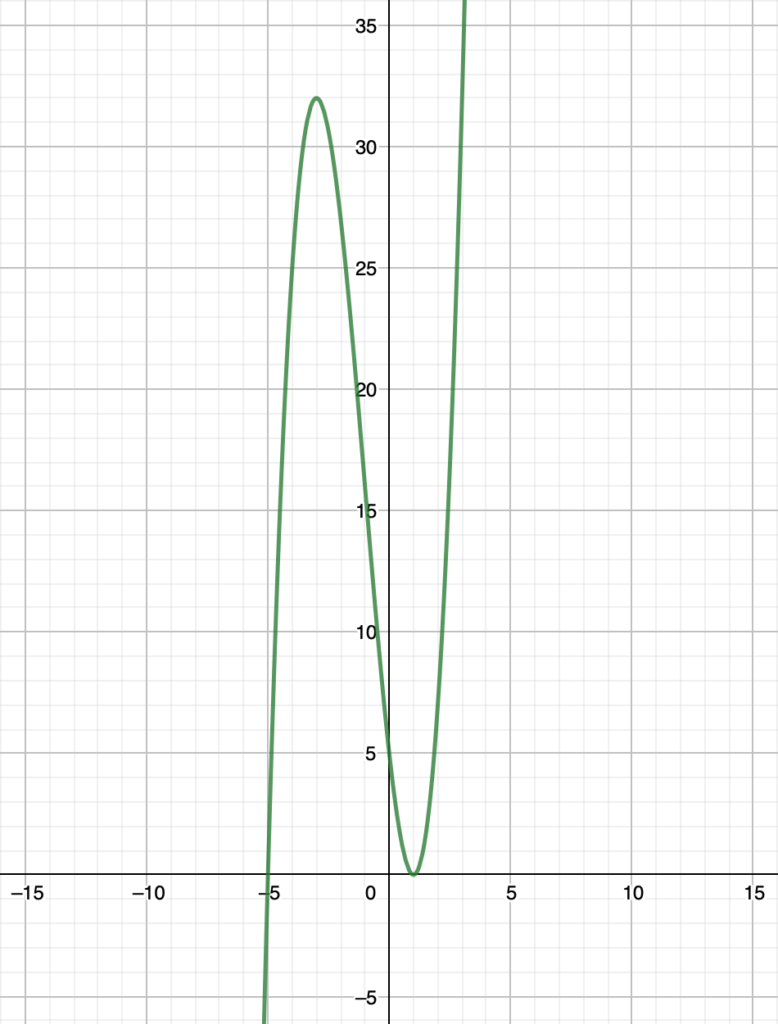
（解答終わり）

演習３〜グラフと軸で囲む図形の面積〜

【問題】次の関数のグラフとx軸で囲まれてできる図形の面積を求めなさい。

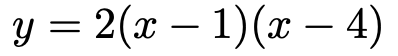
【解答】与えられた式は２次関数です。右辺を展開しても解けますが，ここでは新しい解き方を紹介するため，展開せずに解いてみます。

まず，この関数のグラフとx軸との交点の座標は，式を見てすぐにわかります。関数のグラフとx軸との交点を求めるには，y＝０を代入して，次の式の解を求めますよね。

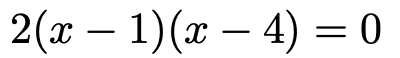
この解はx＝１，４で，問題で与えられた関数を見たときにここまではわかります。では，グラフをかいてみましょう。下に凸の（上に開いた）放物線で，x軸と（１，０），（４，０）で交わるから，次のようになりますね。

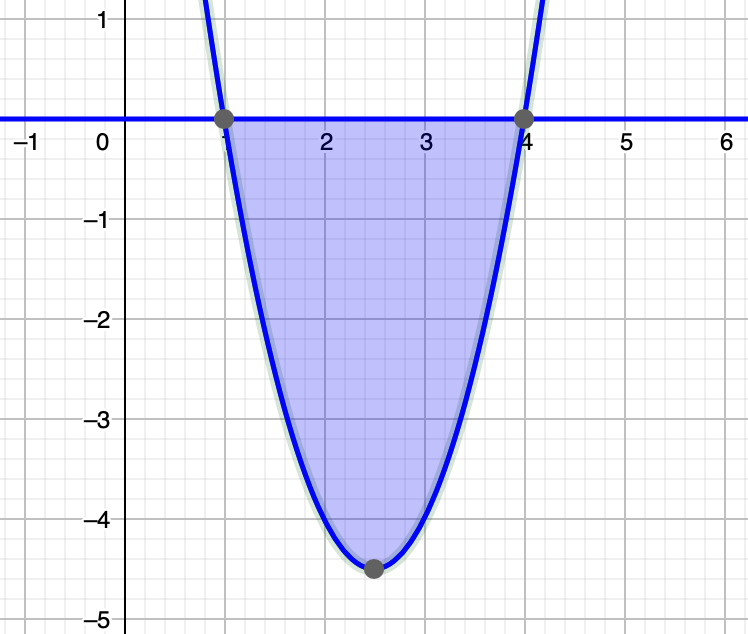
求めるのは色のついた部分の面積です。この領域を縦長の長方形で分割するイメージを持ってください。長方形の縦の長さはどう表せるでしょうか。この関数のy座標ではないですよ。１≦x≦４の範囲では，y座標は０以下なので，長方形の縦の長さは，ー（y座標）としてあげないといけませんね。そこで，面積を求める式は次のようになります。

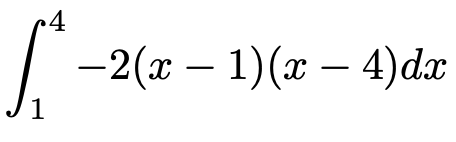
これまで説明した方法では，被積分関数（積分される関数）の式を展開してから積分の計算をする順番になりますが，ここでは展開せずに求める方法を解説します。もちろん，展開して求めてもOKです。ここでは，少しずるいですが，大学受験数学で俗に「６分の１公式」などと呼ばれる次の式を使います。話を簡単にするため，a＞0，β＞αだと考えてください。

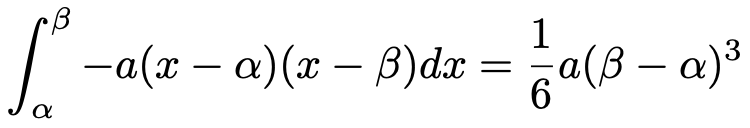
左辺と右辺をそれぞれ地道に計算すれば等しいことはわかるので，この式の証明は省略します。求めるべき積分の式と，この公式を比べると，次のように対応しているのがわかりますね。

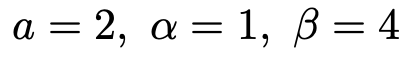
よって，求める面積は次のように計算できます。

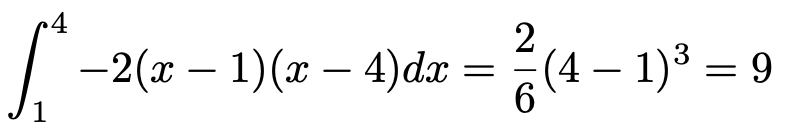
（解答終わり）

演習４〜連続一様分布の期待値と分散〜

【問題】a＜bとして，確率密度関数が次のように表される連続型確率変数Xが従う確率分布を連続一様分布と言う。

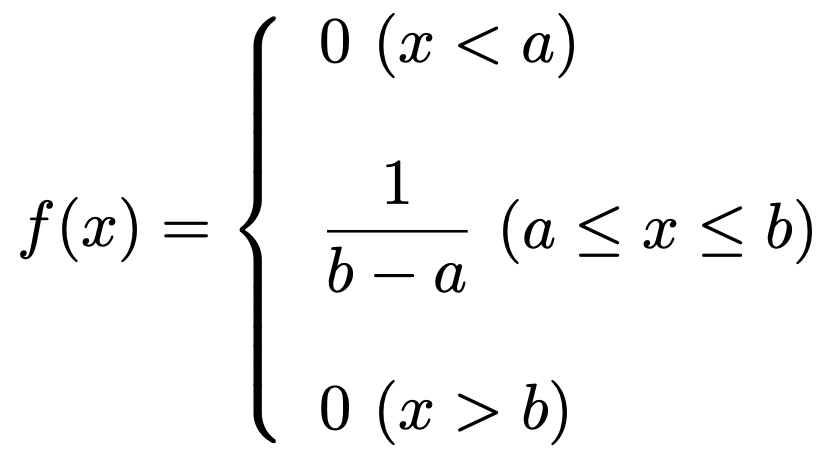
このとき，Xの期待値と分散を求めなさい。

【解答】この問題とは直接的には関係ありませんが，参考までに連続一様分布の確率密度関数y＝f(x)を図示すると次のようになります。

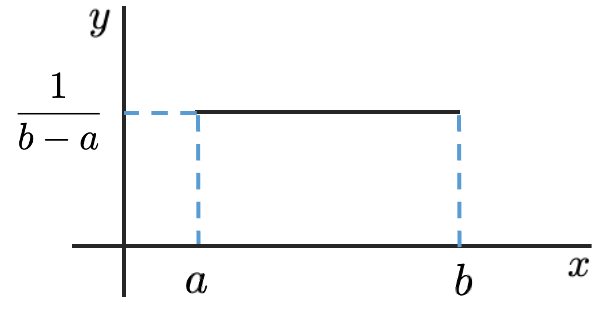
a≦x≦bの部分にできる長方形の面積が１になり，すべてのxについてf(x)≧０であることから，確率密度関数の条件を満たしていることがわかります。

では，期待値を計算します。期待値の定義式では，積分範囲がー∞から＋∞になっていますが，確率密度関数が０のときには積分の値は０なので，期待値の計算はa≦x≦bの部分だけを考えれば十分です。このことに注意すると，連続一様分布の期待値は次のように計算できます。

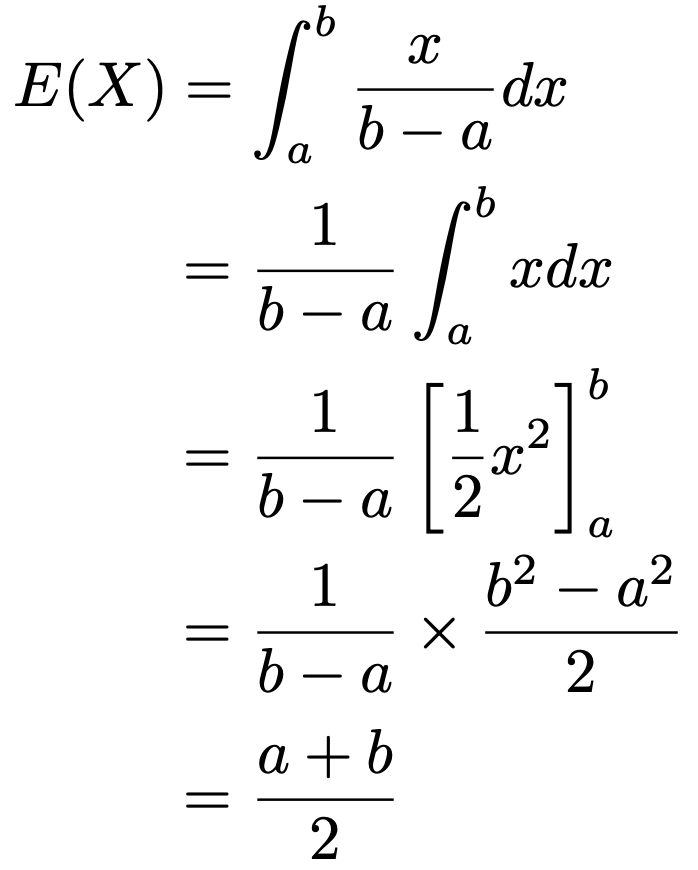
この値は，aとbの中点ですね。確率密度関数のグラフの対称性を考えると，こうなるのは自然ですよね。

次に分散を計算します。分散もa≦x≦bの部分だけを考えればいいので，分散の定義式に連続一様分布の確率密度関数と期待値をあてはめて計算すると次のようになります。

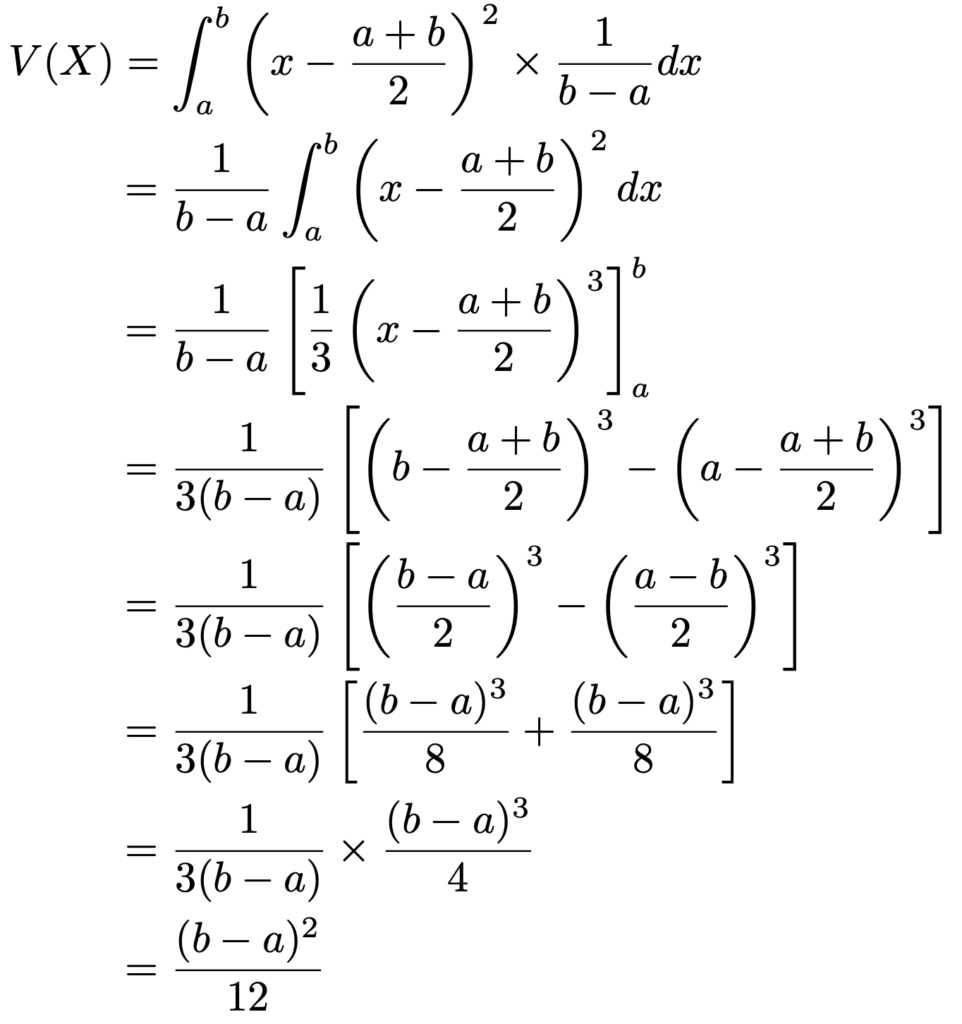
（解答終わり）

演習５〜連続型確率変数の文章題〜

【問題】ある携帯電話会社の料金プランについて，契約者１人当たりの１か月のデータ使用量（単位：GB）は連続型確率変数Xで表され，その確率密度関数f(x)は次の式で与えられるものとする。

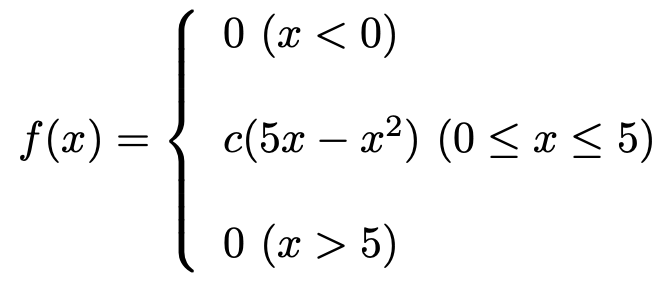
ただし，cは定数であり，c＞0である。一方，契約者１人当たりの１か月のデータの使用料金は，データ使用量が３GB未満では980円，３GB以上５GB以下では1480円であるとする。

（１）cの値を求めなさい。

（２）契約者１人当たりの１か月のデータ使用量の期待値を求めなさい。

（３）契約者１人当たりの１か月のデータの使用料金の期待値を求めなさい。

【解答】

（１）まず，考えやすいようにc＝１として，２次関数についての基本事項を確認しておきます。

最右辺の式を展開して整理すれば，上の式の変形が正しいことは確認できると思います。最右辺の式への変形のことを，２乗の形をつくるという意味で，平方完成と言います。最右辺の第１項は０以下なので，全体ではxの値が２分の５のときに最大で４分の25という値をとることがわかります。

また，次の２次方程式の解はx＝０，５ですね。

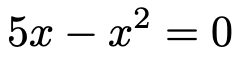
よって，この２次関数のグラフはx軸と２点（０，０），（５，０）で交わることがわかります。このグラフは上に凸（下に開いた）放物線だから，c＝１のときのグラフは次の図のようになることがわかります。

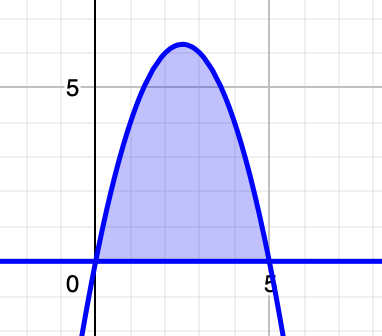
このグラフの頂点の座標は次のようになります。

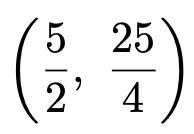
さて，本題に戻りましょう。f(x)という関数は，０≦x≦５の範囲以外では０という値をとっているので，０≦x≦５だけを考えればいいです。この範囲に全確率が集まっていますので，次の式で表されるような，グラフとx軸で囲まれた部分の面積が１になるように定数cの値を決めてあげればいいのです。

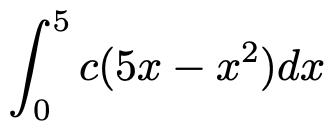
この積分を計算するために，まず，次の式のように，定数cを積分の外に出してしまいましょう。

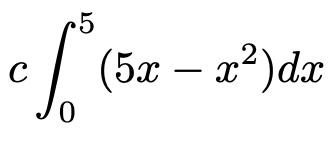
インテグラルはシグマの性質を受け継いでいるので，こういう変形ができるのでしたね。では，積分を計算していきましょう。普通に計算してもいいですが，演習３で紹介した「６分の１公式」を使ってみましょう。「６分の１公式」において，次の値を代入します。

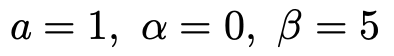
定数cを除いた積分を，この方法で計算すると，次のようになります。

この結果を使うと，０≦x≦５の範囲で面積が１になることから，cの値は次のように求められます。

（２）ここからは，（１）の結果を踏まえて，cを125分の６で置き換えて計算していきます。Xの期待値を求める一般式を思い出しておくと，次の式でしたね。

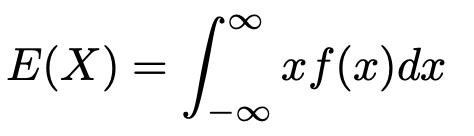
この問題では，０≦x≦５の範囲以外ではf(x)の値は０なので，積分範囲は０≦x≦５にしてしまっていいです。そして，この範囲での被積分関数は次のようになります。

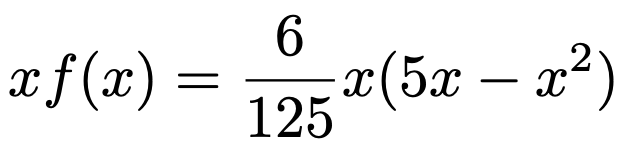
よって，Xの期待値は次のように求められます。

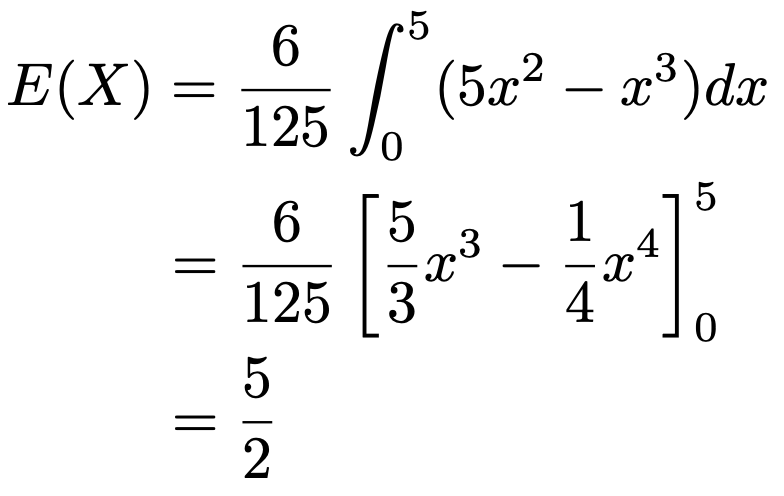
これで，データ使用量の期待値は２分の５GBだとわかりました。

ところで，確率密度関数である２次関数のグラフは，次の直線を対称の軸とする線対称な図形です。

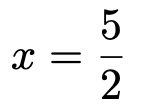
したがって，グラフの対称性から考えて，期待値が２分の５なのは当然だと言えます。

（３）１か月のデータの使用料金が980円（データ使用量が０GB以上３GB未満）となる確率，1480円（データ使用量が３GB以上５GB以下）となる確率はそれぞれ次のように求められます。

よって，データの使用料金の期待値は次のように計算できます。

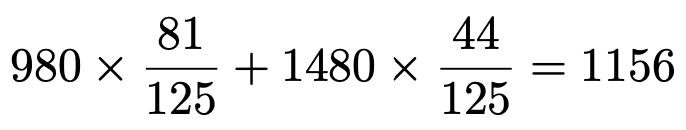
答えは1156円です。

（解答終わり）

第６回は以上となります。最後までお付き合いいただき，ありがとうございました！
引き続き，第７回以降の記事へ進んでいきましょう！

2023年1月に「統計検定２級公式問題集[CBT対応版]（実務教育出版）」が発売されました！（CBTが何かわからない人はこちら）
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが，本書は分野ごとにその形式の問題を並べた構成になっていて，最後に模擬テストがついています。CBT対策の新たな心強い味方ですね！

さらに実戦に向けた演習を積みたい人は，「統計検定２級公式問題集2018〜2021年（実務教育出版）」を手に取ってみてください！

また，もっと別の問題を解いてみたい人は，さらにさかのぼって「統計検定２級公式問題集2016〜2017年（実務教育出版）」を解いて実力に磨きをかけましょう！