「確率の和と積の使い分け方がわからない」「確率の問題はいつも何となく解いているだけ」なんて思っている人はいませんか。しっかり理解すれば,確率の問題にも自信を持って答えを出せるようになります。その鍵になるのが次の3つです。
- 同様に確からしいとは何か
- 互いに排反な事象と確率の和
- 独立な事象と確率の積
統計検定2級で出題される確率の問題を解くためには,高校1年生までの数学で学習する内容の理解が必要になります。この1つの記事だけで,確率の計算方法を網羅的に解説しますので,統計検定2級を受検する人のみならず,大学入試の確率の問題がスラスラ解けるようになりたい人にとっても有益であるはずです。ただし,「条件付き確率とベイズの定理」と組合せは別の記事を用意していますので,そちらをご覧ください。記事を読み終わる頃には,確率の和と積を使いこなせるようになっているはずです。それでは,確率・統計の旅のはじまり,はじまり〜。
事象と試行,排反
まずはじめに,言葉を3つだけ覚えてください。確率の話をするための基本的な語彙(確率用語)です。
試行とは,例えば,サイコロを投げることのように,確率を計算する対象となる実験のことです。また,事象とは,例えば,1の目が出ることのように,試行の結果,確率的に起こる事柄のことです。つまり,試行をすると,事象が起きるわけです。3つ目として,排反という言葉を覚えましょう。「互いに排反の関係である」というのは,一方の事象が起これば,他方の事象は起こらないという関係のことです。例えば,サイコロを1回投げるとき,1の目が出れば,2の目は出ませんよね。このとき,1の目が出る事象と2の目が出る事象は互いに排反の関係になります。
確率とは
この講座では,確率とは次のような性質を持つものであると考えることにします。
- 事象の起こりやすさを0以上1以下の数で表したもの
- 全く起こらない事象の確率は0,必ず起こる事象の確率は1
- 事象AとBが互いに排反であるとき,AまたはBが起こる確率は,Aが起こる確率とBが起こる確率の和に等しい
- 同様に確からしい事象の確率は等しいものとする
一読しただけでは少し意味がわかりにくいかもしれません。この後の説明を読み終わった後に理解できていれば十分です。ちなみに,確率は英語でProbabilityですから,確率を表すために「P」という記号をよく用います。では,はじめにポイントとして挙げたものの1つである「同様に確からしいとは何か」を次に説明します。
同様に確からしいとは何か
次のような問題を考えてみましょう。
【問題】サイコロを1回投げるとき,1の目が出る確率を求めなさい。
おそらく,即答できる方が多いと思いますが,ちょっと待ってください。なぜ,その答えになるか,「同様に確からしい」という言葉を使って,説明してみます。
【解答】1の目が出る確率,2の目が出る確率,…を,次のように目の数をPの右下につける形(添字)で表すことにします。

このとき,1の目のほうが2の目より出やすいのであれば,
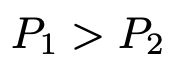
となるわけですが,直感的にそうは思えないですよね。どの目も同じ確率で出ると思えるので,
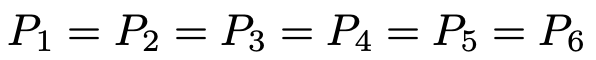
が成り立つといえます。このことを同様に確からしいというわけです。「確からしさ=確率」が同じくらいという意味ですね。この式を使うと,確率を数として求めることができます。確率の性質の2と3によって,
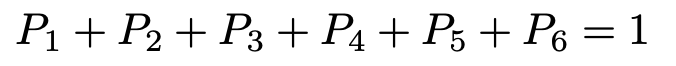
が成り立ちます。つまり,1から6の目が出る事象は同時には起きない(互いに排反である)し,必ずこのうちのどれかは起きるから,これらの確率の和は1になる,ということです。よって,

とおいて代入すると,

このように,答えが求められるわけです。(解答終わり)
同様に確からしいという仮定が効いて,答えが求められていることがポイントです。
確率と樹形図
次の問題は,中学2年生の内容です。
【問題】5本のうち2本があたりのくじがある。2本同時にくじをひくとき,2本ともあたりくじである確率を求めなさい。
【解答】2本のあたりくじには「あ」の右下に1,2の添字をつけ,3本のはずれくじには「は」の右下に1,2,3の添字をつけて樹形図をかくと,次のようになります。
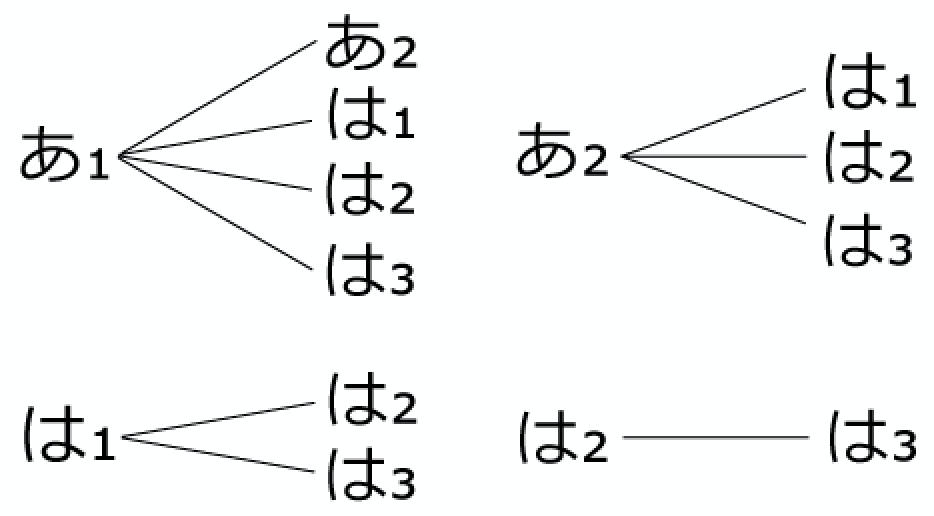
全部で10本の枝を,4つのブロックに分けてかいてあります。この中で,2本ともあたりであるのは,左上の枝の1つだけです。同様に確からしい事象が全部で10通りあり,そのうちの1通りだけが条件を満たすので,答えは10分の1です。(解答終わり)
この問題を通して理解していただきたい大事なことは,次の2つです。
- 確率の問題を解くときの基本姿勢は,図や表にしてもれなく数え上げること
- 同じ「あたりくじ」,同じ「はずれくじ」でも,もじや数字等をつけて区別して数えること
繰り返しますが,「同じものにも別の名前をつけて数える」ことは,確率において超重要です。
事象の独立と確率の積
確率の積の法則などと呼ばれたりもしますが,ここでのポイントは次の内容になります。
事象AとBが独立であるとき,Aが起きて,さらにBが起こる確率は,(Aが起きる確率)×(Bが起きる確率)で求められる。
ここで,今回4つ目の確率用語である独立が登場しました。この言葉は,【中学の数学からはじめる統計検定2級講座第2回】の記事で改めて説明しますが,ここでは次のようなものとして考えましょう。コインを2回投げるとき,1回目の表裏の結果は2回目の表裏の結果に何ら影響を与えませんよね。このような関係が独立です。つまり,一方の事象が他方の事象に全く影響を与えない,という意味です。では,このことを踏まえて,次の問題を考えてみましょう。
【問題】ある陸上選手が,競技Aで勝つ確率,競技Bで勝つ確率はそれぞれ,

である。この選手がAとBの両方の競技で勝つ確率を求めなさい。ただし,2つの競技の勝敗は独立であるものとする。
【解答】この陸上選手が勝つ場合を「○」,負ける場合を「×」で表して樹形図をかくと,次のようになります。
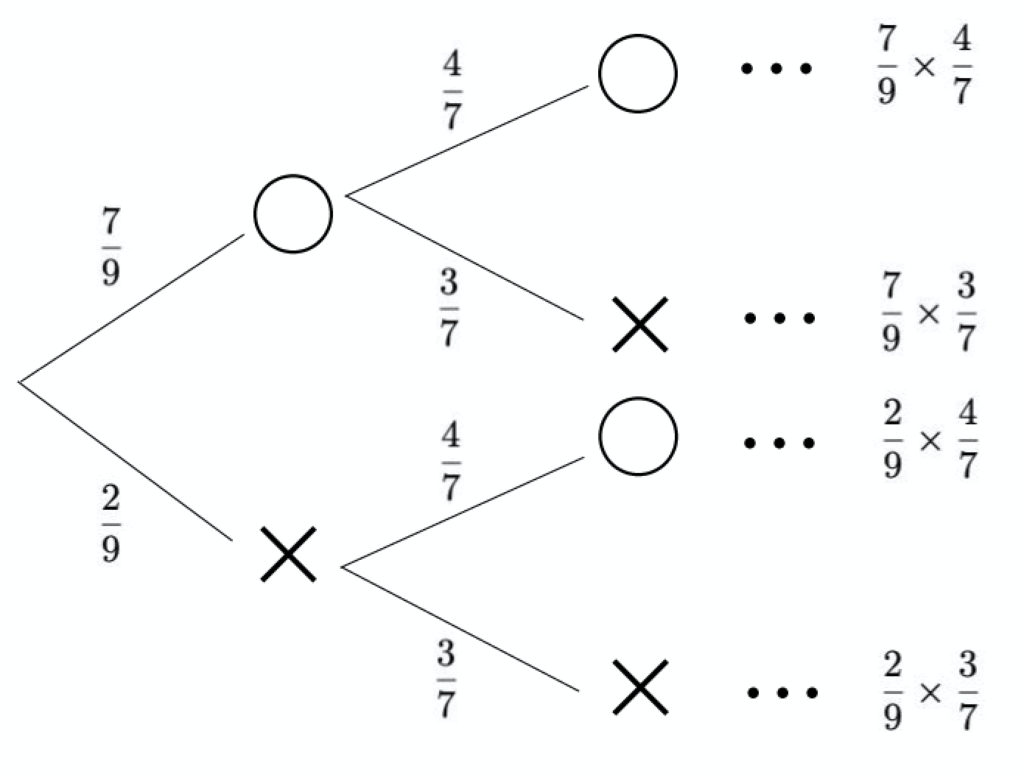
全部で4本の枝があります。それぞれ,左側が競技Aの結果,右側が競技Bの結果です。AとBの両方の競技で勝つ場合というのは,いちばん上の枝になります。2つの競技の勝敗は独立ですから,競技Aで勝つ確率×競技Bで勝つ確率として計算すると,求める確率は,
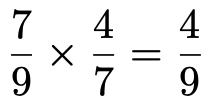
となります。(解答終わり)
総合問題
ここまでで理解したことを使うと,大学入試でたびたび出題されている次のような問題を解くことができます。
【問題】nを2以上の自然数とする。サイコロをn回投げるとき,出た目の最大値と最小値の差が1となる確率を求めなさい。
【解答】出た目の最大値と最小値の差が1となる場合を具体的に考えましょう。
例えば,n回とも1か2の目しか出ないとき,最大値が2,最小値が1ですから,その差は1になっています。条件に合う場合は他にもありますので,記号を使って表してみましょう。(最小値,最大値)の形で表すと,(1,2),(2,3),(3,4),(4,5),(5,6)の5通りがあります。どの場合でも,同じように確率を求められるので,(1,2)の場合を考えることにします。
最大値が2,最小値が1となるn回の目の出方は,次のようになります。

1回目も,2回目も,…,n回目も,6つの目のうち,1または2のいずれかが出れば良いので,確率はそれぞれ3分の1ですね。各回は独立ですから,n回とも,1または2の目しか出ない確率は,かけ算によって,
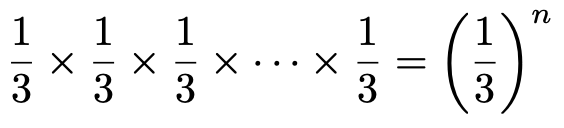
と求められます。でも,ここで気をつけなければならない点があります。上の表では,各回とも「1または2」となっていますが,「n回とも1」や「n回とも2」の場合も含まれています。「n回とも1」だと,最大値が1,最小値も1となって,条件に合いませんね。1も2も1回以上出てもらわないと困るわけです。そこで,n回とも1が出る確率を求めてみましょう。先ほどと同じように考えて,
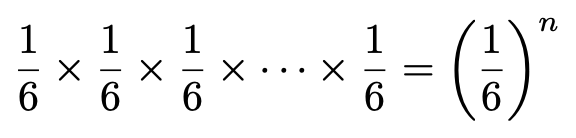
と求められます。また,n回とも2が出る確率も全く同じですよね。さて,ここで,確率の和についての性質3を思い出してください。「n回とも1または2が出る事象」は「n回とも1が出る事象」と「n回とも2が出る事象」と「n回とも1または2が出て,1も2も1回以上出る事象」という互いに排反な3つの事象に分けることができるので,「n回とも1または2が出る確率=n回とも1が出る確率+n回とも2が出る確率+n回とも1または2が出て,1も2も1回以上出る確率」という式が成り立ちます。つまり,n回とも1または2が出て,1も2も1回以上出る確率は,次のように求められます。
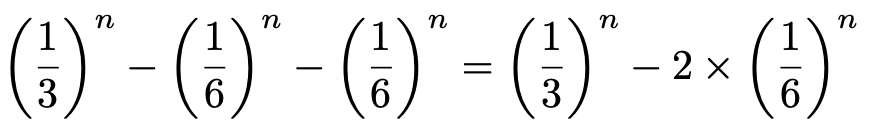
できました! これが(1,2)となる確率です! 出た目の最大値と最小値の差が1となる事象は,(1,2),(2,3),(3,4),(4,5),(5,6)の5つの互いに排反な事象に分けることができるのでした。そして,(2,3),(3,4),(4,5),(5,6)となる確率も全く同じなので,確率の和についての性質3を使うと,出た目の最大値と最小値の差が1となる確率は,(1,2)の確率+(2,3)の確率+(3,4)の確率+(4,5)の確率+(5,6)の確率によって,先ほど求めた確率の5倍となり,次のようになります。

(解答終わり)
ここまで,確率の計算について,統計検定2級を目指す上で必須の内容を解説しました。この後は,参考図書の紹介に続けて,さらに理解を深めるための演習問題ですので,余力があればぜひチャレンジしてみてください。
参考図書
本稿を執筆するにあたり,次の書籍を参考にしました。
ハッとめざめる確率(安田享著,東京出版)
確率が苦手な人は,高校数学の確率を扱った書籍を1冊だけでも読んで,確率の基礎をガッチリ固めるのが良いでしょう。この本はおすすめの1冊で,基礎から解説しつつも,「同様に確からしい」とは何なのかという本質を語りかけてくれます。
演習1〜同様に確からしいの極意〜
【問題】1〜5の5つの自然数が1つずつ書かれた5枚のカードがある。この中から1枚ずつ3枚のカードを選び,順に左から並べて3桁の整数をつくるとき,できた整数が3の倍数である確率を求めなさい。
【解答】整数は,各位の数字の和が3の倍数であるときに限り,3の倍数になります。例えば,123という数の各位の数字を加えると,1+2+3=6となって3の倍数なので,123は3の倍数です。
さて,確率の問題を解くときには,まずはじめに全体像を把握します。つまり,事象が全部でいくつあるのかを数えます。数え方の基本は,樹形図でしたね。次の図のようになります。

5つの数から,3つの数の組をつくると,全部で10通りあるわけです。この10通りの事象の起こりやすさはどうでしょうか。(1,2,3)の組や(2,3,5)の組が特に起こりやすいなんてことはありますか? ないですよね。10通りは同様に確からしいと考えられます。その中で和が3の倍数になっているものは,●印をつけた4通りなので,答えは,
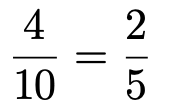
となります。(解答終わり)
あれ?「同じ1,2,3の組でも,231や312など複数の整数ができるので,数の並べ方を考える必要があるんじゃないか」って思いますか? 結論からいうと,並べる必要はありません。なぜなら,3つの数の組を決めた時点で,並べ方に関係なく3の倍数かどうかは確定しているので,この問題で本質的に問われているのは数の組の選び方だからです。とはいえ,解き方は人に押し付けられるものではなく,自分で納得できるものが良いと思いますので,数の並べ方まで考慮した別解も示しておきます。
【別解】1枚目に取り出す数の決め方は5通り,2枚目に取り出す数の決め方は,1枚目に取り出した数を除く4通り,3枚目に取り出す数の決め方は,1,2枚目に取り出した数を除く3通りであるから,できる3桁の整数は全部で,5×4×3=60(通り)です。もし,この式がかけ算になることがわからなければ,面倒臭がらずに樹形図をかいてみてください。かいてみればわかると思います。慣れてくれば,樹形図をかかずにかけ算で計算したほうが早いと感じるようになるでしょう。
このうち,3の倍数であるような3つの数の組は,上の樹形図のように4通りあります。例えば,(1,2,3)の組であれば,123,132,213,231,312,321の6通りの3桁の整数がつくれます。他の数の組も同じように6通りずつの3桁の数ができるから,条件に合う3桁の整数は,4×6=24(通り)となります。よって,求める確率は,
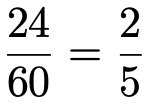
となり,はじめに求めた答えと一致します。(解答終わり)
このように,考え方によって,すべての事象(全事象といいます)の数は変わるので,確率の求め方は1つとは限りません。
演習2〜和事象と余事象〜
【問題】WAKARUの6つのアルファベットが1つずつ書かれた6枚のカードを並べかえるとき,「WA」という文字列(WとAが隣り合ってこの順に並ぶ)と「KA」という文字列(KとAが隣り合ってこの順に並ぶ)をどちらも含まない確率を求めなさい。
【解答】前問と同じように,まず全体像を把握しましょう。6つのアルファベットの中には,Aが2つ含まれています。この2つを同じものと考えて数える方法もありますが,ここでは別々のものとして区別して考えることにします。どちらでも同じ答えを出せますが,区別するほうが基準が明確でわかりやすいと思います。次のような6つの文字だと考えましょう。
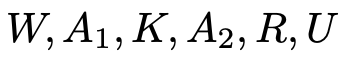
6枚のカードを左端から順に決めていきます。いちばん左端に現れる文字は何通りの可能性があるでしょうか。どの文字の可能性もあるので,6通りですよね。左端の文字を1つ決めた後,左から2番目に現れる文字を決めます。何通りの可能性があるでしょうか。左端のカードで使った文字以外の5通りがありえますね。同じように数えていくと,左から3番目以降は,4通り,3通り,2通りとなって,右端は残った1通りに決まります。つまり,6枚のカードの並べ方の総数は次の通りです。
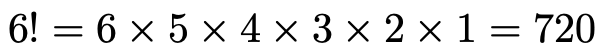
6!という記号は「6の階乗」と読みます。1から6までのすべての自然数の積を表す記号です。一般的に表現すれば,異なるn個のものを一列に並べるとき,その並べ方の総数は,次のようになります。
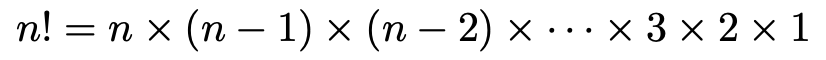
便利な記号なので,知らない人はこの機会に覚えてしまいましょう。
さて,本題に戻ります。「WA」という文字列と「KA」という文字列をどちらも含まない場合が何通りあるかを求めるんでしたね。この条件に合うカードの並べ方を考えてみると,例えば,

など,いろいろ考えられそうです。でも,このまま考えてみても,つかみどころがないと思いませんか? むしろ,「WA」という文字列と「KA」という文字列を含む確率のほうが求めやすそうです。この状況をベン図で整理してみると,次のようになります。
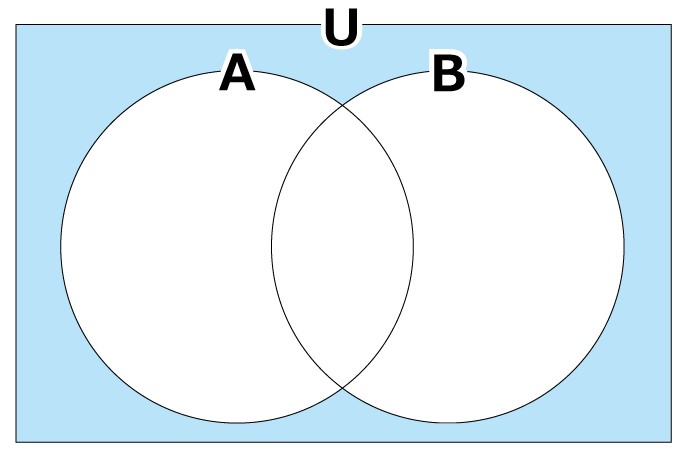
ここで,U,A,Bとは次のような事象を表しています。
- U:全事象
- A:「WA」という文字列を含む事象
- B:「KA」という文字列を含む事象
2つの円を合わせてできる図形全体は,『「WA」という文字列と「KA」という文字列の少なくとも一方を含む事象』を表しています。このAとBを合わせてできる事象を,AとBの和事象といいます。この問題で問われているのは,AとBの和事象の外側の色のついた部分の確率です。この色のついた部分の確率が直接的には求めにくそうなので,全体の確率の1からAとBの和事象の確率をひいて求めようというのが方針です。ちなみに,一般的に,A以外の事象全体のことをAの余事象(補事象)といいますので,問題で問われている事象の余事象であるAとBの和事象の確率を求めようということです。
さて,AとBの和事象の確率を考えます。2つの事象AとBが互いに排反であれば,この2つの確率をたして終わりなのですが,互いに排反ではないですよね。A とBは同時に起こることがあります。例えば,問題に登場している「WAKARU」という順に並んだ場合がそうです。「WA」という文字列と「KA」という文字列を同時に含む並び方があるわけです。こういう場合にどうするか,についての一般的な方法を説明します。まず,2つの事象AとBが同時に起こるという事象を,AとBの積事象といいます。そして,和事象と積事象の確率について,次の式が成り立ちます。
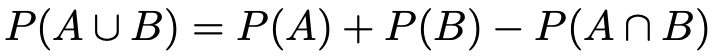
この式において,P(A),P(B)は,それぞれ「事象Aが起こる確率」,「事象Bが起こる確率」を表していますが,あと2つ,見覚えのない記号がありますね。
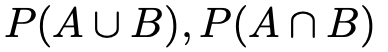
これらは,左から順に,「事象AとBの和事象が起こる確率」,「事象AとBの積事象が起こる確率」を表しています。さて,みなさんの中には,和事象の確率と積事象の確率を結びつける上の式を知っている人もいるでしょう。また,もし知らなくても,この式が成り立つことは,直感的に理解できるかもしれません。AとBを重ね合わせて和事象を求めようとするときに,ダブルカウントになる積事象の部分をひきましょう,ということです。厳密には,この式は確率の性質3から導かれます。上のベン図内の円で分けられてできる4つの領域に対応する事象が互いに排反であることから示すことができます。ここでは,これ以上の脱線を避けるため,説明は割愛します。
さて,事象Aが起こる確率を求めましょう。6枚のカードを並べたときに,「WA」という文字列が含まれる確率です。これには,典型的な解き方が存在します。WとAを1つのカードとみなして固定し,5枚のカードを並べると考えてしまうのです。いま,Aが2種類あると考えているので,この5枚のカードとして次の2組を考えます。

それぞれ5!通りの並べ方があります。この2種類は互いに排反でしょうか。Wの右隣りにくるAは1種類しか選べませんので,これらは互いに排反ですね。だから,事象Aは,これらの並べ方を合わせて,2×5!通りあります。また,事象Bについても,いまの話のWをKにおきかえるだけなので,全く同じように考えて,事象Bが起こる確率は,2×5!通りあります。では,次にAとBの積事象の確率を求めます。6枚のカードを並べたときに,「WA」という文字列と「KA」という文字列がどちらも含まれる確率です。やはり,隣り合う2枚のカードを1枚とみなして,4枚のカードの並べ方として考えます。次の2種類のパターンがあります。
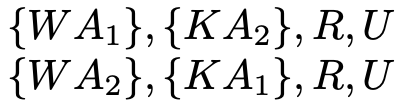
いずれの並べ方も4!通りで,互いに排反なので,合わせて2×4!通りあります。これで,準備が整いました! 事象AとBの和事象の確率は,次のように求められます。
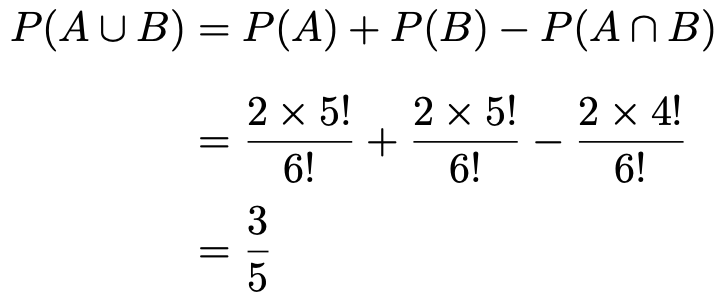
問題で問われている確率は,全体の確率の1からこの確率をひけばいいので,
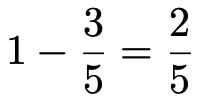
となります。(解答終わり)
演習3〜日本シリーズ型の勝敗〜
【問題】AチームとBチームはどちらかが先に4勝するまで試合を行い,4勝したチームを優勝とする。過去の対戦成績から,1試合でAチームがBチームに勝つ確率は60%であることがわかっている。このとき,4勝1敗でAチームが優勝する確率を求めなさい。ただし,各試合の勝敗は独立であるものとし,引き分けはないものとする。
【解答】4勝1敗でAチームが優勝するのは,どういう場合があるかを具体的に考えましょう。各試合で,Aチームの勝ちを○,Bチームの勝ちを×として表すと,次のようになります。
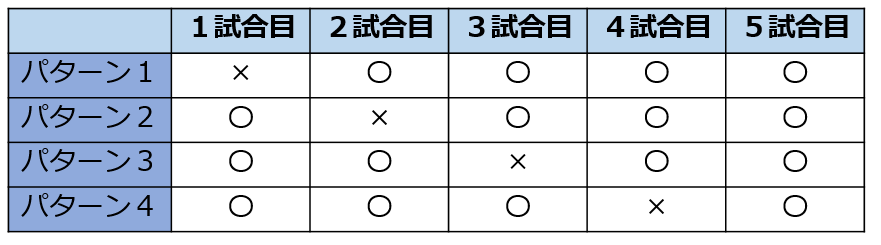
つまり,1試合目〜4試合目のうち,1試合だけAチームが負けて,5試合目にAチームが勝てば良いですね。では,表のパターン1の,Aチームが1試合目だけに負けて,2試合目〜5試合目に4連勝する場合を考えてみましょう。1試合目に負ける確率は40%(=5分の2)で,2試合目に勝つ確率は60%(=5分の3),3試合目に勝つ確率も60%,4試合目に勝つ確率も60%,5試合目に勝つ確率も60%です。各試合の勝敗は独立なので,この1〜5試合目の結果がすべて起きる確率は,それぞれの確率の積で求められるのでしたね。つまり,次のような式になります。
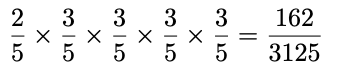
また,Aチームが2試合目だけに負けて,1試合目と3〜5試合目に勝つ確率は次のようになります。
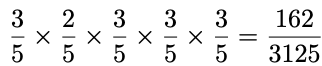
先ほどの確率と比べると,かけ算の順序が違うだけで,積は同じです。つまり,上の表のパターン1〜4の確率はすべて同じで,互いに排反ですから,求める確率はパターン1の確率の4倍になります。よって,

となります。(解答終わり)
演習4〜袋と箱〜
【問題】1,2,3,4の数字が1つずつ書かれた4枚のカードが入っている箱Aと,5,6,7,8の数字が1つずつ書かれた4枚のカードが入っている箱Bと,赤玉3個と白玉2個が入った袋が1つある。はじめに,袋から玉を1個取り出し,赤玉なら箱Aから,白玉なら箱Bからカードを1枚取り出す。玉とカードをもとに戻した後,同じ操作をもう一度行い,取り出したカードに書かれた数を順に左から並べて2桁の整数をつくる。このとき,できる整数が3の倍数である確率を求めなさい。
【解答】まず,問題文を理解していきましょう。つくるものは,2桁の整数です。十の位になりうる数は何通りあるでしょうか? 1〜8の8通りです。一の位も同じです。ということは,できる2けたの整数は全部で,8×8=64(通り)あるわけです。この64通りが同様に確からしいかというと,残念ながら同様に確からしくはないんです。袋から玉を取り出すとき,赤玉のほうが白玉よりも袋から取り出される確率が高いことによって,箱Aのほうがカードが取り出されやすくなります。この点を踏まえて整理していきましょう。

このような4つのパターンに大きく分けることができます。さらに具体的に考えましょう。①の16通りの中で,3の倍数は何通りあるでしょうか。12,21,24,33,42の5通りありますね。では,12になる確率はどれくらいでしょうか。12になるには,赤玉→1のカード→赤玉→2のカードの順に取り出せばいいですね。赤玉を取り出す確率が5分の3で,1のカードを取り出す確率はさらにその4分の1なので,図に表すと次のようになります。
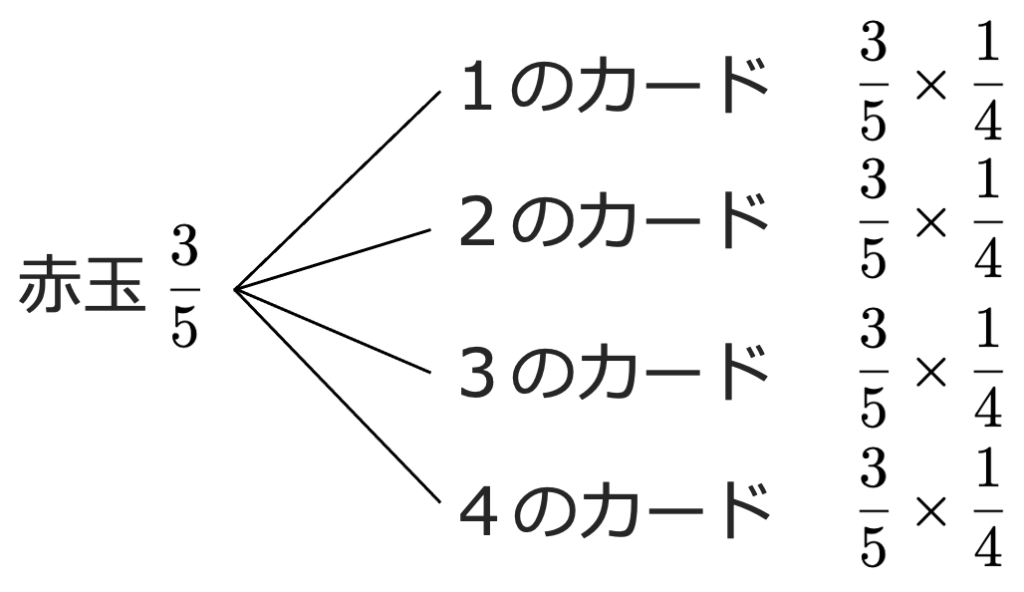
後半の「赤玉→2のカード」となる確率も同じなので,12になる確率は,
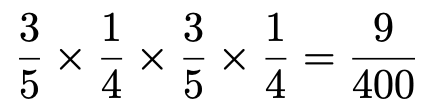
他の21,24,33,42の場合も同じように計算できるので,①の場合の確率は,この確率を5倍して,

となります。約分は最後にやれば良いです。次に②の場合を考えましょう。②の16通りの中で3の倍数は,15,18,27,36,45,48の6通りありますね。では,15になる確率はどれくらいでしょうか。赤玉→1のカード→白玉→5のカードの順に取り出せばいいので,
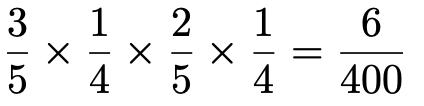
他の18,27,36,45,48の場合も同じように計算できるので,②の場合の確率は,この確率を6倍して,
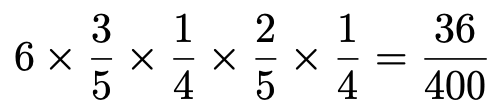
①,②の場合と同じように,③,④の場合も計算していきます。③の16通りの中で,3の倍数は,51,54,63,72,81,84の6通りあるので,③の場合の確率は,
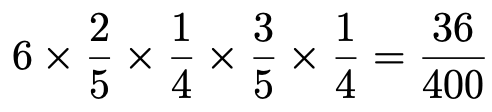
となります。さらに,④の16通りの中で,3の倍数は,57,66,75,78,87の5通りあるので,④の場合の確率は,
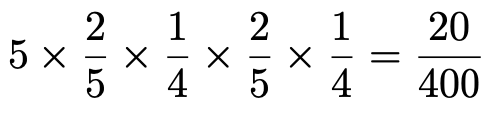
となります。①〜④は互いに排反なので,求める確率は,確率の和を使って,
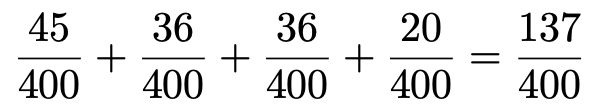
やりました! これが最後の問題の答えです! 結局,最後に約分はできませんでした。途中で約分すると,最後に通分という無駄な作業が発生するので,そこを見越して途中の約分はしないようにしましょう。(解答終わり)
ということで,第1回は以上となります。最後までお付き合いいただき,ありがとうございました!
引き続き,第2回以降の記事へ進んでいきましょう!
2023年1月に「統計検定2級公式問題集[CBT対応版](実務教育出版)」が発売されました!(CBTが何かわからない人はこちら)
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが,本書は分野ごとにその形式の問題を並べた構成になっていて,最後に模擬テストがついています。CBT対策の新たな心強い味方ですね!
さらに実戦に向けた演習を積みたい人は,「統計検定2級公式問題集2018〜2021年(実務教育出版)」を手に取ってみてください!
また,もっと別の問題を解いてみたい人は,さらにさかのぼって「統計検定2級公式問題集2016〜2017年(実務教育出版)」を解いて実力に磨きをかけましょう!



![統計検定2級公式問題集[CBT対応版]](https://m.media-amazon.com/images/I/51q3GfZId3L._SL500_.jpg)



コメント