「線形代数がわからなくてワークブックが読めない…」と感じているのはあなただけではありません。ベクトルや行列は統計検定2級では必要なかったので,大学で線形代数の勉強をしたことのない人にとっては準1級の勉強をするにあたっての障害になりやすいです。そこで,本稿では,中学までの数学と私の統計検定2級講座の内容を理解している人を想定して,線形代数をゼロから解説し,その応用として分散共分散行列とマハラノビス距離を最後に説明します。
ただし,大学1年の線形代数をすべて網羅すると,かなりの分量になってしまうため,一般的な線形代数のテキストに掲載されているような行列の連立方程式への応用,基底,ベクトル空間など,準1級に直接的に必要ない内容はカットしつつ,スペクトル分解に到達するのに必要な内容にしぼりました。
本稿だけでも学習が完結するように構成しましたが,本稿で学習の道筋を確認しつつ,専門書でより詳しく学習するといった使い方も考えられます。本稿の下部にオススメの線形代数の書籍を挙げておきましたので,そちらも参考にしてください。
では,はじめていきましょう!
ベクトル
ベクトルや行列の計算をしたことのない人でも,実はそれらと同等な計算はしたことがあるはずです。次の例を見てみましょう。
(例)あるカフェで売られている大・中・小の3種類のカフェラテを次の表のように購入した。
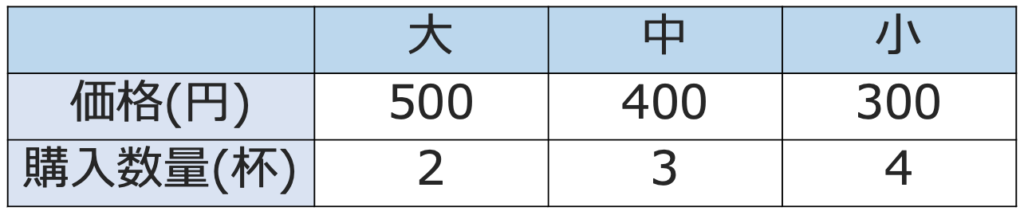
3種類のカフェラテの購入金額の合計は,500×2+400×3+300×4で求められますね。この計算は,ベクトルの内積と呼ばれる計算と同じものとみなすことができます。そのことを確認するために,まずはベクトルとは何かを説明します。
ベクトルとは次のように複数の数や文字をかっこでまとめたものです。
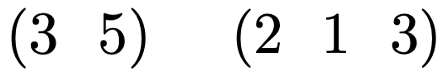
これらのベクトルでは,数が横に並んでいるので,横ベクトルとか行ベクトルと言います。行ベクトルは,次のように「,」を書いてもかまいません。
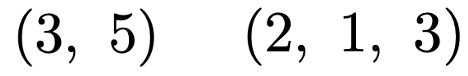
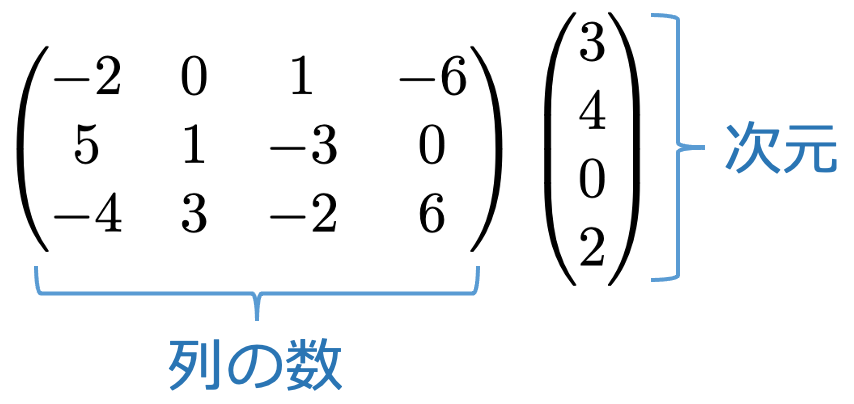
かっこの中に並べられている数を成分と言い,成分の数が次元です。本稿では,成分として用いる数はすべて実数です。左上のベクトルのように成分が2つであるベクトルが2次元のベクトル,その右のベクトルは3次元のベクトルです。行ベクトルの成分は,左から順に第1成分,第2成分,第3成分と呼びます。
また,次のように数を縦に並べたベクトルを,縦ベクトルとか列ベクトルと言います。
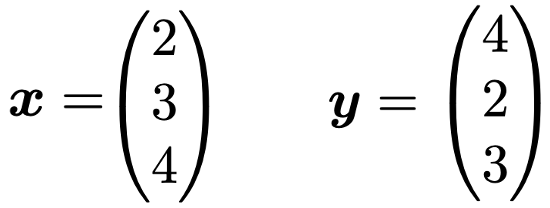
ベクトルは,アルファベットの小文字で表すことが多いですが,普通の数を表す文字と区別するため,上のように太字のアルファベットを使ったりします。列ベクトルの成分は,上から順に第1成分,第2成分,第3成分と呼びます。上の2つのベクトルx,yは,2と3と4を成分として持っていますが,それらの順番が異なるため,x≠yです。カフェラテの購入数量を表すベクトルだと考えると,xは大を2つ,中を3つ,小を4つ購入する場合で,yは大を4つ,中を2つ,小を3つ購入する場合に対応しているので,2つのベクトルが等しいのは,すべての成分が等しい場合に限るということが納得できるでしょう。これ以降,本稿で単に「ベクトル」と書いた場合には「列ベクトル」を表すものとします。
次に,ベクトルの基本的な演算として,和・スカラー倍・内積を紹介します。ベクトルの和とは次のように成分ごとに加える演算です。
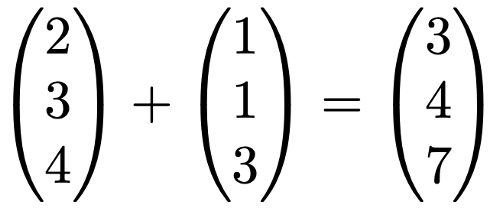
これもカフェラテの例で言えば,第1成分は大のサイズの購入数量,第2成分は中のサイズの購入数量,第3成分は小のサイズの購入数量を表していると考えて,先週は大を2つ,今週は大を1つ買ったので,2週間で3つ買ったことになる(第1成分)というイメージです。この計算ができるためには,和の計算をしようとしている2つのベクトルの次元が等しくないといけませんね。
次に,ベクトルのスカラー倍は,次のようにすべての成分に同じ数をかける演算のことです。
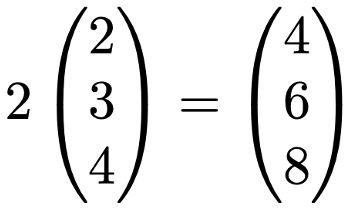
スカラーというのは,ベクトルと対比して普通の数のことを指す言葉で,上の式の左辺の先頭の2がスカラーです。上の式では,左辺のベクトル全体を2倍する計算をしています。より一般的にkをスカラーとすると,ベクトルxのkによるスカラー倍は,次のように表せます。
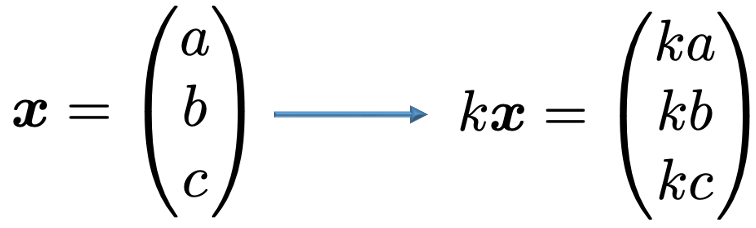
ここで,k=0のときには,スカラー倍した結果は次のようになります。
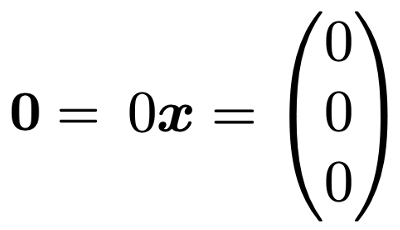
このようなすべての成分が0のベクトルをゼロベクトルとか零ベクトルと言って,太字の0で表します。ベクトルの和の計算方法からわかるように,次のようにどんなベクトルaにゼロベクトルを加えても,和はaのままになるので,普通の数の0と和に関して同じような働きをすることがわかります。
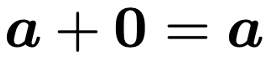
上のスカラー倍でk=ー1とすると,次のようになります。
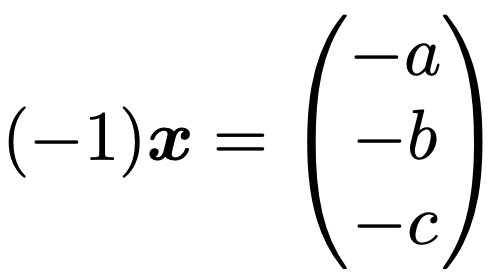
このベクトルと,もとのベクトルxとの和は,ベクトルの和の計算方法から,次のようにゼロベクトルになることがわかります。
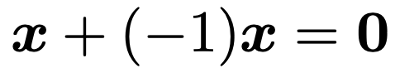
よって,このベクトルは通常の数の世界と同じように「ーx」と表すことにしましょう。
x,y,zを次元の等しいベクトルとすると,ベクトルの和について次の計算規則が成立することは,実際に成分を計算してみればわかるでしょう。
交換法則
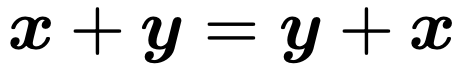
結合法則
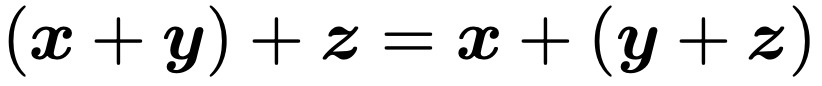
k,lをスカラーとして,ベクトルのスカラー倍について次の計算規則が成立することも,実際に成分を計算してみればわかるでしょう。
スカラー倍の結合法則
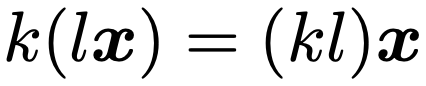
分配法則①
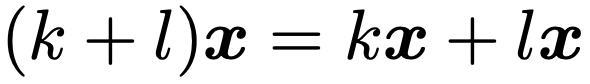
分配法則②
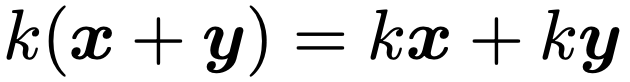
次に,ベクトルの内積を説明します。次のように,サイズごとの単価を並べたベクトルと購入数量を並べたベクトルの内積は3種類のカフェラテの購入金額の合計の計算と一致します。
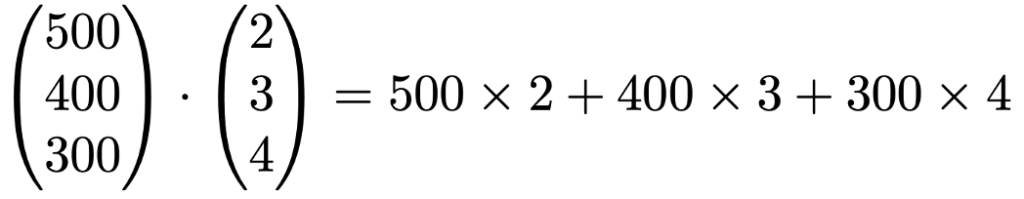
つまり,内積とは対応する成分どうしの積を合計したものであり,1つの数になります。ベクトルの和やスカラー倍の結果はベクトルでしたが,ベクトルの内積の結果はスカラーになる点には注意してください。
内積の定義をより一般的に表しておきましょう。次の2つのn次元ベクトルx,yを考えます。
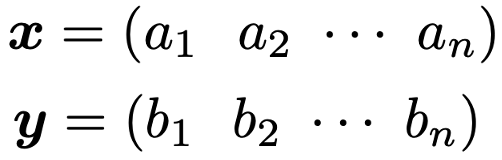
ベクトルx,yの内積は次の式で定義できます。
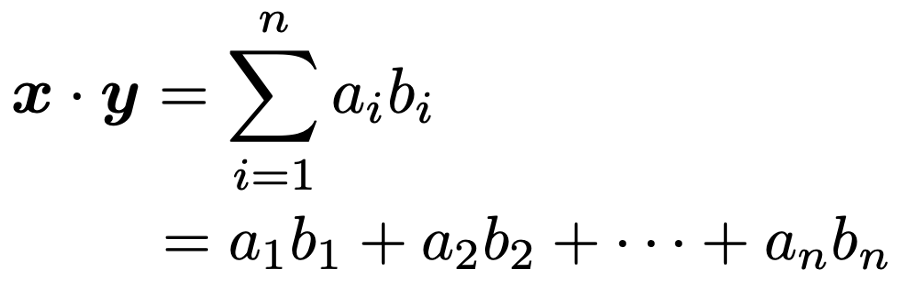
内積には複数の表し方がありますが,本稿では上の式の左辺のようにxとyの間に「・」を打って表すことにします。
行列
行列とは,次のように複数の数や文字を長方形(正方形を含む)に並べてかっこでまとめたものです。

行列についても,イメージがしやすいように,前のセクションで取り上げたカフェラテの例を取り上げてみます。Aさん,Bさん,Cさんの3人が大,中,小のカフェラテを次の個数だけ買うとしましょう。
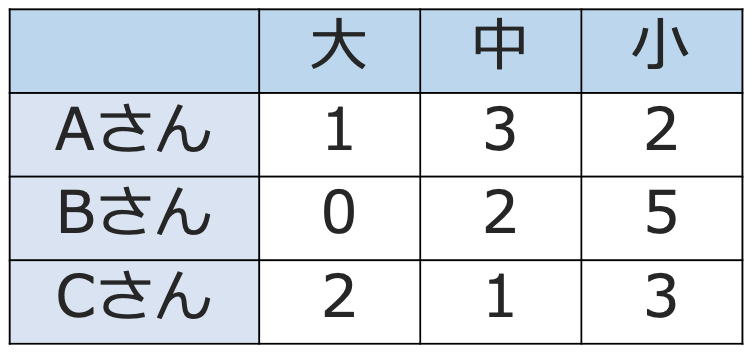
購入数量を表す9個の数に着目すると,上で紹介した行列と一致していますよね。ベクトルでは1人の購入数量しか表せませんでしたが,行列を使えば複数の人の購入数量を表すことができるわけです。このように,行列はベクトルよりも多くの情報を詰め込むことのできる入れ物だと考えられます。
行列の横の並びを行,縦の並びを列と言います。上で紹介した行列では,(1,3,2)が第1行,(0,2,5)が第2行,(2,1,3)が第3行です。また,この行列には列も3つあるので,3次正方行列と呼びます。次の行列も見てみましょう。
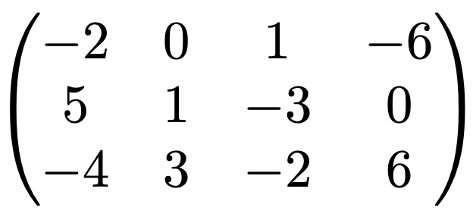
この行列には行が3つ,列は4つあるので,3行4列の行列とか3×4行列と呼びます。このとき,3×4行列と4×3行列は異なることに注意してください。また,ベクトルも行列の一種とみなすことができて,n次元の行ベクトルは1行n列の行列,n次元の列ベクトルはn行1列の行列です。このような行列の行の数と列の数のことを行列のサイズと言います。
次の行列には9個の数が並んでいますが,これらをベクトルのときと同じように成分と言います。本稿では,成分として用いる数はすべて実数です。例えば,次の図で2つの四角形が重なっている部分は,3行目2列目の成分を表していて,これを(3,2)成分と言います。
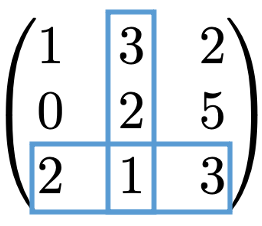
2つの行列が等しいというのは,サイズが同じで,すべての成分が同じであることを指します。
次に,行列の演算を説明します。行列の和・スカラー倍は,ベクトルの和・スカラー倍と同じように定義できます。まず,行列の和はサイズが同じである行列に対して,次のようにすべての成分を加えたものです。

また,スカラー倍は,すべての成分に同じスカラーをかけます。下の左辺の行列を3人の1週間分の購入数量だとすると,2によるスカラー倍で2週間分の購入数量を計算していることになります。
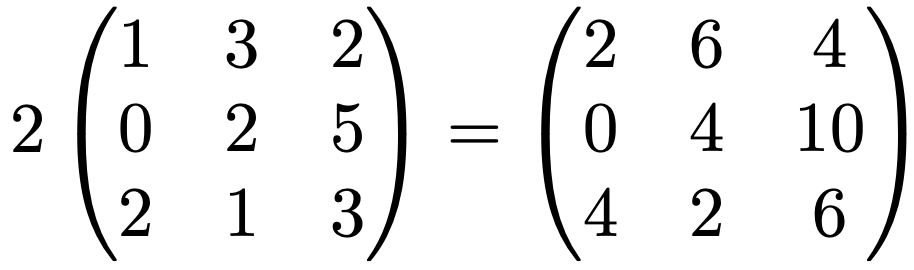
より一般的にkをスカラーとすると,3次正方行列Aのkによるスカラー倍は,次のように表せます。
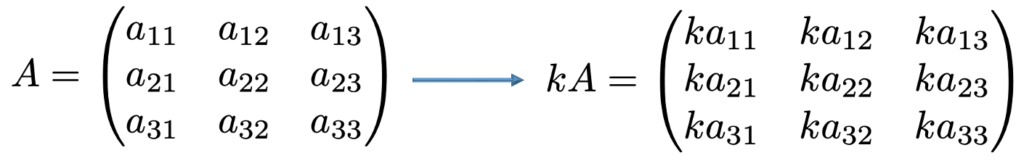
ここで,k=0のときには,スカラー倍した結果は次のようになります。
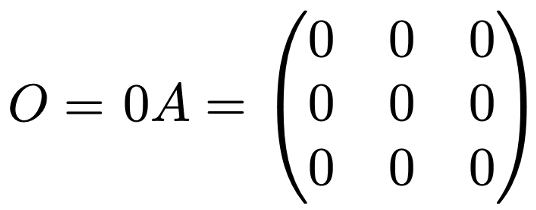
このようなすべての成分が0の行列をゼロ行列とか零行列と言って,アルファベット大文字のOで表します。次のようにどんな行列Aに零行列を加えても和はAのままであることは,和の計算方法からわかりますね。
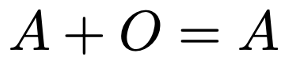
また,k=ー1によるスカラー倍の結果は次のようになります。
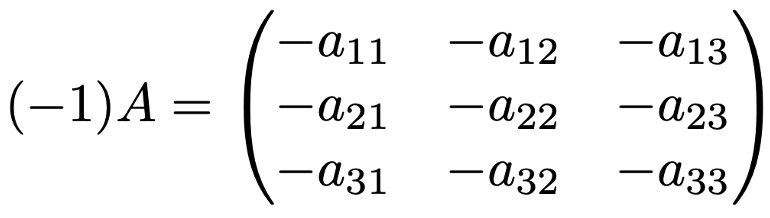
この行列と,もとの行列Aとの和は,行列の和の計算方法から,次のように零行列になることがわかります。
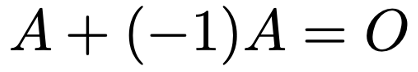
そこで,この行列を「ーA」と表します。
もう1種類だけ,特別な行列を紹介しておきます。それは,次のような左上から右下にかけての対角線上の成分(対角成分)以外が0であるような行列で,対角行列と言います。

次のように,対角行列の和は対角行列です。
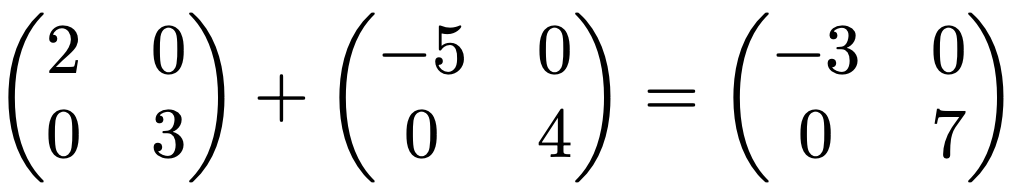
また,次のように対角行列のスカラー倍も対角行列です。
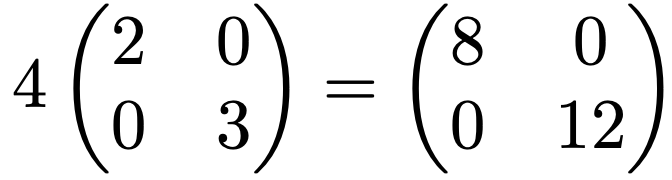
次に,行列とベクトルの積を説明します。もう一度,サイズごとの3人の購入数量を並べた次の表を思い出します。

カフェラテの単価は,大中小の順に,500円,400円,300円だったので,3人がそれぞれ支払う金額は次の通りですよね。
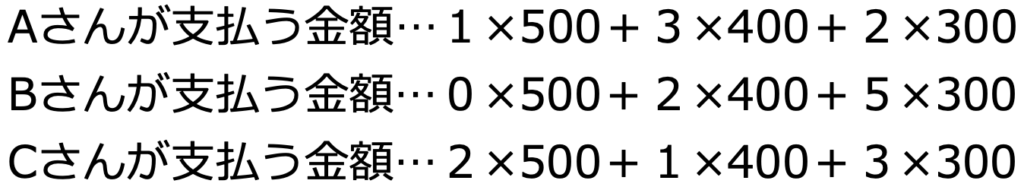
実は,この計算が行列と列ベクトルの積なんです。行列とベクトルの形で表すと,次のようになります。
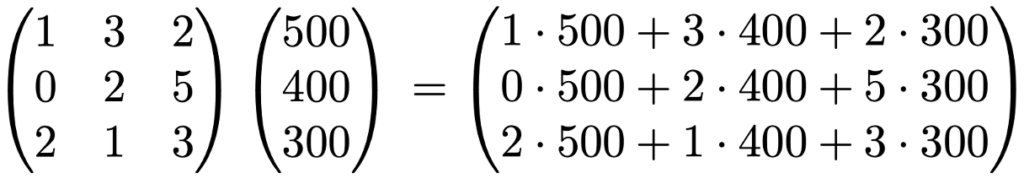
つまり,行列と列ベクトルの積では,左の行列の各行と列ベクトルの内積を計算し,それを上から順に成分として並べて,列ベクトルをつくることになります。
もちろん,次のような正方行列ではない行列と列ベクトルとの積も考えることができます。
上の計算では,左の行列の列の数と右のベクトルの次元が合っているので,3組の内積が計算できますが,それらが一致しない行列とベクトルの間では積が計算できないことに注意しましょう。
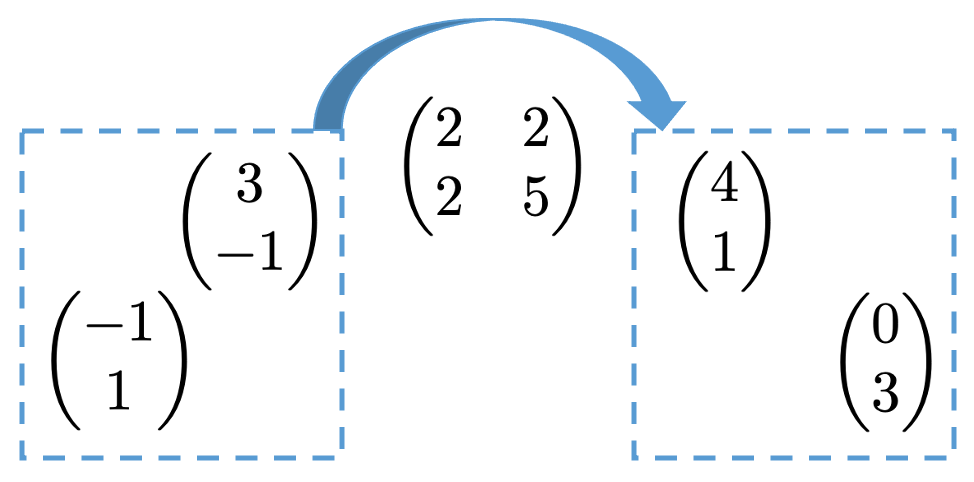
ここで,2次正方行列と2次元の列ベクトルの積を次のように計算してみます。
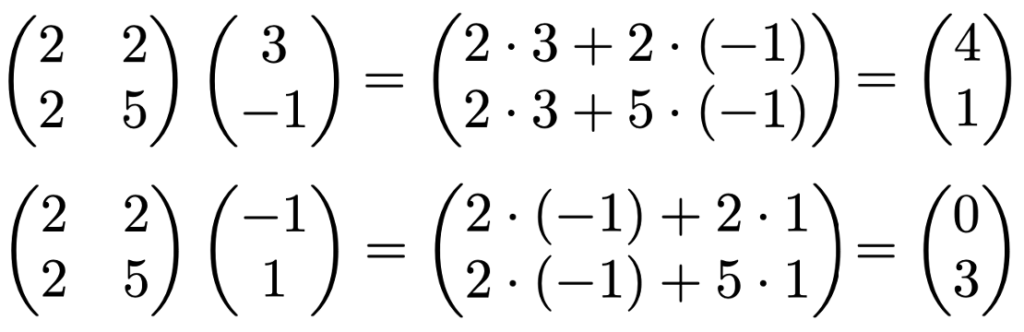
上の計算で,最左辺のように,行列をベクトルにかけることで,最右辺のベクトルが得られると考えると,2次正方行列を2次元のベクトルにかけることは,次の図のように2次元のベクトル全体の集まりをシャッフルするようなイメージで同じベクトル全体の集まりに移していると考えられます。
このような行列のベクトルに対する作用を一次変換とか線形変換と言います。2次正方行列が2次元のベクトルの間の一次変換を定めるのと同じように,3次正方行列は3次元のベクトルの間の一次変換を定めます。
この一次変換を図形的にイメージできることは,本稿全体を理解する上で重要なので,ここで2次元のベクトルの図形的な解釈について触れておきます。
次の図のように,第1成分が3で,第2成分が2のベクトルを,原点(0,0)から(3,2)に向かう矢印と同一視します。
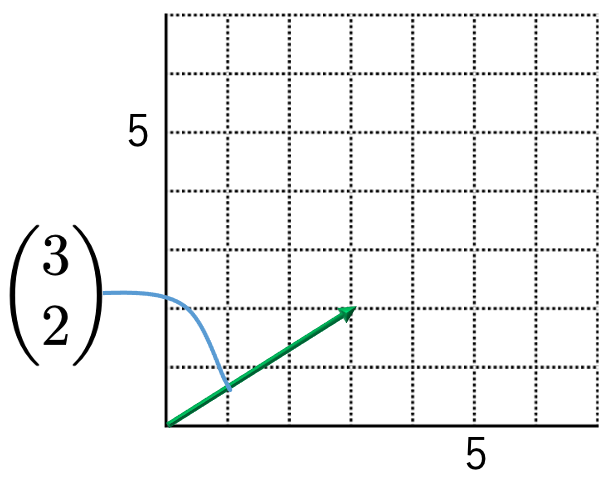
もちろん,第1成分がaで,第2成分がbのベクトルならば,原点(0,0)から(a,b)に向かう矢印と同一視します。次に,ベクトルの長さを,対応する矢印の長さとして定めます。第1成分が3で,第2成分が2のベクトルであれば,上の図で三平方の定理を用いると,次のように長さが求められます。
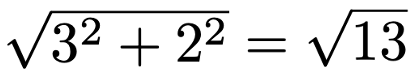
より一般に,第1成分がaで,第2成分がbのベクトルの長さは次のように計算し,自分自身との内積の正の平方根に等しいことに注意します。
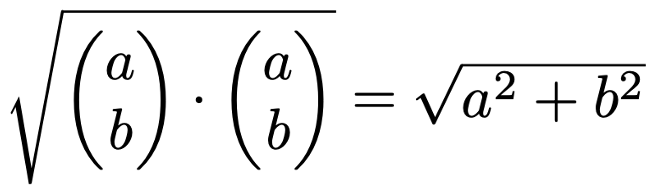
次に,ベクトルの和が図形的にどのように表せるのかを確認します。次の計算を見てみましょう。

上の式の3つのベクトルを次のように図に表してみると,右辺のベクトルは,左辺の2つのベクトルをとなり合う2辺とする平行四辺形の対角線になっていることがわかります。
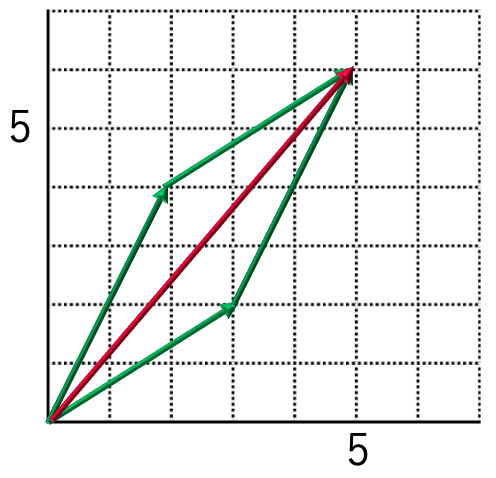
一般に,平行でない2つのベクトルx,yの和x+yはx,yをとなり合う2辺とする平行四辺形の対角線になります。
今度は,スカラー倍です。次の計算を見てみましょう。
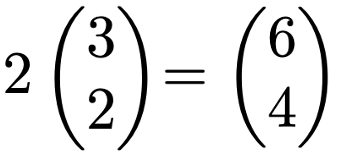
スカラー倍する前のベクトルと,スカラー倍した後のベクトルは,次の図のように表すことができ,方向を変えないまま矢印の長さをスカラーの倍率で伸ばしていることがわかります。
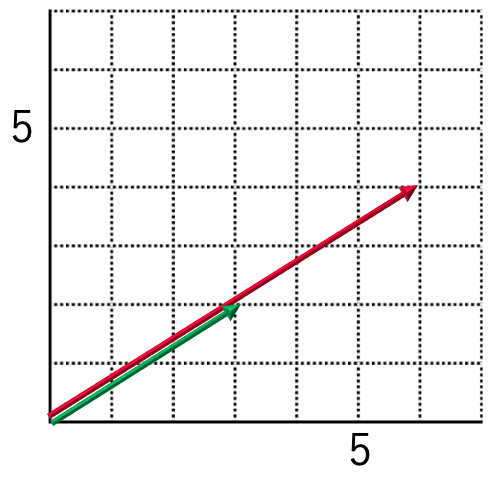
一般に,k>0ならば,ベクトルkxに対応する矢印はベクトルxに対応する矢印の長さをk倍したものになります。k<0ならば,ベクトルkxに対応する矢印はベクトルxに対応する矢印の長さを|k|倍して,向きを逆にしたものになります。
さて,(1,0)や(0,1)のように,1つの成分だけが1で,残りの成分が0であるようなベクトルを基本ベクトルと言います。次の行列と2次元の基本ベクトルの積を計算してみると,あることに気づきます。
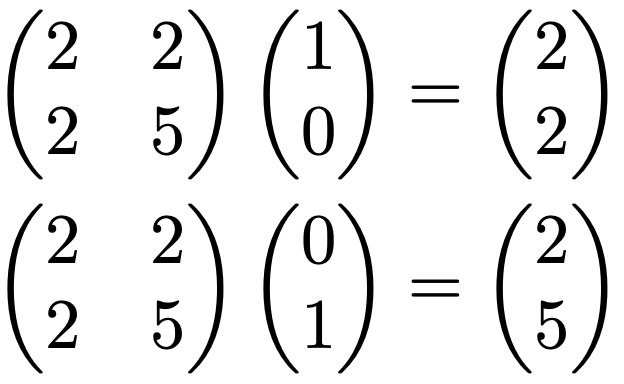
基本ベクトルは,行列の第1列や第2列を取り出す役割を果たしていますね。このように,行列によって基本ベクトルが移る先のベクトルに着目すると,その行列による一次変換を理解しやすくなります。まず,次の式を見てください。
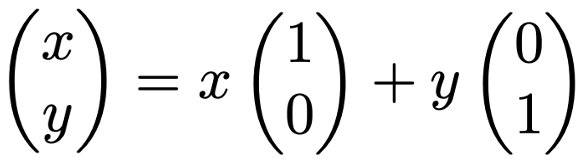
上の式の左辺は一般的な2次元のベクトルです。それは右辺のように,2つの基本ベクトルをスカラー倍して和をとったものに等しくなっています。次に両辺に左から2次正方行列Aをかけてみます。
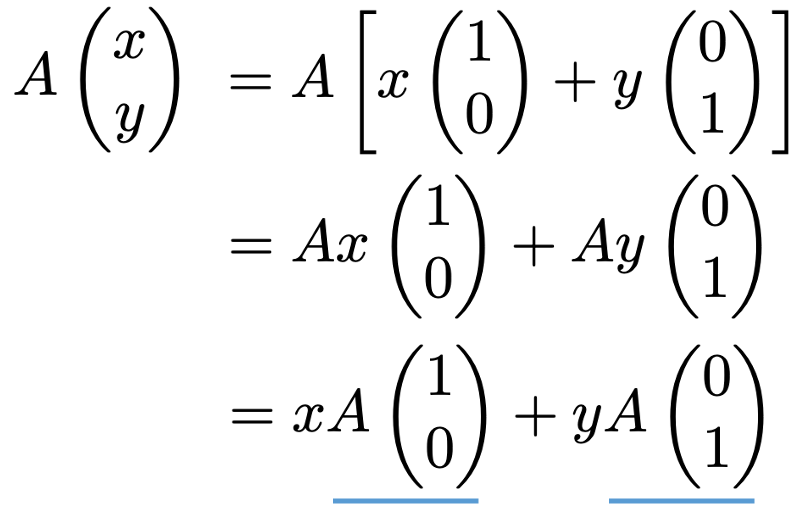
上の1行目から2行目の変形では行列の分配法則,2行目から3行目の変形では行列とスカラー倍の順序を交換できることを使っています。下線をひいた部分は基本ベクトルが移る先のベクトルであり,行列をかける前にこの位置にあったのは基本ベクトルだったことに注意しましょう。
では,すでに登場している次の計算に今の見方を適用してみましょう。次の式の最右辺は,基本ベクトルが移る先のベクトルを使って表したものです。
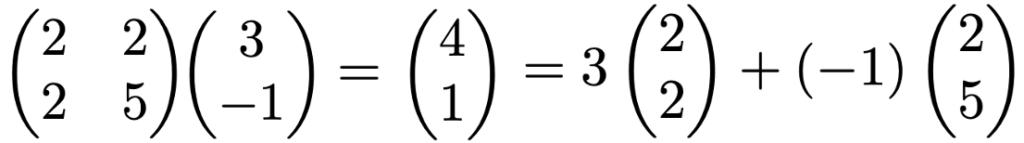
この一次変換を図に表すと,次のようになります。
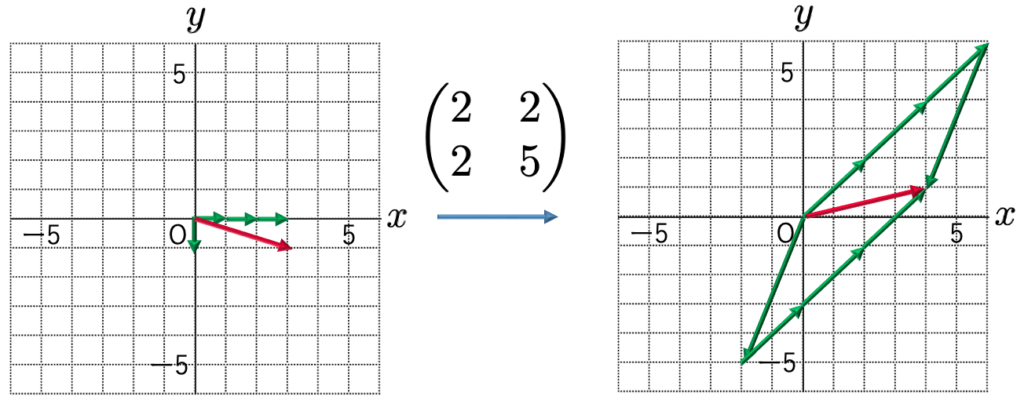
左上の図では,基本ベクトルをそれぞれ3倍,ー1倍したものを2辺とする平行四辺形(この場合は長方形)の対角線になっていたベクトルが,右上の図では,基本ベクトルが移る先のベクトルをそれぞれ3倍,ー1倍したものを2辺とする平行四辺形の対角線になるのです。
このような行列とベクトルの積について,kをスカラー,A,Bを行列,v,wをベクトルとして次の計算規則が成り立ちます。
スカラー倍と行列の作用の順序交換
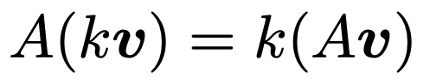
分配法則①

分配法則②
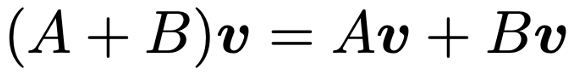
次に,一次変換を連続して行うことを考えます。一次変換の結果として得られたベクトル(4,1)に,さらに次のようにもう一度同じ一次変換を作用させたら,(10,13)へと変化します。
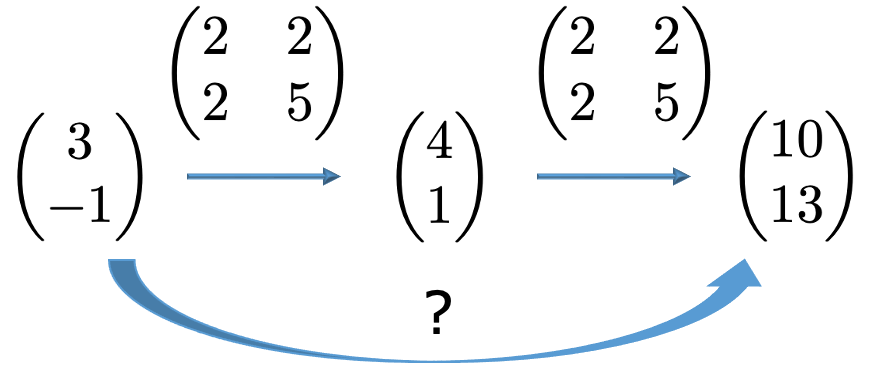
では,(3,ー1)を一度で(10,13)に対応させる行列は何でしょうか。その答えを与えてくれるのが行列の積です。これから説明する行列の積の計算を使うと,上の行列の2乗は次のように計算できるので,(3,ー1)を(10,13)に移すことも確認できます。
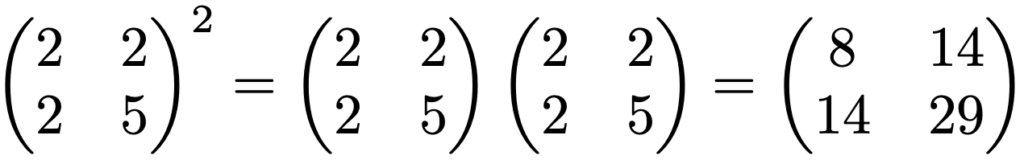
行列の積を理解するため,もう一度カフェラテの例を取り上げます。次の1行目の左の行列は,サイズごとの3人の購入数量を並べたものです。

上の計算の1行目の青い枠で囲んだ部分は,カフェラテの単価を並べた列ベクトルを表しています。この列とその左の購入数量を表す行列との積が,2行目の青い枠で囲んだ部分になります。つまり,購入数量を表す行列と青い枠で囲んだ部分だけをみれば,これまでに学習した行列とベクトルの積になっているのがわかると思います。
次に,カフェラテの単価が100円ずつ値上げされたとしましょう。上の計算で値上げ後の単価を表しているのが1行目の右の行列の第2列です。サイズごとの3人の購入数量は変わらないものとして,購入数量を表す行列と右の行列の第2列の積を計算すると,その結果は2行目の行列の第2列に現れます。これが行列の積の計算です。行列の積では,左の行列の行と右の行列の列の間で内積を計算するので,左の行列の列の数と右の行列の行の数が一致していないと計算できません。上の例では,左の行列のサイズが3×3,右の行列のサイズが3×2なので,積が計算できています。一般的に言うと,l×m行列とm×n行列はmがそろっているので積が計算できて,積の結果はl×n行列になります。
ここで,上の計算を振り返ってみると,積の結果として得られる行列の(1,1)成分は,もとの2つの行列のうち,左の行列の第1行と右の行列の第1列の内積になっていて,(2,1)成分は,左の行列の第2行と右の行列の第1列の内積となっているのがわかると思います。より一般的には,積の結果として得られる行列の(i,j)成分は,左の行列の第i行と右の行列の第j列の内積になります。行列の積をこのように定めることで,行列を続けて2回作用させた結果と,行列の積を計算した後で1回作用させた結果が一致します。このことを文字を使って一般的に表すと,2つの行列A,Bは積が計算できるサイズであるとすれば,次のような結合法則が成り立ちます。
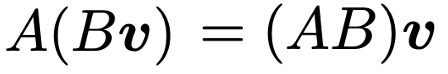
この積について,次のような対角成分が1で非対角成分が0であるような行列は特別な存在であり,どんな行列にかけても,もとの行列を変化させません。
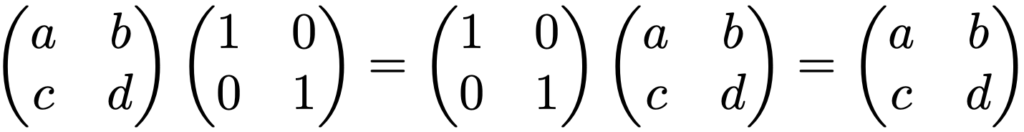
このような行列を単位行列と言い,I(”identity”の頭文字)で表します。数学の専門書では,ドイツ語に由来するEを使う場合が多いですが,本稿ではIを用います。
また,行列の積では,普通の実数の積とは異なり,一般には順序の交換ができません。例えば,次の2つの行列の積を見比べてみましょう。
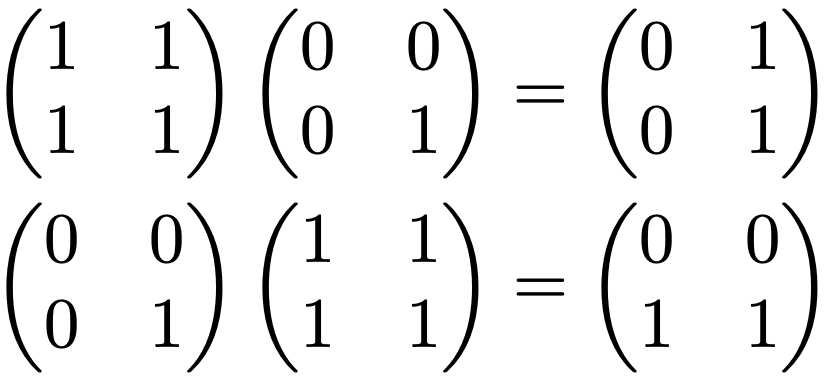
積を計算する行列の左右を入れ替えただけで結果が変わりましたよね。実数a,bの積では,ab=baは当たり前でしたが,それは行列の場合には当たり前ではないのです。その結果として,実数の場合に成り立った展開の公式は,行列の場合には次のようになります。
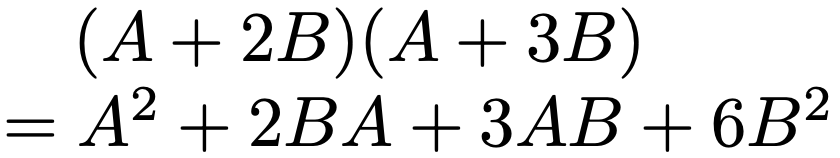
一般には,BA≠ABであるために,2BA+3ABを5ABとまとめることはできませんが,AAは順序を気にする必要がないので,A2と表すことができます。このような行列の積について,kをスカラー,A,B,Cを行列として,次の計算規則が成り立ちます。
スカラー倍と行列の積の順序交換
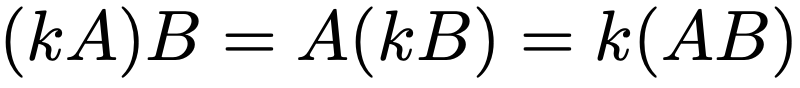
行列の積の結合法則
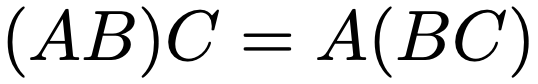
行列の積の分配法則①
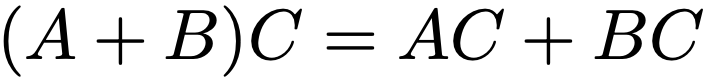
行列の積の分配法則②
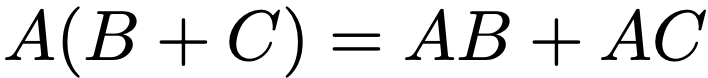
次に,一次変換の逆変換を調べましょう。次の変換をもとに戻すのはどんな行列でしょうか。
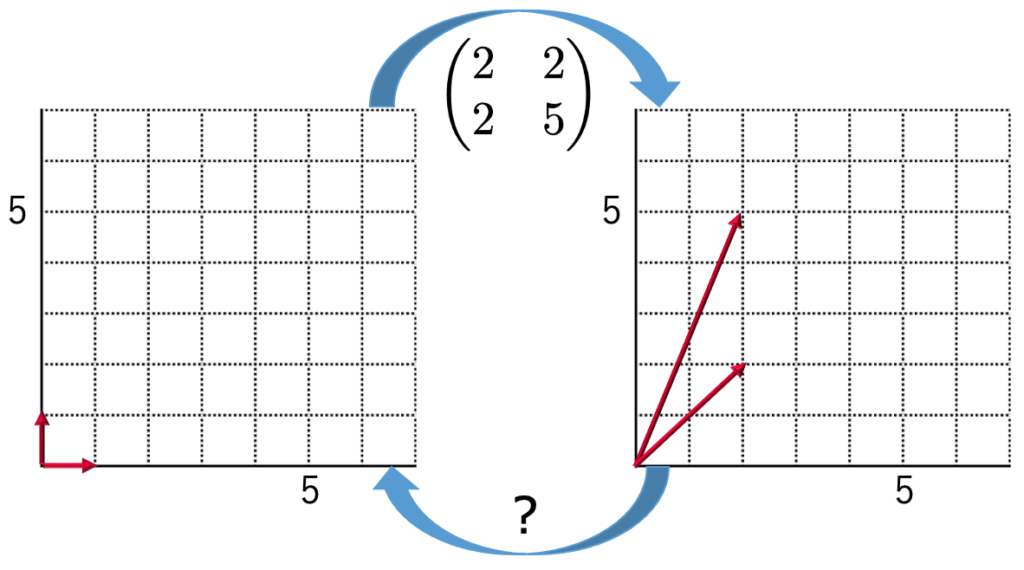
逆変換を調べるために,一次変換による面積の変化を考えます。この変換では,次の図のように正方形が平行四辺形に移っています。
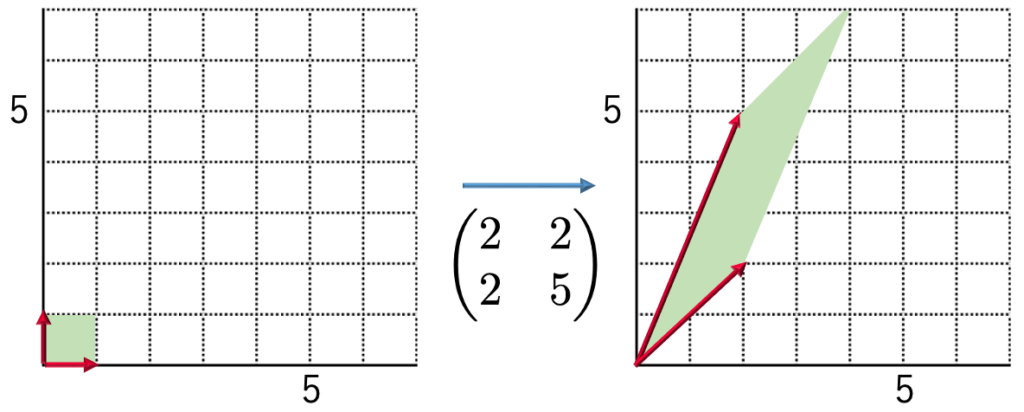
左の正方形の面積は1で,右の平行四辺形の面積は6なので,面積は6倍になっていますよね。この一次変換によって,平面全体がこのような倍率で引き延ばされているのです。この倍率を教えてくれるのが行列式であり,次の2次正方行列の行列式はadーbcによって計算できます。
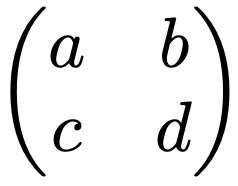
実際に,上の一次変換を表す行列の成分をあてはめてみると,adーbc=2・5ー2・2=6となります。3次以上の正方行列でも行列式を考えることができて,その場合の行列式の絶対値は(一般化された意味での)体積の拡大率を教えてくれます。なお,行列Aの行列式を,detAや|A|で表します。
さて,行列式を使うと,上の一次変換の逆変換を表す行列が次のように求められます。

先頭のスカラーの分母にあるのが行列式です。実際に,もとの行列との積を計算すると単位行列になることから,はじめの一次変換によって変化したすべてのベクトルをもとに戻す行列であることがわかります。
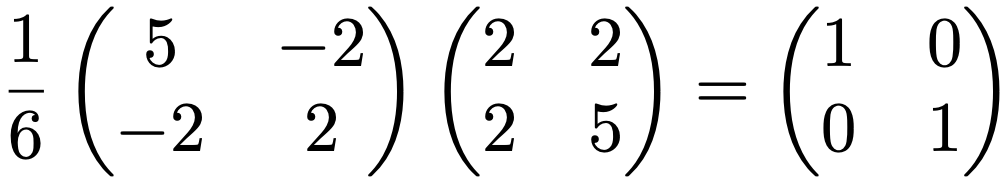
このように,n次正方行列Aに対して,あるn次正方行列Bが存在して,AB=BA=Iを満たすとき,BをAの逆行列と言います。Aの逆行列は存在すれば一意に定まるので,Aー1(Aインバースと読みます)と表します。ちょうど0でない実数aの逆数がただ1つ存在してaー1と表し,aaー1=1を満たすのと同じようなものです。零行列は逆行列をもちませんが,逆行列をもたないものは他にも考えられます。例えば,次の2次正方行列は逆行列をもちません。
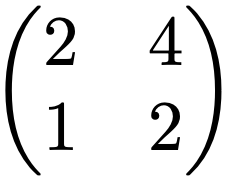
上の行列は,1つの行(列)のスカラー倍がもう1つの行(列)に一致していますね。行(列)の間に従属関係があるということです。このときには,行列式が0になります。実際に,上の行列の行列式は,2・2ー4・1=0となります。一般的に,行列式が0となる場合には逆行列をもちません。行列式の絶対値は面積(体積)の倍率だったことを思い出すと,「面積(体積)が0倍になってしまう=長さのあるベクトルが零ベクトルにつぶれてしまう」というイメージです。
逆に,左下の2次正方行列がadーbc≠0を満たすならば,右下の行列が逆行列になります。
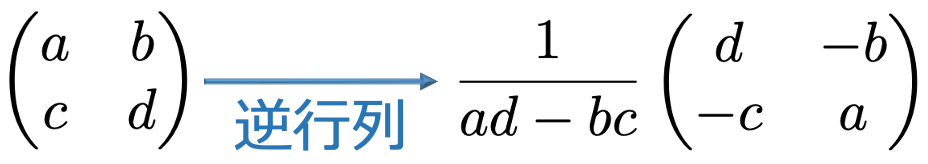
上の2つの行列の積は単位行列になりますので,ご自身で計算してみてください。逆行列をもつ行列のことを正則行列と言うので,2次正方行列の場合にはadーbcが0かどうかを調べることで正則行列であるかどうかを判定することができます。3次以上の逆行列の求め方は準1級のためには不要なので,本稿では扱いません。
なお,AとBが同じサイズの正方行列で,逆行列をもつならば,積ABの逆行列はBー1Aー1となります。なぜなら,(AB)(Bー1Aー1)=A(BBー1)Aー1=AAー1=Iとなるからです。
転置行列と直交行列
次の列ベクトルと行ベクトルには,行と列の違いしかありません。列を行(行を列)に入れ替えれば,一方は他方に一致します。
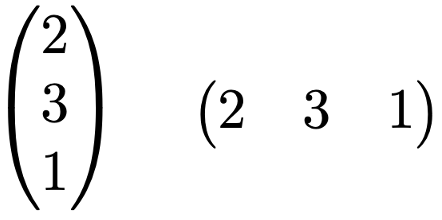
上の一方のベクトルを他方のベクトルに入れ替えるように,行を列(列を行)に入れ替える操作を転置と言います。行列に対する転置も考えることができます。右下の行列の第1列は,左下の行列の第1行と一致していて,右下の行列の第2列は,左下の行列の第2行と一致しています。
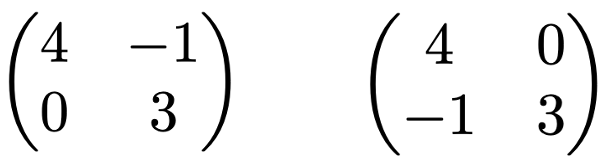
このように,行列Aの第1行,第2行,…を,第1列,第2列,…にもつ行列をAの転置行列と言って,本稿ではATと表します。Tは transpose(転置)の頭文字です。別の言い方をすれば,Aの(i,j)成分をaijとするとき,ATの(i,j)成分はajiです。同じ行列に転置を2回行えばもとの行列に戻るので,(AT)T=Aです。
次のように,3行2列の行列の転置行列は,2行3列の行列になります。
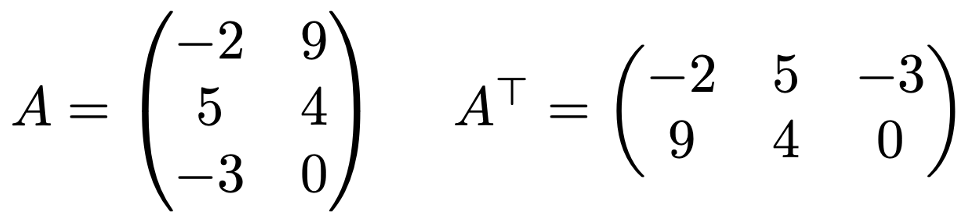
次に,行列の演算と転置をとる操作の関係を確認しておきます。はじめに,(A+B)T=AT+BTという関係が成り立ちます。つまり,行列の和と転置をとる操作の順番を入れ替えても結果は変わりません。具体的に成分を計算してみれば,これが成り立つことは明らかですが,念のため,理由を示しておきます。AとBが同じサイズの行列だとして,Aの(i,j)成分をaij,Bの(i,j)成分をbijと表すことにします。まず,(A+B)Tの(i,j)成分はA+Bの(j,i)成分に等しく,(aji+bji)です。一方で,ajiはATの(i,j)成分,bjiはBTの(i,j)成分なので,AT+BTの(i,j)成分も(aji+bji)であり,上の等式が成り立ちます。
次に,(AB)T=BTATという関係についてです。これは,行列の積と転置をとる操作の順番を入れ替える場合には,積の順番が変わるということであり,この性質は転置行列を使う計算でよく用いられるので注意しましょう。まず,等式の両辺の行列のサイズを確認します。行列Aをm行n列,行列Bをn行l列とすると,積ABはm×l行列です。一方で,BTはl×n行列でATはn×m行列なので,BTATはl×m行列であり,確かに(AB)Tと行列のサイズが一致していることがわかります。では,一般的にこれが成り立つ理由を述べておきましょう。積ABの(i,j)成分はAのi行とBのj列の内積なので,(AB)Tの(i,j)成分はAのj行とBのi列の内積です。一方で,BTATの(i,j)成分はBTのi行とATのj列の内積ですが,それはBのi列とAのj行の内積に等しいです。よって,(AB)T=BTATが成り立ちます。
行列の演算と転置をとる操作の関係の3つ目として,(Aー1)T=(AT)ー1という関係が成り立ちます。つまり,逆行列をとる操作と転置をとる操作の順番を入れ替えても結果は変わりません。これが成り立つ理由も示しておきます。Aー1A=Iの両辺の転置行列を考えると,(Aー1A)T=ITとなります。右辺はIT=Iですよね。左辺は,(Aー1A)T=AT(Aー1)Tとなるので,AT(Aー1)T=Iとなります。よって,(Aー1)T=(AT)ー1です。
次に,ベクトルの内積を転置の記号を使って表すことに慣れましょう。同じベクトルどうしの内積は行ベクトルと列ベクトルの行列としての積によって次のように計算できます。
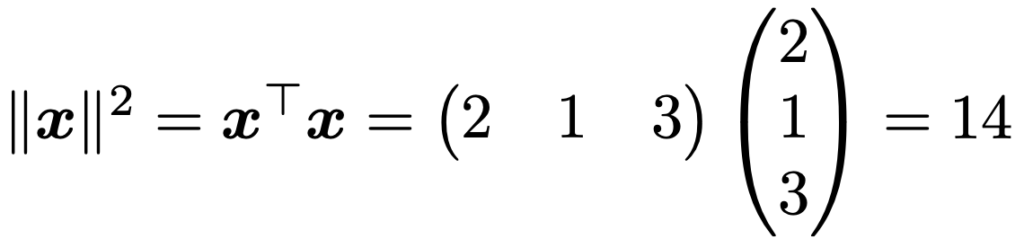
これはベクトルxの長さの2乗でもあり,一般的には,ベクトルxのノルムと言って,最左辺の2重の縦棒の記号で表します。
この内積と似て非なるものがxxTです。xを上と同じ列ベクトルとすると,xxTは次のような3次正方行列になるので,注意が必要です。
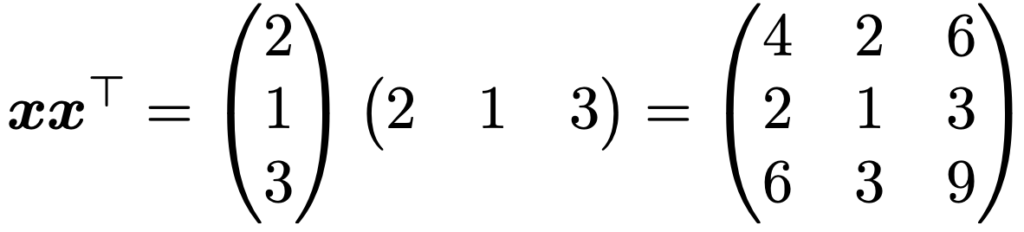
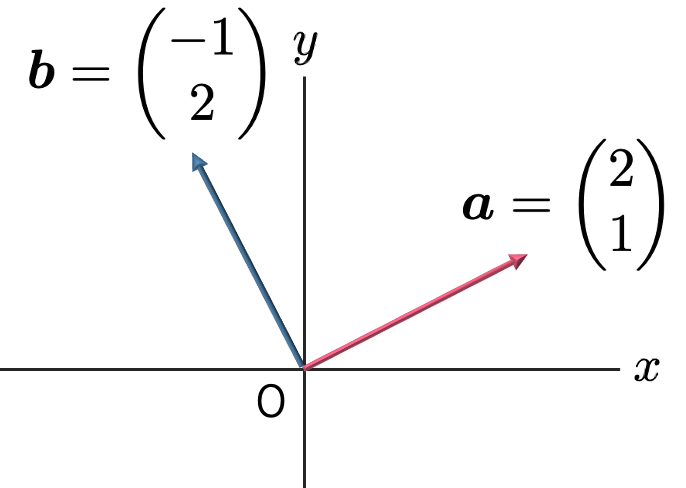
さて,2つのベクトルx,yに対して,内積xTy=0であるとき,ベクトルx,yは直交すると言います。このとき,x,yが2次元や3次元の(ゼロベクトルでない)ベクトルならば,幾何的に垂直になります。例えば,次の2つのベクトルは幾何的に垂直であり,内積は,aTb=2×(ー1)+1×2=0です。
次に,QTQ=Iを満たす正方行列Qを直交行列と言います。言い換えると,QT=Qー1ということであり,直交行列は正則です。
直交行列Qがn次正方行列であるとして,列ベクトルを並べて次のように表せるものとしましょう。
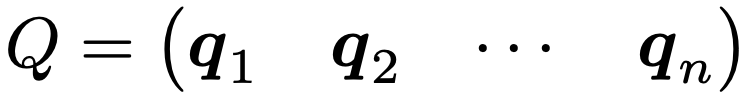
上の列ベクトルの表示を使うと,QTQ=Iは次のように書き直せます。
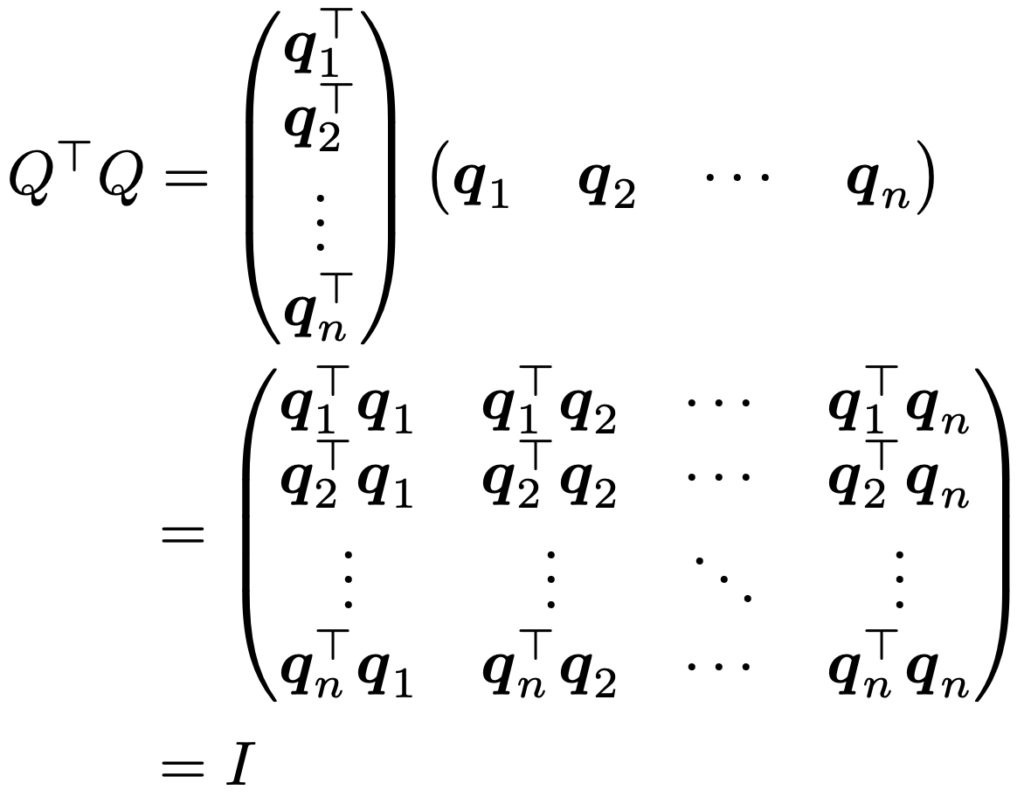
上の変形の最後の等号から,Qの各列について,次の関係が成り立つことがわかります。
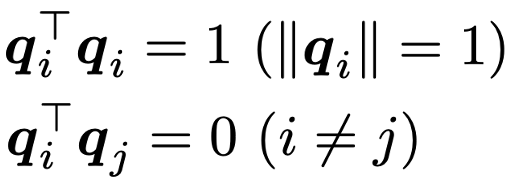
つまり,直交行列の各列は,ノルムが1で互いに直交する列ベクトルであるということです。直交行列の例として,次のセクションでは回転行列を紹介します。
三角関数と回転行列
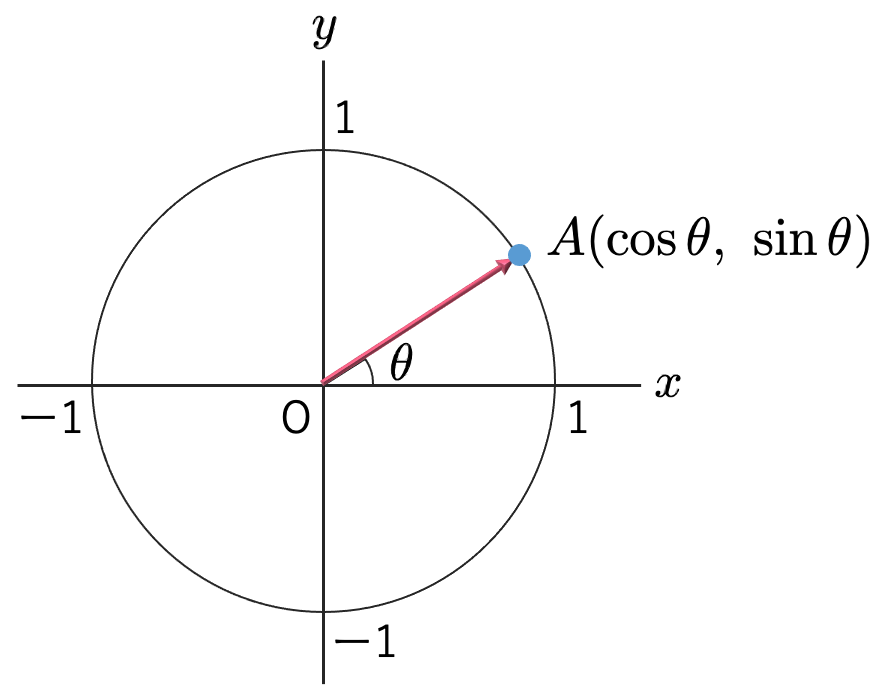
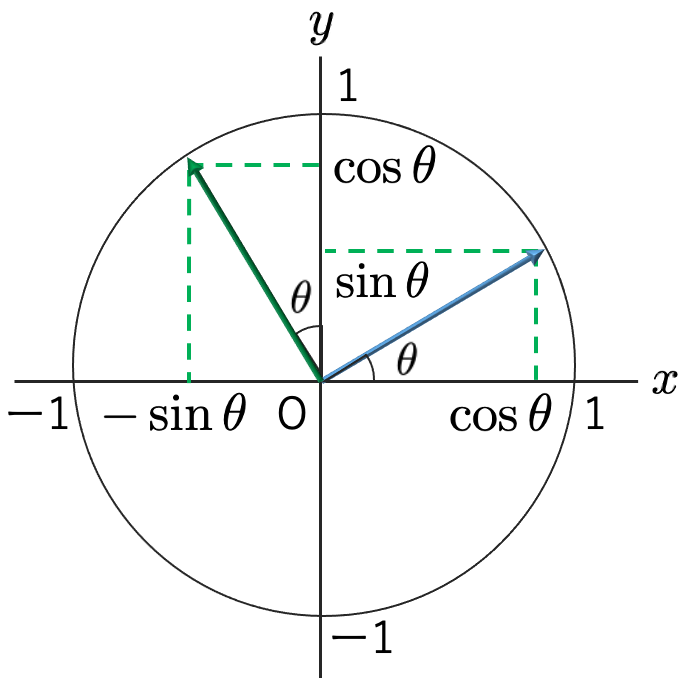
まずは,三角関数の定義の確認からはじめます。次の図のように,原点を中心とする半径1の円(単位円)の周上の点Aと原点を結ぶ線分が,点(1,0)と原点を結ぶ線分を反時計回りに角度θ(>0)だけ回転させたものと一致するとき,Aのx座標をcosθ,y座標をsinθと表します。
次の図のように,時計回りにθ(>0)だけ回転させる場合には,角度はーθとします。
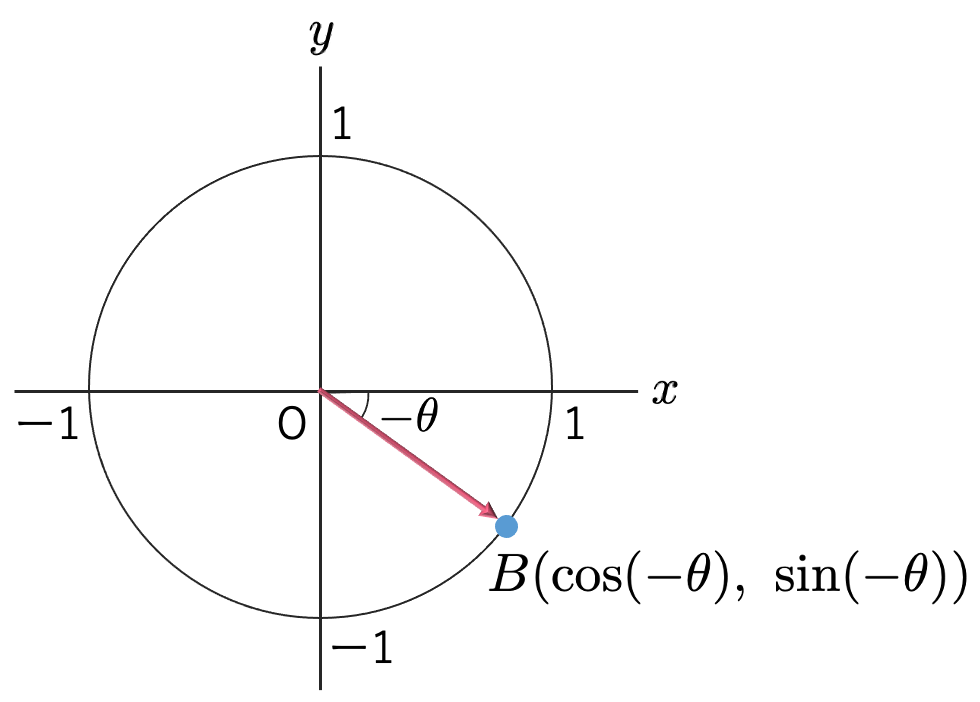
単位円上の点(x,y)と原点との距離が1であることから,単位円の方程式はx2+y2=1であることがわかります。そして,点Aが単位円上にあることから,次の式が成り立ちます。
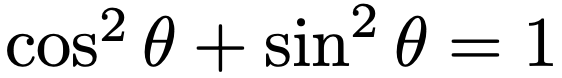
では,特定のθに対して,cosθとsinθの値を具体的に求めてみましょう。その際に,角度θの単位が問題となりますが,ひとまず中学までで学習している度数法ではじめることにします。
次の図は,θ=60°の場合です。
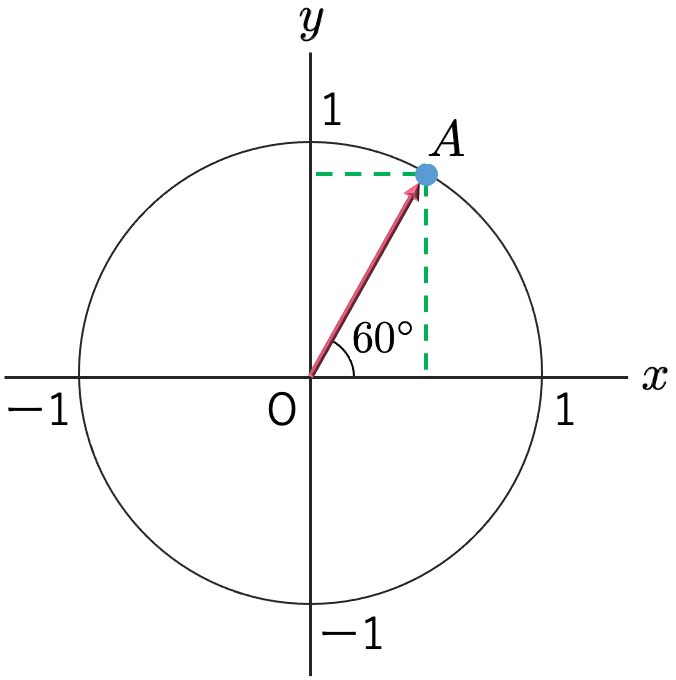
直角三角形の3辺の比から,上の図の点Aのx座標とy座標は次のようにわかります。
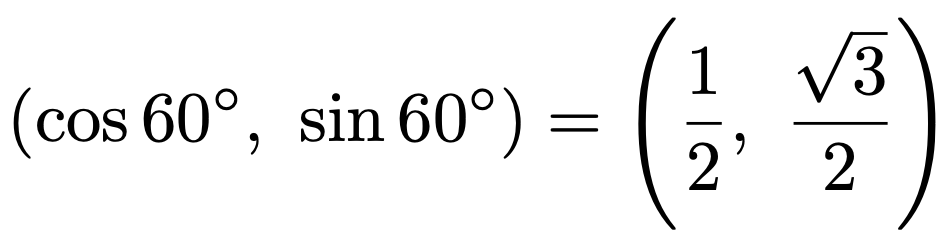
また,次の図は,θ=45°の場合です。
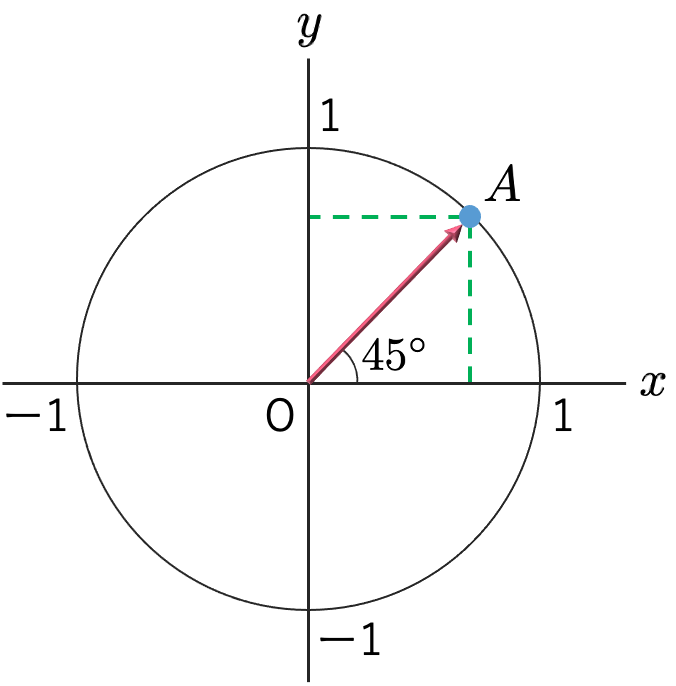
直角三角形の3辺の比から,上の図の点Aのx座標とy座標は次のようにわかります。
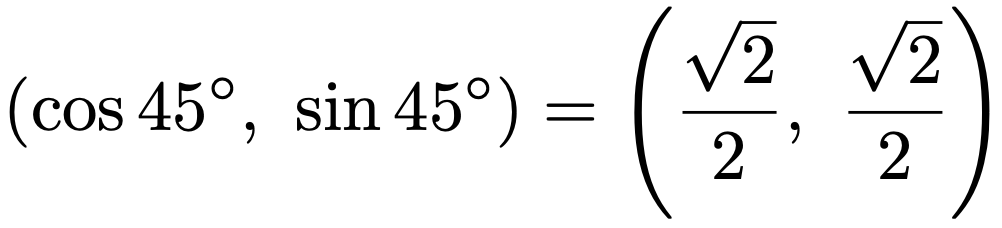
このように,θを0°から180°まで動かしながら,単位円上の点で座標が簡単に求められる点を調べると,次の9個が見つかります。
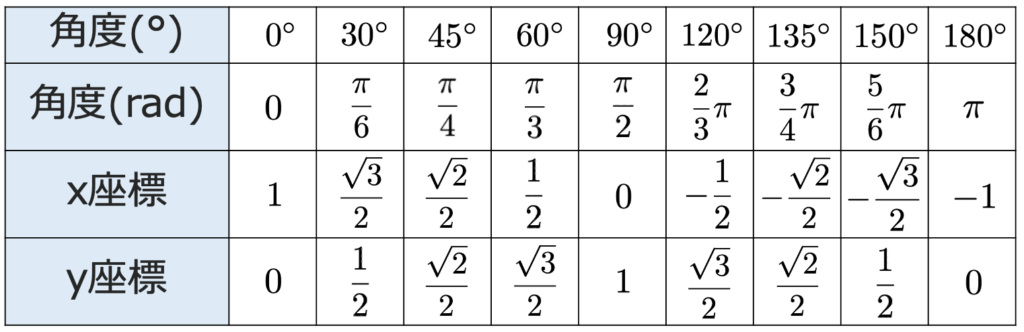
θが180°から360°まで動くときにも同じような表をつくることができますが,原点に関して点対称な点が上の表に載っていることを利用すればその座標は求められます。
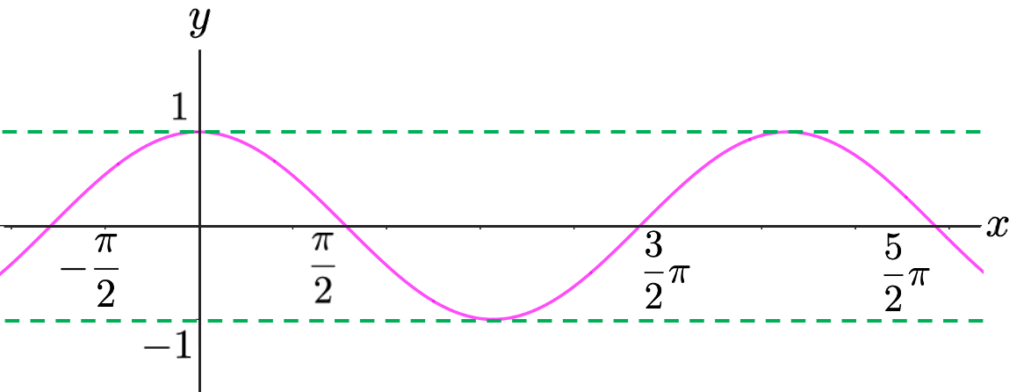
さて,中学の数学までは度数法を用いるのが通常ですが,高校以上の数学では,応用上の都合のよさを考慮して,度数法ではなく,弧度法を用います。弧度法は弧の長さによって角度を表す方法です。まず,単位円の円周の長さは2πであり,それに対応する中心角は360°です。また,単位円の円周の長さの半分はπであり,それに対応する中心角は180°です。そこで,反時計回りに1周する角度を2π[rad(ラジアン)]と定めます。反時計回りに45°の回転であれば1周の8分の1なので,2π[rad]を8でわって4分のπ[rad]です。時計回りに半周する角度はーπ[rad]です。このような弧度法を使うとき,y=cosxやy=sinxを三角関数と言います。例えば,y=cosxはすべての実数xに対して定義することができて,次のようなグラフになります。
さて,三角関数の知識を使うと,平面上のベクトルを一定の角度θだけ回転させるような一次変換を表す行列を求めることができます。行列は基本ベクトルが移る先のベクトルによって表せることを思い出しましょう。次の図のように,原点を中心として反時計回りに角度θの回転によって(1,0)は(cosθ,sinθ)に移り,(0,1)は(ーsinθ,cosθ)に移ることがわかります。
よって,(cosθ,sinθ)Tを第1列,(ーsinθ,cosθ)Tを第2列とする次の行列は平面上のベクトルを原点を中心として反時計回りに角度θだけ回転させる一次変換を表します。
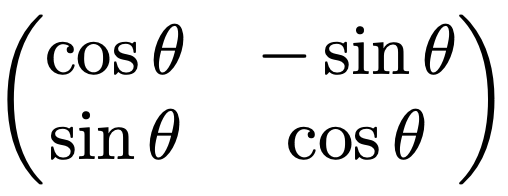
例えば,原点を中心として反時計回りに60°の回転を表す回転行列は次の行列になります。
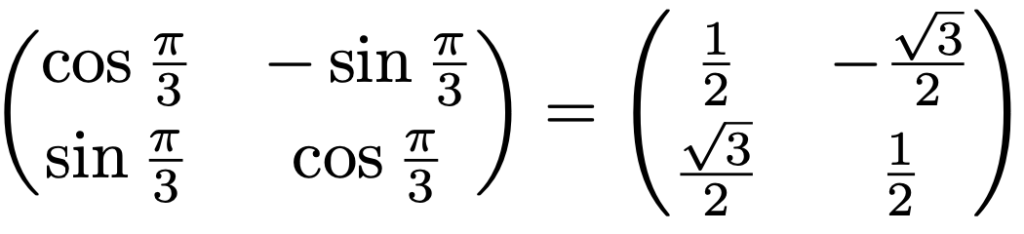
実際に,上の回転行列をベクトルにかけてみると,次のようになります。
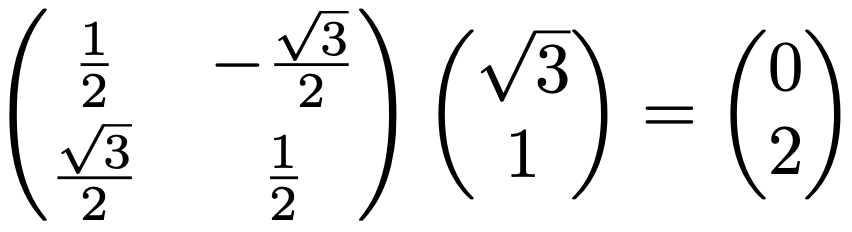
上の回転行列をかけることによって,次の図のように,ベクトルは確かに原点を中心として反時計回りに60°回転しているのがわかります。
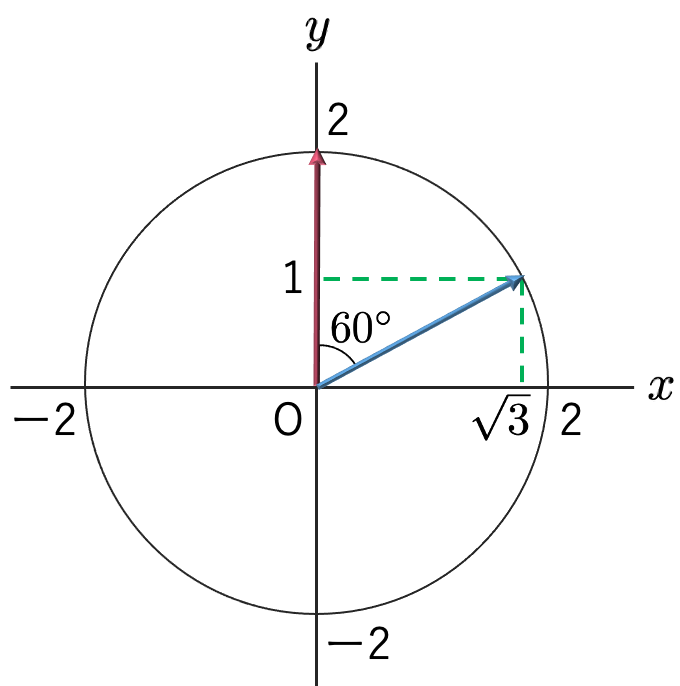
回転行列は直交行列です。実際に,角度θの回転行列とその転置行列との積は,cos2θ+sin2θ=1を利用して次のように単位行列になります。
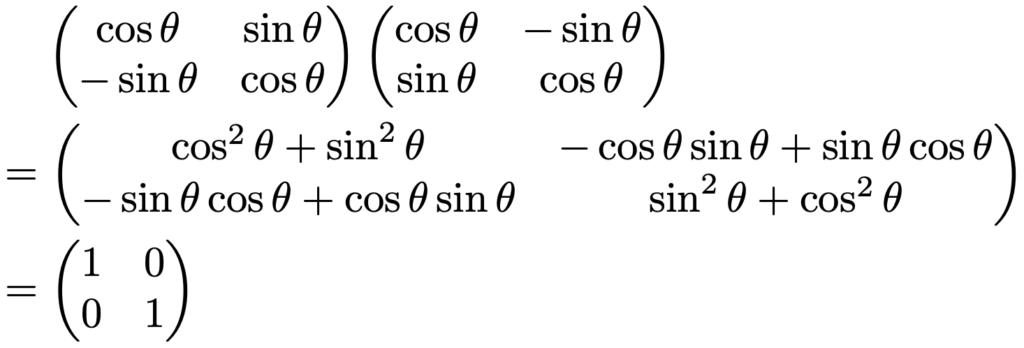
これ以降,原点を中心として反時計回りに角度θの回転行列をR(θ)と表すことにします。
射影行列
数学では「射影」という言葉をいくつかの意味で用いますが,本稿での「射影」は,真上から光を当てて影をつくる操作をイメージしてください。次の図は,b=(4,3)Tをy=2xという直線上に射影した影に相当するベクトルをpとしたものです。
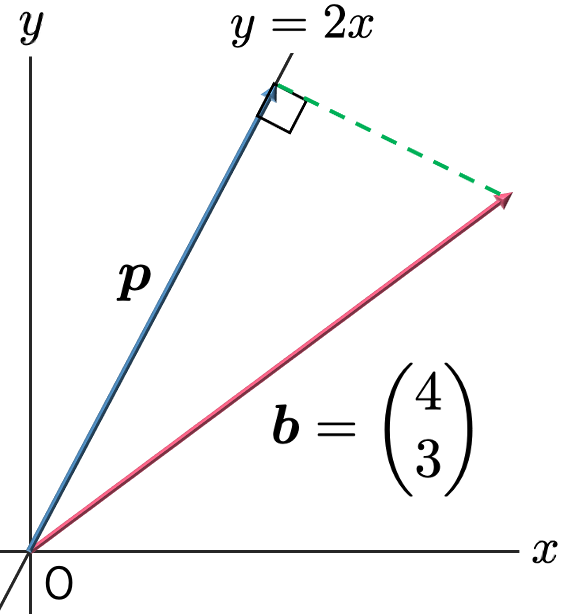
直線y=2xの向きを表すベクトルとして,次のaをとることにします。
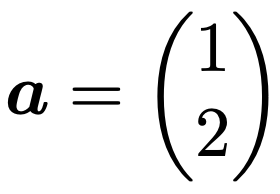
ベクトルpは,直線y=2xと同じ向きなので,次のように,ある実数kを用いてaのk倍と表すことができます。

pが,bを直線y=2x上に射影したときの影に相当するベクトルになるように実数kを決める必要があります。そのためには,次の図のように,ベクトルbーkaとベクトルaが直交することを使います。
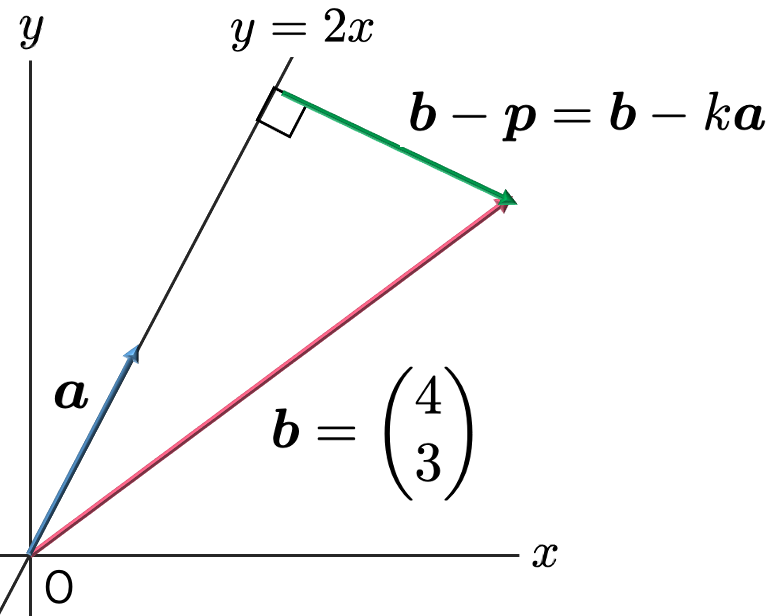
「2つのベクトルが直交」と言えば「2つのベクトルの内積=0」です。そこで,次の式がつくれます。

この式を解くと,kは次のように表せます。
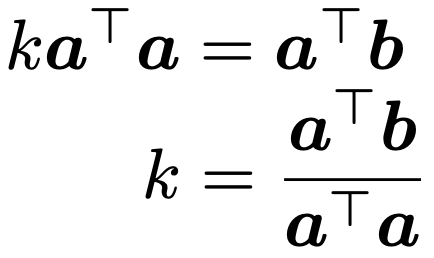
aTaやaTbは数なので,上のような計算ができます。kの値を求めるため,aTaを計算すると,次のようになります。
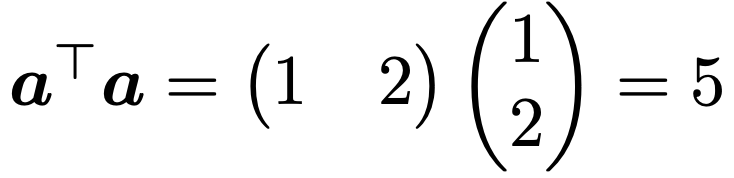
同じように,aTbを計算すると,次のようになります。
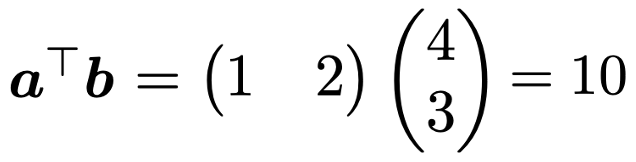
これらを代入してkの値を求めると,k=2となります。つまり,bを直線y=2x上に射影したときの影に相当するベクトルは,aの2倍になりました。
さて,ベクトルpの式に,上で求めたkを内積の商で表した式を代入し,次のように変形します。
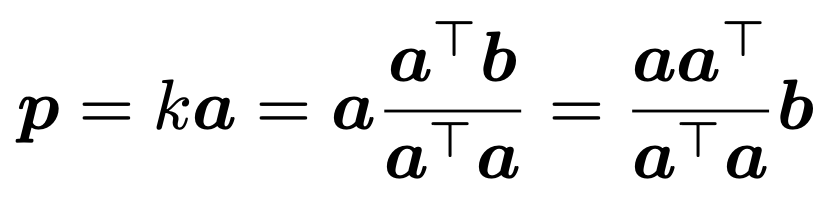
上の式の最後の等号では,a(aTb)=(aaT)bという性質(行列の積の結合法則)を使っています。ここで,aaTは行列です。aaTをaTaでわった行列は,aと同じ次元のすべてのベクトルを,原点を通りベクトルaの向きを向いた直線上へ射影した影に対応させる射影行列です。例えば,上の例では次の行列になります。
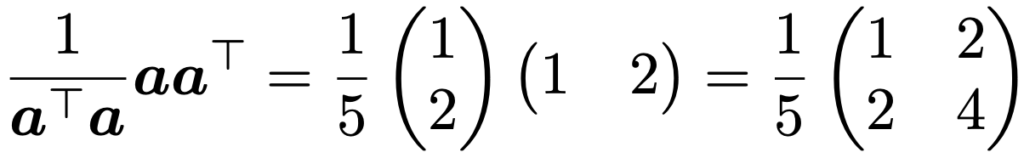
この行列をbにかければ2aに一致します。また,この行列をaにかけてもaのまま変化しません。この行列の作用は直線y=2x上に影を落とすものであり,この直線上のベクトルはすでに影なので,それ以上は変化しようがないのです。したがって,一般に射影行列Pについて,P2=Pが成り立ちます。
なお,ベクトルaのノルムが1のとき,原点を通りベクトルaの向きを向いた直線上にベクトルbがつくる影pは,aTa=1を代入して,次のように表せます。
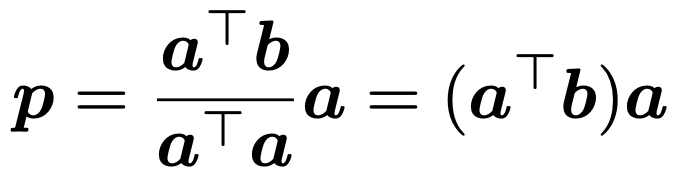
上の式からベクトルpのノルムは次のようになります。
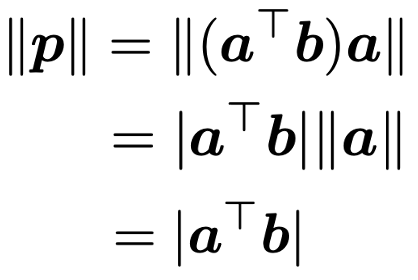
つまり,ベクトルbが原点を通る直線上につくる影の長さが知りたければ,その直線上の単位ベクトルとベクトルbの内積(の絶対値)を計算すればいいことになります。
楕円
次のセクションで説明する固有値,固有ベクトルを理解しやすくするため,ここで楕円の基本事項をおさらいしておきましょう。まず,円の方程式をベクトルを使って表してみます。三角関数のセクションでも説明したように,円は中心からの距離が一定の点の集まりであることから,方程式を導くことができます。例えば,原点を中心とする半径aの円の方程式は次のようになりますよね。
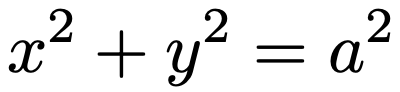
上の式の左辺は,点(x,y)と原点との距離の2乗です。これをベクトル(行列)を使って表すと,次のようになります。
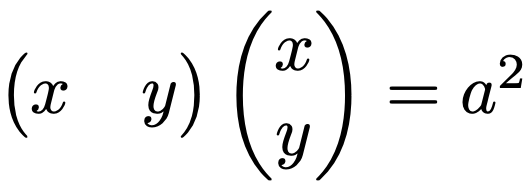
上の式の左辺は同じベクトルどうしの内積であり,それはベクトルの長さの2乗であるというのはすでに説明した通りです。「2地点の距離=2地点を結ぶベクトルの長さ」なので,距離の2乗は同じベクトルの内積で表せます。
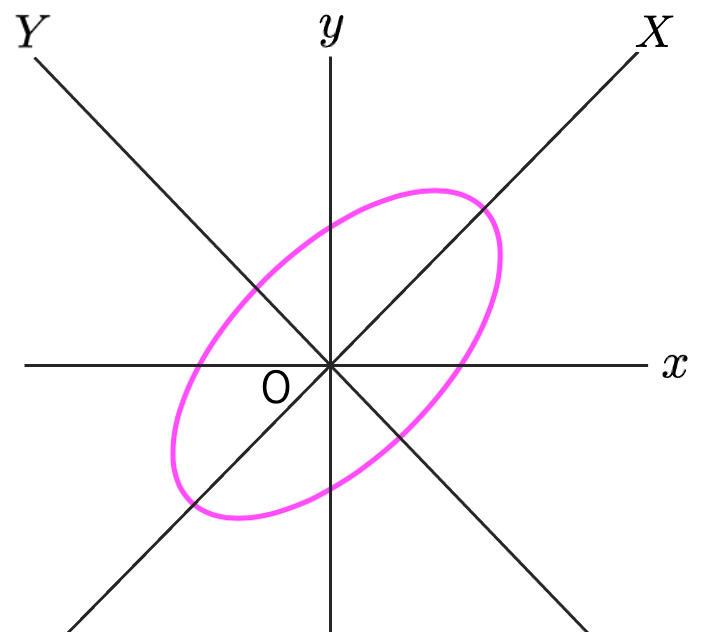
今度は楕円について考えます。次の図は単位円をx方向に2倍してできる楕円です。
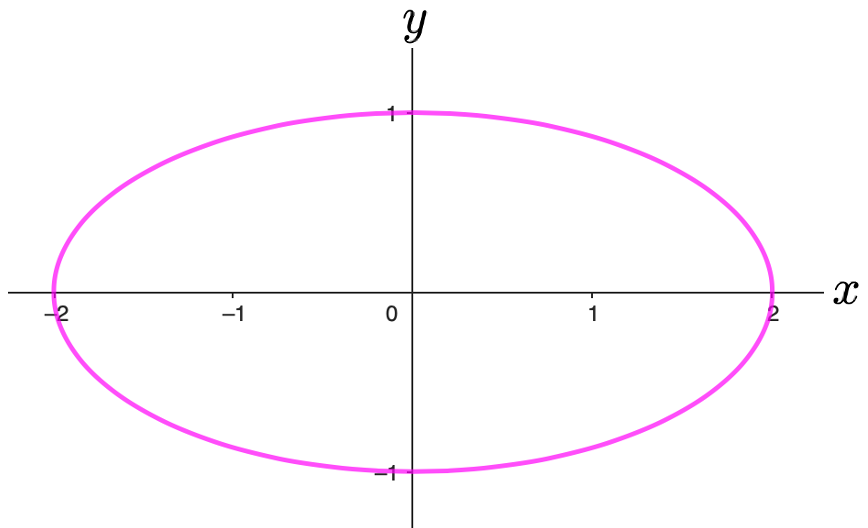
円は中心からの距離が一定の点の集まりですが,楕円上の点は中心からの距離が一定ではありませんね。上の楕円上で中心である原点から最も離れているのが点(2,0)と点(ー2,0)です。このときの2を長半径,点(2,0)と点(ー2,0)を結ぶ線分を長軸と言います。一方で,原点に最も近い楕円上の点は点(0,1)と点(0,ー1)であり,このときの1を短半径,点(0,1)と点(0,ー1)を結ぶ線分を短軸と言います。そして,次の式が上の楕円を表す方程式です。

上の楕円の方程式を行列を使って表すと,次のようになります。
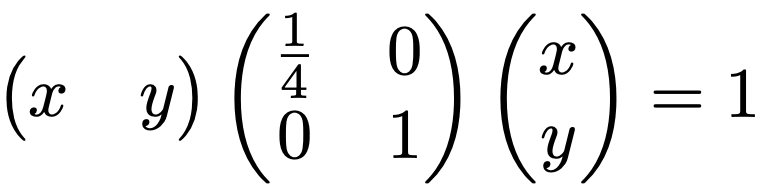
上の式の左辺の真ん中にはさまれている行列が単位行列(の正のスカラー倍)ならば円の方程式になりますが,対角成分に異なる正の数が並ぶと楕円になります。
さて,上の方程式が楕円を表すことを納得するため,円の方程式との関係を確認してみましょう。まず,点(a,b)が単位円上にあるとき,a2+b2=1が成り立ちますよね。次に,点(a,b)のx座標だけを2倍すると点(2a,b)に移りますが,a2+b2=1であることから,x=2a,y=bは上の楕円の方程式を満たしています。つまり,上の楕円の方程式は,単位円上の点のx座標だけを2倍した点の集まりです。
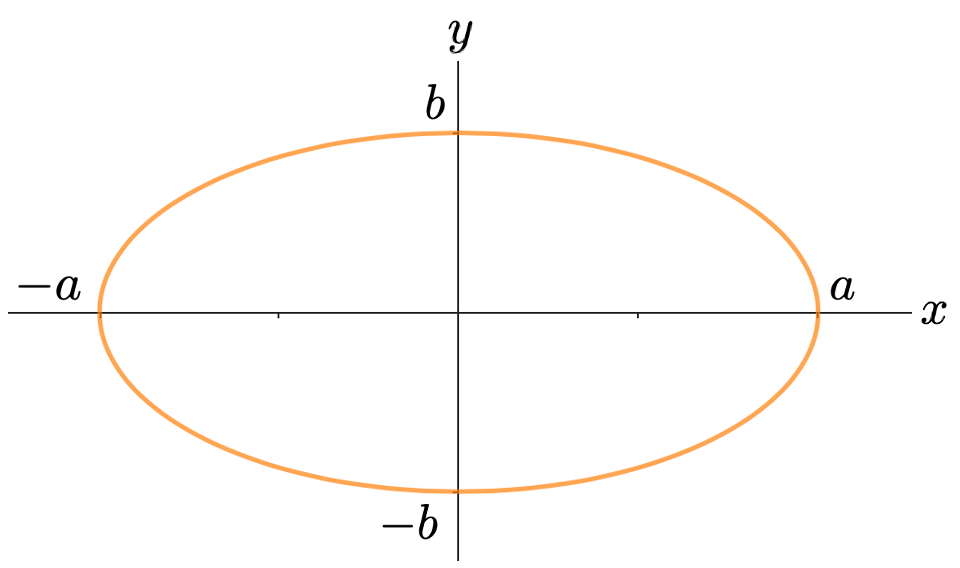
より一般的に,楕円の標準形は,a>0,b>0として,次の方程式で表されます。
この方程式のグラフは,次の図のようにx軸との交点が(±a,0),y軸との交点が(0,±b)であるような楕円になります。
さて,ここからが本題です。次の式は実は楕円の方程式です。
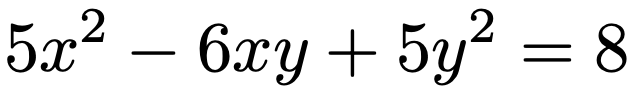
楕円の標準形とは形が異なるので,楕円の方程式かどうかがわかりにくくなっています。そこで,座標系をx,y以外のものにとりかえることで,楕円の標準形に書き直してみましょう。まずは上の方程式を次のように行列を使って書き直します。
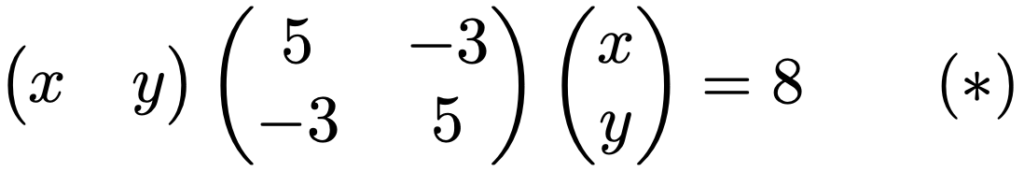
これまで学習してきた行列の積の計算ルール通りに左辺のベクトルと行列の積を計算すれば,もとの方程式と一致することが確かめられるはずです。左辺の中央に現れた行列が次の式の右辺の行列の積に等しいことを,次のセクションで説明します。
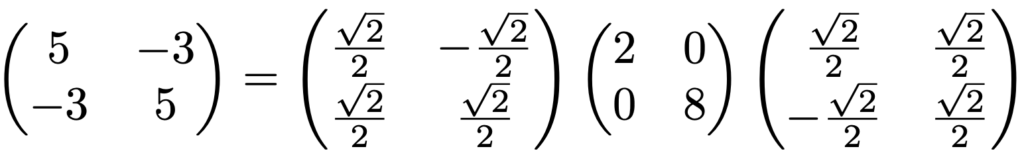
このことをいったん認めて,(*)の式に代入すると,次のようになります。
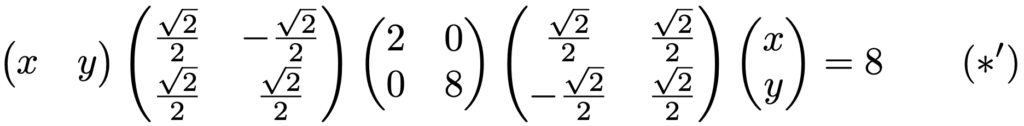
ここで,新しい座標(X,Y)を次の式で定めることにします。
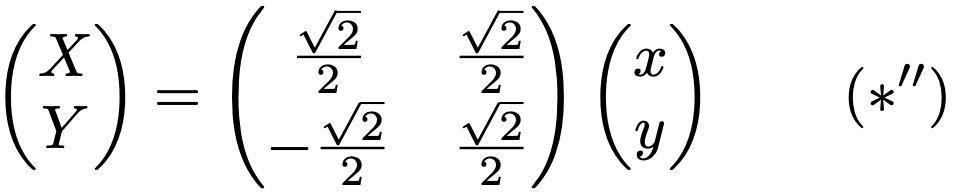
(X,Y)を使うと,(*’)の式は次のように変形できます。
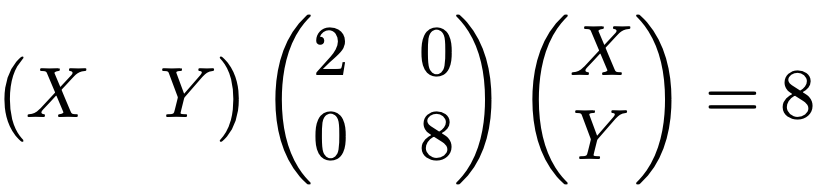
再び,行列の積の計算ルール通りに左辺のベクトルと行列の積を計算すれば,次の方程式が得られます。
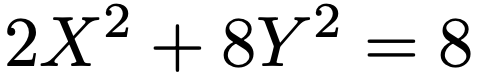
両辺を8でわると,次のような楕円の標準形の方程式が得られます。
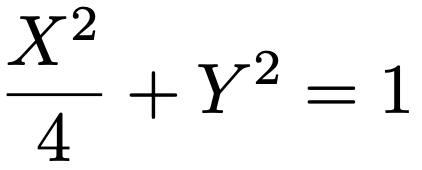
というわけで,もとの座標(x,y)で表示したときの楕円の方程式は「xyの項」を含んでおり,標準形ではなかったのですが,新しい座標(X,Y)で方程式を表示し直すと,標準形で表すことができました。なぜこんなことができるのかを考えてみましょう。(*”)の座標変換の式に,右辺の行列の逆行列を左からかけることで,次の式になります。
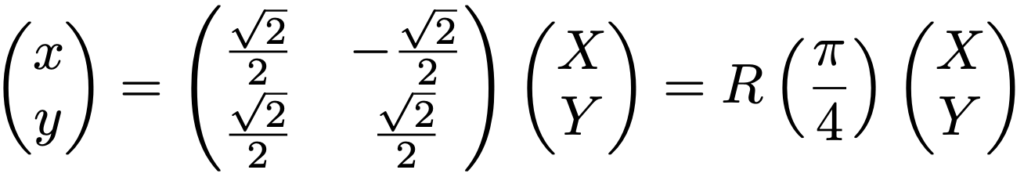
この式から,XY座標軸は,xy座標軸を原点を回転の中心として反時計回りに45°回転したものであることがわかります。つまり,ここで考えていた楕円は,次の図のように長軸がX軸,短軸がY軸の方向を向いているために,(X,Y)座標で表すと標準形で表されるのです。
固有値と固有ベクトル
前のセクションでは,次のような行列の計算を利用することで,楕円の方程式を標準形になおすことができることを示しました。
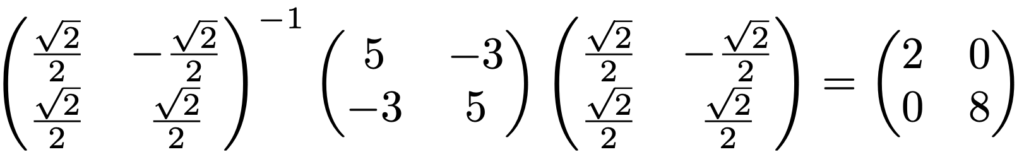
上のように,もとの行列(左辺の中央の行列)に左右から正則行列とその逆行列をかけることで対角行列にする変形を対角化と言います。どんな行列でも対角化できるわけではないので,対角化できる行列は対角化可能であると言います。
では,もとの行列が対角化可能である場合,左右からどんな行列をかければ,上のように対角化できるのでしょうか。その鍵になる固有値と固有ベクトルを定義しておきましょう。Aを正方行列として,ある数λに対して,次の式を満たすゼロベクトルでないベクトルvが存在するとき,λを固有値,vを固有ベクトルと言います。
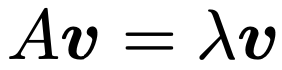
ベクトルに行列を左からかけると,ベクトルの向きが変わるのが普通ですが,固有ベクトルの場合には向きが変わらずに,λ倍の伸縮だけになるというのが上の式が主張していることです。とは言え,具体的に固有値や固有ベクトルを求めてみないと理解しにくいでしょうから,求め方の話に進みます。上の固有値を定義する式で,項を左辺にまとめると次の式になります。

もし,左辺の行列(AーλI)が正則であれば,上の式の両辺に(AーλI)の逆行列を左からかけることで,v=0となってしまいます。固有ベクトルはv≠0を満たすベクトルなので,(AーλI)が正則であれば,固有ベクトルは存在しないことになります。よって,固有ベクトルが存在するならば,(AーλI)が正則でない,つまり逆行列を持たないことが必要であり,このとき,次のように(AーλI)の行列式が0という式が成り立ちます。

固有値は上の方程式を解くことで求めることができます。実際に,前のセクションで取り上げた次の行列Aの固有値を計算してみましょう。
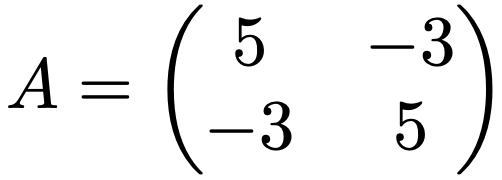
この行列AからλIをひいた行列の行列式が0となるように,次の方程式をつくります。
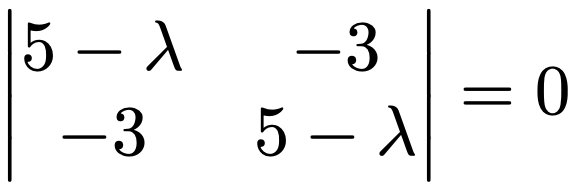
左辺の行列式を計算して方程式を解くと,次のようになります。
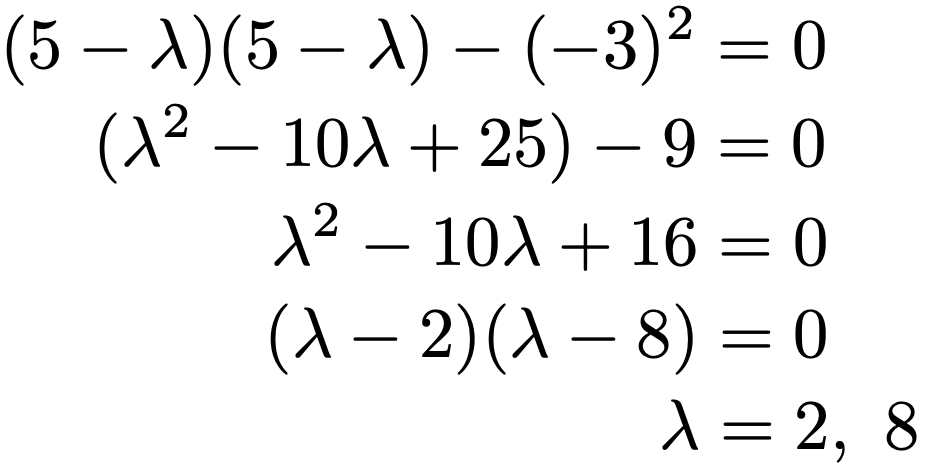
これで固有値が2と8であることがわかりました。次に固有ベクトルを求めます。固有値2に対する固有ベクトル(x,y)Tは次の式を満たします。
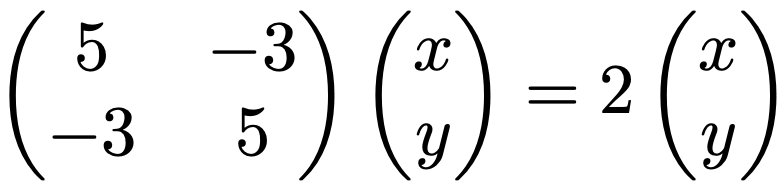
左辺の行列とベクトルの積を計算すると,次の連立方程式が得られます。
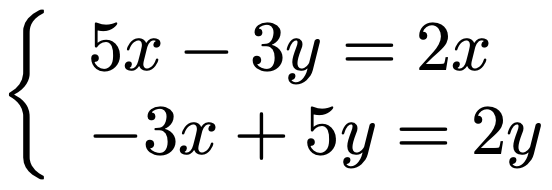
それぞれの式を整理すると,どちらもx=yになります。固有ベクトルは,この式を満たすようにとればいいので,無数の決め方がありますが,ここでは長さが1である次の(x,y)Tを選ぶことにしましょう。
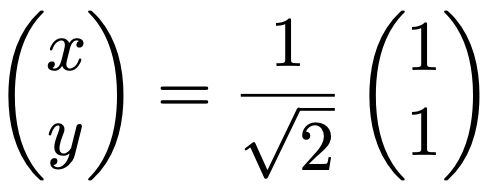
これが固有値2に対する固有ベクトルです。次に固有値8に対する固有ベクトルは,次の式を満たす(x,y)Tです。
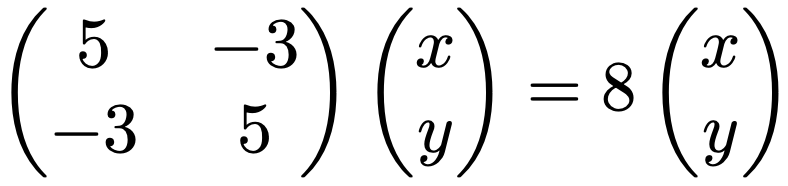
左辺の行列とベクトルの積を計算すると,次の連立方程式が得られます。
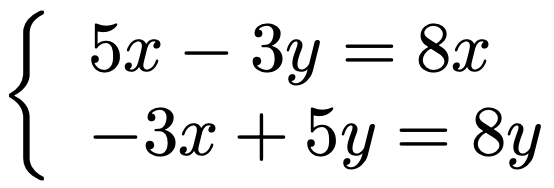
それぞれの式を整理すると,どちらもx=ーyになります。固有ベクトルは,やはり長さが1になるように次の(x,y)Tを選ぶことにしましょう。
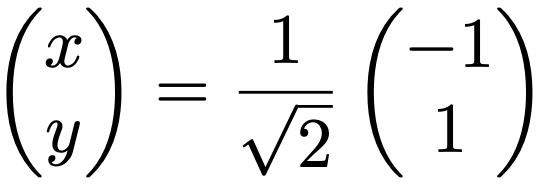
これが固有値8に対する固有ベクトルです。これで2組の固有値と固有ベクトルが求められました。もう一度ふり返ると,固有値2については次の式が成り立っていました。
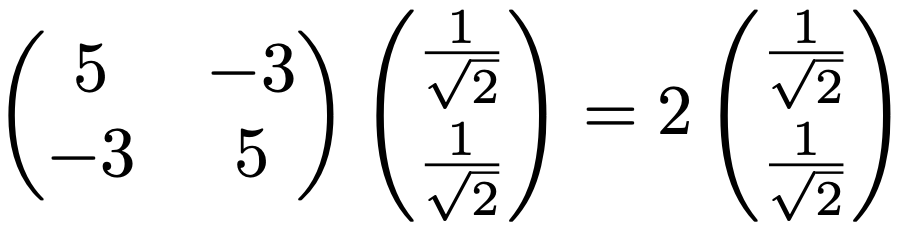
また,固有値8については次の式が成り立っていました。
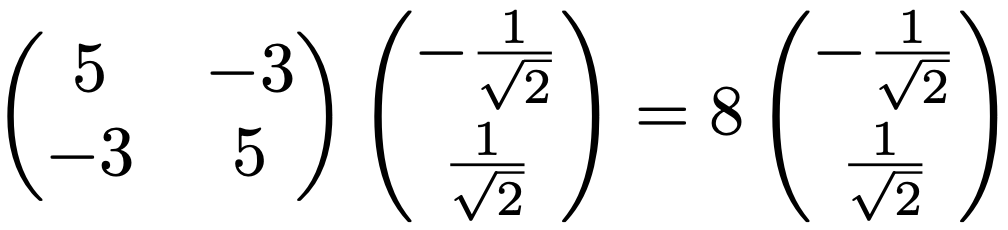
上の2本の式をまとめて次のように表すことができます。
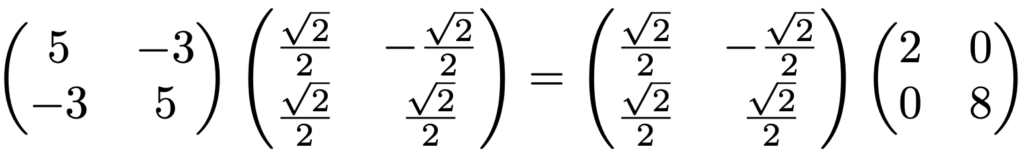
両辺の左の行列と右の行列の第1列の積が固有値2に関する等式,右の行列の第2列との積が固有値8に関する等式になっています。これらの固有ベクトルを並べてできた行列をPと表すと,もとの行列はAだったので,次のようになります。
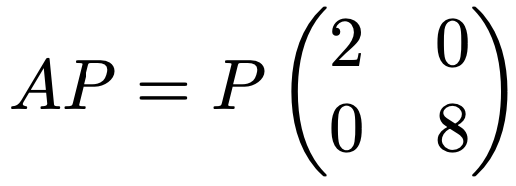
両辺に左からPー1をかけると,次のように表せます。
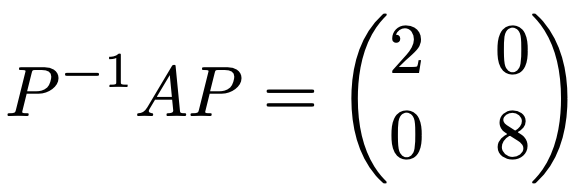
A自体は対角行列ではありませんが,このようにPー1APが対角行列に等しくなるようにPを選ぶことができたわけです。これが対角化です。このように,n次正方行列が互いに異なるn個の固有値をもつならば,そのn本の固有ベクトルを並べた行列をPとして,もとの行列を対角化することができます。
さて,上の式の両辺に左からP,右からPー1をかけると次のようになります。
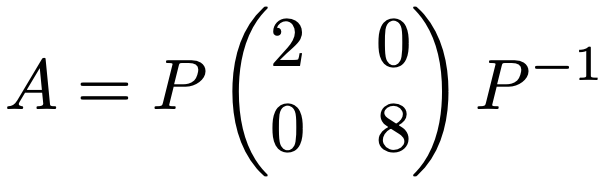
上の式を使うと,Anを比較的簡単に計算することができます。実際に,行列Aの2乗,3乗,…を計算して,10乗や100乗がどんな行列になるかを予想してみてください。結構,難しいです。しかし,上の式を利用することで,10乗の計算も100乗の計算も劇的に簡単になります。ここでは,成分の桁数が大きくなりすぎるため,A5を計算することにします。まず,固有値を対角成分に並べた対角行列をΛと表すと,Anは一般的に次のように計算できます。
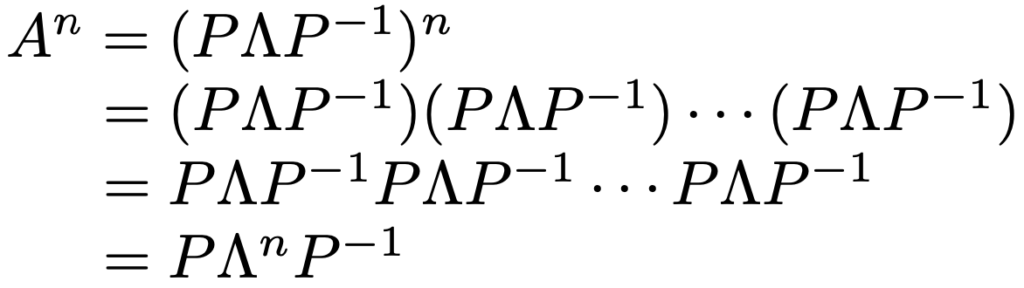
上の計算の3行目から4行目で,途中のPー1Pがことごとく単位行列Iになることが1つ目のポイントです。2つ目のポイントは,対角行列Λのn乗は対角成分をn乗すればいいので,簡単に計算できるということです。よって,今の例では,A5は次のように計算できます。
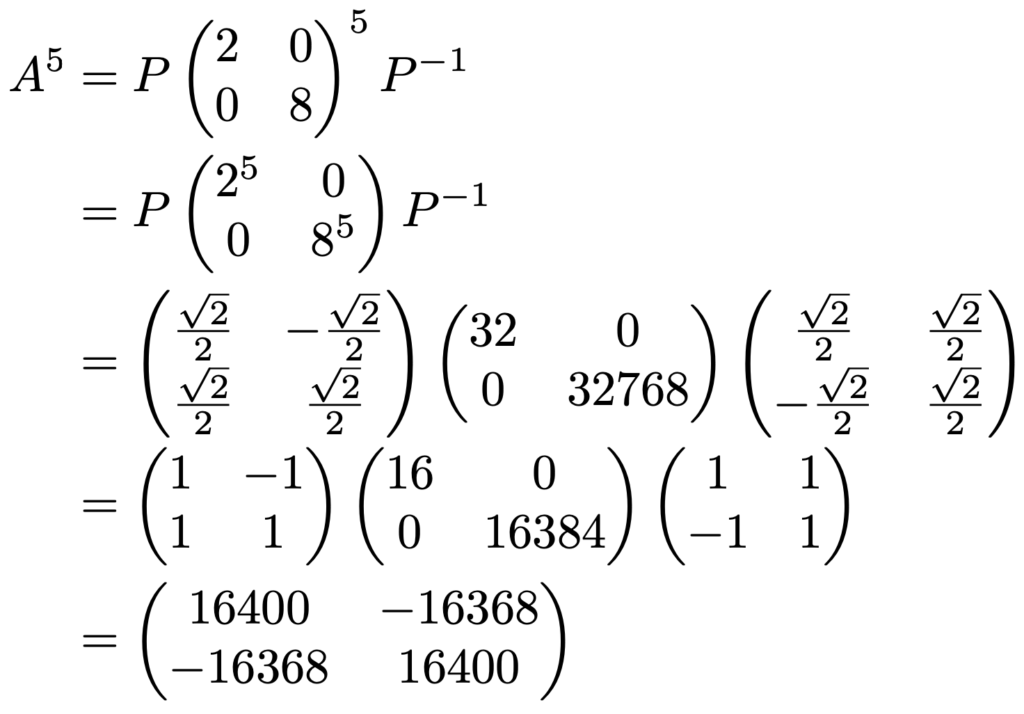
楕円を標準形に変形するだけでなく,このように行列のn乗も対角化を利用すれば簡単に計算できるのです。
なお,固有値はつねに実数とは限りません。例えば,次の行列を考えてみましょう。
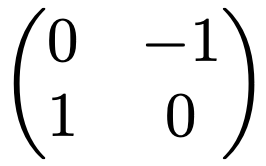
この行列の固有値は,次の行列式を「=0」とおいた方程式の解なので,実数の範囲では解をもちません。

しかし,次のセクションで説明する(実)対称行列の場合には固有値は実数であることが保証されます。
対称行列
正方行列AがAT=Aを満たすとき,Aを対称行列と言います。つまり,転置行列がもとの行列と一致するような行列です。ここで,前のセクションで扱った行列を思い出すと,次の左辺の行列は対角化を利用して右辺のように表せました。
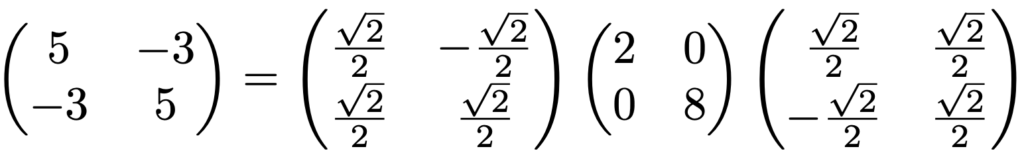
左辺の行列は,転置行列がもとの行列と一致するので対称行列です。右辺のいちばん左の行列は45°の回転を表す回転行列で,いちばん右の行列はー45°の回転を表す回転行列なので,次のように書き直せます。
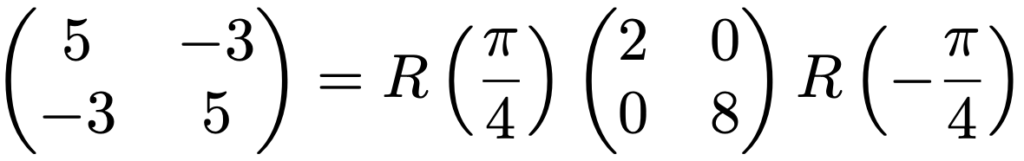
回転行列は直交行列でしたね。対角化するときに使う正則行列Pがいつでも直交行列になるわけではありませんが,今の場合にはもとの行列が対称行列であったために,Pを直交行列にとることができました。実は,対称行列には,異なる固有値に対する固有ベクトルは互いに直交するという著しい特徴があり,ノルムを1にした直交する固有ベクトルを並べて正則行列をつくると,直交行列になります。それが上の回転行列です。
では,回転行列と成分が実数の対角行列の積に分解できると何が良いのかを説明します。一言で言えば,この対称行列による一次変換のようすが克明に理解できます。上の行列は成分がやや大きいので,両辺を2分の1倍した次のBという行列で考えてみましょう。
次のように,ベクトル(x,y)Tに対称行列Bを作用させることは,右辺の3つの行列を右から順番に作用させることと同じです。
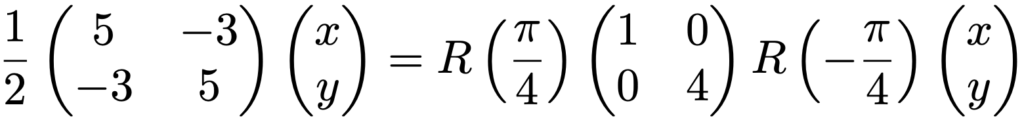
次の図は,長さが1である8つのベクトルを考え,矢印の先を点で表したものです。回転の様子がわかるように1つだけ色を変えてあります。はじめに原点を回転の中心としてー45°回転すると,次のようになります。
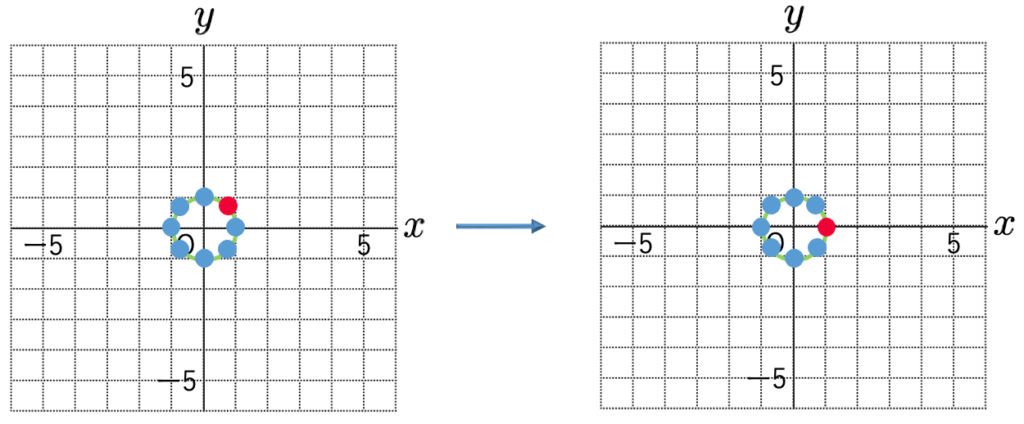
今度は対角行列を作用させて,次のようにx座標を1倍,y座標を4倍します。
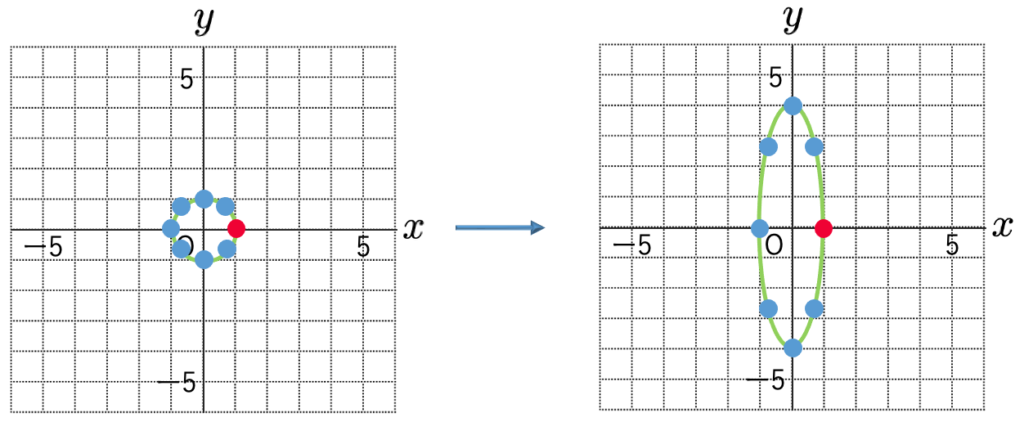
さらに,原点を回転の中心として45°回転すると,次のようになります。
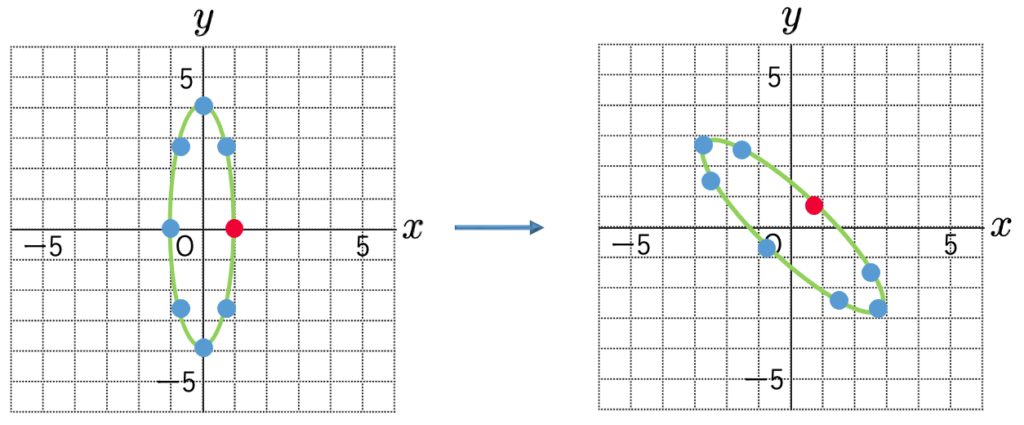
結局,Bという行列による一次変換では,円が楕円に移りましたね。楕円の長軸,短軸は,固有ベクトルの方向と一致しているということに注意しましょう。
次に,一般的に,n次対称行列Sが互いに異なるn個の固有値λ1,λ2,…,λnをもつものとしましょう。これらの固有値に対するノルム1の固有ベクトルをそれぞれq1,q2,…,qnとすると,これらは互いに直交し,次の行列はn次直交行列になります。
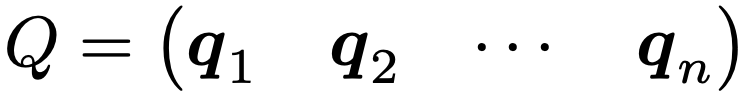
対称行列Sは,この直交行列Qを使って次のように対角化できます。

ただし,Λは次のように対角成分にn個の固有値を並べてできる対角行列です。
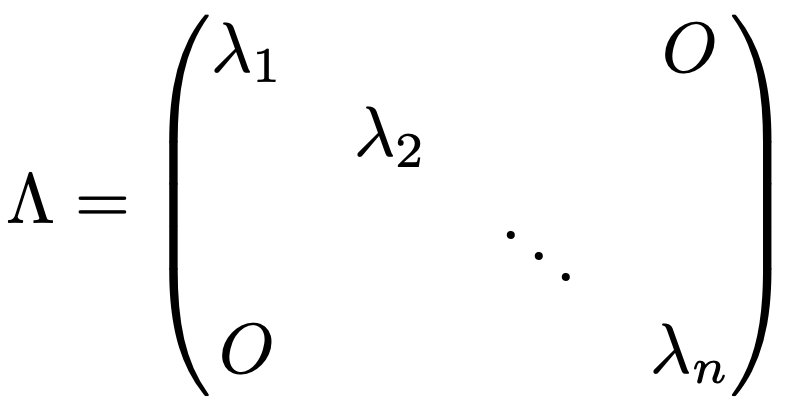
上のSを対角化した式の両辺に,左からQ,右からQTをかけると,Sは次のように表すことができます。
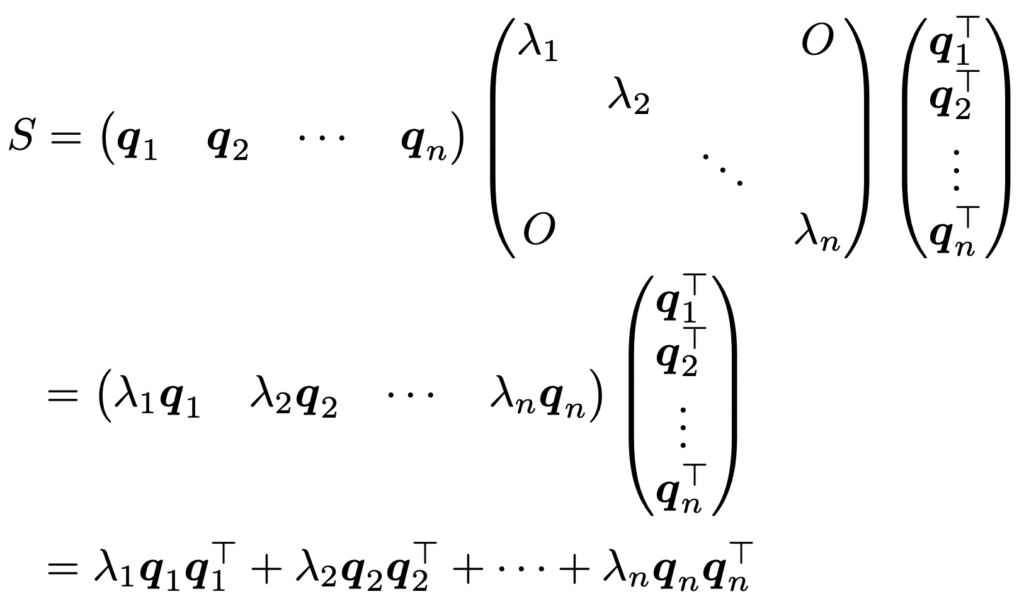
特に,上の3行目の形を対称行列Sのスペクトル分解と言います。スペクトル分解は主成分分析や因子分析で本質的な役割を果たします。これは,次のセクションで説明する分散共分散行列が対称行列であることに起因します。
スペクトル分解の式に登場しているqiqiTは,それぞれの固有ベクトルの方向へ射影するような射影行列ですね。このことを,前のセクションで対角化した行列Aを例として,具体的に確認していきましょう。まず,行列Aのスペクトル分解は次のようになります。
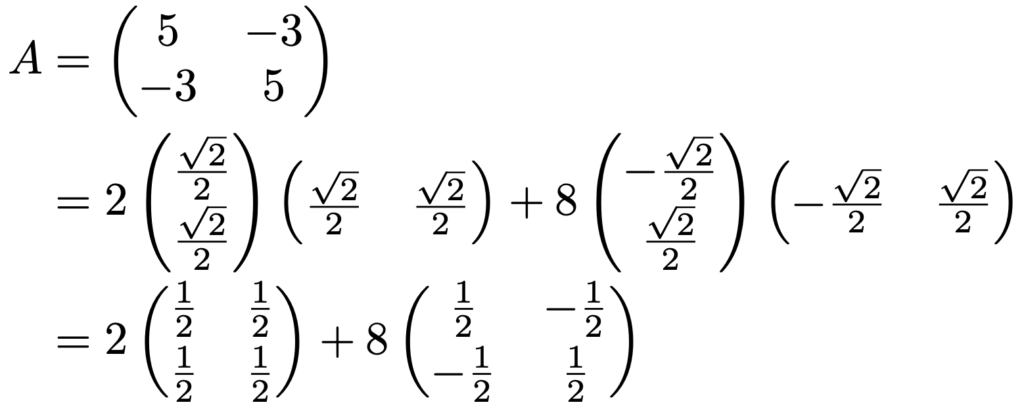
例えば,上の行列Aをベクトル(4,2)Tに作用させると,次のようになります。
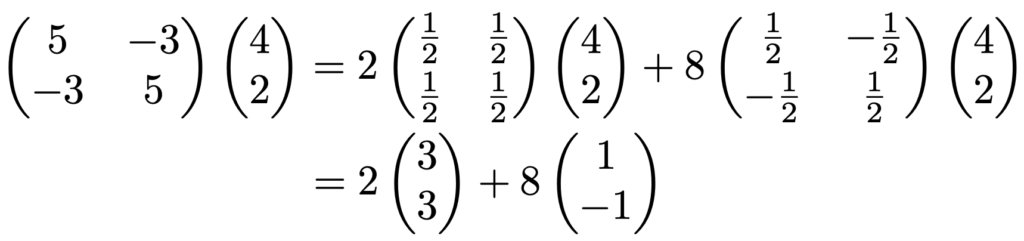
この一次変換を図に表すと,次のようになります。
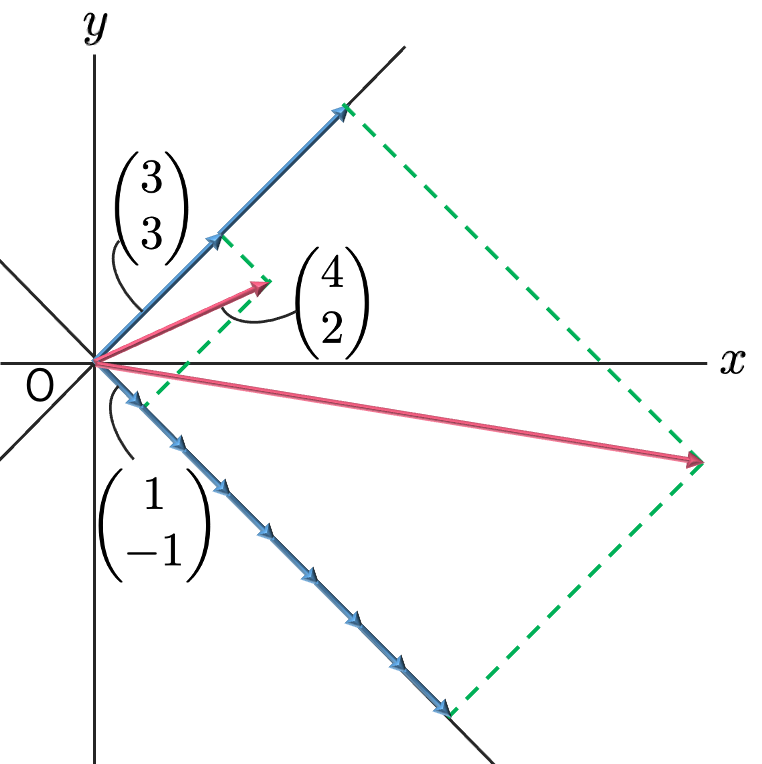
ベクトル(4,2)Tを固有値2に対する固有ベクトルの方向に射影すると,(3,3)Tになり,固有値8に対する固有ベクトルの方向に射影すると,(1,−1)Tになるので,射影されたベクトルをそれぞれ2倍,8倍して再び合成してできるベクトルが(4,2)Tの移る先になるわけです。対称行列による一次変換は,このような固有ベクトルの方向への射影を固有値倍する操作を加えたものに等しくなります。
また,対称行列Sのn個の固有値λ1,λ2,…,λnの中に0が含まれていなければ,Sは逆行列をもち,Sー1は次のスペクトル分解をもちます。
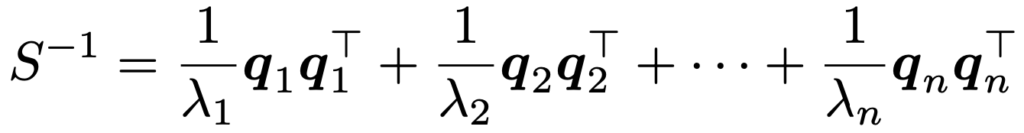
実際に,S=QΛQTとQΛー1QTの積を計算すれば単位行列Iに等しくなることから,Sー1=QΛー1QTであり,このことから上のSー1のスペクトル分解が導けます。
さて,この後のセクションのためにいくつかの言葉を定義しておきます。Aをn次対称行列,xをn次元ベクトルとして,xTAxをAによる2次形式と呼びます。例えば,x=(x,y)Tとして,原点を中心とする半径rの円の方程式は,xT Ix=r2と表すことができ,Dを対角成分が正の対角行列とすれば,楕円の方程式の標準形は,xTDx=1と表せました。2次形式というのはこれらの方程式の左辺のような2次の多項式です。
また,円の方程式の左辺xT Ixはx=(x,y)Tと原点との距離の2乗とも解釈できましたよね。実は,楕円の方程式の左辺xTDxも2つの座標が対等ではないような一般化された距離の2乗と解釈することができます。例えば,入学試験の傾斜配点では,国語と数学の点数を単純に合計せずに,数学の点数だけを2倍するなどの操作をして,あえて対等には扱わないようにしますが,それと同じように変数ごとに扱いを変えたときの距離の2乗がxTDxです。最後のセクションで登場するマハラノビス距離も,このような2次形式で定義される一般化された距離の仲間です。そこで,これらの一般化された距離と区別して,xT Ixの正の平方根で表される通常の距離をユークリッド距離と呼びます。
さて,対称行列Sによる2次形式によって,次のような距離を定めたいとします。
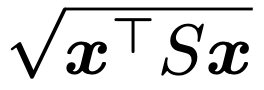
そのためには,どんなxに対しても2次形式xTSxが0以上でないと,ルートの中が負の数になって困ってしまいます。そこで,2次形式の符号を考えます。どんなxに対しても2次形式xTSxの符号が一定であるとき,Sを定符号行列と言い,どんなxに対してもxTSx≧0が成り立つとき,Sを半正定値行列(または非負定値行列)と言います。また,どんなx≠0に対してもxTSx>0が成り立つとき,Sを正定値行列と言います。よって,2次形式xTSxに用いる行列Sが(半)正定値であれば,上のように距離が定義できます。
唐突に正定値という概念が出てきましたが,「どんなx≠0に対してもxTSx>0」という定義ではわかりにくいですよね。わかりやすく表現し直すと,対称行列Sが正定値行列であるとは,Sの固有値がすべて正であるということです。例えば,2次対称行列Sの固有値λ1,λ2が正であるとき,直交行列Qを用いてSを次のように表したとしましょう。
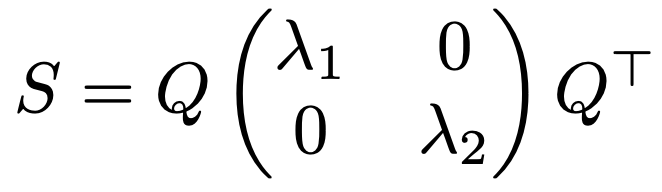
このとき,x≠0に対して,Sによる2次形式は次のように正になります。
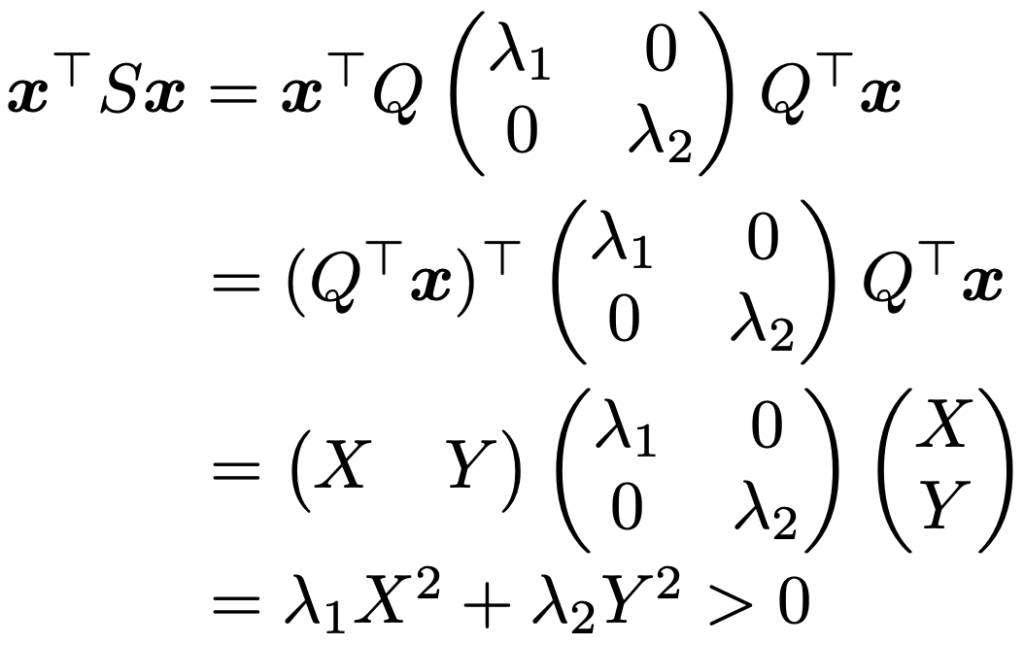
ただし,上の計算の2行目から3行目の変形では,次のようにおきました。
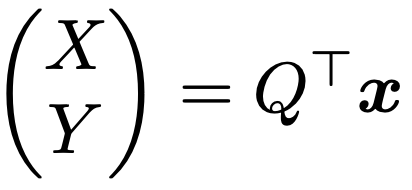
x≠0の場合を考えると,(X,Y)T≠0も成り立つため,λ1X2+λ2Y2>0となります。本稿ではここまでにしておきますが,逆にSが正定値行列であれば,Sの固有値がすべて正であることも示すことができます。
分散共分散行列
ここまで学習してきた線形代数の知識を使うと,多変量のデータを効率よく扱うことができます。まず,確率変数をベクトルの形でまとめて表したものを確率変数ベクトルと言い,k次元の確率変数ベクトルx=(x1,x2,…,xk)Tに対する平均ベクトルを次の式で定義します。
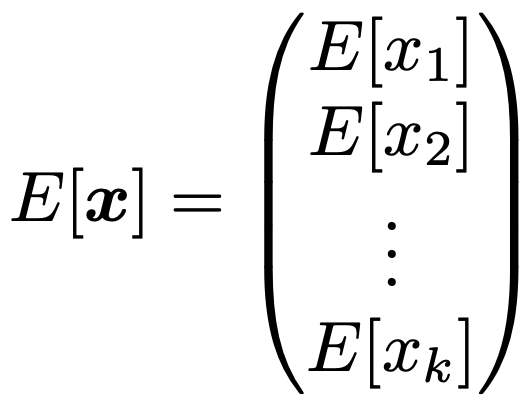
上のxに対して,Aをr行k列の行列,bをr次元の定数ベクトルとして,次の式が成り立ちます。
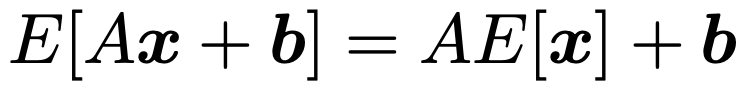
1変数の確率変数について成り立ったE[aX+b]=aE[X]+bという公式と同じ形の式が確率変数ベクトルに対して成り立つのは驚きですね。上の式が成り立つことは,両辺の第i成分に着目すると,Aの(i,j)成分をaij,bの第i成分をbiとして,期待値の性質によって次の等式が成り立つことからわかります。
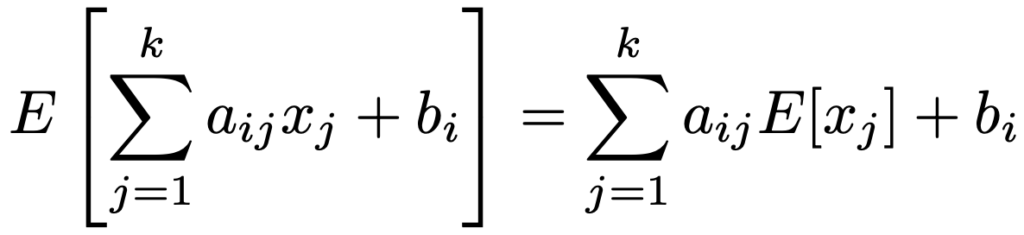
次に,多次元のデータの散らばりの表し方を考えてみましょう。例えば,2次元のデータの場合,次の図のように横軸方向の分散と縦軸方向の分散に分けて計算すれば良さそうです。
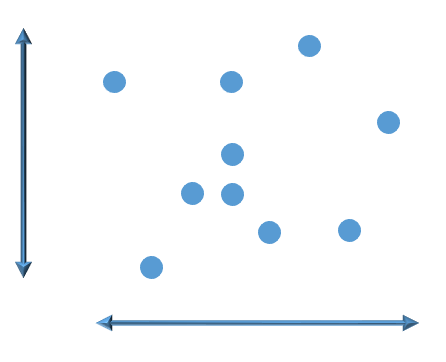
次のデータは,上のデータと横軸方向の分散も縦軸方向の分散もほぼ同じです。しかし,上のデータはほぼ無相関であるのに対して,次のデータには正の相関があります。
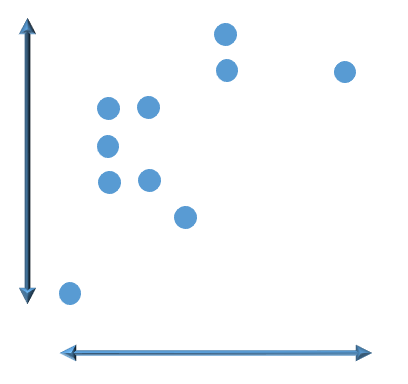
このように,各変数の分散を考えるだけでは上の2組のデータを区別することができないので,多次元のデータでは分散に加えて変数間の共分散(または相関係数)の情報まで把握することがデータの分布の理解に役立ちそうです。そこで,これらをまとめて1つの行列に表したものが分散共分散行列(または共分散行列)であり,x=(x1,x2,…,xn)の分散共分散行列とは,次のようにn個の確率変数x1,x2,…,xnについて,Cov[xi,xj]を(i,j)成分に並べてできるn次正方行列です。
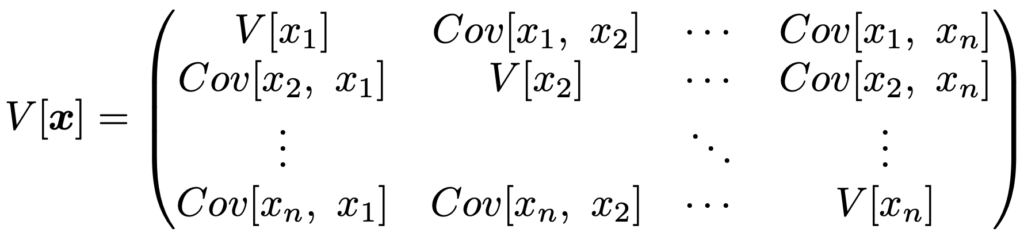
Cov[xi,xj]=Cov[xj,xi]であるため,分散共分散行列は対称行列です。
いきなりn変数だとわかりにくいという場合には,2変数の場合から考えましょう。そのときの分散共分散行列は次のように表されます。
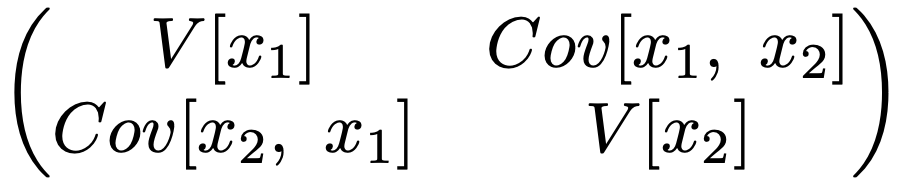
上の2次正方行列で,例えば,V[x1]=V[x2]=1,Cov[x1,x2]=0とすれば,次のような単位行列になります。
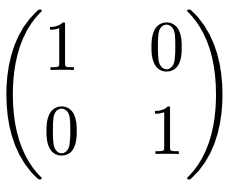
このように,x1とx2が無相関であれば,分散共分散行列は対角行列になります。n変数の場合でも,すべての変数が互いに無相関であれば,分散共分散行列は対角行列になりますね。
さて,1変数の分散は次のように定義しました。
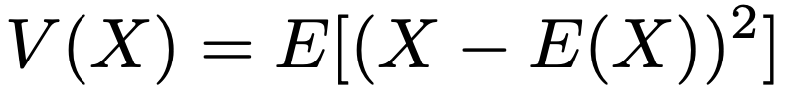
同じように,ベクトルx=(x1,x2,…,xn)Tに対して,平均ベクトルをE[x]=(E[x1],E[x2],…,E[xn])Tとすると,次の式が成り立ちます。
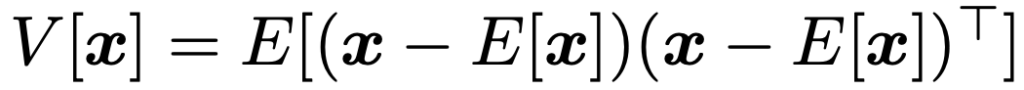
ただし,成分が確率変数である行列を確率変数行列と言い,確率変数行列X=(xij)に対して,E[X]=(E[xij])と定めるものとします。この式が成り立つことを示しておきます。E(xi)=μi(i=1,2,…,n)とおくと,
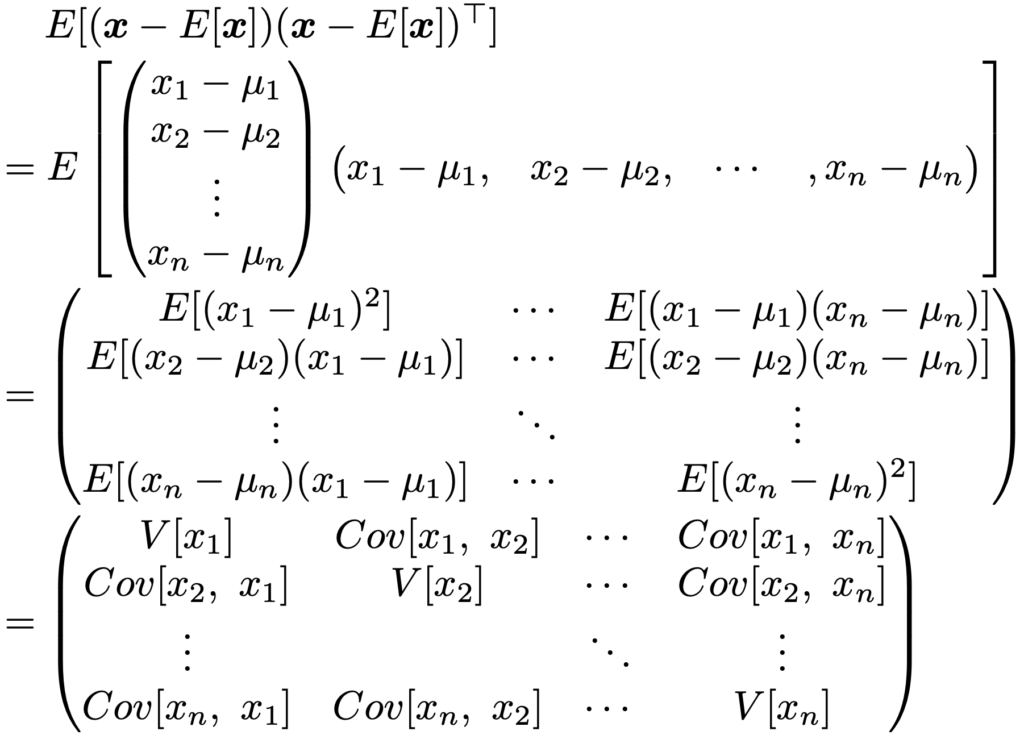
ところで,分散共分散行列が対称行列であることはすでに述べましたが,実は半正定値でもあります。なぜなら,任意のn次元ベクトルaに対して,次のようになるからです。
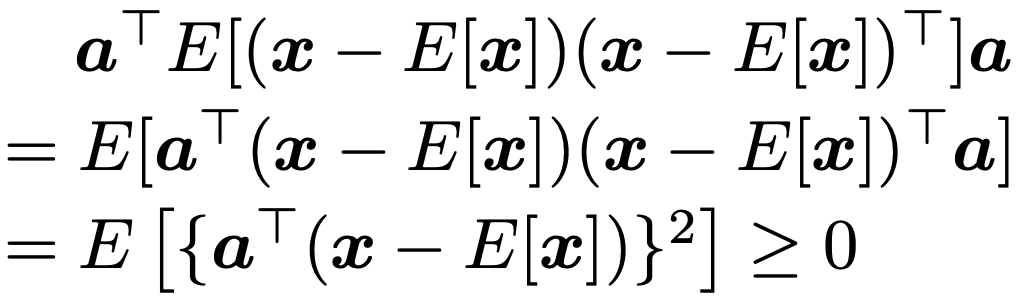
上の計算の1行目から2行目では,確率変数行列Xをk×ℓ行列,定数行列Aをm×k行列,定数行列Bをℓ×n行列として,E[AXB]=A・E[X]・Bという公式が成り立つことを使っています。この式にさらにm×n定数行列Cを追加して,E[AXB+C]=A・E[X]・B+Cという公式が成り立つので,その理由を述べておくと,X,A,B,Cの(p,q)成分をそれぞれxpq,apq,bpq,cpqとして,期待値の性質によって両辺の(i,j)成分について次の等式が成り立つことからわかります。
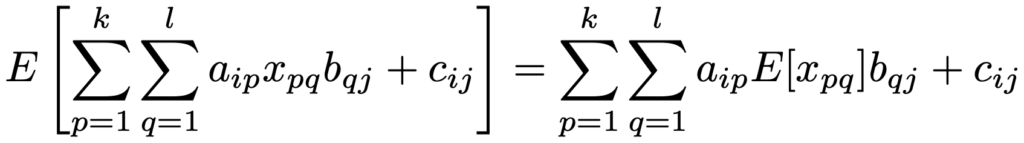
なお,分散共分散行列は必ずしも正定値であるとは言えません。例えば,データが(1,1),(1,ー1)の2つであるとき,その分散共分散行列は次の通りです。
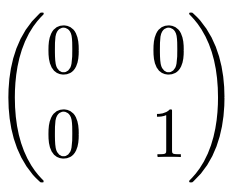
1つの固有値が0なので,正定値にはなりません。実際のデータ分析においては,母集団の分散や共分散はわからないのが普通なので,サンプルをもとに分散共分散行列を計算しますが,このような分散共分散行列は正定値であることが多いです。これを標本分散共分散行列と言い,次のセクションでは正定値であると仮定します。
マハラノビス距離
次の図は2変量のデータ(青い点)の散布図です。黄色い点はそれぞれの変量の平均を表しているものとします。
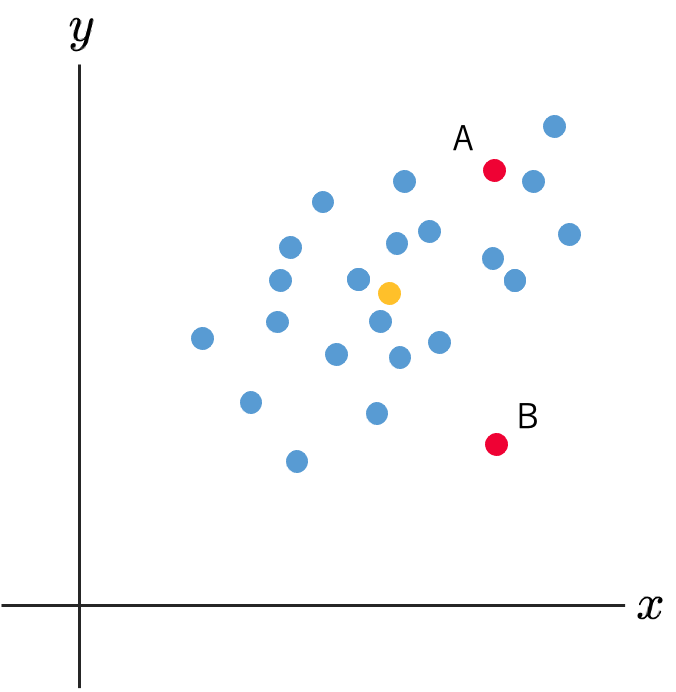
ここに新しいデータAとB(赤い点)を追加します。AとBはどちらも黄色い点とのユークリッド距離は等しいのですが,BよりもAのほうがもとのデータと同じ母集団から取り出されているような印象を受けます。それはデータに相関があるからです。このデータの母集団分布として2変量正規分布を仮定してみると,このことがよりはっきりします。次の図は,上のデータを2変量正規分布の確率密度の等高線と一緒に描いたものです。
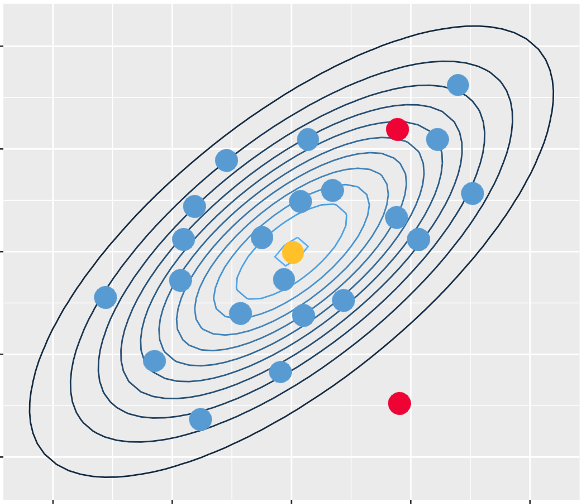
こうして見ると,Bの赤い点に対応するデータは,この母集団からは得られにくい(確率密度が小さい)ことがわかります。このような2変量正規分布の確率密度の等高線は黄色い点x=(x,y)からのマハラノビス平方距離が一定となる点の集まりであり,データ(x1,y1),(x2,y2),…,(xn,yn)の標本分散共分散行列をSとして,xとx=(x,y)のマハラノビス平方距離を次の式で定義します。
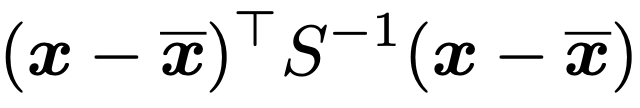
Sー1が対称行列であることから,マハラノビス平方距離は2次形式であることがわかりますね。その正の平方根がマハラノビス距離です。
さて,マハラノビス(平方)距離が一定となる点の集まりは楕円になります。次の式を見てください。rは正の定数です。
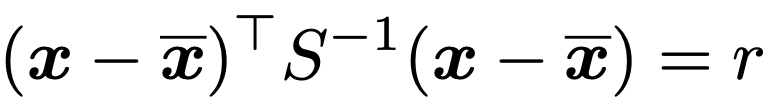
ここまで読んできてくれた人ならば,上の式が楕円を表していることは説明しなくてもわかると思いますが,確認してみましょう。まず,Sー1が正定値対称行列であることから,Sの固有値をλ1,λ2(λ1>0,λ2>0)として,適切な直交行列Qを使って次のように表せます。
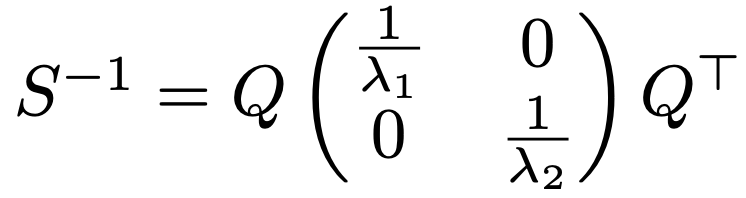
上の「…=r」の式で,xーx=zとおいて,Sー1の式を代入すると,次のように表せます。
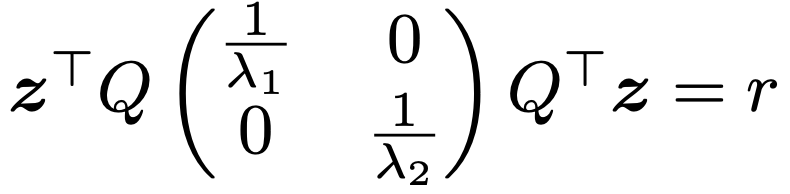
ここで,次のように新しい変数(z,w)Tをおきます。
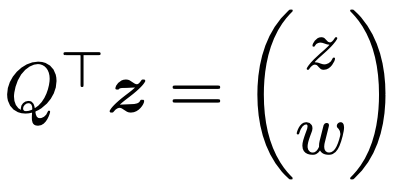
zTQ=(z,w)であることに注意すると,上の「…=r」の式は次のように変形できます。
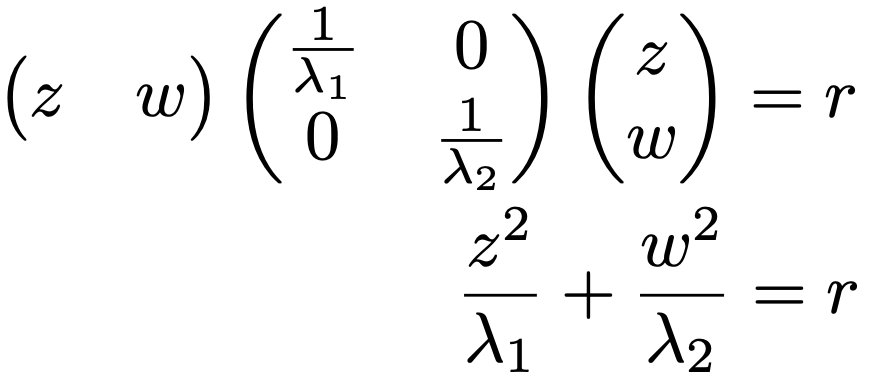
λ1>0,λ2>0より,これは楕円の方程式です。この楕円の長軸,短軸はrが大きいほど,長くなります。2変量正規分布の同時確率密度関数では,マハラノビス平方距離に負の係数がついているので,rが大きくなるほど,山を下りるように確率密度が小さくなっていきます。つまり,xとx=(x,y)のマハラノビス(平方)距離とは,データが多変量正規分布にしたがうことを仮定したとき,xがxからどのくらい離れた(等確率密度の)楕円上にあるかを計算しているのです。
なお,多変量正規分布については,統計検定準1級講座(リンクはこちら)で解説します。
参考図書
本稿を執筆するにあたり参考にした書籍を挙げておきます。線形代数を独学する際に役立つものばかりです。①,②,③は応用を念頭においた書籍,④と⑤は数学者の手による純粋に数学的な書籍,⑥はその両方の側面を持つ書籍です。
①機械学習のエッセンス(加藤公一,SBクリエイティブ)
本書は,Pythonを使って統計的なアルゴリズムを実装するための方法をゼロから解説した良書ですが,第3章だけは「機械学習に必要な数学」というタイトルで数学の解説にあてられています。この章では,集合を導入した後,50ページほどかけて線形代数の解説が続きます。ここでは,ベクトルや行列をはじめて学ぶ人でもわかるように基本的な演算の説明からはじまり,転置行列の性質,固有値や対称行列の正定値性など,準1級で必要な線形代数の知識をある程度カバーしています。数学が苦手でも読めるように易しく書かれているので,最小限の労力で合格したい人に適しています。本書の正誤表も出版社のサポートページに掲載されていますが,初版本は誤植が多いので,最新のものを購入されることをおすすめします。
②初歩からの多変量統計 (三土修平,日本評論社)
本書は,タイトルの通り,多変量解析のテキストであり,「主成分分析と因子分析は,線形代数的に何をやっているのか?」を説明するところに主眼があります。線形代数の解説にあてられているのは第5,6,9章で,多変量解析を理解するために必要な線形代数を「行列やベクトルとは何か」というところから説明してくれています。スペクトル分解という線形代数の知識が主成分分析や因子分析とどのように関わるのかを説明してくれているので,ぜひ読んでみてください。数学に苦手意識のある文系の学生を読者として想定しており,全体的に平易に書かれています。また,章末の練習問題も充実しており,巻末に解答もついています。
③計量経済学のための数学(田中久稔,日本評論社)
ワークブックの第16章(重回帰分析)を理解するくらいの線形代数を学びたい人は,本書の第Ⅰ部(第1〜6章)を読んでみてほしいです。ベクトルや行列を導入するところからはじまり,射影,対角化,2次形式あたりまでを具体的な例題を通して学ぶことができます。線形代数の学習項目のうち,計量経済学に直結する内容にしぼった構成になっており,特に射影の概念を通して回帰分析を理解することは本書の目標の1つであるようです。各章に演習問題がついており,解答も巻末に掲載されているので,具体的な問題を通して理解を深められるところが良いです。ただし,第Ⅱ部(第7〜11章)は測度論的確率論に踏み込むので,やや難しいです。
④手を動かしてまなぶ線形代数(藤岡敦,裳華房)
行列の基礎から対称行列の対角化までを,数学的な厳密さに配慮しつつ,読者が行間(論理の飛躍)を感じないように丁寧に解説した書籍です。正定値性の話題などは出てきません。また,連立方程式,置換,行列の指数関数,ベクトル空間など,準1級の勉強には不要な部分もありますが,質・量ともに重すぎず,数日間で読み通せる点が魅力です。各節末の問題だけでなく,本文中の例題も解説を読む前に自分で解くように進めると,タイトルの通り「手を動かして学ぶ」ことができます。節末の問題の略解は巻末についていますが,詳細な解説が見たい場合には出版社のホームページからPDFをダウンロードする必要があります。
⑤線型代数[改訂版](長谷川浩司,日本評論社)
2次行列を解説する第1部,n次行列の一般論を展開する第2部,ジョルダン標準形などの応用を解説する第3部という3部構成になっています。改訂版では,高校数学から行列がなくなったことを踏まえて,行列をはじめて学ぶ人でもわかるように0章を追加してくれています。準1級のための線形代数の勉強としては,3次以上の正方行列に関する一般的な議論はひとまず飛ばしても差し支えないので,まずは第1部で2次正方行列の固有値や対称行列の正定値性などを理解しましょう。本文の説明も丁寧で,章末の練習問題の解答も巻末にしっかり書かれており,十分に独習可能です。
⑥線形代数 基礎と応用(新井仁之,日本評論社)
500ページを超える厚い書籍で,射影,特異値分解,コレスキー分解など,多変量解析を本質的に理解するために大切な内容がもれなく扱われています。線形代数の数学的な扱いだけではなく,主成分分析や回帰分析にどのように応用できるかについても触れられています。数学的な理論は,複素行列の場合も含めて一般的な書き方をしているので,後半に進むにつれて難易度は高くなります。「与えられた行列に対して,基底のとり方を変えることで表現行列が対角行列にできる」ことのロジックなどが極めて明快に説明されており,数学的な本質をしっかりと理解したい人にオススメです。
本稿はここまでとなります。最後までお読みいただき,ありがとうございました!
引き続き,勉強をがんばっていきましょう!










コメント
3Cを勉強したことがない文系人間が、統計を学ぶことを目的として線形代数を理解するのに最適なコンテンツだと思います。ありがとうございます😊