「分散分析って何? 分散を分析するの?」「分散分析表の結果は読み取れるけれど,意味はよくわからない」なんて思いますよね。エクセルや統計ソフトを使えば,意味がわからなくても分散分析は実行できます。しかし,分散分析がどういう仮定のもとで成り立っているのかがわからなければ,結果を用いて正しい判断をすることは困難でしょう。また,近年の統計検定PBTでは,分散分析表を読み取るだけでなく,検定統計量の立式などの途中のプロセスを問うような問題も増えてきています。
そこで,この記事では,分散分析の初学者の人に向けて,分散分析のイメージと仕組みがわかるように,例題を解きながら,わかりやすく説明していきます。
この記事で前提とする知識は,第5回の記事で説明したΣΣ(シグマが2つ続く)の内容,第12回の母比率の差の検定の記事で説明したP値の内容,第13回の記事で説明したカイ二乗分布の性質,第14回の記事で説明したF分布の性質,第15回の記事で説明した母平均の差の検定の概念になりますので,これらの内容に不安がある人は,先にそちらの記事を読んでください。
では,はじめていきましょう!
分散分析とは
分散分析は,分散を使って,2群以上の母平均の差を検定する分析手法のことです。分散を分析するわけではありませんので,注意してください。2群の場合には,第15回で解説したt検定によって母平均の差の検定ができますので,3群以上の場合に使われることが多いです。また,分散分析は英語で,”analysis of variance”と呼ばれますので,これを略して「ANOVA(アノバ)」と呼ぶこともあります。
母平均の差の検定なので,帰無仮説は「すべての群の母平均が等しい」というものです。対立仮説は「すべての群の母平均が等しい」の否定なので,「少なくとも1つの群の母平均の値が異なる」となります。
さて,分散分析とはどういうものか,具体的に見ていきましょう。ここでは,例として,あるコンビニエンスストアの各店舗で,商品Aを陳列棚の上から何段目に並べるかによって,売れる個数に差があるかどうかを調べたいとしましょう。無作為に9店舗を選び,3店舗は1段目に,別の3店舗は2段目に,また別の3店舗は3段目に商品Aを並べたとき,1日の販売個数のデータが次の表のようになったとします。
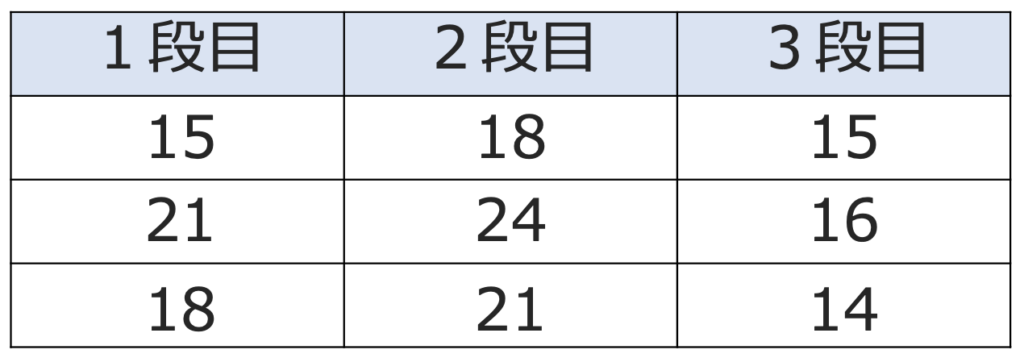
ここで,分散分析で重要な2つの言葉を紹介します。この例では,売れる個数に影響を与える可能性のあるものとして,「陳列棚の何段目に並べるか」に注目しています。このように,観測データ(この場合ならば,売れる個数)に影響を与える可能性のあるものを要因と言います。これと同じ意味で因子という言葉が使われることがありますが,この言葉は統計検定2級の問題文で使われていないので,この記事では使用しないことにします。
上の例では,1つの要因が,「1段目」,「2段目」,「3段目」という3つの場合に分かれています。このような要因がとりうる一つひとつの条件のこと(要因を独立変数とみなしたときの値に相当するもの)を水準と言います。この例では,3つの水準があり,3水準=3群の母平均の差の検定ということになります。各水準の標本の大きさは,同じでも異なっていても,どちらでもかまいません。
そして,タイトルにある一元配置分散分析というのは,要因が1つの分散分析のことを指します。二元配置分散分析と比べてみると,その意味がはっきりとわかるでしょう。次の表を見てください。
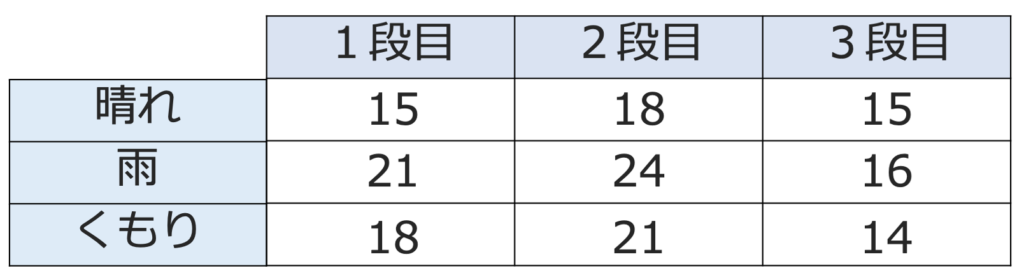
これは,「陳列棚の何段目に並べるか」という要因に加えて,「その日の天気」というもう1つの要因を追加したものです。このように,要因が2つの分散分析を二元配置分散分析と言いますが,統計検定2級では出題範囲外なので,この記事では扱いません。
さて,分散分析では前提条件として次の3つを仮定します。
- 観測値は独立であること(無作為標本)
- 各水準内でデータはほぼ正規分布に従う
- すべての水準で母分散がほぼ等しい
つまり,第15回で解説した等分散を仮定できる場合の2標本t検定と同等な仮定をおくことになります。
このセクションの最後として,分散分析の限界についてコメントしておきます。水準の数をm個とすると,分散分析によってわかるのは,これらのm個の水準のどこかに母平均が異なるものがある(可能性が高い)というだけであり,母平均が異なるのはどの水準なのかについてはわかりません。これを調べる方法を多重比較と言いますが,統計検定2級の範囲を超えるので,この記事では扱いません。
分散分析のイメージ
式を使った説明に入る前に,分散分析のイメージをつかんでおきましょう。次の図は,青と赤の2つの水準(正規母集団)について,無作為抽出された標本を,それぞれ青と赤の点で表したものです。背後にある母集団の平均(赤と青の縦線)がわからない状態で,標本だけを観察して母平均に違いがあるのかを判断したい状況を考えます。

この図の場合には,それぞれの母集団から抽出された標本の値だけを見ても,母平均に差がありそうだとわかりますね。このように,「水準どうしのバラツキ」のほうが「標本のバラツキ」よりも明確に大きいときには,標本だけを見て,母平均に差があることを確信できるわけです。
一方で,次の図はどうでしょうか。
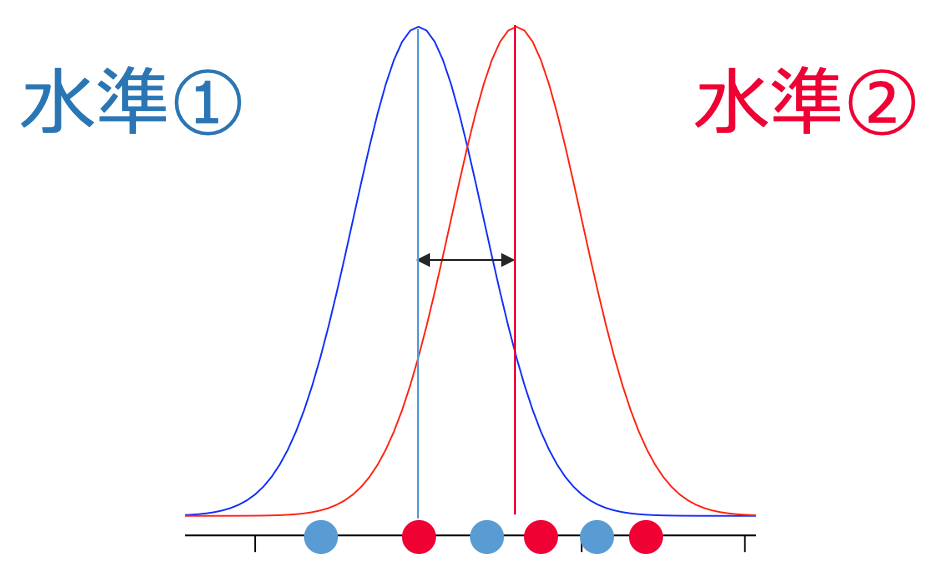
この図の場合には,2つの母集団の平均の差が小さく,標本だけを観察しても,母平均に差があるかどうかがわかりにくいですよね。つまり,「水準どうしのバラツキ」に比べて「標本のバラツキ」が大きいときには,標本だけを見て,母平均に差があるかどうかの結論を出すことは難しいわけです。
では,母平均に差があるという確信が持てるのは,「水準どうしのバラツキ」が「標本のバラツキ」に対してどれくらい大きいときでしょうか。この疑問に答えるため,次のセクションでは「水準どうしのバラツキ」と「標本のバラツキ」をそれぞれ式で表して,これらの大きさの比較がF分布につながっていくことを確認していきます。
分散分析の定式化
では,一元配置分散分析を式を使って一般的に捉えていきます。
1つの要因について,m個の水準があるものとします。標本の大きさを水準ごとに,n1,n2,…,nm(全部で,Σnj=Nとする)とし,各水準の母平均を,μ1,μ2,…,μmとすると,帰無仮説は次の式で表せますね。
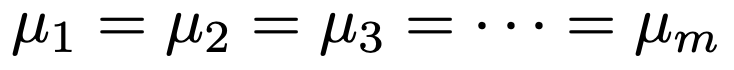
次に,j(j=1,…,m)番目の水準の標本を次のように表します。
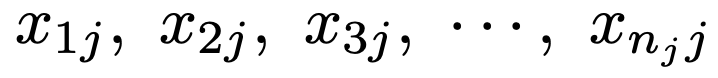
また,標本全体の平均とj(j=1,…,m)番目の水準に属する標本の平均を次のように表します。
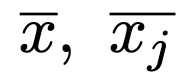
これらの記号を使って,すべての標本と標本全体の平均との偏差平方和は次のように表すことができます。
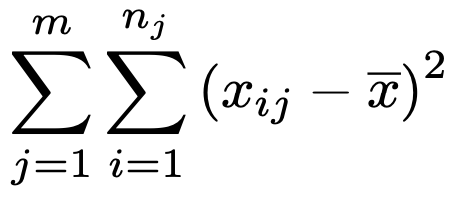
これを総平方和とか,全平方和と呼びます。この記事では後者で呼称することにします。ちなみに,この全平方和を標本の大きさでわったものが分散ですよね。
この全平方和が水準間のばらつきと標本誤差のばらつきに分解できるという事実が,分散分析の根幹となります。そこで,全平方和を次のように変形します。
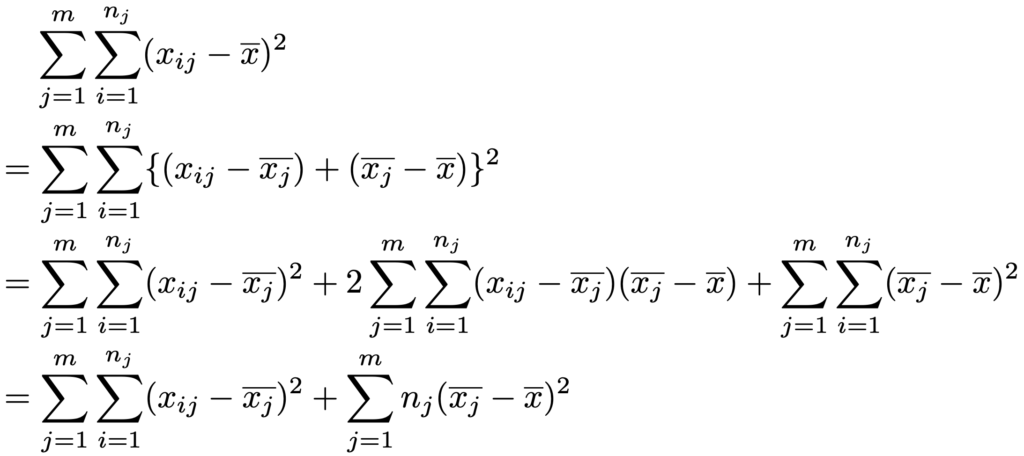
下から2行目の第2項が0になるのがポイントで,すべてのjについて次の式が成り立つことを使っています。
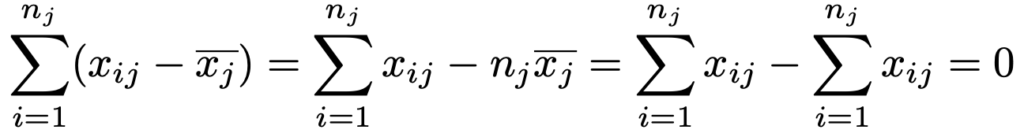
上の式変形によって,全平方和が最終的に2つの平方和で表されましたね。このうちの第1項が残差平方和で,次の式で表されます。
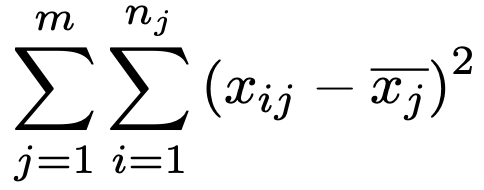
各水準内における標本と水準内平均との偏差平方和をすべての水準について加えたものです。
また,上の変形後の第2項が水準間平方和であり,次の式で表されます。
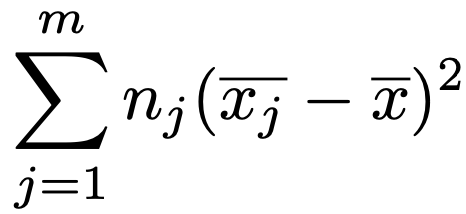
水準内平均と全体の平均の偏差平方和ですが,それぞれの平方を各水準の標本の大きさの数(=nj)だけ加えることに注意してください。
さて,大事なのは,これらを使うと,よく知られた確率分布に従う確率変数がつくれるということです。
そのことを確認するために,母分散をσ2として,3種類の平方和を母分散σ2でわってみましょう。帰無仮説を仮定すると,xijは1つの正規母集団からの大きさN(=Σnj)の無作為標本であるとみなせるので,第13回の記事で学習したことから,全平方和を母分散でわってできる次の確率変数は自由度Nー1のカイ2乗分布に従います。
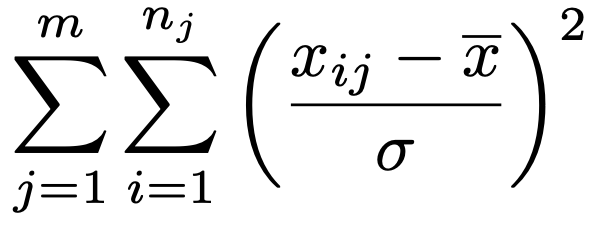
次に,残差平方和を母分散でわってできる次の確率変数もカイ2乗分布に従いますが,その自由度はどうなるでしょうか。

この式の一部である次の部分は,j番目の水準に対応していて,これは自由度njー1のカイ2乗分布に従いますね。
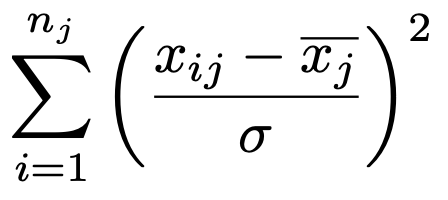
カイ2乗分布に従う独立な確率変数の和は,自由度がそれぞれの自由度の和に等しいカイ2乗分布に従う性質がありましたから,次のように,njー1をjについて和をとって,残差平方和を母分散でわってできる確率変数の自由度はNーmになります。
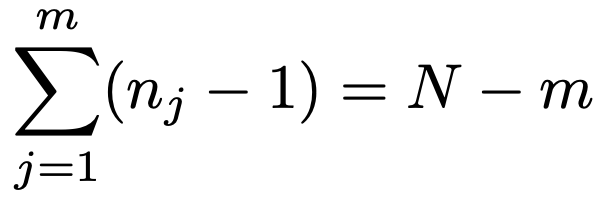
また,水準間平方和を母分散でわってできる確率変数は,次のような変形によって,帰無仮説のもとで自由度mー1のカイ2乗分布に従うことがわかります。
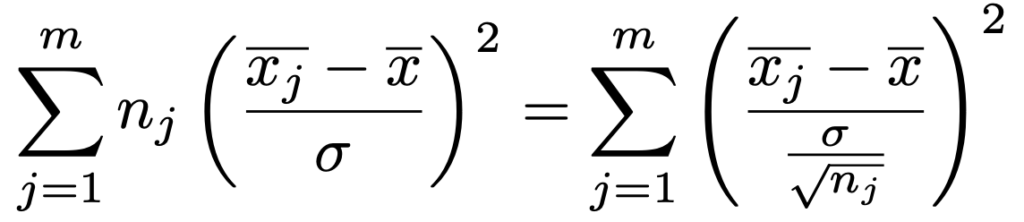
よって,帰無仮説を仮定するとき,次の等式の3つの項はそれぞれカイ2乗分布に従っていて,各辺の自由度の合計はNー1で等しくなっています。
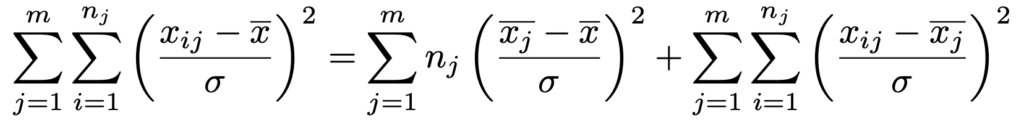
したがって,次の確率変数は分子が自由度mー1のカイ2乗分布に従い,分母が自由度Nーmのカイ2乗分布に従っています。
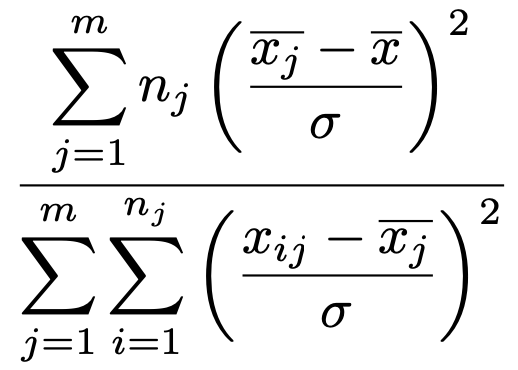
分母と分子にσ2をかけた後,分母と分子をそれぞれカイ2乗分布の自由度でわってできる次の確率変数は,第14回の記事で学んだことから,F(mー1,Nーm)に従います。
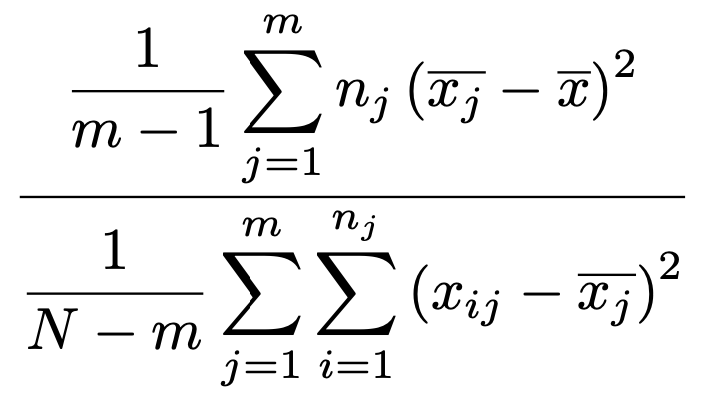
上の分数の分母と分子にある「平方和を自由度でわったもの」を平均平方と言います。分子は水準間平均平方,分母は残差平均平方です。残差のばらつきよりも水準間のばらつきのほうが大きいだろうという予想のもとに対立仮説を設定しているので,この確率変数は1よりも大きい値をとることが期待されます。したがって,この確率変数が検定量(検定統計量)であり,F分布のグラフの右側の裾を使って,右片側検定を行います。
大事なことをもう一度繰り返しておくと,水準間平均平方を残差平均平方でわってできる確率変数は,第1自由度が「水準の数ー1」,第2自由度が「すべての水準の標本の大きさの合計ー水準の数」のF分布に従います。
次のセクションでは,最初に挙げた例を使って,具体的に計算していきましょう。
分散分析表
分散分析の結果は,次のような分散分析表に表すことが多いです。
この表の左から順に計算していきます。
統計検定2級では,平方和は問題で与えられることが多いのですが,はじめに,簡単な数値例を使って平方和を計算するところからやっていきましょう。
【問題】あるコンビニエンスストアチェーンの店舗で,商品Aを陳列棚の上から1段目,2段目,3段目のどこに並べるかによって,1日に売れる個数に差があるかどうかを調べるため,無作為に選んだ9店舗で1日に売れた個数をまとめたところ次の表のようになった。

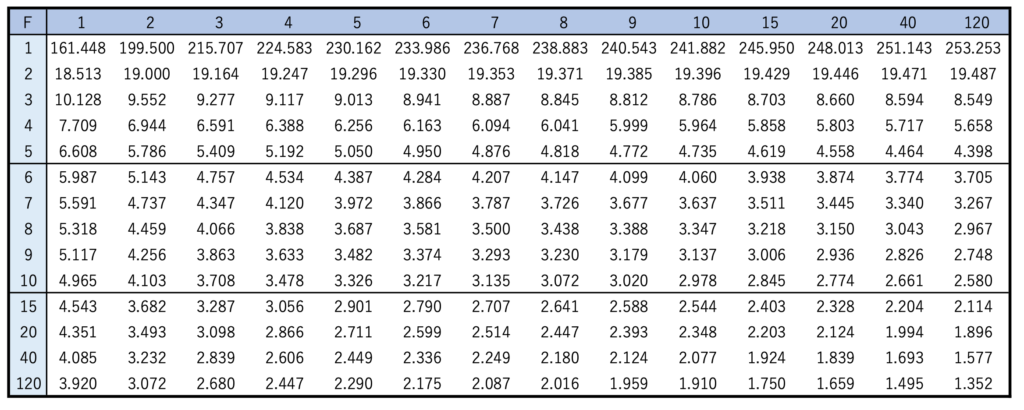
正規性と等分散性を仮定し,上から何段目に並べたかを要因とする一元配置分散分析を行った。1段目,2段目,3段目にそれぞれ並べたときの1日に売れる個数の母平均をμ1,μ2,μ3,帰無仮説をμ1=μ2=μ3,対立仮説を「μ1,μ2,μ3のうち少なくとも1つは異なる」として,有意水準5%で検定しなさい。必要ならば,上側5%点を示した次のF分布表(いちばん上の行が第1自由度,いちばん左の列が第2自由度を表している)を用いなさい。
【解答】1要因3水準の分散分析ですね。まず,水準内平均をそれぞれ求めましょう。
売れた個数の平均は,1段目が,(15+21+18)÷3=18(個),2段目が,(18+24+21)÷3=21(個),3段目が,(15+16+14)÷3=15(個)になります。
全体の平均は,(18+21+15)÷3=18(個)なので,水準間平方和は次のように計算できます。
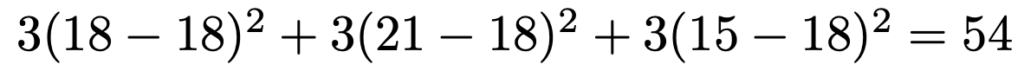
残差平方和は次のように計算できます。
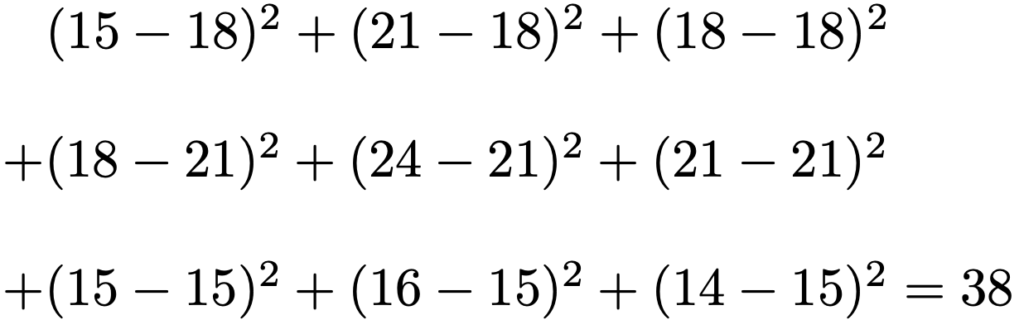
次に,平均平方を計算します。水準間平方和を母分散でわってできる確率変数のカイ2乗分布としての自由度は,水準の数の3より1小さい2だから,水準間の平均平方は,54÷2=27
残差平方和を母分散でわってできる確率変数のカイ2乗分布としての自由度は,標本の大きさの9より水準の数の3だけ小さい6だから,残差の平均平方は,38÷6≒6.33
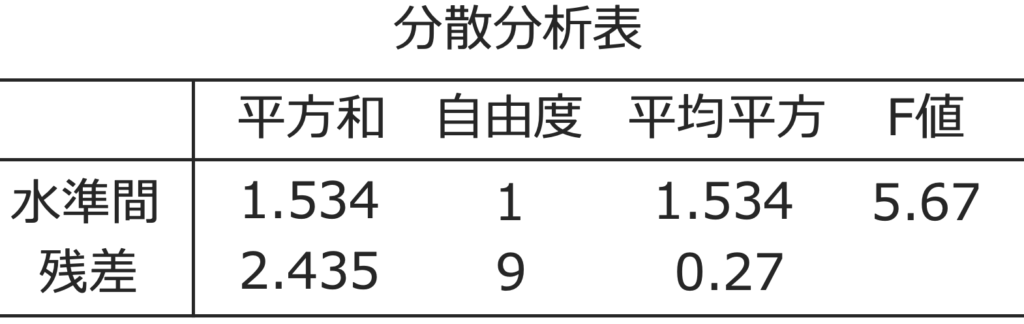
F値は,27÷6.33≒4.26となります。ここまでを分散分析表にまとめると,次のようになります。
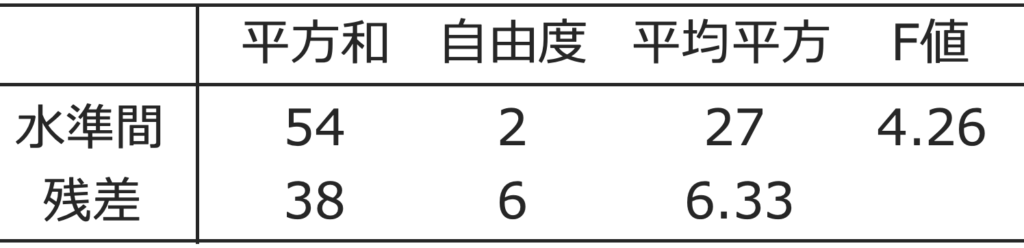
さて,問題の帰無仮説の検定に進みます。2つの自由度から,F(2,6)の上側5%点とF値の4.26を比べればよいことになります。F分布表から,F(2,6)の上側5%点は約5.14なので,4.26<5.14より,この値は棄却域には入らないことになります。よって,帰無仮説を受容し,母平均に差があるとは言えないという結論になります。
(解答終わり)
さて,統計検定2級では,実際のデータをもとに出題されることが多く,平方和から計算することは事実上不可能なので,次のような出題パターンになります。
・平方和が与えられて,自由度以降を計算させる
・分散分析表全体が与えられて,読み取って検定結果等を答える
では最後に,このタイプの実戦的な問題を解いておきましょう。
【問題】みかんを生産する7つの地域から,それぞれ無作為に抽出された18個のみかん(合計126個)を使って,1個あたりのカリウムの含有量(単位:mg)に差があるかどうかを調べた。正規性と等分散性を仮定し,地域を要因とする一元配置分散分析を行ったところ,次の結果を得た。

(1)分散分析表の空欄をうめなさい。ただし,ウ,エ,オにあてはまる数は小数第2位まで求めなさい。
(2)地域ごとのカリウムの含有量の母平均をμi(i=1,…,7)とする。帰無仮説を「μiはすべて等しい」,対立仮説を「μiのうち少なくとも1つが異なる」として,有意水準5%で検定しなさい。必要ならば,上のF分布表を用いなさい。
【解答】
(1)アは,「水準間」の自由度なので,(水準の数ー1)で求められます。地域を要因として考えているので,7水準だから,自由度は,7ー1=6
イは,「残差」の自由度なので,(すべての水準の標本の大きさの合計ー水準の数)で求められます。データの大きさの合計は126個なので,水準の数の7をひくと,自由度は,126ー7=119
ウにあてはまる数は,水準間平方和を自由度でわって,377.76÷6=62.96
エにあてはまる数は,残差平方和を自由度でわって,2710.78÷119≒22.78
オにあてはまる数は,水準間平均平方を残差平均平方でわって,62.96÷22.78≒2.76
よって,答えは,ア=6,イ=119,ウ=62.96,エ=22.78,オ=2.76です。
(2)(1)の結果から,F値を求めるための確率変数はF(6,119)に従います。上のF分布表にはF(6,119)の上側5%点は記載されていませんが,F(6,120)の上側5%点が2.175であることが示されていますので,ほぼ等しい値であると考えられます。なお,F(6,40)の上側5%点が2.336であり,F(6,119)の上側5%点はそれより小さい値であることから考えてもかまいません。いずれにしても,F値の2.76のほうが大きいので,棄却域に落ちます。帰無仮説を棄却し,対立仮説を採択します。つまり,有意水準5%で母平均のうち,少なくとも1つが異なると言えます。
(解答終わり)
一元配置分散分析についての基本的な説明は以上になります。この後は,参考図書の紹介に続けて,さらに理解を深めるための演習問題ですので,余力があればぜひチャレンジしてみてください。
参考図書
本稿を執筆するにあたり,次の書籍を参考にしました。
基本統計学 第5版(宮川公男,有斐閣)
検定量がF分布に従うことを示す式変形,およびその自由度の考え方がしっかりと書かれています。
演習1〜分散分析表の穴うめ〜
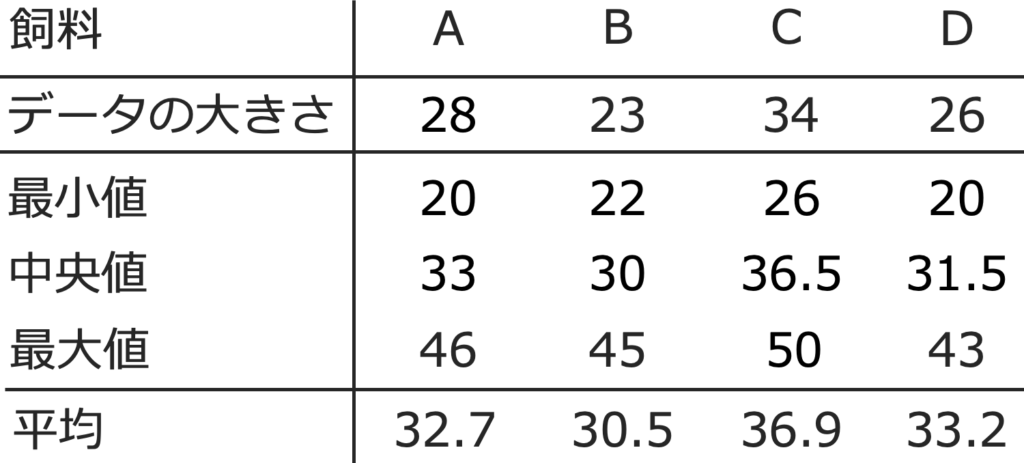
【問題】次の表は,ある魚の養殖場で,4種類の飼料A,B,C,Dのうち1種類だけを与えて3年間育てた後の体長(単位:cm)を調べ,飼料の種類別にまとめた要約統計量である。
飼料によって3年後の体長に差があると言えるかどうかを考察したい。正規性と等分散性を仮定し,飼料の種類を要因とする一元配置分散分析を行ったところ,次の分散分析表を得た。
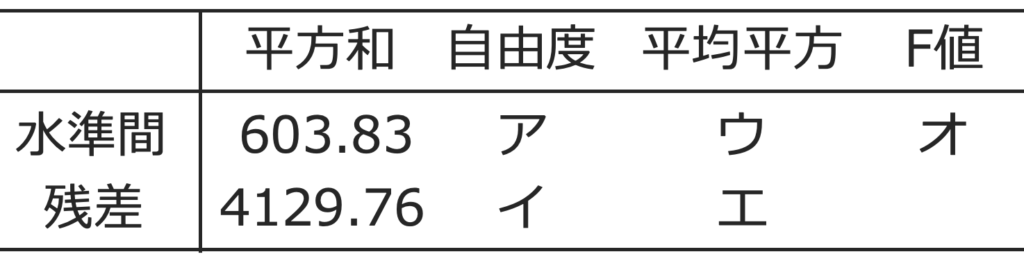
(1)分散分析表の空欄をうめなさい。ただし,ウ,エ,オにあてはまる数は小数第1位まで求めなさい。
(2)飼料ごとの3年後の体長の母平均をμi(i=1,2,3,4)とする。帰無仮説を「μiはすべて等しい」,「対立仮説をμiのうち少なくとも1つが異なる」として,有意水準5%で検定しなさい。必要ならば,上のF分布表を用いなさい。
【解答】
(1)アには,水準間平方和を母分散でわってできる確率変数のカイ2乗分布としての自由度があてはまります。飼料を要因として考えているので,4水準になりますから,自由度は,4ー1=3
イには,残差平方和を母分散でわってできる確率変数のカイ2乗分布としての自由度があてはまります。データの大きさの合計(標本となる魚の数)は,28+23+34+26=111なので,水準の数の4をひくと,自由度は,111ー4=107
ウにあてはまる数は,水準間平方和を自由度でわって,603.83÷3≒201.3
エにあてはまる数は,残差平方和を自由度でわって,4129.76÷107≒38.6
オにあてはまる数は,水準間平均平方を残差平均平方でわって,201.3÷38.6≒5.2
よって,答えは,ア=3,イ=107,ウ=201.3,エ=38.6,オ=5.2です。
(2)(1)の結果から,F値を求めるための確率変数はF(3,107)に従います。上のF分布表にはF(3,107)の上側5%点は記載されていませんが,F(3,120)の上側5%点が2.680,F(3,40)の上側5%点が2.839であることから,F(3,107)の上側5%点はこの間の値であることがわかります。よって,F値の5.2のほうが大きいので,棄却域に落ちます。帰無仮説を棄却し,対立仮説を採択します。つまり,有意水準5%で母平均のうち,少なくとも1つが異なると言えます。
(解答終わり)
演習2〜2水準の一元配置分散分析とt検定〜
【問題】ある自動車メーカーは,小型車Aを使って,晴れの日と雨の日でそれぞれ燃費(燃料1Lあたりの走行可能距離)を測定する実験を行った。晴れの日に5台,雨の日に6台を走らせて測定した結果は次の表(単位:km/L)のようになった。
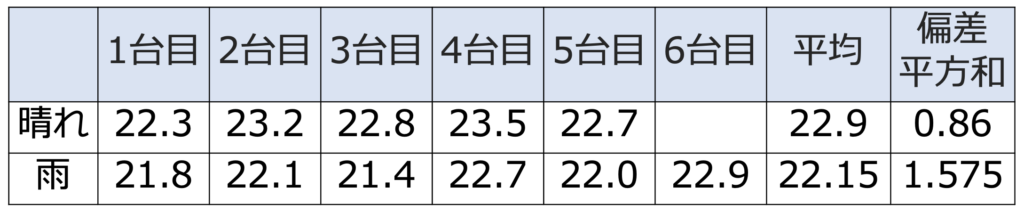
正規性と等分散性を仮定し,小型車Aの晴れの日と雨の日の燃費について,帰無仮説を「母平均が等しい」,対立仮説を「晴れの日の母平均のほうが雨の日の母平均より大きい」として,有意水準5%で検定しなさい。必要ならば,上のF分布表を用いなさい。
【解答】第15回で学習したt検定を使ってみましょう。片側検定になります。
プールした分散は,次のように計算できます。

これを使うと,検定量(t値)は次のように求めることができます。
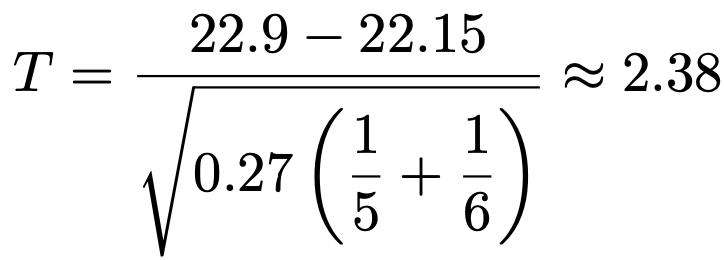
5+6ー2=9より,自由度9のt分布の上側5%点を調べると,(t分布表は載せてませんが)およそ1.833であることから,棄却域に落ちます。帰無仮説を棄却し,対立仮説を採択します。つまり,有意水準5%で母平均に差があると言えます。
(別解)
次に,分散分析を使って,同じ仮説を検定します。まず,全体の平均は次のようになります。
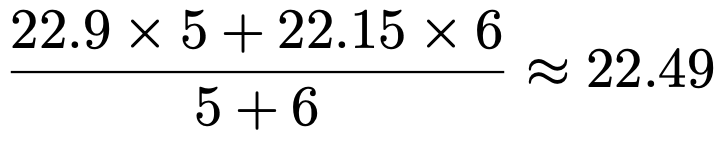
これを使うと,水準間平方和は次のように求めることができます。
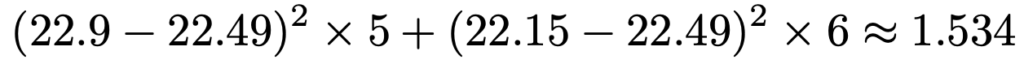
残差平均平方はt検定のところで計算したプールした分散そのものですから,分散分析表は次のようになります。

F値を求めるための確率変数はF(1,9)に従います。上のF分布表から,F(1,9)の上側5%点はF分布表から5.117だとわかるので,F値の5.67のほうが大きいので,棄却域に落ちます。帰無仮説を棄却し,対立仮説を採択します。つまり,有意水準5%で母平均のうち,少なくとも1つが異なると言えます。
(解答終わり)
【補足】上で求めたt値の2.38を2乗すると,F値の5.67に(四捨五入の誤差を除いて)等しくなります。したがって,どちらで計算しても検定の結果が変わることはありません。
演習3〜一元配置分散分析(Rによる出力)〜
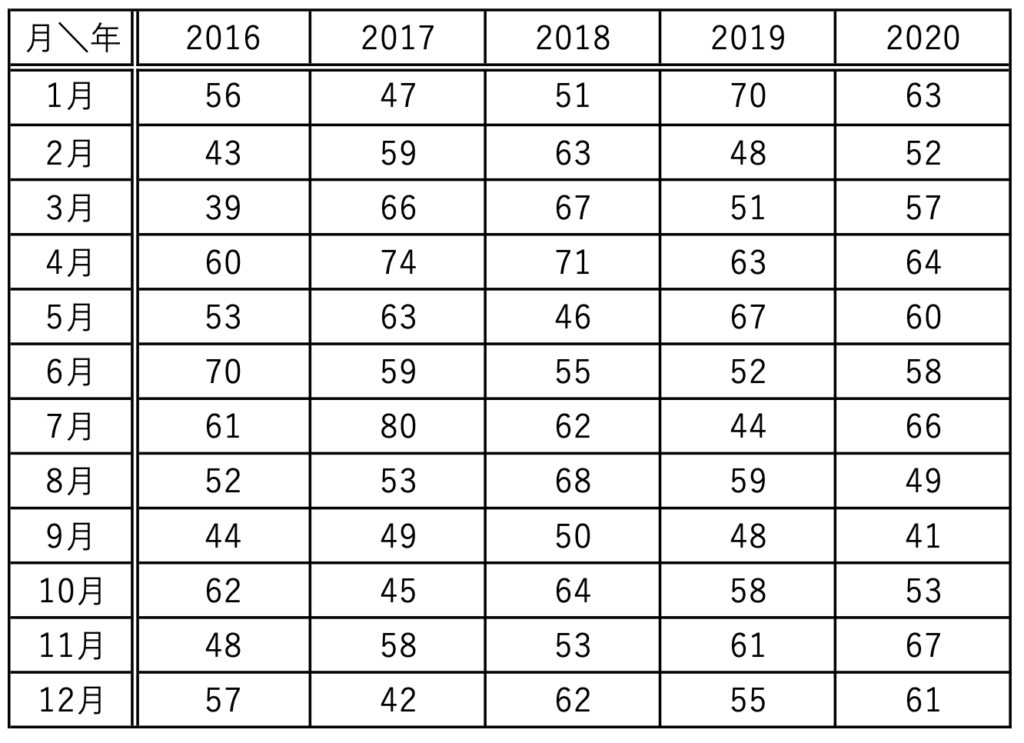
【問題】次の表は,ある企業の月別の売上高(単位:億円)を2016年から2020年までの5年間集計したものである。月ごとの売上高に差があるといえるかどうかを考察したい。
正規性と等分散性を仮定し,このデータを用いて月を変動要因とする一元配置分散分析を行った結果,次の表を得た。

(1)60か月の売上の不偏分散を小数第1位まで求めなさい。
(2)j年i月の売上高をyij(i=1,…,12,j=2016,…,2020)とし,月ごとの平均をyi・,年ごとの平均をy・j,全体の平均をy・・とする。これらの文字を使って,水準間平均平方と残差平均平方をそれぞれ表しなさい。
【解答】
この英語表記の分散分析表は統計ソフトのRによる出力結果で,2017年の統計検定2級の試験でも同種の分散分析表が出題されています。
DfはDegree of freedomの略で自由度を,Sum SqはSum of Squaresの略で平方和を,Mean SqはMean Squareの略で平均平方を表しています。F valueはF値,PrはP値です。
(1)不偏分散は,全平方和を標本の大きさより1だけ小さい59でわって求めることができます。全平方和=水準間平方和+残差平方和より,全平方和は,1582+2969=4551
よって,不偏分散は,4551÷59≒77.1
(2)月を変動要因としているので,水準は12個あります。まず,水準間平方和は次のようになります。
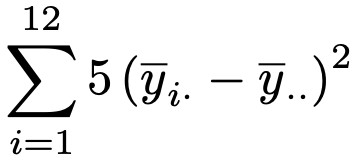
5年分のデータがあり,各水準のデータは5個ずつあるので,5をかけるのを忘れないようにしましょう。分散分析表から水準間の自由度は11なので,水準間平均平方は次のようになります。

次に残差平方和は次のようになります。
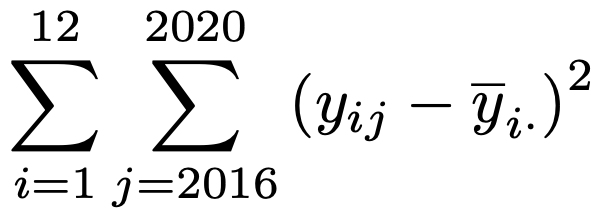
iについてのΣとjについてのΣは逆でもかまいません。分散分析表から残差の自由度は48なので,残差平均平方は次のようになります。
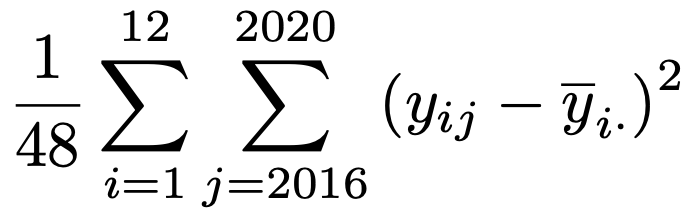
(解答終わり)
第16回は以上となります。最後までお付き合いいただき,ありがとうございました!
引き続き,第17回以降の記事へ進んでいきましょう!
2023年1月に「統計検定2級公式問題集[CBT対応版](実務教育出版)」が発売されました!(CBTが何かわからない人はこちら)
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが,本書は分野ごとにその形式の問題を並べた構成になっていて,最後に模擬テストがついています。CBT対策の新たな心強い味方ですね!
さらに実戦に向けた演習を積みたい人は,「統計検定2級公式問題集2018〜2021年(実務教育出版)」を手に取ってみてください!
また,もっと別の問題を解いてみたい人は,さらにさかのぼって「統計検定2級公式問題集2016〜2017年(実務教育出版)」を解いて実力に磨きをかけましょう!


![統計検定2級公式問題集[CBT対応版]](https://m.media-amazon.com/images/I/51q3GfZId3L._SL500_.jpg)




コメント