記述統計学としての回帰分析と推測統計学としての単回帰分析をわかりやすく解説していきます。回帰分析は非常に奥の深い理論ですが,統計検定2級で問われるのは,ほんの入り口の部分だけです。この記事では,統計検定2級の回帰分析を表面的に理解することにとどまらず,その背後にある理論の一部分を紹介し,回帰分析とt分布の関係などを式を使って解説していきます。
なお,この記事で前提とする知識は,第4回の期待値と分散の内容,第5回の共分散と相関係数の内容,第8回のt分布の内容,第11回の仮説検定の内容,第12回の母比率の差の検定の記事で説明したP値の内容,第13回の記事で説明したカイ2乗分布の内容になりますので,これらの内容に不安がある人は,先にそちらの記事を読んでください。では,はじめていきましょう!
記述統計学
統計学は大きく分けて次の2つに分類できます。
- 記述統計学:データの特徴を見つけてわかりやすく整理する
- 推測統計学:標本から母集団の性質を推測する
この講座でこれまで時間をかけて説明してきた推定や検定は,後者の推測統計学に属します。回帰分析はこの2つのどちらにも登場するので,まずはこのセクションでいったん記述統計学を概観して,次のセクション以降で記述統計学における回帰分析,推測統計学における回帰分析を順に説明していきます。
記述統計学では,データの特徴を見つけるためによく使う指標があります。それらは,データの平均,分散,相関係数などです。この講座ではすでに確率変数の期待値,分散,相関係数として学習済みですが,少し違いがあるので改めて紹介していきます。
まず,次のようなn個のデータを考えます。例えば,畑で獲れたn個のじゃがいもの重さなどをイメージしましょう。
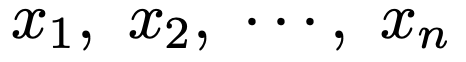
データの平均とは「標本のデータを全部たして個数でわったもの」だから,次の式のようになりますね。
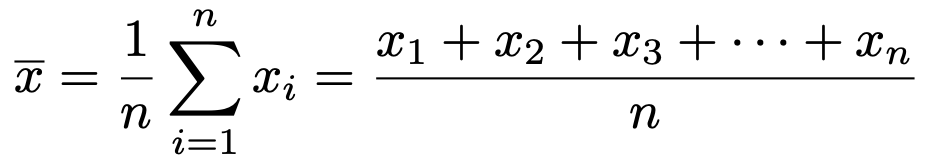
これは,小学校以来学んできた平均そのものなので,大丈夫ですよね。これを第4回で学習した確率変数の期待値と比べてみましょう。期待値は次のような式で表せました。
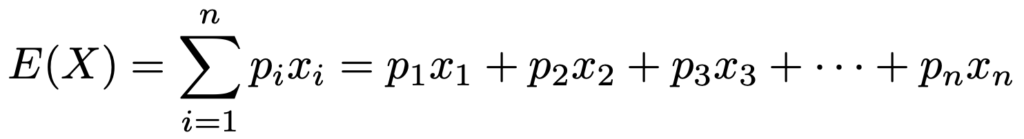
すべてのデータが等確率で現れると考えて,期待値の式でpi=1/nとおくことで平均の式を導くことができます。
次に,データの分散は下の式で表されます。
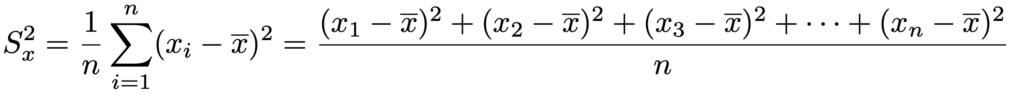
偏差の2乗の平均と言えますね。第4回で学習した確率変数の分散と比べてみましょう。次のような式で表せました。
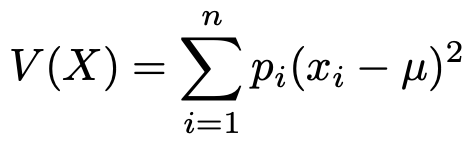
期待値と同じようにV(X)の式でpi=1/nとおくと,μ=xとなり,上のSx2の式を導くことができます。
また,第4回の記事で紹介したように,確率変数の分散と期待値については次の公式が成り立ちました。

これに対応するデータの分散と平均の公式は次のようになります。
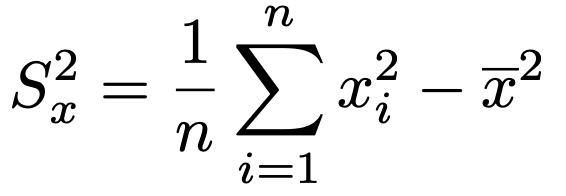
つまり,データの分散はxの2乗の平均からxの平均の2乗をひいたものに等しいわけです。この式の証明は,この後に紹介する共分散の公式の証明から自動的に導かれます。
次に,標準偏差は分散の正の平方根でしたね。分散をSx2で表したので,標準偏差はSxで表します。
標準偏差に関連して,次のような新しい指標も紹介しましょう。

つまり,標準偏差を平均でわったものです。これを変動係数と言います。統計検定2級でも出題されるので,確実に理解しておきたいところです。
では,変動係数を具体例で確認していきましょう。次の表を見てください。
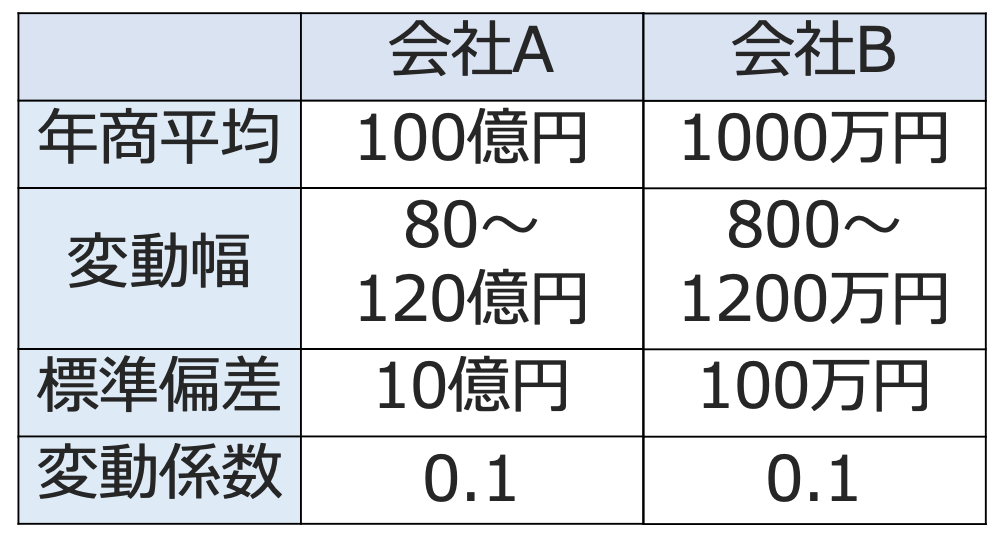
年商が100億円の会社Aがあるとします。毎年,年商は80〜120億円の間で変動して,標準偏差が10億円であるとします。このときの変動係数は,10(億円)÷100(億円)=0.1です。
次に,年商が1000万円の会社Bがあるとします。もし,年商のばらつき方が会社Aと同じであるならば,年商は800〜1200万円の間で変動して,標準偏差が100万円であればいいですね。実際に変動係数を計算してみると,100(万円)÷1000(万円)=0.1となり,会社Aの変動係数と一致します。
このように,平均が大きくなると標準偏差も大きくなる傾向があるので,単純に標準偏差だけを比べるわけにはいかず,標準偏差を平均でわった変動係数が有効になります。
次に,下のようなxとyの2種類のデータの組がn個ある場合を考えます。例えば,国語と数学の点数の組がn人分あるようなイメージです。
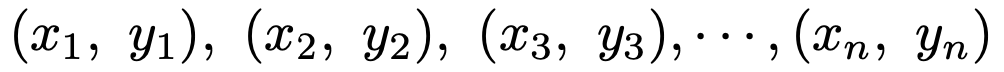
このデータに対して,共分散は次のように定義できます。
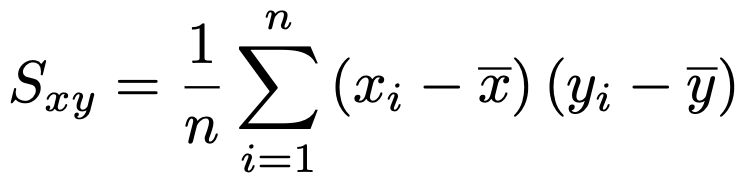
x=yとおくと,データの分散の式に一致しますね。
ここで,第5回で学習した確率変数の共分散を思い出します。次の式で表されました。

この式で,すべてのデータが等確率で現れるとして計算すると,上のデータの共分散の式に一致するわけです。
また,確率変数の共分散については次の公式が成り立ったことを思い出しておきましょう。
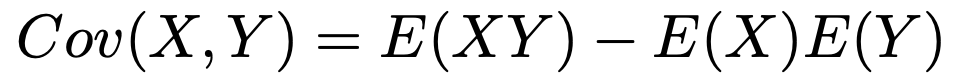
これに対応するデータの共分散の公式は次のようになります。
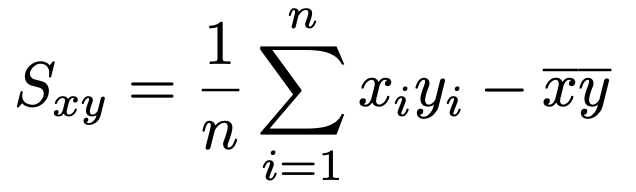
つまり,データの共分散はxとyの積の平均からxの平均とyの平均の積をひいたものに等しいわけです。念のため,この式を証明しておくと,次のようになります。
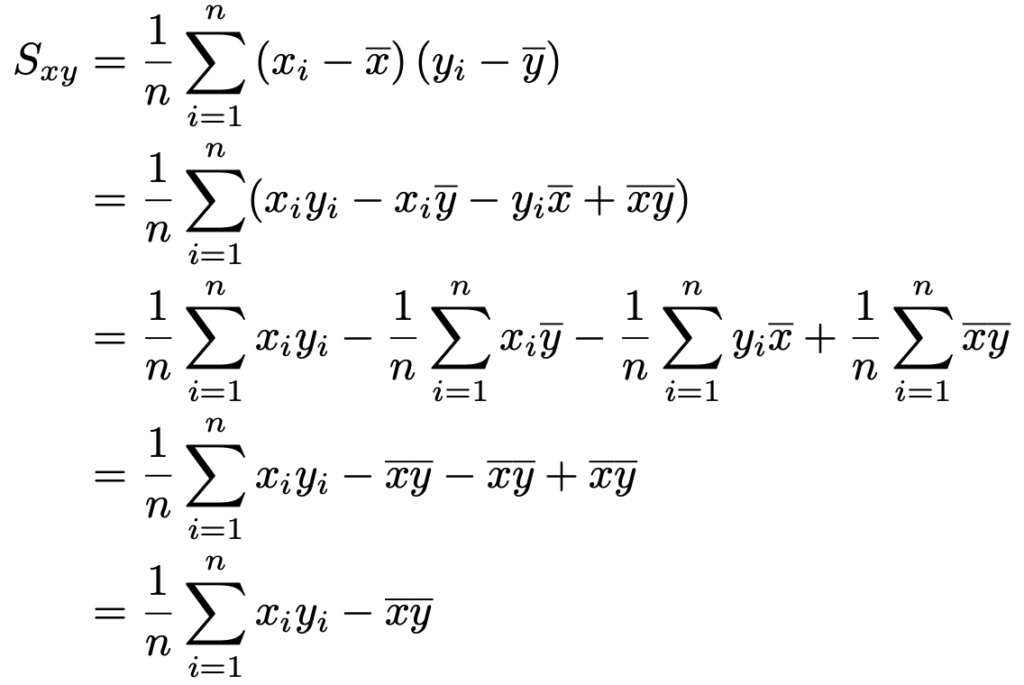
この式で,x=yとおくと,先ほど保留した分散の公式が導かれます。
今度は,xとyの2種類のデータの組を座標と見て,図に表してみましょう。次のようにxy平面上に図示したものを散布図と言います。
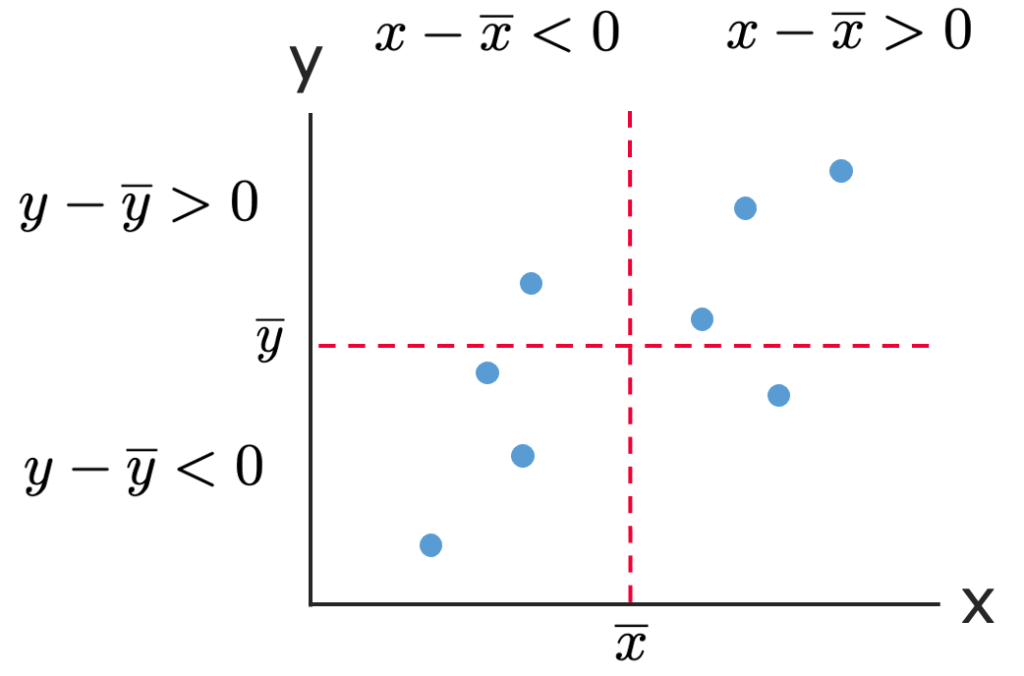
共分散はxの偏差とyの偏差の積(偏差積)の平均になっていたことを頭に浮かべながら,この図を見てみましょう。
xの平均を表す縦の線とyの平均を表す横の線をひくことで,散布図を4つの領域に分けてみます。このうち,右上と左下の領域のデータは偏差積が正に,右下と左上の領域のデータは偏差積が負になるので,右上と左下の領域に点がたくさんあると,共分散は正になることがイメージできることでしょう。ざっくり言うと,点が右上がりに並ぶと,共分散は正になりやすいということです。
次に,相関係数はここまで定義した共分散と標準偏差を使って,第5回で学習した確率変数の相関係数と同じ形の式で表されます。
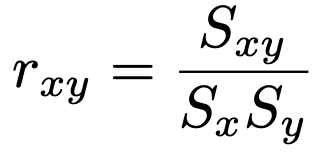
通常,相関係数と言えばこの式で定まるものを言いますが,実は,相関係数と呼ばれるものは他にもあります。そこで,この相関係数のことをより詳しく,ピアソンの積率相関係数と呼ぶことがあります。第5回で学習したように,相関係数はー1以上1以下の値をとり,その符号は共分散の符号と一致します。
相関係数が定義できるのは,2つの分散がともに0でないときのみですが,分散が0というのはすべてのデータが同じ値の場合ですので,その場合は除いて考えても差し支えないでしょう。
また,データの相関係数は,散布図と相性が良いです。次の図のように,散布図でデータがおおよそ右上がりの直線に近い形で並ぶとき,相関係数は正の値をとり,正の相関があると言います。

また,次の図のように,データがおおよそ右下がりの直線に近い形で並ぶとき,相関係数は負の値をとり,負の相関があると言います。
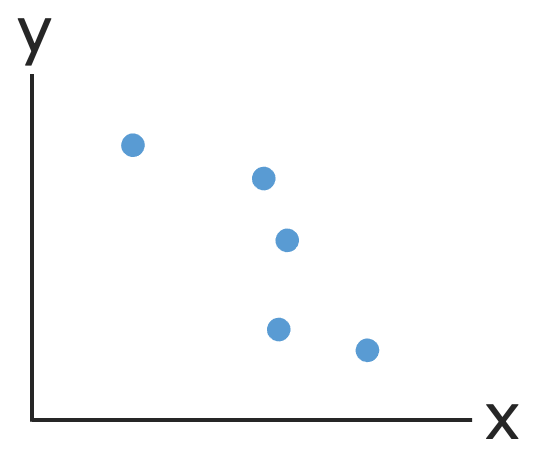
さらに,次の図のように,右上がりでも右下がりでもないとき,相関係数は0に近い値をとり,無相関であると言います。

散布図では2つの変量の関係は対等ですが,一方のxという変数を使って,もう一方のyという変数を説明するのが次のセクションで学ぶ回帰分析になります。
回帰分析とは
変数xと変数yの平均的な値の間に関数関係を想定した分析のことを回帰分析と言います。この関数の形はいろいろあるのですが,統計検定2級では1次関数だけを考えてもらえば十分です。
xによってyの平均的な値を説明するという関係があるので,xを説明変数,yを被説明変数と言います。yは知りたい対象(目的)なので,目的変数と呼ばれることも多いですが,この記事では統計検定2級の問題文の表現に合わせて,被説明変数と呼びます。
よくある例として,ある会社の広告費をx億円,売上をy億円として,xによってyがどのように説明できるかを調べることが考えられます。例えば,過去のデータから,おおむねy=2x+30という関係があることがわかれば,広告費を1億円増やせば,売上が平均して2億円増えると予測できるようになります。こんな強みを持つのが回帰分析です。
回帰分析は説明変数の数によって大きく2つに分けられます。
説明変数が1つのときを単回帰分析と言います。このときのxとyの関係式は次のような見慣れた1次関数になりますね。
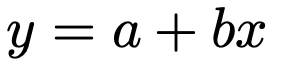
次に,説明変数が2つ以上のときを重回帰分析と言います。このとき,説明変数と被説明変数の関係式は,次のようなものになります。
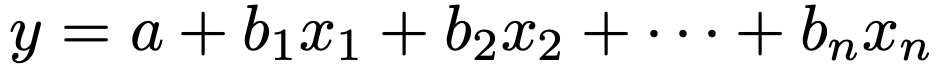
この式のx1,x2,…,xnが説明変数で,どの説明変数についても1次の関数になっています。重回帰分析の解説は第18回の記事に譲ることにして,ここからは単回帰分析の解説をしていきます。
単回帰分析では,次の図のように,散布図上の点に最も良くフィットする直線を見つけることが肝になります。
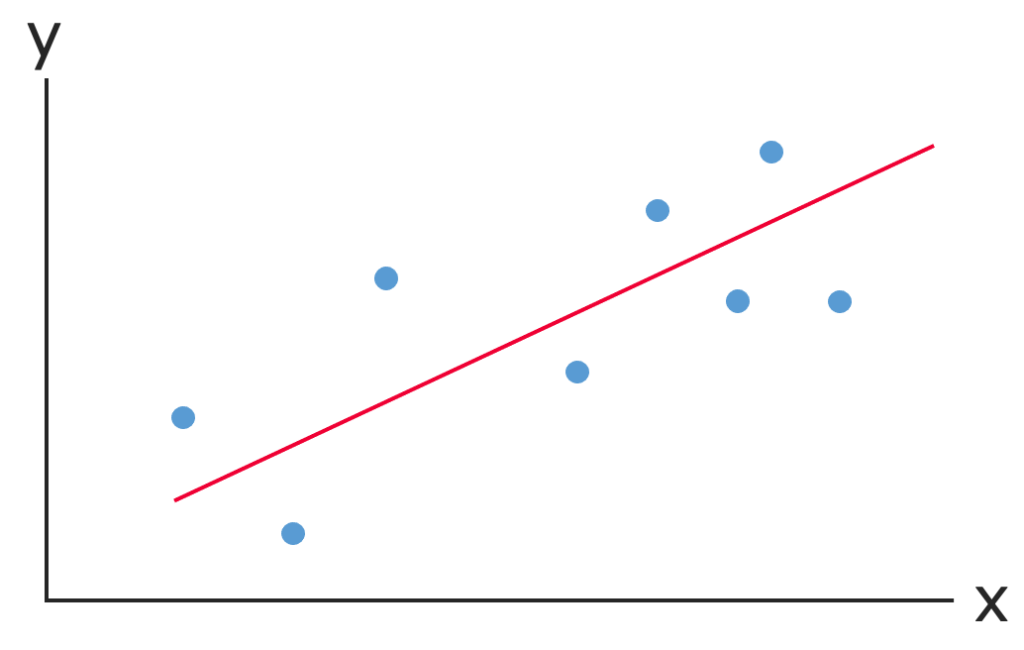
この直線を回帰直線と言います。
では,この直線をどのように求めるのかを説明していきます。
まず,データは次のn組であるとしましょう。
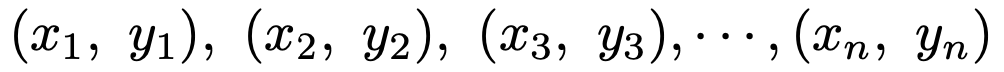
求めたい回帰直線の式をy=a+bxとおいて,それぞれのデータのxiを代入すると,次のようになります。
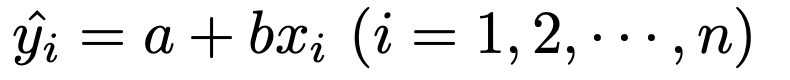
この左辺は,yiの上に帽子(ハット)がついていますので「yiハット」と読み,予測値と言います。回帰分析では,よく「ハット」の記号を使います。
また,次の式のような実測値yiと予測値との差を,ここでは直線からのズレと呼ぶことにしましょう。
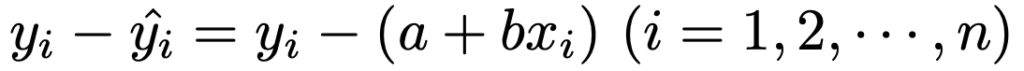
予測値と直線からのズレの関係は,次のように図に表せます。
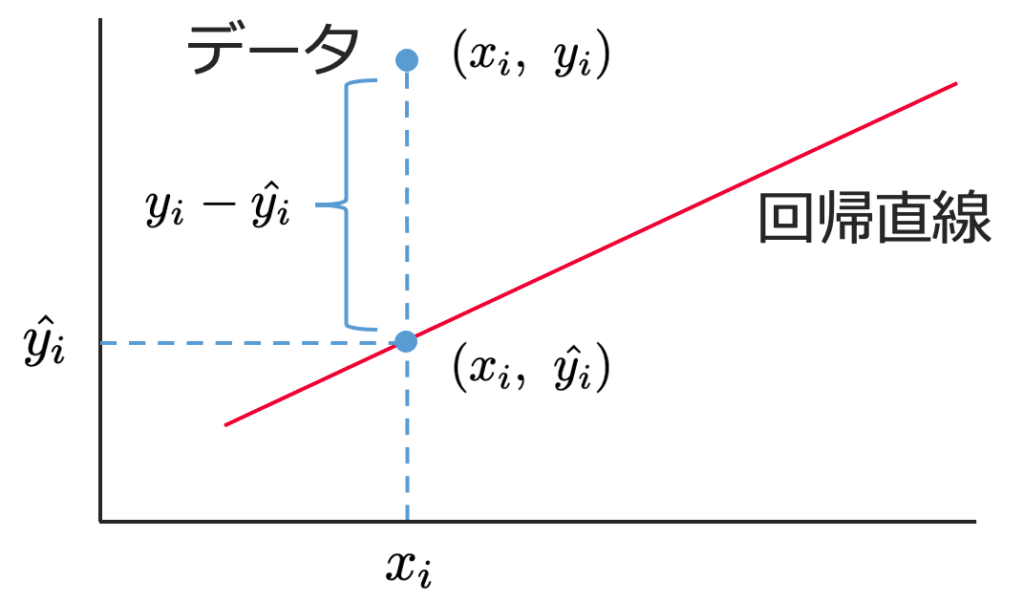
次の2つの図で,直線からのズレを表す破線の線分の長さの合計を比べてみると,図2のほうが小さそうですよね。データが同じであっても,直線の傾きを変えると,直線からのズレの大きさが変わるのがわかります。
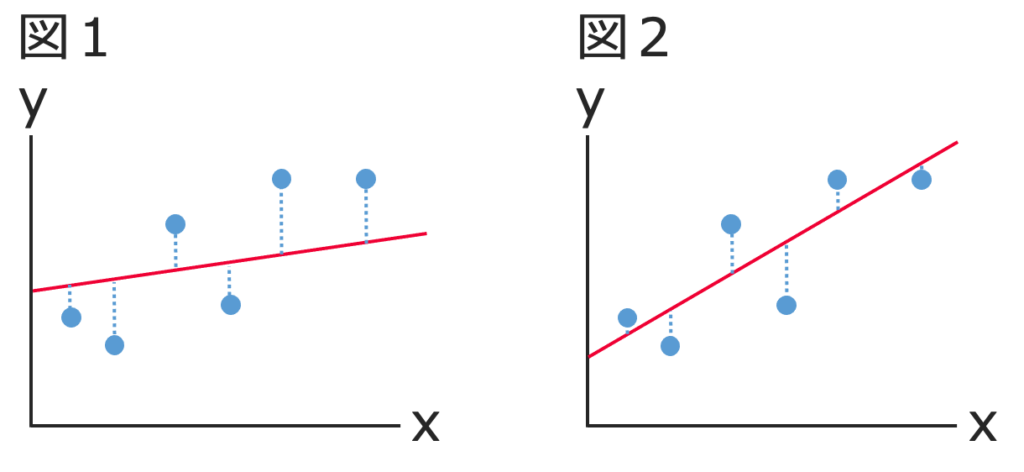
そこで,散布図上の点に最も良くフィットする直線とは,直線からのズレの2乗の和を最小にするように求めようというわけです。n組のデータについて,これを式で表すと次のようになります。
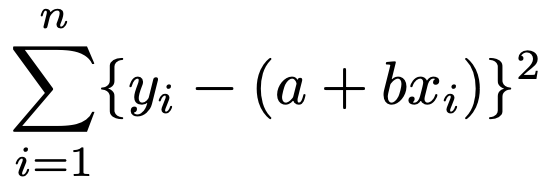
この和が最も小さくなるように,a,bの値を決める方法を最小2乗法と言います。最小2乗法は英語で,”ordinary least squares”と言いますので,「OLS」と呼ばれることもあります。
次の(*)から(**)まで,最小2乗法の計算方法の説明をしますが,統計検定2級では問われないので,興味がない人は読み飛ばしてください。
(*)このa,bの値をデータを使って求める公式を導出するために,次の2つの方法がよく使われます。
- 平方完成
- 偏微分
はじめて偏微分と聞いた人は,「偏微分? 何それ? 難しそう」と思うかもしれませんが,ふつうの微分(1変数の微分)がわかっていれば,偏微分はすぐに理解できます。偏微分は独立変数が2種類以上ある式を,独立変数が1種類しかないかのように微分することで,最大・最小などの極値をとる条件式を導き出すことができます。
ただ,高校で数学ⅡやⅢを学習していない人は極値という概念に慣れていないでしょうから,ここではより直感的に理解しやすい平方完成を使うことにします。2次関数の平方完成は,第5回の記事でも使っていますので,よくわからない人はそちらもご覧ください。
はじめに,テクニカルではありますが,yの項とbxの項を作り出すことで,直線からのズレの2乗の和を次のように変形します。
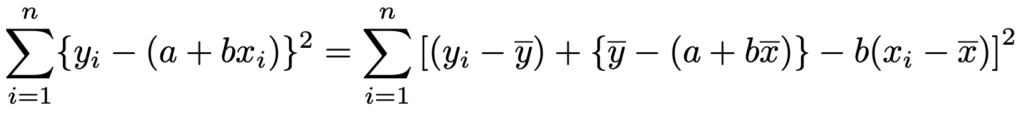
かっこの中の項を整理すれば,両辺が等しいことがわかるはずです。
3つのかっこを維持したまま2乗を展開すると,6つの項が出てきますが,そのうち次の2つの項は,偏差の和が0であることから,0になります。
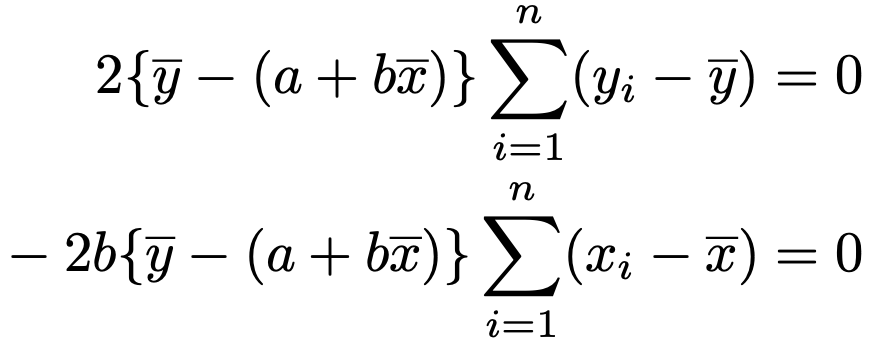
展開して出てくる残り4つの項のうちの3つを,式を簡略化するために次のようにおき直します。
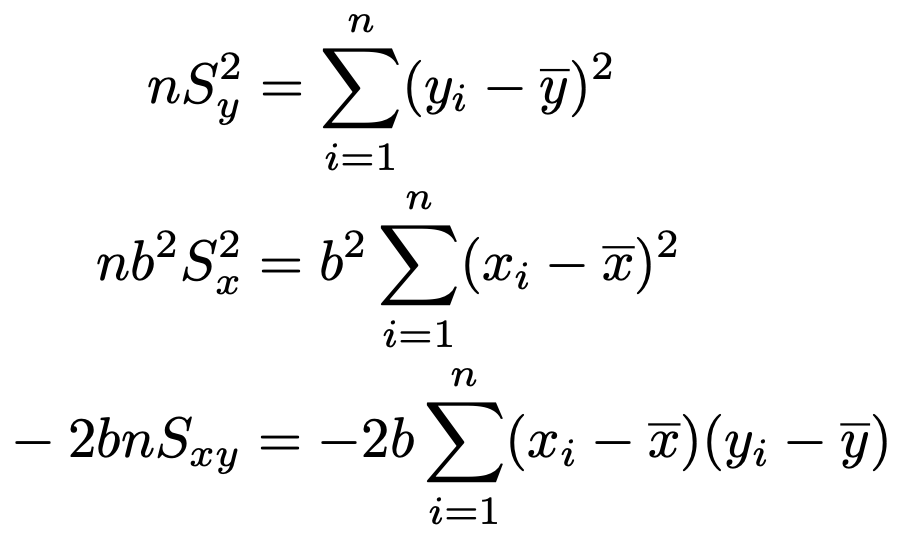
よって,直線からのズレの2乗の和を展開した式は次のようになります。
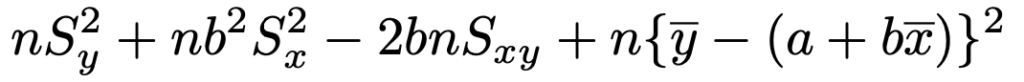
この式をbの2次関数とみて平方完成してまとめると,次のようになります。
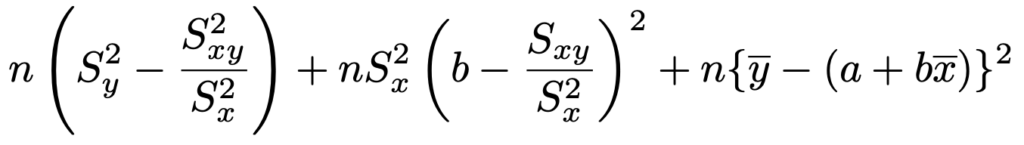
第2項と第3項は,かっこの2乗の部分が0以上であり,かっこの前の係数は正の数です。よって,第2項のかっこの中と第3項のかっこの中が同時に0になるようなaとbがあれば,そのときに全体として最小になります。(**)
よって,直線からのズレの2乗の和が最小になるときのbは次の式で表せます。
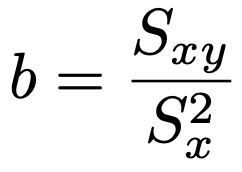
また,直線からのズレの2乗の和が最小になるときのaは次の式を満たします。
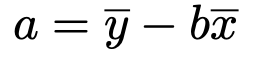
このようにして求められるa,bの値を回帰係数と言います。
さて,最後のaの値を求める式を,移項して書き直すと次のようになります。
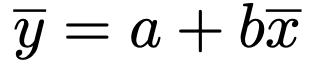
この式から,回帰直線y=a+bxは点(x,y)を通ることがわかります。この性質は大事なので,覚えておきましょう!
さて,このセクションの最後に,決定係数を紹介しておきます。
統計検定2級では,決定係数という名前とその使用目的がわかっていれば大丈夫なのですが,ここでは少し式を使って説明をしていきます。なんとなく決定係数の雰囲気がつかめたら,細かい式変形は読み飛ばしてください。
まずは,次の図が出発点になります。データから求めた回帰直線がy=a+bxで,データの1つが(xi,yi)です。
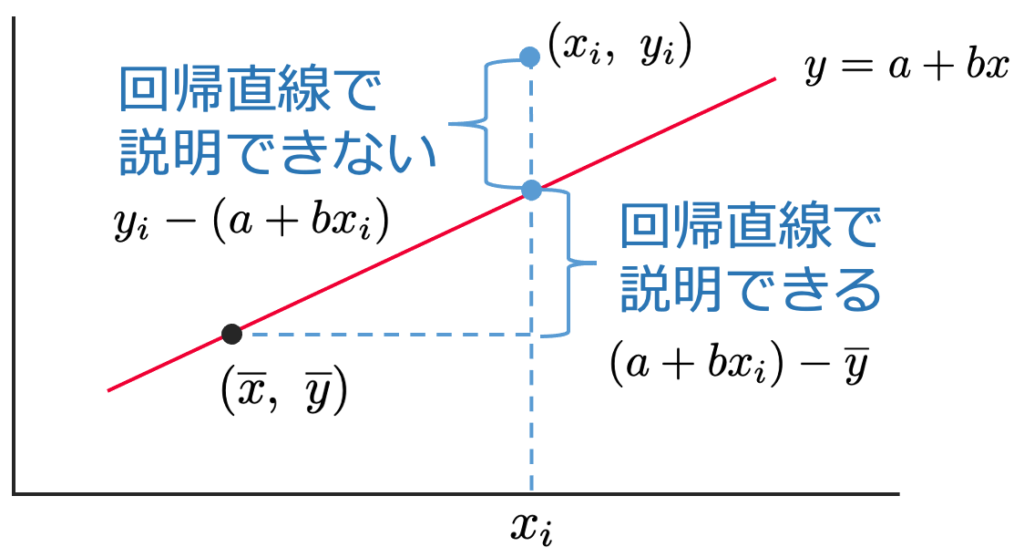
点(x,y)から点(xi,yi)へ移るとき,x軸方向に動いた後のy軸方向への移動は,回帰直線で説明できる部分と回帰直線で説明できない部分に分けられます。それを式で表すと,次のようになります。
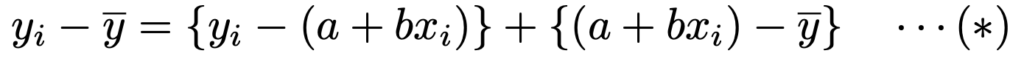
両辺を2乗して,i=1,2,…,nについて和をとると,実は次の式のようになります。
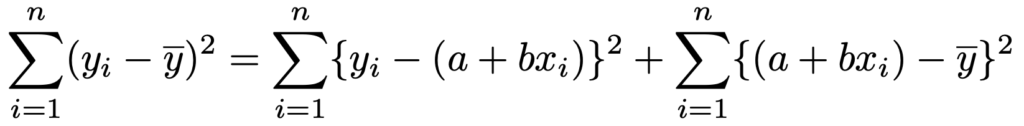
左辺はそのままですが,右辺はそうではないので,これを示しましょう。まず,(*)の式の右辺を2乗して展開すると,次のようになります。
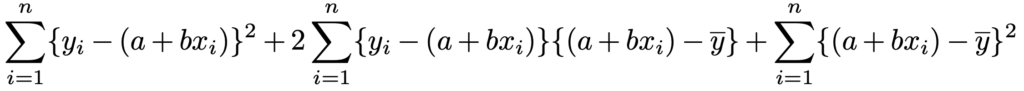
この式の第2項が0になればいいですね。そのためには,次の式を思い出します。
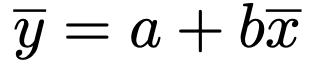
先ほどの第2項のyにこの式を代入すると,次のようになります。
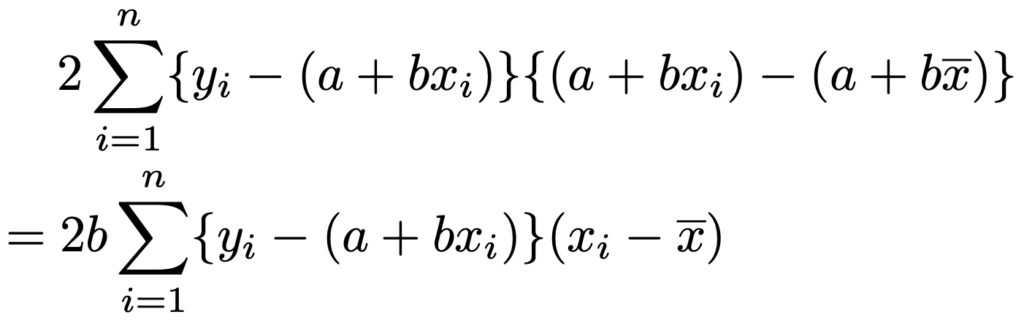
さらに,a=yーbxを代入すると,次のようになります。
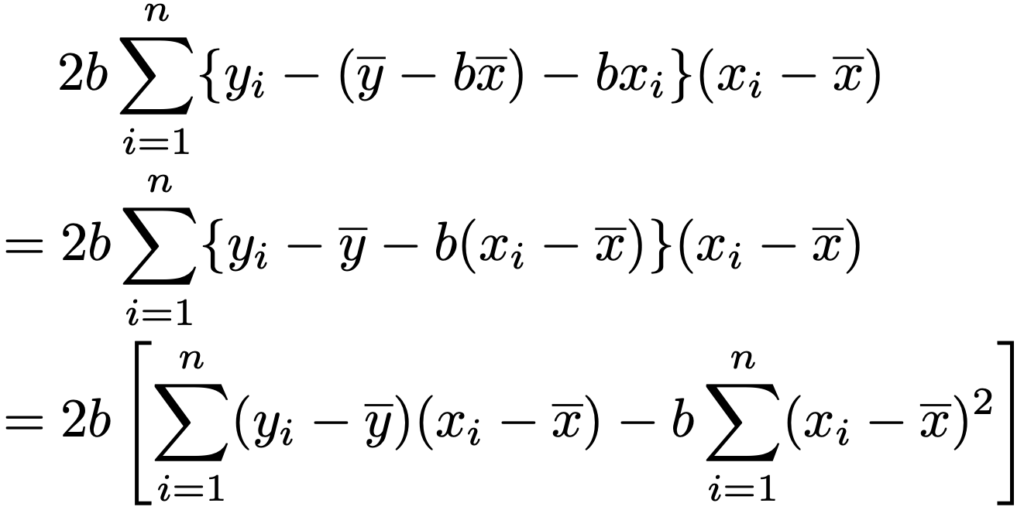
ここで,説明変数の係数bは,xとyの共分散をxの分散でわったものだったことを思い出すと,次の式のように表せるので,上の式の大かっこの中が0であることがわかります。
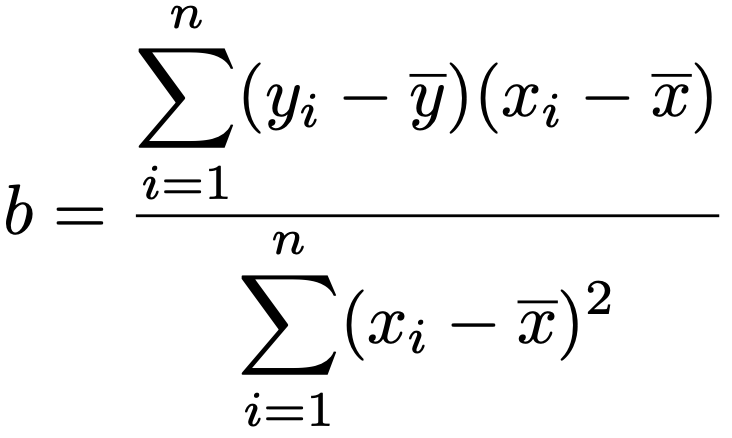
これで,次の式が示せました。
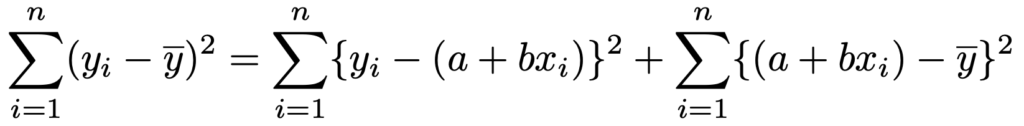
この式の左辺をnでわるとyの分散ですね。yiが平均のまわりにどれだけばらついているかを表しています。右辺の第1項は,yiのばらつきのうち,回帰直線で説明できない部分,第2項は回帰直線で説明できる部分をそれぞれ表しています。決定係数は,yiのばらつきのうちの回帰直線で説明できる部分の割合であり,次の式のR2のことです。
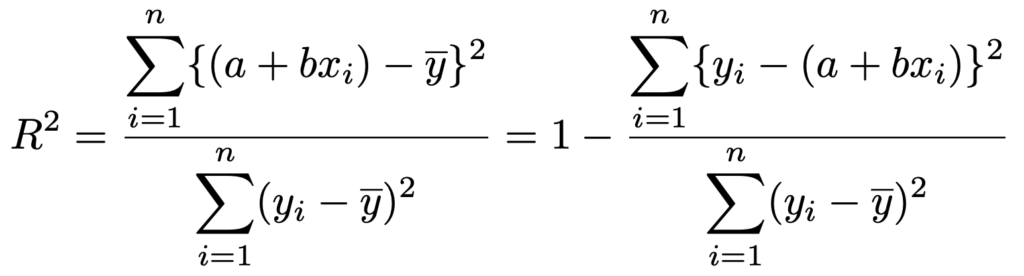
決定係数が大きいほど,回帰直線がデータをうまく説明できているということです。定義から,0≦R2≦1が成り立つことがわかります。R2=1となるのは,すべてのデータが直線上に並ぶときです。
また,決定係数がR2と表されるのには理由があり,実は相関係数の2乗に等しくなっています。これは次のように示すことができます。
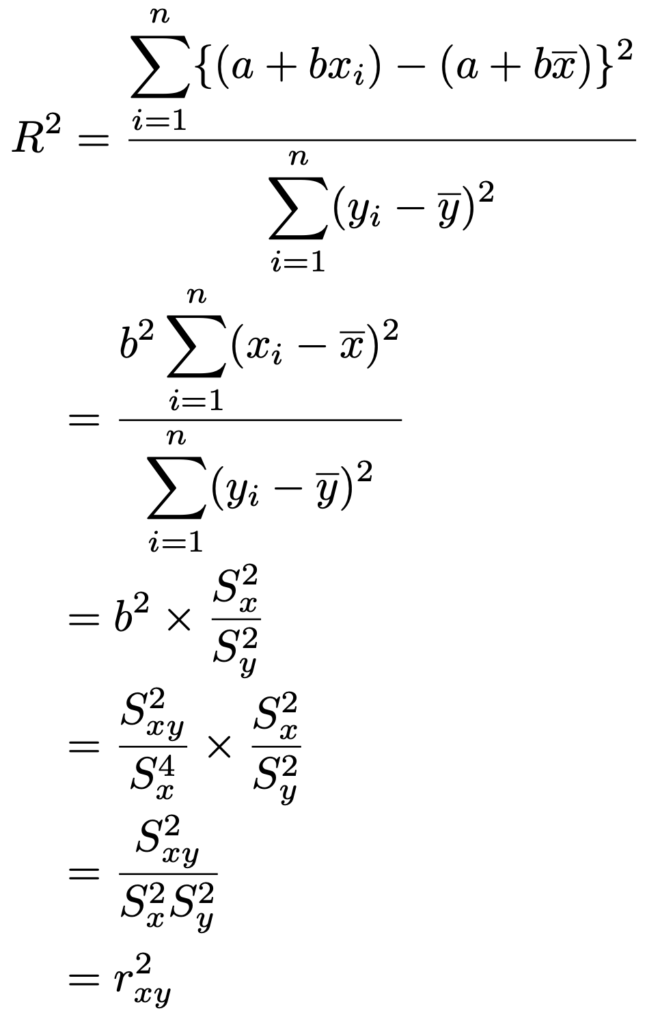
よって,相関係数は決定係数の正の平方根に共分散の符号をつけたものであり,ー1以上1以下の値をとることがわかります。
さて,ここまでの計算はなかなかハードでした。決定係数を説明しようとするとこれくらいの数式が必要になるのですが,統計検定2級の合格のためには「決定係数って,回帰直線がデータをどれくらい説明できるかの割合のことだよね」という感じで意味がわかればOKです。
単回帰分析
このセクションでは,推測統計学における回帰分析の説明をしていきます。
「記述統計学における回帰分析との違いは何か?」と言うと,データを母集団から抽出された標本だと考えるという点にあります。つまり,ある標本から推定される回帰直線と,別の標本から推定される回帰直線は違うものになるかもしれないわけです。
これだと困ったことになるのはわかりますか?
ビジネスの現場で「回帰直線が右上がりだと思っていたけれど,別の標本を抽出してみたら,やっぱり右下がりでした!」なんてことになったら笑えないですよね。会社の方針が真逆に変わってしまうわけですから。
そこで,回帰直線の(特に)傾きの誤差がどれくらいあるのかに興味がわいてくるのです。誤差がわかると推定や検定ができるようになるからです。そして,誤差を知るために,確率変数の概念を持ち込むことになります。
本題に入る前に,統計検定2級で問われる単回帰分析のポイントを紹介しておきます。
2級では,与えられた表を読み取って正しい選択肢を選ぶことが中心となります。計算が必要な問題はあまり多くなく,言葉の意味がわかっていればほとんど正解できてしまいます。
そんな中でよく問われるのは次のわり算です。
t値=回帰係数÷標準誤差
この式も覚えてしまえば問題は解けますが,せっかくなので「なぜこの関係が成り立つのか」,そしてt値という名前から察することができるように「なぜt分布と関係しているのか」というところを説明していきます。
また,仕組みを深く理解できているほうが内容を忘れにくいですし,忘れても頭の中で組み立て直せるという側面もあります。
では,説明を始めていきます。
次の大きさnの標本を考えます。
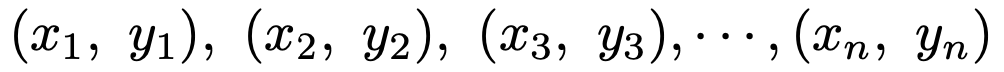
回帰直線をy=a+bxとおくと,前のセクションで学習したように,最小2乗法によってa,bの値を求めることができます。このa,bの値が標本によって変わりうるので,a,bを確率変数として考えていきます。
では,どう考えればa,bが確率変数になるかと言うと,xiからyiが決まる仕組みに確率変数で決まる誤差を導入します。
まず,x1からy1が次の仕組みで決まるものと考えます。
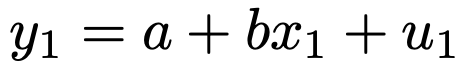
このu1が確率変数で,誤差項と呼ばれます。
x2,x3,…からy2,y3,…が決まる仕組みもこれと同様で,一般的には次の式になります。
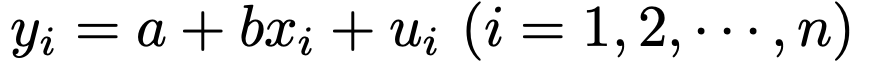
uiが確率変数なんですが,どんな確率分布に従うのかを決めておく必要がありますよね。誤差なので,0に近い値をとる確率が高く,0よりも大きく離れた値をとる確率は低いと考えるのが自然です。そこで,uiが従う確率分布を次のように考えるわけです。
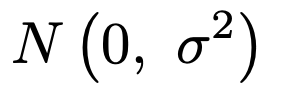
分散の値はわからないけれど,すべてのuiで分散が同じ値であること(等分散性)を仮定します。そして,すべての確率変数uiは独立であるとします。各xiにおける誤差なので,独立と考えるのが自然なのは納得できるのではないでしょうか。
上のn本の式は,母集団において次の式で表されるような構造が存在していることを仮定しています。この構造のことを単回帰モデルと言います。
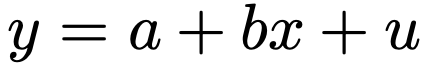
なお,xiは確率変数とは考えません。xiを確率変数と考えるモデルもありますが,それは統計検定2級のレベルを超えます。
では,これらのことを使うと,a,bが確率変数になることを確認していきましょう。
最小2乗法によるa,bの推定値は次のように表されるんでしたね。
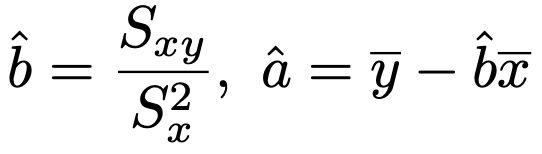
上の式では,a,bの上に帽子(ハット)がついています。これは,a,bを標本から推定した値という意味で,母集団における真の値と区別するためにこの記号をよく使います。また,これらを最小2乗推定量と言います。では,この推定量を確率変数として表し,その確率分布がどのようなものなのかを調べていきます。
なお,このあたりの説明は,統計検定2級の範囲を超えるプラスアルファの内容になりますので,一例としてbの推定量の確率分布だけを紹介し,aの推定量の確率分布は割愛します。
まず,次の式が成り立つことを示します。

この式を利用すると,この推定量がbの不偏推定量(不偏推定量は第8回で学習済み)であることを示すことができます。つまり,次の式が成り立ちます。
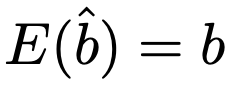
では,これを証明していきます。まず,次の式が出発点です。
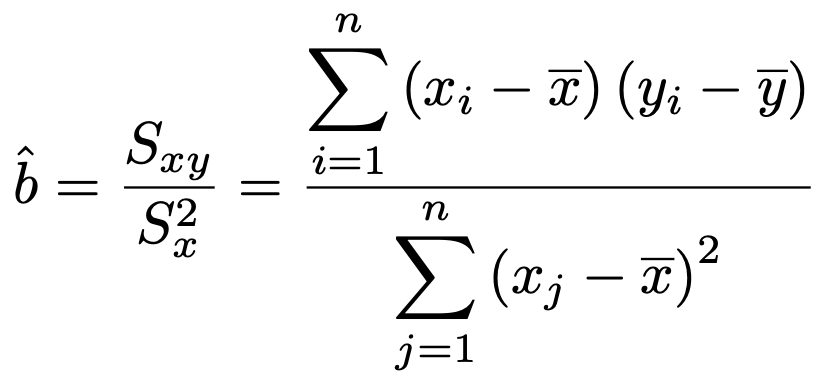
最右辺の分子を次のように書き直します。
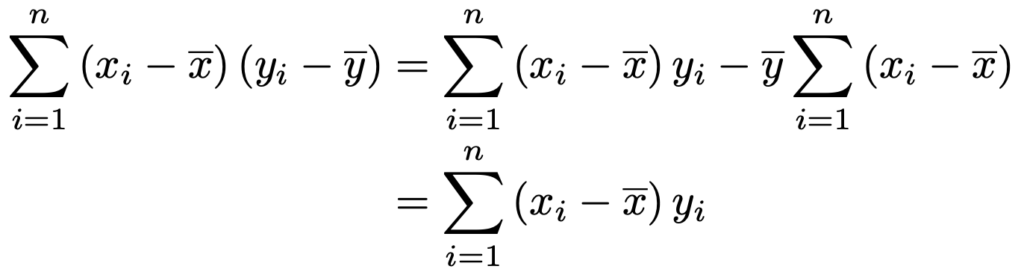
今の計算で,第2項のΣの式が無くなったのは,偏差の和は0だからです。
さらに,推定量の式にyiの式を代入して次のように変形します。
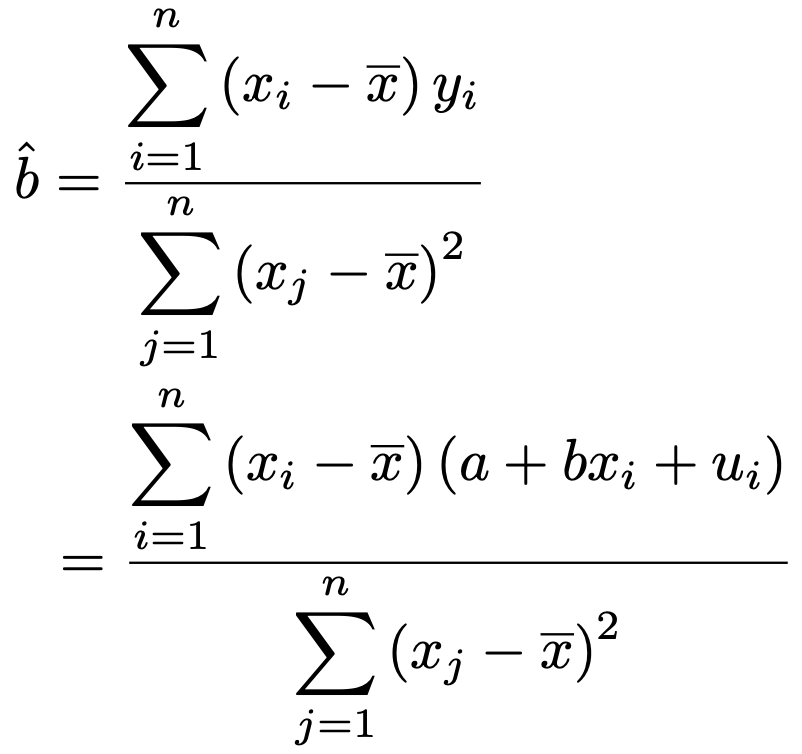
ここで,分子を展開して出てくる次の項は,偏差の和が0であることから0になります。
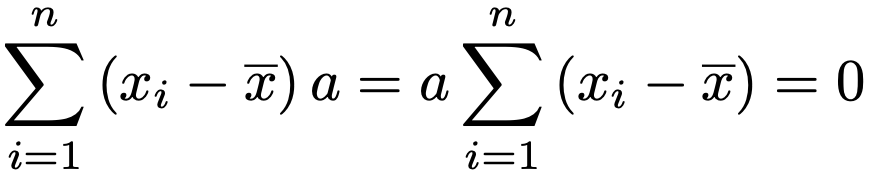
また,分子を展開して出てくる次の項も変形しておきます。
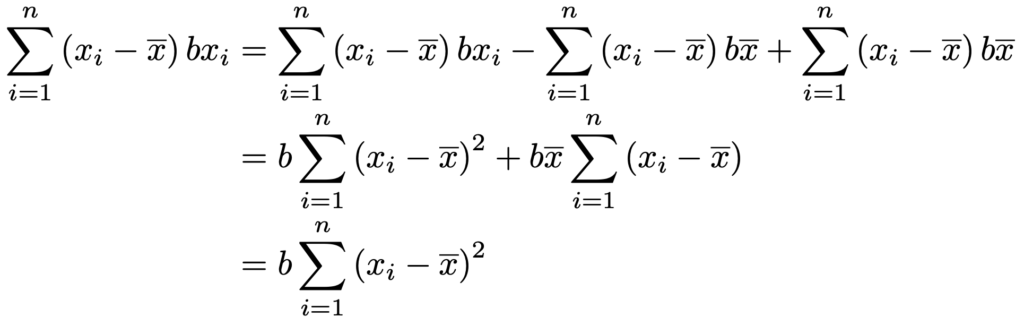
これらのことから,bの推定量が次の式で表されることがわかります。

この式を使うと,E(ui)=0であることから,期待値は次のように計算できます。
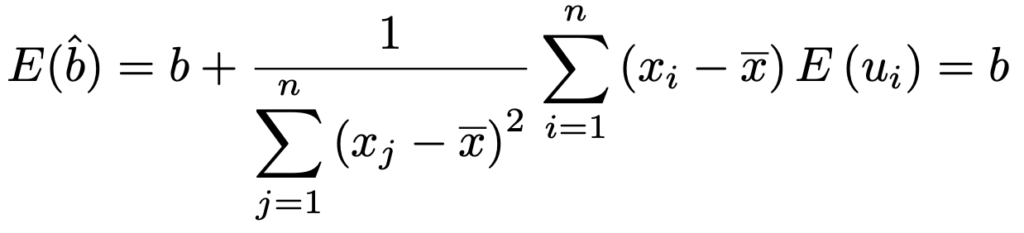
bの推定量の式の右辺は,真の値bと誤差を表すuiの和で構成されています。確率変数はuiだけで,uiが互いに独立に同一の正規分布に従うことから,正規分布の再生性より,bの推定量は期待値bの正規分布に従うことになります。では,その分散はどうなるでしょうか。bの推定量の分散は次のようになります。
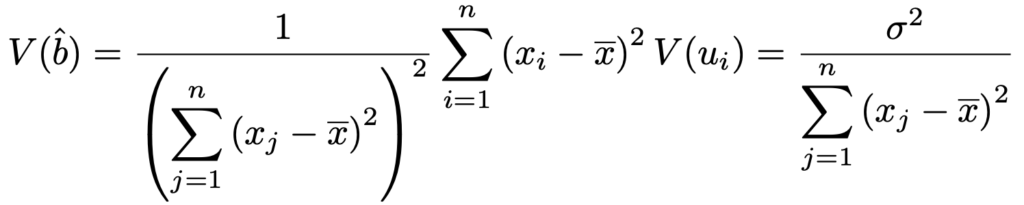
この計算では,V(ui)=σ2であることから分子を次のように式変形し,分母と約分しています。
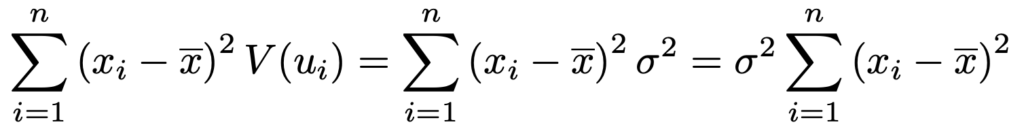
よって,bの推定量は次の正規分布に従います。
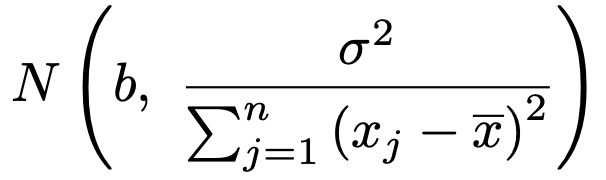
さて,傾きbの推定や検定をするのに,これで十分でしょうか。いや,そうでもなさそうです。分散の分子にあるσ2がわからないので,まだ誤差が特定できていません。
σ2は誤差項uiの分散ですが,これを標本から推定する必要があります。そのために大切な統計量が残差で,次の式で定めます。
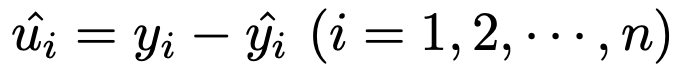
つまり,残差は,次の図のように,標本を表す点と同じx座標の推定された回帰直線上の点とのy座標の差を表しています。
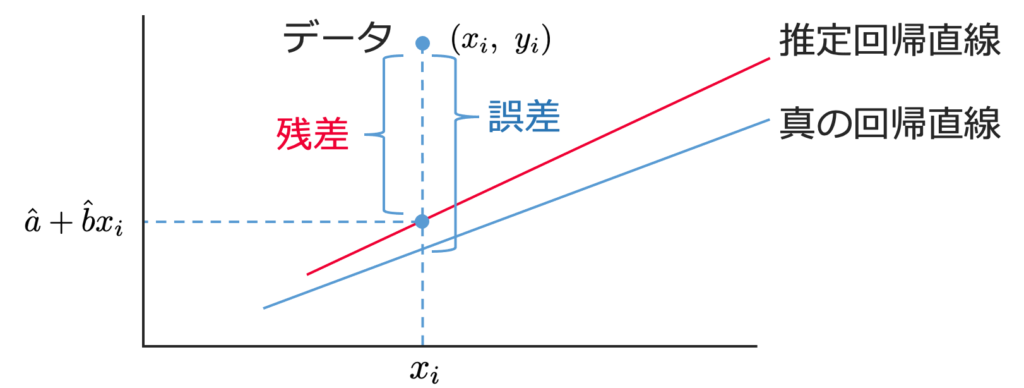
また,標本を表す点と同じx座標の真の回帰直線上の点とのy座標の差を誤差と言います。
次に,残差をそれぞれ2乗して加えた次の式で表される確率変数が残差平方和です。
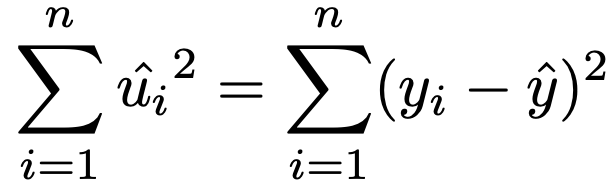
そして残差平方和について,次の定理が成り立ちます。
誤差項uiが互いに独立に次の正規分布に従うものとする。
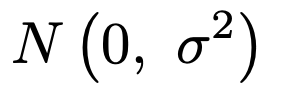
残差平方和を誤差項の分散でわってできる次の確率変数は,自由度nー2のカイ2乗分布に従う。
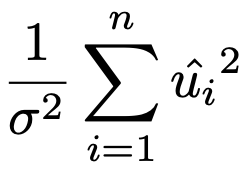
また,残差平方和を自由度のnー2でわってできる確率変数は誤差項の分散の不偏推定量であり,次の式が成り立つ。
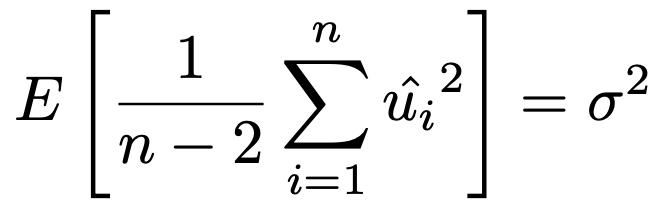
これ以上の脱線を避けるため,この証明は割愛します。証明を知りたい人は,例えば,「線形回帰分析(蓑谷千凰彦著,朝倉書店)」を参照してください。
これで準備が整ったので,いよいよ回帰係数の仮説検定を説明していきます。最もよく行われるのは,bの値について,帰無仮説をb=0,対立仮説をb≠0とする両側検定です。まず,検定統計量を求めていきます。
bの推定量が従う正規分布の期待値と分散がわかっていたので,標準化した次の確率変数ZはN(0,1)に従います。
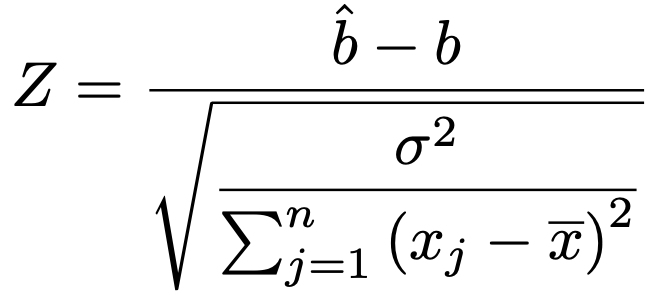
ここで,分母のσ2を,残差平方和を自由度のnー2でわったものにおきかえると次のようになります。
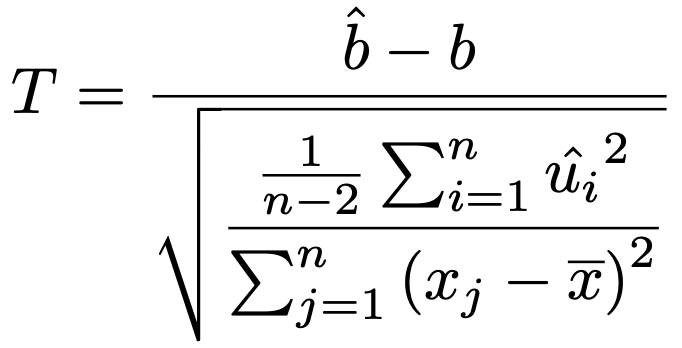
このT が自由度nー2のt分布に従うことは次のようにわかります。
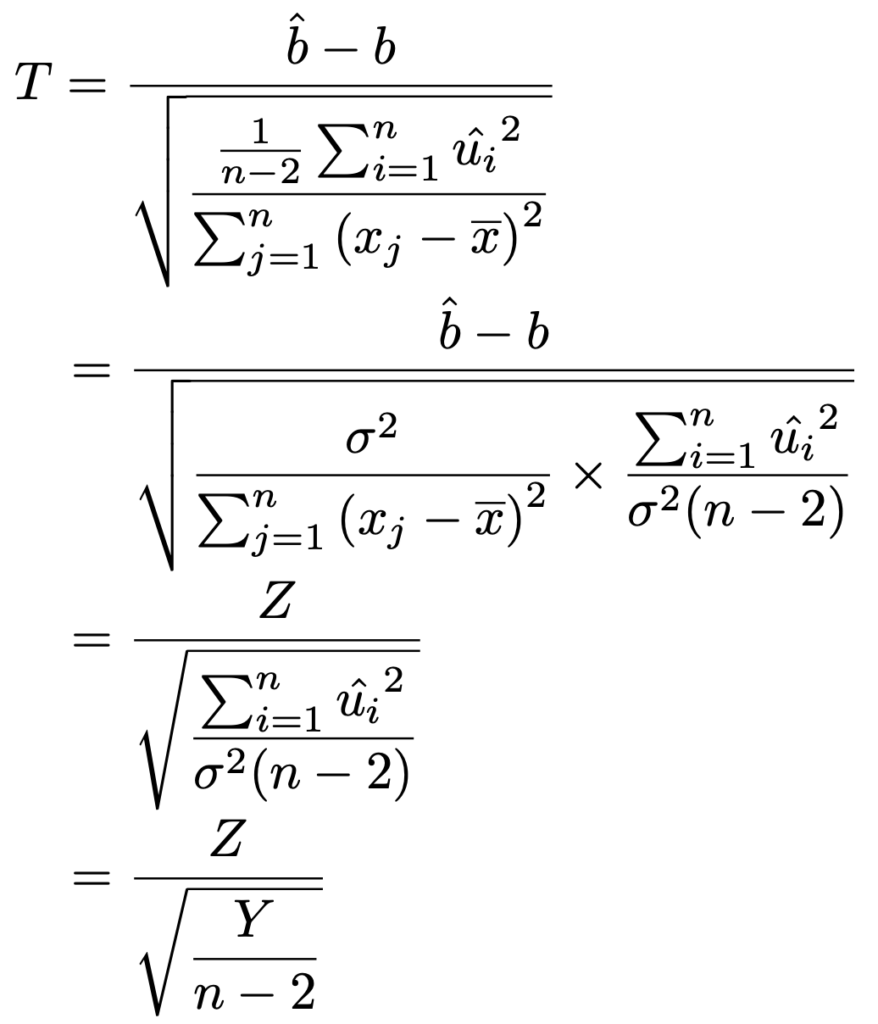
この変形で登場したZは,すぐ上で説明済みのbの推定量を標準化した確率変数で,Yは次の確率変数です。
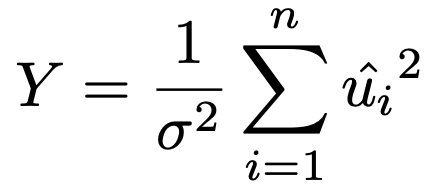
Yは,上の「残差平方和の性質」として紹介した定理から,自由度nー2のカイ2乗分布に従います。
よって,第15回の記事で紹介した命題①によって,T は自由度nー2のt分布に従います。
ここで,帰無仮説b=0を仮定すると,次の式が検定統計量になります。
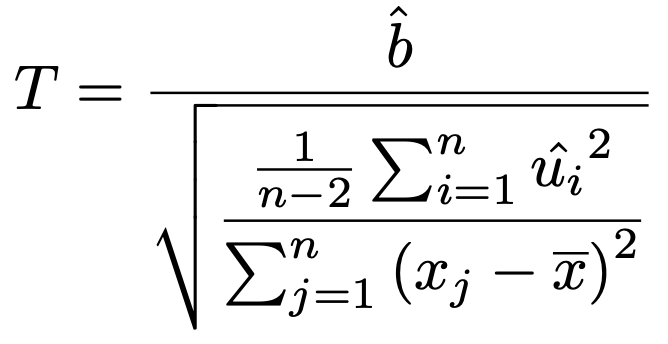
この検定統計量の実現値をt値と言います。また,この式の分母はbの推定量の標準偏差です。一般に,推定量の標準偏差のことを標準誤差と言います。この2つの用語は回帰分析では欠くことのできないものになりますので,必ず覚えましょう。
さて,これで次の式が成り立つことがわかりました。
t値=回帰係数÷標準誤差
標準誤差は回帰係数のばらつきの大きさを表しているので,標準誤差の値が小さいほど回帰係数は狭い範囲の値しかとらないことが示唆されます。その結果,t値が大きくなり,P値が小さくなります。こうなると,回帰係数の検定において,回帰係数が0であるという帰無仮説が棄却され,0ではないとほぼ断言できるようになります。
では,これを踏まえて実戦的な問題を解いていきましょう。
【問題】ある高校の志願者数が,前年の入学試験の合格最低点で説明できるかどうかを検証するため,年ごとの志願者数yを被説明変数,その前年の入学試験の合格最低点xを説明変数,互いに独立に正規分布に従う誤差項をuとする次の単回帰モデルを考える。
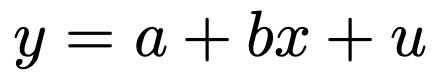
上記の単回帰モデルを15年分のデータを用いて最小2乗法で推定したところ,次の結果が得られた。なお,出力結果の一部を加工している。
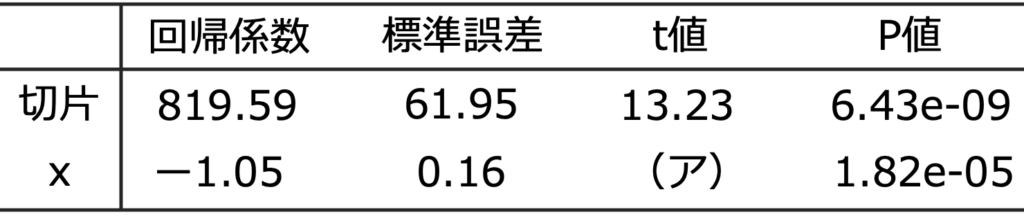
(1)(ア)にあてはまる数値を四捨五入して小数第2位まで求めなさい。
(2)合格最低点が390点だった年の翌年の志願者数の推計値を,四捨五入して整数で求めなさい。
(3)残差の標準誤差(誤差項の分散の不偏推定値の正の平方根)は5.05だった。このとき,残差平方和を求めなさい。
【解答】
まず,表のP値をチェックしましょう。
xの係数(傾き)のP値は「1.82e-05」となっていますが,この数値の意味はわかるでしょうか。次のことを表しています。
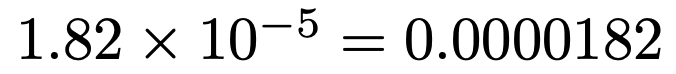
このP値はとても小さいです。0.01よりも小さいので,回帰係数は有意水準1%で有意であると言います。
つまり,有意水準1%で回帰係数が0であるという帰無仮説は棄却されます。
(1)t値は,回帰係数÷標準誤差で求められるので,(ー1.05)÷0.16=ー6.5625
小数第3位を四捨五入して,ー6.56 …(答)
(2)推定された回帰直線の式は,y=ー1.05x+819.59です。x=390を代入すると,y=ー1.05×390+819.59=410.09
よって,志願者数の推計値は,小数第1位を四捨五入して,410人 …(答)
(3)誤差項の分散の不偏推定量は,残差平方和をその自由度でわったものです。つまり,残差平方和は,誤差項の分散の不偏推定値に自由度をかけて求めることができます。
「15年分のデータを用いて」とあるので,標本の大きさは,n=15です。
与えられた残差の標準誤差を2乗したものが誤差項の分散の不偏推定値なので,残差平方和は,
5.052×(15ー2)=331.5 …(答)
(解答終わり)
単回帰分析についての基本的な説明は以上になります。この後は,参考図書の紹介に続けて,さらに理解を深めるための演習問題ですので,余力があればぜひチャレンジしてみてください。
参考図書
本稿を執筆するにあたり,次の書籍を参考にしました。
①基本統計学[第5版](宮川公男,有斐閣)
決定係数の説明の仕方について参考にしました。本書は,記述統計学分野では回帰直線を具体的に計算する問題例が豊富であり,推測統計学分野では回帰係数の区間推定が解説されているところに特徴があります。
②入門統計解析(倉田博史・星野崇宏,新世社)
記述統計学としての回帰分析と推測統計学としての回帰分析のどちらも詳しく書かれている書籍です。特に,回帰係数の確率分布を計算する過程を参考にしました。
演習1〜変動係数〜
【問題】次の表は,あるクラスの数学と英語のテストの得点の平均と標準偏差をまとめたものである。このとき,数学と英語の変動係数をそれぞれ求めなさい。
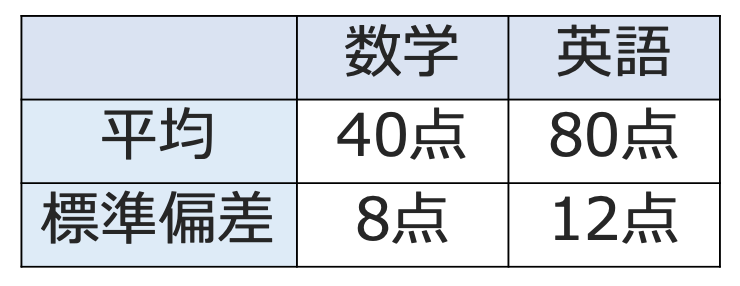
【解答】標準偏差を平均でわればいいですね。数学の変動係数は,8÷40=0.2 …(答)
英語の変動係数は,12÷80=0.15 …(答)
つまり,標準偏差は英語のほうが大きいですが,平均に対する得点のバラツキは数学のほうが大きいと言えるわけです。
(解答終わり)
演習2〜回帰直線〜
【問題】次の表の5組のデータに対して,xを説明変数,yを被説明変数として,回帰直線を求めなさい。
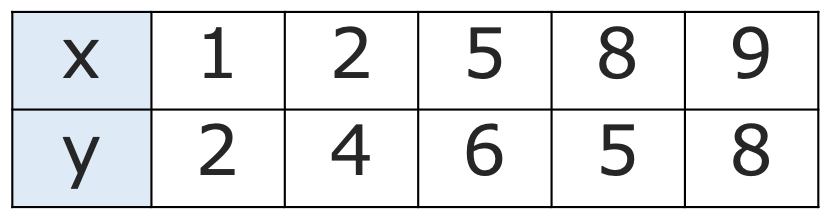
【解答】回帰直線は次の式で求められるんでしたね。
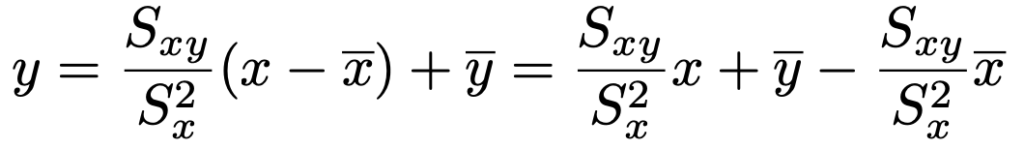
求めるのに必要なのは,xの分散,xとyの平均,xとyの共分散なので,これらを順に求めます。まず,xの平均は次のようになりますね。
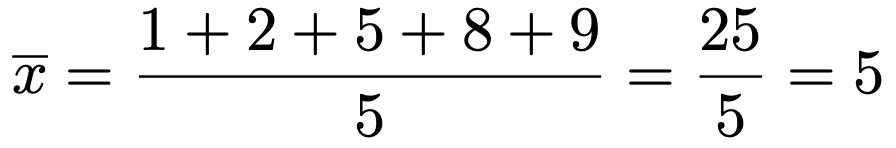
また,xの分散を求めるためにxの2乗の平均を計算すると,次のようになります。
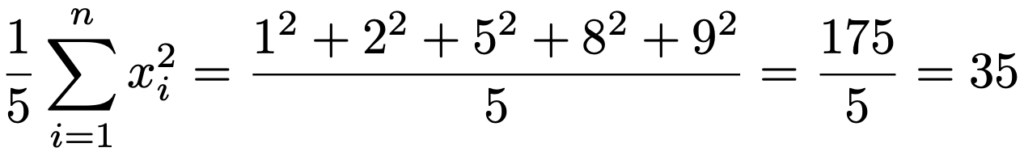
よって,xの分散は次のようになります。
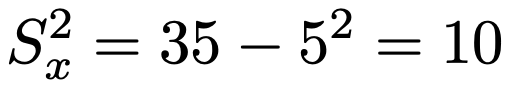
次に,共分散を計算していきます。積xyは次の表のようになりますね。
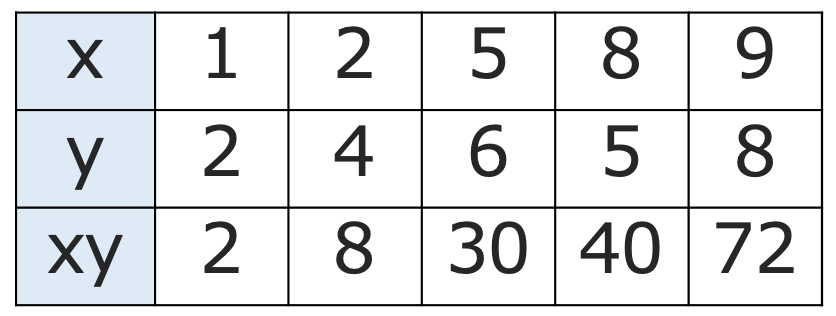
よって,積xyの平均は次のように計算できます。
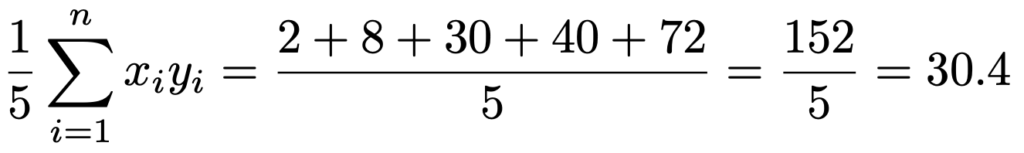
また,yの平均は次のようになります。
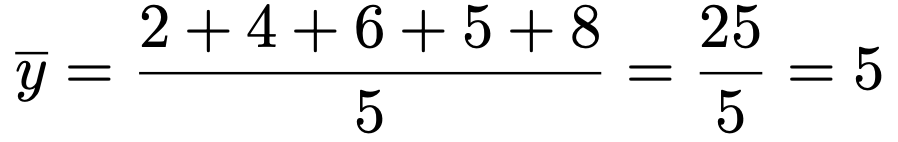
これらを使って,共分散は次のように計算できます。
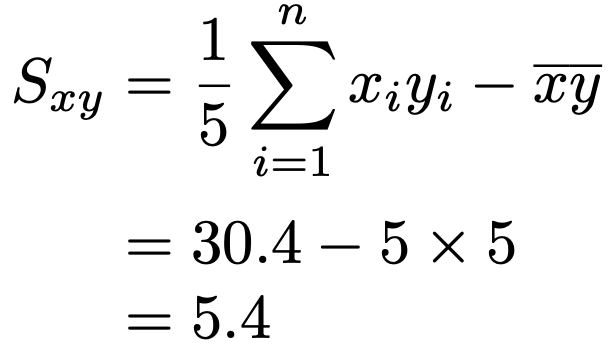
したがって,回帰直線は次のようになります。
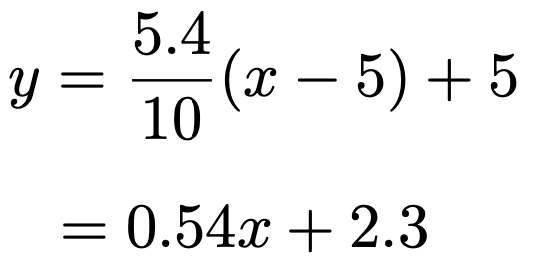
…(答)
(解答終わり)
演習3〜回帰係数の検定〜
【問題】演習2の5組のデータを標本とみて,回帰直線の傾きbについて,有意水準5%のもとで帰無仮説をb=0,対立仮説をb≠0として回帰係数を検定しなさい。
【解答】対立仮説が等号を否定する形なので両側検定です。演習2の回帰直線の式にxの値をそれぞれ代入して,yの予測値を求めると次のようになります。
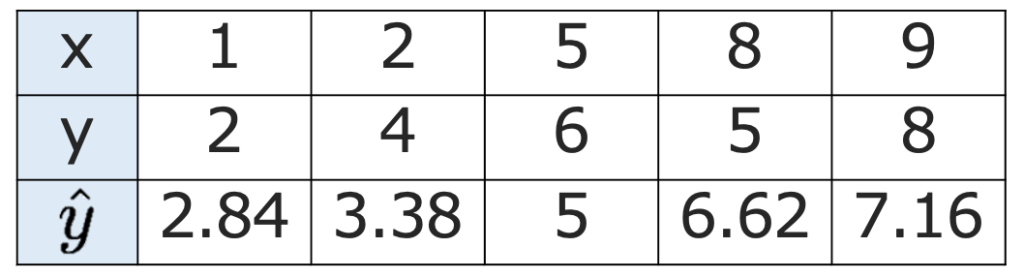
よって,残差平方和は次のように計算できます。
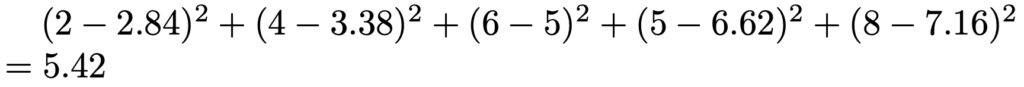
残差平方和の自由度は,5ー2=3なので,残差平方和を自由度の3でわると,
5.42÷3≒1.8
また,演習2でxの分散が10であることを計算しているので,xについての偏差平方和は,
5×10=50
よって,回帰係数の推定量の標準誤差は次のように計算できます。
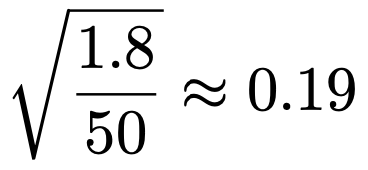
したがって,t値は,0.54÷0.19≒2.84
自由度3のt分布の上側2.5%点を調べると3.182だから,有意水準5%で帰無仮説を受容します。傾きが有意に0でないとは言えません。
(解答終わり)
演習4〜回帰統計の読み取り〜
【問題】ある時点で,都道府県ごとのオンライン診療を行っている医療機関の数がその都道府県の人口で説明できるかどうかを検証するため,都道府県ごとのオンライン診療を行っている医療機関の数yを被説明変数,都道府県の人口x(万人)を説明変数,互いに独立に正規分布に従う誤差項をuとする次の単回帰モデルを考える。
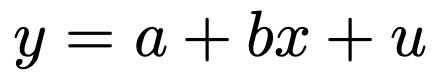
上記の単回帰モデルを最小二乗法で推定したところ,次の結果が得られた。
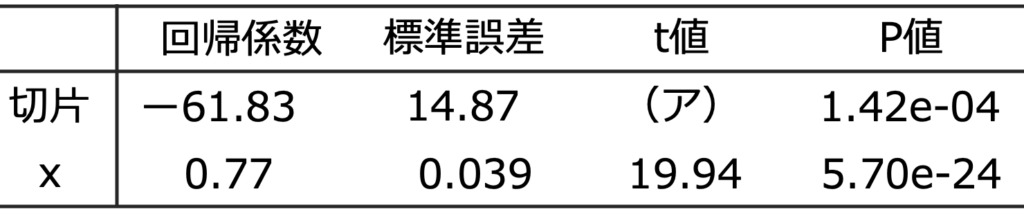
(1)(ア)にあてはまる数値を四捨五入して小数第2位まで求めなさい。
(2)P値はt分布を用いて計算されている。このt分布の自由度を求めなさい。
(3)オンライン診療を行っている医療機関の数の予測値の平均が144.47となった。このとき,47都道府県の人口の平均を1万の位まで求めなさい。
【解答】
(1)t値は,回帰係数÷標準誤差で求められるので,(ー61.83)÷14.87=ー4.158…
小数第3位を四捨五入して,ー4.16 …(答)
(2)標本の大きさがnのとき,単回帰モデルの回帰係数の検定統計量の従うt分布の自由度はnー2です。標本の大きさは都道府県の数の47なので,自由度は,47ー2=45 …(答)
(3)推定された回帰直線の式は,y=ー61.83+0.77xです。よって,予測値は次の式で求められます。
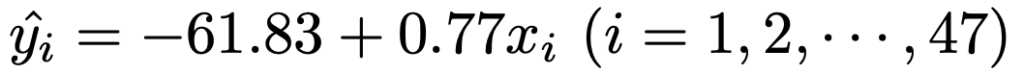
この47本の式のそれぞれの辺をすべて加えて47でわると,次の式になります。
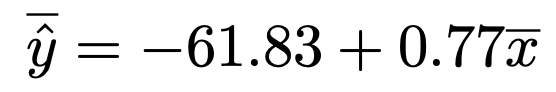
この式の左辺に,オンライン診療を行っている医療機関の数の予測値の平均の144.47を代入すると,次の式になります。
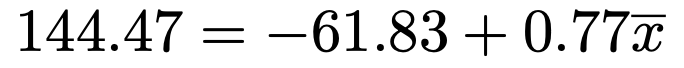
この式を解いて,x=267.92より,268万人 …(答)
(解答終わり)
第17回は以上となります。最後までお付き合いいただき,ありがとうございました!
引き続き,第18回以降の記事へ進んでいきましょう!
2023年1月に「統計検定2級公式問題集[CBT対応版](実務教育出版)」が発売されました!(CBTが何かわからない人はこちら)
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが,本書は分野ごとにその形式の問題を並べた構成になっていて,最後に模擬テストがついています。CBT対策の新たな心強い味方ですね!
さらに実戦に向けた演習を積みたい人は,「統計検定2級公式問題集2018〜2021年(実務教育出版)」を手に取ってみてください!
また,もっと別の問題を解いてみたい人は,さらにさかのぼって「統計検定2級公式問題集2016〜2017年(実務教育出版)」を解いて実力に磨きをかけましょう!





![統計検定2級公式問題集[CBT対応版]](https://m.media-amazon.com/images/I/51q3GfZId3L._SL500_.jpg)



![統計学が最強の学問である[数学編]【おすすめ本】 統計学が最強の学問である[数学編]【おすすめ本】](https://images-na.ssl-images-amazon.com/images/I/51p4aPUyeOL._SX344_BO1,204,203,200_.jpg)
コメント