ベストセラーとなった「統計学が最強の学問である」は,すべての大人に統計学の世界を紹介するための「読み物」でしたが,続編である本書は統計学と機械学習で必要な数学的な道具立てをビジネスマン向けに解説したものです。
統計学や機械学習に必要な数学がコンパクトにまとまっているので,統計学や機械学習を学びたいけれど,高校以上の数学に自信がないという人におすすめしたい一冊です。この記事では,【中学の数学からはじめる統計検定2級講座】を執筆している私の目線で内容を紹介していきますので,本書に興味がわいたら,ぜひ手にとってみてください!
本書はどんな人に役立つか
著者は本書の目的について次のように述べています。
本書はこれからの時代の全ての大人にとって必要な,統計学と機械学習を勉強するための素養となる数学について説明していきたいと思います。
つまり,中学で習う数学から大学1年生が習う線形代数と微積分までの内容のうち,統計学と機械学習で必要な部分に絞って学習できるように作られています。
これはありがたいですね。だって,数学を学び直したいとしても,統計学の全体像が見えていなければ「何が必要な数学なのか」という判断がつきませんので。自分で数学のテキストを選んで手探りで勉強を進めていくのは無駄が発生しやすいです。そんなときには全体像が見えている著者のお力を借りましょう。
本書が向いているのは,例えば「これから統計学と機械学習を学んでいきたいけれど,数学的な理解が不足していて専門書はすぐには読めない。でも,大人になった今,高校生が勉強に使っているようなテキストを自分で買って勉強するのはちょっと抵抗があるな…」と思っている人ですね。
今の世の中,数学が苦手な人に向けて書かれた「数式を最小限におさえた統計学や機械学習の入門書」が数多く存在します。でも,それを読んでも統計学や機械学習の雰囲気がわかるだけで,その先で数学が必要になったときに太刀打ちできません。ただ,数式を避けて通っただけだからです。本気で専門書を読めるようになりたいなら,どこかできちんと数学を学ぶことが必要になります。少なくとも高校数学,できれば大学初年級の線形代数と微積分はできるようにしておきたいです。そこで,本書が役に立ちます。というのも,本書はわりとガチめに数学と向き合っています。そして,予備知識ゼロの読者を想定した解説になっているので,学び直しにうってつけです。
本書の全体像と読み方
本書は,数学的な内容を第1章から積み上げていく形式になっています。そこで,第1章をいちばん下の土台として第6章まで上がっていくようにして内容をまとめると,次の表のようになります。
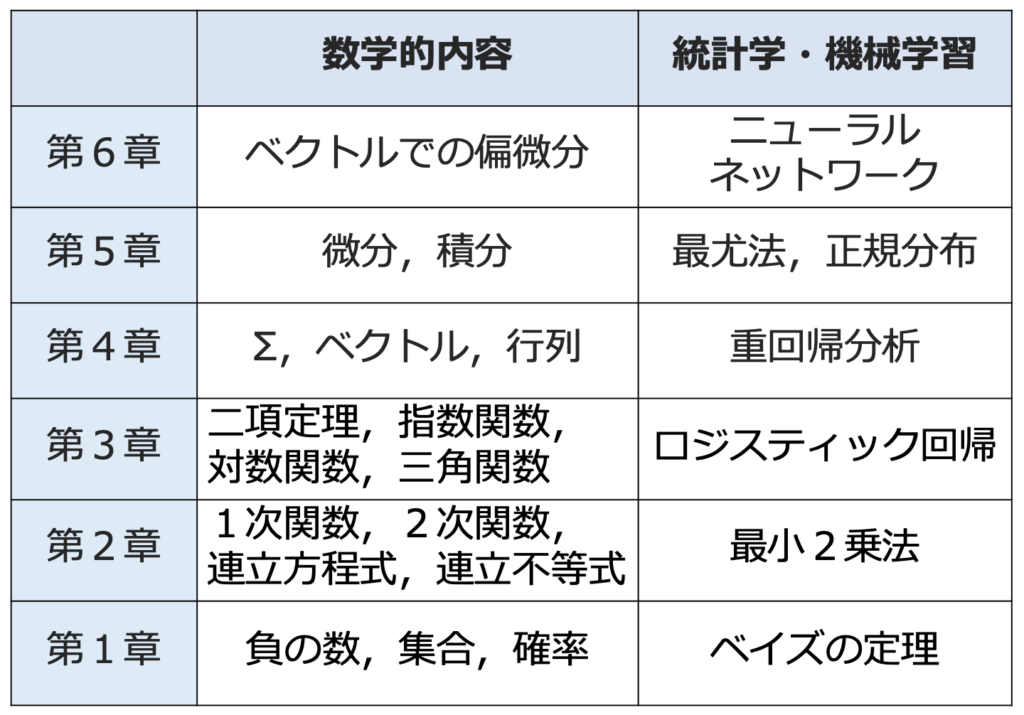
この表が示すように,各章で学んだ数学がどのように統計学や機械学習に結びつくかが示されていて,同時に学ぶことができるところが本書の素晴らしい点ですね。
統計学と機械学習の中核をなすアイデアは「データに最もよくあう数学的なモデルをどう推定するかであり,共通している」と本書中で述べられています。そのために必要なのが(ベクトルでの偏)微分であり,本書は全体として,そこに到達するまでのピラミッドになっています。
ただし,中学で習う数学から始まるので,おそらく知っている内容もあるはずです。歴史的な背景なども説明されているので,わかっている部分も読み物として楽しむことができますが,全部で約550ページくらいありますので,はじめから全てを読んでいく人はあまりいないでしょう。たいていの場合,自分が知りたい部分だけをつまみ喰い的に読んでいくことになりますね。
では,次のセクションからは章ごとに内容を紹介していきましょう。
第1章 統計学と機械学習につながる数学の基本
正直に言うと,第1章は読み飛ばすのもありでしょう。
と言うのも,この章で扱われる「負の数」「文字式」「1次方程式」「集合」「確率」は知っている人も多いでしょうし,扱う内容の易しさのわりに説明が厳密で「理学部数学科かよ…」と思わざるをえない解説がなされているからです。例えば,「負の数」の説明では,次のような事柄がテーマになっています。
- なぜひき算を負の数のたし算として考えるのか
- わり算を分数のかけ算として処理するとどんなメリットがあるのか
- ー1とー1の積はなぜ1になるのか
これらを数の演算規則に基づいて説明していくので,数学を「使えれば十分」と考える人からすると,ありがたみは薄いでしょう。もちろん,これらに数学的に興味がある人は別ですが。
ただし,「集合には自信がない」という人はそこだけでも読んでみたほうが良いですね。確率や統計(そもそも数学)を学ぶ上で,集合の知識は必須ですので。
第2章 統計学と機械学習につながる2次関数
この章のテーマは多項式関数です。ここも「楽勝」と思える人は読み飛ばしても後の章で差し支えはないです。
扱う数学としては,「座標とは何か」という中学1年の内容から始まり,1次関数,2次関数へと話を進めていきます。中学〜高校1年くらいまでの易しめの内容ではありますが,2次関数の平方完成をビジネスシーンでの課題解決に役立てているところがこの章の見どころですね。
具体的には,顧客の平均購買額を最大化するDMの送付回数を求めることを題材として,はじめに2次関数のグラフのあてはめによって分析していきます。過去の営業成績を表す点を座標平面上にとり,2次関数のグラフ上にのっているとみなすことで最大値を計算していきます。
そして,メインは回帰分析です。2次関数のグラフ上にのっているとみなしたデータを「実は直線的な関係があり,生データだから誤差を含んでいる」と考え直して,最小二乗法を使ってあてはまりの良い直線を見つけていきます。
このようなビジネスでも使われる(単)回帰分析が2次関数の平方完成という易しめの数学だけで実現できるということがよくわかるので,このような計算をしたことのない人はやってみると発見があるでしょう。
第3章 統計学と機械学習につながる二項定理,対数,三角関数
この章では,統計学や機械学習でも頻繁に登場するネイピア数(自然対数の底)e=2.71…が,ロジスティック関数やロジット関数を使ったロジスティック回帰に結びつくことを理解できます。
ネイピア数は高校の数学Ⅲで学習しますが,極限を使った定義式は一見すると不思議な形をしているので,納得できていない高校生も多いことでしょう。本書では,次のような例を示して,この数を説明しています。
あなたは「1年後に倍にして返すから100万円を貸して欲しい」と友人に頼み込んだ。つまり年利100%の借金ということである。
友人は「年利100%ではなく半年ごとに50%の複利という計算でもよいか?」と聞き,あなたは承諾する。すると友人はさらに「四半期ごとに25%でもよいか?」…
という具合にどんどん期間を短くしていきます。実際に計算してみるとわかりますが,複利は利息に利息がつくので,期間を短くするほど返済額がどんどんふくらみます。では,無限に増え続けるかというと,ある一定のライン(=元本の約2.71倍)以上には増えないのです。ここにネイピア数が現れるというわけです。
ネイピア数という名前はジョン・ネイピアというイギリスの貴族の名前に由来しています。本書によると,ネイピア数を発見したのはネイピアではないそうなのですが,彼が確かに発明したと言えるものが,この章のもう1つのテーマである対数です。対数は大きな数のかけ算に対して威力を発揮します。
例えば,みなさんは暗算で次の計算ができますか。
「90日間は何秒か」
小学生でも答えられる問いではありますが,暗算はどうでしょうか。6の5乗が計算できればいいんですが,私にはちょっと無理そうです…。
本書で紹介されている計算には対数の値をまとめた数表を使うので,本当の暗算ではないですが,こういう計算を一度はやってみるのも面白いですね。数表はネイピアが苦労してまとめ上げたもので,その功績によって後の天文学者の寿命を伸ばしたとさえ言われています。
この章の最後には三角関数を学習します。直角三角形の辺の比として素朴に定義される三角比に始まり,弧度法を踏まえて座標平面上の単位円上の点の座標として一般化できることが解説されています。この章だけでは,三角関数と統計学との関わりは見えませんが,次の第4章でベクトルの内積として,第5章で極座標として活かされていきます。
第4章 統計学と機械学習のためのΣ,ベクトル,行列
この章で扱われるΣ,ベクトル,行列は,本書の言葉を借りれば,どれも「情報を高密度に記述するもの」です。
和を表すΣ記号は統計検定2級を目指すために,ベクトルと行列は統計検定準1級を目指すために必要なので,苦手な人はぜひ読んでみてほしいです。
Σとベクトルの基本事項を確認した後,それを踏まえてベクトルの内積と相関係数の関係が説明されます。相関係数の解説中に”cos”が登場するところが興味深いです。
そして,この章のメインは行列です。みなさんは,次の式を見て,意味がわかるでしょうか。ただし,X Tで行列Xの転置行列を表しています。
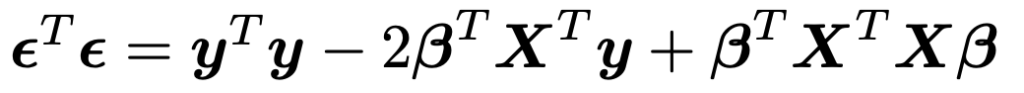
この式をベクトルβで微分しようというわけです。これらの記号に慣れていない人には,「謎の古代文字」のように見えるかもしれませんね。
統計学や機械学習の専門書で多変量解析を勉強しようとすると,こういった計算は避けては通れません。統計検定準1級を目指す人の中には,このあたりにつまずく人も少なくないでしょうから,きっと本書が役に立つはずです。
第5章 統計学と機械学習のための微分・積分
この章では,統計学と絡めて微分積分を基礎から学びます。次の文章は,この章で取り上げられている例題の書き出しです。ビジネスマンならドキッとするのでは?
あるエンジニアは上司から作業時間の見積もりが甘いというお叱りを受けた。上司から彼にふられる業務は基本的にいつも同じような内容であり,1週間(5営業日)ほどで完了することが多いため上司にもそう伝える。…
みなさんなら,業務の作業時間の見積もりを上司に伝えるときに,どんなことに気をつけるでしょうか。まさか,平均的な作業時間を伝えないですよね。それだと間に合うかどうか,五分五分で危険すぎです…。
この章では,「95%大丈夫な作業時間」はどれくらいになるのかを,確率密度関数を仮定して計算しています。そこで積分が必要になります。本書では,積分の基本的な性質だけでなく,イメージもしっかり書かれています。次の表現からそのことをうかがうことができるでしょう。
微分は関数を細かく分けて,関数の変化量を細かい「点」で捉えたもの,積分は細かく分けて考えた関数の値をいっぱいあつめて,「面」や「立体」などの大きさを捉えるもの
私も数学的な概念をいかに上手に言葉にするかを日頃から考えていますが,こういう表現に著者の洞察の深さがにじみ出るものですね。
微分積分が一通り解説された後,最尤法の基本的な部分が説明される流れになっていて,統計学や機械学習に興味がある読者のモチベーションを刺激します。
本章のもう1つの見どころは,正規分布の解説です。ふつうの統計学の入門書は,正規分布の確率密度関数を天下り的に示した上で
「それはさておき,正規分布の確率を求めるには正規分布表というものがありまして…」
と続いていくのですが,本書は違います。この章で学んだ微分積分の知識を駆使して,正規分布の確率密度関数はなぜあの形になっているのかというナゾに正面から立ち向かっていきます。人類史上,最も有名な数学者であるガウス(C.F.Gauss)がいかにして正規分布にたどり着いたのか,という歴史的な視点も絡めた展開は読みごたえがあります。
とは言え,このあたりの話題は「使えればいい」という人には必要のない内容ではありますので,読み飛ばすのもありでしょう。私は個人的に気に入っている部分なので,興味のある方はどうぞ。
この章の最後の話題は重積分です。正規分布の確率密度関数の係数部分を決定するのに2変数での積分が必要になるので,極座標を使って計算していきます。本書では,積分区間が「ー∞〜+∞」の積分をしれっと登場させていますが,広義積分についての説明があるとなお良かったですね。
第6章 ディープラーニングを支える数学の力
この章の目的は,前章までで学んだ内容を活かして,ニューラルネットワークを線形代数的に表現する方法を理解することにあります。これができれば,機械学習の最新の研究成果なども含めて「読み解ける資料の幅が大きく広がる」と著者は述べています。
数学的には,スカラーの場合の偏微分の計算方法を紹介した後,ベクトルによる微分について成り立つ計算ルール(例えば,2次形式に対する微分)を解説してくれています。統計学を学ぶのであれば,少なくとも偏微分は理解しておきたいですし,統計検定準1級レベルを目指すのであれば,ベクトルによる微分も理解したいところです。
その後に続くニューラルネットワークの話題は本書の最難関の部分です。第1章で負の数の解説をしていたかと思えば,第6章で「これほど高いところまで数学の山を登ってきたのか」と気づかされます。
ディープラーニングは,「どういうモデルを考えるか」という部分と「どういうアルゴリズムでパラメーターを推定するか」という部分に分けることができます。「企業が効率的な採用活動のために過去の採用者のデータをどう活用すべきか」などの現実的な課題設定のもとで,前者についてはシグモイド関数の重ね合わせとその線形代数的な表現,後者については最急降下法や微分のチェーン・ルールに基づくバックプロパゲーションが取り上げられています。なかなか読み進めるのも体力が必要な話題ですが,興味のある人はぜひ読んでみてほしいです。
まとめ
統計検定2級は,中学校の数学が理解できていれば大半の問題は解けるのですが,Σや積分ができるとさらに解ける問題が増えます。また,記述統計の何気ない問題で指数の知識が必要になったり,重回帰分析の問題中に(知らなくても解けるとは言え)対数が出てきたりするので,高校数学全般の理解があるほうが有利ではあります。
そこで「2級の勉強にあたり本書を傍に置きつつ,必要に応じて高校数学を復習し,行列などの部分は準1級の勉強を始めるときに読む」といった使い方も考えられるでしょう。
なお,欲を言えば「数列」の解説も本書に盛り込んで欲しかったですね。統計学を勉強していると,数列の知識が活きる場面が出てくるので。
また,本書はあくまで統計学や機械学習の専門書へ進む前段階となる数学の本ですが,実際に統計学なり機械学習をさらに勉強したい人のために巻末に著者がおすすめの書籍を多数挙げてくれているのも助かります。ただし,本書には索引がないので,この記事も参考にしてどの章にどんな数学が登場するのかを把握してください。
では,本書に興味がわいたら,ぜひ手にとってみてください!

![統計学が最強の学問である[数学編]【おすすめ本】 統計学が最強の学問である[数学編]【おすすめ本】](https://images-na.ssl-images-amazon.com/images/I/51p4aPUyeOL._SX344_BO1,204,203,200_.jpg)



コメント