条件付き確率とベイズの定理【中学の数学からはじめる統計検定２級講座第２回】

「条件付き確率って，分母と分子に分数の確率が入るから，よくわからないなぁ…」「P(A|B)なのか，P(B|A)なのか，忘れちゃうよ！」「統計の教科書で，ベイズの定理って見かけたけど，式が複雑すぎて覚えられない！」と思ったことはありませんか。こんなモヤモヤを抱える人が多い分野ですが，いったん理解してしまえば悩む必要なんてなかったときっと思えることでしょう。統計検定２級でほとんど毎回出題されている重要単元なので，苦手意識はなんとしても克服したいところです。そのために，「条件付き確率とベイズの定理がスッキリわかる」ような記事にしてあります。また，ベイズの定理は機械学習の基礎になっているので，AIに関わる仕事を目指す人にも有益です。

なお，この記事では，【中学の数学からはじめる統計検定２級講座第１回】の内容を既知であるものとして話を進めます。確率の計算の基本を確認したい方は，第１回の記事を先にご覧ください。

では，はじめていきましょう！

ベイズの定理【中学の数学からはじめる統計検定２級講座第２回】

条件付き確率とは
ベイズの定理
ベイズ更新
参考図書
演習１〜場合の数の商として計算する条件付き確率〜
演習２〜事前確率がわからないときのベイズの定理〜
演習３〜ベイズの定理（原因が２つの場合）〜
演習４〜ベイズの定理（原因が３つの場合）〜

条件付き確率とは

まず，【中学の数学からはじめる統計検定２級講座第１回】で扱った確率の積の話を思い出しましょう。忘れてしまった人はもう一度見直してみてください。次のような内容でした。

事象AとBが独立であるとき，Aが起きて，さらにBが起きる確率は，(Aが起きる確率)×(Bが起きる確率)で求められる。

式で表すと，次のようになります。

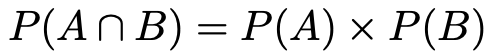
ここで，左辺は事象AとBが両方とも起きる確率，右辺は事象Aが起きる確率と事象Bが起きる確率の積を表しています。

では，事象AとBが独立ではないときには，どうなるのでしょうか。実はこの場合でも，次のような式が成り立ちます。

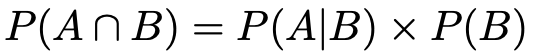
２つの式を見比べると，P(A)のところがP(A|B)に変わりました。P(A|B)は，事象Bが起きたという条件のもとで事象Aが起きる確率を表しています。これが条件付き確率です。AとBが独立ではない場合には「Bが起きたという条件のもとでAが起きる確率」が右辺に現れますが，AとBが独立ならばBの影響はないのでただのP(A)で良いわけです。

また，P(A|B)とP(B|A)を混同してしまうということがよく起こります。そうならないためには，この記号の成り立ちをしっかり理解しましょう。

縦棒は英語で”given”と読まれたりしますが，日本人の感覚としては，”when”だと思うのがわかりやすいでしょう。縦棒を”when”で置き換えると，P(A|B)のかっこ内は「A when B」と読めます。「A when B」を日本語に訳すと，「BのときA」となります。つまり，P(A|B)はBのときAが起きる確率を表していて，縦棒の右に書かれたBが条件を表しているんです。P(A|B)はBのときAが起きる確率，P(B|A)はAのときBが起きる確率です。

では，具体例で確認していきましょう。

【問題】６本のうち２本があたりのくじがある。Aさんが１本のくじをひき，ひいたくじをもとに戻さずに，Bさんが１本のくじをひくとき，２人ともあたりくじをひく確率を求めなさい。

【解答】Aさんがひいたくじをもとに戻せば，１回目にひいたくじの結果と２回目にひいたくじの結果は独立なのですが，もとに戻さない設定のため，Aさんがあたりくじをひくか，はずれくじをひくかによって，Bさんがあたりくじをひく確率が変わるわけです。だから，Aさんがひく１回目の結果とBさんがひく２回目の結果は独立ではないですよね。

さて，確率を求めてみましょう。２人ともあたりくじをひく確率です。まず，Aさんがくじをひくとき，６本の中に２本のあたりくじがありますので，あたりくじをひく確率は６分の２ですね。次に，Bさんがくじをひくとき，５本の中に１本のあたりくじがありますので，Bさんがこの状況であたりくじをひく確率は５分の１です。Aさんがはずれくじをひいたという別の状況であれば，Bさんがあたりくじをひく確率は５分の２であったはずです。

では，記号を使って式を書いてみましょう。Aさんがあたりくじをひく確率をP(A)，Bさんがあたりくじをひく確率をP(B)とすると，AさんとBさんが２人ともあたりくじをひく確率，Aさんがあたりくじをひいたという条件のもとでBさんがあたりくじをひく確率はそれぞれ次のように表されます。

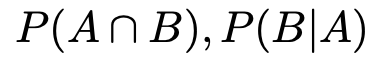
このとき，次の式が成り立つのでしたね。

先ほど書いたように，この式の右辺の２つの確率は次のようにわかっています。

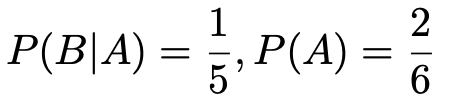
したがって，答えは次のように求められます。

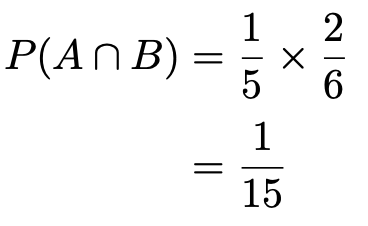
（解答終わり）

さて，条件付き確率を求める式は，先ほどの式をP(B|A)について解いて，次のようになります。

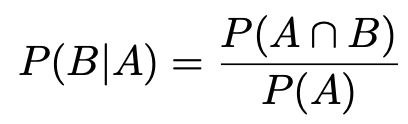
上の問題ではP(B|A)とP(A)が先にわかる設定でしたが，P(B|A)が残りの２つの確率によって求められるという場合には，この式を使います。この式の分母がP(A)であることは「事象Aが起きた場合のみを考えて，Aが起きない場合は考えない」ということを意味しています。このように，全事象を特定の事象が起きた場合に絞り込むのが条件付き確率です。このことがよくわかる問題を，この記事の下のほうの演習１に入れてありますので，そちらを解いて条件付き確率の理解を深めてください。

ここで，事象Aと事象Bの順番について大事な注意を１つしておきます。実は，上の問題で，あとからくじをひくBさんの結果がAさんがあたりくじをひく確率に影響を与えるということもあるのです。たとえば，Aさんは，Bさんがひいたくじの結果を確認するまで，自分のひいたくじは確認しないという状況を考えてみましょう。「Bさんがあたりくじをひいた」という事実を知ったら，Aさんはきっとがっかりするでしょう。その時点で，Aさんが握っているくじがあたりである確率が小さくなるからです。逆に，「Bさんがはずれくじをひいた」という事実を知ったら，Aさんはきっと喜ぶでしょう。Aさんが握っているくじがあたりである確率が大きくなるからです。このように考えると，先に起きた事象が後に起きる事象に影響を与えるだけでなく，後に起きた事象が先に起きた事象に影響を与えることもあるわけです。どういう情報をもとに考えるかによって，確率は変わるのです。

このことを式で確認しておきましょう。２人ともあたりくじをひく確率は，先にAについての情報が判明するか，Bについての情報が判明するかによって，次の２通りの書き方が可能です。

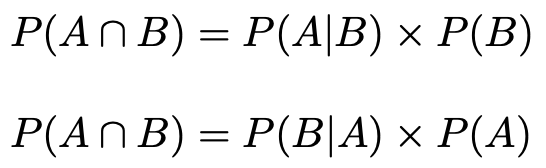
左辺は等しいので，右辺も等しくなります。よって，

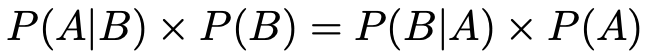
上の式で，例えば，Aが先に起きる原因で，Bが後に起きる結果だと考えてみましょう。一般的に「原因A→結果B」の条件付き確率はわかっているケースが多いので，上の式を利用すると，「原因A→結果B」の条件付き確率から「結果B→原因A」の条件付き確率を求めることができます。

ある結果Bが起こったことから，原因がAであった条件付き確率を求めることができるのが，次のセクションで紹介するベイズの定理のミソになります。

ベイズの定理

ベイズの定理は，トーマス・ベイズ（Thomas Bayes）の名前に由来します。ベイズは牧師だったのですが，生前にはこの定理が数学界で大きな評価を受けることはありませんでした。しかし，彼の死後，別の数学者によってその意義が見出され，ベイズの名前が付けられたという逸話があります。

さて，ベイズの定理の式を一般的な形で書き直すと，次のようになります。

この式を見て，一気にやる気をなくす人もいるかもしれませんが，大丈夫です。この式は参考のために書いただけで，覚える必要はありません。ベイズの定理は覚えるものではなく，仕組みを理解して使うのです。では，問題を通して確認してみましょう。

【問題】ある製品をA，B，Cの３台の機械で作っている。この製品の60％は機械Aで，25％は機械Bで，15％は機械Cで作られている。また，作った製品のうちの不良品の割合は，Aが２％，Bが３％，Cが５％である。この製品の１つが不良品であることが判明したとき，それが機械Aで作られたものである確率を求めなさい。

【解答】１つの製品を取り出したとき，それが機械Aによって作られた確率，機械Bによって作られた確率，機械Cによって作られた確率をそれぞれ次のように表すことにします。

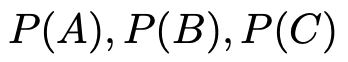
また，１つの製品が機械Aによって作られたものであるときに不良品である確率，機械Bによって作られたものであるときに不良品である確率，機械Cによって作られたものであるときに不良品である確率をそれぞれ次のように表すことにします。

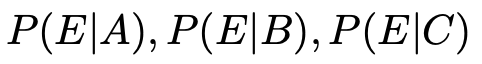
この表し方にならうと，求める確率は，不良品であることがわかったとき，それが機械Aが作ったものである確率なので，P(A|E)と表せますね。この確率は，条件付き確率の定義から，次のように表せますね。

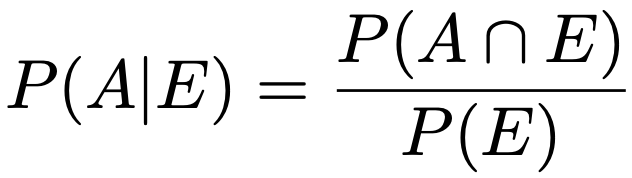
上の式の右辺の分母は，１つの製品を取り出したとき，それが不良品である確率です。不良品は，Aの不良品，Bの不良品，Cの不良品の３つに分けることができるので，次のように書き直すことができます。

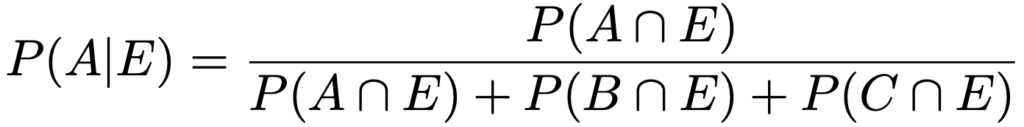
そして，右辺の分母，分子の各項は，前のセクションで学習したことから，次のように表すことができます。

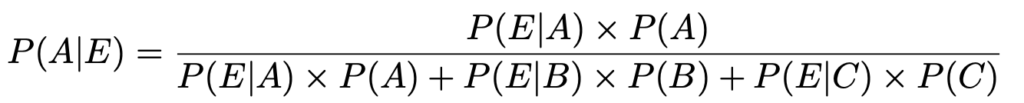
この式は，ベイズの定理の一般式において，右辺の分母の項を３つにしたものです。では，この式が意味するところを，次の図で確認してみましょう。

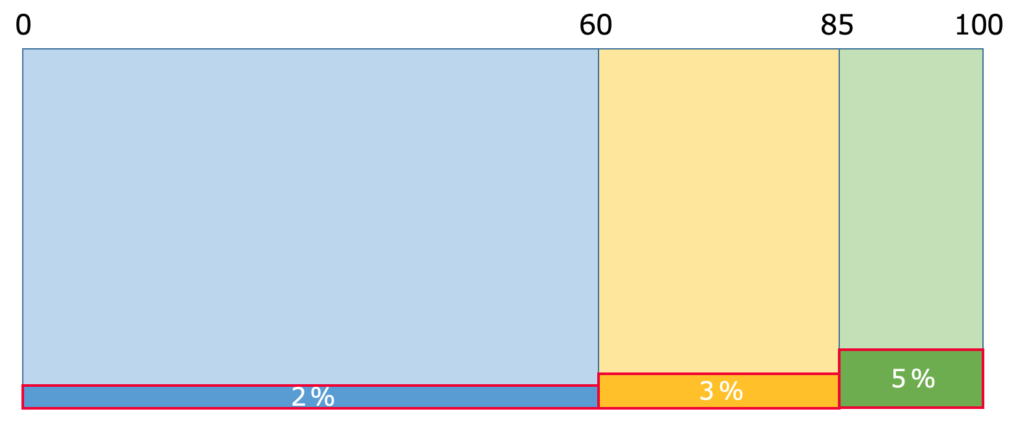
青い部分が機械Aで作られた製品の割合，黄色い部分が機械Bで作られた製品の割合，緑の部分が機械Cで作られた製品の割合を表しています。そのうち，赤線で囲まれた部分が不良品にあたります。この長方形全体の面積を１と考えます。そのうちの60％（＝P(A)）が機械Aで，さらにその２％（＝P(E|A)）が機械Aの不良品なので，P(E|A)×P(A)によって，製品全体に対する機械Aの不良品の割合が表されます。同じように，P(E|B)×P(B)で製品全体に対する機械Bの不良品の割合，P(E|C)×P(C)で製品全体に対する機械Cの不良品の割合を表しますので，先ほどのベイズの定理の式が，製品全体に占める不良品の割合に対する機械Aの不良品の割合を表すわけです。

では，確率を計算していきます。１つの製品を取り出したとき，機械Aによって作られた不良品である確率は，機械Aによって作られる確率と，機械Aの製品であるときの不良品である確率との積であるから，次のように計算できます。

この数は，求めたい確率を計算する式の右辺の分子であるのと同時に，分母の第１項ですね。同じように，右辺の分母の第２項と第３項を求めましょう。１つの製品を取り出したとき，機械Bによって作られた不良品である確率と，機械Cによって作られた不良品である確率は次のように計算できます。

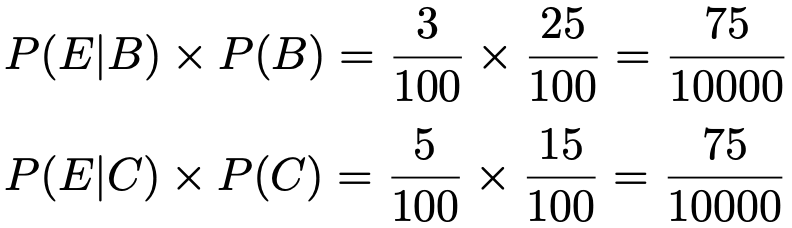
したがって，上に書いた求めたい確率を計算する式の右辺の分母だけを計算すると，次のようになります。

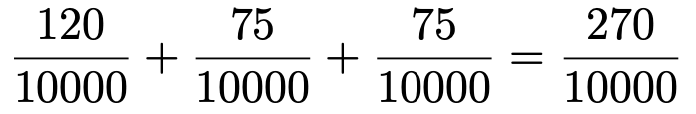
よって，求めたい確率は次のように計算できます。

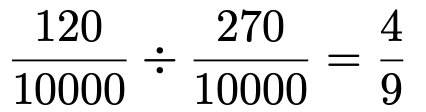
（解答終わり）

ベイズの定理は，解釈の仕方が大切です。もともと，１つの製品を選んだときに，Aによって作られた製品である確率は60％だったのですが，その製品が不良品であるという情報が入ってきたので，Aによって作られた製品である確率がベイズの定理にしたがって更新される，という見方がミソです。この考え方があるので，P(A)を「情報が入る前の確率」ということで事前確率，P(A|E)を「情報が入った後の確率」ということで事後確率と呼びます。

９分の４＝約44％なので，不良品を１つ見つけたとき，それが機械Aによって作られた確率は，もとの60％から少し下がった，とみることができます。機械Aの不良品率がBやCと比べて低いためにこのようになるのですが，新しい情報によって確率が更新されるという考え方を次のセクションでさらに詳しく見ていきます。

ベイズ更新

【問題】ある地域で，病気Aにかかっている人は，人口の0.1％である。検査方法は不完全であり，病気Aに罹患している人について，正しく陽性と判定する確率は99％，罹患していない人について，誤って陽性と判定する確率は10%である。
（１）この検査を受けて陽性だと判定された人が，実際に罹患している確率を求めなさい。
（２）病気Aの検査を１回受けて陽性だと判定された人が，再検査を受けて陽性だと判定されたとき，実際に罹患している確率を求めなさい。

【解答】

（１）まず，求める確率を式で表すと，次のようになります。

ここで，病気Aに罹患している確率をP(A)，検査で陽性になる確率をP(E)としています。左辺は，検査で陽性だと判定されたときに，実際に罹患している確率を表しています。右辺の分母の第１項と分子は，実際に罹患していて，陽性だと判定される確率を表しています。右辺の分母の第２項は，実際には罹患していないのに，陽性だと判定される確率を表しています。この項のAの上についている横棒には否定の役割があり，「Aでない」つまり「病気Aに罹患していない」という意味です。右辺の分母の２つの項を合わせると，検査で陽性だと判定される確率，つまりP(E)に等しくなります。

では，確率の計算をしていきましょう。右辺の各項は，問題で与えられた条件から次のように計算できます。

これらを代入すると，求めたい確率は，

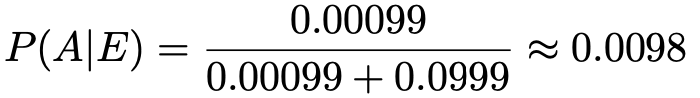
（解答終わり）

四捨五入すると約１％ですから，病気Aに罹患している確率は事前確率の10倍に跳ね上がりました。とはいえ，陽性だと判定されても，本当に罹患している確率がたったの１％というのは驚きではないでしょうか。罹患していないのに陽性だと判定された人がたくさんいるので，このようになります。次に，同じ人がもう一度検査を受けて陽性だと判定された場合を考えてみましょう。

（２）１回検査を受けて陽性だと判定されている時点で，この人が病気Aに罹患している確率は，先ほどの計算の通り，約１％です。したがって，事前確率P(A)＝0.01として，先ほどと同じように計算すると次のようになります。

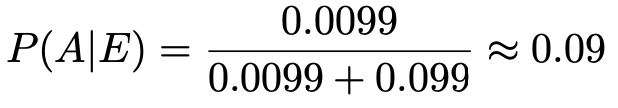
ということで，事後確率は約９％になりました。（解答終わり）

【補足】
より正確に言えば，（１）のP(A)と（２）のP(A)は意味が異なりますから，１回目の検査で陽性だと判定される確率をP(E₁)として，（２）のP(A)をP(A|E₁)と書いたほうがベターです。
この場合，２回目の検査で陽性だと判定される確率をP(E₂)として，求める確率はP(A|E₁,E₂)となります。
上の計算と結果は変わりませんが，この記号を使って式を改めて書いておくと，次のようになります。

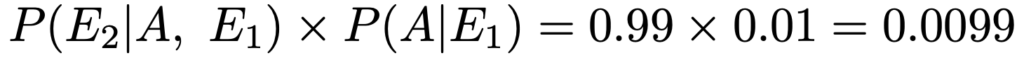
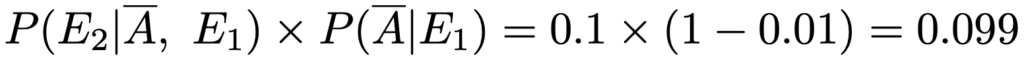
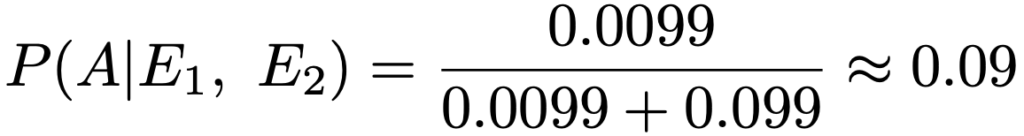
やっていることは同じなので，上記解答では簡略化した表記を使っています。

（補足終わり）

このように，ベイズの定理は，事前確率を入力すると，自動的に事後確率を出力する仕組みを提供してくれています。このプロセスを繰り返すことで，どんどん確率が情報に合わせて更新されていくわけです。これをベイズ更新といいます。

確率は分数で表されることが多いので，ベイズの定理や条件付き確率の定義式の分母や分子には分数をあてはめることになります。「分母や分子に分数を書くなんて複雑だな」とはじめは思うかもしれませんが，確率更新のプロセスにおける入力と出力になっていて，コンピューターに計算させることを考えれば，この形のほうが便利なのです。

条件付き確率とベイズの定理についての基本的な説明は以上になります。この後は，参考図書の紹介に続けて，さらに理解を深めるための演習問題ですので，余力があればぜひチャレンジしてみてください。

参考図書

ベイズの定理の式の意味がわからないという人には，次の書籍がおすすめです。

完全独習ベイズ統計学入門（小島寛之，ダイヤモンド社）

こちらの書籍は，ベイズの定理と同等の条件付き確率の計算を，ベイズの公式を使うことなく，面積図だけを使って解説しています。割合と面積図さえ正しく使えれば，ベイズの定理は不要であるということがよくわかるでしょう。また，本稿で紹介した事前確率，事後確率，ベイズ更新といった用語も本書中に登場します。

ちなみに，本書の後半は準１級レベルのベイズ統計です。ベイズ統計の入門書としても，限りなく平易に書かれた数少ない一冊です。

完全独習ベイズ統計学入門

演習１〜場合の数の商として計算する条件付き確率〜

【問題】ある学校のテニス部の男子36人と，女子32人が合宿に行き，１つのフロアを貸し切った。男子のうち，メガネをかけているのは12人，女子のうち，メガネをかけているのは8人である。テニス部が宿泊しているフロアでメガネの落とし物が見つかったとき，それが男子のものである確率を求めなさい。

【解答】部員は全部で，36＋32＝68(人)ですが，メガネをかけている人だとわかった時点で，12＋8＝20(人)に絞られます。

この「メガネをかけている人」という情報によって，確率の分母が68から20に変わり，確率を求める対象全体が絞られるのが条件付き確率です。

いきなりですが，答えを求めてみましょう。メガネをかけている20人の中で男子は12人なので，求める確率は，

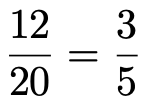
（解答終わり）

【別解】

あっさり答えが出てしまったのですが，条件付き確率の公式を使ってみましょう。無作為に１人を抽出したとき，それが男子である確率をP(A)，メガネをかけている確率をP(B)とします。求めたいのは，メガネをかけている人であることがわかったとき，男子である確率なので，P(A|B)です。これは，次の式によって求められます。

上の条件付き確率の式の右辺の分母は次のようになります。

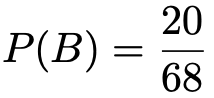
上の条件付き確率の式の右辺の分子は「１人を無作為に抽出したとき，メガネをかけた男子である確率」だから，次のようになります。

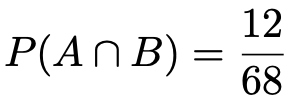
これらを代入して計算すると，求める確率は，

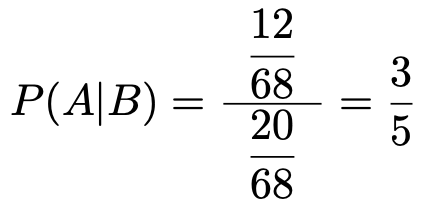
（解答終わり）

68が分母と分子に共通しているので，約分してしまうと，はじめに求めたのと同じ答えが出るわけです。分母と分子で相殺されることははじめからわかっているので，このタイプの問題であれば，前者の求め方のほうがスマートです。

条件付き確率の公式は，ベイズの定理として使うときにその真価を発揮します。闇雲に使わないことに注意しましょう。

演習２〜事前確率がわからないときのベイズの定理〜

【問題】兄と弟は，２つの袋AとBから玉を取り出すゲームを行う。袋Aには，赤玉が２個と白玉が４個入っており，袋Bには，赤玉が１個と白玉が５個入っている。兄は，この２つの袋のどちらか一方から玉を取り出し，それを弟に渡す。弟が赤玉を渡されたとき，兄が玉を取り出した袋が袋Aである確率を求めなさい。

【解答】袋Aから取り出す確率をP(A)，袋Bから取り出す確率をP(B)，赤玉を取り出す確率をP(R)とすると，求める確率は，次の式で表すことができます。

求めるものは，赤玉であるという条件のもとで，袋Aから取り出された確率なので，P(A|R)と表せます。ここで，弟の立場からは，兄がどちらの袋を選ぶかは同様に確からしいと考えて，事前確率を次のように設定します。

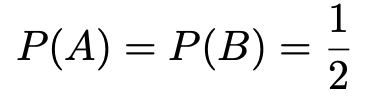
この事前確率の設定ははっきりいうと主観です。そのため，このような確率を主観確率と呼ぶことがあります。

それぞれの袋から赤玉を取り出す確率は次のようになります。

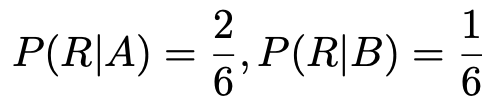
これらを代入して計算すると，次のようになります。

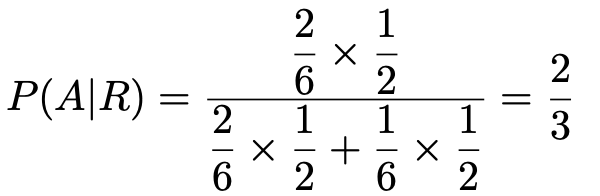
（解答終わり）

答えの３分の２は直感的には明らかです。この問題の設定は，袋Aに入っている玉と袋Bに入っている玉を１つの箱の中に入れてしまい，箱から玉を１個取り出す試行と同じです。箱から赤玉が取り出されたとき，それがもともと袋Aに入っていた赤玉である確率を求めなさい，と言っているのと同じです。箱の中には３個の赤玉があり，そのうち２個がもともと袋Aに入っていた赤玉です。だから，３分の２なのです。

演習３〜ベイズの定理（原因が２つの場合）〜

【問題】ある資格試験の受検資格は，専門学校の卒業生と，通信講座の受講修了者にのみ与えられる。この試験の受検者を調べたところ，専門学校の卒業生が30％，通信講座の受講修了者が70％であった。また，この試験に合格する確率は，専門学校の卒業生であれば25％，通信講座の受講修了者であれば20％であることがわかっている。この試験の合格者を無作為に１人選んだとき，その人が専門学校の卒業生である確率を求めなさい。

【解答】専門学校の卒業生である確率をP(A)，通信講座の受講修了者である確率をP(B)，合格者である確率をP(E)とすると，求める確率は，次の式で表すことができます。

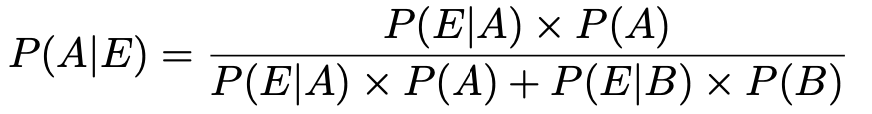
左辺は，合格者であることがわかったときに，それが専門学校の卒業生である確率であり，これが求めたいものです。右辺の分母は，合格する確率を表していて，第１項は専門学校の卒業生が選ばれて合格する確率，第２項は通信講座の受講修了者が選ばれて合格する確率です。右辺は，合格者全体に対する専門学校を卒業した合格者の割合を計算していることになります。では，計算していきましょう。

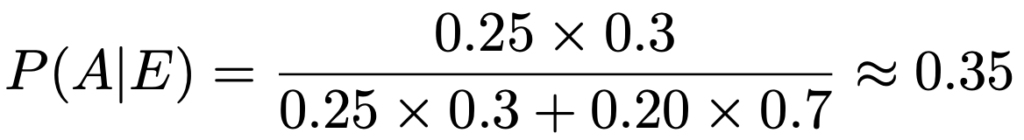
（解答終わり）

つまり，約35％ですね。受検者にしめる専門学校の卒業生の割合は30％ですが，専門学校の卒業生は合格率が少し高いので，合格者を対象に調べると，その割合が高くなっているわけです。

演習４〜ベイズの定理（原因が３つの場合）〜

【問題】ある市場では，A県産とB県産とC県産の白菜が並べられていて，この市場の白菜のうち，A県産は40％，B県産は35％，C県産は25％である。しかし，A県産の白菜の３％，B県産の白菜の４％，C県産の白菜の２％は出荷基準に適合しないことがわかっている。この市場の白菜を無作為に１つ選んだところ，出荷基準に適合しないものであった。この白菜がB県産である確率を求めなさい。

【解答】白菜がA県産である確率をP(A)，B県産である確率をP(B)，C県産である確率をP(C)，出荷基準に適合しない白菜である確率をP(E)とすると，求める確率は，次の式で表すことができます。

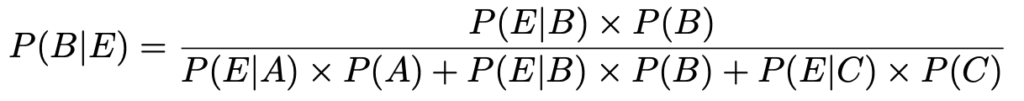
求めるのは，白菜が出荷基準に適合しないことがわかったときに，それがB県産である確率なので，P(B|E)と表せます。右辺の分母は，出荷基準に適合しない確率で，分子はB県産で出荷基準に適合しない確率です。問題で与えられた数値を代入すると，次のようになります。

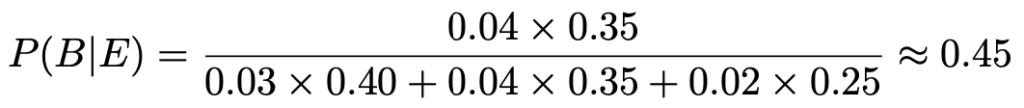
（解答終わり）

これだけ問題を解けば，ベイズの定理はバッチリだと思います。第２回は以上となります。最後までお付き合いいただき，ありがとうございました！
引き続き，第３回以降の記事へ進んでいきましょう！

2023年1月に「統計検定２級公式問題集[CBT対応版]（実務教育出版）」が発売されました！（CBTが何かわからない人はこちら）
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが，本書は分野ごとにその形式の問題を並べた構成になっていて，最後に模擬テストがついています。CBT対策の新たな心強い味方ですね！