ベイズ法の勉強をすると,唐突にガンマ分布・ベータ分布に出会います。これらの確率分布に慣れていないせいで,ベイズ法の勉強でつまずいてしまうのは非常にもったいないです。なぜなら,これらはシンプルでよくできたモデルを与えてくれるので,ベイズ法の勉強の端緒として都合がいいからです。本稿を通して,ガンマ分布やベータ分布は恐れるようなものではなく,パラメータを調節することで自在に確率密度関数の形を変えられる便利な確率分布であるということを納得してもらえればうれしいです。
本稿の目的は,ガンマ分布・ベータ分布を解説すること以外にもう1つあり,それはガンマ分布・ベータ分布を理解するために必要な数学を解説することです。【統計検定準1級のための数学】と題した記事では,統計検定2級からスムーズに準1級に進めるように,ギャップをうめるために必要な数学も解説していきます。本稿では,ガンマ分布・ベータ分布に関連して置換積分,ガンマ関数,ベータ関数,極値を解説します。
この記事で前提とする知識は,【中学の数学からはじめる統計検定2級講座】の第3回の確率変数,第4回の期待値と分散,第6回の連続型確率変数,第7回の広義積分,【統計検定準1級のための数学】の②(指数関数)と③(指数分布)の内容になります。これらの内容に不安がある人は,先にそちらの記事を読んでください。
では,はじめていきましょう!
置換積分
指数分布の記事で紹介した部分積分と同じように,積分を効率的に計算するための方法の1つが置換積分です。次の図のように,被積分関数のf(x)とx=φ(t)という変数変換のための関数を組み合わせた合成関数f(φ(t))を考えることで,積分を計算しやすく変形します。
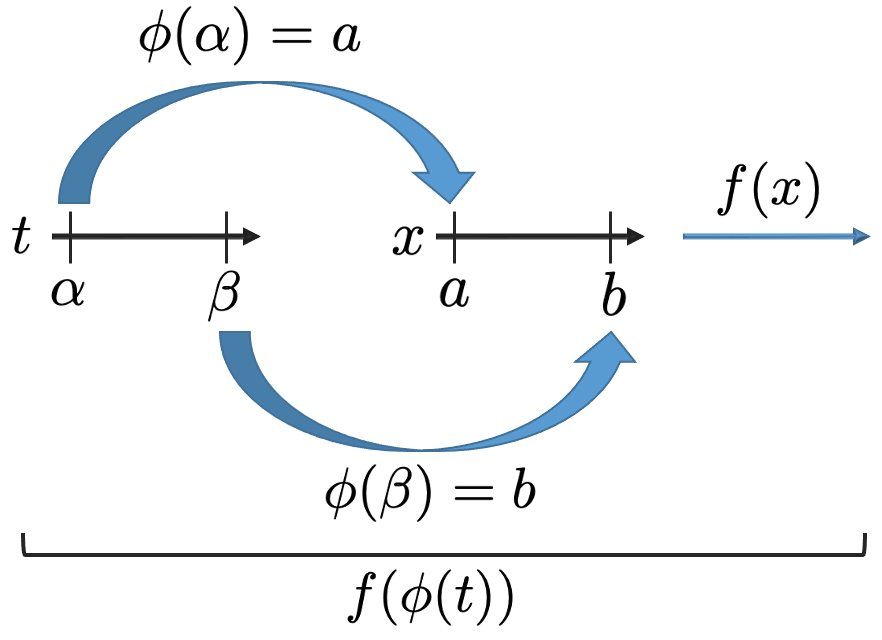
xでの積分をtでの積分に置き換える計算では,次の命題のようにφ(t)の微分をかけることに注意します。
関数φ(t)は閉区間[α,β]を閉区間[a,b]に移し,φ(α)=a,φ(β)=bであり,C1級(微分可能で導関数が連続)であるものとする。このとき,連続関数f(x)に対して,次の等式が成り立つ。
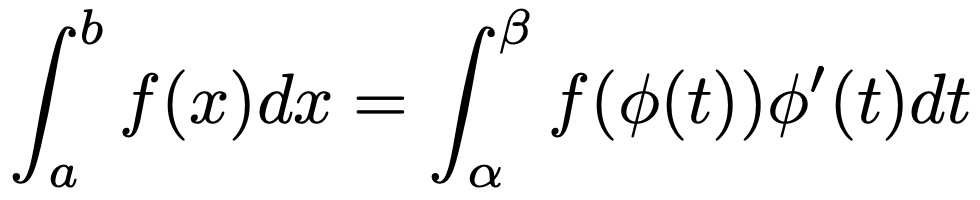
(上の命題の証明)f(x)の原始関数の1つをF(x)として,y=F(x),x=φ(t)とおくと,合成関数の微分によって,次の式が成り立ちます。

つまり,上の式の最右辺の原始関数として,F(φ(t))をとることができるので,次のように置換積分の公式が示せます。
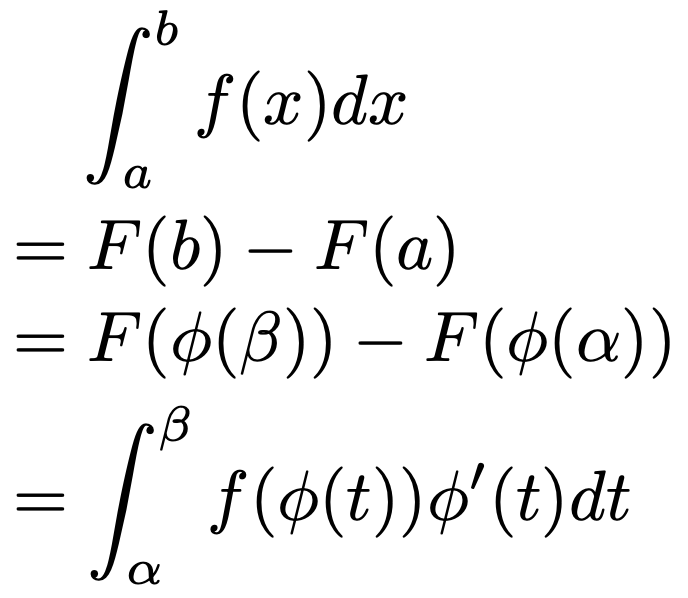
(証明終わり)
ということで,置換積分の公式は合成関数の微分を使うと証明できますが,証明よりも使えることが大事です。そこで,次の問題を解いてみましょう。
【問題】次の定積分の値を求めなさい。
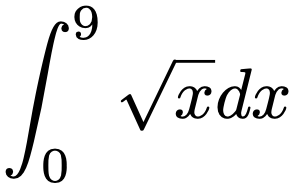
【解答】この定積分は,置換積分を使わずにそのまま計算できますが,ここでは練習のためx=t2と置換して計算してみます。この変換によって,次の表のようにx=0とt=0,x=9とt=3がそれぞれ対応していることに注意します。
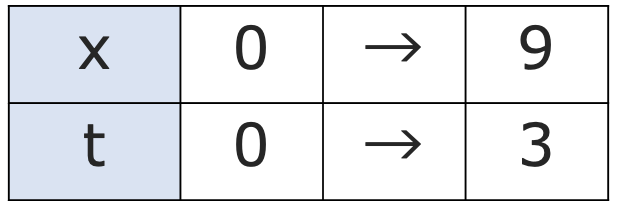
上の命題と見比べると,φ(t)=t2になっているので,(被積分関数にt2を代入した関数)×(t2を微分して得られる2t)dtと変形して,次のように求められます。
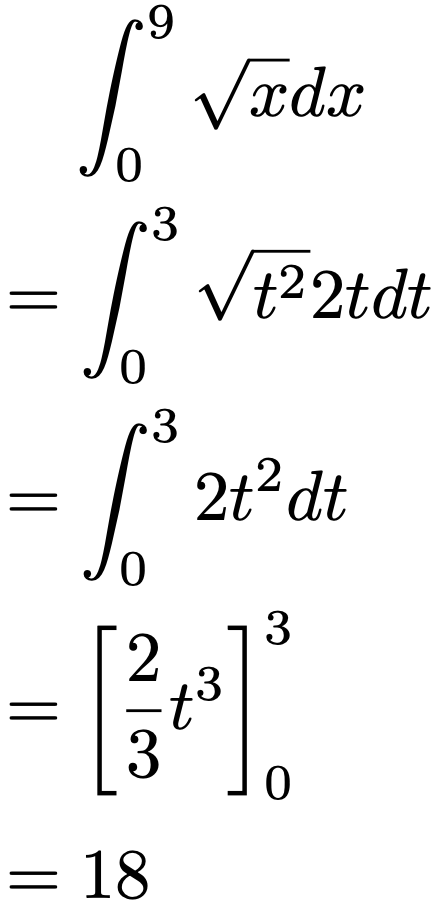
冒頭で断ったように,この積分は置換積分を使わずに計算できます。実際に計算してみると,次の通りです。
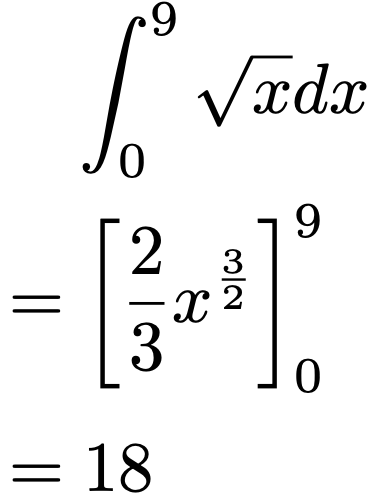
確かに同じ結果になりましたね。
(解答終わり)
置換積分に慣れるために,定積分の計算をもう1つやってみましょう。
【問題】次の定積分の値を求めなさい。
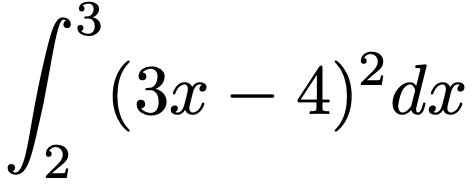
【解答】この定積分も置換積分を使わずに計算できますが,ここでは3xー4=tと置換して計算してみます。この変換によって,次の表のようにx=2とt=2,x=3とt=5がそれぞれ対応していることに注意します。
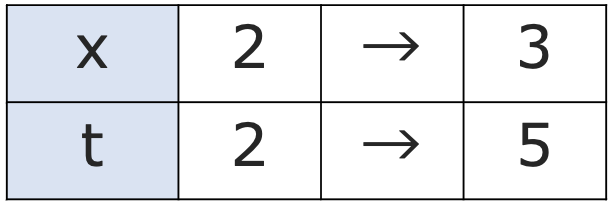
次に,dxとdtの置き換えですが,上の命題と無理に合わせると,次のようにxについて解いてから右辺をtで微分することになります。

しかし,実はxについて解く手間は必要ありません。dxとdtの関係式は,xの微小な変化量とtの微小な変化量の対応関係を示しています。次の図を見てください。
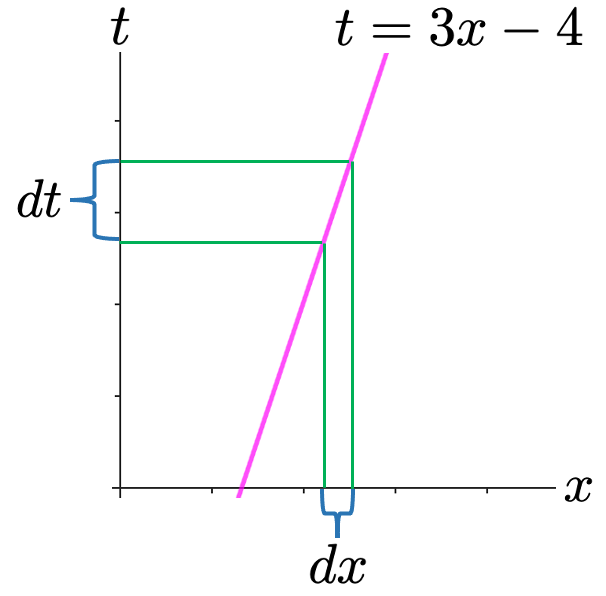
tをxで表した式の変化の割合(直線の傾き)が3なので,t方向の変化量はx方向の変化量の3倍になります。よって,dt=3dxが成り立つのです。これを形式的に計算するには,3xー4=tの左辺をxで微分し,右辺をtで微分して,左辺にはdxを,右辺にはdtを追加すれば,3dx=dtが得られます。つまり,置換積分は次の3つのステップを実施することで計算できます。
- 積分範囲を対応させる
- 被積分関数の変数をおきかえる
- 微小量をおきかえる
よって,定積分の値は次のように求められます。
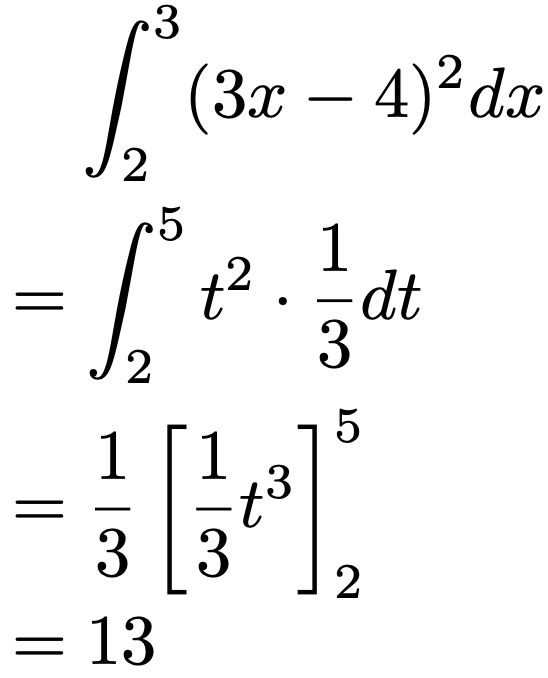
(解答終わり)
ガンマ関数
ガンマ分布を述べるための準備として,ガンマ関数を説明していきます。まず,ガンマ関数を定義します。x>0のとき,正の実数tに対して次の式で定義される関数f(t)を考えます。
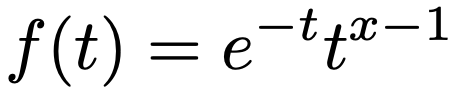
関数f(t)は(0,∞)で広義積分可能(証明が知りたい人は参考図書①を見てください)なので,ガンマ関数を次のように定義します。
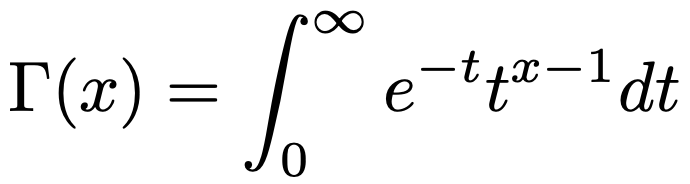
f(t)>0より,Γ(x)>0です。ちなみに,ガンマとは,アルファベットの”c”に対応するギリシャ文字であり,”Γ”という記号で表されます。Γ(x)の式を見て「右辺の積分は計算しないの?」と思うかもしれませんが,被積分関数が多項式の場合とは異なり,積分結果を簡単な形で表すことができないため,上の式のように定義します。右辺はtで積分しているので,「積分した結果」にtは含まれず,xだけの関数になります。
ガンマ関数が何やら得体のしれない積分で定義されてしまいましたが,「ガンマ関数とは何者なのか」に対する1つの回答は「階乗の一般化」と言うことができます。このように言える理由は,次の式からわかります。
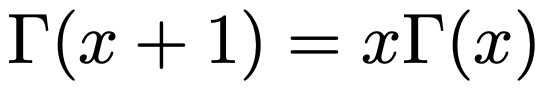
上の式は指数分布の記事(リンクはこちら)で解説した部分積分を使うことで次のように示すことができます。
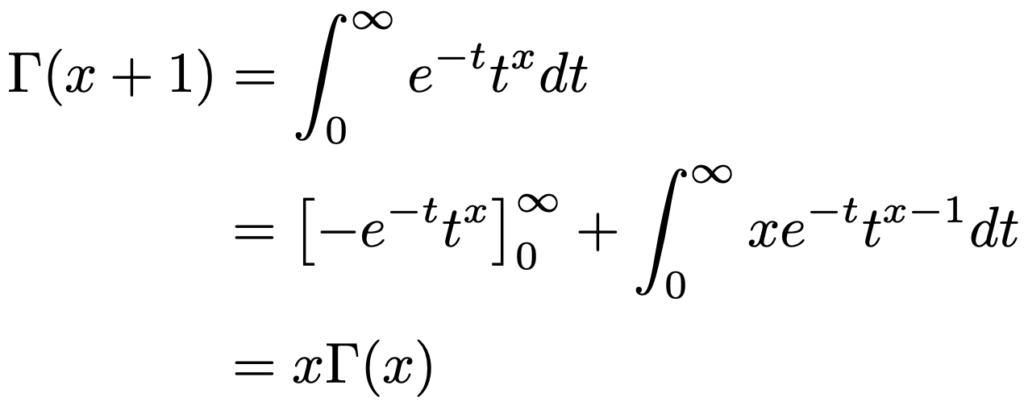
さて,この性質から,nを自然数としてΓ(n)=(nー1)!を示すことができます。まず,次のnー1本の式が成り立ちますよね。
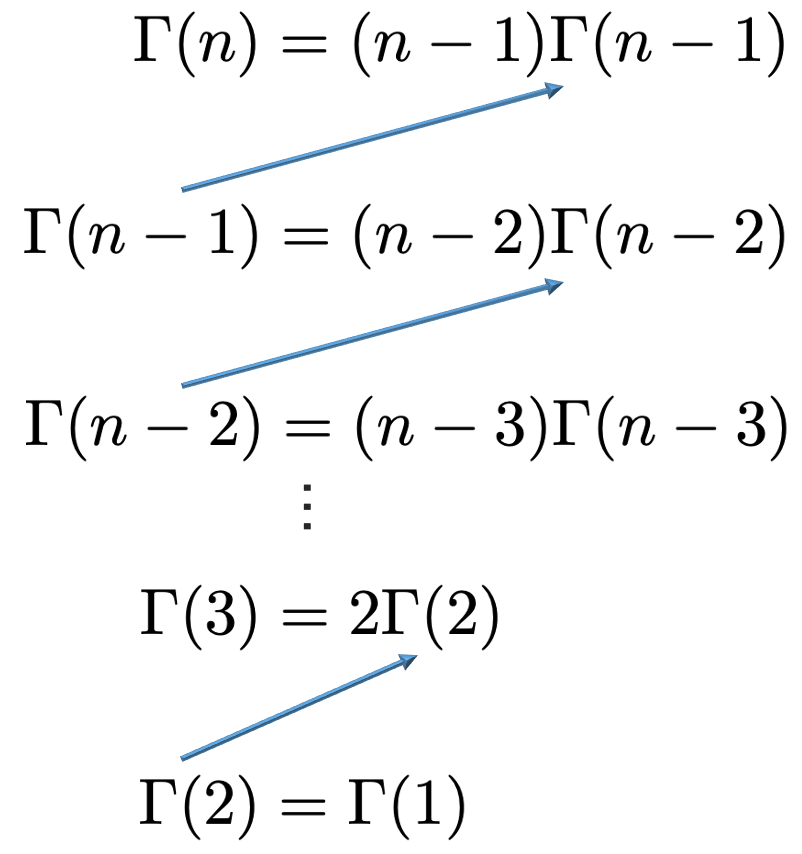
上の矢印のように,次々に代入していくと,次のようになります。
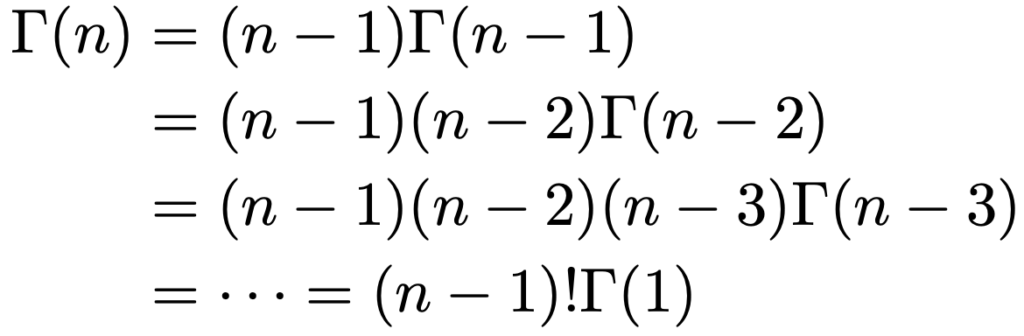
ここで,Γ(1)の値は,次のように計算できます。
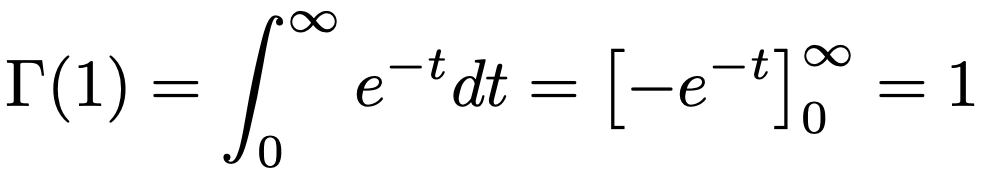
よって,Γ(n)は(nー1)!と一致します。これが「階乗の一般化」と言える理由で,ガンマ関数を使えば,自然数以外の数に対しても「階乗のようなもの」を考えることができます。特に,次の値は統計学でもよく使いますので知っておくといいでしょう。
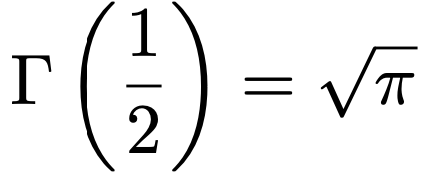
上の値は,次のセクションで紹介するガンマ関数とベータ関数の関係式を使うと,比較的簡単に求められます。
ベータ関数
名前から察しがつくと思いますが,ベータ分布を定義するために必要なものがベータ関数です。まずは定義からはじめます。x>0,y>0のとき,0<t<1に対して次の式で定義される関数g(t)を考えます。
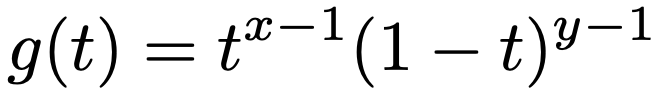
関数g(t)は(0,1)で広義積分可能(詳細は参考図書①を見てください)であり,ベータ関数を次のように定義します。
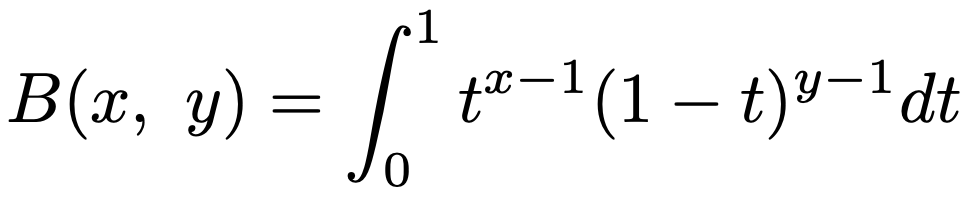
g(t)>0より,B(x,y)>0です。ちなみに,ベータはアルファベットの”B”に対応するギリシャ文字です。
ベータ関数もガンマ関数と同じく,上の式の右辺は「積分した結果」をよく知る関数で簡単に表示することができないため,積分の形で定義します。右辺はtで積分しているので,「積分した結果」にtは含まれず,xとyの2変数関数になります。
この2つの変数xとyは,次の式が成り立つという意味での対称性を持ちます。
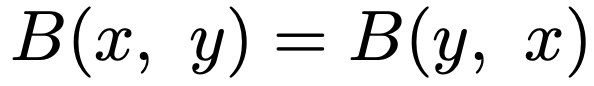
これが成り立つことを示すには,t=1ーsによって変数変換します。実際に計算してみると,dt=ーdsに注意して,次のようになります。
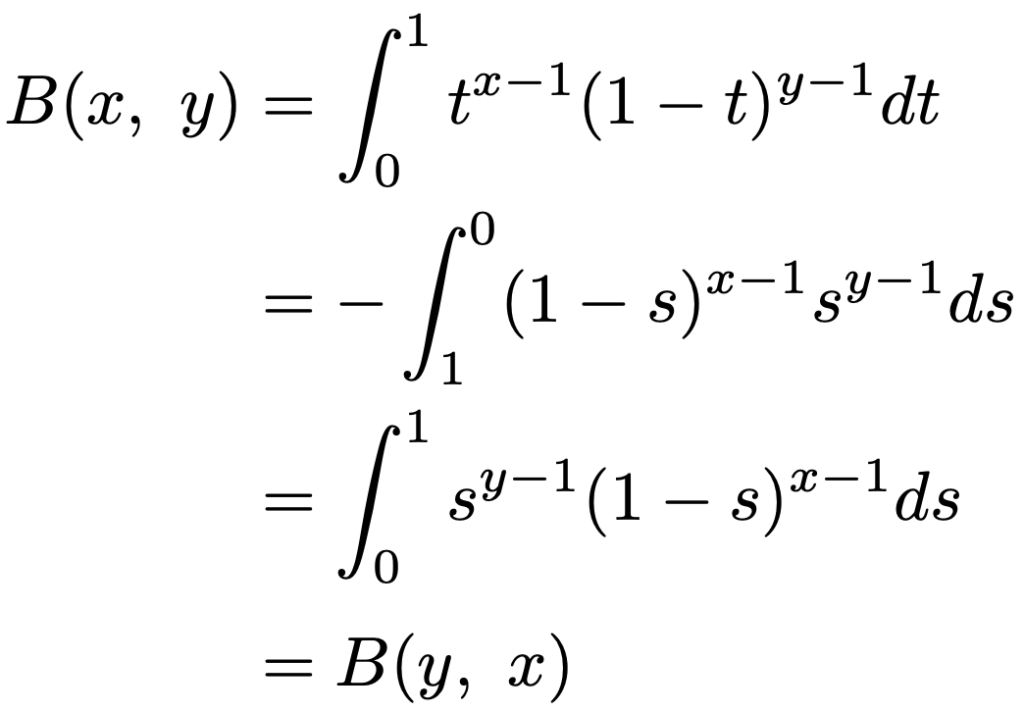
また,次の値は後で使うので覚えておいてください。
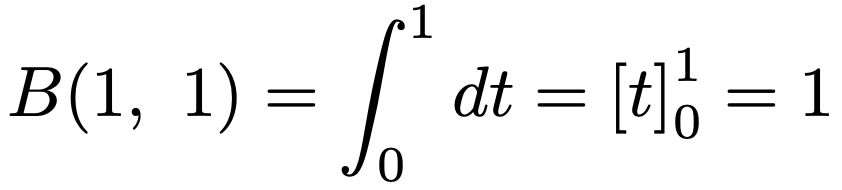
さて,実は,ガンマ関数とベータ関数の間には,次の関係式が成り立ちます。
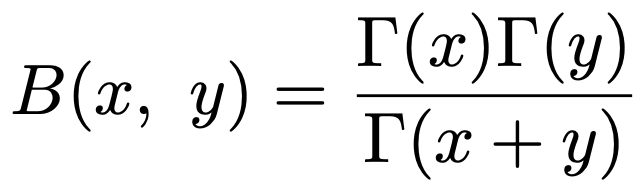
上の関係式が成り立つことの証明を知りたい人は,参考図書①を見てください。この関係は非常に大切なので,結果だけは覚えましょう。せっかくなので,この関係を使って,自然数m,nに対して次の等式が成り立つことを証明しておきます。
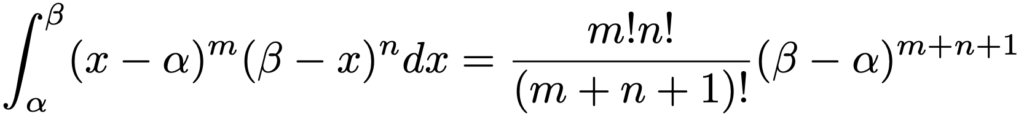
これは,高校数学範囲の積分を計算するときに重宝する公式であり,m=n=1のときには,俗に6分の1公式と呼ばれる次の式になります。
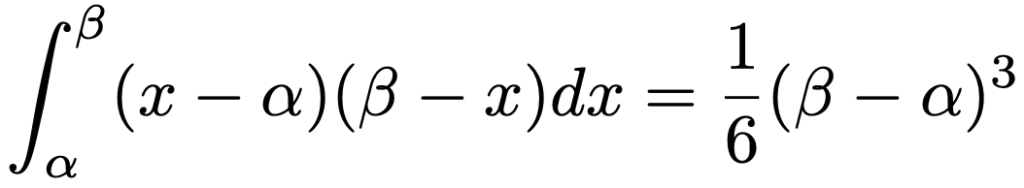
では,証明していきます。まず,次の変数変換を考えます。
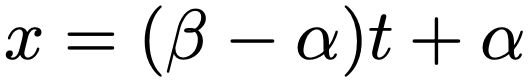
この変換によって,次の表のようにx=αとt=0,x=βとt=1がそれぞれ対応していることに注意します。
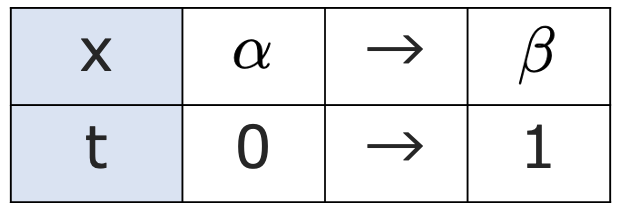
また,変数変換の式の両辺の微分を考えることにより,次の微小量の間の関係が成り立ちます。
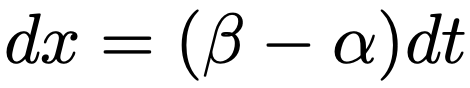
よって,示すべき式の左辺は次のように変形できます。
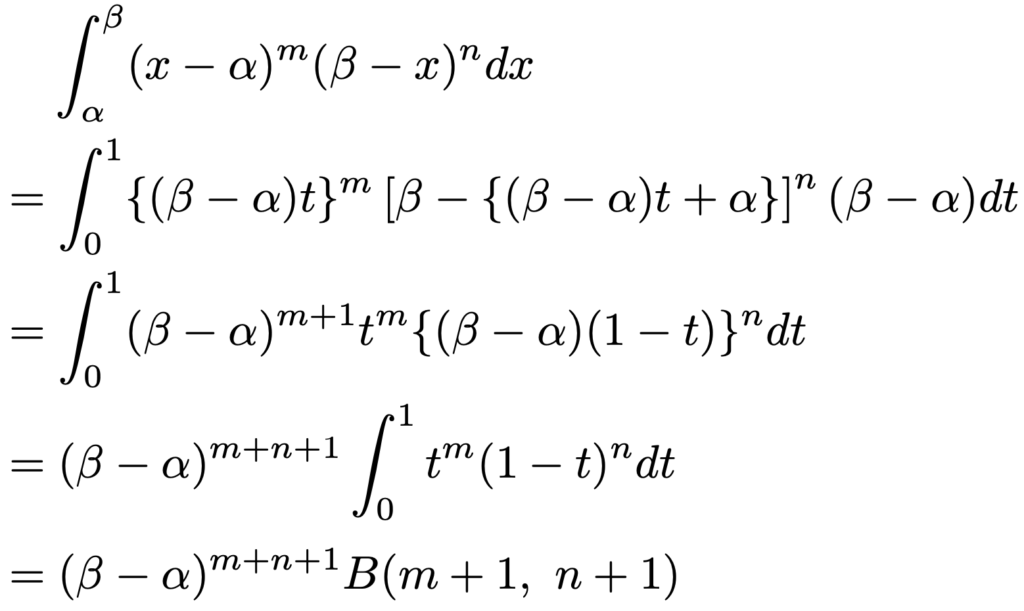
ここで,ガンマ関数とベータ関数の関係式と,自然数m,nに対するガンマ関数の値が階乗で表せることを使うと,示したかった式は次のように導くことができます。
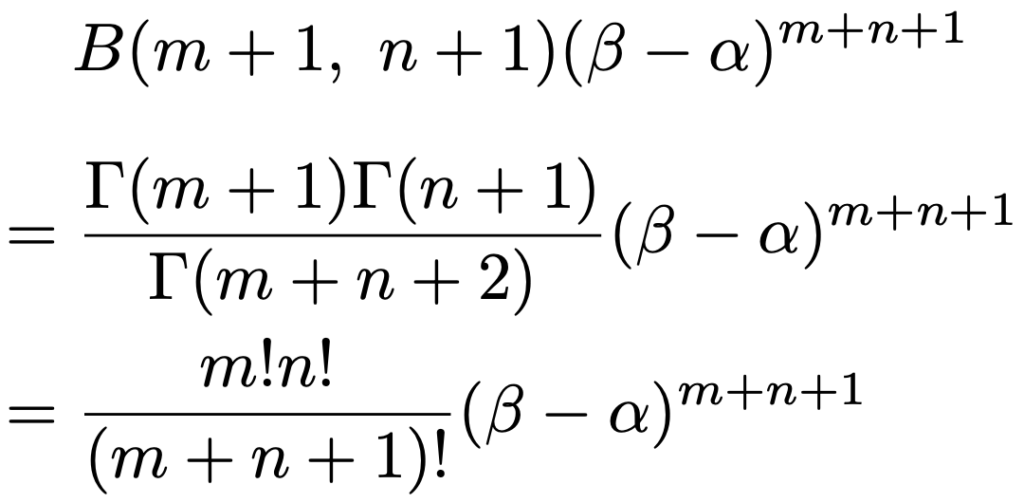
ガンマ分布
まず,指数分布の記事で登場した次の図を思い出すところからはじめてみましょう。

緑の点は魚が釣れた時刻を表しているのでしたね。そして,1匹の魚が釣れてから,次の1匹が釣れるまでの時間がしたがう確率分布が指数分布でした。実は,指数分布自体もガンマ分布の一種であり,上の例で魚釣りをはじめた時刻を0としたときのn匹目の魚が釣れる時刻がしたがう確率分布もガンマ分布の一種なのです。つまり,独立に同じパラメータの指数分布にしたがう確率変数の和がしたがう確率分布はガンマ分布(この場合のガンマ分布は別名アーラン分布と言います)になります。
ガンマ分布は(0,∞)上の連続型確率分布で,2つのパラメータ(本稿ではa,bで表す)を持っており,このパラメータを調節することで,指数分布やアーラン分布を含むさまざまな分布を表現できます。では,ガンマ分布を定義します。a>0,b>0に対して,確率変数Xの確率密度関数が次の式で表せるとき,Xがしたがう確率分布をガンマ分布と言います。
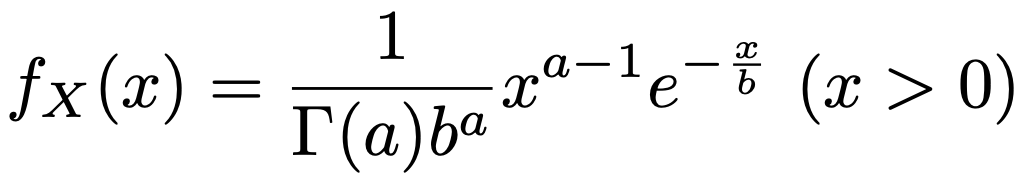
Xがパラメータa,bのガンマ分布にしたがうことを,本稿では次のように表すことにします。
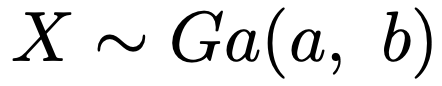
fX(x)の式は複雑そうですが,その正体をとらえてみましょう。b=1を代入し,変数をyに変えると次の式になります。

fY(y)は,ガンマ関数の被積分関数と同じ形の式をΓ(a)でわったものになっています。つまり,ガンマ関数をベースに,定義域全体での積分が1になるようにΓ(a)でわって,確率密度関数にしたものがfY(y)です。ここで,X=bYという変数変換を行うと,実は,もとの確率密度関数fX(x)を導くことができます。このように,ガンマ関数をもとにして,さらにパラメータを増やしてできたものがガンマ分布の確率密度関数です。なお,X=bYという変数変換によって,期待値はb倍,分散はb2倍になるので,bというパラメータはスケールをb倍にするような効果を持っています。そこで,bを尺度母数と呼ぶことがあります。
では,他のガンマ分布の例も見てみましょう。fX(x)にa=1を代入すると,Γ(1)=1であることから,次の式になります。
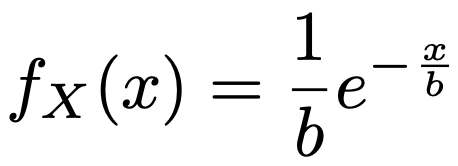
これは,b分の1をパラメータとする指数分布です。確かに,指数分布はガンマ分布の特殊な場合になっていました。a=1,b=2のガンマ分布(指数分布)の確率密度関数のグラフは次の図の緑の曲線になります。
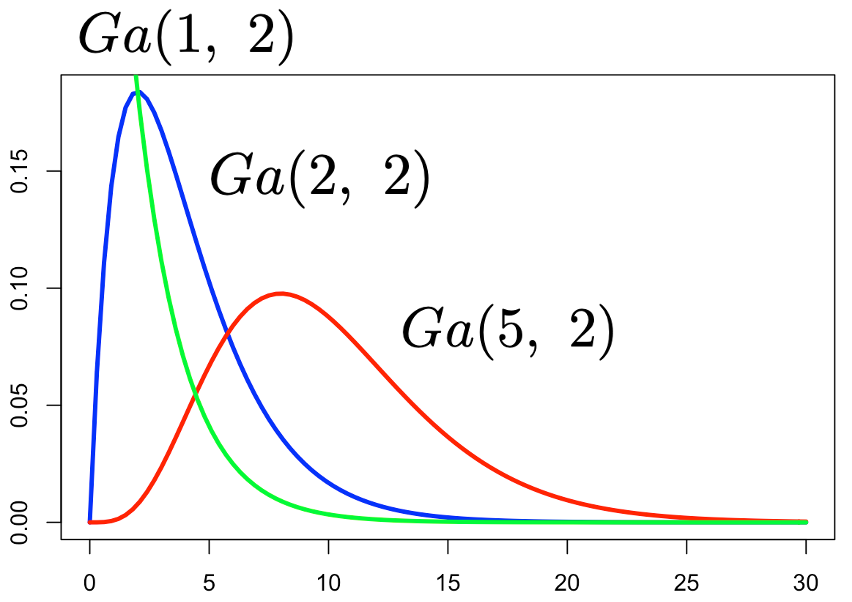
a=1,2,5の場合のグラフを比べると,aが小さいときにはグラフの偏りが大きく,a=5になると左右対称な形に近づいているのがわかります。このように,パラメータのaはグラフの形を決めているので,形状母数と呼ばれることがあります。
では,念のため,fX(x)が確率密度関数であることを確かめましょう。fX(x)≧0であることは,Γ(a)>0と定義から明らかなので,(0,∞)で積分して1になることを示します。そのために,fX(x)において次の変数変換を行います。
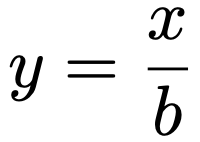
変数をyにおきかえても積分範囲は変わらず,dy=(1/b)dxとなるので,fX(x)の(0,∞)での積分は次のように計算できます。
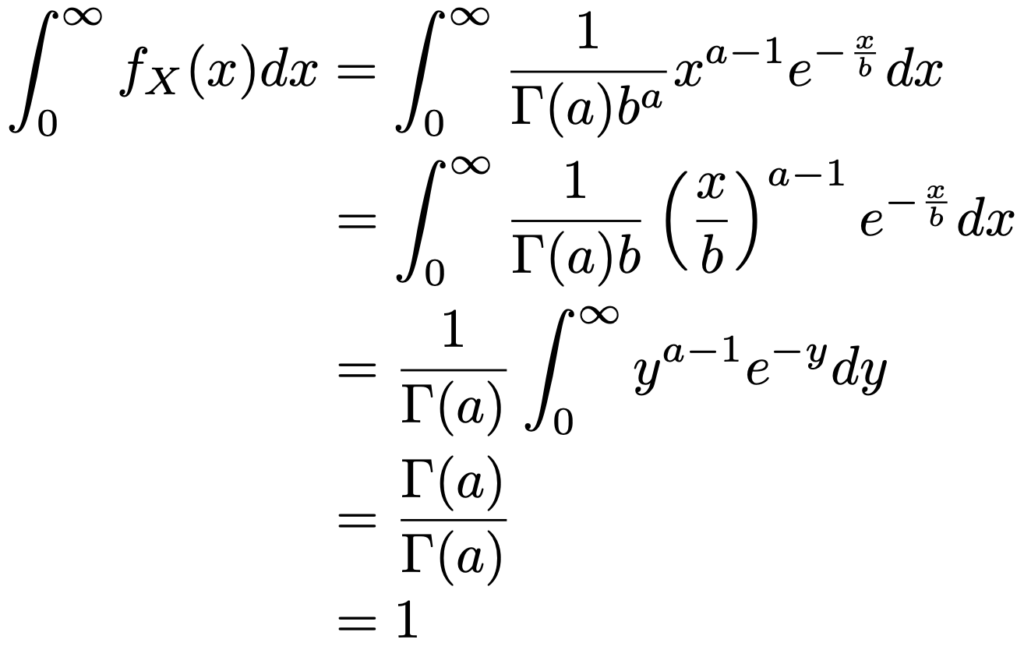
これで,fX(x)が確率密度関数であることがわかりました。いまの計算からわかる通り,確率密度関数の係数の分母にあるΓ(a)は積分が1になるようにするためのものです。
次に,ガンマ分布の期待値を計算してみましょう。確率変数Xがガンマ分布Ga(a,b)にしたがうとして,Xの期待値は次のように計算できます。
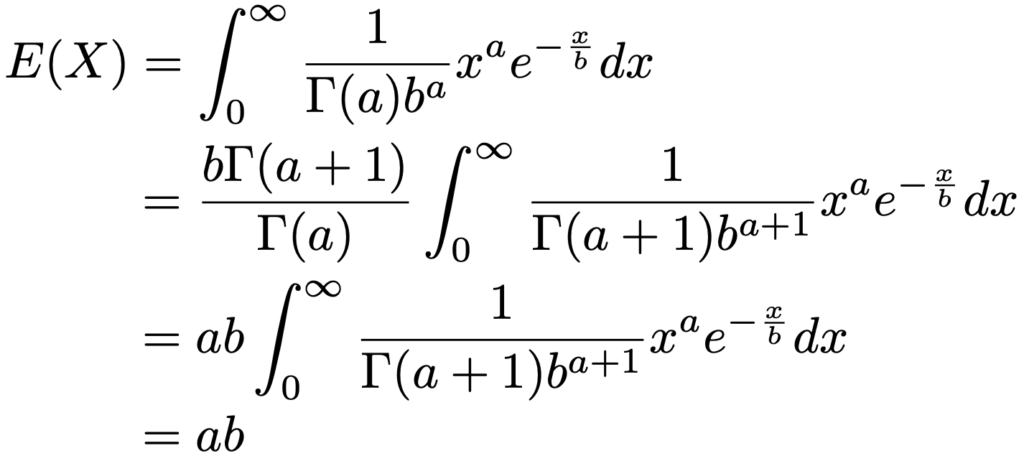
上の計算では,2行目から3行目の変形で,次の関係を使っています。
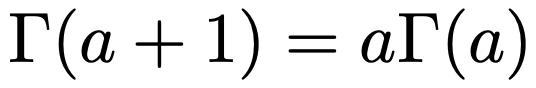
また,3行目の積分の被積分関数はパラメータa+1,bのガンマ分布の確率密度関数になっているので,積分すると1になります。積分を直接的に計算することを避けて,ガンマ分布の確率密度関数に帰着できるように変形しました。
期待値は2つのパラメータの積になりましたね。何らかの分布をガンマ分布でモデリングしたい場合には,その分布の平均を利用してパラメータの見当をつけることができます。例えば,平均が10の分布をガンマ分布でモデリングするなら,ab=10になるようなaとbを選びますよね。a=2,b=5とすると次の図の青い曲線のようにピークの位置が左に寄り,a=5,b=2とすると次の図の赤い曲線のようにピークの位置が右に寄ります。平均と分布の左右の偏り具合をもとにしてパラメータを調整できるわけです。
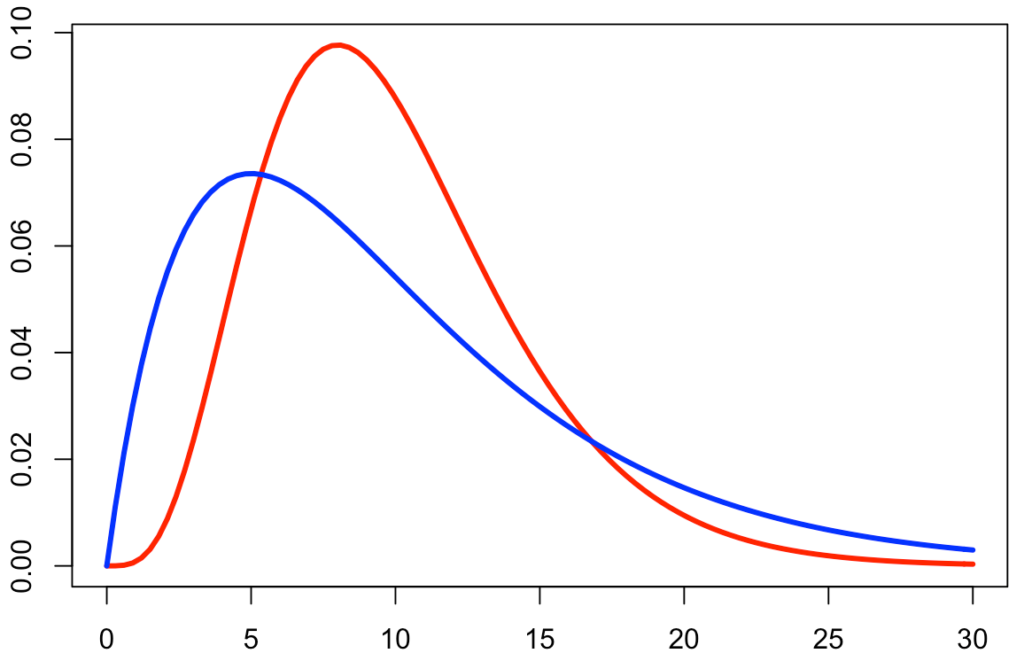
次に,分散を計算するためにXの2乗の期待値を次のように計算します。
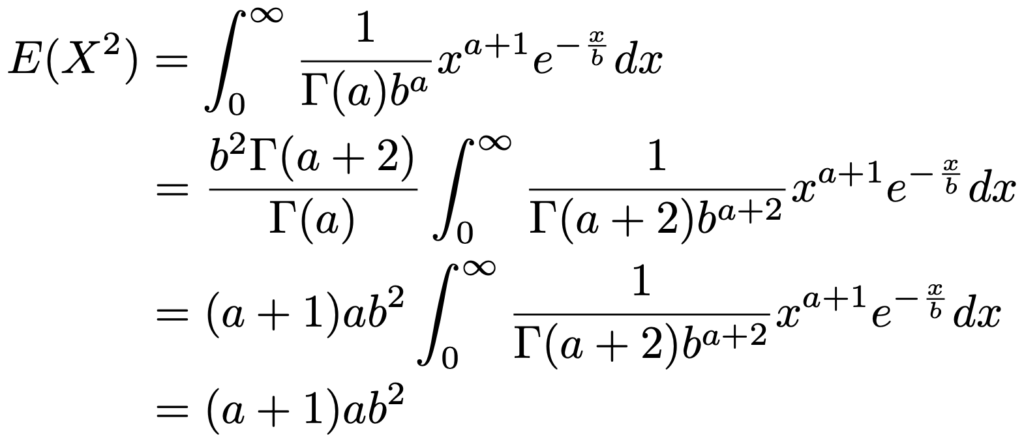
上の計算でも,2行目から3行目の変形で,次の関係を使っています。
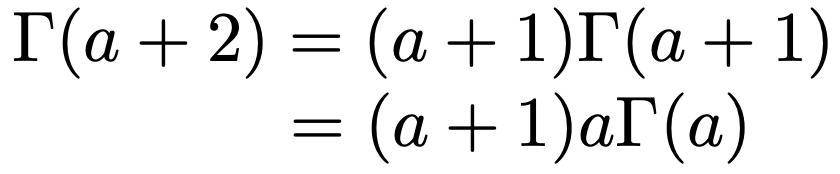
また,3行目の積分の被積分関数はパラメータa+2,bのガンマ分布の確率密度関数になっていることを利用しています。よって,分散は次のように計算できます。
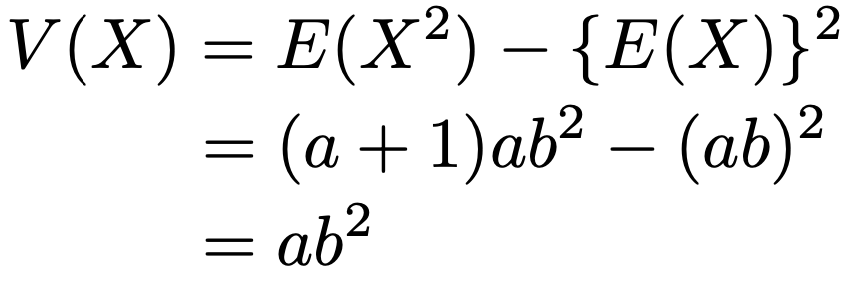
ここで陥りやすいのが,「V(X)=ab2だったかな? V(X)=a2bだったかな?」という「どちらのパラメータを2乗すればいいか」という問題です。暗記できないときには,原理に立ち返りましょう。すでに説明したように,ガンマ分布の確率密度関数は,ガンマ関数の被積分関数と同じ形の式をΓ(a)でわったfY(y)がベースになっています。E(Y)=V(Y)=aであり,X=bYという変数変換によって,期待値はb倍,分散はb2倍になるので,E(X)=ab,V(X)=ab2になるのです。このように考えると,尺度母数を2乗すればいいということを記憶しやすくなります。
さて,ガンマ分布の性質をもう1つだけ紹介して,このセクションを締めくくります。指数分布(ガンマ分布の一種)にしたがう確率変数の和がアーラン分布(ガンマ分布の一種)にしたがうことはすでに書いた通りですが,それをより一般的に述べたものがガンマ分布の再生性という性質です。2つの確率変数X,Yがそれぞれ独立に次のガンマ分布にしたがっているとします。
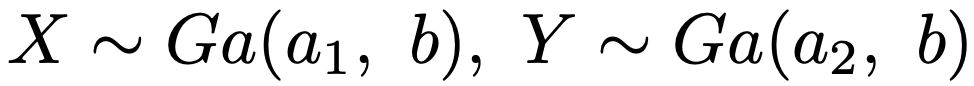
このとき,X+Yは次のガンマ分布にしたがいます。
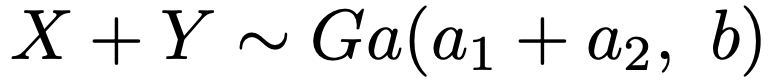
この再生性の証明が知りたい人は,参考図書②を参照してください。
ベータ分布
まず,次の例を考えてみましょう。
(例) くじを10回引いたら,3回当たった
さて,あなたはこのくじを1回引くときの当たる確率を知らないものとします。上の結果だけしか情報がないとするとき,あなたは当たる確率をいくらだと推定するでしょうか。もちろん,0.3ですよね。でも,絶対に0.3とは言い切れないですよね。0.4かもしれないし,0.2かもしれないです。もしかしたら,当たる確率は0.8なのに,たまたま3回しか当たらなかったという可能性も0ではないはずです。
では,くじ引きの例について,もう少し考えを進めてみます。くじを1回引くときの当たる確率をpとして,くじを10回引いて3回当たる確率は,p3(1ーp)7と表せます。「いや,違います。二項係数が前につきます!」と思ったあなたは正しいのですが,定数倍の部分はすぐ後で調整されてしまうので,二項係数は無視します。p3(1ーp)7のpに0と1の間の様々な数を代入すると,それぞれのpのときの「10回引いて3回当たる確率」が求められます。そのような確率をたくさん計算して線で結ぶと,おおよそ次のようなグラフになります。
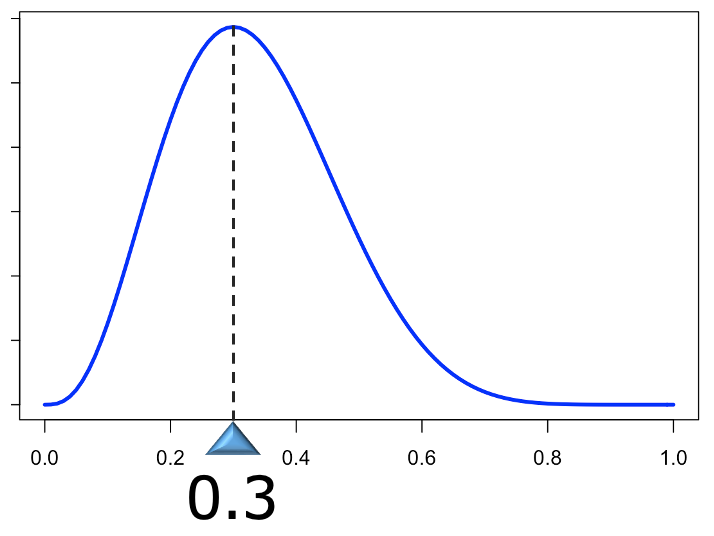
もし,この「10回引いて3回当たる確率」を表す曲線を確率密度関数にしたいと思ったら,上の青い曲線と横軸で囲まれた部分の面積を積分で求めてp3(1ーp)7をそれでわればいいですね。この面積は,ベータ関数を使って,次のように表せます。
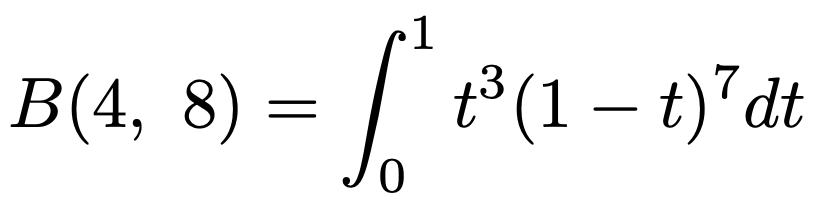
よって,「10回引いて3回当たる確率」をベースにした確率密度関数は次のようになります。
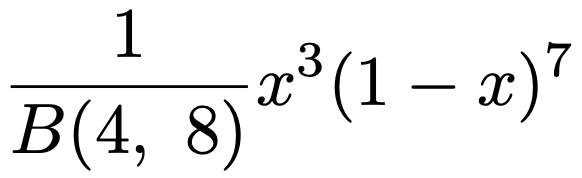
実は,これはベータ分布の確率密度関数の一種になっています。このように,ベータ分布は確率pの確率分布をモデル化するのに役立つ(0,1)上の連続型確率分布であって,そのグラフは,パラメータを調整することで,さまざまな形状をとれるので便利なのです。定義を一般的に述べると,a>0,b>0に対して,確率変数Xの確率密度関数が次の式で表せるとき,Xがしたがう確率分布をベータ分布と言います。
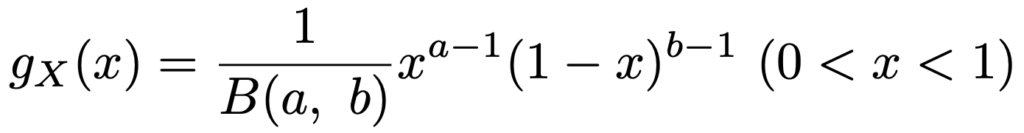
Xがパラメータa,bのベータ分布にしたがうことを,本稿では次のように表すことにします。
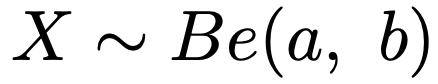
ここまでの話を踏まえると,gX(x)が確率密度関数であることは,ほぼ明らかです。なぜなら,B(a,b)>0より,gX(x)>0であり,(0,1)での積分値でわった式で定めたので,積分は1になるはずです。念のため積分してみると,次のようになります。
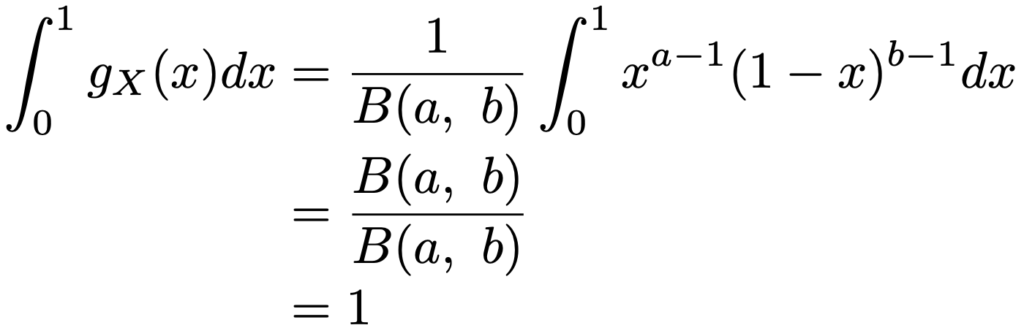
ベータ分布の確率密度関数のグラフは「パラメータを調整することで,さまざまな形状をとれる」と述べましたが,実際にパラメータの値を決めて調べてみましょう。まず,a=1,b=1のとき,B(1,1)=1であることからgX(x)=1となるので,(0,1)上の一様分布になります。したがって,ベータ分布は一様分布を一般化したものと言うことができます。
次に,a=0.5,b=0.5のとき,次の式のように確率密度関数の分母にxと1ーxが現れます。
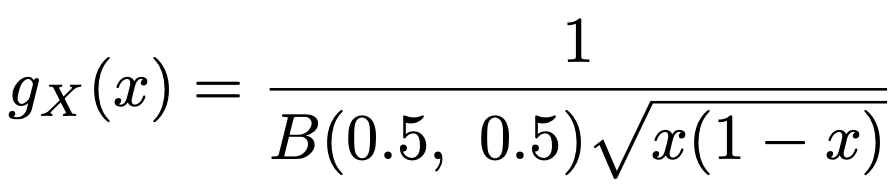
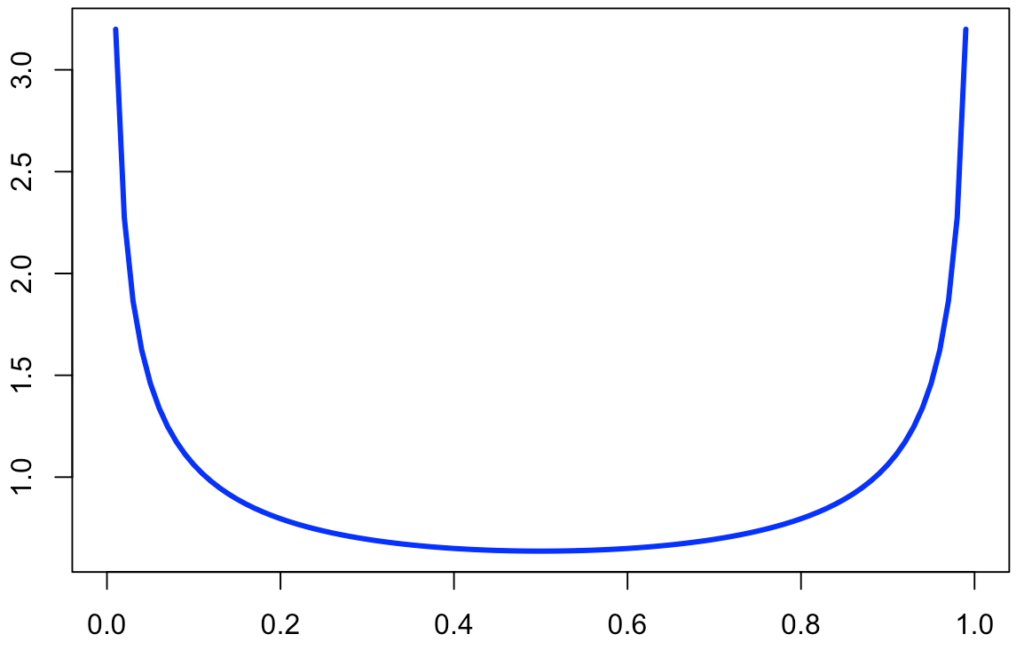
xを0または1に近づけるとgX(x)の値はどこまでも大きくなるので,このときの確率密度関数のグラフは次の図のようになります。
次に,a=0.5,b=1のとき,次の式のように確率密度関数の分母にxが現れます。
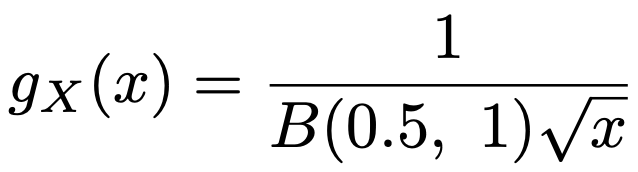
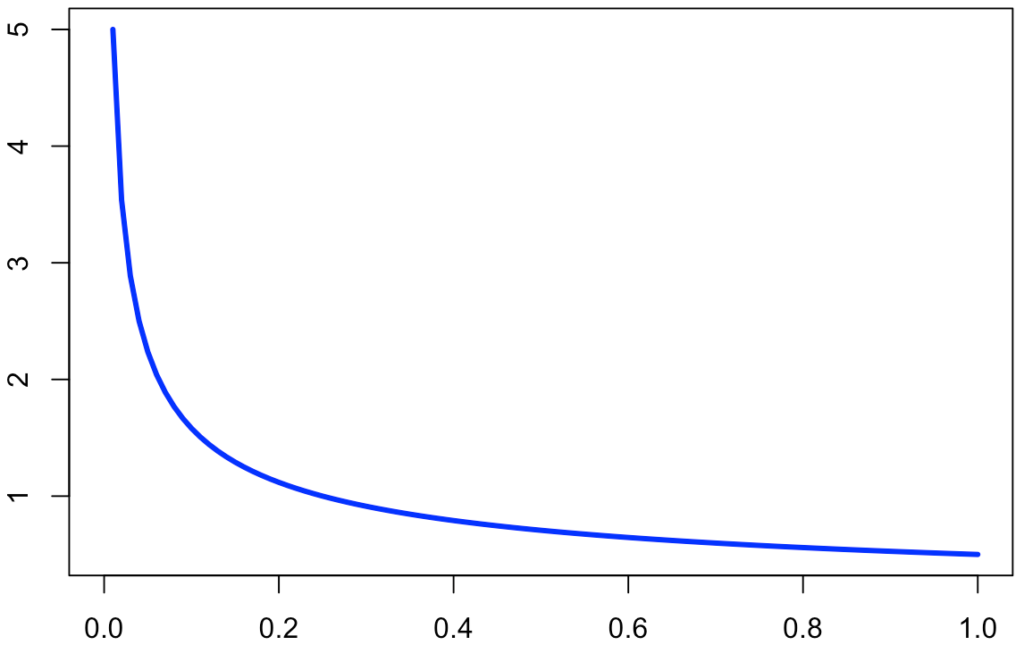
xを0に近づけるとgX(x)の値はどこまでも大きくなり,xを大きくしていくとgX(x)の値は0に近づいていくので,このときの確率密度関数のグラフは次の図のようになります。
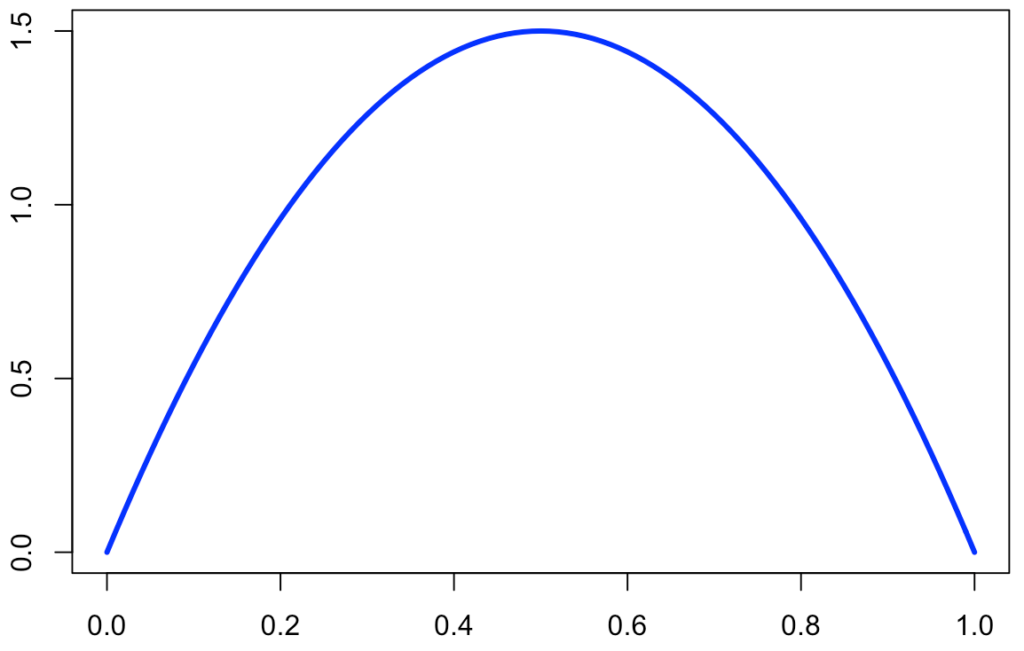
次に,a=2,b=2のとき,次の式のように確率密度関数は2次関数になります。
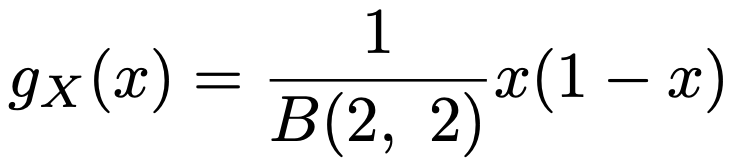
よって,このときの確率密度関数のグラフは次の図のようになります。
aとbの値に差をつけると,確率密度関数のグラフは非対称になります。例えば,Be(2,5)のグラフは次の図のようになります。
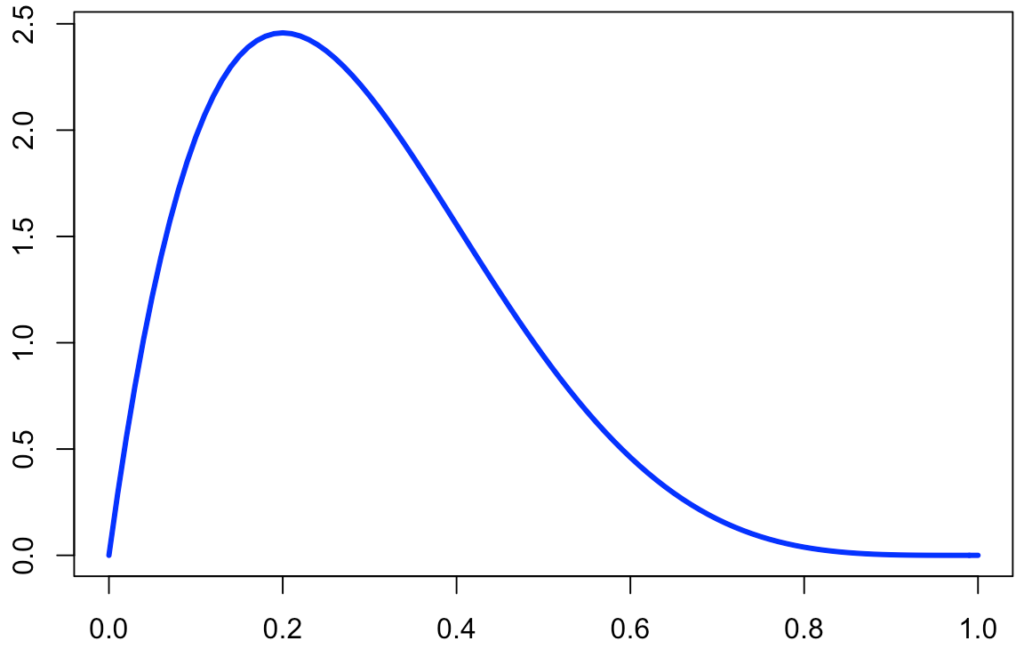
このグラフからも想像できるように,aを固定してbを大きくすると期待値は0に近づきます。逆に,bを固定してaを大きくすると期待値は1に近づきます。では,実際に期待値を計算して,そのことを確認してみましょう。確率変数Xがベータ分布Be(a,b)にしたがうとして,期待値は次のように計算できます。
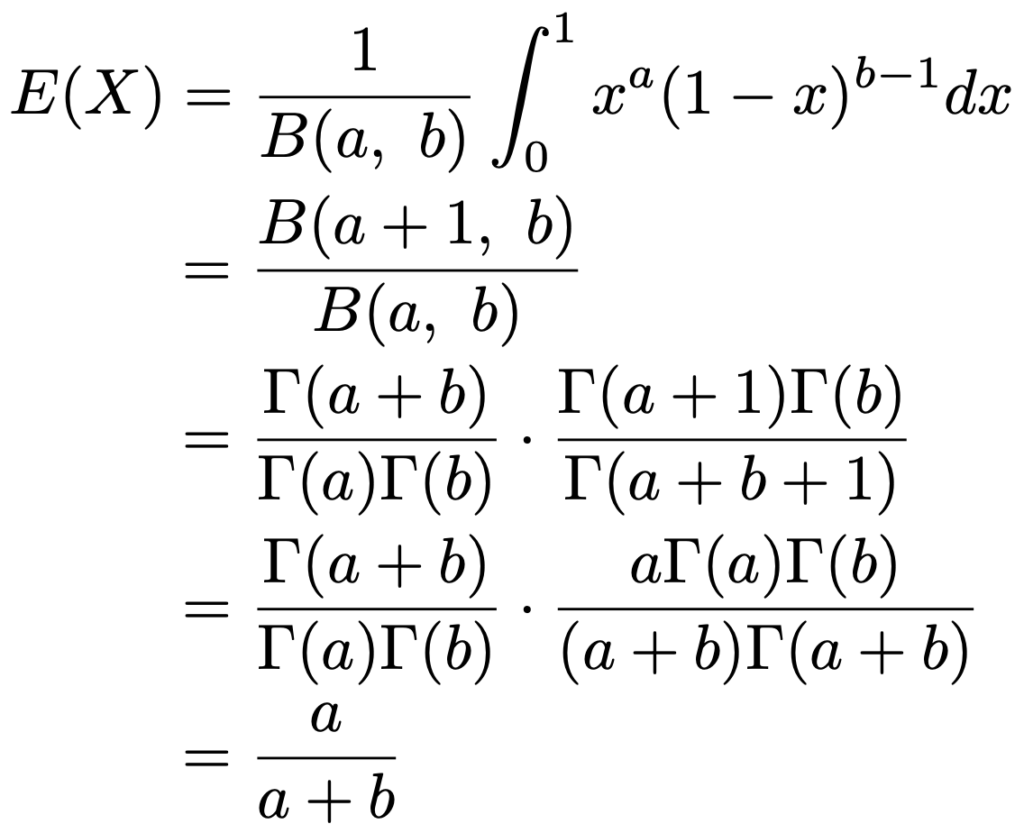
この計算結果から,確かに,aを固定してbを大きくすると期待値は0に近づき,bを固定してaを大きくすると期待値は1に近づくことがわかりますね。
次に,分散を計算するために,Xの2乗の期待値を次のように計算します。
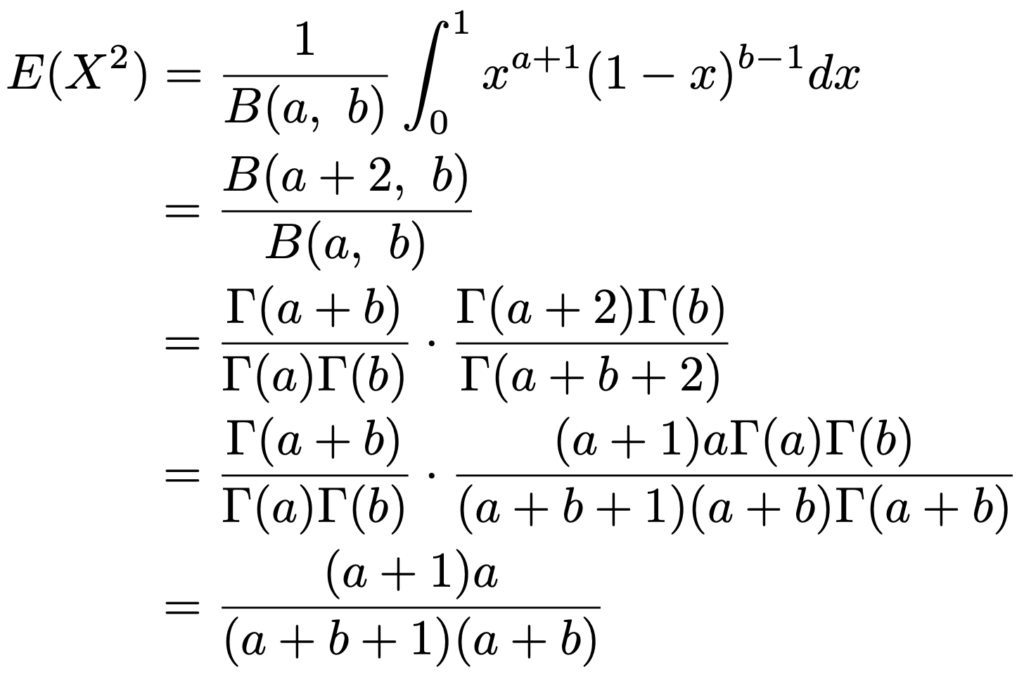
よって,分散は次のように計算できます。
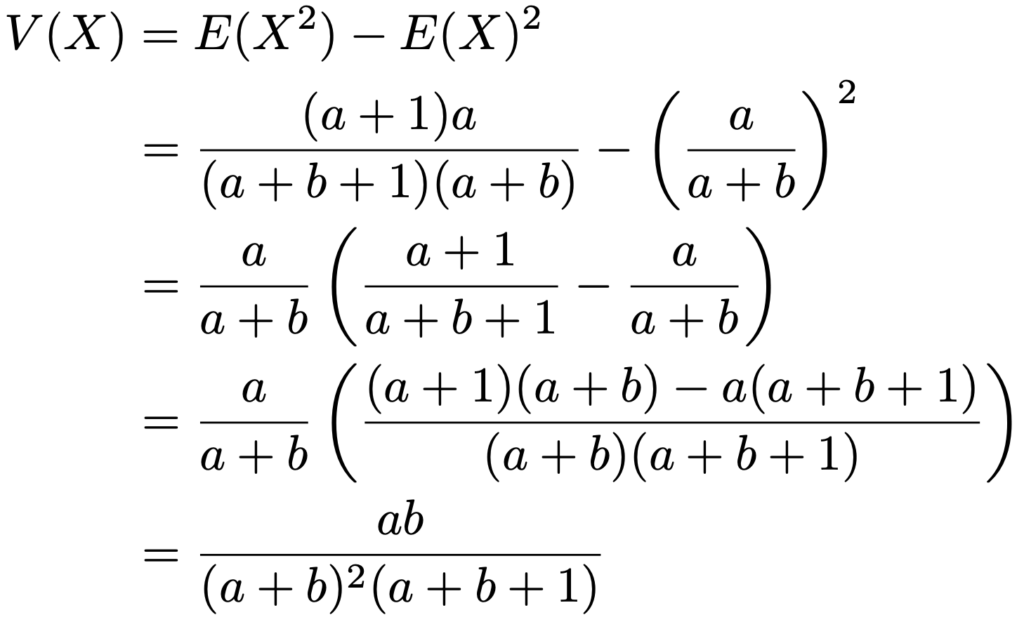
最後に,ベータ分布とガンマ分布の関係に触れておきます。2つの確率変数X,Yがそれぞれ独立に次のガンマ分布にしたがっているとします。
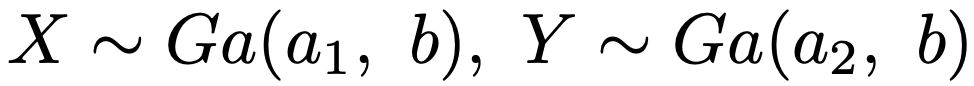
このとき,次の確率変数はベータ分布にしたがいます。
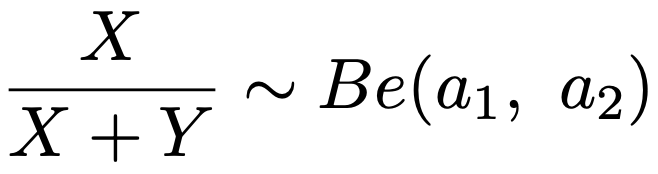
つまり,独立にガンマ分布にしたがう2つの確率変数の「割合のようなもの」を考えると,ベータ分布が現れるということですね。この証明は統計検定1級相当なので,ここでは省略しますが,興味がある人は参考図書②を参照してください。
最頻値
ガンマ分布とベータ分布は,次の2つの性質を持っているため,ベイズ法の導入としてよく使われます。
- 2つのパラメータを調整することで様々な確率密度関数を表現できる
- ガンマ分布はポアソン分布の,ベータ分布は二項分布の共役事前分布になる
ベイズ法では,これらの確率分布の最頻値がよく使われるため,ここで基本的な事項を整理しておきます。連続型確率変数の最頻値とは,確率密度関数f(x)の値が最大になるようなxのことです。例えば,ガンマ分布Ga(a,b)の確率密度関数のグラフは,a>1のとき,次の図のような山が1つの形になります。

ここで求めたいのは,上の図の三角形が示している横軸の値です。どのように求めるかと言えば,極値というものに着目します。次の図を見てください。
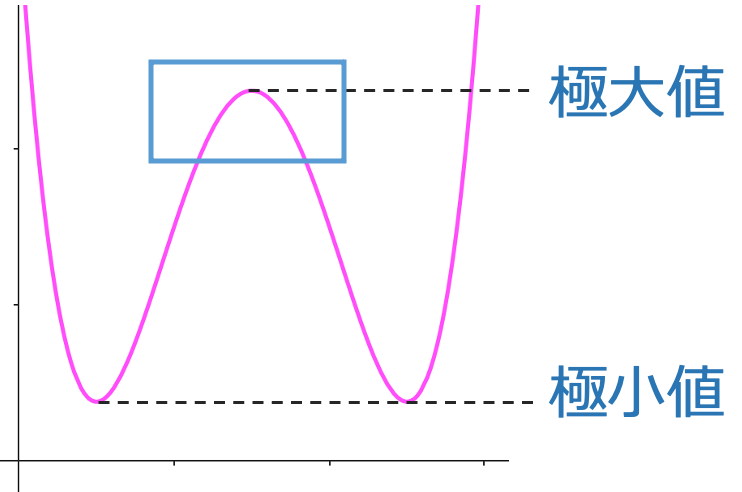
四角で囲んだ部分の山の頂上は,この関数の最大値ではありませんが,四角の中だけを見れば,いちばん大きな値になっています。このようにその点の近くだけを見たときに他にその点より大きい値をとる点がないとき,その値を極大値と言います。極小値も同様に定義し,極大値と極小値を合わせて極値と言います。最大値は極大値ですが,極大値は必ずしも最大値であるとは限りません。最小値と極小値の関係も同様です。
次に,(定義域全体で)微分可能な関数を考えます。次の図は,関数f(x)がx=cで極大値をとっていることを表していますが,その点でのグラフの接線の傾きが0になっています。
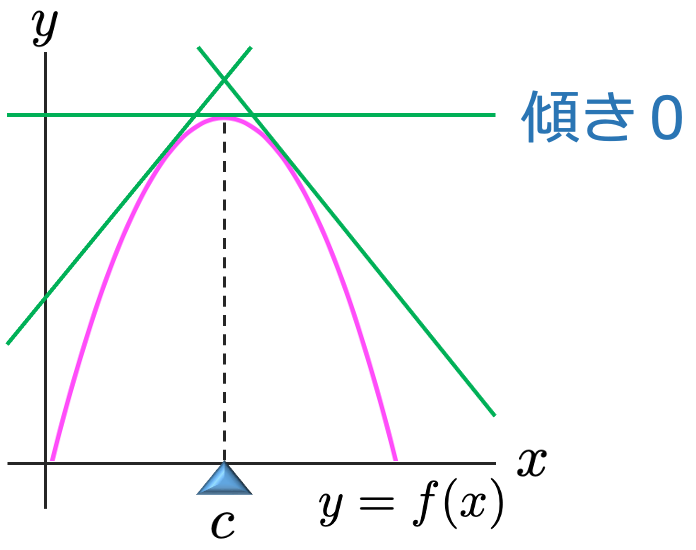
f(x)の導関数f'(x)のx=cでの値f'(c)を微分係数と言いますが,上の図ではf'(c)=0となっているということです。そして,x<cでは微分係数(接線の傾き)が+,x>cでは微分係数(接線の傾き)がーになっています。このように,微分係数が,+→0→ーと変化するときに極大値になるわけです。極小値の場合の微分係数の符号の変化も,同じようにグラフをかいて考えれば,ー→0→+となることがわかります。
さて,これで極大値や極小値となる点のx座標の求め方は,次の2ステップであることがわかりました。
- 方程式f'(x)=0の解x=cを求める
- x=cの前後での導関数f'(x)の符号の変化を調べる
では,ガンマ分布とベータ分布の最頻値を求めていきます。まず,ガンマ分布Ga(a,b)で,a>1のときを考えます。ガンマ分布の確率密度関数の係数を除いた部分を微分すると,次のようになります。
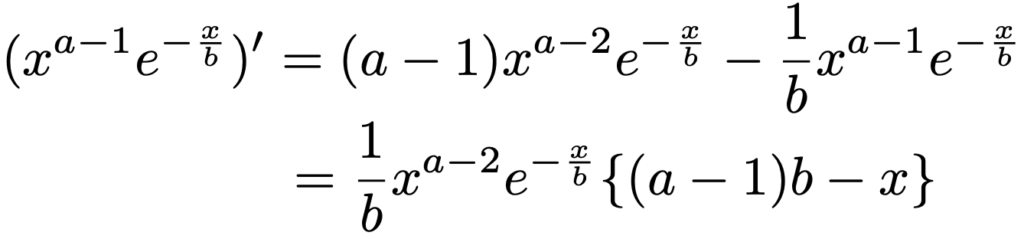
よって,x=(aー1)bで確率密度関数の微分係数が0になることがわかります。また,x<(aー1)bで導関数は正の値,x>(aー1)bで負の値をとるので,+→0→ーという符号の変化をしているため,この点で極大値をとることがわかります。この点は最大値でもあるので,ガンマ分布Ga(a,b)の最頻値は(aー1)bです。
次に,ベータ分布Be(a,b)で,a>1,b>1のときを考えます。ベータ分布の確率密度関数の係数を除いた部分を微分すると,次のようになります。
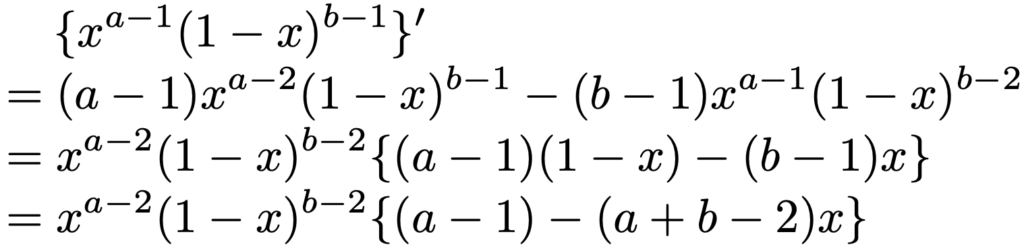
よって,次のxで確率密度関数の微分係数が0になることがわかります。
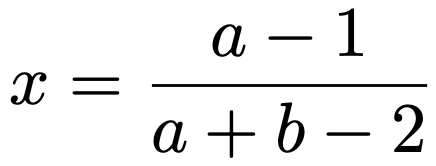
また,その前後で,導関数の符号が+→0→ーと変化しているため,この点で極大値をとることがわかります。この点は最大値でもあるので,ベータ分布Be(a,b)の最頻値は上記のxの値になります。
参考図書
本稿を執筆するにあたり,次の書籍を参考にしました。
①手を動かしてまなぶ微分積分(藤岡敦,裳華房)
数学的な厳密さと,行間(論理の飛躍)のなさのバランスのとれた良書です。大学1年の微分積分を短期間で学習したい人にオススメです。
②数理統計学(黒木学,共立出版)
統計検定1級相当のテキストで,確率分布の解説が全体的に詳しいです。
本稿はここまでとなります。最後までお読みいただき,ありがとうございました!
引き続き,勉強をがんばっていきましょう!






コメント