確率変数と標本平均【中学の数学からはじめる統計検定２級講座第３回】

「確率変数って，何のこと？」「標本平均って，ただの平均でしょ」なんて声が聞こえてきそうですが，意味を正しく理解できている自信はありますか。今回の最重要テーマは，「標本平均が確率変数であることの理解」です。はじめに，これから統計学を語るための言語の役割を果たす確率変数の概念を解説します。確率変数が１つの確率分布から確率変数が複数である同時確率分布に話を展開し，のちに統計学の本論である推定や検定で重要な役割を果たす標本平均へと進んでいきます。

【第１回】確率の計算の内容は既知であるものとして説明しますので，もし内容に不安のある方は，先にそちらの記事からご覧ください。

では，はじめていきましょう！

離散型の確率変数
連続型の確率変数
離散型確率変数の同時確率分布
確率変数の和・標本平均
標本平均の中央値と最頻値
参考図書
演習１〜確率変数の最頻値〜
演習２〜独立性〜
演習３〜標本平均〜

離散型の確率変数

確率変数とは，いろいろな値をとる変数であって，その値と確率がひもづいているもののことです。と言ってもピンとこないでしょうから，この後，具体例を確認しながら理解していきましょう。

確率変数には離散型と呼ばれるものと，連続型と呼ばれるものがあります。このセクションでは離散型の確率変数について，次のセクションでは連続型の確率変数について，それぞれ確認していきましょう。

では，離散型の確率変数を具体的に見ていきます。

確率変数が，整数のように，とびとびの値をとる場合，この確率変数を離散型と呼びます。次の例のように，中２〜高１の確率で習うものは，すべて離散型の確率変数に対応しています。

（例）サイコロの目，コインの表裏，玉に書かれた数等

離散型の確率変数については，変数としてとる値と確率の対応関係を表にすることが可能です。例えば，１が書かれたカード３枚と，２が書かれたカード２枚と，３が書かれたカード１枚の合計６枚のカードが入った袋の中から１枚を取り出す試行を考えてみましょう。

確率変数Xを，取り出したカードに書かれている数とします。一般に，確率変数はXやYなどのアルファベットの大文字で表されるのが通例です。

【第１回】で説明したように，６枚のカードは，書かれている数が同じでも，異なるものと考えます。したがって，２が書かれたカードを取り出す（X＝２）確率は，６枚中の２枚ということで，３分の１になります。このことを，次のように表します。

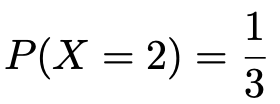
一般的に，確率変数Xについて，Xの値がkであるときの確率を，P(X＝k)と表します。

この例で，X＝１やX＝３の場合も含めて表にまとめると，次のようになります。

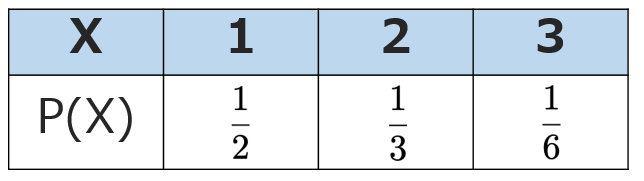
この表を見れば，Xがとる値とそのときの確率がはっきりとわかりますよね。このようにXの値と確率がひもづいているので，Xは確率変数です。また，この表のように，Xのすべての値と確率P(X)の対応関係を一覧にしたものを離散型確率変数の確率分布といいます。

連続型の確率変数

連続型の確率変数とは，次の例のように，確率変数のとる値がとびとびではなく，連続的であるということです。

（例）身長や体重，製品の重さ，電池の寿命等

連続的であるということは，とる値が無限にありますので，離散型とは異なり，変数の値と確率の対応関係を表にすることはできません。連続型の確率変数では，変数の値と確率の対応関係を確率密度関数という式で表します。

次の図は，ある集団に属する人の体重の平均が50kgであるとして，その確率密度関数のグラフの一例を示したものです。

グラフとx軸で囲まれる領域を区切ってできる部分の面積が確率に対応します。次の図で，色のついた部分は，体重が51〜51.5kgの範囲に入る確率を表しています。

また，確率の最大値は１でしたから，面積が確率に対応するということは，次の図で色のついた部分のように，全範囲の面積は１に等しくなります。

こういった面積を求めるのに，一般的には積分が必要になりますので，連続型の確率変数の確率を確率密度関数を使って定義するのにも積分を使います。

そこで，高校で積分を習っていない人や，習ったけれども意味がよくわからないという人のために，第６回の記事で，「積分とは何か」を含めて，連続型の確率変数の確率の求め方を解説します。ということで，今回の記事では，連続型の確率変数はここまでにします。

離散型確率変数の同時確率分布

ここまでは，１つの確率変数のとりうる値と確率の対応関係のみを扱ってきましたが，次は，２つ以上の確率変数のとりうる値の組に対して１つの確率が対応する例を扱います。何やら難しそうに聞こえるかもしれませんが，例えば，「サイコロを２回投げるとき，出た目の数の和が８になる確率を求めよ」みたいな問題を解いたことがある人は多いでしょう。１回目に出た目の数をX，２回目に出た目の数をYとすると，確率変数が２つあり，そのとりうる値の組に対して１つの確率が対応していますよね。こういった例について「確率分布を調べてみよう」というのが，このセクションでやりたいことです。では，次の問題で確率分布を考えてみましょう。

【問題】３が書かれたカード３枚と，２が書かれたカード２枚と，１が書かれたカード１枚の合計６枚のカードが入った袋がある。この中から，１枚のカードを取り出した後，カードをもとに戻さずに続けて２枚目のカードを取り出す。１枚目のカードに書かれた数をX，２枚目のカードに書かれた数をYとするとき，XとYの同時確率分布を求めなさい。

【解答】X，Yのとりうる値の組と確率の対応関係を表にまとめると，次のようになります。

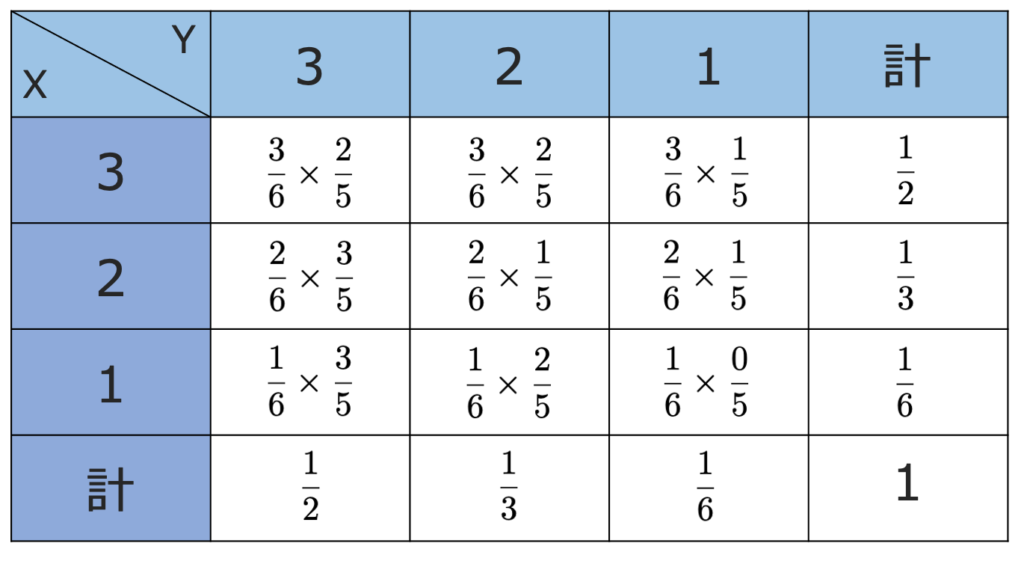
（解答終わり）

この表からわかるように，この問題では，XとYの値の組の１つずつに対して，１つの確率が定まっています。確率変数が１つのときの確率分布と同じように，この表は２つの確率変数の確率分布だといえますね。これを２次元同時確率変数（X，Y）の同時確率分布といいます。また，いちばん右の列はXのみの確率分布，いちばん下の行はYのみの確率分布を表していますね。このように，同時確率分布を表に表したとき，いちばん右やいちばん下といった「周辺」に現れる１つの確率変数についての確率分布を，周辺確率分布といいます。

では次に，確率変数の独立について説明します。上の表の白い部分の左上のマスを見てください。ここは，X＝３，Y＝３のときの確率を表していますね。これを次のように表します。

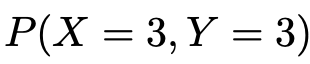
このマスの分数のかけ算を計算することで，次のことがわかりますね。

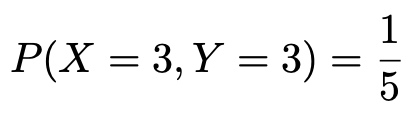
一方で，X＝３となる確率や，Y＝３となる確率は次のようになっています。

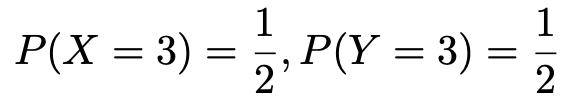
ということは，次の式が成り立っていますね。

この問題では，１回目に３のカードが取り出されるかどうかによって，２回目に３のカードが取り出される確率が変わります。XとYが互いに影響を与え合う関係にあるので，独立ではないということになります。

逆にいえば，２つの確率変数XとYが独立であるとは，XとYがとりうるすべての値a，bに対して，次の式が成り立つことをいいます。

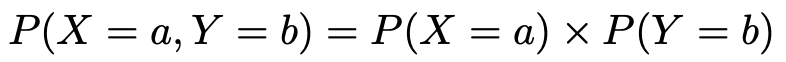
これが確率変数の独立の定義です。【第１回】の記事で紹介した事象の独立と区別して覚えておきましょう。

確率変数の和・標本平均

同時確率分布では，複数の確率変数の組を考えましたが，複数の確率変数から別の新しい確率変数をつくるということも，統計学ではよく行います。例を挙げて説明します。

１，３，５の数が１つずつ書かれた３枚のカードから１枚を取り出し，取り出したカードをもとに戻してから，もう１枚のカードを取り出します。このとき，１回目に取り出したカードに書かれた数を表す確率変数をX₁，２回目に取り出したカードに書かれた数を表す確率変数をX₂と表すことにします。どちらの確率変数も１，３，５の値をとりますので，２つの値の組み合わせは９通りあります。

さらに，この２つの確率変数を用いて，新しい確率変数Xを次の式で定めます。

つまり，取り出した２枚のカードに書かれた数の和をXとするわけです。例えば，X＝４となるのは，次の場合です。

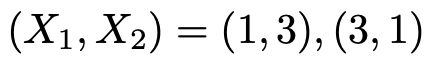
９通りあるX₁とX₂の値の組は同様に確からしいので，その確率はすべて９分の１です。このことから，Xの確率分布は次の表のようになります。

新しい確率変数をつくる方法は，確率変数をたし合わせるだけではありません。例えば，サイコロを１回投げて出た目の数を表す確率変数をXとすると，Y＝10X+40で定まる確率変数Yの確率分布は次のようになります。

そして，このような新しい確率変数をつくる方法の中で，統計学においてとても重要なものが，次に紹介する標本平均です。

まず，何らかの調査をしたい対象となる全体のことを母集団と言います。標本とは母集団の一部分のことであり，母集団からかたよりなく取り出される必要があります。この取り出し方を無作為抽出と言います。次のn個の確率変数を考えます。

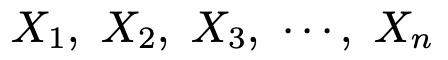
これらは，同じ母集団から取り出された大きさnの標本であり，それぞれが母集団と同じ確率分布に従い，独立であるものとします。このとき，標本平均とは，次の式で定まる確率変数です。

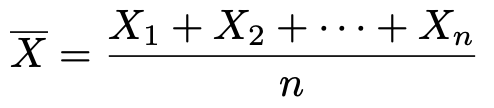
確率変数の和は確率変数であり，全体にn分の１をかけても確率変数なので，標本平均は確率変数なのです。

例えば，世論調査で内閣の支持率を推測するために，1000人に聞き取り調査をするのなら，母集団は有権者全体であり，標本の大きさは1000です。1000人の回答結果にX₁〜X₁₀₀₀までの（それぞれ独立に，支持するなら１，支持しないなら０という値をとる）確率変数を割り当てると，次の標本平均は内閣の支持率の真の値を推定するのに使うことができます。

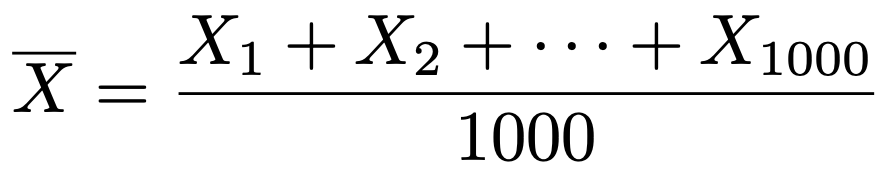
世論調査での内閣の支持率は，1000人の選び方によって変わる確率変数として考えることができるのです。

標本平均の中央値と最頻値

データを値の小さい順に並べたときにちょうど真ん中にくる値を中央値（メディアン），最も多い値を最頻値（モード）と呼びます。これは中学１年の学習内容で，知っている人も多いと思いますが，同じ言葉を確率変数に対しても使います。

まず，離散型確率変数Xの最頻値とは，P(X)が最大になるようなXの値のことです。

次に中央値ですが，離散型確率変数の中央値には２つの場合があります。データの中央値にも２つの場合がありましたよね。データの個数が奇数個のときにはデータを大きさの順に並べたときにちょうど真ん中に位置する値があり，この値をデータの中央値と呼びました。これに対応する離散型確率変数の中央値の１つ目の定義は，次のようになります。

（中央値の定義１）離散型確率変数Xのとりうる値aのうち，次の２つの不等式を同時にみたすものが存在するとき，このaの値をXの中央値という。

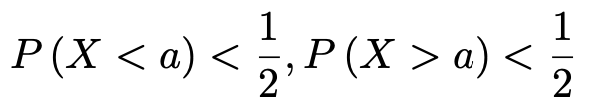
一方で，データの個数が偶数個のときには，データを大きさの順に並べてもちょうど真ん中に位置する値はないので，データの中央値の定義が変わります。データを値が大きいほうの半分と小さいほうの半分に分け，値が小さいほうのグループの最大値と値が大きいほうのグループの最小値の平均をデータの中央値と呼びました。これに対応する離散型確率変数の中央値の２つ目の定義は，次のようになります。

（中央値の定義２）離散型確率変数Xのとりうる値a，b（a＜b）のうち，次の２つの等式を同時にみたすものが存在するとき，aとbの平均をXの中央値という。

では，これを踏まえて，次の問題を解いていきましょう。

【問題】既知の母集団{２，８，16，20，28}を考える。この母集団から大きさ２の標本を無作為復元抽出し，順にX₁，X₂とする。
また，この標本に対する標本平均を次のように定める。

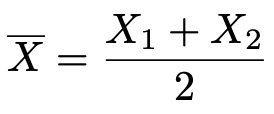
このとき，標本平均の中央値と最頻値を求めなさい。

【解答】「無作為」に取り出すので，１回の抽出で５つの数のどれを取り出す確率も５分の１です。また，「復元抽出」するとは，１回目に取り出した数をもとに戻してから２回目を取り出すという意味ですから，２回目の抽出で５つの数のどれを取り出す確率も５分の１です。よって，次の表のように，５×５＝25（通り）の取り出し方があり，どの取り出し方も同様に確からしいので，それぞれの確率は25分の１です。

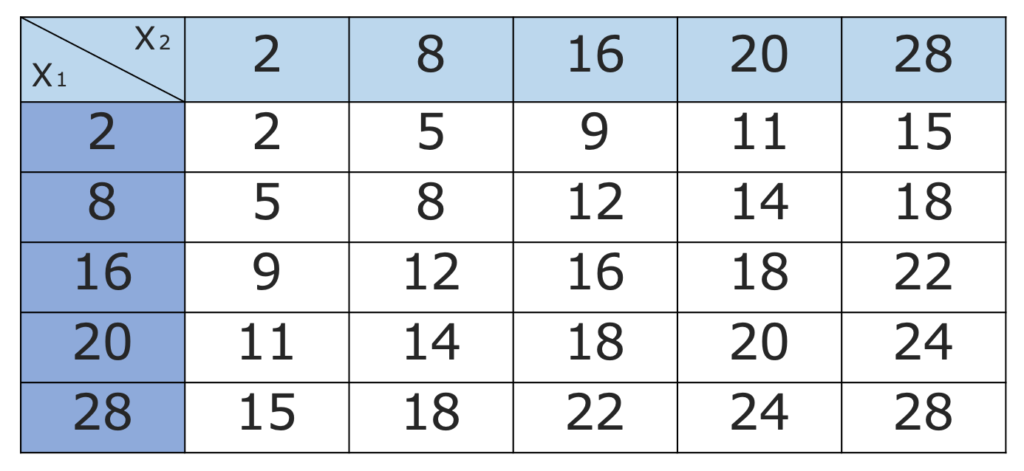
上の表の白い部分は，標本平均の値を表しています。したがって，標本平均の確率分布は次の表のようになります。

最頻値は，確率が最も大きい標本平均の値なので，この表から，標本平均の最頻値は18だとわかります。中央値については，（中央値の定義１）の不等式が次のように成り立つので，標本平均の中央値は15です。

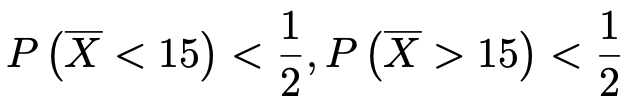
（解答終わり）

離散型の確率変数の基本的な解説は以上になります。この後は，参考図書の紹介に続けて，さらに理解を深めるための演習問題ですので，余力があればぜひチャレンジしてみてください。

参考図書

本稿を執筆するにあたり，参考にした図書を２つ挙げます。

①基本統計学　第５版（宮川公男，有斐閣）
標本の抽出について丁寧に解説されており，標本平均が確率変数であることもしっかり説明されています。

基本統計学[第５版]

②実用統計用語辞典（岩崎学・中西寛子・時岡規夫，オーム社）
離散型確率変数の中央値の定義は，こちらを参考にしつつ少し言い換えてわかりやすくしました。

実用統計用語辞典

演習１〜確率変数の最頻値〜

【問題】１から10までの整数が書かれた10枚のカードがある。この中から３枚のカードを同時に取り出すとき，３の倍数の数が書かれたカードの枚数をXとする。確率変数Xの最頻値を求めなさい。

【解答】「３枚を１枚ずつ続けて取り出す」という場合には，取り出す順番を考えるので，「順列」を使い，「同時に３枚を取り出す」という場合には，取り出す順番を考えなくて良いので，「組合せ」を使うというのが一般論です。でも，３枚を１枚ずつ取り出そうが，同時に取り出そうが，３の倍数のカードが取り出される確率が変わるはずはありません。ここでは，【第１回】で学習した範囲内で済ませるため，「３枚を１枚ずつ続けて取り出す」と考えて，確率を求めていきます。

まず，起こりうるすべての場合の数を求めましょう。１枚目は10通りの場合があり，２枚目は１枚目で取り出したカード以外の９通りの場合があり，３枚目は１〜２枚目で取り出したカード以外の８通りの場合があるので，すべての場合の数は，

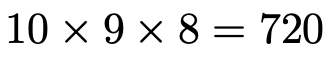
これが確率を求めるときの分母にくる数です。次に，それぞれの場合の分子を求めて，確率を計算していきましょう。３の倍数は，３，６，９の３枚あります。この中から３枚を取り出すので，X＝０，１，２，３の４つの場合があります。

X＝０のとき，３の倍数ではない７枚のカードから１枚ずつ３枚を取り出すことになります。分母を計算したときと同じ考え方で，１枚目は７通り，２枚目は６通り，３枚目は５通りの場合があるので，X＝０となる場合の数は，

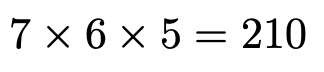
X＝１となるのは，例えば，１，２，３の３枚のカードのように，３の倍数のカードを１枚，３の倍数ではないカードを２枚取り出す場合です。１枚目に３の倍数を取り出すとすると，１枚目は，３，６，９の３通りの決め方があり，２枚目は，３の倍数以外の７通り，３枚目は，２枚目で取り出した数を除く６通りとなります。３の倍数が２枚目の場合や３枚目の場合も全く同じように計算できるので，X＝１となる場合の数は，

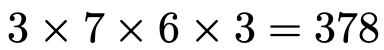
X＝２となるのは，例えば，１，３，６の３枚のカードのように，３の倍数のカードを２枚，３の倍数ではないカードを１枚取り出す場合です。１枚目に３の倍数ではないカードを取り出すとすると，１枚目は，３の倍数以外の７通り，２枚目は，３，６，９の３通り，３枚目は，２枚目で取り出していない３の倍数の２通りがあります。３の倍数でない数が２枚目の場合や３枚目の場合も全く同じように計算できるので，X＝２となる場合の数は，

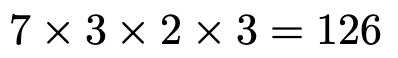
X＝３のとき，３，６，９の３枚のカードを取り出すことになります。この３枚のうち，どのカードを何回目に取り出すか（＝３枚のカードの並べ方）を計算すれば良いので，X＝３となる場合の数は，

よって，確率分布は次の表のようになります。

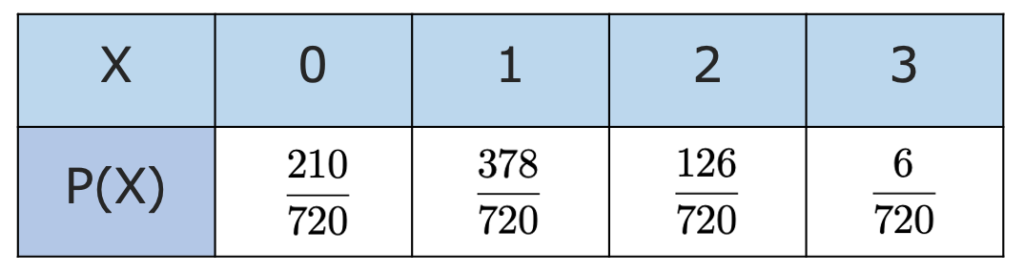
最頻値とはP(X)が最大になるXの値のことでした。上の表から，確率が最も大きいのはX＝１のときなので，最頻値は１です。（解答終わり）

演習２〜独立性〜

【問題】プロ野球パリーグの各球団の人気選手20人ずつ，６球団で合計120人の姿が１人ずつ描かれた野球カードがあり，各球団の20枚のうち，３枚には選手のサインが入っている。120枚の中から１枚を取り出すとき，取り出したカードに描かれた選手の所属球団の昨年の順位をX，サインの有無をYとする（サイン入りをY＝１，サインなしをY＝０とする）。このとき，XとYは独立であるといえるか。

【解答】XとYの同時確率分布は次のようになります。

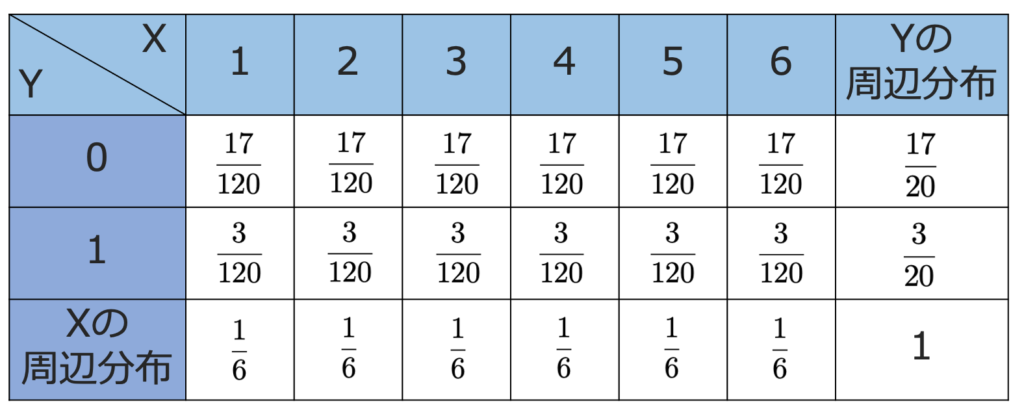
例えば，左上のマスは，次のことを示しています。

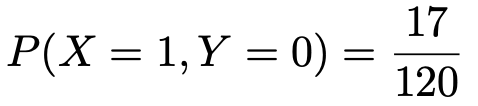
このマスと同じ列のいちばん下の行の確率と，同じ行のいちばん右の列の確率との積は，次のようになっています。

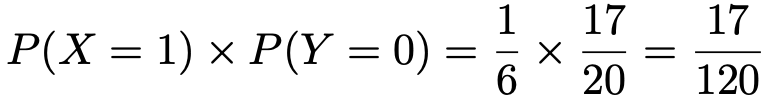
よって，次の式が成り立っています。

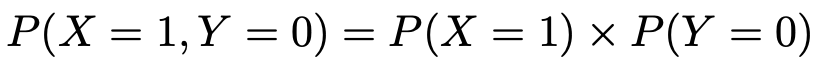
同じように，12個のマスすべてについて，次の式が成り立っています。

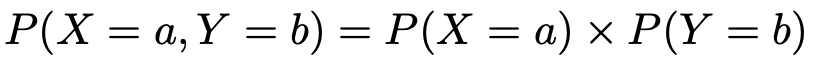
したがって，XとYは独立であるといえます。（解答終わり）

演習３〜標本平均〜

【問題】既知の母集団{１，５，７，９}を考える。この母集団から大きさ２の標本を無作為復元抽出し，

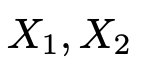
とする。この標本に対する標本平均を

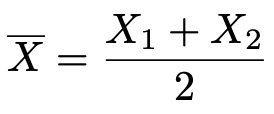
とするとき，標本平均の中央値を求めなさい。

【解答】標本平均の値をまとめると，次の表のようになります。

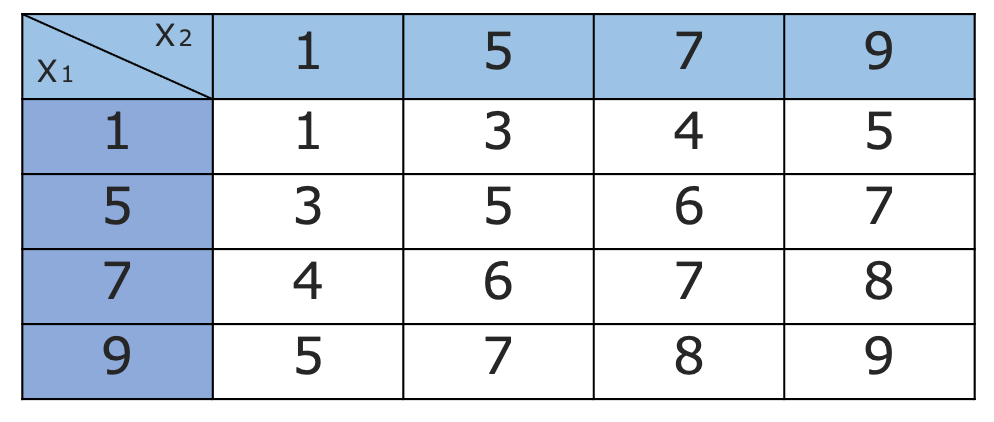
したがって，標本平均の確率分布は次の表のようになります。

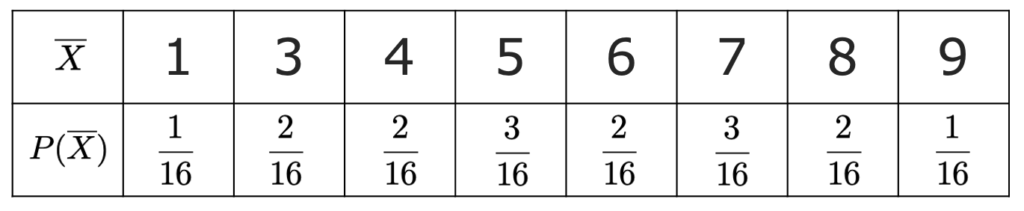
標本平均の中央値については，標本平均の値が５以下となる確率が２分の１，６以上となる確率が２分の１なので，確率変数の中央値の定義２から，５と６の平均の5.5です。（解答終わり）

第３回は以上となります。最後までお付き合いいただき，ありがとうございました！
引き続き，第４回以降の記事へ進んでいきましょう！

2023年1月に「統計検定２級公式問題集[CBT対応版]（実務教育出版）」が発売されました！（CBTが何かわからない人はこちら）
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが，本書は分野ごとにその形式の問題を並べた構成になっていて，最後に模擬テストがついています。CBT対策の新たな心強い味方ですね！