幾何分布のポイントは,期待値や分散,無記憶性です。統計検定2級では期待値や分散の結果を知っていれば,ほとんどの問題に対応できますが,準1級を受ける人にも役に立つように,本稿では幾何分布の諸性質を証明つきで紹介していきます。
本稿の目的は,幾何分布を解説すること以外にもう1つあり,それは幾何分布を理解するために必要な数学を解説することです。【統計検定準1級のための数学】と題した記事では,統計検定2級からスムーズに準1級に進めるように,2級と準1級のギャップをうめるために必要な数学も解説していきます。本稿では,幾何分布に関連して数列や無限等比級数を解説します。
本稿で前提とする知識は,【中学の数学からはじめる統計検定2級講座】の第1回の確率,第2回の条件付き確率,第4回の期待値と分散,第5回のΣ(シグマ),第6回の極限,第10回のベルヌーイ分布の内容になります。これらの内容に不安がある人は,先にそちらの記事を読んでください。
では,はじめていきましょう!
等差数列と等比数列
このセクションでは,幾何分布と関連の深い等比数列について,ゼロから説明していきます。すでに知っている人は,読み飛ばして次のセクションに進んでください。
数列というのは,数を規則的に並べたものでしたね。多くの人がはじめに思いつく数列は,自然数を1から順に並べた次のような数列でしょう。
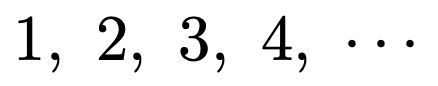
これは,1から始まって,1ずつ増える数列ですね。となり合う数の差が一定なので,等差数列と呼ばれます。また,最初の1のことを初項,となり合う数どうしの差の1のことを公差と言います。
別の例を挙げると,次の数列は,初項2,公差3の等差数列です。

一般的に,等差数列は,初項をa,公差をdとして,次のように表すことができます。
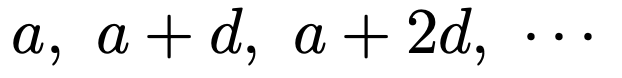
そして,等差数列と同じくらい基本的で重要なのが等比数列です。等差数列ではとなり合う2つの項の差が一定でしたが,等比数列ではとなり合う2つの項の比が一定で,前の項にある決まった数(公比と言います)をかけることで次の項が求められます。
次の数列は,初項2,公比2の等比数列で,前の項に2をかけると次の項が得られます。
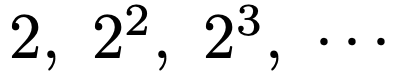
一般的に,初項a,公比rの等比数列は次のように表せます。
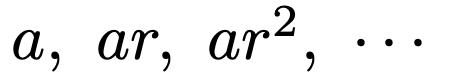
さて,次のセクションの準備として,等比数列の初項から第n項までの和を求める公式を紹介しておきます。その公式は,初項a,公比r(≠1)として次のようになります。
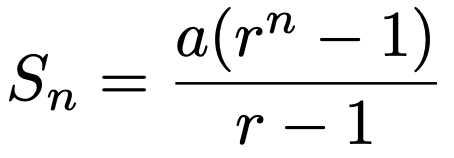
例えば,上に例として挙げた初項2,公比2の等比数列の初項から第n項までの和は,次のように計算できます。
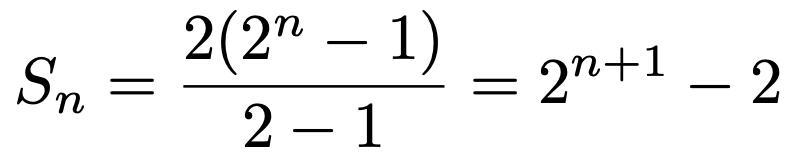
では,このような等比数列の和の公式がどのようにして導かれるのか,確認してみましょう。初項a,公比rの等比数列の初項から第n項までの和を次のようにおきます。
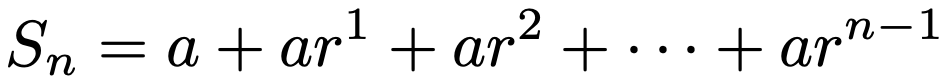
この式の両辺をr倍すると,次のようになります。
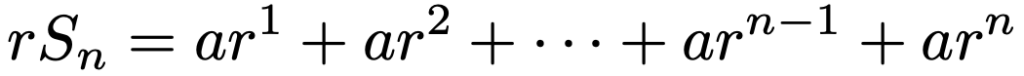
各辺について,上の式から下の式をひくと,次のように右辺のほとんどの項が相殺されて,2つの項だけが残ります。
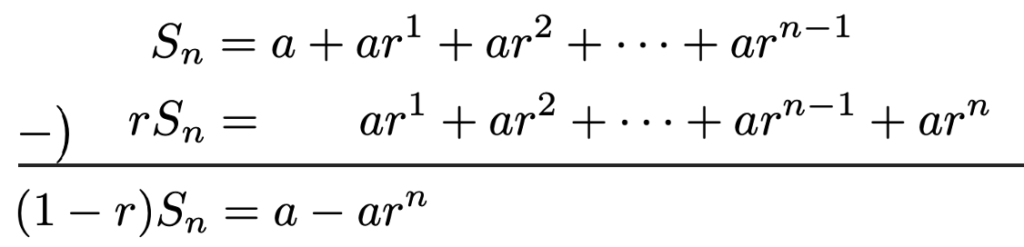
r≠1と仮定したので,両辺を1ーrでわることができて,整理すれば上に挙げた式と一致することがわかります。
さらに,等比数列の和の応用を2つ紹介します。
1つ目は,次のように等比数列の各項を無限に加えた場合の和についてです。
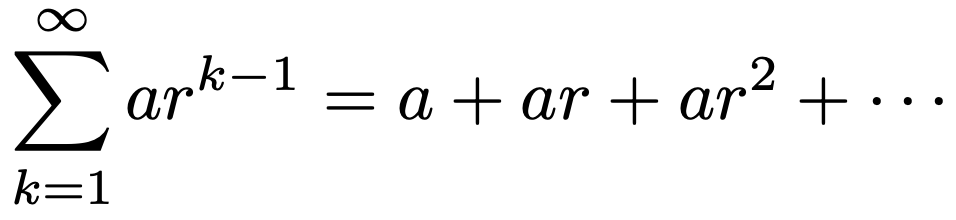
「無限に加えるとは何か?」という疑問がわくかもしれませんね。無限に加えた和というのは,次の式の右辺のように初項から第n項までの和をnの式で表した上で,n→∞の極限をとったものを指します。
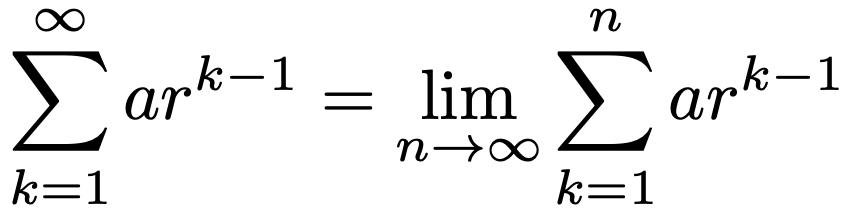
このような等比数列を無限に加えた和のことを無限等比級数と呼び,公比rの絶対値が1より小さい(ー1<r<1)とき,極限が定まります(収束すると言います)。
実際に等比数列の和の公式において,ー1<r<1とすると,rnはnが大きくなるにつれてどんどん0に近づいていくことから,初項a,公比rの無限等比級数の和は次のように計算できます。
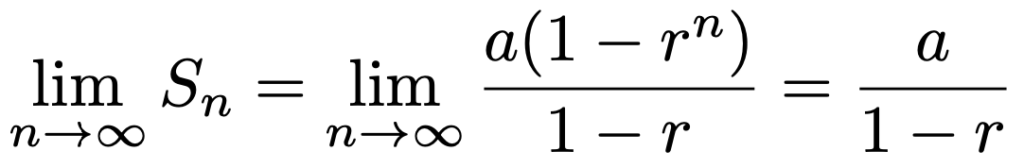
では,等比数列の和の応用の2つ目です。それは,次のような数列の和に関するものです。
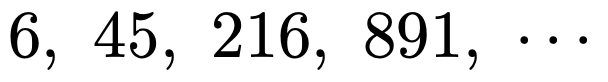
おや,今度は等差数列にも等比数列にもなっていないようです。この数列を次のように書き直すと,その正体がわかります。
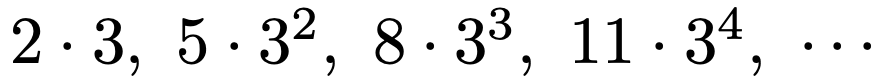
各項の左側の数を順に見ていくと「2,5,8,11,…」となっていますので,これは初項2,公差3の等差数列です。また,各項の右側の数を順に見ていくと,初項3,公比3の等比数列ですよね。つまり,等差×等比の形になっているわけです。
では,この数列の初項から第10項までの和を求めてみましょう。まず,求める和を次のようにおきます。
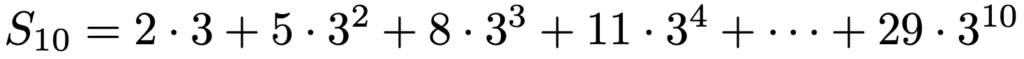
この式の両辺を3倍すると,次のようになります。
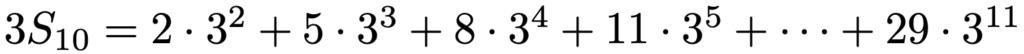
各辺について,上の式から下の式をひくと,次のようになります。
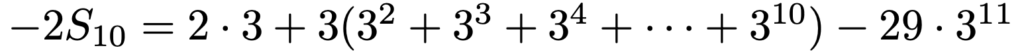
右辺のかっこの中は,初項9,公比3,項数9の等比数列なので,等比数列の和の公式から次のように書き直すことができます。
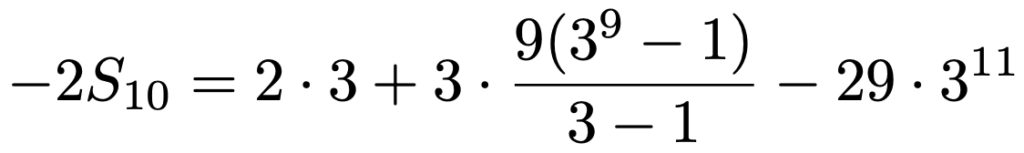
両辺をー2でわって,右辺を整理すると,次のように求められます。
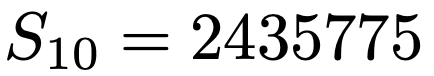
今回は初項から第10項までの和を求めましたが,同じように計算すれば,第n項までの和も計算できます。つまり,等差×等比の形の数列の和は等比数列の和を使って求めることができるわけです。
では,これらの等比数列の知識を踏まえて,次のセクションで幾何分布の説明をしていきます。
幾何分布
【中学の数学からはじめる統計検定2級講座第10回】では,独立にベルヌーイ分布に従う確率変数の和で定まる確率変数が二項分布に従うことを学習しましたね。そして,ベルヌーイ分布に従う確率変数の代表例は,1枚のコインを投げるとき,表が出たら1,裏が出たら0という値をとるものでした。表が出ることを成功,裏が出ることを失敗と便宜上呼ぶことにすると,コイン投げを何回行っても,成功の確率と失敗の確率はどちらも2分の1です。この試行のように,結果が2通りで,各回の成功確率が一定である試行をベルヌーイ試行と言います。
幾何分布は,このベルヌーイ試行を使って定めることができます。例えば,1枚のコインをくり返し投げるとき,はじめて表が出るまでに裏が出た回数をXとすると,Xも確率変数になりますよね。実は,このXが従う確率分布が幾何分布なんです。ベルヌーイ試行によって起こる2通りの事象を「成功」と「失敗」と呼ぶことにすると,最初から失敗が続いた後,はじめて成功するまでに失敗する回数が従う確率分布です。
では,幾何分布の確率関数を求めてみましょう。離散型確率変数Xの確率関数というのは,次の式を満たすようなf(x)のことです。
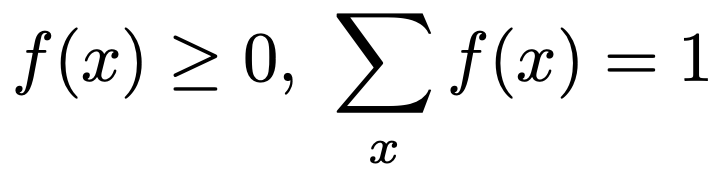
つまり,どのxでも値が0以上であって,すべて加えると1になるということです。
幾何分布は独立なベルヌーイ試行のくり返しによって定まるので,2つの独立な事象A,Bの確率について,次の式が成り立つことを思い出しましょう。
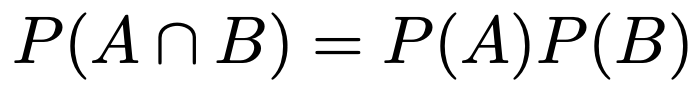
つまり,AとBがどちらも起こる確率は,それぞれの確率の積で計算できるわけです。
この式を踏まえて,1回あたりの成功確率をp(0<p<1)とすると,はじめて成功するまでにx回失敗する確率は次のように計算できます。
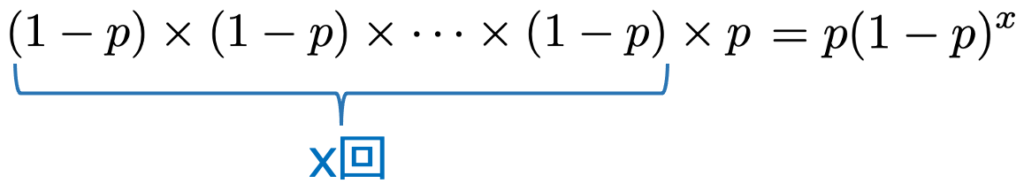
よって,幾何分布の確率関数は次のようになります。
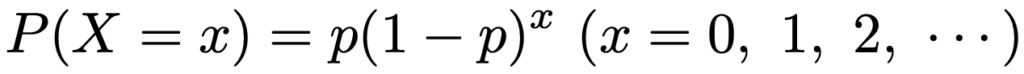
幾何分布を英語で”geometric distribution”と言うので,これ以降はこの幾何分布をGeo(p)という記号で表すことにします。例えば,1個のサイコロをくり返し投げるとき,はじめて1の目が出るまでに1以外の目が出る回数をXとすると,成功確率6分の1のベルヌーイ試行のくり返しなので,Xは次の幾何分布に従います。
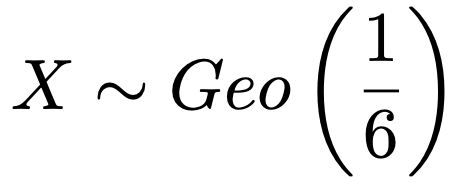
このとき,X=2となる確率は次のように求めることができます。
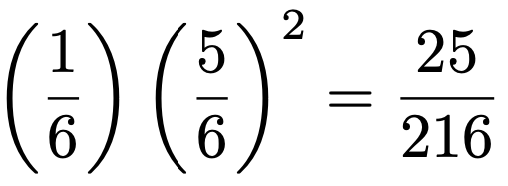
ここまで,幾何分布とは「はじめて成功するまでに失敗する回数が従う確率分布」と説明してきましたが,実は「はじめて成功するまでの試行の回数が従う確率分布」を幾何分布とする場合があります。はじめて成功するまでの試行の回数をYとすると,はじめて成功するまでに失敗する回数Xに最後の1回を加えれば試行の回数になるので,Y=X+1という関係があります。よって,Yの確率関数は次の式になります。
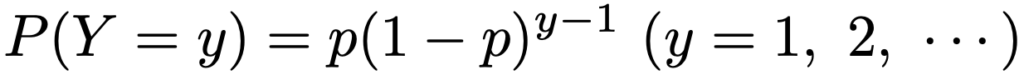
さて,P(X=x)が確率関数になっていることを確認してみましょう。まず,P(X=x)の右辺に,x=0,1,2,…のように整数を代入してみると,それぞれの場合の確率は次のように表せます。

これは,初項p,公比1ーpの等比数列になっていますね。実は,等比数列の別名が幾何数列であることから,幾何分布の名前がついていると言われています。0<p<1より,上の数列の各項が正の数なのは明らかですが,P(X=x)が確率関数であるためには,次のような確率の和が1になる必要がありますね。
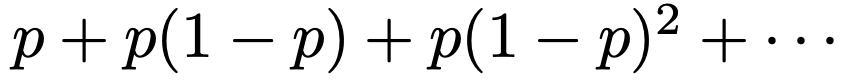
正の数を無限に加えていくので,等比数列の知識がない人が見たら,和が無限に大きくなるように感じてしまうかもしれません。でも,みなさんは大丈夫ですよね。初項がp,公比が1ーpの無限等比級数であり,0<1ーp<1なので,この和は前のセクションで学習した公式を使うと,次のように計算できます。
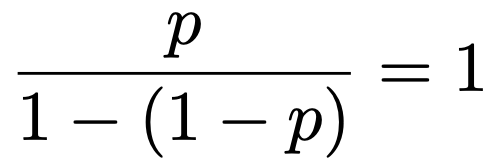
よって,すべての確率の和が1になり,P(X=x)が確率関数であることがわかりました。
このセクションの最後として,幾何分布のグラフを確認しておきましょう。次のグラフは,1個のサイコロをくり返し投げるとき,はじめて1の目が出るまでに1以外の目が出る回数をXとして,横軸でXのとる値,縦軸で確率を表したものです。
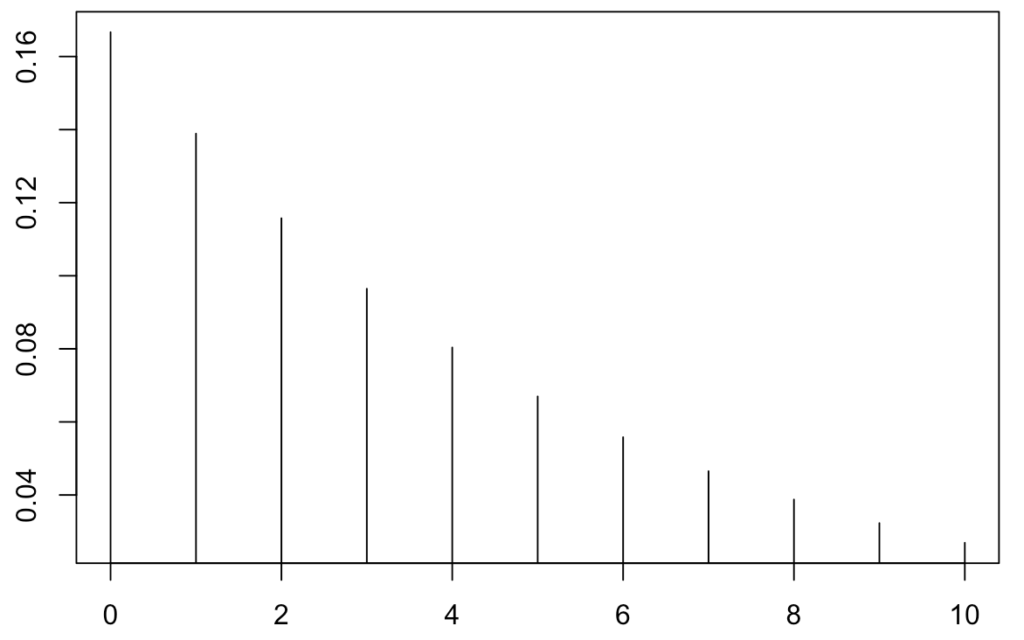
x=0,1,2,…と無限に確率が続いていき,確率が0になることはありません。
幾何分布の期待値と分散
結論から言えば,はじめて成功するまでに失敗する回数をXとするとき,Xの期待値と分散は次のようになります。
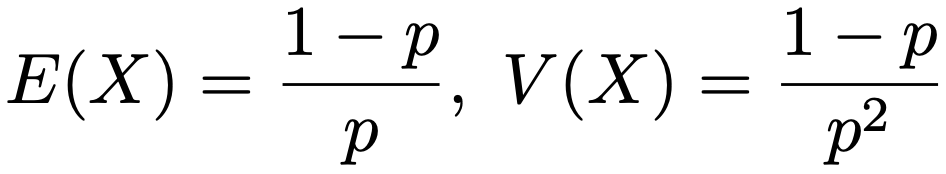
また,はじめて成功するまでの試行の回数をYとするとき,Yの期待値と分散は次のようになります。
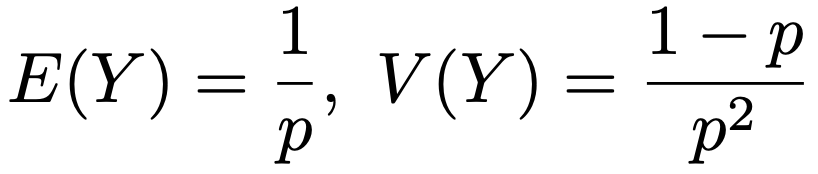
Y=X+1という関係があるので,Xの期待値,分散を利用すれば,Yの期待値,分散を導くことができます。まず,期待値は次のようになります。
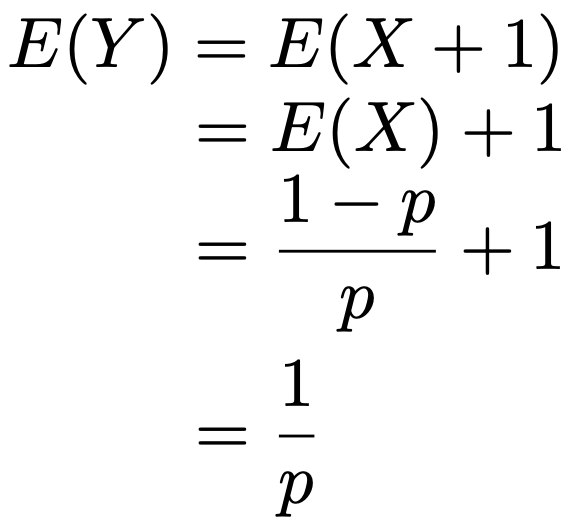
分散については,定数を加えても分散は変わらないことから,V(Y)=V(X)です。2級や準1級では,この結果を覚えておいて,すぐに書けるようにしておきましょう。
では,等比数列の知識を使って,Xの期待値,分散を導出してみましょう。Xの期待値は,期待値の定義から次のようになります。
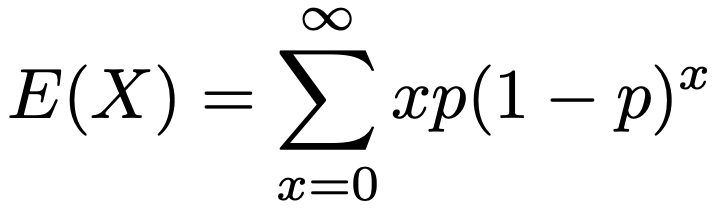
わかりやすいようにシグマを使わずに表すと,次のようになります。
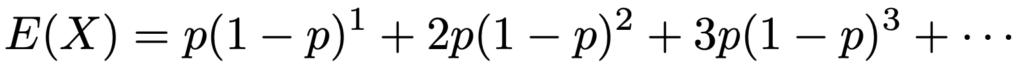
すべての項にかけられている「p」を除くと,それぞれの項は,1,2,3,…と等差数列的に増えていく部分と(1ーp)の1乗,2乗,3乗,…と等比数列的に増えていく部分の積で成り立っていることがわかりますね。つまり,等比数列のセクションで学習した等差×等比の形の数列になっているので,この考え方を使って,和を求めることができそうです。
ここで,式を簡略化するため,q=1ーpとおいて,求める和をSとします。
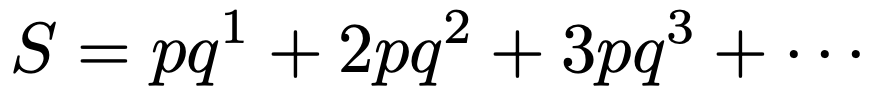
等比数列のセクションでやったように公比であるqを,上の式の両辺にかけると,次のようになります。
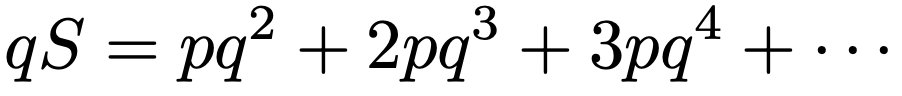
上の2つの式の各辺をひき算すると,次のようになります。
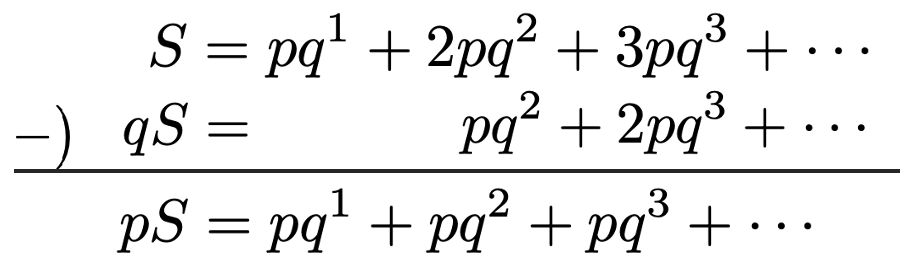
左辺では,1ーqをpでおきかえました。両辺のすべての項がpの倍数になったので,両辺をpでわると次のようになります。
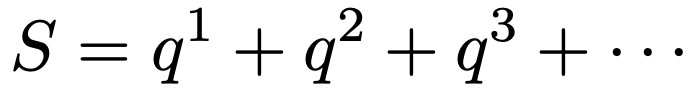
上の式の右辺は,初項q,公比qの無限等比級数なので,次のように計算できます。
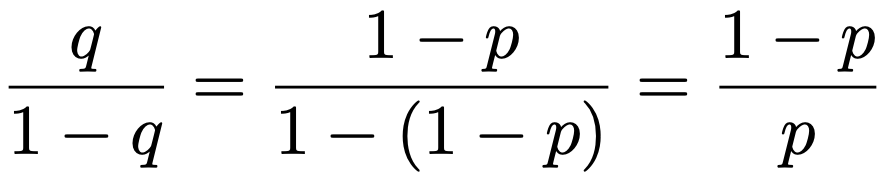
これで,期待値が求まりました。
次に,Xの分散の計算をしていきます。次の分散の公式を利用しましょう。
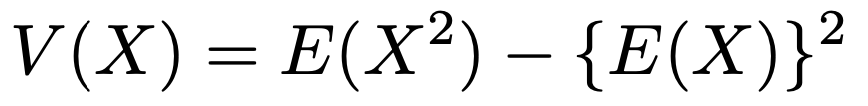
この式の右辺の第2項には,先ほど計算した期待値を代入すれば良いので,右辺の第1項のX2の期待値を計算すれば良いですね。定義から,次の計算をすることになります。
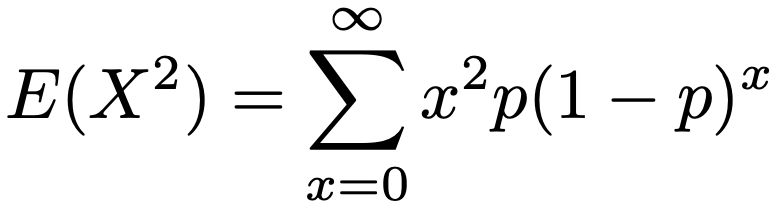
これをシグマを使わずに表してみると,次のようになります。
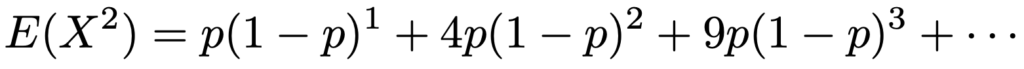
今回は,等差×等比の形にはなっていないのですが,期待値と同じ方針でやってみます。式を簡略化するため,q=1ーpとおいて,求める和をTとします。
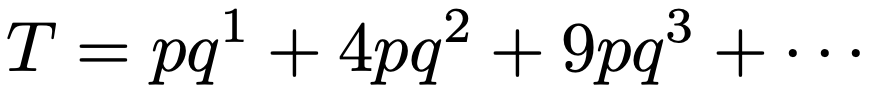
公比であるqを,上の式の両辺にかけると,次のようになります。
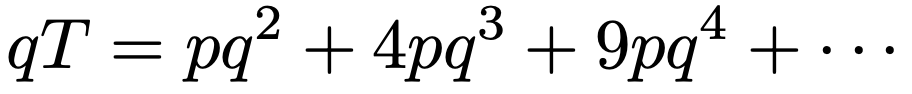
上の2つの式の各辺をひき算すると,次のようになります。
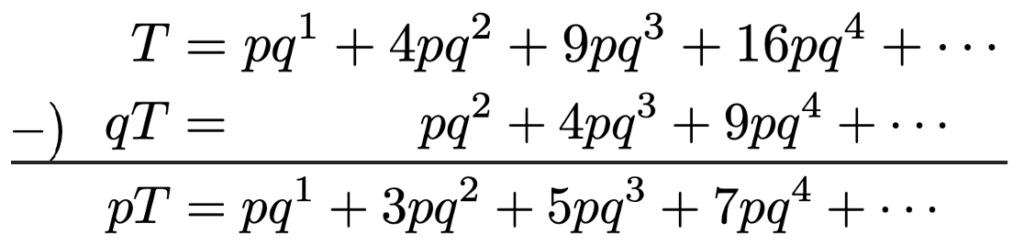
期待値のときと同じように,左辺では,1ーqをpでおきかえました。さらに,両辺をpでわると次のようになります。
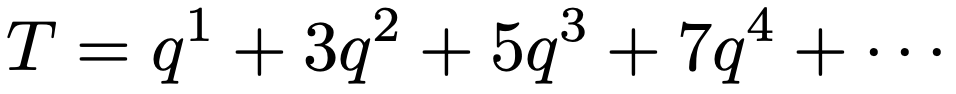
この式の右辺は,等差×等比の形になっていますね。もう一度,両辺にqをかけてひき算をしてもいいのですが,そうしなくてもTの値を求めることができます。まず,次のように右辺をΣで表し,式変形します。
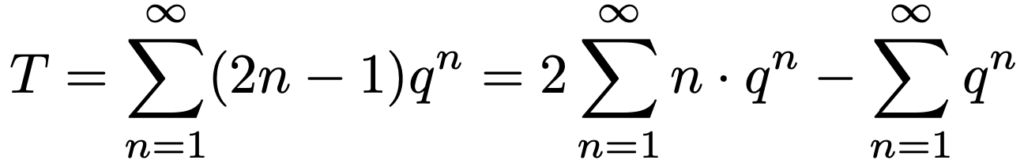
最右辺の第1項のΣの部分は,期待値をpでわったものになっていて,第2項は初項q,公比qの無限等比級数なので,次のように計算できます。
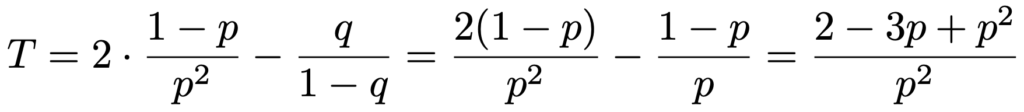
よって,求める分散は次のように計算できます。
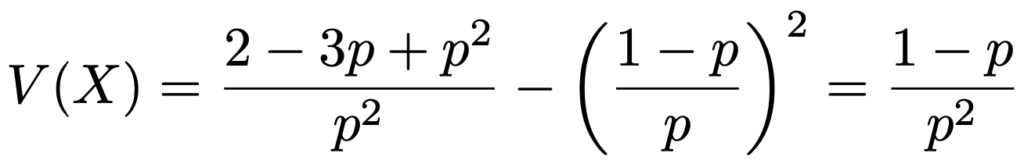
無記憶性
幾何分布を特徴づける大事な性質として,無記憶性があります。擬人化して表現すれば,幾何分布はまるで過去のことを覚えていないかのような性質を持っているのです。数式を使うと,どんな0以上の整数m,nに対しても次の式が成り立つこととして表現できます。
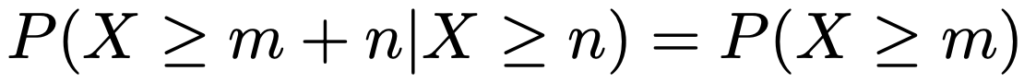
この式の左辺は条件付き確率で,「はじめのn回は失敗の連続だったことがわかっている前提で,次のm回も失敗の連続になる確率」を表しています。それが右辺の「はじめのm回は失敗の連続になる確率」に等しいのです。例えば,10回続けて失敗だったことがわかっても,そのことはこれから成功する確率には影響せず,これから試行をはじめる場合と変わらないことを意味しています。
では,幾何分布Geo(p)において,この性質が成り立つことを示してみましょう。上の無記憶性の式の左辺は,条件付き確率の定義から次の式の右辺のように書き直すことができますよね。
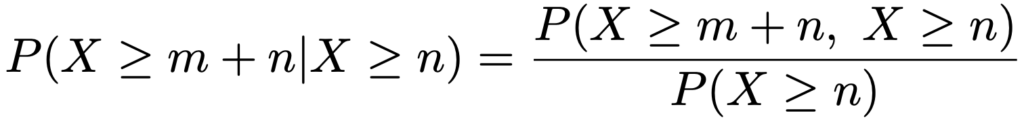
右辺の分子は「X≧m+nであって,しかもX≧nとなる確率」を表していますが,X≧m+nならばX≧nとなるのはあたり前なので,これはつまりP(X≧m+n)に他ならないですよね。その確率は次のように計算できます。
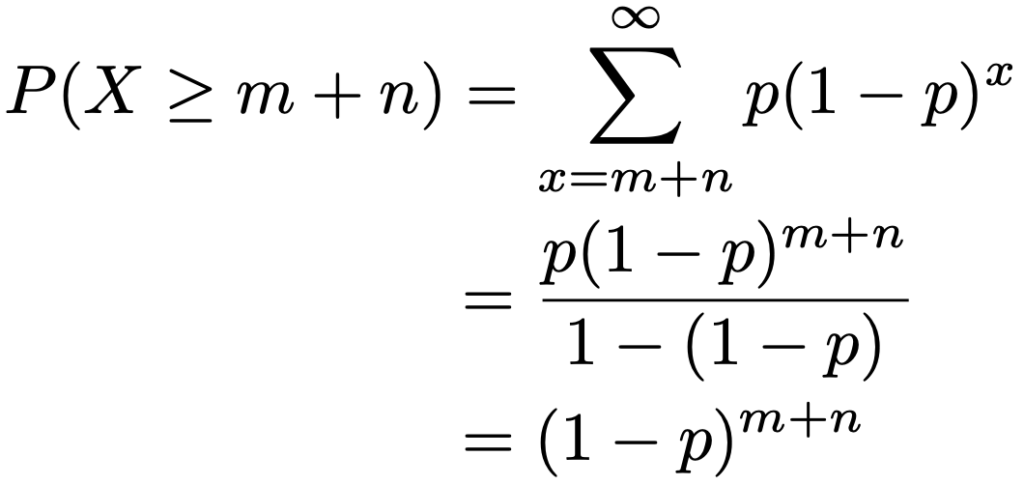
分母も同じように計算できるので,もとの条件付き確率は次のように計算できます。
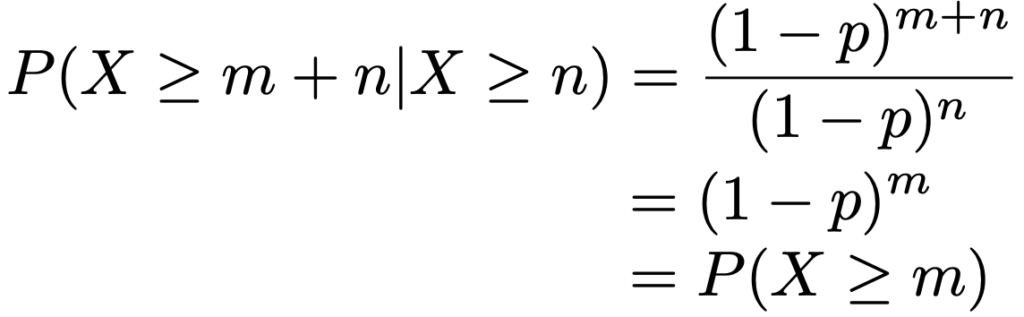
これで「幾何分布は無記憶性を持つ」ということが示せました。また,逆に,X=0,1,2,…という値をとる離散型確率分布のうち,無記憶性を持つのは幾何分布のみであることも知られています。つまり,離散型確率分布では「無記憶性と言えば幾何分布」なわけです。
幾何分布についての基本的な説明は以上になります。この後は,さらに理解を深めるための演習問題と参考図書の紹介です。
演習1
【問題】袋の中に赤玉,青玉,白玉,黒玉の4個の玉が入っている。この袋の中から1個の玉を取り出して,色を確認した後,玉を袋の中に戻すという試行を繰り返す。このとき,4種類の玉すべてが少なくとも1回取り出されるまでの試行の回数の期待値を求めなさい。
【解答】※この解答では,はじめて成功するまでの試行の回数が従う確率分布を幾何分布とします。
1回目の試行で,4種類の玉のうちの1種類目が必ず取り出されます。
では,2種類目は2回目に取り出されるでしょうか。そうとは限りませんよね。1回目の試行で取り出された玉を2回目の試行でも取り出すかもしれないからです。
2回目以降の試行では,2種類目の玉が取り出される確率は4分の3なので,はじめて2種類目の玉が取り出されるまでの試行の回数は,成功確率4分の3の幾何分布に従います。よって,その期待値は,4分の3の逆数の3分の4になります。
同じように,2種類目の玉が取り出された後の試行では,3種類目の玉が取り出される確率は4分の2なので,はじめて3種類目の玉が取り出されるまでの試行の回数は,成功確率4分の2の幾何分布に従います。よって,その期待値は,4分の2の逆数の2になります。
最後に,3種類目の玉が取り出された後の試行では,4種類目の玉が取り出される確率は4分の1なので,はじめて4種類目の玉が取り出されるまでの試行の回数は,成功確率4分の1の幾何分布に従います。よって,その期待値は,4分の1の逆数の4になります。
よって,4種類の玉すべてが少なくとも1回取り出されるまでの試行の回数をYとすると,Yの期待値は次のように計算できます。
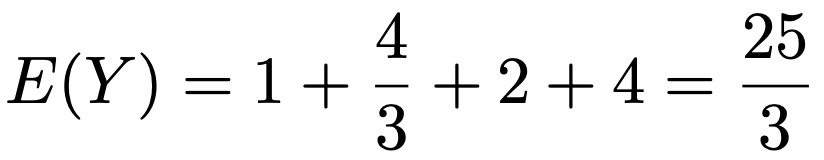
(解答終わり)
演習2
【問題】ある映画を映画館で観ると,入場時に映画の一場面を切り取った12種類のフィルムのうちの1つを等確率でもらうことができる。すでに10種類のフィルムを持っている人が,まだ持っていない2種類のフィルムをどちらとも入手するまで映画を観に行くとき,これからの入場回数の期待値を求めなさい。
【解答】※この解答では,はじめて成功するまでの試行の回数が従う確率分布を幾何分布とします。
10種類のフィルムを持っていて新たに入場するとき,まだ持っていないフィルムを手に入れる確率は12分の2=6分の1です。はじめて11種類目のフィルムを入手するまでの入場回数をXとすると,Xは次の幾何分布に従います。
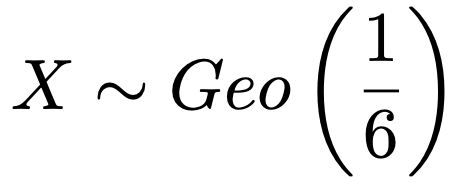
よって,Xの期待値は次のようになります。
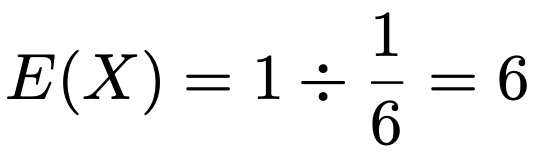
同じように,11種類のフィルムを持っていて新たに入場するとき,まだ持っていないフィルムを手に入れる確率は12分の1です。はじめて12種類目のフィルムを入手するまでの入場回数をYとすると,Yは次の幾何分布に従います。
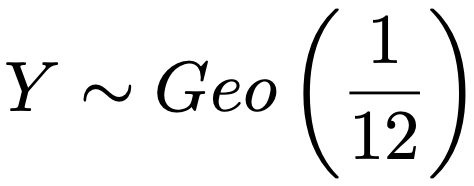
よって,Yの期待値は次のようになります。
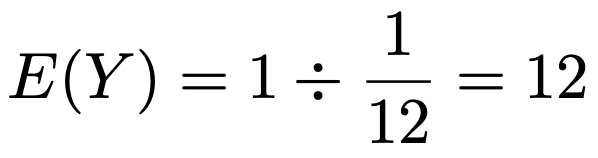
したがって,求める入場回数の期待値は,6+12=18(回)
(解答終わり)
参考図書
本稿を執筆するにあたり,次の書籍を参考にしました。
これからはじめる統計学(蓑谷千凰彦,東京図書)
本書は,無記憶性なども解説されており,本稿では取り上げなかった幾何分布の待ち時間分布としての側面も具体例とともに解説されています。
本稿は以上となります。最後までお付き合いいただき,ありがとうございました!





コメント