ポアソン分布の確率関数をはじめて見たら,誰でも目が点になりますよね。この式の謎を解明しつつ,統計検定の2級〜準1級で問われるポアソン分布の諸性質を証明つきで解説していきます。
本稿の目的は,ポアソン分布を解説すること以外にもう1つあり,それはポアソン分布を理解するために必要な数学を解説することです。【統計検定準1級のための数学】と題した記事では,統計検定2級からスムーズに準1級に進めるように,2級と準1級のギャップをうめるために必要な数学も解説していきます。本稿では,ポアソン分布に関連して指数関数とべき級数を解説します。
なお,本稿で前提とする知識は,【中学の数学からはじめる統計検定2級講座】の第1回の確率,第4回の期待値と分散,第6回の極限と微分,第7回の正規分布,第10回の階乗と二項分布の内容になります。これらの内容に不安がある人は,先にそちらの記事を読んでください。
では,はじめていきましょう!
指数関数
指数と言えば,23=8の3や24=16の4のように,数の右肩にのった数のことですよね。この後で示す具体例のように,指数として使える数は自然数だけではなく,どんな実数でも指数として使うことができます。そこで,次の式で表されるような「2の実数乗」という関数を考えることができ,これを底が2の指数関数と言います。
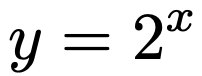
この場合の2のように,何乗かされる数のことを底と呼びます。底を1つの正の数に固定したとき,1つの指数関数が定まります。
では,自然数以外の指数をどのように考えればいいのかを紹介していきましょう。その際に鍵になるのが指数法則です。例えば,次のような計算が成り立ちますよね。
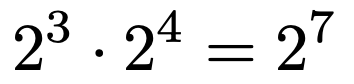
「2を3回かけたものと2を4回かけたものをかけたら,2を7回かけたものに等しい」というのは当たり前ですね。これを一般的に表すと,次のようになります。
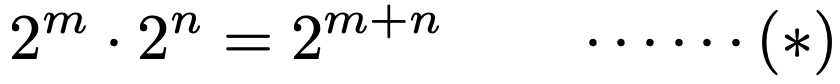
この式は,底が同じであれば,左辺のようなかけ算は,右辺のように指数部分のたし算で計算できるということを意味しています。mやnが自然数なら,この式が成り立つことは直感的にわかりやすいですが,mやnがすべての実数で成り立つと考えると,いろいろなことがわかってきます。
例えば,(*)の式にn=0を代入すると,次の式が成り立ちますよね。
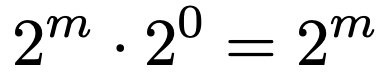
2mは0ではないので,上の式の両辺を2mでわると,20=1となります。この計算過程は,底が2でなくても同じになりますので,結局のところ,正の数の0乗は1になるわけです。
次に指数部分が負の整数になるときを考えましょう。(*)の式で,nにーmを代入すると,次の式が成り立ちます。
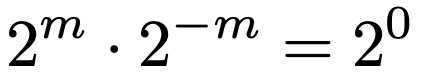
右辺の2の0乗は1だったので,上の式の両辺を2mでわると,次のようになります。
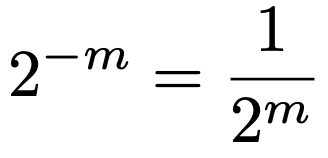
上の式の左辺の数のように指数部分が負の整数である数は,指数部分の符号を正に変えた数の逆数に等しいわけです。
次に,指数部分が分数のときを考えましょう。(*)の式のmとnをどちらも2分の1とすると,次の式が成り立ちます。
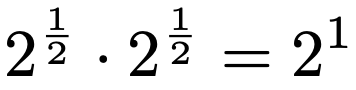
2の2分の1乗を2回かけると2に等しくなるわけです。これは,みなさんがよく知っているルート2の性質そのものです。つまり,次の式が成り立ちます。
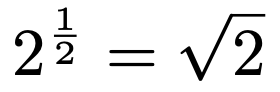
では,2の3分の1乗はどんな数でしょうか。次のように(*)の式を2回使うことで,2の3分の1乗を3回かけると2に等しくなりますね。
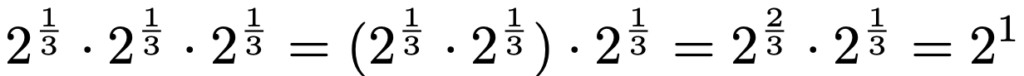
2回かけて2に等しくなる数を2の平方根と呼んだように,3回かけて2に等しくなる数を2の3乗根と言います。次の式で表されるように,正の数で2の3乗根となる実数がただ1つ存在します。

より一般的に,自然数nに対して,2のn分の1乗は2のn乗根となる正の数です。
このように,すべての実数xに対して2のx乗の値を定めることができ,それぞれのxの値に対して2のx乗の値をy座標としてグラフに表すと,次のようになります。
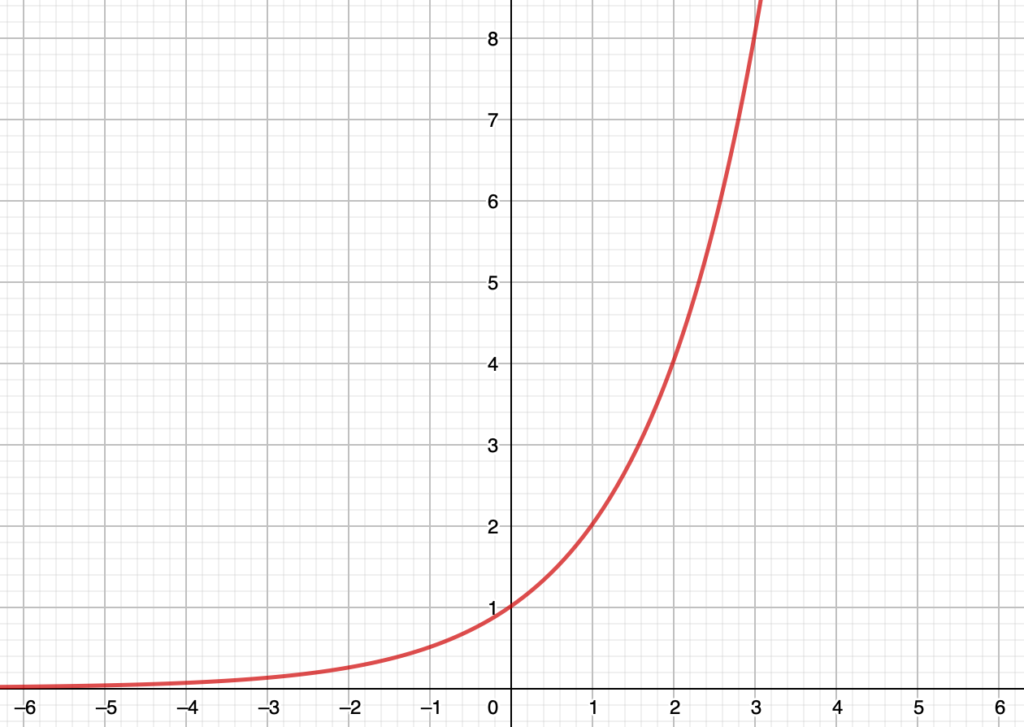
これが,指数関数y=2xのグラフです。
さて,ここまで底が2の指数を考えてきましたが,底が他の正の数の場合でも同じことが言えますよね。そこで,正の数a,bを底として,指数法則を一般的な形で書いておきます。x,yを実数として,指数法則は次の3つの条件から成り立ちます。
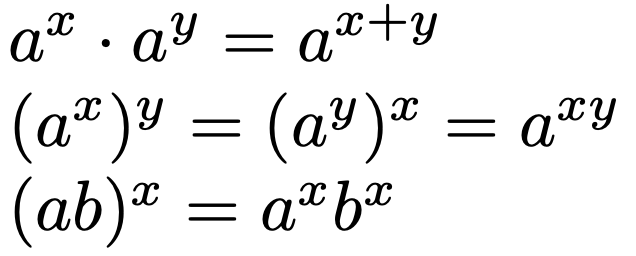
上の説明で登場したのは,指数法則の1つ目ですね。後のセクションの証明の中で,指数法則の2つ目を使います。
ネイピア数とべき級数
前のセクションで紹介したように,指数関数の底となりうる数は2,3,…のような自然数だけでなく,さまざまな正の数が考えられます。その中で,指数関数の底として最も重要なものは次の数です。
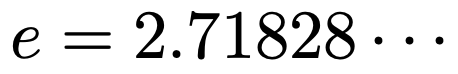
この数は,小数第何位までも無限に続き,小数点以下の数の並びに規則性は現れません。こういう性質を持った数を,みなさんは他にも知っているはずです。そう,円周率も同じように無限に小数が続きますよね。こういう数のことを無理数(その中でも特に超越数)と言います。
「小数点以下が無限に続く数」のままでは不便なので,円周率にはπという記号を与えました。同じように,上の数にはeという記号が与えられています。この数をネイピア数,または自然対数の底と言います。「自然対数とは何か」については別の記事で説明するので,本稿ではネイピア数と呼ぶことにします。
ここで,ネイピア数の定義を紹介しておきます。次の式を見てください。
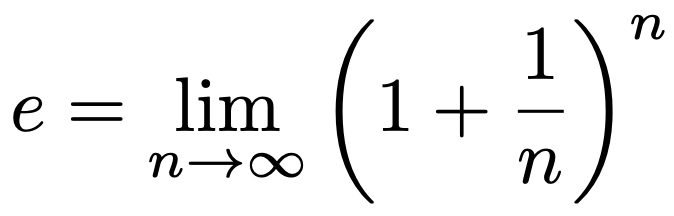
上の式の右辺の極限は1つの実数を定めます。それがネイピア数です。試しに,上の式の右辺の文字式に,n=2,3,4をそれぞれ代入して計算すると,次のようになります。
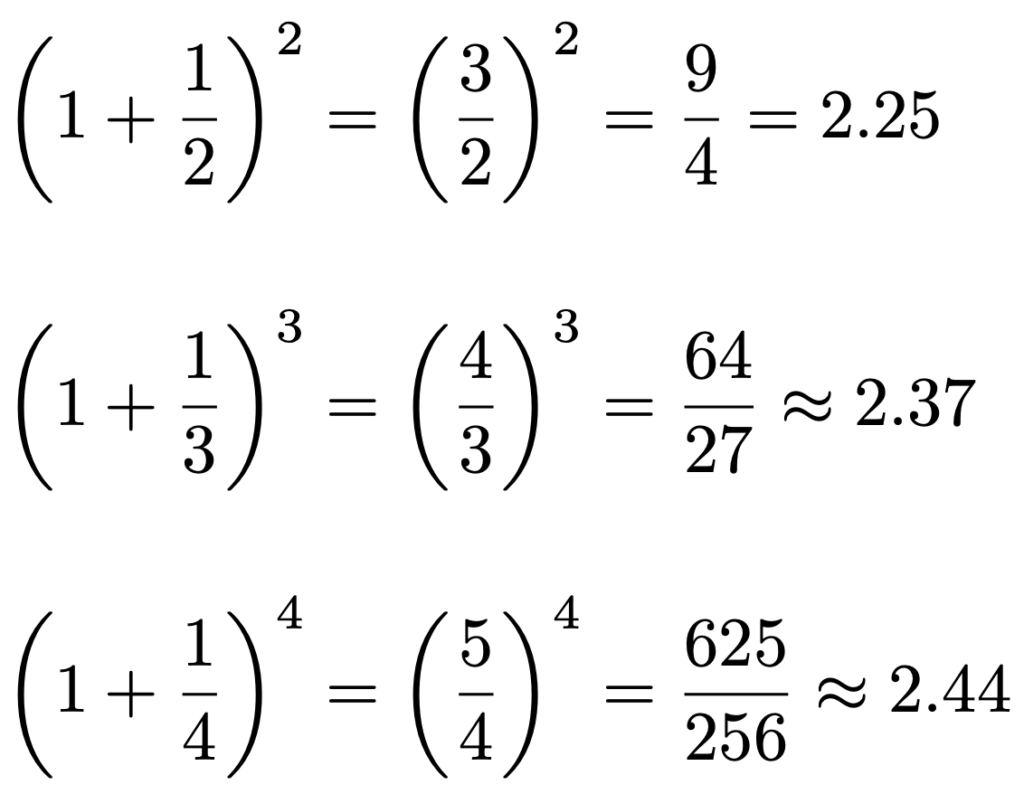
確かに,2よりも大きい数で,少しずつ大きくなっている感じがしますよね。不思議なことに,nをどれだけ大きくしても3を超えることはなく,2.71828…というネイピア数にどんどん近づいていくことが知られています。
あとで使うため,ネイピア数の定義を少し変形しておきます。上の定義式で,x=1/nとおくと,次の式になりますね。
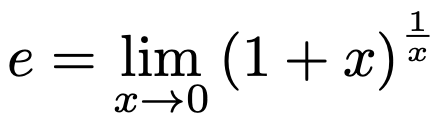
n→∞のときに,x→0であることに注意しましょう。こちらをネイピア数の定義の2つ目と呼ぶことにします。他にもネイピア数の定義式は考えられますが,本稿ではここまでにしておきます。
では,このようなネイピア数が何の役に立つのでしょうか。実は,ネイピア数を底とする指数関数については,実数全体で次の式の右辺と関数として等しいです。

上の式の右辺のように,多項式が無限に続くような形をしたものをべき級数と言います。そのべき級数の形から,ネイピア数を底とする指数関数は微分しても形が変わらないことがわかります。上のべき級数は,次のようにひとつずつの項ごとに微分することができます。
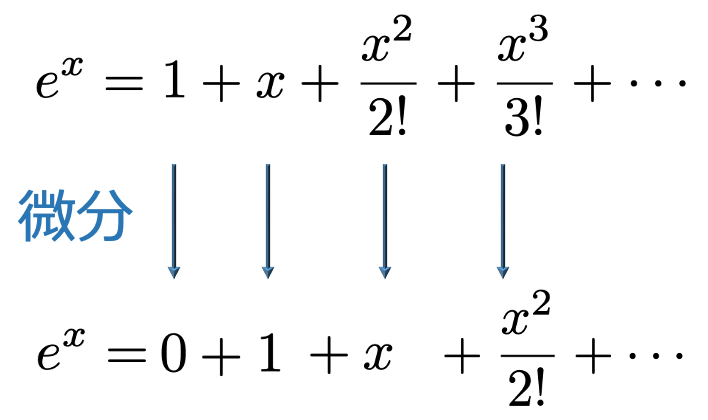
微分した後のべき級数をもとのべき級数と比べると,全体としては一致することがわかります。つまり,ネイピア数を底とする指数関数は微分しても形が変わらないという特徴をもっており,指数関数の中で最も重要なものとして様々な分野で応用されています。
では,ネイピア数を底とする指数関数が上の式の右辺のべき級数のように表せることを感覚的に納得してもらうため,グラフを見ていきましょう。
次の図で,ピンクの曲線が指数関数y=exのグラフで,緑の直線が1次関数y=x+1のグラフです。x=0の付近(y軸と交わるあたり)では,2つのグラフが近づいていますよね。
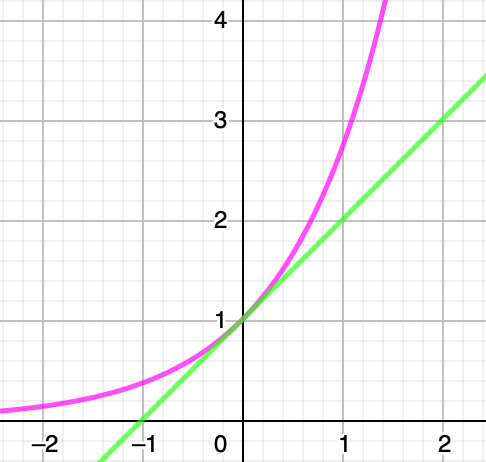
今度は,次の図を見てみましょう。
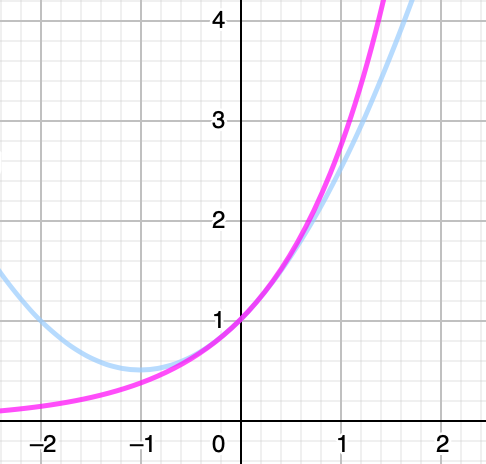
ピンクの曲線は先ほどと同じ指数関数のグラフで,薄い青の曲線が次の2次関数のグラフです。
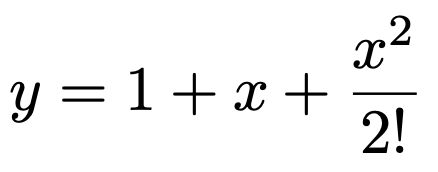
1次関数のときよりも2次関数のほうが,x=0の付近を中心としてより広い範囲で重なっているように見えますよね。
今度は,次の図を見てみましょう。
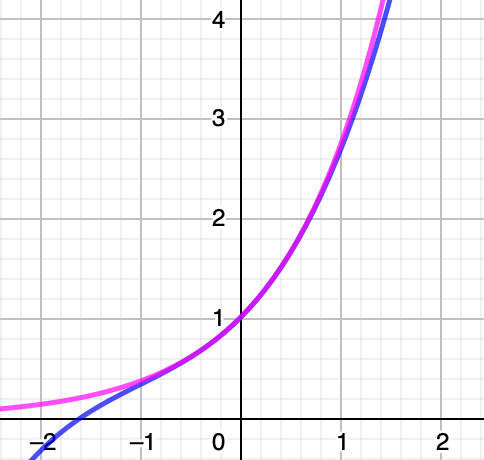
ピンクの曲線は先ほどまでと同じグラフで,濃い青の曲線が次の3次関数のグラフです。
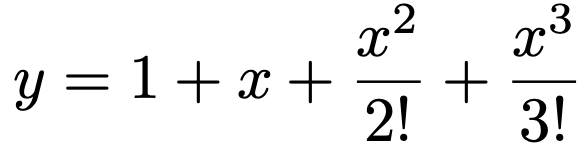
2次関数のときよりも3次関数のほうがさらに広い範囲で指数関数のグラフと重なっているように見えます。
このように,より高い次数の項をつけ加えていくと,多項式関数のグラフは指数関数のグラフにさらに広い範囲で重なるようになり,無限に項を加えたべき級数は指数関数とピッタリ一致します。
ポアソン分布
ポアソン分布は,ある条件のもとで二項分布をより簡便に扱えるようにしたものであり,それだけにはとどまらない応用範囲も持っています。
例えば,次のような設定を考えてみましょう。
(例1)5000分の1の確率で不良品が発生する機械がある。この機械で10000個の製品を作ったとき,不良品が3個となる確率はいくらか。
この問題を解いてみましょう。10000個の製品について,不良品となる確率が5000分の1,不良品とならない確率が5000分の4999なので,不良品の個数をXとすると,Xは次の二項分布に従います。
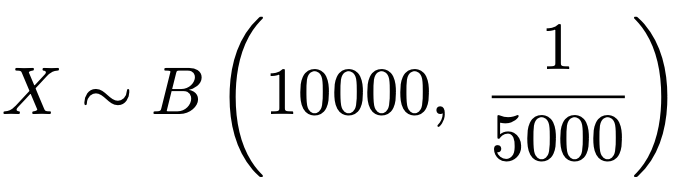
よって,X=3となる確率は次の式で計算できます。
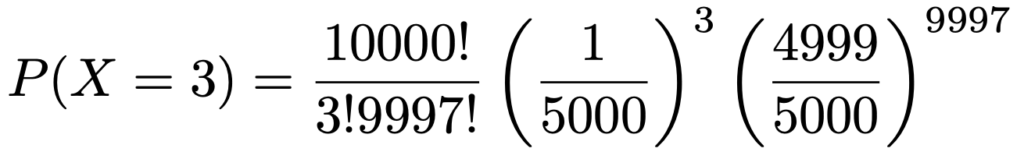
これって,電卓を使っても直接計算するのは無理ですよね…。このように,nが大きくpが小さい二項分布はよく現れるのですが,扱いにくいんです。これを簡便に計算できる方法があったら便利ですよね。実は,その方法を与えてくれるのがポアソン分布なんです。
では,そのポアソン分布とは具体的にどのような確率分布なのでしょうか。平均λのポアソン分布の確率関数は次の式で表されます。
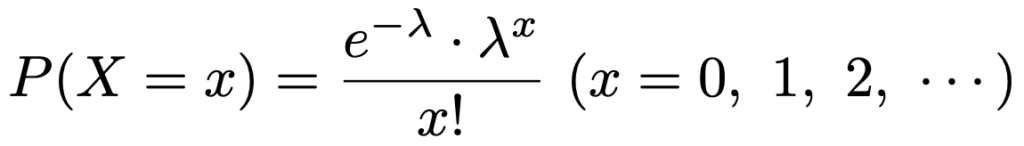
eは前のセクションで説明したネイピア数,分母の「!」は階乗です。
「…と言われても,複雑すぎて意味がわからない…」って思いますよね,わかります。順を追って説明するので,あきらめずについてきてください。
では,この式がどこからきているのかと言うと,それが次の定理です。
λを正の定数とするとき,np=λのもとで,n→∞(つまり,p→0)とした極限について次の式が成り立つ。
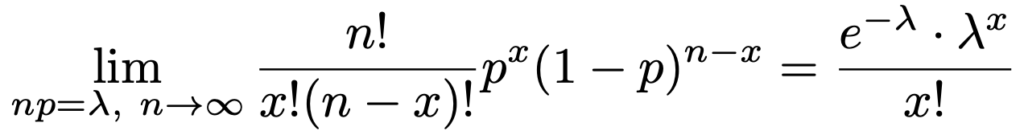
つまり,nが非常に大きくpが非常に小さい二項分布は,平均np=λのポアソン分布に近似的に従うということです。ちなみに,この少数の法則をはじめて証明したのがフランス人の数学者のポアソンです。
なお,本稿では確率変数Xが平均λのポアソン分布に従うことを次のように表します。
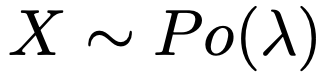
では,先ほどの(例1)の答えをポアソン分布を使って求めてみましょう。不良品の個数Xが従う二項分布は次のようなものでしたね。
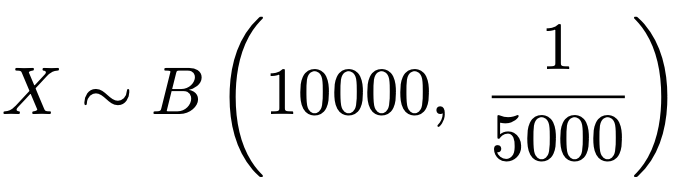
よって,期待値は次のように求められます。

次に,同じ期待値のポアソン分布を考えます。XはPo(2)に近似的に従っているとみなせるので,X=3となる確率は,ポアソン分布の確率関数でλ=2,x=3として,次のように計算できます。
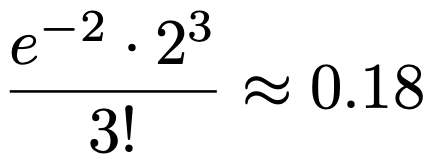
どうですか? このほうが二項分布で計算するより簡単ですよね。二項分布はnとpを決めると定まり,ポアソン分布はλを決めると定まるので,実はポアソン分布のほうがシンプルなんです。
ここで,上の定理の証明をしておきます。この証明は1級で出題されたことはありますが,2級や準1級の合格のためには不要ですので,興味のない人は読み飛ばしてください。
まず,np=λという条件があるので,二項分布B(n,p)の確率関数に,p=λ/nを代入すると,次の式になります。
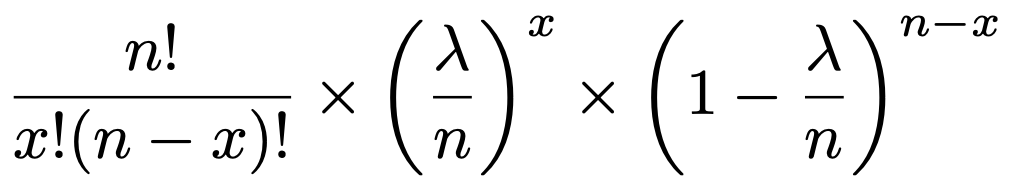
「×」の記号で示したように,3つの部分のかけ算とみたときの左の2つの積を次のように書き直します。
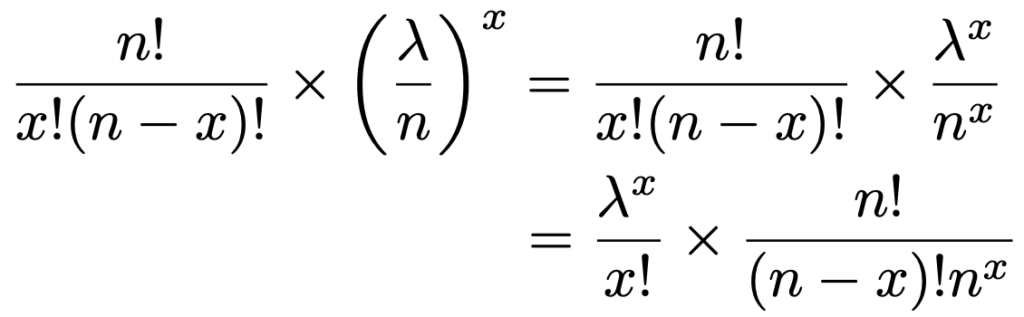
次に,上の3つの部分のかけ算の式で残っていた3つ目を次のように変形します。
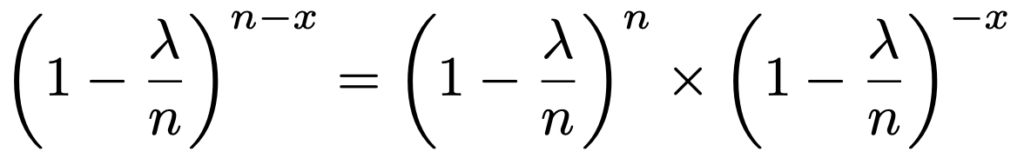
この2つの変形を組み合わせると,最初の式は次の式に変形できます。
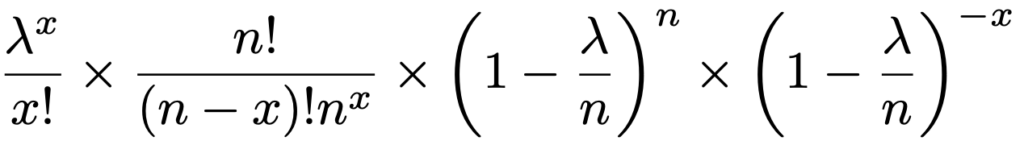
この式を,4つの部分のかけ算とみたときのいちばん左の部分は,ポアソン分布の確率関数として最後まで残りますので,2つ目以降を処理する必要があります。まず,2つ目は,次のように変形することで,n→∞のとき1に近づくことがわかります。
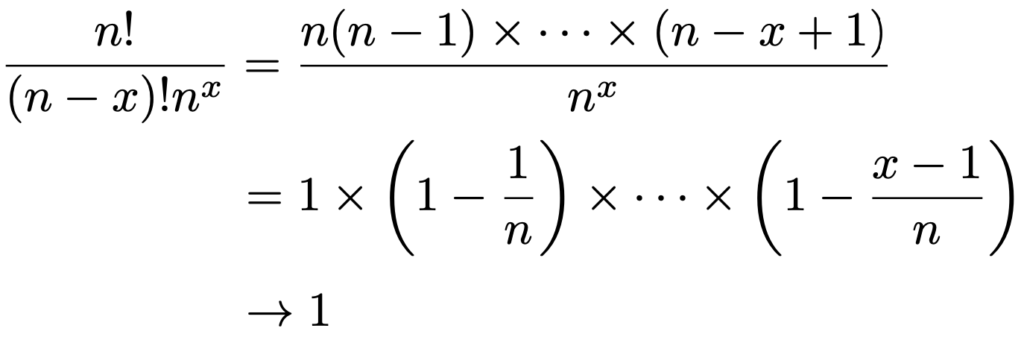
上の4つの部分のかけ算の式で,いちばん右の部分は,n→∞のときλ/n→0なので,1に近づきます。
残るは,4つの部分のかけ算の式の右から2番目の部分です。唐突ですが,この部分を次のように変形します。
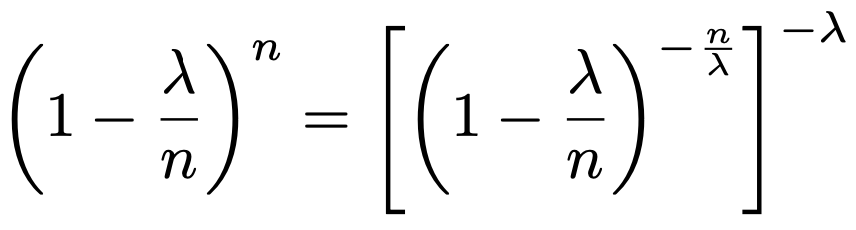
左辺と右辺が一致することは,指数法則の2つ目からわかります。そして,上の式の右辺の大かっこの中の式のn→∞の極限は,ネイピア数eの2つ目の定義式で,x=ーλ/nとしたものと一致します。
よって,次のように,ポアソンの少数の法則が示されたことになります。
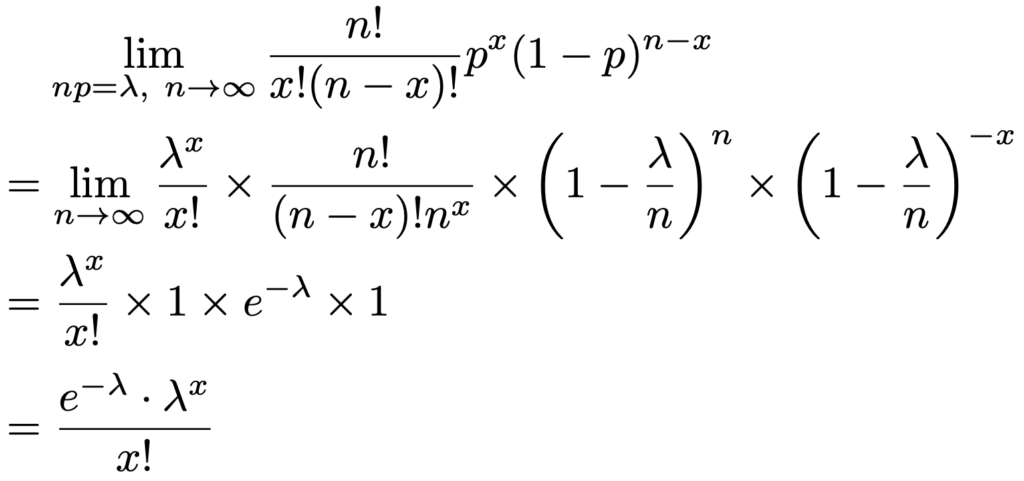
ここまで,ポアソン分布の二項分布の代用品としての側面を紹介しましたが,この確率分布の真価は単なる代用品にはとどまらない応用の可能性にあります。
例えば,次のような設定を考えてみましょう。
(例2)あるお店では,平均的に1時間に3人の客が来る。1時間に客が1人も来ない確率はいくらか。
この例は,もはや二項分布ではないですが,一定の条件のもとではポアソン分布を仮定することができます。それは,時間的(あるいは,空間的)にまばらにしか起きないような事象については,次の図のように,時間の単位(あるいは,空間の単位)を細かくとると,◯がつくか・つかないか(起きるか起きないか)の2択になり,試行の回数が非常に多く,起きる確率が非常に低い事象とみなすことができるためです。

他にも,あるメールアドレスに1日に送られてくるメールの数など,離散的にしか起こらない事象の確率モデルとしてポアソン分布が有用であることがしばしばあります。
時間的にまばらにしか起きない事象を例として,ポアソン分布を仮定できるかどうかの目安となる3つの条件を示すと,次のようになります(本稿下部の参考図書②を参照)。
- 微小時間内に事象が起きる確率は過去の起こり方に影響されない(独立性)
- 上の生起確率は時点によって変化しない(定常性)
- 微小時間内に事象が2回以上起きる確率は無視できるほど小さい(希少性)
また,統計検定準1級の過去問では,上記以外にも「過去のデータから期待値と分散がほぼ等しいと想定できる」ということをポアソン分布の妥当性の判断基準としている出題がありますので,この点も頭に入れておきましょう。
いずれにしても,時間的(あるいは,空間的)にまばらにしか起きないような事象にポアソン分布をあてはめて確率を計算する問題が統計検定で出題される場合には,問題文中に「ポアソン分布に従うと仮定して解きなさい」といった指示がありますので,それに従って解けば迷うことはないでしょう。
さて,ポアソン分布がどういうものかがそろそろ見えてきたのではないでしょうか。しかし,まだ大切なことを確認していませんでした。それは「そもそもポアソン分布は確率分布になっているの?」という点です。
ポアソン分布の確率関数に,x=0,1,2,3,…をそれぞれ代入すると,それぞれの確率は次のようになりますよね。
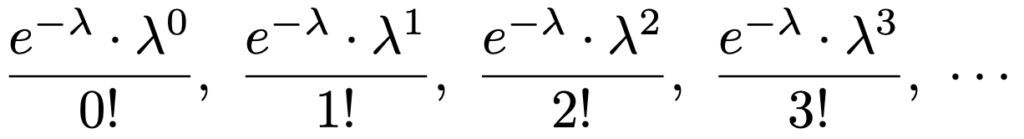
正の数を何乗しても正の数なので分子は正の数,0以上の数の階乗も正の数なので分母も正の数であり,無限個の正の数の和になっています。では,これらの和は1だと言えるでしょうか。一見しただけではわかりそうもないですよね。ここで役に立つのが,前のセクションで紹介したexをべき級数で表した式で,x=λを代入すると,次のようになりますね。
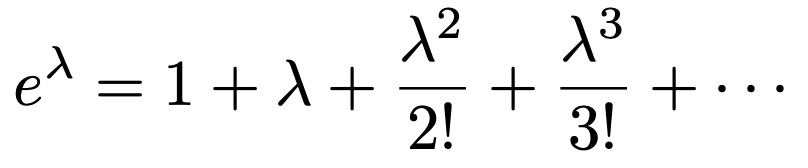
この式の両辺にeーλをかけると次のようになります。
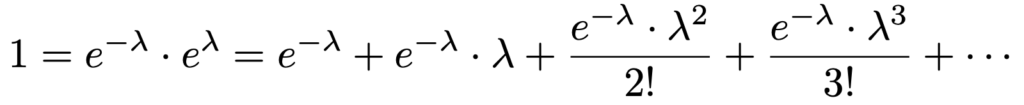
この式の最右辺は,ポアソン分布の確率関数に,x=0,1,2,3,…をそれぞれ代入して得られる確率の和になっています。つまり,ポアソン分布のすべての確率の和が1であることを示せたことになります。
これで,ポアソン分布が確率分布であることがわかりました。ポアソン分布の確率関数は複雑ですが,すぐ上の式をイメージすると簡単に思い出すことができますので,すべての確率の和が1であることを導く練習をしてみてください。
では,このセクションの最後として,ポアソン分布のグラフを確認しておきましょう。
平均2のポアソン分布のx=0〜10の確率をグラフに表すと,次の図のようになります。
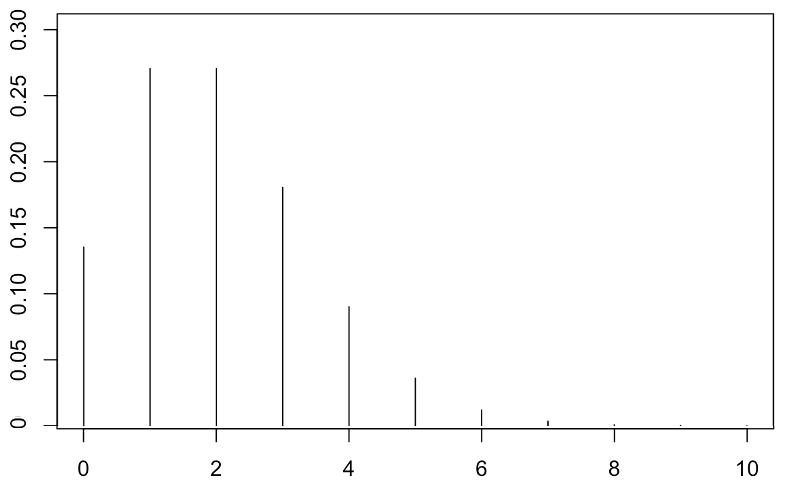
x=1,2で確率は最大になっていますね。また,x=8以上の確率が小さすぎて,ほとんど見えませんが,xがどれだけ大きくなっても確率は0にはなりません。
同じように,平均5のポアソン分布のx=0〜10の確率をグラフに表すと,次の図のようになります。
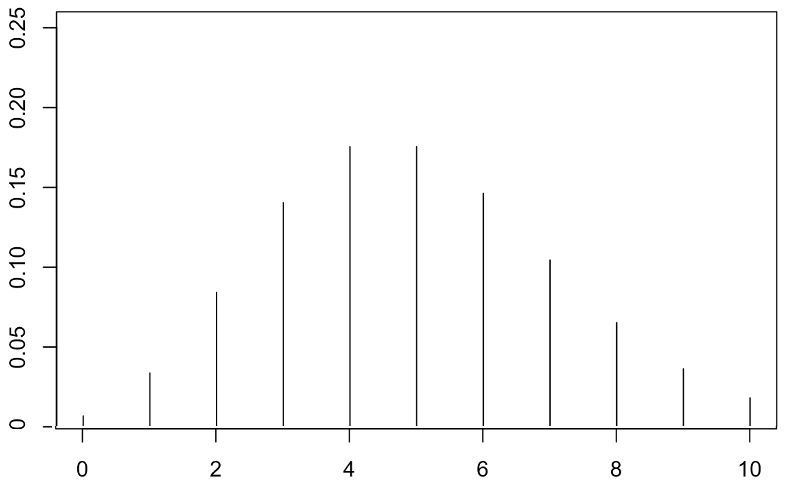
こちらは,x=4,5で確率が最大になっていますね。
さらに極端に平均を大きくして,平均30のポアソン分布のグラフを確認してみましょう。
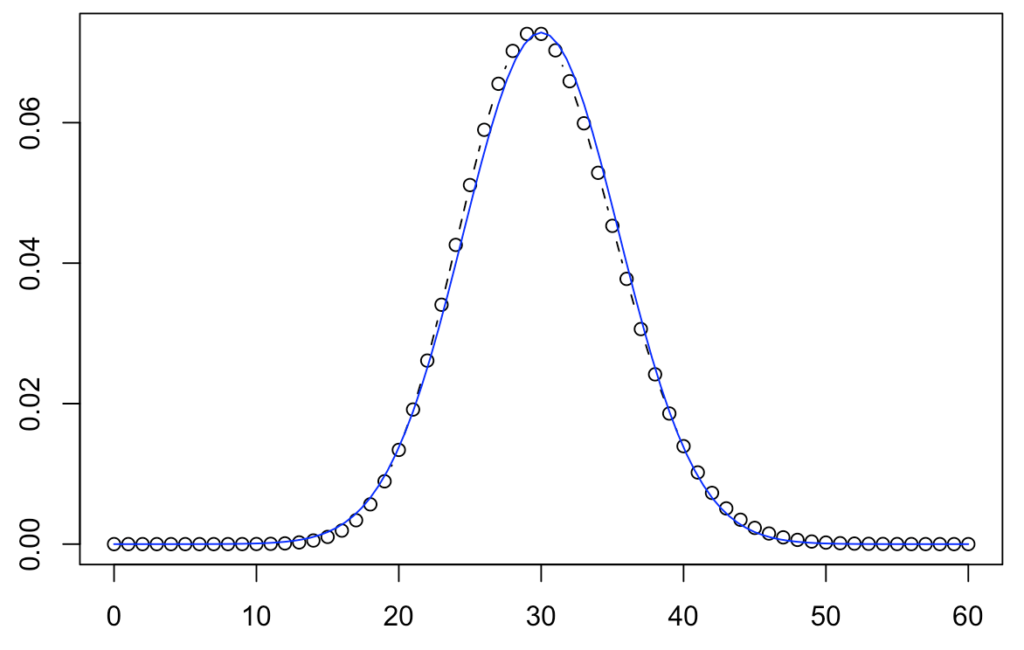
上の図で,丸印はλ=30のポアソン分布の確率,青い曲線はμ=30,σ2=30の正規分布の確率密度関数を表しています。λがこれくらい大きいときには,正規分布とほぼ一致することがわかると思います。
二項分布はnが十分に大きいときには正規分布で近似できるという性質がありましたが,ポアソン分布もパラメーターのλが大きいときには正規分布で近似することができます。
ポアソン分布を正規分布で近似することを利用する問題は,統計検定2級で出題されたことがあります。このタイプの問題を,下の演習2に入れておきましたので,そちらも確認してみてください。
ポアソン分布の期待値,分散,再生性
期待値と分散
ポアソン分布の大きな特徴の1つは期待値と分散が等しいことです。
もとをたどると,二項分布B(n,p)において,np=λとおいたわけですよね。この二項分布の分散はnp(1ーp)で,pが非常に小さい場合を考えるので,1ーp≒1とすれば,期待値と分散はともにnp=λになります。だから「期待値と分散が等しい」として済ませてしまっても良いのですが,念のため,ポアソン分布の確率関数を使って,期待値と分散がともにλになることを定義から求めておきましょう。
以下では,Xを平均λのポアソン分布に従う確率変数とします。
まず,期待値を定義通りに計算すると,次のようになります。
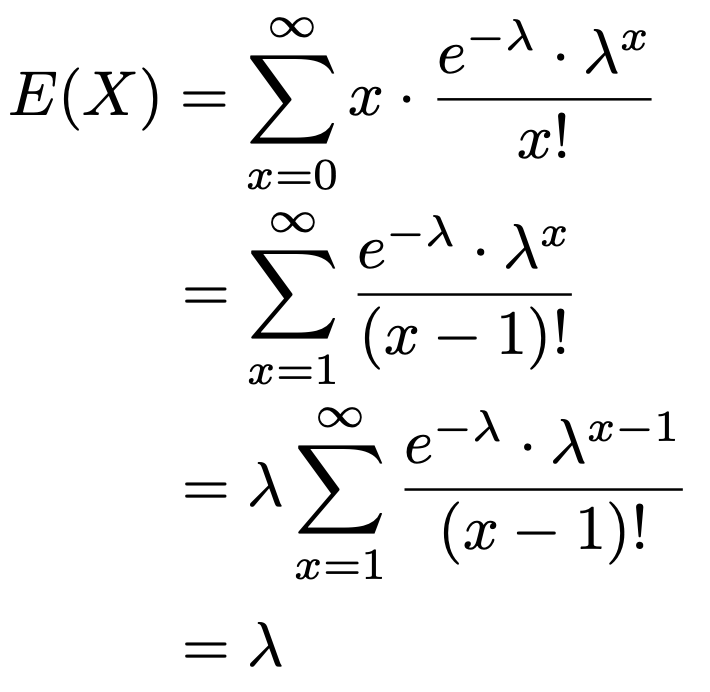
次に,分散はいつものように次の公式を利用します。
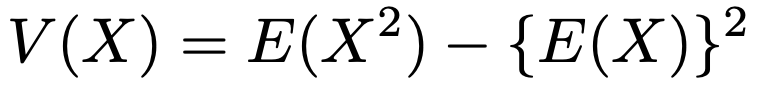
ここで,もうひと工夫します。次のように変形しておくと,階乗の計算と相性が良くなります。
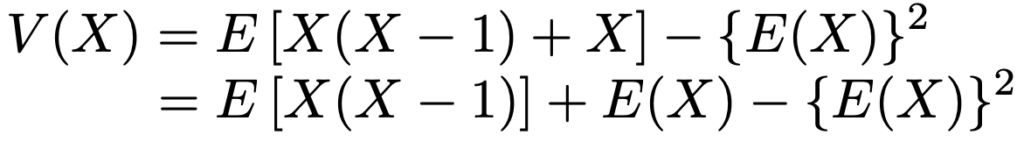
E(X)は求めてあるので,E[X(Xー1)]を計算すればいいですね。定義通りに計算すると,次のようになります。
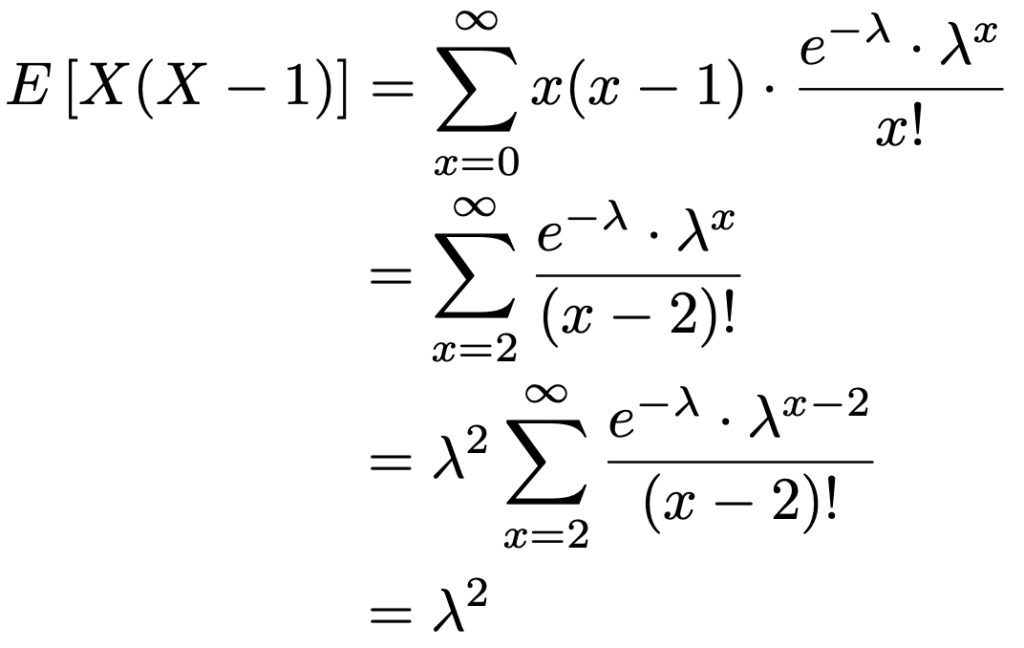
よって,分散は次のように計算できます。
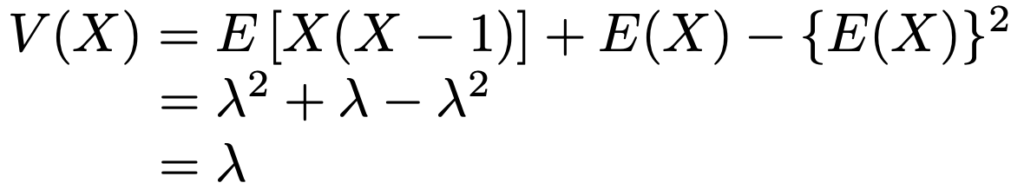
再生性
正規分布は再生性と呼ばれる性質を持っていましたが,ポアソン分布にも同様の性質があります。それが次の定理です。
XとYが次のようにそれぞれポアソン分布に従う確率変数で独立であるとする。
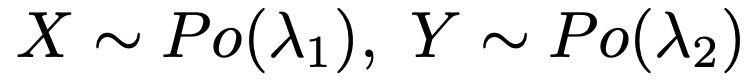
このとき,X+Yは次のポアソン分布に従う。

この性質は準1級で出題されたことがありますので,結果は覚えておきましょう。念のため,証明をしておきますが,興味のない人は読み飛ばしてもらって大丈夫です。
まず,X+Y=nとなる場合は,「X=0,Y=n」の場合から「X=n,Y=0」の場合までのn+1通りありますので,次の式が成り立ちます。
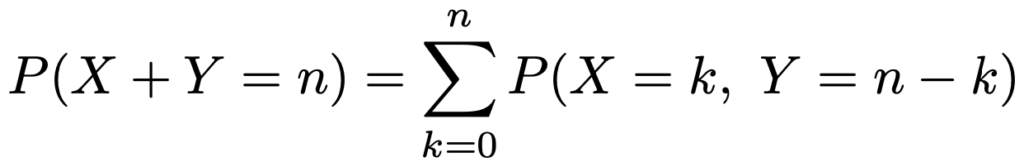
そして,XとYが独立ならば,次の式の左辺の確率は,右辺のような積に書き直すことができます。
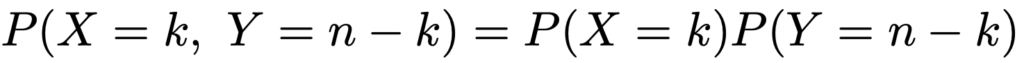
これらのことを使うと,次のようにX+Yが期待値λ1+λ2のポアソン分布に従うことが示せます。
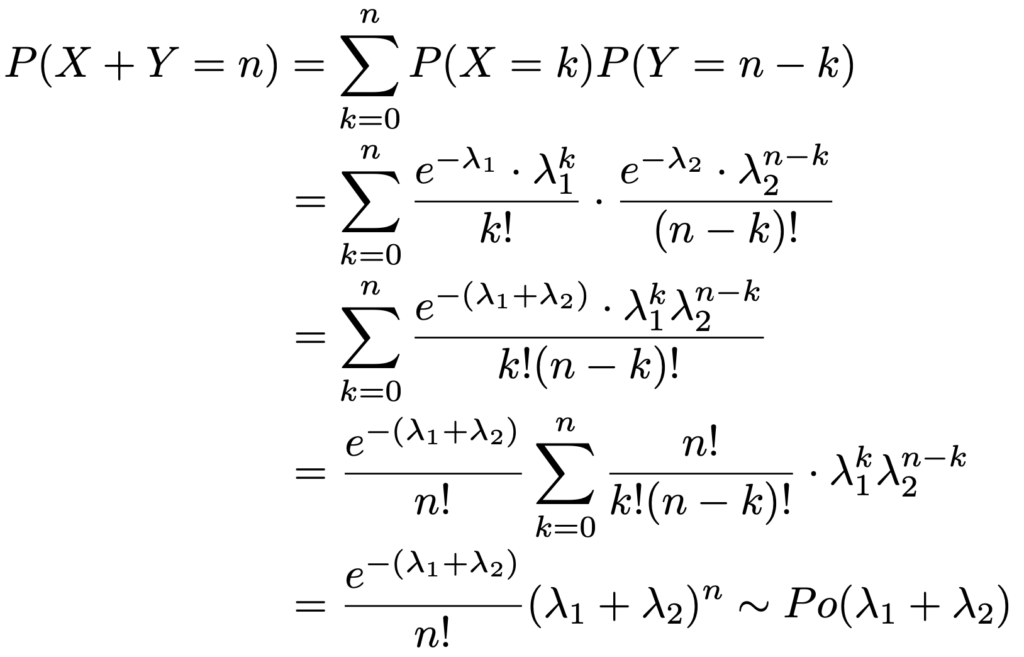
下から2行目から最後の行への変形では,次の二項定理を使っています。
nを自然数として,次の式が成り立つ。
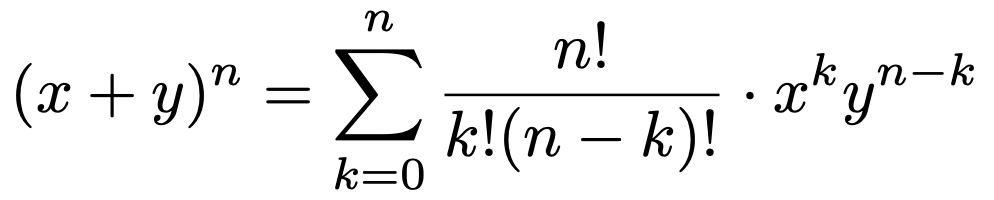
二項定理は,左辺の展開公式です。n=2の場合は,中学で学習する次の式です。
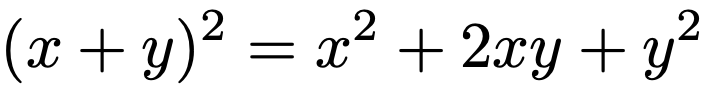
また,n=3の場合は,高校で学習する次の式です。
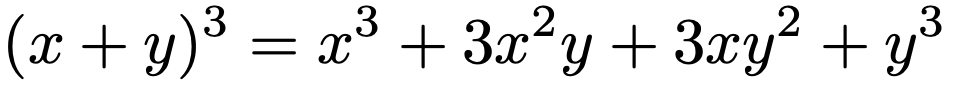
これらを一般化したものが上の二項定理です。
展開された式の係数を取り出すと,n=2なら「1,2,1」,n=3なら「1,3,3,1」となっていますね。これらは次の図のように表すことができて,これをパスカルの三角形と言います。
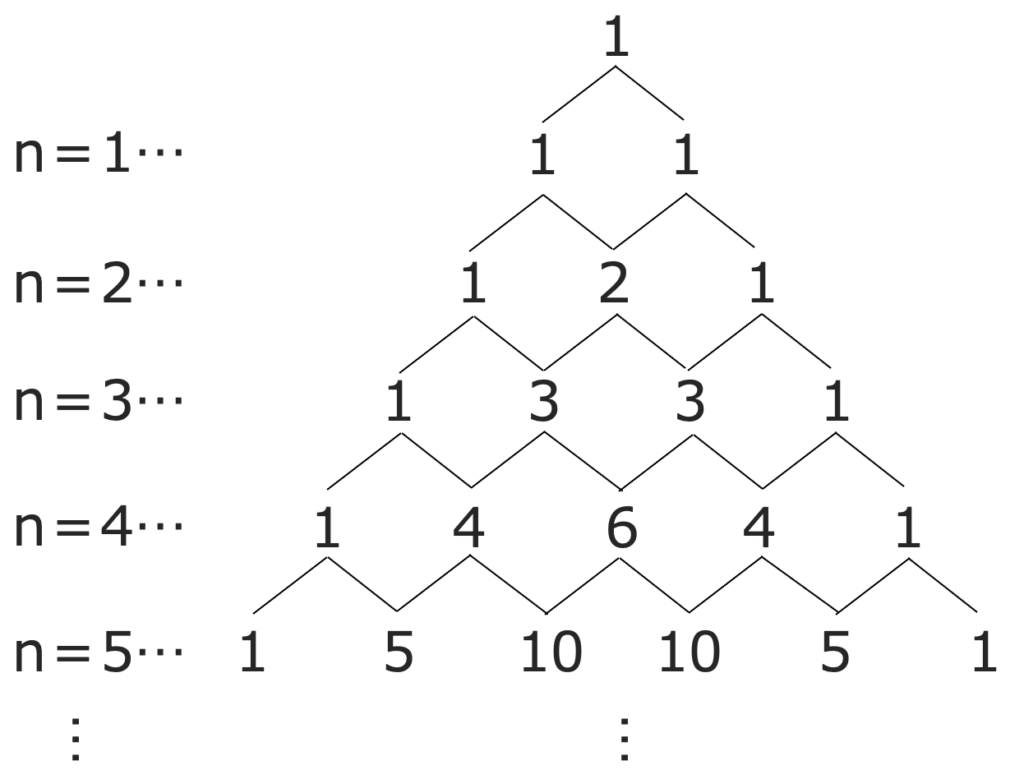
この図では,上から順にとなり合う数を加えることで線分で結ばれた真下の数が求められる仕組み(ただし,各段の両端は1)になっています。この係数は,二項定理の式のように階乗で表すことができて,例えば,n=4ならば次のようになります。
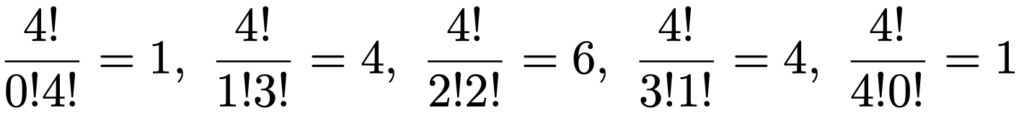
二項定理はいろいろな場面で役に立ちますので,知らなかった人は覚えておきましょう。
ポアソン分布についての基本的な説明は以上になります。この後は,さらに理解を深めるための演習問題と参考図書の紹介です。
演習1 売り切れの確率
【問題】ある店に訪れる客の商品Aに対する需要は,1日に平均3.2(個)のポアソン分布に従うものとする。ある日の閉店時までに商品Aが品切れで買えない客が発生する確率を5%未満にするためには,開店時に商品Aを何個用意しておけばよいか。ただし,必要に応じて次の近似値を用いなさい。
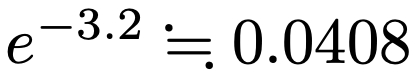
【解答】平均3.2のポアソン分布の確率関数は次の式になりますね。
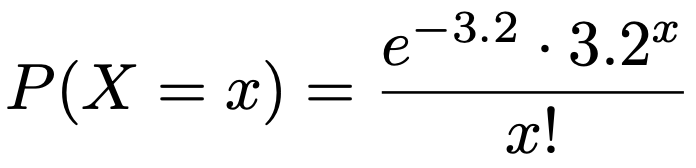
1日の商品Aに対する需要が0個となる確率を求めるには,上の式にx=0を代入すればいいですね。問題で与えられた近似値を使うと,次のようになります。
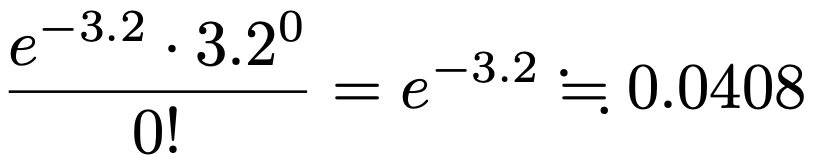
同じように,1日の商品Aに対する需要が1個の確率を求めてみると,上の確率関数にx=1を代入して,次のようになります。
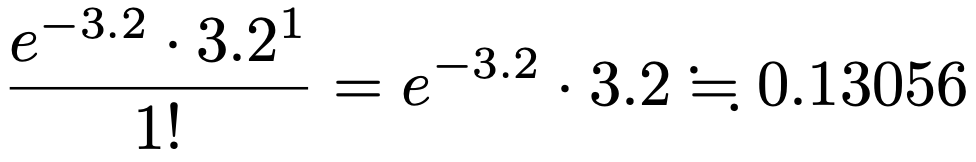
このような確率をまだまだ計算する必要があるので,もう少し計算の効率を上げてみましょう。x=2となる確率は,次のようにx=1となる確率に3.2をかけて2でわったものです。

よって,x=2となる確率は,0.13056×3.2÷2≒0.208896
同じように,x=3となる確率は,0.208896×3.2÷3≒0.222822,x=4となる確率は,0.222822×3.2÷4≒0.178258,x=5となる確率は,0.178258×3.2÷5≒0.114085,x=6となる確率は,0.114085×3.2÷6≒0.060845となるので,これらの確率を四捨五入して小数第4位までにして表にまとめると,次のようになります。

表では,1日の商品Aに対する需要をXとしています。
x=0〜5の確率の合計は約0.896だから,需要が5個以下である確率は約90%です。また,x=0〜6の確率の合計は約0.956だから,需要が6個以下である確率は95%を超えます。よって,開店時に用意した商品Aの個数が5個ならば,閉店時までに商品Aが品切れで買えない客が発生する確率は約10%,開店時に用意した商品Aの個数が6個ならば,閉店時までに商品Aが品切れで買えない客が発生する確率は5%未満となることから,求める答えは6個です。
(解答終わり)
演習2 ポアソン分布の正規近似
【問題】平日の13時に開店するケーキ屋があり,ケーキを買いにきた客は開店前から列をつくる。平日の12時から13時の間に新しく列に並ぶ客の数は平均25人のポアソン分布に従うものとする。ある平日の12時の時点でこのケーキ屋の列に並んでいる客の数が15人のとき,開店時に並んでいる客の数が50人以上となる確率を求めなさい。ただし,平均λが20以上のポアソン分布は,正規分布で近似して良いものとし,必要ならば,次の正規分布表を用いなさい。
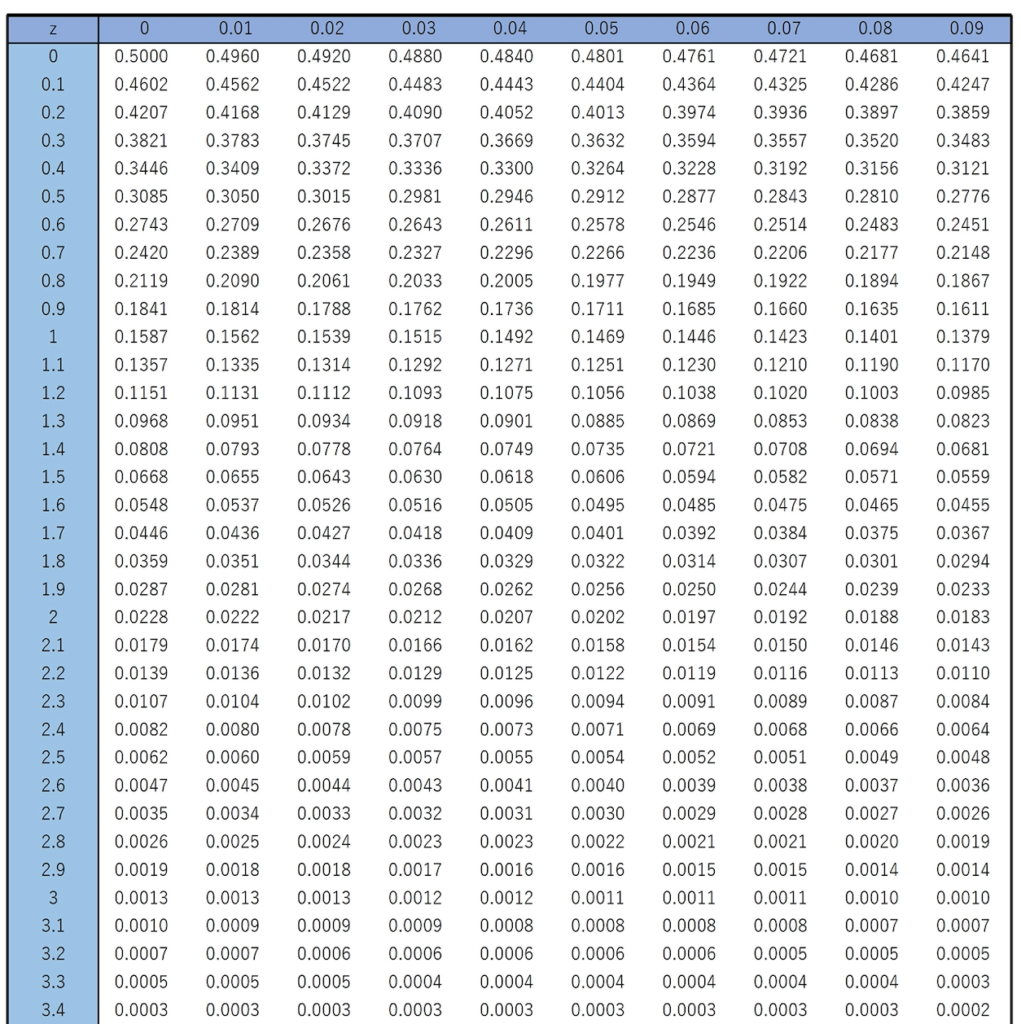
【解答】ポアソン分布の期待値と分散は等しいので,平均25人のポアソン分布に従う確率変数の分散は25です。これは平均が20以上のポアソン分布だから,この確率変数は期待値25,分散25の正規分布に近似的に従うものと考えます。
12時の時点で列に並んでいる客の数が15人で,13時の時点で列に並んでいる客の数が50人以上となるには,この1時間で35人以上の客が新しく列に並ぶことになります。12時から13時の間に新しく列に並ぶ客の数をXとすると,求める確率は次の式のようになります。
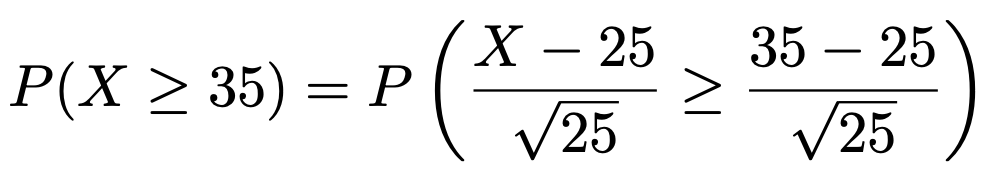
Xが近似的に期待値25,分散25の正規分布に従うことから,上の式の右辺のかっこ内に登場する次の確率変数は標準正規分布に従うことに注意しましょう。
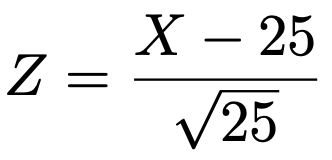
よって,求める確率は次のようになります。
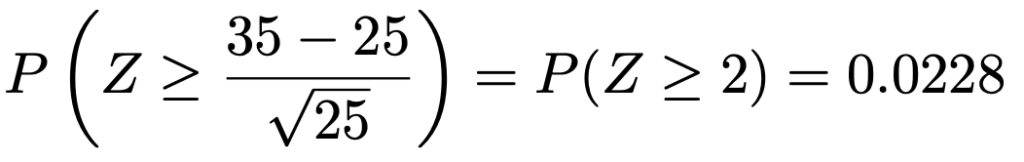
(解答終わり)
参考図書
本稿を執筆するにあたり,次の書籍を参考にしました。
①これからはじめる統計学(蓑谷千凰彦,東京図書)
本書では,ポアソン分布がよくあてはまる5つの具体例が紹介されています。また,コラムも充実しており,シメオン・D・ポアソンという数学者の略歴についても説明されています。
②確率・統計解析の基礎(久保木久孝著,朝倉書店)
時間的(あるいは,空間的)にまばらにしか起きないような事象について,ポアソン分布とみなすことができるかを判断するための3つの条件(独立性,定常性,希少性)が記載されています。
③数理統計学の基礎(尾畑伸明著,共立出版)
本書は,再生性の証明などについて参考にさせてもらいました。
本稿は以上となります。最後までお付き合いいただき,ありがとうございました!







コメント