重回帰分析【中学の数学からはじめる統計検定２級講座第18回】

「重回帰分析が苦手」という人は多いですが，統計検定２級で必要な範囲内に限れば決して難しいものではないので，要点をしぼってわかりやすく解説していきます。この記事を読んで，２級のヤマ場である重回帰分析を乗り越えてしまいましょう！
なお，重回帰分析を理解するためには，第17回の記事で扱った単回帰分析の理解が前提になりますので，不安がある人は先にそちらの記事を読んでください。
では，はじめていきましょう！

重回帰分析
演習１〜重回帰式による推計〜
演習２〜ダミー変数〜

重回帰分析

重回帰分析とは，説明変数が２つ以上の回帰分析ですから，重回帰モデルは次のような式で表されることになります。

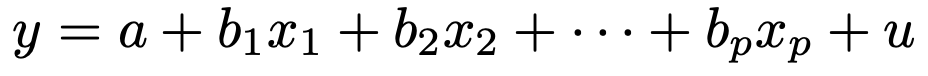
単回帰モデルと同じように，誤差項uは期待値０の正規分布に従うものとし，すべてのu_iは独立で分散が同じ値であること（等分散性）を仮定し，説明変数x₁，x₂，…，x_pは確率変数ではないと考えます。

また，重回帰モデルにおける回帰係数（偏回帰係数と呼ばれることもあります）は，単回帰モデルと同じように最小２乗法を使って推定しますが，今回はその詳細には立ち入りません。

大事なのは，回帰係数が意味するところを正しく理解することです。それは，回帰係数が「他の説明変数が一定である条件のもとで，１つの説明変数が１単位増えたときにyがどれくらい増えるか」を表しているという点です。このことを，次の具体的な問題を通して確認してみましょう。

【問題】ある県での農作物Aの収穫量を説明するため，10年分のデータをもとに重回帰モデルを用いて推計を行った。被説明変数は農作物Aの収穫量（単位：t），説明変数はその年の６〜９月の平均降水量（単位：mm）と平均気温（単位：℃）である。この重回帰モデルを最小二乗法で推定したところ，次の表のようになった。

平均降水量が一定の場合，平均気温が１℃上昇すると農作物Aの収穫量は平均して何t増加すると推定できるか。なお，出力結果の一部を加工している。

【解答】一般的に，２つの説明変数を使った重回帰モデルは次のように表せます。

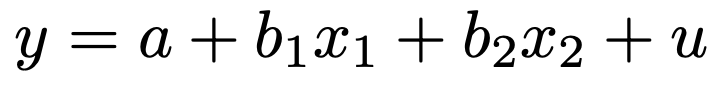
ここで，yは農作物Aの収穫量（単位：t），x₁は６〜９月の平均降水量（単位：mm），x₂は６〜９月の平均気温（単位：℃）を表していると考えることにしましょう。このとき，問題の表から回帰係数を読み取ると，推定された回帰式は次のようになります。

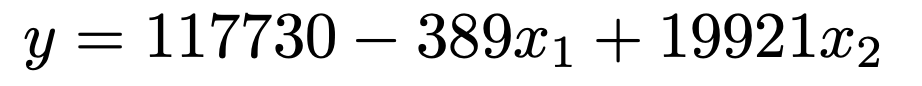
回帰係数は，他の説明変数が一定である条件のもとで，１つの説明変数が１単位増えたときにyがどれくらい増えるかを表すんでしたね。

上の回帰式から，平均気温が一定であるという条件のもとで，平均降水量が１mm増えると農作物Aの収穫量は平均して389t減少し，平均降水量が一定であるという条件のもとで，平均気温が１℃上昇すると農作物Aの収穫量は平均して19921t増加すると推定できます。

ちなみに，この問題に解答するだけならば，問題の表のx₂の係数が19921であることを確認すればいいだけです。

（解答終わり）

回帰係数のt検定

単回帰分析と同じように，各回帰係数が０になる確率が十分に低いことを示すために，帰無仮説をb_i＝０，対立仮説をb_i≠０（i＝１，２，…，p）とする両側検定を行います。

このときの検定量は，単回帰分析と同じように，（回帰係数の推定量ー０）÷標準誤差という形であり，自由度nーpー１のt分布に従います。単回帰分析では，この自由度はnー２でしたよね。それは説明変数が１個（p＝１）だからです。

上の問題では，「10年分のデータを用いて」とあるので，標本の大きさはn＝10です。説明変数が２個なので，t分布の自由度は，10ー２ー１＝７となります。この自由度は，（標本の大きさ）ー（定数項を含む推定するパラメータの数）と考えると覚えやすいです。

上の問題のx₂を例にとると，最小２乗法で推定した回帰係数が19921で，標準誤差が5956と読み取れます。t値は回帰係数の値が標準誤差の約3.34倍であることを示しています。つまり，回帰係数の値が期待値から標準偏差の3個分以上ずれてはじめて値が０になるわけです。t分布表で自由度７の上側2.5％点が2.365であることから，有意水準５％で有意だということになります。

統計検定２級では，上の問題のように表でP値が与えられるので，その数を見るだけでx₁，x₂の回帰係数が有意であるかどうかを確認できます。

回帰係数のF検定

統計検定２級での主たる出題は回帰係数のt検定ですが，選択肢の中でF検定が問われることがありますので，簡単に紹介しておきます。

回帰係数のF検定の帰無仮説は「すべての説明変数の係数の値が０」，対立仮説は「少なくとも１つの説明変数の係数が０でない」となります。説明変数の係数がすべて０だと，説明変数の中に被説明変数を説明できているものが１つもないことになるので，もはやその回帰モデルは全く役に立たないことになります。そこで，分析を進めるにあたり，少なくともこのF検定で帰無仮説が棄却されることが前提となります。

第16回で解説した分散分析でもF検定を行い，水準間平均平方を残差平均平方でわったものが検定量でしたね。回帰係数のF検定もこれと同様の式をつくりますが，詳細は統計検定２級では不要なので省略します。

なお，F検定の自由度については，下の演習２で補足しています。

ダミー変数

上の問題では，収穫量，降水量，気温という数値で表せる変数を扱いました。こういうものを量的変数と言います。一方で，数値では表せないものを扱う変数を質的変数と言います。

回帰分析では，説明変数として質的変数を扱うことができます。例えば，上の問題で，農作物Aを育てるのに使う肥料Bがあったとします。このとき「肥料Bを使ったかどうか」によって収穫量がどれくらい変わるかを調べたいとしたら，「肥料Bを使った」場合には１，「肥料Bを使わなかった」場合には０という値をとる第３の独立変数x₃を追加すればいいわけです。

このように，質的変数を０と１の２つの値をとる変数として回帰モデルの説明変数にしたものをダミー変数と言います。

多重共線性

重回帰分析を行う前には，それぞれの説明変数と被説明変数との相関を調べたり，単回帰分析をしたりして，被説明変数を説明できる変数を見つけ出します。しかし，被説明変数を説明できる変数を片っ端から重回帰モデルに入れてしまうのは逆効果になる場合があります。もし，説明変数どうしの相関が高い場合には，回帰係数のバラツキが大きくなってしまい，重回帰モデルの安定性が損なわれるなどの問題が起きてしまうのです。これを多重共線性と言います。

個別に単回帰分析をすると有意な説明変数であっても，相関が高い場合にはどれか１つに絞ることが有効です。

自由度調整済み決定係数

第17回の単回帰分析の記事では，回帰直線のデータへのあてはまりの良さを示す決定係数を紹介しました。

重回帰分析においても，決定係数を考えることができるのですが，注意点があります。実は，被説明変数を説明できない説明変数であっても，説明変数の数を増やすだけで決定係数は大きくなってしまうのです。これでは，データへのあてはまりの良さを数値化するためのせっかくの決定係数が台なしですよね。

そこで，その分の調整を加えたものが自由度調整済み決定係数で，次のような式で表されます。

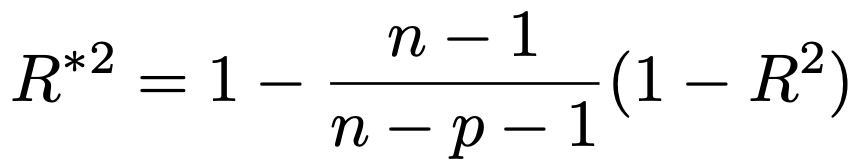
統計検定２級ではこの式は覚えなくていいですが，この式を使って自由度調整済み決定係数が決定係数以下の値をとることを示すと，次のようになります。

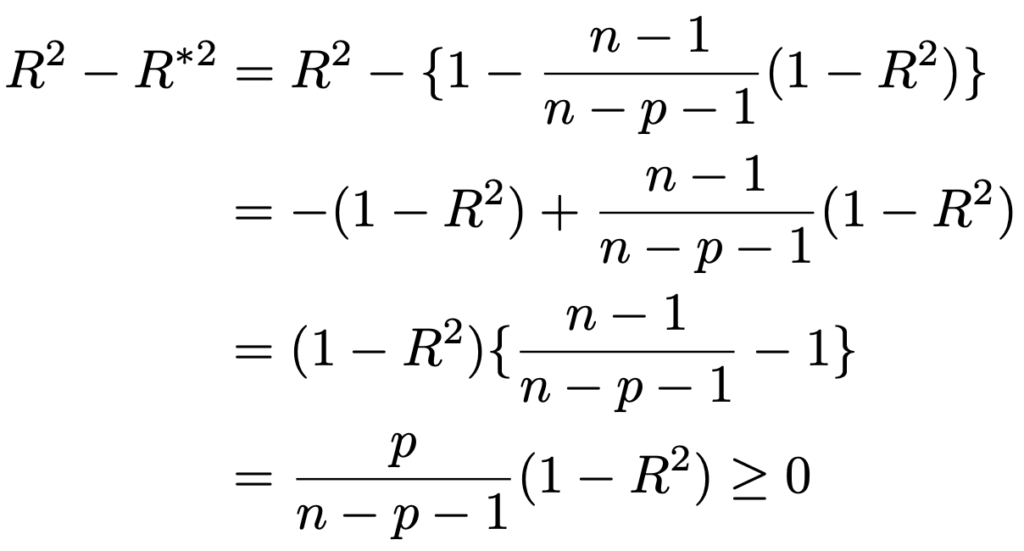
この結果から，R²＝１の場合を除けば，単回帰モデルでも重回帰モデルでも自由度調整済み決定係数の値は決定係数の値より小さいことがわかりますね。
自由度調整済み決定係数は説明変数の数が増えたことによる決定係数の値の増加を調整したものなので，データへのあてはまりの良いモデルを選択するときには，決定係数ではなく自由度調整済み決定係数をもとに判断します。

外挿

データが得られた範囲の外側でも回帰式が成り立つと仮定して被説明変数を予測することを外挿と言います。

例えば，上の問題で使った平均気温のデータの範囲は，実は21〜24℃なのですが，この範囲外の気温に対しても上の問題で推定した回帰係数が適切かどうかの保証は全くありません。平均気温の回帰係数は19921と推定しましたが，気温が高すぎたり，低すぎたりすれば，収穫量にマイナスの影響が出てくることが考えられます。それにもかかわらず，上で求めた回帰式に平均気温30℃などをあてはめて計算することは，外挿になるので注意が必要だということなのです。

これは，範囲外でも回帰式が成り立つという別の根拠がない限り正当化されません。あくまで，データの範囲内で使うのが通例で，この使用法のことを内挿と言います。

では，ここまでの内容を踏まえて，実戦的な問題に取り組んでいきましょう。

【問題】ある資格試験の受検者の得点を説明するため，資格試験での受検者の得点yを被説明変数，受検者それぞれの勉強時間x₁と，この資格試験の対策講座を受講した受検者は１，受講していない受検者は０をとる対策講座ダミーx₂を説明変数，互いに独立に正規分布N(０,σ^２)に従う誤差項をuとする次の重回帰モデル

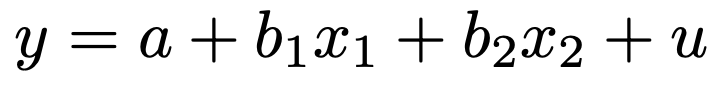
を25人分のデータを用いて最小二乗法で推定したところ，次のような出力結果が得られた。なお，出力結果の一部を加工している。

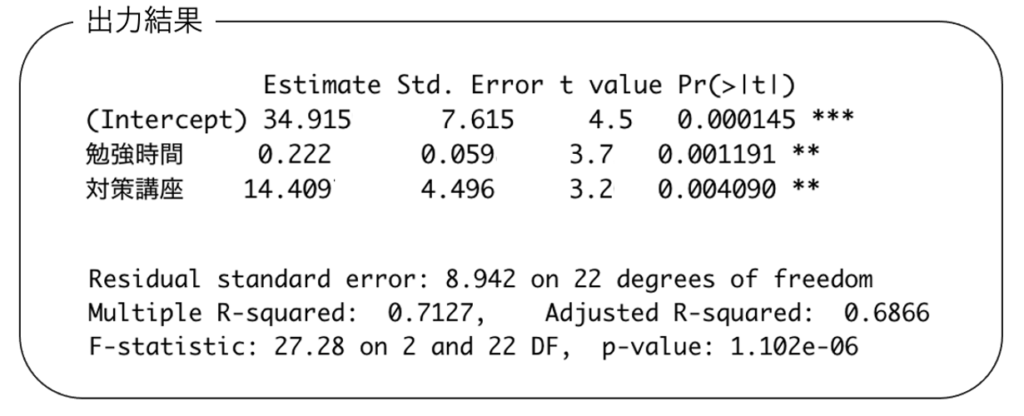
（１）勉強時間が150時間で対策講座を受講した人の資格試験での得点の推計値を，四捨五入して整数で求めなさい。
（２）説明変数にかかるすべての係数は０であるという帰無仮説は有意水準１％で棄却されるか。
（３）b₁の値は0.4であるという主張があったとする。この説を検証するため，帰無仮説b₁＝0.4，対立仮説b₁≠0.4として仮説検定を行うとき，帰無仮説は有意水準５％で棄却されるか。

【解答】統計検定２級の試験では，このような英語表記の（統計ソフトのRによる）出力結果が与えられることが多いです。それぞれの英単語が表していることがらがわかれば，日本語のものと変わりませんので恐れる必要はありません。Estimateは回帰係数の推定値，Std.Errorは標準誤差，t_valueはt値，Pr（p-value）はP値，Interceptは切片，Multiple R-squaredは決定係数，Adjusted R-squaredは自由度調整済み決定係数，F-statisticはF統計量です。

（１）問題の出力結果を読み取ると，回帰式は次のように表せます。

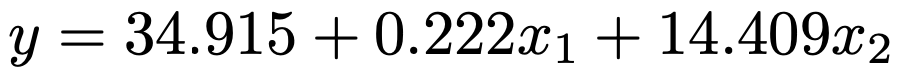
x₁＝150，x₂＝1をそれぞれ代入して計算すると，資格試験での得点の推計値は次のように求められます。

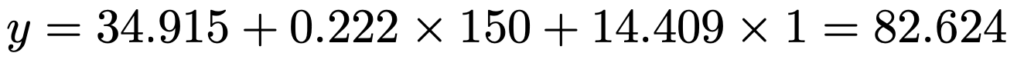
四捨五入して整数で求めると，約83点です。

（２）F-statisticの欄を見ると，F値が27.28という大きな値をとっていて，F(2，22)の上側１％点を十分に超えています。

そもそも，P値が「1.102e-06」という0.01よりもずっと小さい値をとっているので，有意水準１％でF検定の帰無仮説は棄却されます。

（３）対立仮説が「≠」なので，両側検定です。

帰無仮説を仮定し，「（回帰係数の推定量ー回帰係数の真の値）÷標準誤差」にあてはめると，検定量の値は次のように計算できます。

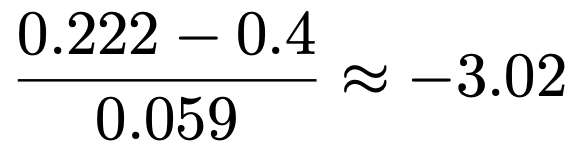
検定量は自由度nーpー１＝25ー2ー1＝22のt分布に従います。t分布表を見ると，自由度22のt分布の上側2.5％点は2.074です。

ー2.074＞ー3.02より，ー3.02という値は棄却域に落ち，帰無仮説は棄却されます。

（解答終わり）

重回帰分析についての基本的な説明は以上になります。ここからは，さらに理解を深めるための演習問題ですので，余力があればぜひチャレンジしてみてください。

演習１〜重回帰式による推計〜

【問題】あるプロサッカーリーグの次年度の各チームのホームゲームの平均観客動員数を説明するため，重回帰モデルを用いて推計を行った。次年度の平均観客動員数y（単位：人）を被説明変数，主力選手の前年の年俸の総額x₁（単位：億円）と，各チームのホームスタジアムの収容人数x₂（単位：万人）を説明変数，互いに独立に正規分布N(０,σ^２)に従う誤差項をuとする次の重回帰モデル

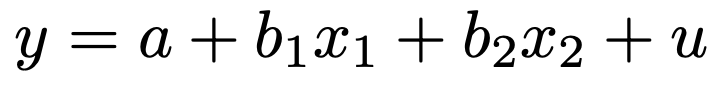
を最小二乗法で推定したところ，次の表のようになった。なお，出力結果の一部を加工している。

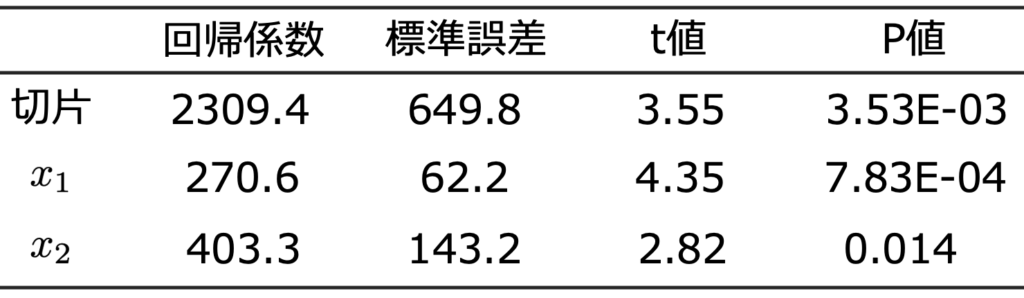
主力選手の前年の年俸の総額が30億円，ホームスタジアムの収容人数が５万人のチームの次年度の平均観客動員数を，四捨五入して整数で推計しなさい。

【解答】問題の表から回帰係数を読み取ると，推定された回帰式は次のようになります。

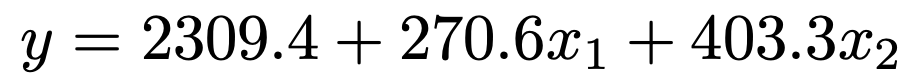
x₁＝30，x₂＝５をそれぞれ代入して計算すると，次年度の平均観客動員数は次のように求められます。

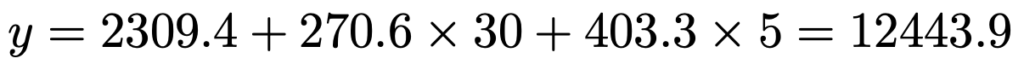
小数第１位を四捨五入して，約12444人となります。

（解答終わり）

演習２〜ダミー変数〜

【問題】ある商業施設では，３社の通信事業者A，B，Cのwifiが無料で提供されている。スマホ１台あたり，いずれか１種類のwifiと接続し，下りの通信速度と通信事業者の関係を調べたい。B社ダミーを，B社なら１，それ以外なら０をとる変数とする。同様に，C社ダミーを，C社なら１，それ以外なら０をとる変数とする。下りの通信速度（単位：Mbps）yを被説明変数，B社ダミーx₁，C社ダミーx₂を説明変数，互いに独立に正規分布N(０,σ^２)に従う誤差項をuとする次の重回帰モデル

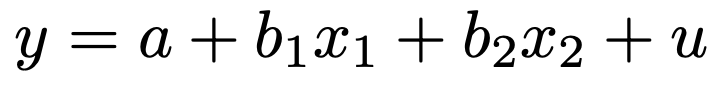
をスマホ30台分のデータを用いて最小二乗法で推定したところ，次のような出力結果が得られた。

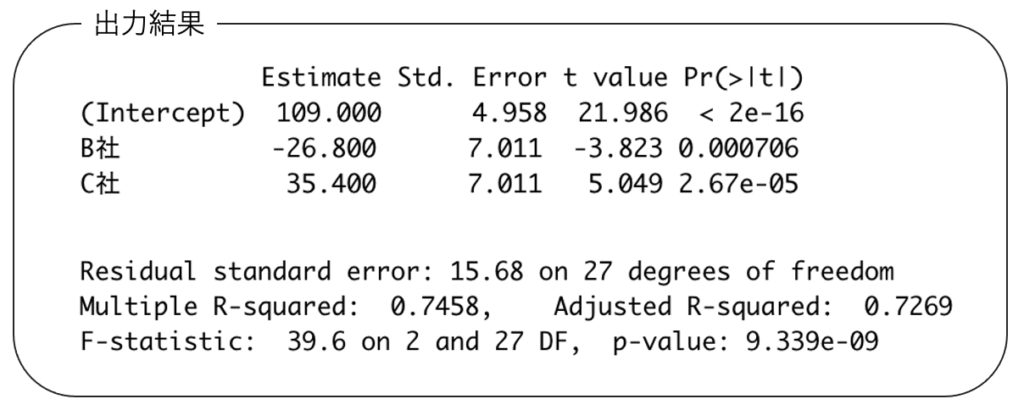
（１）P値はt分布を用いて計算されている。このt分布の自由度を求めなさい。

（２）C社のwifiはB社のwifiと比べて，下りの通信速度は平均的に何Mbps速い傾向があるか。

【解答】

（１）標本の大きさが30，説明変数の数が２なので，回帰係数の検定量は自由度nーpー１＝30ー2ー1＝27のt分布に従います。
なお，F-statisticの欄を見ると，すぐにこの自由度がわかります。回帰係数のF検定における第１自由度は帰無仮説で「＝０」と仮定した係数の数，第２自由度はt分布の自由度と同じで，（標本の大きさ）ー（定数項を含む推定するパラメータの数）です。

（２）問題の出力結果から回帰係数を読み取ると，推定された回帰式は次のようになります。

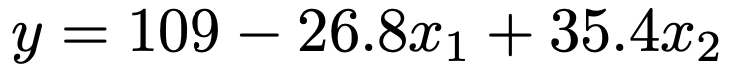
x₁とx₂がともに０のときはB社でもC社でもないので，A社のwifiの下りの通信速度になります。それが定数項の109です。

x₁＝１，x₂＝０のときがB社のwifiを使っている状態で，下りの通信速度は，109ー26.8＝82.2（Mbps）

x₁＝０，x₂＝１のときがC社のwifiを使っている状態で，下りの通信速度は，109＋35.4＝144.4（Mbps）

よって，C社のwifiはB社のwifiと比べて，下りの通信速度は平均的に，144.4ー82.2＝62.2（Mbps）速い傾向があります。

（解答終わり）

第18回は以上となります。最後までお付き合いいただき，ありがとうございました！
第１〜18回の記事でカバーできていない内容は「統計検定２級チートシート」の記事で扱っていますので，こちらも参考にしてください！

2023年1月に「統計検定２級公式問題集[CBT対応版]（実務教育出版）」が発売されました！（CBTが何かわからない人はこちら）
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが，本書は分野ごとにその形式の問題を並べた構成になっていて，最後に模擬テストがついています。CBT対策の新たな心強い味方ですね！