【統計検定１級・統計応用】人文科学のススメ

統計検定１級は，学部３年次程度の統計学の理解を問う試験です。近年，人工知能の発展とともに，機械学習の基礎理論を与える統計学にも注目が集まっており，１級の受験者も増加傾向にあります。

この記事を読んでくださっている方々は，統計検定２級や準１級のイメージをお持ちだと思いますので，それらの試験と１級の試験の違いを紹介するところからはじめて，人文科学での受験がオススメである理由，私自身の合格体験を踏まえた試験対策などを解説していきます。なお，１級の試験は，午前に実施される「統計数理」と午後に実施される「統計応用」の２種類の試験から成り，両方に合格して，はじめて１級の合格となります。本稿では，統計応用（人文科学）の対策を説明し，統計数理の勉強法については別の記事で紹介します。

統計検定１級とはどんな試験か

１級の試験は，外出自粛により中止された2020年を除き，毎年11月20日頃に大学等の会場で実施される紙ベースの試験（PBT）です。近年，準１級以下の試験は完全にCBTに移行しており，多肢選択式であるために答えがわからなくても正解することができますが，１級では正しい答えを出すか，正しい解法を示せなければ得点できません。つまり，まぐれでは合格できません。

試験会場では，難関大学の理系学部の大学入試っぽい雰囲気を感じました。受験者層（男性が多い）や，試験問題の難易度，試験時間中に鉛筆の動きが止まらない人とほとんど動かない人に２分される雰囲気，そして何より，全問自由に思考過程を記述する形式が難関国立大学の２次試験っぽいです。問題番号すら自分で記入する形式で，問題番号を書き忘れたら，たぶんそのページは０点扱いです。それから，１級の成績優秀者として公表されている人の所属を見ると，「難関大学の理系学部の試験」を突破している人が多いように感じます。そういう人たちとガチの試験をして５人に１人くらいしか受からないのが，統計検定１級です。

では，試験の特性を踏まえて，合否を分けるポイントを説明します。しっかりと対策をして試験に臨むことを大前提として，合格のために重要になるのが時間の使い方です。統計数理，統計応用のどちらにもあてはまりますが，効率よく解かないと時間がたりないです。どちらの試験も５大問の中から３問を選んで解答しますが，時間の効率性の点で，どの３問を選ぶかがめちゃくちゃ大事になります。５大問をすべて解く時間はないので，問題文を読んで最後まで完答できそうな問題を３問選ぶことになります。この最初のステップでしくじると，致命傷になりかねません。

また，だだっ広い解答用紙にどのように解答を記述していくのかによっても，かかる時間が大きく変わります。１級には，「答えを書くように求められる問題」と「言葉や数式で説明するように求められる問題」の２種類がありますが，前者の場合でも，答えだけでなく，途中の過程も書くようにしましょう。なぜなら，前者の場合で答えが合っていない場合に，途中経過を書いておけば部分点をもらえる可能性があるからです（問題冊子の表紙にそのような記載がある）。ただし，丁寧に書きすぎると時間がかかるので，部分点のための途中経過は，思考の流れが採点者に伝わる程度のちょうど良い塩梅を目指します。思いつくままに解答を書いていくのではなく，あらかじめ余白に解いた上で整理した内容を解答用紙に書くようにしましょう。

さらに細かい点を挙げると，記号の使い方を事前に決めておくといいです。期待値・分散をはじめ，設問に解答するには多種多様な記号を用いますが，人によって記号の書き方が異なるものが少なくありません。過去問を解いたときに，よく使う記号をリストアップしておき，試験中にそれらが必要になったらどのように書くか，そして自分で使う記号を採点者にどのように伝えるのかを予め決めておけば，試験中に悩む必要がなくなります。くれぐれも，自分にしかわからないような記号を何の断りもなく使うことのないように注意してください。

ここまで，「効率的に解くべき」という話をしてきましたが，もうひとつの勝負の分かれ目が計算ミスの多寡です。「解けたつもりになっていた問題が実は計算ミスで間違っていた」という経験をしたことはないでしょうか。計算ミスはトレーニングによって減らせます。難関大学に合格する人は，こういう無駄な失点をなくすためにハンパない量のトレーニングを積んでいます。それゆえ，自分の計算が正しいことに自信が持てます。もし，あなたが模範解答を見るまで自分の解答に自信が持てないのだとすれば，「ハンパない量のトレーニング」を積んで，合格者層との実力差をうめる必要があります。

ここまで読んで自信をなくしてしまった人もいるかもしれませんが，これで気落ちするくらいのメンタルでは統計検定１級は勝ち抜けません。「よし，やってやる！」と思える人はぜひチャレンジしてみてください。ちなみに，統計数理は数学的な色彩が強く，統計応用はどちらかと言えば統計学の知識に比重があります。両方合格して１級合格ではありますが，数学に自信がない人は今年は統計応用だけを受けて，来年までに数学を強化して統計数理を受けるといったプランを立てることも可能です。統計応用（数理）に合格した場合には，翌年の統計応用（数理）の受験は免除可能です。

あと，合格最低点は公表されていません。おそらく，試験を実施した後に，得点の分布を見て合格最低点を調整しているものと思われます。なので，「○点以上ならば合格」とは言えませんが，一つの目安として，選んだ３大問は「パーフェクトまたは１ミス」くらいの得点は取れるように準備しておきましょう。

なぜ人文科学か

統計応用は，人文科学，社会科学，理工学，医薬生物学という４つの分野に分かれており，そのうちの（少なくとも）１つに合格する必要があります。統計応用の出題範囲には準１級にはない内容も含まれていますが，ざっくりとしたイメージで言えば，準１級の内容を共通部分のある４つの領域に分割して，それぞれの分野をさらに深く掘り下げた感じです。

どの分野を受験するかは，試験当日ではなく，１級の受験の申込みまでに決める必要があります。さて，どの分野で受験しましょうか。例えば，あなたが製薬会社に勤務していれば「医薬生物学で合格したい」と思うかもしれませんし，その通りに受験すればいいでしょう。でも「特に受けたい分野はない」という人もいるはずです。もし，あなたが「受けたい分野はなく，とにかく１級に合格しさえすればいい」というのなら，私は人文科学をオススメします。

人文科学をオススメする理由は，その過去問が他の選択分野と比べて易しいからです。特に，2019年や2018年は，問１〜問４が非常に易しいため，この２年の人文科学の平均点は，他の選択分野の受験者の平均点と比べて，かなり高かったものと推察されます。2020年に中断をはさんだ後の2021年，2022年はその点が改善され，１つの題材を複数の視点から考えるような工夫された出題が見られ，易しい問題でも文章量を増やすことで，人文科学の問題の難度は底上げされてきています。しかし，それでもまだ，他の選択分野と比べて数学的なハードさがない分，取り組みやすいと言えます。

このように人文科学の過去問が相対的に易しいことは，準１級の知識でも解ける問題が毎年５大問中の３大問くらいあることにも表れています。その中には，２級の知識だけで解ける大問すらあります。そして，準１級の範囲外で人文科学の受験のために学習しなければならない内容も多くなく，深くもありません。だから，仕事をしながらでも１か月で十分に対策することが可能です。

とは言え，難しさの感じ方は個々人によって異なるので，最終的には自分の目で見て判断してください。なお，人文科学系の専攻であるかどうかによる有利不利はほとんどないので，これまで人文科学とは縁のなかった他分野を専攻している人でも選択しやすいです。

出題範囲と過去の出題の分析

人文科学の出題範囲は概ね次のようなものです。

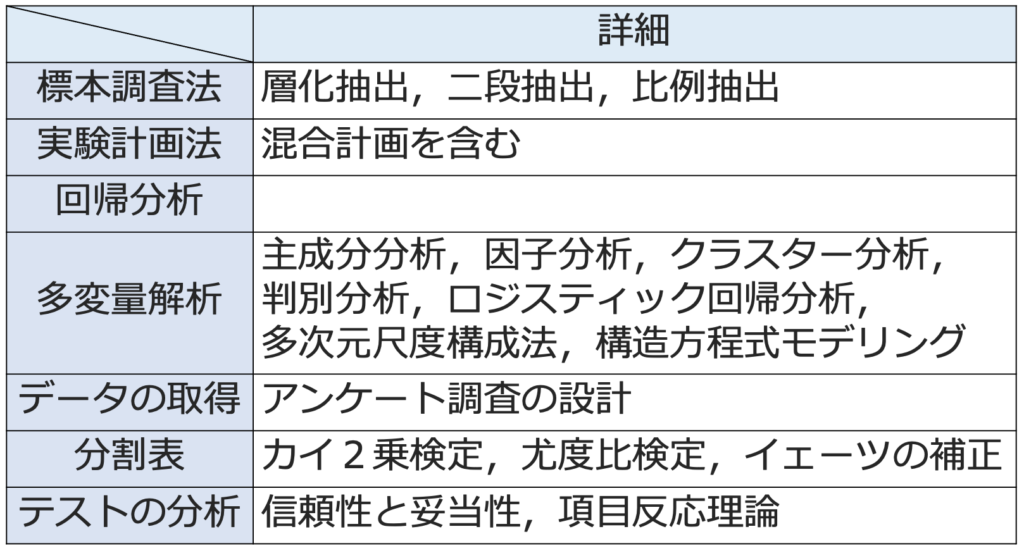
上の表は，統計検定が発表している試験範囲から「実際には過去10年で出題されていないもの」を除いてシンプルにしたものです。表には書かれていませんが，基本的な確率分布はもちろん問われます。準１級の範囲にないものは，確認的因子分析，構造方程式モデリング（パス解析，共分散構造分析），アンケート調査の設計，項目反応理論ですが，標本調査法も準１級のレベルを超える出題が見られるので勉強し直す必要があります。とは言え，多くの内容が準１級範囲と重なっており，重なっていない分野は知識偏重型なので，統計応用の４分野の中では最も取り組みやすいと感じる人が多いはずです。

個々の過去問の評価の前に全体的な講評を述べておきます。2013年は特別に易しい大問も難しい大問もなく，それぞれの大問に統計学の知識を問う要素と数学的な処理能力を問う要素があり，バランスの良い出題でした。2014年以降は大問ごとに難易度が大きくばらつくようになり，易しい大問が極端になりすぎていて，人文科学以外の他の３分野に比べて得点しやすい構成になっていました。すでに述べたように，2020年の中断の後はその点が改善され，大問ごとの難易度の差が小さくなり，かつどの大問も容易には完答できないような工夫された出題になりました。おそらく，この傾向は今年以降も続くことでしょう。

では，過去10年の全問の難易度と講評を紹介します。準１級でどのくらい深く掘り下げて学習したのかは人によって差がありますが，明らかに準１級の出題内容からはずれる問題については，問の番号に赤マーカーをつけています。大問ごとの難易度は★の数による５段階評価で表しており，★が多いほど難しいことを意味します。難易度の評価は10年間で基準をそろえるように努めましたが，主観を排除できないことはご承知おきください。

2022年

【問１】（★★）やや長めの会話文を読んだ上で，その後の問題に答えていく珍しい形式。読まなければいけない文字数が多いので飛ばしたくなる問題だが，実は会話文は読まなくても解けるようになっており，しかも全問が２級レベルの知識で解けるので，ミスなく完答したい。４小問のうちのはじめの３問は平均，分散，相関係数といった統計量に関する基本的なものだが，要注意なのは１問目。勝ったチームの得点の分散と負けたチームの得点の分散から全体の得点の分散を求めるが，この公式を自分でひねり出すには普段からの訓練が必要。４問目は正規分布表を使って確率を求める易問。

【問２】（★★★）母集団がそれぞれ２変量正規分布にしたがう２群の判別の問題。４小問のうちの１問目では，２変量正規分布から導かれる１変量正規分布の期待値と分散を計算し，２問目では，マハラノビス平方距離を計算して判別境界を求める。３問目と４問目は誤判別の確率をテーマとし，２群判別のしきい値を与えて誤判別の確率を求めるのが３問目で，誤判別の確率を最小にするような２群判別のしきい値を求めるのが４問目。準１級の知識があれば特段難しくはないが，４問目を解き切れるかどうかは数学的な基礎力にかかっているように思われる。

【問３】（★★）クラスター分析がテーマである。枝問を含めた５問のうちの１問目から３問目は，最短距離法と最長距離法の基本問題であり，デンドログラムを描き，２つのクラスターに分け，クラスター内変動を問題で与えられた式にしたがって計算する。４問目と５問目はk-means法の問題で，４問目では初期クラスターからクラスターを更新する計算を行う。この際に，クラスター内変動の計算式として問題で与えられている２つの式の関係を理解しているかどうかで計算量が大きく変わってしまうので，注意が必要。５問目のk-means法の記述問題は典型的な内容だが，答えるべき内容が２つあるので漏れのないようにしたい。

【問４】（★★）クロンバックのα係数がテーマであるが，その定義は問題文に与えられており，測定の信頼性と妥当性について記述する１問目を除いて特別な知識は必要ない。２問目は，与えられたクロンバックのα係数の式を平均を使った式に書き直し，それが０や１になるのはどういうときかを答えるもの，３問目は，その式に値を代入して変数の数を求めるもので，いずれも易しく，初見で十分に解ける。最後の２問では，因子分析モデルを仮定し，クロンバックのα係数や因子負荷量を求めるが，準１級相当の因子分析の知識があれば，基本的な計算で楽に得点できる。

【問５】（★★★★）２変量正規分布の条件付き期待値や条件付き分散を中心とした問題。５小問のうちのはじめの２問は公式をあてはめるだけで解ける計算問題に，平均への回帰に関する記述を加えたもの。３問目からはモデルの設定が追加されて難度が上がるが，準１級の勉強をした人ならば，３問目までは完答したいところ。最後の２問はこのモデルと条件付き分布との関係を正しく理解する必要があるため，やや難しい。全体的に計算量の少ない小粒な問題ばかりだが，小問ごとに答えるべき数値が複数あり，最後まで完答するのは骨が折れる。

2021年

【問１】（★★★）枝問を含めた７問のうち，はじめの５問は，アンケート調査と標本抽出についての理解を問う記述問題が並んでおり，得手不得手が分かれやすい。有意抽出，非標本誤差，無回答バイアスなどの用語を説明させるものや，アンケート調査票を見てその問題点を指摘するものなど，難しくはないが慣れていないと答えにくい問題が並ぶ。最後の２問は計算問題で，母比率の信頼区間を求めるものと，適合度検定に関するものである。これらも難しくはないが，間違いやすいポイントはあるので，注意深く計算したい。

【問２】（★★）２×２の分割表をテーマとした問題で，４小問のうちのはじめの３問では，ファイ係数とカイ２乗統計量をひたすら計算する。１問目は定義通りに計算するだけで易しいが，２問目と３問目では最大値と最小値をそれぞれ求めるため，整理してケアレスミスを防止することが大切。また，４問目は超幾何分布を利用して確率と期待値を計算する。３問目と４問目は，列和と行和を固定した設定で，考えられる分割表が３通りしかないので難しくはない。

【問３】（★★★★）２因子の因子分析モデルに関する問題で，最終小問にだけ主成分分析が関わる。与えられた因子負荷量行列から相関行列を求める１問目では，４次正方行列を計算しなければならないが，難しくはない。しかし，２問目はこの４次正方行列の固有値を求めるものであり，線形代数の知識の有無によって明暗が分かれる。３問目は，与えられた因子負荷量行列を単純構造に近づける回転行列を求める問題で，同種の問題の経験があれば解けるだろう。最後の４問目では，因子分析としての累積寄与率と主成分分析としての累積寄与率を比較し，それらが異なる理由を答えるものであり，因子分析と主成分分析の類似性と違いについての理解が問われている。全体的に表面上の理解だけでは太刀打ちできない構成であり，特に２問目を迷わずに処理できる線形代数の理解があるかによって差がつく。

【問４】（★★）２要因混合計画に関する問題で，５小問のうちの１問目はこの名称を答えるもの。２問目は分散分析のF値と検定の結果を答えるもので準１級相当の基本問題。３問目は参加者間要因の効果が交互作用に現れることを指摘するもので，４問目ではそれが等分散を仮定した２標本t検定と同等であることを確認する。さらに５問目では，２標本t検定をダミー変数を用いた単回帰分析で表現することが問われている。混合計画の基本をおさえていれば，後は２級〜準１級の知識を組み合わせることで対応できる。

【問５】（★★★）感度と特異度を中心とした問題であるが，用語の定義は問題文に書かれているため，特別な知識は必要ない。５小問のうちのはじめの４問は正規分布とベイズの定理を使って確率を計算するものなので，方針は明確であるが，小問ごとに答えるべき数値が複数あるため，根気よく正確に計算していくことが求められる。５問目は，偽陰性率と偽陽性率のトレードオフに関する記述問題であるが，問題の意図を汲むことができるかどうかが分かれ目になる。

2019年

【問１】（★★）受験者の得点が正規分布にしたがうと仮定し，得点の上位半分が合格するという設定で，正規分布の右半分を考えるよくある問題。４小問のうちのはじめの２問は，正規分布表の読み取りや偏差値の定義がわかればすぐに解けるので，易しい。残りの２問は，切断された正規分布の確率密度関数についての問題で，条件付き期待値・分散の計算にはなるが，変数変換が正しくできればスムーズに解ける標準的なもの。最後の小問の計算量に鑑みて，難易度は「★★」とした。

【問２】（★）クラスター分析の基本的な問題。４小問のうちのはじめの２問は，最短距離法によるデンドログラムの作成とクラスター分けを問うものであり，準１級の勉強をした人ならば簡単に答えられるはず。残りの２問は，k-means法についての問題。サイズ６のデータのうちの２つを初期代表点としたときのクラスターの更新を手計算する３問目も，初期値依存性について記述させる４問目も易しい。

【問３】（★）項目反応理論におけるロジスティックモデルの基本的な問題で，５小問のうちの４問目は項目情報関数，５問目は当て推量パラメータを知っているだけで即答できる。計算が必要な問題もあるが計算量は少なく，１問目は項目反応関数に代入するだけ，３問目は偏微分するだけである。２問目も困難度パラメータの値から答えはすぐにわかるが，その判断理由を説明しようとしたら迷うかもしれない。

【問４】（★）共分散構造分析の基本的な概念がわかっていれば解ける問題。５小問のうちの２問目から４問目は直接効果や間接効果，構造方程式に関するもので，与えられたパス図とパラメータの推定値を使って，それぞれ10秒程度で答えられる。１問目と５問目は，それぞれ標準解と同値モデルについての簡単な記述問題であり，こちらも基本事項を理解していれば迷うことはなく，満点をとりやすい。

【問５】（★★★★）適合度検定の問題であり，枝問まで含めて５問構成。難しくはないが，答えにくい問題が含まれているため，難易度を高めにした。１問目は，与えられた度数について適合度検定統計量を手計算する問題で，２級レベルである。２問目は１問目の設定を引き継いでいることが問題に示されていないので，迷うかもしれない（問題の不備）。３問目は適合度検定統計量が近似的にカイ２乗分布にしたがう理由を述べる問題で，どこまで説明すべきか悩ましい。最後の２問は，ラグランジュの未定乗数法を使って最尤推定値を求めるもので，素直に計算すれば解けるものの，５問目の答え方には迷う余地がある。

2018年

【問１】（★）２×２の分割表をテーマとする基本的な出題。問われているのは，超幾何分布，オッズ比，ファイ係数，イェーツの補正，フィッシャーの正確検定などであり，何のひねりもないので，準１級の知識があれば，苦労せずに満点がとれる。逆に言うと，これらの知識に穴がある場合には避けなければならない問題である。５小問だが，１小問の中で答えるべきものが２つ以上あったりするので，解答漏れに注意したい。

【問２】（★★）２群の線形判別をテーマとする出題で，４小問のうちのはじめの３問は易しい。１問目では分散共分散行列から相関係数を答え，２問目ではユークリッド平方距離から判別境界線を求める。３問目では，マハラノビス距離を用いた判別を問われているが，判別境界線は問題で与えられているので，計算する必要はない。２問目と３問目は記述を伴うが，マハラノビス距離などの基本事項が理解できていれば迷うことはない。一方で，４問目は誤判別率に関する記述問題で，難しくはないものの，どのように解答すべきか悩むかもしれない。

【問３】（★★★）パス解析の基本的な問題。５小問のうちの１問目はパス図を解釈するもの，２問目は擬相関を指摘するものであり，知識があれば易しい。３問目から４問目では，構造方程式をつくり，その両辺に変数をかけて期待値を計算する典型的な流れであり，解き慣れていれば迷う余地はない。５問目では，パス係数が１つ与えられているので，それをもとにすべてのパス係数が求めやすくなっていて，前問ができていれば難なく総合効果を求められる。しかし，逆に言えば，３問目や４問目でつまずくと，その後の問題は解けなくなるという難しさはある。

【問４】（★★）クラスター分析がテーマであり，５小問のうちのはじめの２問は，最短距離法とデンドログラムに関する基本的な問題。残りの３問は，最短距離法とウォード法を比較しながら論述させる問題。いずれも準１級のレベルを超える内容ではないが，ワークブックでは鎖効果に言及されていないため，他の書籍で勉強したことがなければ，答えられないかもしれない。記述が３問あるものの，計算する要素が全くなく，記述を苦にしない人ならば楽に完答できる。

【問５】（★★★★★）２つの正規分布の混合分布の確率密度関数のグラフがふた山になるための条件を考える問題。４小問のうちの１問目は，混合分布の期待値と分散を確率密度関数を使って計算するもので，方針は明確だが，１問目にしては計算が多め。２問目は，平均と分散の異なる２つのグループを合併したときの平均と分散を計算するもので，特に分散の計算は勘違いしやすいので注意が必要。３問目は，混合分布の確率密度関数を２回微分するだけなので，これも方針は明確だが計算量が多い。４問目はふた山になるための条件を式で表すもので，３問目で２階の導関数を求めさせている意図を読み取ることができれば，解答を簡単にまとめることができる。全体的に計算量が多く，完答のハードルは高い。

2017年

【問１】（★）因子分析の基本的な問題。５小問のうちの１問目は，バリマックス回転後の因子負荷量とプロマックス回転後の因子負荷量を見分けるもので，５秒程度で判断でき，２問目は１秒で即答できる。３問目と４問目は因子間の相関を考慮に入れた因子負荷量の計算をともなうが，せいぜい２次方程式くらいなので，５分もかからない。５問目は因子軸の回転を論じる標準的な記述問題。準１級のワークブックではプロマックス回転に触れられていないため，他の書籍で因子分析を勉強したことのない人だと対応できないだろうが，難易度としては準１級レベルを超えるものではなく，容易に完答できる。

【問２】（★）一元配置分散分析の基本的な問題で，５小問のうちのはじめの４問は２級の知識だけで解けるし，５問目も２級の知識を応用すれば解ける。４問目までは，与えられた記号を用いて，平方和の分解や検定統計量を式で表し，自由度や対立仮説，検定の有意性，確率分布を答えるもので，失点したくない基本問題である。５問目は，３群のうちの２つの群の母平均が等しいという帰無仮説の場合の母平均の検定を問うもので，経験がないと戸惑うかもしれないが，特別な知識はなくとも解ける。

【問３】（★★）２回のテストの得点が２変量正規分布にしたがうという設定のよくある問題。５小問のうちのはじめの２問は，２変量正規分布の条件付き期待値，分散および確率を求めるもので，公式を運用することで解くことができる。３問目は，切断された正規分布の期待値を積分によって求めるもので，これも準１級の過去問に類題がある。しかも，４問目は，３問目ができると即座に解答できる易問なので，ここまでは計算ミスに気をつけて確実に得点したい。５問目は，期待値を比べて論述する問題で，難しいわけではないが，問われていることを適切に捉えて解答する必要がある。

【問４】（★★★★★）問題で与えられた復元単純無作為抽出の場合の母集団総計の推定量とその分散を使って，母平均の推定量を考えていく４小問の構成。１問目は与えられた分散を用いて標本平均の分散を表すもの，２問目は層化抽出法のときの標本平均の不偏性を示し，その分散を１問目と同様に表すもの。問題で与えられた推定量と結びつけるように式を変形していくが，慣れていないと難しいだろう。３問目は，１問目と２問目の結果を比較するものだが，平方和の分解を用いて層化抽出法のメリットを示すという方向を見出し，説明を完遂するのはやや難しい。４問目は，ここまでの結果を踏まえて２つの標本抽出案を比べるものであり，２問目までができていれば分散の比較を行うのは易しいが，それ以外に何を記述すべきかは悩ましい。全体的に途中でつまずくと後の設問にひびく構成であり，全問正解の難易度は高い。

【問５】（★★★）二項分布や正規分布を用いて，確率，期待値，分散，信頼区間などを求める問題で，２級の知識だけで解ける。５小問のうちのはじめの２問は，２つのグループに学生を割り付ける２種類の方法について，それぞれ確率，期待値，分散を求めるもの。１問目は二項分布なので公式によって簡単に解けるが，２問目は地道に確率を計算する必要があり，確率をミスすれば期待値も分散も答えが合わなくなってしまうので気をつけたい。これらの具体的な計算を踏まえ，３問目では，２種類の方法の期待値，分散の大小関係を一般的に考察・記述するもので，特に分散の大小関係をどう説明するのかは悩ましい。４問目と５問目は一転して信頼区間に関するもので，母集団が正規分布にしたがう場合の母平均の信頼区間の幅の求め方や，二項分布の正規近似など，基本的な知識と若干の計算力があれば解ける。

2016年

【問１】（★）因子間の相関を考慮に入れて，変数どうしの相関や独自性などを計算する問題。ワークブックに沿って因子分析の勉強をした人は，プロマックス回転を学習していない可能性が高いが，共分散の項を０にせずに計算することさえできれば全体的に易しい。４小問のうちのはじめの３問は，10秒前後で解答できる。また，４問目の直交回転と斜交回転の違いも，模範解答を見る限り，ごく簡単なことが書けていれば良さそうなので，１〜２分もあれば完答できる。

【問２】（★★）試験の得点を題材とする正規分布絡みの問題。３小問のうちの１問目の数値を答える部分は，コースごとの平均から全体の平均を求める小学生でも解ける内容だが，それを用いて記述する部分では，２年間の比較でコースごとの平均はどちらも上がっているのに，全体の平均は下がっていることについての論述であり，差がつきやすい。２問目は２級レベルの正規分布表の読み取りで易しい。３問目は，500点以上の得点の平均と500点未満の得点の平均をそれぞれ求める問題で，切断された正規分布の期待値の計算である。準１級の知識で十分に解け，計算量も多くはないが，標準正規分布を利用して手際よく処理できることが大切。

【問３】（★★★★★）地域のM校の中から学校を抽出し，選ばれた学校で生徒を抽出する二段抽出をテーマとする問題。４小問のうちの１問目は地域の生徒から１人を選ぶときの期待値，分散を求めるもの，２問目は地域の学校が１校だけのときの期待値，分散を求めるもので，どちらの問題も同様の考え方で解けるが，統計モデルの仕組みを理解することが難しい。３問目は，単純無作為抽出の場合と二段抽出の場合の期待値と分散を，前問までの結果を用いて比べるもので，その結果を踏まえて，４問目では両者の精度の違いやコストの違いを論じる。本問は１問目から難度が高く，前問の出来が次の問題に影響し続けるため，完答するのはハードルが高い。

【問４】（★★）確認的因子分析に関する問題で，計算はほとんど必要ない。５小問のうちのはじめの３問は，順に，モデルの母数，自由度，測定方程式を答えるものだが，基本的な知識があれば即答できる。４問目は分散共分散行列の空欄をうめるもので，分散と共分散の計算方法がわかっていれば１分程度で答えられるでしょう。５問目は，モデルの自由度と識別性に関する記述問題で，モデルの自由度の計算原理がわかっていないと答えられないため，差がつきやすい。

【問５】（★★★★）２群の母平均の推定と検定に関する問題。３小問のうちの１問目は，１群の母平均の信頼区間をt分布を使って求めるもので，２問目は，等分散を仮定したときの２群の母平均の差の検定と，母平均の差の信頼区間を求めるものであり，ここまでは２級の知識で完答できる。３問目は，各群の母平均の信頼区間の重なり具合と，母平均の差の検定の有意性の関係を数式で説明する問題であり，これも２級の知識で解けるものの，完答するには数学力を要する。

2015年

【問１】（★★★）項目反応理論における１母数のプロビットモデルとロジスティックモデルをテーマとする問題。両モデルを使って尤度関数をつくり，能力母数θの最尤推定値を数式と数値で表すのが５小問のうちのはじめの３問であり，基本的だが標準正規分布の累積分布関数の微分で戸惑うことのないようにしたい。４問目と５問目は，母数θの最尤推定値が正答数の関数になることを一般的に式で表し，その意味を述べるもので，項目ごとの正解・不正解を表す文字x_jを自分でおいて尤度関数をつくれるかどうかで結果がわかれるだろう。

【問２】（★★★）４小問のうちの１問目は主成分分析に関する問題で，２問目以降は因子分析に関する問題である。全体的に教科書に書いてあるような内容を記述させるものであり，計算力はほとんど必要ない。１問目は主成分分析はどんな関数の最大化に基づくものであるかを答えるもの，２問目は直交モデルの因子分析の仮定を述べるもの，そして４問目は独自因子の分散が意味することを説明するものであり，両分野を普通に勉強してきた人ならば迷わずに答えられるだろう。３問目は因子分析のパラメータの次元を答えるもので，直交回転による不定性を考慮する必要があるため，知識として知っていないと難しく，点差がつきやすい。

【問３】（★★★★）多次元尺度構成法に関する問題。４小問のうちの１問目は対象間のユークリッド距離を式で表すもの，４問目は解の直交回転による不定性に関するもので易しい。２問目は距離の２乗を成分とする行列の二重対角化の結果が座標行列Xとその転置行列の積に一致することを示すもの，３問目は解Xの具体的な形を示すもので，多次元尺度構成法の理論の数式を追うだけでなく，自分で再構成した経験がないと太刀打ちできないだろうが，よく知られた内容を問うているだけとも言える。

【問４】（★★★★）観測変数が正規分布にしたがう場合のベイズ判別に関する問題。１問目で，対数確率比に正規分布の確率密度関数を代入して判別式を求め，２問目では，１問目の結果を踏まえて誤判別の確率を求めるため，１問目を間違えると，２問目も正解できない。３問目と４問目では２変量正規分布を用い，１問目，２問目と同じように，３問目で判別式を構築し，４問目で誤判別の確率を求めるため，３問目を間違えると，４問目も正解できない。このような小問の構成であることと，３問目と４問目でベクトルと行列の計算の習熟度が問われることから，全問正解の難易度は高め。

【問５】（★★）二元配置分散分析がテーマで，５小問のうちの１〜４問目は，分散分析表の空欄をうめ，交互作用効果を説明し，検定統計量がしたがう確率分布を答え，平方和の分解を式で答えるという流れであり，準１級の分散分析の理解を問うのに非常に良い問題。逆に，１級の出題としては易しめであり，５問目で誤差分散の最尤推定値と不偏推定値の関係を答えられるかどうかで差がつくと思われる。

2014年

【問１】（★★★）(X，Y)が２変量正規分布にしたがうときのX+Yの確率分布についての問題。４小問のうちの１問目と２問目は，準１級相当の２変量正規分布の基礎的な知識が必要であり，X+Yが正規分布にしたがうことと，２変量正規分布では無相関と独立が同値であることを使う。３問目と４問目は切断された正規分布の期待値，分散の計算問題。正規分布の上側25％の分散を求めるときの計算量がやや多いので，日頃から訓練しておきたい。

【問２】（★★）10点満点の試験について，得点が上位の群と下位の群に分けてダミー変数を用いた回帰分析を適用する３小問の構成。１問目は妥当性を含めた各小問の特徴を述べるもので，合計点との相関が唯一負になっているNo.10に言及するのは簡単だが，それ以外に何を書くのかは悩ましい。２問目は回帰係数と上位の群および下位の群の平均の関係式を証明するもので，公式の通りに計算すればよいので易しい。３問目は，相関係数と各小問の標準偏差，上位の群の平均，下位の群の平均の間に成り立つ式を自分で見つける必要があるが，相関係数を計算してみれば関係式はすぐに見える。

【問３】（★★）ロジスティック回帰の基本的な問題であり，準１級レベルの知識で概ね対応できる。３小問だが，それぞれ答えるべき事柄が複数あるので，漏れのないように解答したい。１問目は，ロジットモデルをpについて解き，グラフを描いて単回帰モデルとの違いを記述するもので，２問目は，ロジットモデルの係数と対数オッズの関係を問うものである。ここまでは標準的な内容なので得点しやすいが，３問目はモデル選択についての記述問題で，明確な答えがあるタイプではないため，やや書きにくい。AICやP値の数値だけで選ぶわけではなく，変数どうしの相関や変数の意味合いも考慮する必要がある。

【問４】（★）クラスター分析がテーマであり，最短距離法の場合と最長距離法の場合について，デンドログラムを描いていく。３小問のうちの１問目はデンドログラム作成の途中経過（２番目と４番目）を答えるもので，２問目は完成したデンドログラムを描くものであり，どちらも基本的であるがゆえにケアレスミスをしないように注意したい。３問目は２つのデンドログラムを比べて，最短距離法における鎖効果を中心に記述させるものであり，この分野をきちんと勉強したことのある人にとっては易しい。

【問５】（★★★★★）２×２の分割表におけるサンプリングの仕方による確率分布の違いについての問題。４小問のうちの１問目は，独立性の検定の統計量を計算するだけなので易しいが，２問目は行和を固定したときの独立性の検定の解釈を説明する必要があり，しっかりとした理解がないと厳しい。３問目は，３種類のサンプリング計画ごとの確率分布を与えられたパラメータを使って表すもので，テクニカルな式変形と計算量の多さからすれば，初見で解くのは困難だと思われる。４問目は，行和と列和を固定したときの超幾何分布に基づく検定と独立性の検定の関係を述べるもので，やはり経験がないと難しいだろう。

2013年

【問１】（★★★）項目反応理論における３母数のロジスティックモデルがテーマ。４小問のうちの１問目は３つの母数の意味を答える易しい問題で，２問目も期待値と分散の公式を使うだけのシンプルな問題であり，失点しないようにしたい。３問目は対数尤度関数を微分して能力パラメータθについて解くだけであり，４問目も微分を含む計算をしてθが約分できることを示すだけだが，求められている計算を正しく捉え，適切に処理できるかどうかには，数学的な習熟度の差が出るだろう。

【問２】（★★★）３つの科目の得点が３変量正規分布にしたがうという設定の問題。１問目は３科目の平均が55点以上となる確率を求めるもので，多変量正規分布の線形変換によって得られる１次元の変数が正規分布にしたがうという準１級で頻出の内容に関するもの。２問目は，３変量正規分布にしたがう乱数を発生させる方法を問うもので，いくつかの別解が考えられるが，いずれにしても知識として持っていれば解けるし，知らなければその場で考えるのは厳しい。３問目は，母比率に関する標準誤差の問題で，２級の知識があれば解ける。よって，２問目の解答が思いつく人であれば，完答のハードルは低い。

【問３】（★★★）４小問のうちのはじめの２問は主成分分析に関する計算問題で，あとの２問は因子分析に関する記述問題。１問目は【問２】の１問目と同様に，多変量正規分布の線形変換によって得られた１次元の変数が正規分布にしたがうことを利用するもので，この点さえわかれば，計算は易しい。２問目は主成分得点と合計点の相関係数を計算するもので，初見でこれが解けるかどうかが大きな分かれ目になる。主成分負荷量の導出ができるなら，本問も解けるだろう。３問目は因子数の決定方法，４問目はバリマックス回転について基本的なことを記述すればいいので，準１級の勉強をきちんとしていれば対応できる。

【問４】（★★★）正方分割表における対称性の検定の問題で，１問目で無条件での最大対数尤度，２問目で帰無仮説のもとでの最大対数尤度，それらを用いて３問目で尤度比検定統計量を求め，その自由度を答える３小問の構成。多項分布に基づく尤度関数とラグランジュ乗数を組み合わせて最尤推定値を求める流れは頻出だが，本問では添字が３つあり，シグマを使った計算が複雑になるので，間違えないように丁寧に計算したい。

【問５】（★★★）期末試験の点数を中間試験の点数と平常点によって予測する回帰分析の問題で，この重回帰モデルにおける平常点の係数がなぜ負になるのかがテーマになっている。３小問のうちの１問目では，それぞれの説明変数による単回帰式，およびそのときの決定係数を求める。これは単回帰式の公式と決定係数が相関係数の２乗であることがわかっていれば難しくはない。２問目では，単回帰モデルと重回帰モデルを比較するため，単回帰モデルの自由度調整済み決定係数を求めるが，決定係数や自由度調整済み決定係数の式の成り立ちを理解して，正しく計算する必要があり，差がつきやすい。３問目は重回帰モデルの解釈を述べる記述問題で，様々な答え方があり，平常点の係数が負になる仕組みを知識として知っていれば妥当な解答が書けると思われる。

2012年

【問１】（★★）４小問のうちのはじめの２問は，英語の試験の得点を題材とし，ListeningとReadingの得点の和と差について，標準偏差や相関係数を求めるもの。３問目は，２つのグループの得点について，等分散を仮定した２標本t検定を適用するもので，ここまでは２級の知識だけで解ける。４問目はやや異質で，１年間の授業後の生徒の得点の平均の増加が講師の授業の効果であると言えるかについて記述する。この問題には様々な解答が考えられ，因果推論の考え方も必要になるため，解答の作成方針を決めるのは悩ましい。

【問２】（★★）４小問ともにベイズによる２群判別の問題で，やり方を知っていれば難しくはない。正規分布の確率密度関数と事前確率を用いて，一方の群に分類される確率を計算する２問目が典型的であり，１問目はそれを易しくしたもの，３問目は変数の与え方を変えて少し難しくしたものである。４問目は確率密度関数すら使う必要のない易しい問題だが，問題文を正しく理解し，何を求めるのかを間違わないように注意したい。

【共通・問１】（★★★）サンプルサイズ５の２変量データが３組与えられて，それらに対して単回帰分析を適用する問題。５小問のうちの１問目で３組の回帰係数を求め，２問目ではそのうちの１つを散布図に描くもので，ここまでは易しい。３問目で３組の決定係数と残差平方和を求め，それを利用して４問目で回帰係数の推定誤差について論じ，４問目と５問目を通して目的変数の予測精度について答えていく。決定係数，残差平方和，標準誤差は迷うことなく書き下せるように準備しておかなければならない。概ね準１級範囲におさまっているが，５問目の目的変数の条件付き期待値の95％信頼区間だけは範囲外とみなした。

【共通・問２】（★★）ゴール数がポアソン分布にしたがうことを仮定し，そのあてはまり具合を調べていく問題。４小問のうちの１問目はポアソン分布を仮定した理由を記述するもので，様々な答え方があるが，よっぽど的外れでなければ許容されるだろう。２問目は標本平均がポアソン分布のパラメータの点推定値となる根拠を述べるもので，最尤推定値となることを示せば紛れがないだろう。３問目はデータがポアソン分布にしたがうと仮定して適合度検定を行うもので，難しくはないが計算量が多い。４問目はパラメータの95％信頼区間を求めるもので，ワークブックでも扱われている内容なので，準１級の勉強をしてあれば対応できるだろう。

【共通・問３】（★★）与えられた２群のデータに対して，ウィルコクソンの順位和検定を適用することを中心とした問題で，現在の人文科学の試験範囲外だと思われる。５小問のうちの１問目は２標本t検定の仮定と検定結果を述べるもの，２問目は順位和検定の仕組みを説明するもの，３問目は順位和検定のExactな方法を説明するものであり，いずれも２級〜準１級相当の基本的な内容。４問目で帰無仮説のもとでの順位和の期待値を求め，５問目で正規近似に基づくP値を計算し，検定の解釈を述べる。特に難しい要素はないが，５小問のうちの４問が記述を含み，それぞれ正しい理解がなければ得点できないので，基礎力の充実が求められる。

ここまでの10年分を振り返ると，最も出題回数が多いのは，因子分析・構造方程式モデリングであり，過去７年間は毎年何らかの形で出題されています。それに次いで多いのが，クラスター分析と切断された正規分布に関するものです。特定の分野に山を張るのはおすすめしませんが，これらの頻出分野は得点が取りやすいこともあるので，しっかりと練習しておくといいでしょう。

人文科学の試験対策

過去の出題分析で見たように，準１級の知識だけでも対応できる問題がかなり出題されており，準１級の理解（CBTで80点以上）があれば，１級の人文科学の合格までかなり近いところまで来ていると言っていいでしょう。「準１級の勉強をしていない」，または「準１級に合格したけれど，自分で数式を書き下せるほどには理解できていない」という場合には，統計学実践ワークブックの１〜６，９〜12，16〜25，28章を読むか，私が制作した統計検定準１級講座（リンクはこちら）を利用してください。また，人文科学を受験する上で必要な数学的知識も，この講座で前提としている知識と同じと考えてもらっていいです。

そして，言うまでもありませんが，１級の過去問は買いましょう。

統計検定１級公式問題集2019〜2022年（日本統計学会編，実務教育出版）

公式のテキストの増訂版が2023年に発売されました。１級を受験する人はこちらもとりあえず買っておきましょう。

増訂版　統計検定１級対応　統計学（日本統計学会編，東京図書）

本書は，統計数理と統計応用の２部構成になっていて，統計応用は試験に合わせた４分野に分かれています。すべての内容を網羅しているわけではありませんが，統計応用の部分は「クロンバックのα係数って何だっけ？」といったときに辞書的に使ったりするのに適しています。また，統計数理の解説もわかりやすく書かれており，「尤度比検定についてしっかり理解したい」というときにも使えます。他書にはないような例が示されていたりして，参考になります。

標本調査法の理論がよくまとめられているのが次の書籍で，有意抽出法，非標本誤差，無回答などの説明もあります。

概説　標本調査法（土屋隆裕，朝倉書店）

本書は，各抽出法の概念の説明はわかりやすいですが，推定量の期待値，分散の導出過程は十分には示されておらず，他の文献も参考にしながら学習を進めるように意図されて書かれています。それゆえ，はじめて読むとわかりにくいという感想を持つと思います。しかし，逆に言えば，行間を自分で補いながら理解を進めていけば，かなりの力がつくということでもあります。本書と合わせて学ぶのにちょうど良いものとして，統計応用の社会科学の過去問があります。特に，2022年の問１の模範解答などは参考になるはずです。

構造方程式モデリングやその周辺分野は，今後もコンスタントに出題されていくことでしょう。専門書を読むのもいいですが，次の書籍でも十分です。

Rによる多変量解析入門（川端・岩間・鈴木，オーム社）

本書は書名の通り，多変量解析全般を解説したものであり，特定の分野の専門書ではありませんが，確認的因子分析，パス解析，共分散構造分析の要点がよくまとまっており，適度に数式が登場する感じで平易で読みやすいです。書名に「Rによる」とある通り，Rを使いながら学習を進めやすいように作られていますが，Rを使わない人でも各分野の要点を学習する目的で十分に使うことができます。本書を読んで基礎的な知識を得たら，過去問を解いてみてください。

項目反応理論は，過去10年間の人文科学で３回出題されており，得点しやすい問題ばかりでした。これまでと同様の出題であれば，次の書籍で基本的な内容をおさえれば十分です。

項目反応理論[入門編]（豊田秀樹，朝倉書店）

本書は項目反応理論をゆっくりと丁寧に説明した良書で，項目分析を解説した第１章と１〜３母数のロジスティックモデルおよび正規累積モデルを解説している第２章まで読めば人文科学の過去問には対応できます。文章が多めで数式は少なめですが，事前知識として，広義積分とロジスティック回帰くらいを知っておけばスムーズに学習できるでしょう。

ということで，人文科学の対策は，準１級の内容の理論的な理解，過去問，上記の書籍の３本柱になります。人文科学は，統計応用の他分野に比べて，数学にそれほど強くない人でも合格点が取りやすいので，ぜひチャレンジしてみてください！