「仮説検定って何をやっているの?」ってみんな思いますよね。この記事では,母平均を検定する例題を解きながら,その仕組みを具体的にわかりやすく解説していきます。専門用語が多く登場しますが,くり返し学習するなかで慣れていきましょう。
仮説検定を一言で表現すれば,「それが起きたのは偶然か,それとも起こるべくして起きたものなのかを判別する手法」と言えます。有名な統計学者フィッシャーの主著「実験計画法」には,ミルクを入れてから紅茶を入れたミルクティーと,紅茶を入れてからミルクを入れたミルクティーを味だけをもとに見分けることができると主張する婦人が登場します。カップをいくつか用意し,当てることができたカップの数が△杯未満なら偶然の可能性を排除できないが,△杯以上なら偶然とは考えられないという境界線を決める方法を与えてくれるのが仮説検定なんです。
標本平均が従う確率分布を標準化して正規分布表やt分布表を使って結論を出す一連の流れは推定と共通なので,第7回の正規分布,第8回のt分布,第9回の区間推定の内容に不安がある人は,先にそちらの記事を読んでください。では,はじめていきましょう!
仮説検定とは
統計的に検証可能な仮説を設定し,標本を用いてその真偽を確率的に判断する手法のことを,統計的仮説検定または簡単に仮説検定と言います。次の問題をもとにして,仮説検定の考え方を説明していきます。
【問題】ある学校では,昨年まで平日1日あたりの図書室の貸出冊数は72冊だった。今年は新しい生徒会長のもとで読書を推奨する活動を実施したところ,無作為に選んだ平日10日間の図書室の貸出冊数の平均は78冊になった。読書を推奨する活動の効果はあったと言えるか,有意水準5%で検定しなさい。ただし,昨年までの平日1日あたりの図書室の貸出冊数は期待値72冊,標準偏差8冊の正規分布に従うものとする。
昨年まで72冊だったものが,今年になって78冊に増えたのは,取り出した大きさ10の標本がたまたま平均よりも冊数の多い日だったのか,それとも昨年までと比べて本質的に増えている(母平均が増加した)のか,仮説検定を使って統計的な結論を出していきます。そこで,次の2つの仮説を立てます。
仮説1
読書を推奨する活動の効果はなかったが,選んだ10日の貸出冊数がたまたま多かった
仮説2
読書を推奨する活動は効果があった
この場合の仮説検定の目的は,仮説1よりも仮説2のほうが確率的により支持されることを立証することです。仮説1のように,否定したいほうの仮説を帰無仮説,仮説2のように正しいことが期待されるほうの仮説を対立仮説と言います。
ここからの流れは,背理法と似ていますので,先に背理法を復習しておきます。背理法を用いて証明される命題の代表的な例は,「ルート2が無理数である」ことの証明です。統計学の本論から脱線しますが,まずはこの証明を述べてみます。
まず,結論を否定します。つまり,「ルート2が有理数である」と仮定します。有理数というのは,分母と分子がどちらも整数の分数で表せる数のことです。この仮定をおくことで,次のような式をつくることができます。
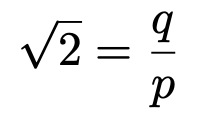
上の式で,pとqは整数で,pは0ではない数です。ルート2が正の数であることを考えれば,pとqは自然数であると言っていいです。背理法というのは,このように証明したいことがらの逆の仮定を設定して式をつくり,その仮定をおいたことで矛盾が起きることを示す論法です。
今の場合も,上の式から矛盾を導くことができます。両辺を2乗して分母を払うと,次のようになります。
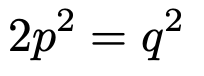
ここで,中学で学習する素因数分解を思い出しましょう。上の式の右辺の自然数も左辺の自然数も素因数分解ができるはずです。そのときに2という素因数に着目します。64=26や100=22×52のように,自然数の2乗を素因数分解すると,各素因数の右肩に乗る指数は偶数になりますが,上の式の右辺のq2を素因数分解すると2の偶数乗が出てきて,左辺の2p2を素因数分解すると2の奇数乗が出てくるので,これは矛盾です。したがって,はじめに「ルート2が有理数である」と仮定したことが誤りだったということになるわけです。これで,ルート2が無理数であることがわかりました。
では,仮説検定の話に戻ります。仮説検定でも,背理法と同じように,正しくないと考えられる仮説(帰無仮説)をはじめに仮定します。そして,その仮定をもとに計算すれば,確率的に極めて起こりにくいことが起きてしまうことを示し,帰無仮説は正しくなく,もう一方の仮説(対立仮説)のほうが正しそうだと言えることになります。背理法の場合には,明確に矛盾が発生するので,仮定は「完全に間違い」と結論づけられるのですが,仮説検定の場合には,「起こりにくいことが起きた」というだけなので,仮説が「完全に間違い」とは言えません。したがって,帰無仮説が疑われるような結果が得られても,帰無仮説が実は正しかったということはありえます。この正しい仮説を誤って否定してしまう確率を危険率と言います。危険率としては,1%や5%がよく使われます。1%や5%の失敗を覚悟して(危険を冒して)確率的に仮説を選ぶのが仮説検定です。
では,上の問題に解答しながら,さらに細かい説明をしていきます。
【解答】帰無仮説を「読書を推奨する活動は効果がなかった」とし,対立仮説を「読書を推奨する活動は効果があった」とします。ここで,危険率を5%に設定します。本当は帰無仮説が正しいのに,対立仮説のほうを正しいと認めてしまう確率が5%です。まず,上の背理法の流れと同じように,正しくないと思われる帰無仮説を仮定します。昨年までの平日1日あたりの図書室の貸出冊数は,次の正規分布に従うことが問題で与えられています。
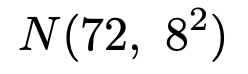
母集団がこの正規分布に従うとき,大きさ10の標本平均は次の正規分布に従います。
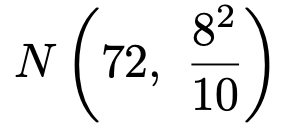
この確率分布を図に表すと次のようになります。
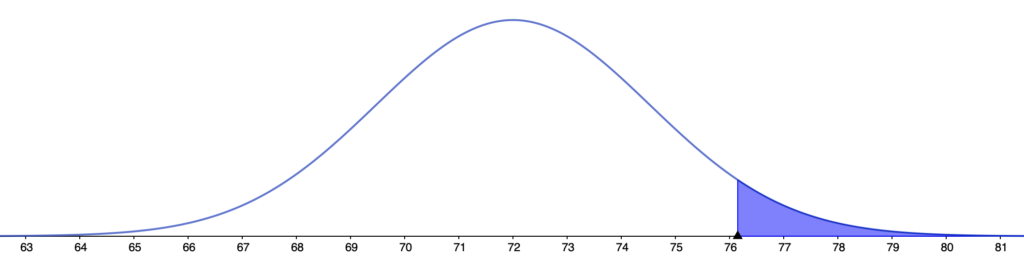
上の図で色のついた部分は,上側確率5%を表しています。標本平均がこの範囲に入る確率は5%しかないので,標本平均がこの範囲に入るならば,帰無仮説が正しくなかったと結論づけることにしようというわけです。
実際に今の標本平均は78であり,この領域に入っていることが図からわかるので,はじめに仮定した帰無仮説が正しくなく,確率分布が変わったんだと考えられます。例えば,母平均が79に変わったとすると,対立仮説の確率分布は次の図のようになります。
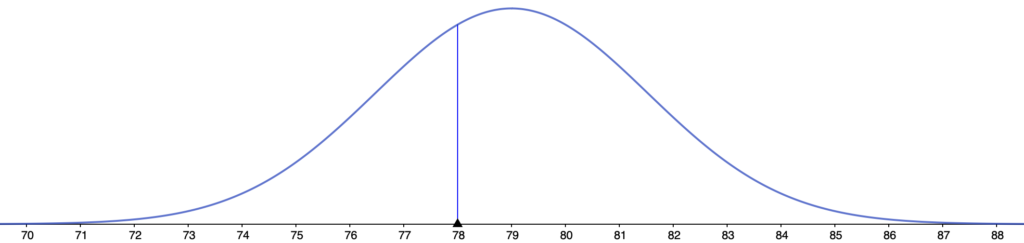
このように母集団の確率分布が変わったのならば,標本平均が78という値をとってもおかしくないわけです。72冊だったものが78冊に増えたのは,標本の取り出し方による偶然ではなく,母集団分布が変わるという「意味のある変化」が起きたからなんだということです。この意味で,2つ上の図で色をつけて表した確率のことを有意水準とも言います。これは,すでに紹介した危険率と同じです。問題で,有意水準5%と言っているのは,正しい帰無仮説を誤って否定してしまう確率(=危険率)を5%にして検定しましょうということです。この場合の78ー72=6という差は,上側5%の部分に入るような確率的に起こりにくいものなので,「意味のある差」ということで有意な差と呼ぶことがあります。
さて,上の図の上側5%にあたる色のついた部分がどのように導かれたのか,という話をしてませんでしたね。実際にどのように計算するのかを知らないと,問題を自分で解くことができませんから,この点を説明しておきましょう。
まず,大きさ10の標本平均Xが従う正規分布の期待値と分散を思い出すと,次の式で定まるZはXを標準化したものになるので,標準正規分布に従います。
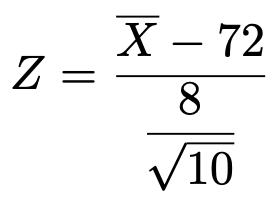
標本平均の実現値を代入すると,次のように計算できます。
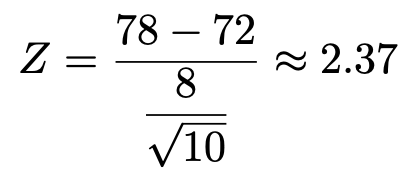
つまり,78という値は,標準正規分布の2.37に対応するわけです。
標準正規分布の上側5%点は約1.64なので,大きさ10の標本平均が78という値をとる確率は5%未満であり,帰無仮説が否定され,対立仮説が肯定されます。よって,読書を推奨する活動の効果はあったという結論になります。
(解答終わり)
上の問題で,最後に計算したZが検定量(検定統計量)です。この問題の場合,検定量の値が1.64を超えれば,帰無仮説が否定されます。この帰無仮説が否定される値の集合を棄却域と言い,帰無仮説を否定することを棄却すると言います。逆に,棄却されない領域(棄却域の補集合)を採択域と言い,帰無仮説が否定されないことを採択する(受容する)と言います。帰無仮説を棄却したときには,同時に対立仮説が採択されます。
上の問題では,棄却域は確率分布の片側だけに設定されましたが,このような検定を片側検定と言います。一方,棄却域を確率分布の両側に設定する両側検定もあり,それについては次のセクションで扱います。
また,仮説検定では,確率的に判断するので,判断を間違える確率が0ではありません。この間違える確率についての用語をまとめておきます。次の図は帰無仮説の確率分布で,棄却域に入る(このことを棄却域に落ちるとも言います)確率を色をつけて表しています。
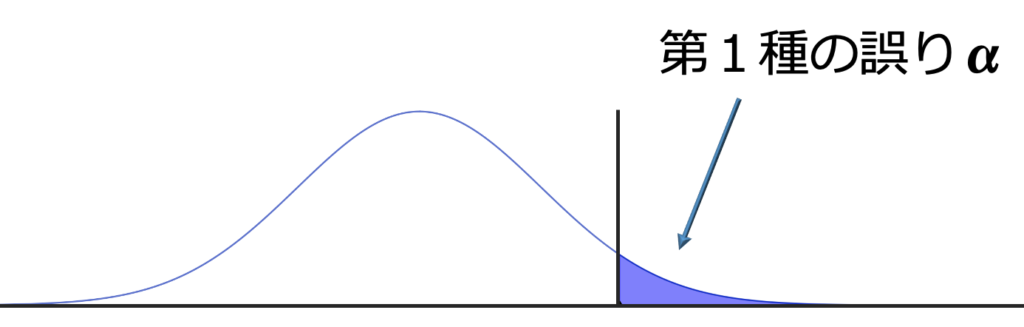
αは危険率であり,上の問題ではα=0.05でした。帰無仮説が正しいとき,正しいはずの帰無仮説を棄却してしまう確率がαなので,αには「帰無仮説が正しいときに対立仮説を採択する誤りを犯す確率」という意味合いがあります。この誤りを第一種の誤り(第一種の過誤)と言います。一方,帰無仮説が正しくないとき,真の確率分布が次の図のように表されるものとしましょう。縦線の位置は上の図と同じだと考えてください。
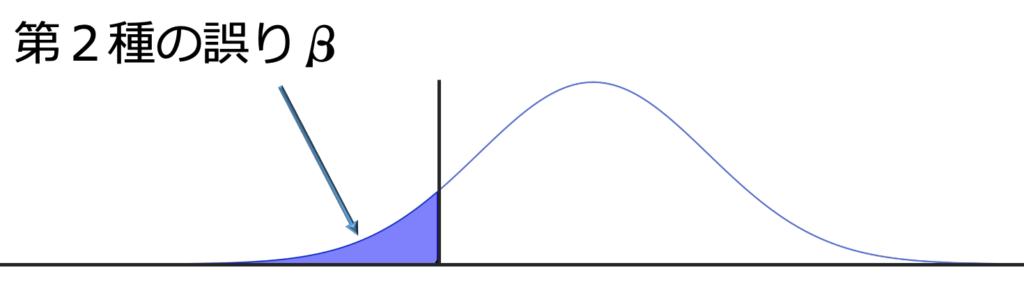
検定量が縦線の右側の値をとれば対立仮説を採択しますが,検定量が縦線の左側の値をとれば正しくないはずの帰無仮説を受容してしまいます。この誤りを第二種の誤り(第二種の過誤)と言い,その確率をβで表します。また,1ーβは「帰無仮説が正しくないときに対立仮説を採択する確率」を表していて,これを検出力と言います。
第一種の誤り(過誤)と第二種の誤り(過誤)を覚えたつもりでも,しばらくすると,どっちがどっちだったか,わからなくなることもあるでしょう。そういうときのために,第一種と第二種を混同しないような覚え方があります。
それは,「あわてんぼうのα,ぼんやりもののβ」という覚え方です。あわてんぼう(awatenbou)とα(alpha)はどちらもaから始まり,ぼんやりもの(bonyarimono)とβ(beta)はどちらもbから始まるのがポイントです。
第一種の誤り(過誤)のどこがあわてんぼうかと言うと,有意な差がないにもかかわらず,有意な差があると早合点して帰無仮説を棄却してしまうからです。また,第二種の誤り(過誤)のどこがぼんやりものかと言うと,有意な差があるにもかかわらず,それを見逃して帰無仮説を受容してしまうからです。よくできた覚え方ですね。
このセクションのまとめとして,改めて仮説検定の手順をまとめると,次のようになります。
- 帰無仮説と対立仮説を設定する
- 有意水準と棄却域を設定する
- 検定量を計算して,棄却域に落ちるかどうかを確認する
母平均の検定(正規母集団で母分散未知の場合)
母集団が期待値μの正規分布に従うとき,第8回で学習したように,標本平均をX,不偏分散の正の平方根をU,標本の大きさをnとすると,次の式で定まるTは自由度n−1のt分布に従います。

母集団分布が正規分布で,母分散がわからないときには,このTが検定量になります。このように,t分布を使う検定をT検定と言います。では,具体的な問題を解いていきましょう。
【問題】ある工場では,内容量20gの袋詰めされたお菓子を作っている。この工場で作られたこのお菓子を無作為に6個抽出し,開封して重さを測ったところ,標本平均と不偏分散は次のようになった。
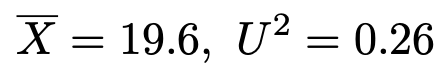
このお菓子の内容量は正規分布に従うものとし,その母平均をμとする。帰無仮説をμ=20,対立仮説をμ≠20,有意水準を5%として,母平均を検定しなさい。
【解答】対立仮説が「μ≠20」のように等号を否定する形で表される場合には両側検定を使います。製品の重さなどのように,それより大きくても小さくてもいけない場合に使われます。有意水準5%で両側検定を行う場合,次の図の両端の色のついていない部分のように,右すその2.5%と左すその2.5%に分け,この領域に検定量の値が入れば帰無仮説を棄却することにします。
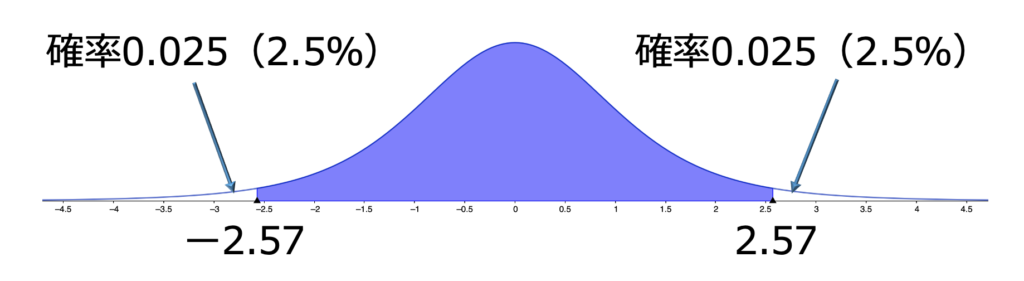
そして,母分散が問題では与えられず,代わりに不偏分散を用いることになるので,上で説明したように,次の式で定まるTが検定量になります。

いま,標本の大きさが6なので,Tは帰無仮説のもとで自由度5のt分布に従います。
帰無仮説は「μ=20」なので,母平均が20gであるとして検定量を計算すると,次のようになります。
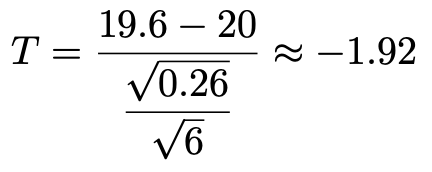
t分布表を調べると,自由度5のt分布の下側2.5%点はー2.57だから,この検定量の値は棄却域には入りません。したがって,帰無仮説は受容されます。
(解答終わり)
ここで,注意してほしいのは,帰無仮説が受容されたからと言って,帰無仮説が正しいことが立証されたわけではないということです。「受容される」というのは,「棄却できるだけの十分な結果は得られなかった」というだけです。
仮説検定についての基本的な説明は以上になります。ここからは,さらに理解を深めるための演習問題ですので,余力があればぜひチャレンジしてみてください。
演習1〜第一種の過誤・第二種の過誤の確率〜
【問題】確率変数Xは,次の正規分布に従うものとする。
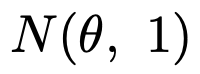
Xについて,帰無仮説をθ=0,対立仮説をθ=2とする仮説検定を考え,Xの観測結果xに対して,棄却域を次の式で定める。
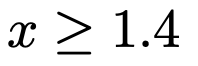
このとき,第一種の過誤の確率および第二種の過誤の確率をそれぞれ求めなさい。なお,必要があれば,上側確率を表した次の正規分布表を使いなさい。
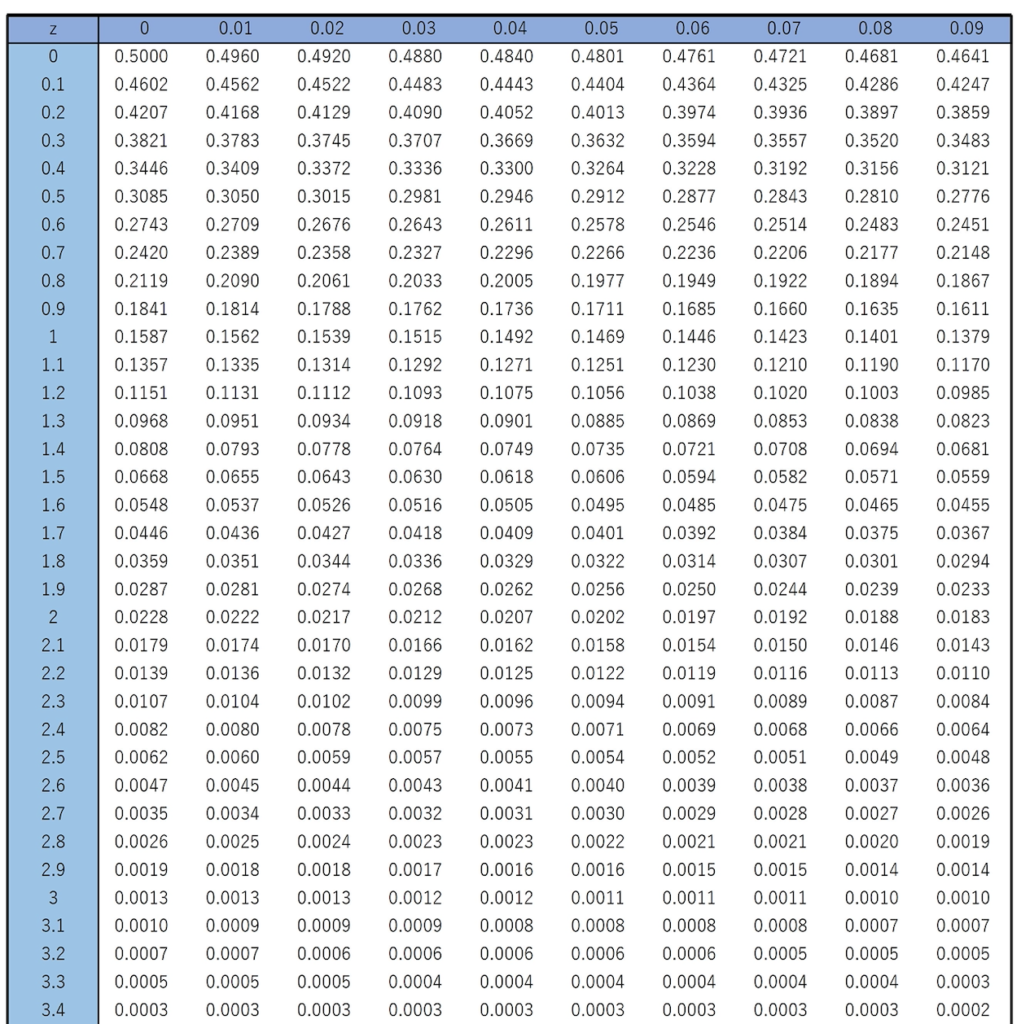
【解答】xが1.4以上の値をとるときに帰無仮説を棄却するわけですから,片側検定です。
第一種の過誤は,帰無仮説が正しいときに誤って帰無仮説を棄却してしまうことでしたね。帰無仮説θ=0が正しいときには,Xが従う確率分布は標準正規分布になり,第一種の過誤の確率を図示すると次の図の色のついた部分になります。
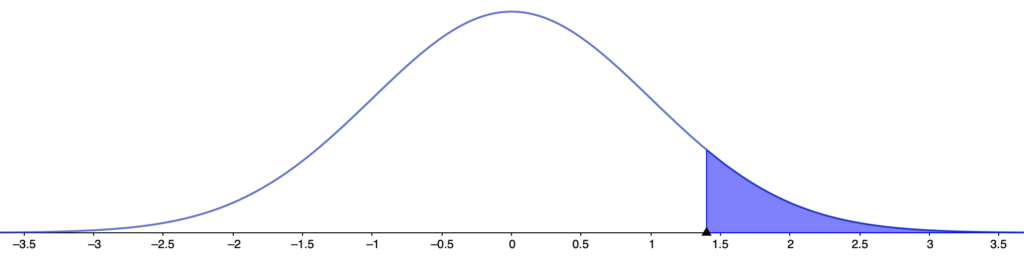
検定量が1.4以上の値をとると,正しいはずの帰無仮説を棄却してしまうわけですから,第一種の過誤の確率は,正規分布表でx=1.4における上側確率を調べることで,0.0808とわかります。
次に,第二種の過誤の確率を求めます。第二種の過誤は,対立仮説が正しいときに誤って帰無仮説を受容してしまうことでしたね。対立仮説θ=2が正しいときには,Xが従う確率分布は次の正規分布になります。
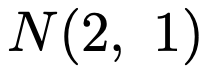
このときの第二種の過誤の確率を図示すると次の図の色のついた部分になります。
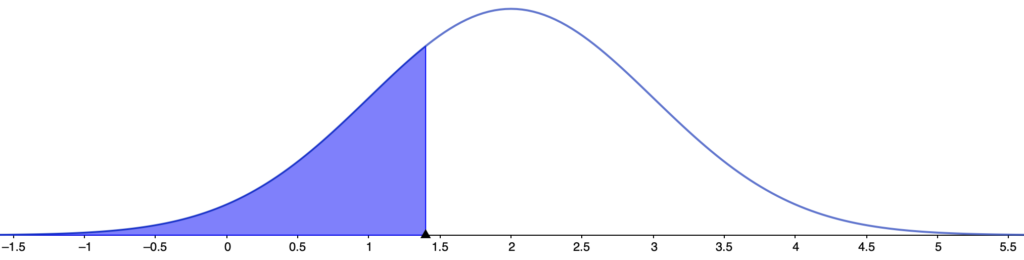
対立仮説が正しいにもかかわらず,検定量が1.4未満の値をとれば,帰無仮説を受容してしまう第二種の過誤を犯してしまうわけです。この色のついた部分は,グラフの対称性から,xが2.6以上の値をとる確率と等しいです。というのも,1.4と2.6のちょうど真ん中が2だからです。そして,このグラフは標準正規分布のグラフを右に2だけ平行移動したものにすぎないことに注意します。2.6ー2=0.6より,このグラフでxが2.6以上の値をとる確率は,標準正規分布でxが0.6以上の値をとる確率と等しいです。よって,正規分布表でx=0.6における上側確率を調べることで,第二種の過誤の確率は0.2743とわかります。
(解答終わり)
演習2〜母平均のz検定(小標本)〜
【問題】ある工場では,太さ0.26mmのヴァイオリンの弦を作っている。この工場で作られた20本の弦を無作為に抽出したところ,太さの平均は0.262mmだった。この工場が作っている弦は規格に沿っていると言えるか,「弦の太さは規格に沿っていない」を対立仮説として有意水準1%で検定しなさい。ただし,この工場が作っている弦の太さは標準偏差0.003mmの正規分布に従うものとする。なお,必要があれば,上の正規分布表を使いなさい。
【解答】弦の太さは太すぎても細すぎても問題がありますので,この問題では帰無仮説を「太さの母平均=0.26」,対立仮説を「太さの母平均≠0.26」としています。対立仮説が「≠」の形で表されるので,両側検定です。
帰無仮説のもとでは,母集団は次の正規分布に従っています。
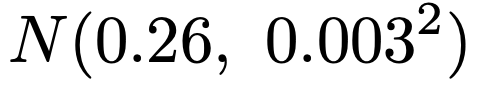
この正規母集団から無作為抽出して得られた大きさ20の標本平均は,次の正規分布に従います。
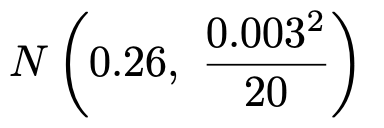
よって,検定量は次のように計算できます。
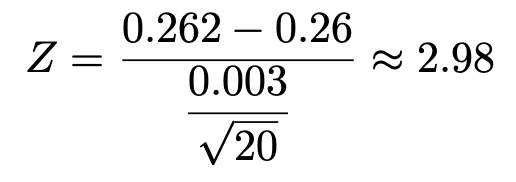
標準正規分布の上側0.5%点は約2.58だから,2.98>2.58より,検定量の値は棄却域に落ち,帰無仮説は棄却されます。したがって,この工場が作っている弦の太さは規格に沿っていないという結論になります。
(解答終わり)
演習3〜母平均のz検定(大標本)〜
【問題】ある地域には,数千店のコンビニがあり,一昨年の1店舗,1日あたりの売り上げの平均は50.4万円,標準偏差は3.6万円であった。昨年,この地域の100店のコンビニを無作為に選んで調査したところ,1店舗,1日あたりの売り上げの平均は51.3万円であった。昨年のこの地域のコンビニの売り上げは,一昨年と比べて増加したと言えるか,「売り上げは一昨年より増加した」を対立仮説として有意水準1%で検定しなさい。なお,必要があれば,上の正規分布表を使いなさい。
【解答】昨年のコンビニの売り上げが一昨年より増加したのは,誤差の範囲なのか,有意な増加なのかを調べるため,この問題では帰無仮説を「売り上げの母平均=50.4」,対立仮説を「売り上げの母平均>50.4」としています。対立仮説が不等式の形で表されるので,片側検定です。
帰無仮説から,母集団は次の期待値,分散の確率分布に従っています。
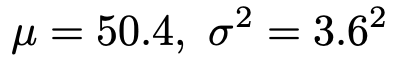
標本の大きさ100は十分に大きいので,中心極限定理によって,標本平均は近似的に次の正規分布に従うと考えられます。

よって,検定量は次のように計算できます。
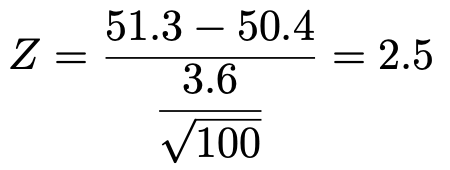
標準正規分布の上側1%点は約2.33だから,2.5>2.33より,検定量の値は棄却域に落ち,帰無仮説は棄却されます。したがって,昨年のコンビニの売り上げは一昨年より増加したという結論になります。
(解答終わり)
演習4〜母平均のt検定〜
【問題】ある電機メーカーが,平均して500回充電して使えると宣伝している電池を5本購入し,使えなくなるまでの充電回数を調べたところ,次のような結果になった。
488回 485回 501回 489回 497回
メーカーが宣伝している内容は誤りであると言えるか,「充電して使えるのは500回未満である」を対立仮説として有意水準5%で検定しなさい。ただし,電池が使えなくなるまでの充電回数は正規分布に従うものとする。なお,必要があれば,上側確率を表した次のt分布表を使いなさい。
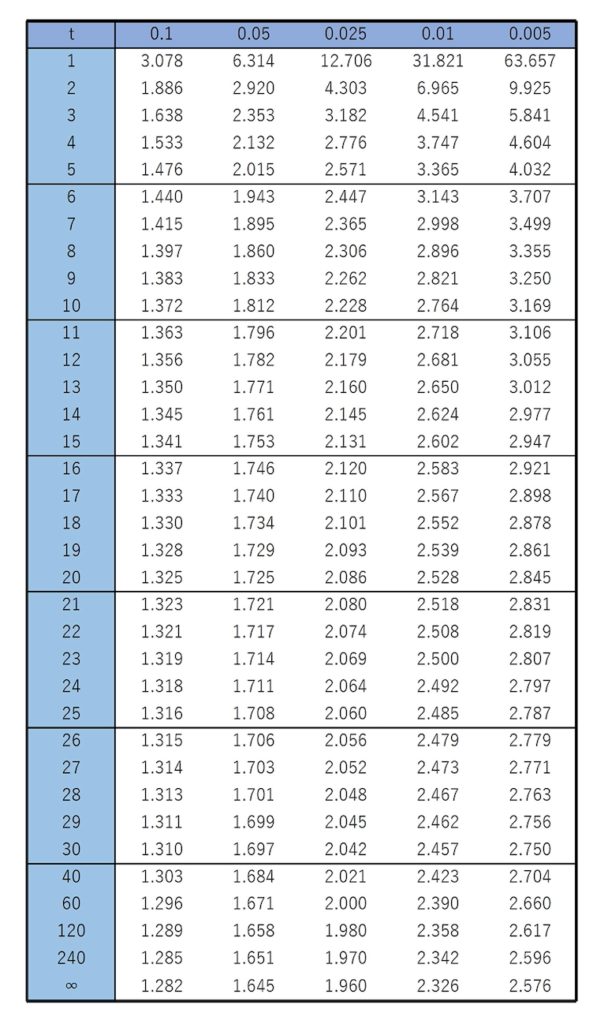
【解答】この問題では帰無仮説を「充電できる回数の母平均=500」,対立仮説を「充電できる回数の母平均<500」としています。対立仮説が不等式の形で表されるので,片側検定です。標本平均は次のように計算できます。
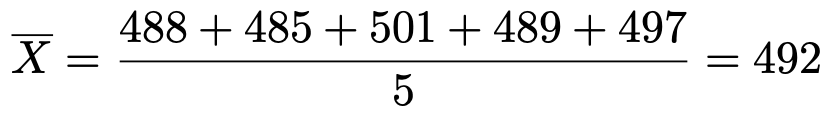
不偏分散は次のように計算できます。
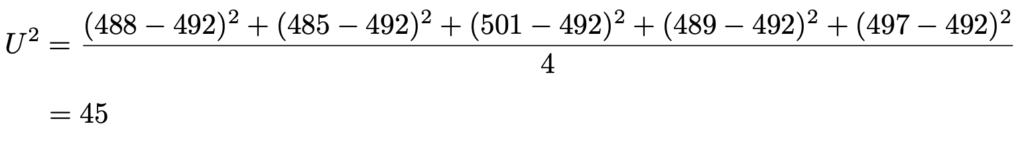
したがって,帰無仮説のもとで,検定量を計算すると,次のようになります。
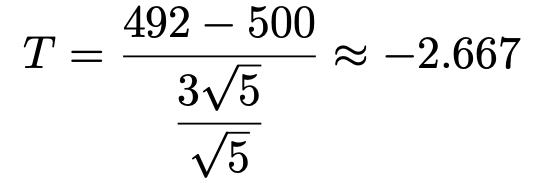
自由度4のt分布の下側5%点はおよそー2.132だから,ー2.667<ー2.132より,検定量の値は棄却域に落ち,帰無仮説は棄却されます。したがって,この電池を充電して使えるのは平均して500回未満であるという結論になります。
(解答終わり)
最後までお付き合いいただき,ありがとうございました!
引き続き,第12回以降の記事へ進んでいきましょう!
2023年1月に「統計検定2級公式問題集[CBT対応版](実務教育出版)」が発売されました!(CBTが何かわからない人はこちら)
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが,本書は分野ごとにその形式の問題を並べた構成になっていて,最後に模擬テストがついています。CBT対策の新たな心強い味方ですね!
なお,さらに実戦に向けた演習を積みたい人は,「統計検定2級公式問題集2018〜2021年(実務教育出版)」を手に取ってみてください!
また,もっと別の問題を解いてみたい人は,さらにさかのぼって「統計検定2級公式問題集2016〜2017年(実務教育出版)」を解いて実力に磨きをかけましょう!


![統計検定2級公式問題集[CBT対応版]](https://m.media-amazon.com/images/I/51q3GfZId3L._SL500_.jpg)




コメント