母比率の差の検定【中学の数学からはじめる統計検定２級講座第12回】

「P値って何？」という疑問に答えつつ，母比率の検定をテーマとして，２つの母集団における母比率の差の検定までを，例題を解きながらわかりやすく解説していきます。

第７回の記事で説明した正規分布の内容，第９回の記事で説明した母平均の区間推定の内容，第10回の記事で説明した母比率の区間推定の内容，第11回の記事で説明した母平均の仮説検定の内容が基礎になりますので，それらの内容に不安がある人は，先にそちらの記事を読んでください。

では，はじめていきましょう！

母比率の検定
P値
母比率の差の検定
演習１〜母比率の検定〜
演習２〜母比率の差の検定〜
演習３〜母比率の差とP値〜

母比率の検定

はじめに，第10回の記事で扱った標本比率が従う確率分布を簡単におさらいしておきます。

母集団の中で，ある性質を持っているものの比率（母比率）がpであるものとして，次の大きさnの標本を取り出します。

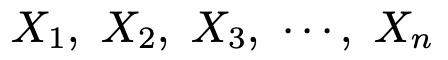
それぞれの確率変数は「注目している性質を持っている→１，注目している性質を持っていない→０」という値をとるものとすると，次の式で定まるXは二項分布B(n,p)に従います。

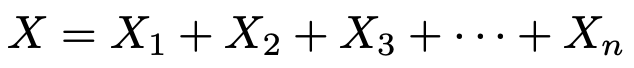
このとき，次の式で定まるものが標本比率です。

そして，nが十分に大きいとき，標本比率は次の正規分布に従います。

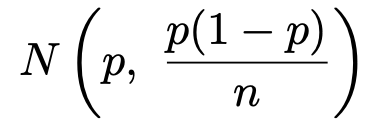
したがって，次の式で定まるZは標準正規分布に従います。

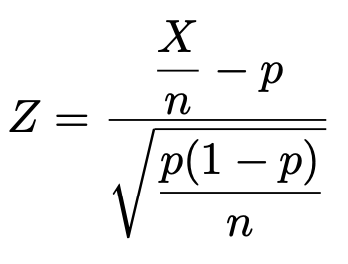
この式で求められる値を検定量（検定統計量）として，母比率の検定をしていきます。

【問題】ある公的機関の発表によると，従業員300人以上の企業のうち，社員が副業することを認めている会社は全体の17％であった。また，同時期に民間の経済団体が，無作為に抽出した従業員300人以上の企業400社を対象に同内容の調査をしたところ，社員が副業することを公式に認めていると回答したのは82社だった。従業員300人以上の企業のうち，社員が副業することを認めている会社の割合をpとする。帰無仮説をp＝0.17，対立仮説をp＞0.17，有意水準を５％として検定しなさい。

【解答】従業員300人以上の企業全体からなる母集団は十分に大きいので，社員が副業することを公式に認めている会社の数Xは二項分布に従うと考えていいです。また，標本は十分に大きいので，帰無仮説のp＝0.17を仮定すると，標本比率は次の正規分布に従います。

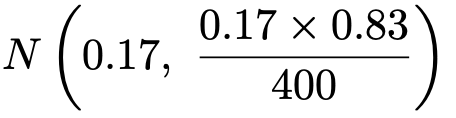
対立仮説が不等号を使った形になるので，有意水準５％で片側検定を行います。検定量は次のように計算できます。

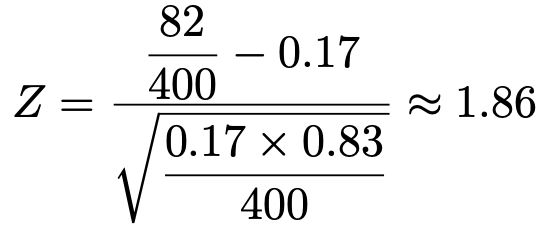
標準正規分布の上側5％点はおよそ1.64だから，検定量の値は棄却域に落ちます。帰無仮説は棄却され，対立仮説が採択されます。母比率は17％より大きいという結論になります。

（解答終わり）

P値

P値とは，検定量の値と等しいか，それより極端な値をとる確率のことです。例えば，前問は片側検定で，検定量の値は1.86でした。これよりも極端な値とは，1.86以上の値のことです。この場合のP値は，次の図の色のついた部分です。

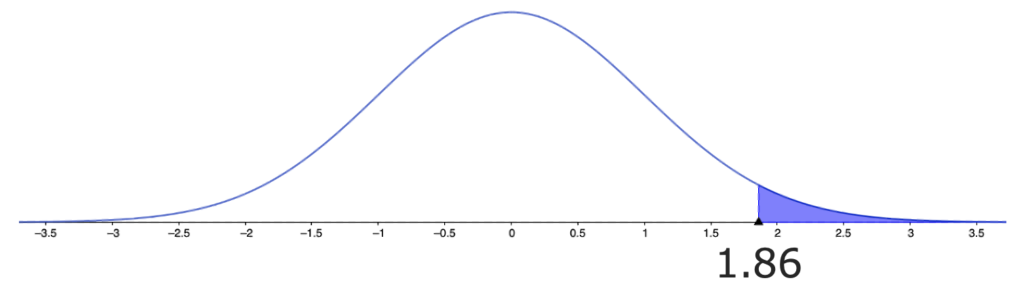
前問での有意水準は，次の図の色のついた部分ですね。

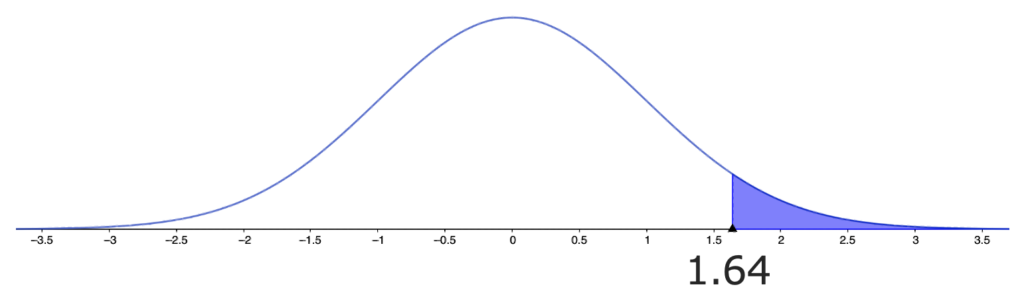
つまり，P値が有意水準よりも小さいとき，帰無仮説は棄却されると言えます。両側検定においても同じように，P値は検定量の値に対して，それと等しいか，それより極端な値をとる確率として定義されます。

母比率の差の検定

第７回の正規分布の記事で，独立な正規分布の一次結合が正規分布になることを紹介しました。今回は，正規分布に従う２つの独立な確率変数の差で表される確率変数を扱いますので，必要な部分に限定して以下に再掲しておきましょう。

確率変数X，Yが独立で，それぞれ次の正規分布に従っているものとします。

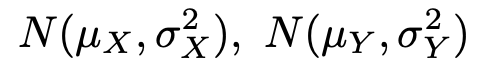
このとき，確率変数XーYは次の正規分布に従います。

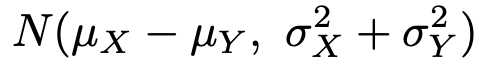
期待値と分散の公式を使えば，XーYが従う確率分布の期待値と分散がこのようになることはすぐに求めることができるのですが，それが正規分布であることを証明することは難しいので，覚えてしまったほうがいいです。というわけで，ここまでが第７回の復習でした。

いま，２つの母集団から独立にそれぞれ大きさn_１，n_２の標本を取り出すことを考えます。標本比率をそれぞれ次のように表します。

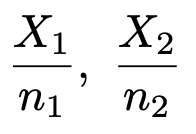
標本の大きさは十分に大きいものとして，それぞれが従う正規分布を次のように表すことにします。

p_１，p_２はそれぞれの母集団における母比率です。このとき，差を表す次の確率変数を考えます。

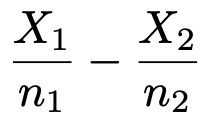
正規分布に従う２つの独立な確率変数の差で表されるので，上で説明したことから，次の正規分布に従うことがわかります。

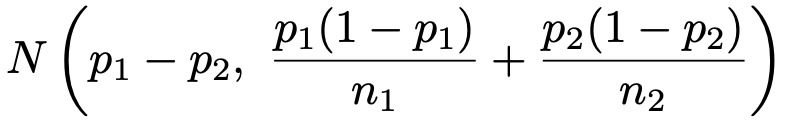
これが母比率の差が従う正規分布です。これらの母比率に差があるかどうかを判定したいとしましょう。この正規分布を標準化する式は次のようになりますね。

たいていの場合，母比率のp_１，p_２はわからないので，第10回の母比率の区間推定でやったのと同じように，これらをそれぞれ標本比率でおきかえてしまうと，次のようになります。

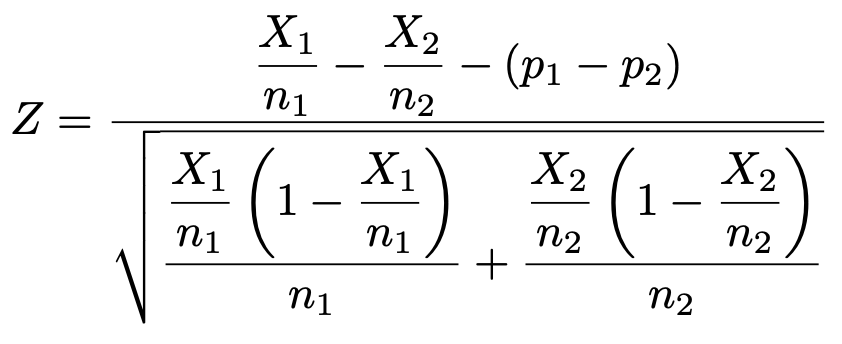
これが母比率の差を検定するときの検定量になります。では，これを使って，２つの母集団の母比率に差があるのかどうかを調べる問題を解いていきましょう。

【問題】ある生活用品メーカーは，販売中の歯ブラシをリニューアルした。東京在住の消費者300人と大阪在住の消費者200人を無作為に抽出し，この歯ブラシのリニューアル前のものとリニューアル後のものの使用感を比べてもらったところ，リニューアル後のほうが良いと回答した人は，東京では192人，大阪では110人であった。東京と大阪で，リニューアル後のほうが良いと回答した人の割合の地域差をpとする。帰無仮説をp＝0，対立仮説をp≠0として検定を行う。このときの連続修正を行わない場合のP値を求めなさい。

【解答】まず，「連続修正」という言葉を補足しておきます。これは，半整数補正とも呼ばれるもので，二項分布のような離散型の確率分布を正規分布のような連続型の確率分布で近似するときに，近似の精度を上げる方法です。例えば，Xが二項分布に従うとき，P（X≦５）を正規分布で近似して求めたいとします。このとき，P（X≦５）の代わりに，P（X≦5.5）を求めたほうがより二項分布の確率に近い値を求められるというものです。この問題では連続修正を考慮しないので，これ以上説明しませんが，詳しく知りたい人は「基本統計学　第５版（宮川公男，有斐閣）」を読んでみてください。

基本統計学[第５版]

この問題では，東京在住の消費者全体という母集団と，大阪在住の消費者全体という母集団の２つを考えています。２つの母集団は十分に大きく，標本も十分に大きいので，前者の母集団におけるリニューアル後のほうを好む人の比率（母比率）をp₁，後者の母集団におけるリニューアル後のほうを好む人の比率（母比率）をp₂とすると，標本比率の差は次の正規分布に従うと考えていいです。

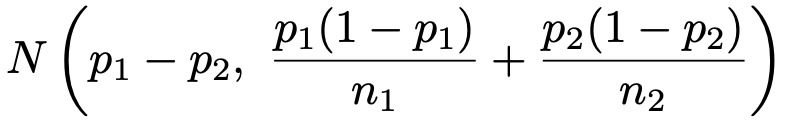
帰無仮説はp_１＝p_２，対立仮説はp_１≠p_２であると言えます。帰無仮説を仮定すると，検定量は次の式で求められます。

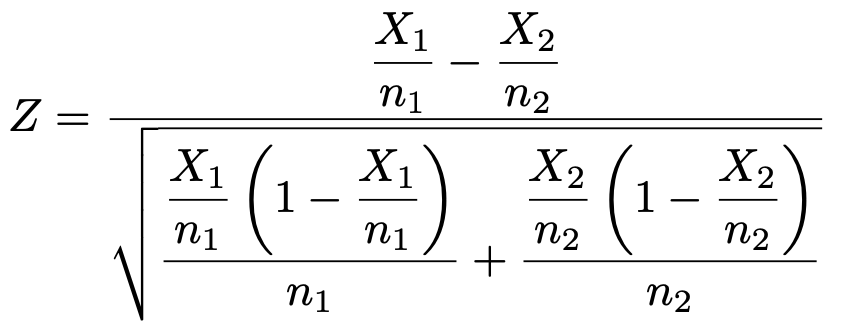
では，数値を代入していきましょう。標本比率の実現値はそれぞれ次のように計算できます。

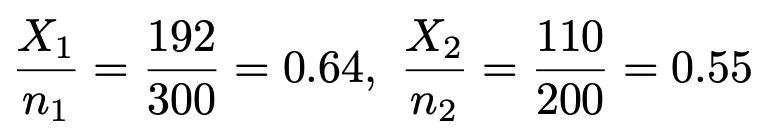
これらを代入すると，検定量は次のように計算できます。

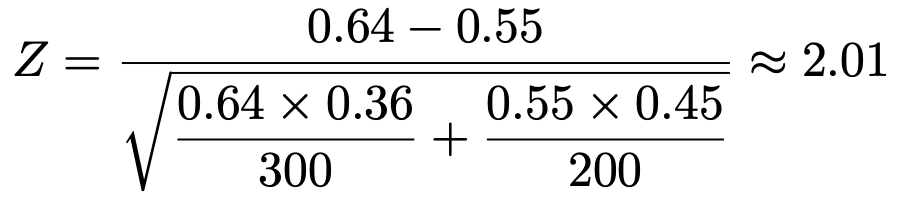
P値は，このZ＝２.01よりも極端な値をとる確率です。正規分布表から，Z＝２.01における上側確率はおよそ0.0222なので，P値は次のようになります。

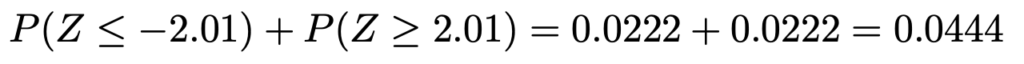
（解答終わり）

母比率の差の検定についての基本的な説明は以上になります。ここからは，さらに理解を深めるための演習問題ですので，余力があればぜひチャレンジしてみてください。

演習１〜母比率の検定〜

【問題】大学生の正答率が10％であると言われる数学の問題がある。この問題を，400人の大学生に解いてもらったところ，正解者は24人だった。この問題の大学生の正答率（母比率）をpとする。帰無仮説をp＝0.1，対立仮説をp＜0.1，有意水準を１％として検定しなさい。なお，必要があれば，次の正規分布表を使いなさい。

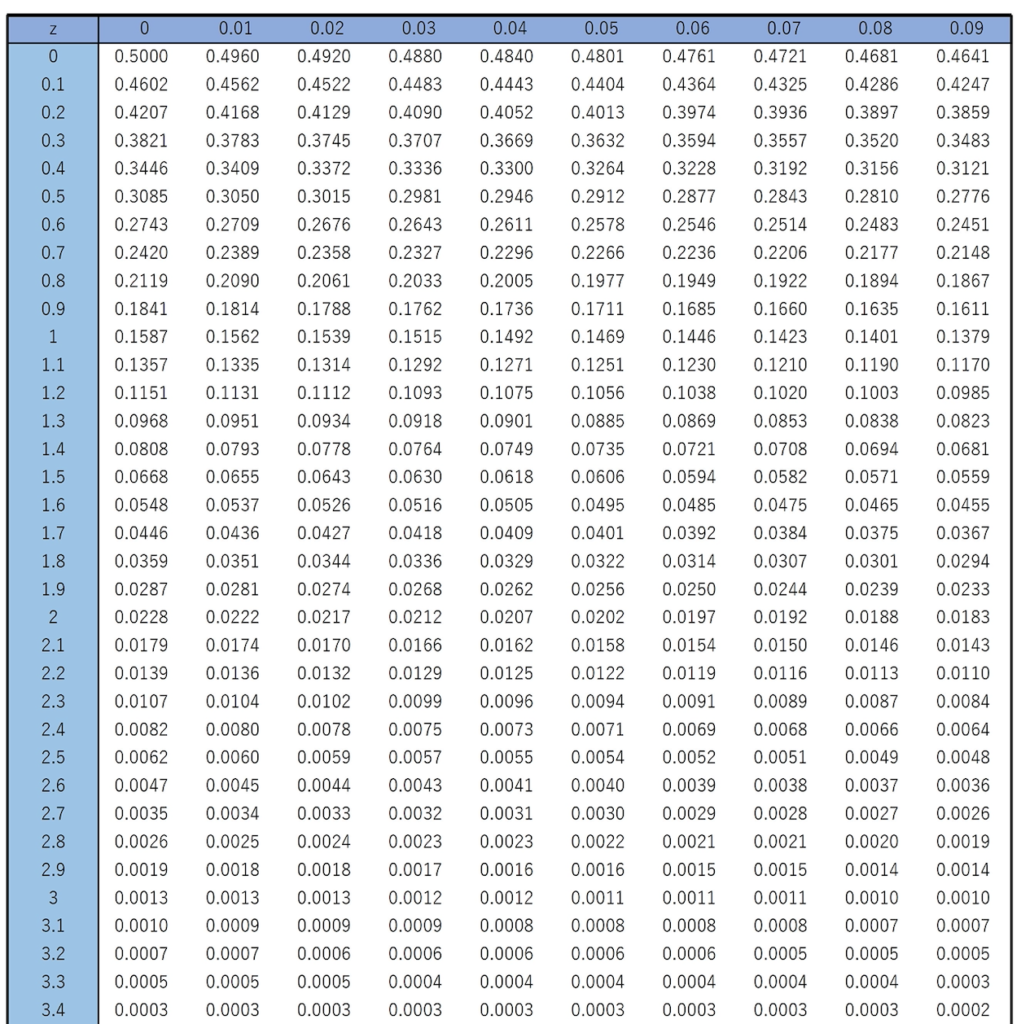
【解答】大学生全体からなる母集団は十分に大きいので，この問題に正解できる大学生の数Xは二項分布に従うと考えていいです。また，標本は十分に大きいので，帰無仮説のp＝0.1を仮定すると，標本比率は次の正規分布に従います。

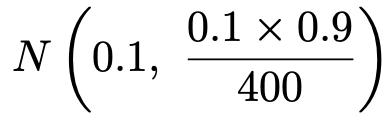
対立仮説が不等号を使った形になるので，有意水準１％で片側検定を行います。検定量は次のように計算できます。

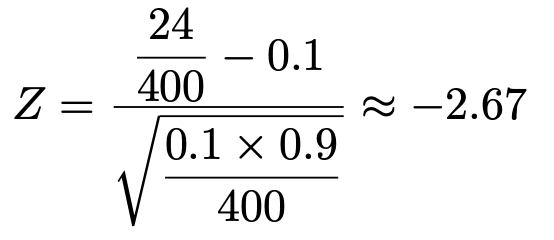
正規分布表を見ると，標準正規分布の下側１％点はおよそー2.33だから，棄却域に落ちます。帰無仮説は棄却され，対立仮説が採択されます。

（解答終わり）

演習２〜母比率の差の検定〜

【問題】ある政令指定都市で，市長が新たな政策を提案したことによる市長の支持率の変化を調べるための調査を行った。この政策を提案する半年前の調査では，2432人から回答を得て，市長を支持したのは1341人だった。また，この政策を提案した直後の調査では，2318人から回答を得て，市長を支持したのは1210人だった。この政策の提案の前後での支持率の差をdとする。帰無仮説をd＝０，対立仮説をd≠0，有意水準を１％として検定しなさい。なお，必要があれば，前問の正規分布表を使いなさい。

【解答】特定の政策の提案前の有権者全体と提案後の有権者全体という２つの母集団を考え，支持率の差があるかどうかを検定します。２つの母集団は十分に大きく，標本も十分に大きいので，前者の母集団における支持率をp_１，後者の母集団における支持率をp₂とすると，標本比率の差は次の正規分布に従うと考えていいです。

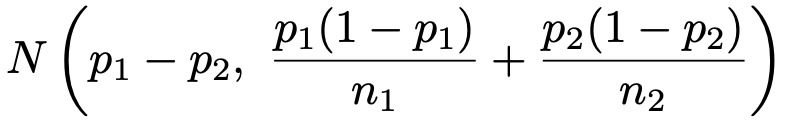
帰無仮説はp_１＝p_２，対立仮説はp_１≠p_２と表せます。「支持率が上がった（下がった）のではないか？」という予想がある場合には片側検定を使いますが，ここでは有意水準１％で両側検定を行います。帰無仮説を仮定すると，検定量は次の式で求められます。

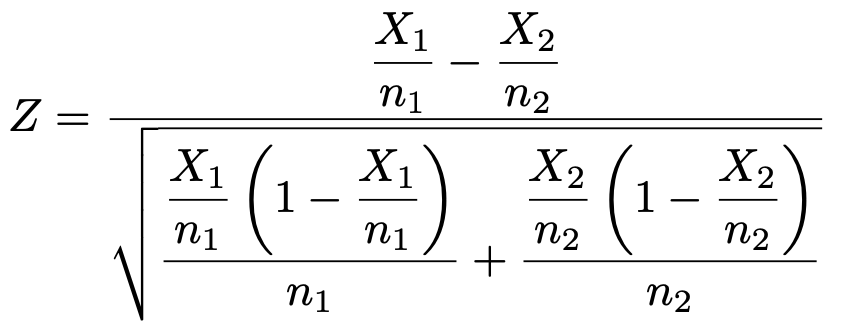
標本比率の実現値はそれぞれ次のように計算できます。

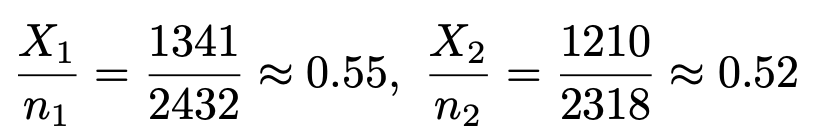
これらを代入すると，検定量は次のように計算できます。

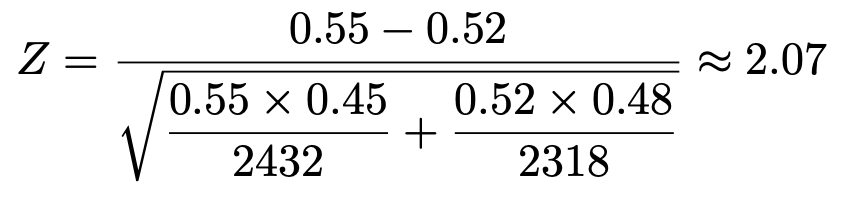
有意水準１％の両側検定なので，上側0.5％点より大きい値であれば帰無仮説を棄却します。標準正規分布の上側0.5％点はおよそ2.58なので，2.07＜2.58となり，帰無仮説は受容されます。

（解答終わり）

演習３〜母比率の差とP値〜

【問題】先週末に放送されたあるテレビ番組の視聴率を調べるため，関東の850世帯と関西の500世帯を無作為抽出して調査したところ，関東では170世帯，関西では85世帯がこの番組を視聴していた。この番組の関東の視聴率（母比率）をp₁，関西の視聴率（母比率）をp₂とする。帰無仮説をp_１＝p_２，対立仮説をp_１＞p_２として検定を行う。このときの連続修正を行わない場合のP値を求めなさい。

【解答】関東のテレビを保有する世帯全体と関西のテレビを保有する世帯全体という２つの母集団を考え，視聴率に差があるかどうかを検定する場合を考えます。２つの母集団は十分に大きく，標本も十分に大きいので，標本比率の差は次の正規分布に従うと考えていいです。

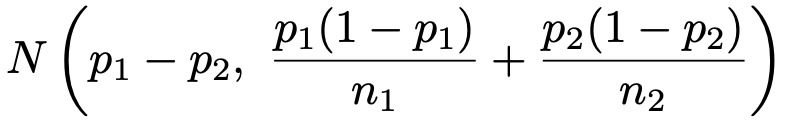
帰無仮説を仮定すると，検定量は次の式で求められます。

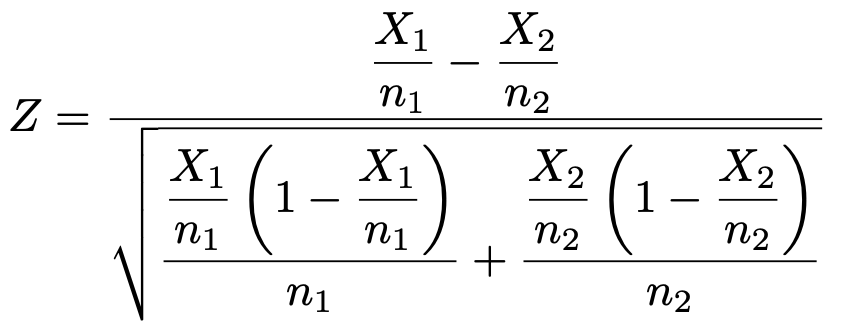
標本比率の実現値はそれぞれ次のように計算できます。

これらを代入すると，検定量は次のように計算できます。

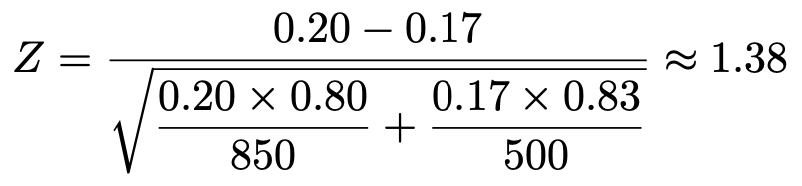
P値は，このZ＝1.38よりも極端な値をとる確率です。正規分布表から，Z＝1.38における上側確率はおよそ0.0838なので，P値は次のようになります。

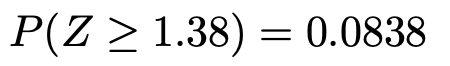
（解答終わり）

第12回は以上となります。最後までお付き合いいただき，ありがとうございました！
引き続き，第13回以降の記事へ進んでいきましょう！

2023年1月に「統計検定２級公式問題集[CBT対応版]（実務教育出版）」が発売されました！（CBTが何かわからない人はこちら）
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが，本書は分野ごとにその形式の問題を並べた構成になっていて，最後に模擬テストがついています。CBT対策の新たな心強い味方ですね！