2×2の分割表を中心にして,統計検定2級〜準1級で頻出の独立性の検定を解説していきます。1つ目のポイントは,2×2の分割表における独立性の検定は,母比率の差の検定としても捉えることができ,それらは等価であることです。2つ目のポイントは,2×2の分割表の場合には,検定統計量を素早く正確に計算できる公式が有効であるということです。また,統計検定準1級の問題文に登場したことがあるクラメールの連関係数やイェーツの補正についても解説します。
この記事で前提知識とする知識は,【中学の数学からはじめる統計検定2級講座】の第1回の確率,第12回の母比率の差の検定,第13回のカイ二乗分布の内容になります。これらの内容に不安がある人は,先にそちらの記事を読んでください。
では,はじめていきましょう!
独立性の検定
例えば,ある市で市長選挙があり,2人の候補者AとBが立候補しているとましょう。有権者はAかBのいずれか一方に投票します。「AとBの支持率は男女で差があるか」を調べるために,1000人を無作為抽出してアンケートをとり,その結果が次の表のようになったとします。
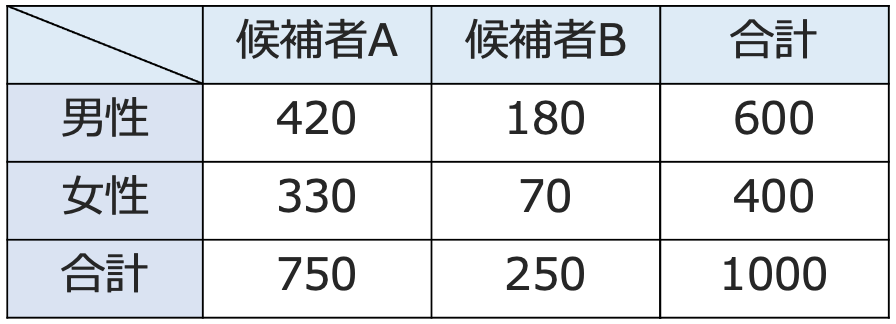
このような表を分割表またはクロス表と言います。特に,この表は行方向に2つのカテゴリー(男・女),列方向にも2つのカテゴリー(候補者A・候補者B)があるので,2×2の分割表(クロス表)と言います。また,このような調査で実際に得られたデータを観測度数と言います。
では,1000人の回答結果から「どちらの候補を支持するか」の割合は男女で差があると言えるでしょうか。このことを調べる方法の1つは,母比率の差の検定を適用することです。これについては第12回の記事で解説していますが,次のセクションで独立性の検定との関係を改めて説明することにします。
そして,もう1つの方法が,今回の主役であるカイ2乗分布を使った独立性の検定を適用することです。
独立性の検定というのは,次の帰無仮説と対立仮説を設定した検定のことです。
- 帰無仮説:行と列の因子は独立である
- 対立仮説:行と列の因子は独立ではない
つまり,独立であることを仮定して検定統計量を計算することで,独立ではないことを示すわけです。
では,上の例で,性別と支持する候補者が独立だと仮定するとどうなるでしょうか。まず,上の分割表で,合計の欄の数以外をすべて消すと次のようになりますよね。
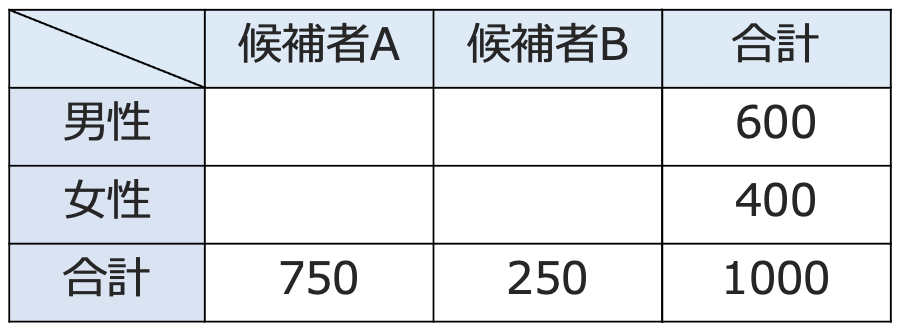
「候補者Aを支持する人」と「候補者Bを支持する人」の人数の比は,男女の合計で,750:250=3:1になっています。もし,性別と支持する候補者が独立だとすると,男性であろうが女性であろうが「候補者Aを支持する人」と「候補者Bを支持する人」の人数の比は3:1になりますよね。人数の比が3:1になるように空欄部分をうめると次のようになります。
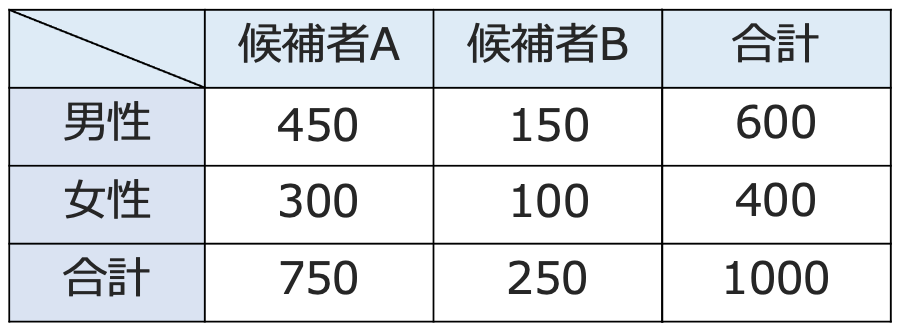
この表の4つのマスの数値のように「行と列の因子は独立である」と仮定したときに各マスに入る数のことを期待度数と言います。期待度数と観測度数のズレが誤差の程度なのか,誤差とは言えないレベルなのかをカイ2乗分布を使って判定します。
では,検定統計量の計算に入る前に期待度数の求め方を振り返っておきましょう。
例えば,上の表の4つのマスのうち,左上のマスに入る450という数を求める式は次のように表すことができます。
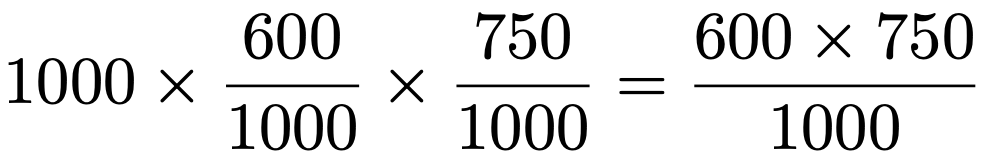
左辺では,全度数の1000に男性である割合の「1000分の600」と候補者Aを支持する人の割合の「1000分の750」をかけています。これには,第1回の記事で説明した独立な事象の確率の性質から,「男性でAを支持する確率=男性である確率×Aを支持する確率」が成り立つことを利用しています。
約分すると右辺のように,1行目の合計と1列目の合計の積を全度数でわったものに等しくなります。つまり,一般的に表現すると,i行目j列目のマスに対応する期待度数は,i行目の合計とj列目の合計の積を全度数でわって求めることができるということです。行の合計や列の合計のことを周辺度数とも言いますので,シンプルに表現すれば「期待度数=周辺度数の積÷全度数」となります。
では,検定の方法の説明に進みましょう。ここまでの準備を踏まえて,次の問題に解答していきます。
【問題】上記の分割表を用いて,ある市長選挙で支持する候補者と性別は独立か,有意水準5%で検定しなさい。
【解答】期待度数からのズレの大きさを数値化するという意味では,適合度検定と同じですから,計算方法も同じになります。つまり(観測度数ー期待度数)2を期待度数でわったものを合計すれば検定統計量が計算できます。上の2×2の分割表の4つのマスについて,この合計を計算すると次のようになります。
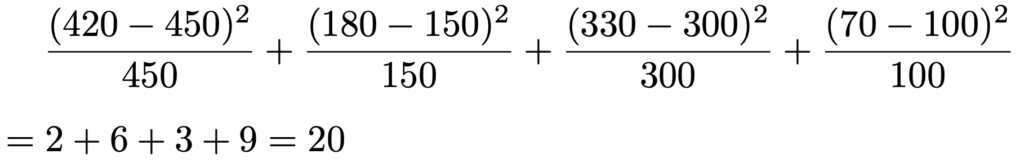
検定統計量の実現値は20ですね。適合度検定と同じように,この統計量は全度数が十分に大きいときに近似的にカイ2乗分布に従いますが,その自由度は2×2の分割表では1になります。この自由度の考え方については後で補足します。20という実現値が自由度1のカイ2乗分布の上側5%点よりも大きければ,有意水準5%で「行と列の因子は独立である」という帰無仮説を棄却することになります。
実際にカイ2乗分布表を使って,自由度1のカイ2乗分布の上側5%点を調べると約3.84であるとわかります。(下の図)

20という実現値は棄却域に入るので,有意水準5%で帰無仮説を棄却し,「行と列の因子は独立ではない」つまり「AとBの支持率には男女差がある」という結論になります。
(解答終わり)
この問題では,検定統計量の実現値が整数の和として計算できたので楽でしたが,ふつうは分割表の数値から計算した(観測度数ー期待度数)2を期待度数でわった値はわりきれないので,計算が煩雑になるだけではなく,四捨五入したときの丸め誤差の影響で正しい検定統計量の値からズレてしまうこともあります。これを防ぐために,2×2の分割表で使える公式を後で紹介します。
では,ここで独立性の検定について一般的にまとめておきます。
まずは,自由度の覚え方です。
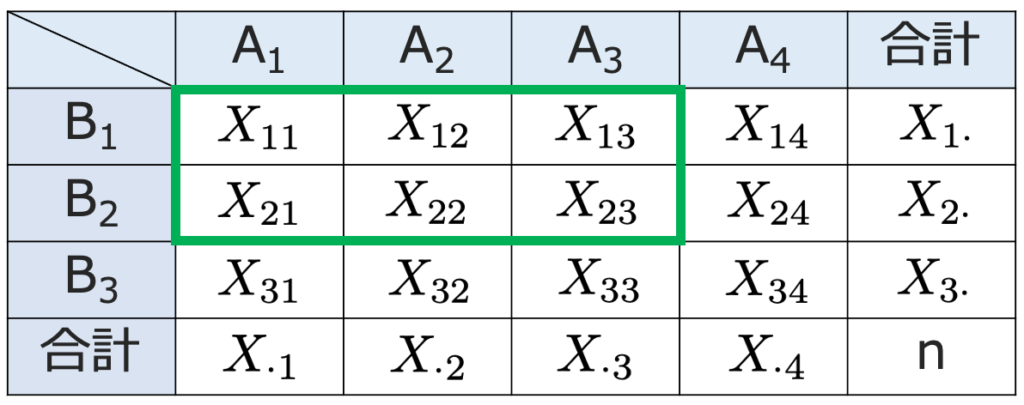
上の3×4の分割表で,周辺度数がはじめから与えられているものとしましょう。このとき,枠で囲んだ左上の6つのマスに入る度数を決めてしまえば,残りのマスに入る数は周辺度数との関係で自動的に決まります。つまり,3×4の分割表ならば,自由に決められるのは2×3の部分であり,k×ℓの分割表ならば,自由に決められるのは(kー1)×(ℓー1)の部分なのです。これが独立性の検定の自由度です。
では,一般的な場合の検定統計量の式を書いておきましょう。k×ℓの分割表で,観測度数を次のようにおきます。
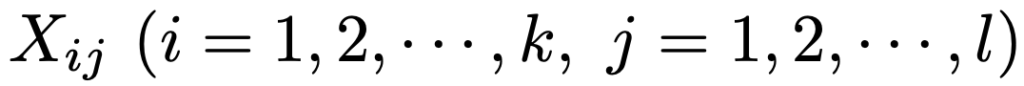
また,周辺度数を次のようにおきます。
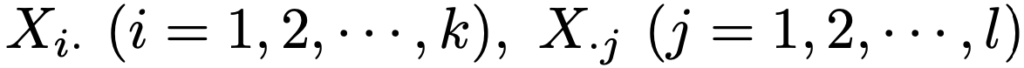
このとき,全度数をnとして,検定統計量は次のように表せます。
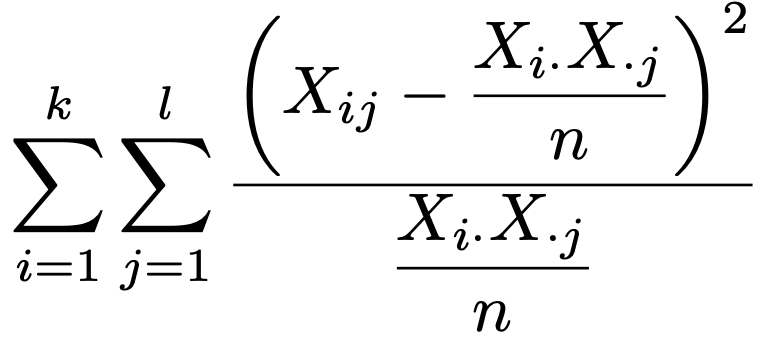
この確率変数は,nが十分に大きいときに近似的に自由度(kー1)×(ℓー1)のカイ2乗分布に従うので,このことを利用して検定を行います。
次のセクションでは,母比率の差の検定と独立性の検定の関係を確認していきましょう。
母比率の差の検定との関係
前のセクションでは「行と列の因子は独立か」と考えましたが,同じ分割表について「どちらの候補を支持するかの割合は男女で差があるか」と考えても同じことですよね。
もし,独立性の検定では有意(独立ではない)になり,母比率の差の検定では有意でない(男女で差がない=独立)という結果になってしまったら困りますよね。
でも,その2つの結果は一致するので大丈夫なんです。母比率の差の検定を適用して,そのことを確認していきます。
次の2×2の分割表は,前のセクションで取り上げたようなアンケート結果だと考えましょう。
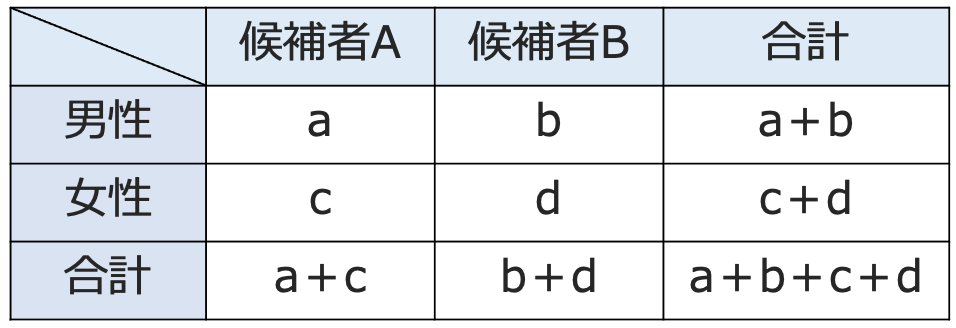
男性の母集団と女性の母集団の2つを考えたときに「候補者Aを支持する」という人の割合に差があるかどうかを調べます。男性で「候補者Aを支持する」と答えた人の標本比率はa÷(a+b)です。女性で「候補者Aを支持する」と答えた人の標本比率はc÷(c+d)です。プールした比率は(a+c)÷(a+b+c+d)なので,母比率の差の推定量の標準誤差は次のように計算できます。
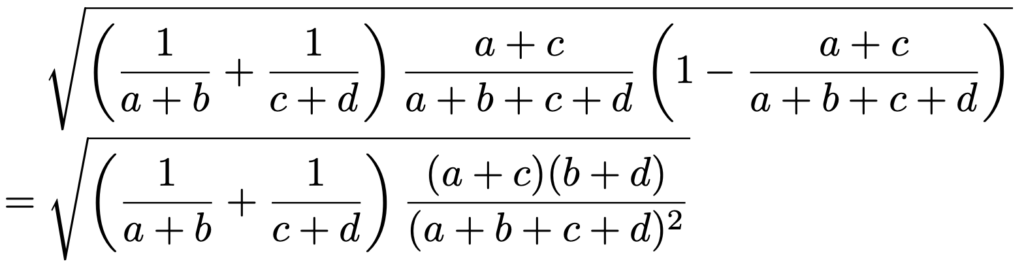
これを使うと,母比率の差の検定の検定統計量の2乗は次のようになります。
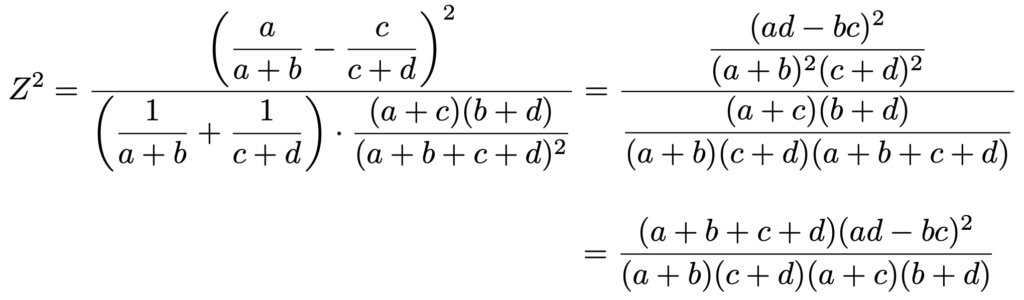
では,同じ2×2の分割表に,独立性の検定を適用してみましょう。4つのマスのうちの左上のマスに対応する期待度数は,周辺度数の積を全度数でわって次のように表せますよね。
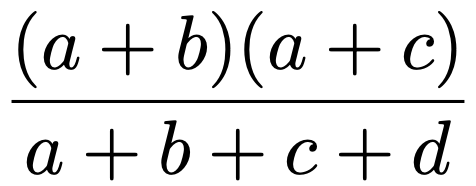
よって,独立性の検定の検定統計量の計算式のうち,左上のマスの数に対応する部分は次のように計算できます。
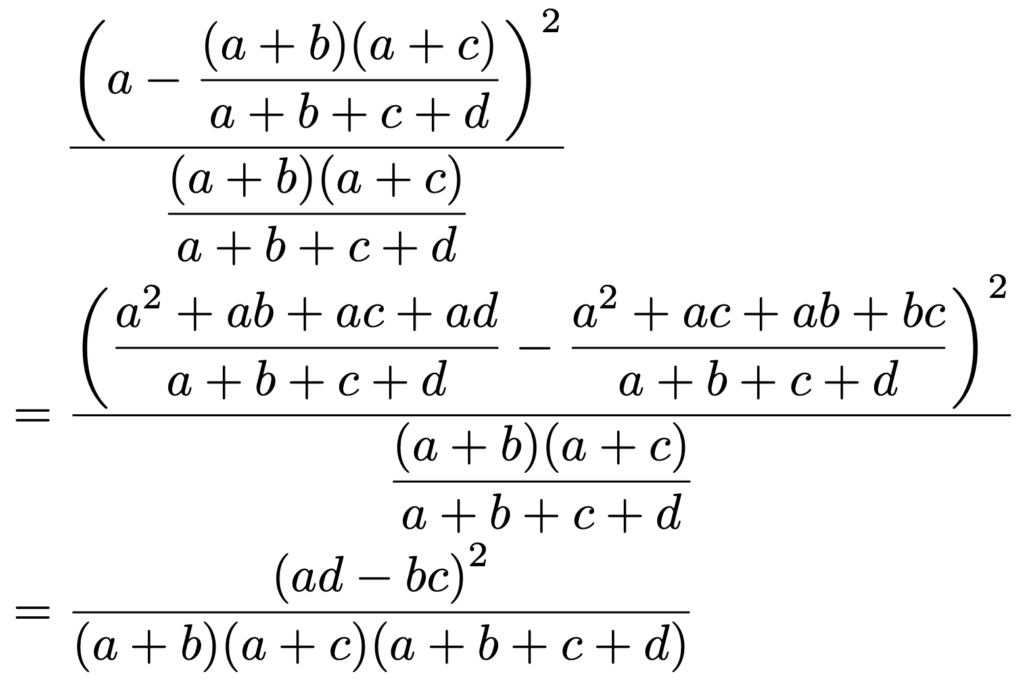
同じように,独立性の検定の検定統計量の計算式のうち,右上のマスの数に対応する部分は次のように計算できます。
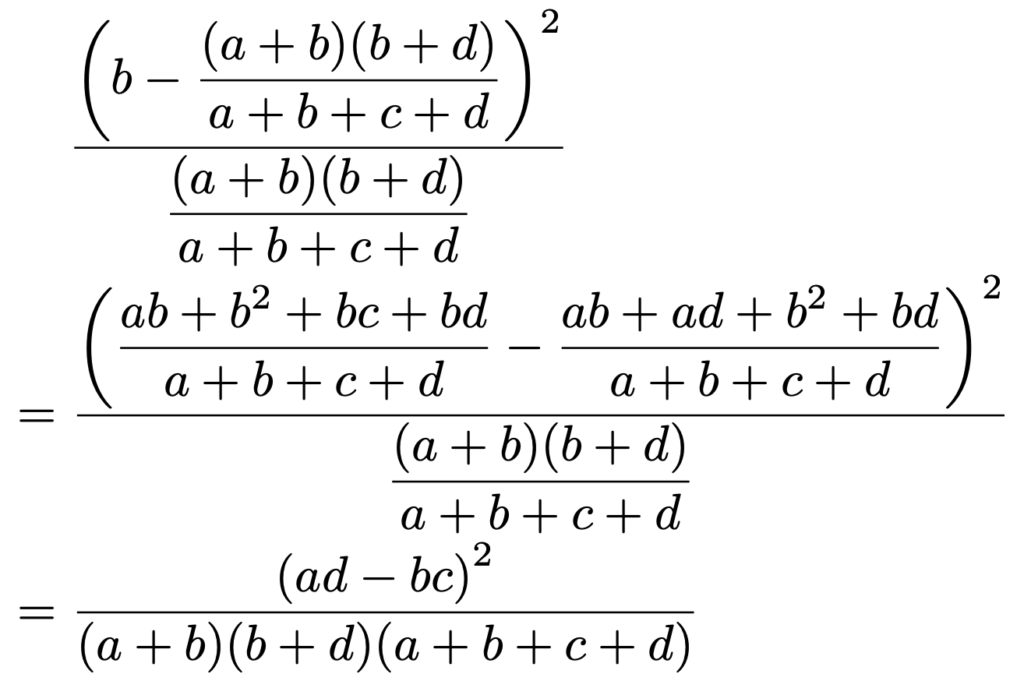
同じように,独立性の検定の検定統計量の計算式のうち,左下のマスの数に対応する部分は次のように計算できます。
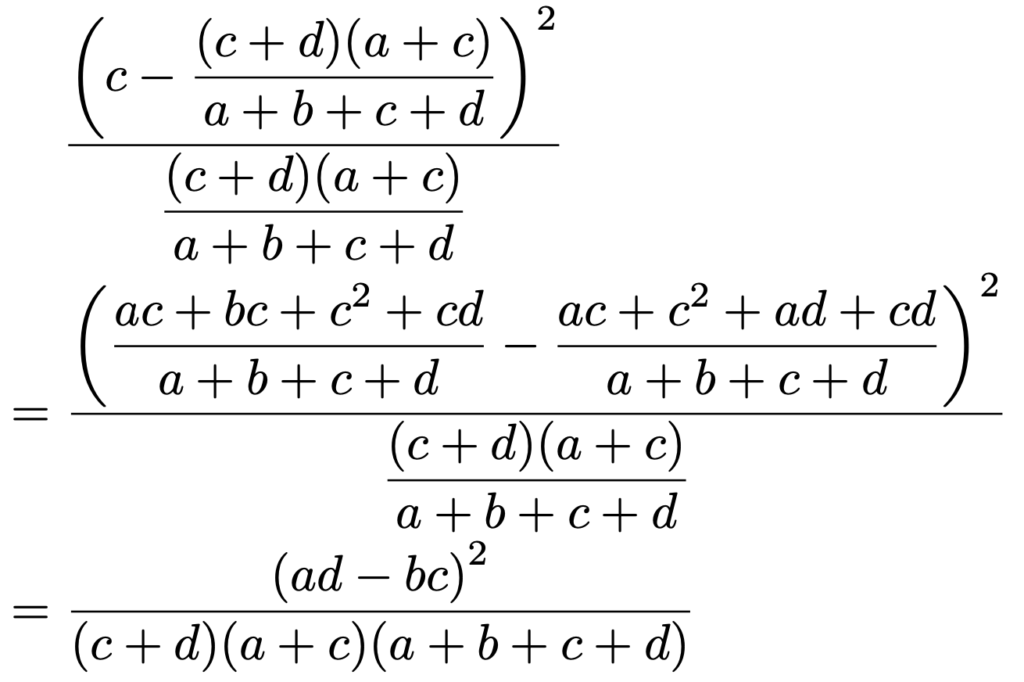
同じように,独立性の検定の検定統計量の計算式のうち,右下のマスの数に対応する部分は次のように計算できます。
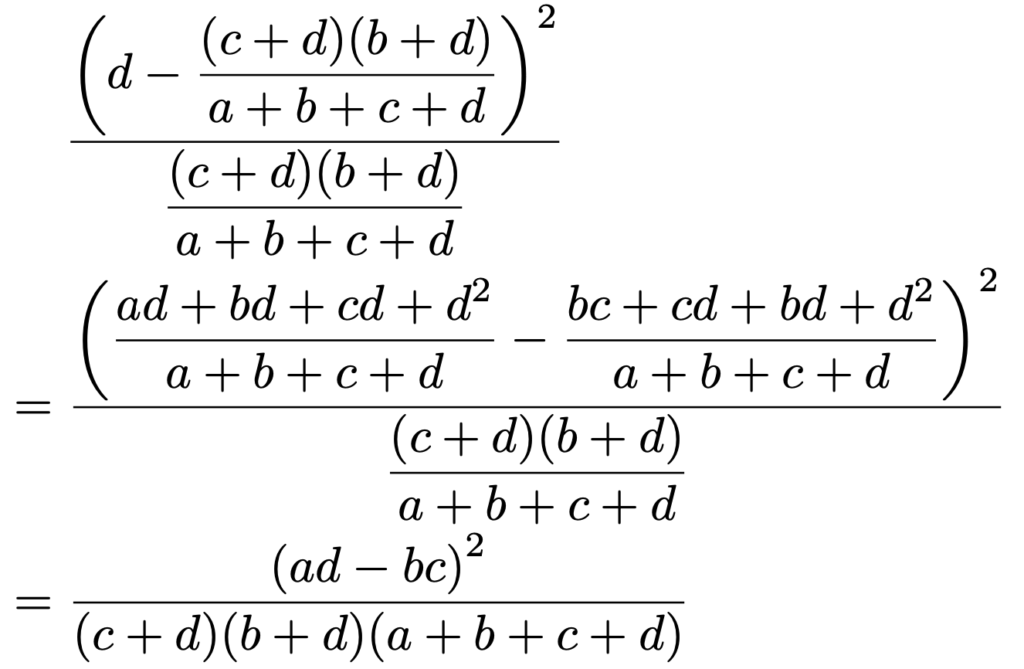
これらをまとめると,次のようになります。
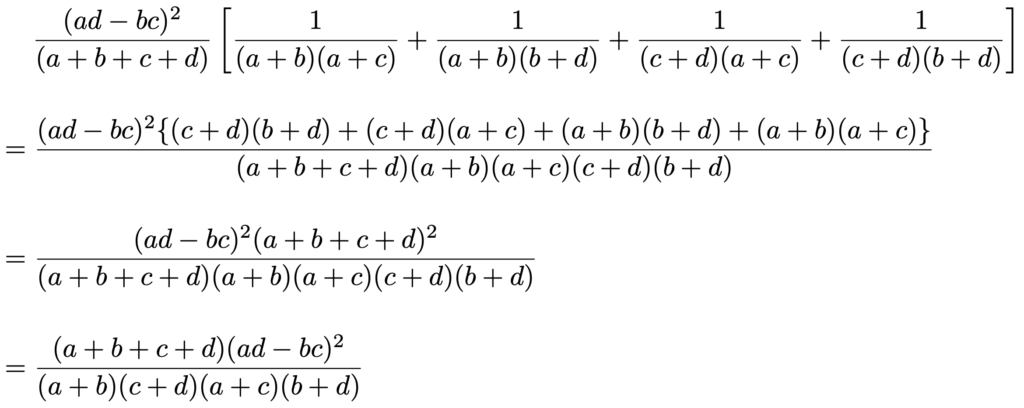
最後の式は,すでに計算してある母比率の差の検定の検定統計量の2乗と一致しています。
2×2の分割表についての独立性の検定の検定統計量は自由度1のカイ2乗分布に,母比率の差の検定の検定統計量は標準正規分布にそれぞれ近似的に従い,標準正規分布に従う確率変数の2乗は自由度1のカイ2乗分布に従うことから,両者の結果は完全に一致します。
さて,ここまでの計算は大変でしたが,大事なことがわかりましたね。それは,2×2の分割表についての独立性の検定の検定統計量は次の式で計算できるということです。

一見,ややこしそうに見える式ですが,adーbcの2乗に全度数をかけて4つの周辺度数でわっているだけなので,それほど苦労せずに覚えられるはずです。この式を使うことで,前のセクションで立式した検定統計量の実現値は,次のように計算できます。
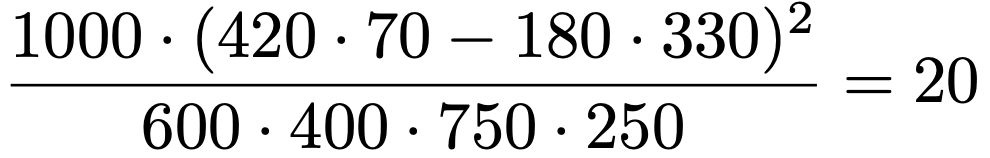
この場合には,どちらで計算してもあまり差が感じられませんが,例えば,後の演習1をこの公式を使わずに計算してもらえれば,この公式のありがたみがわかるかもしれません。
イェーツの補正
分割表に1桁の度数があるような場合,その度数が1ズレただけで,カイ2乗統計量の値が大きく変わってしまうことがあります。そこで第一種の過誤を犯す確率を低くするように,カイ2乗統計量の値を低めに補正するのがイェーツの補正です。
ちなみに,イェーツとは統計学者のFrank Yatesの名前に由来しており,イェイツという呼び方のほうが英語の発音により近いのですが,統計検定準1級の問題文では「イエーツ」と書かれているため,本稿ではイェーツと表記しておきます。
例えば,2×2の分割表で,1行目2列目のbの値が1桁の自然数で,表の中の度数で最も小さい数だとしましょう。このときに,次の表のようにbをb+0.5におきかえます。
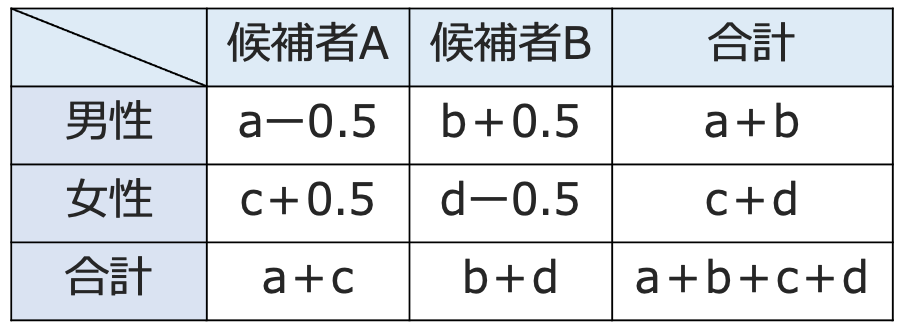
周辺度数を変えないように,bを大きくした分だけ,a,dを小さくし,cは大きくなります。2×2の分割表の公式に代入して計算すると,次のようになります。
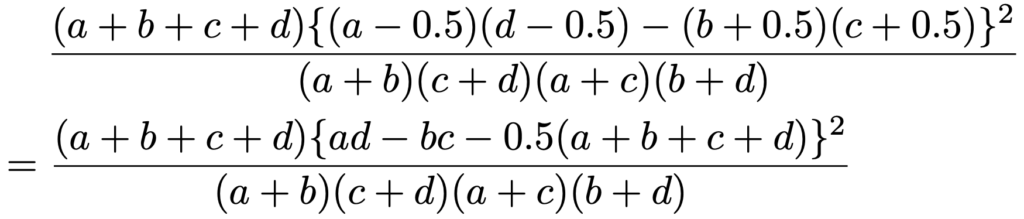
逆に,a,dを0.5だけ大きくして,b,cを0.5だけ小さくする場合もありますよね。その場合も含めてシンプルにまとめると,イェーツの補正を施した2×2の分割表の検定統計量は,a+b+c+d=nとして次の式になります。
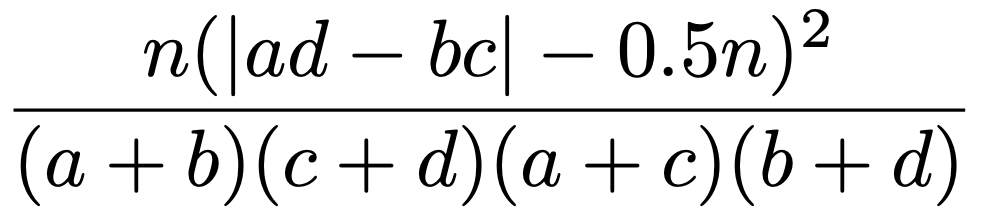
分子の値が小さくなっているので,検定統計量の値が小さくなり,棄却されにくくなっています。したがって,第一種の過誤を犯しにくくなっているのですが,一方で,第二種の過誤は犯しやすくなっています。
補正を施さないと検定統計量は大きめの値になってしまうので,何らかの補正は必要であるものの,イェーツの補正を施すと補正しすぎる傾向があるので,実際にこの補正を行うかどうかは慎重な検討が必要になります。
クラメールの連関係数
すでに紹介したように,k行ℓ列の分割表における独立性の検定の検定統計量は次の式でした。
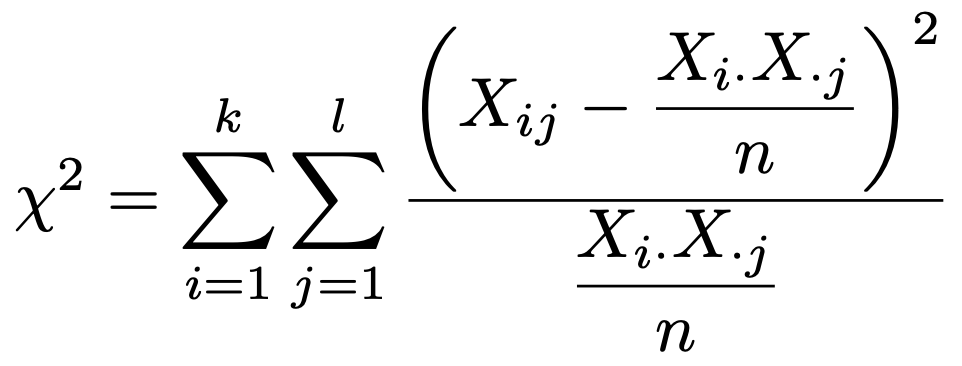
この和の各項は,分子が2乗されているため,全度数nが大きくなるだけで統計量の値は大きくなります。例えば,最初に例に挙げた2×2の分割表で,度数をすべて10倍すると次のようになりますよね。
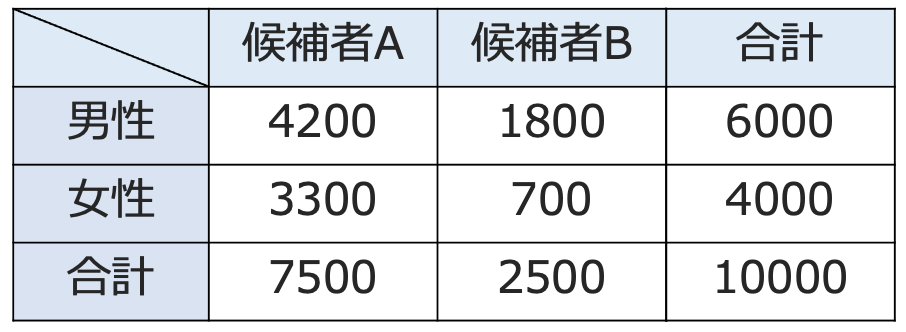
この分割表でカイ2乗統計量を計算すると,各項の分子はもとの100倍,分母はもとの10倍になるので,全体として値が10倍になります。表内の数の比率は変わっていないので,行の因子と列の因子の関連性の度合いは変わっていないはずですが,全度数が大きくなったことで統計量の実現値が大きくなり,棄却されやすくなってしまいます。
そこで,行と列の関連性の度合いを知るには,カイ2乗統計量を標本の大きさでわるような操作が必要だと考えられます。それこそがクラメールの連関係数であり,次の式で表されます。
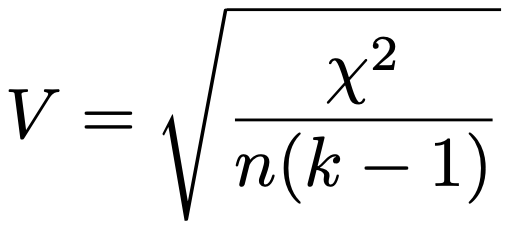
上の式の右辺のルートの中の分子はカイ2乗統計量の値,分母のnは標本の大きさ,kは分割表の行数と列数のうち,大きくないほうの数を表しています。カイ2乗統計量の最大値はn(kー1)なので,カイ2乗統計量をそれでわることで0以上1以下の値をとるようになります。
ちなみに,クラメールとは,数学者・統計学者のHarald Cramerの名前に由来しています。
では,クラメールの連関係数が0以上1以下の値をとることを確認してみましょう。
まず,カイ2乗統計量の値は,観測度数が期待度数とピッタリ一致しているときが最小で,その値は0です。このとき,クラメールの連関係数Vの値も最小の0をとります。このときは,行の因子と列の因子に関連性はない(独立)と考えられます。
では,2×2の分割表で,カイ2乗統計量の値が最も大きくなる場合を考えてみましょう。それは,次のように完全な偏りがある場合です。
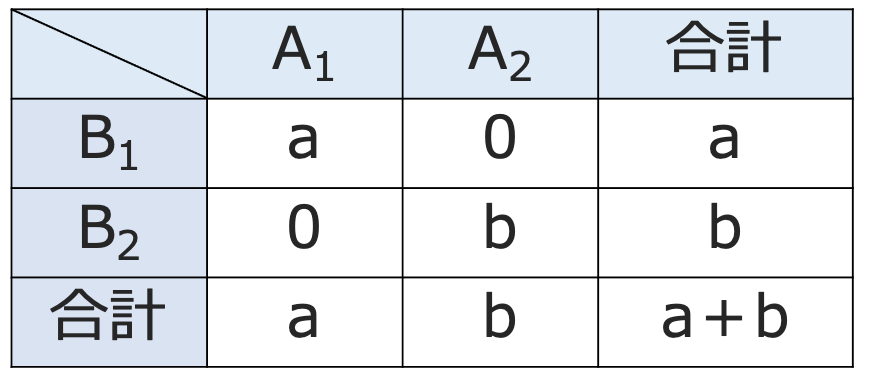
この場合の期待度数は,次のようになりますよね。
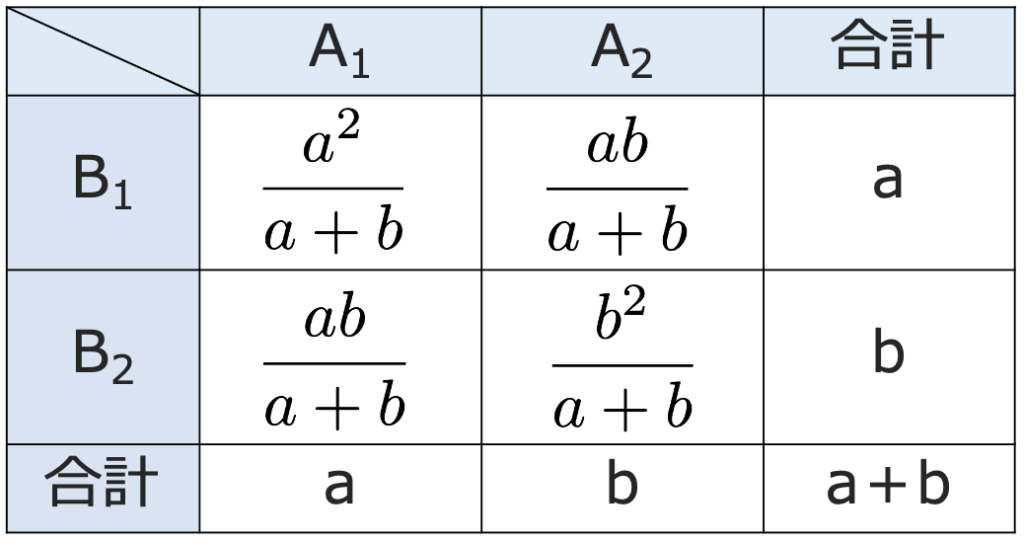
よって,この場合のカイ2乗統計量を計算すると,次のようになります。
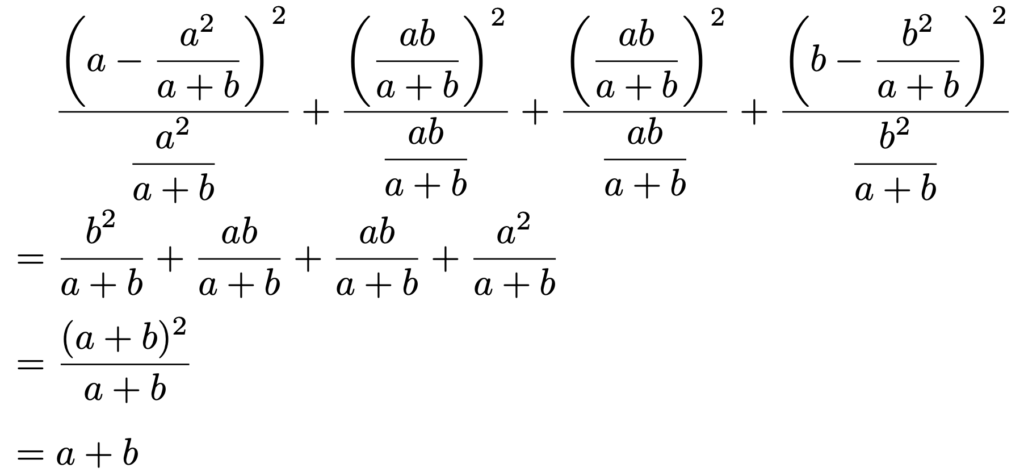
2×2の分割表では,行数と列数のうちの大きくないほうの数は2なので,次のようにクラメールの連関係数は最大値の1をとります。
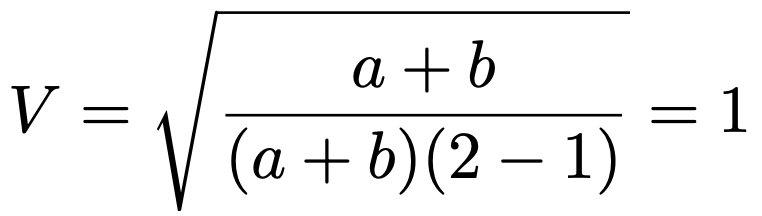
一般的なk行ℓ列(k≦ℓ)の分割表でも,同じように計算することで,カイ2乗統計量の最大値がn(k−1)となることが確認できますので,クラメールの連関係数の最大値は1になるわけです。このときは,行の因子と列の因子に関連性はある(独立ではない)と考えられます。クラメールの連関係数の値が1に近いほど,関連性がある(可能性が高い)と考えることができます。
なお,一般の分割表の場合のクラメールの連関係数の最大値が1であることの証明を確認したい人は本稿下部の参考図書②を参照してください。
演習1 2×2の分割表
【問題】次の分割表は,あるプロ野球チームが5年間に行った702試合における勝敗を本拠地での試合(ホーム)と他球団の本拠地での試合(ビジター)に分けてまとめたものである。
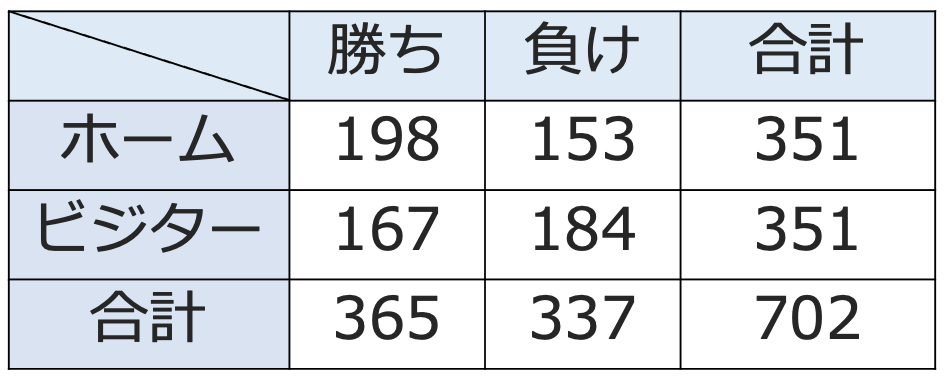
「このチームの勝敗とホームゲームかどうかは独立である」という帰無仮説を有意水準1%で検定しなさい。
【解答】2×2の分割表なので,公式を使いましょう。代入して計算すると,次のようになります。
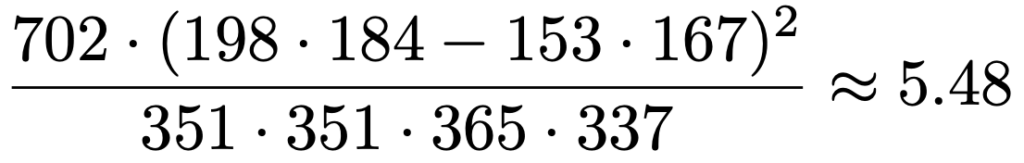
2×2の分割表では統計量が従うカイ2乗分布の自由度は,(2ー1)(2ー1)=1です。カイ2乗分布表から,自由度1のカイ2乗分布の上側1%点は約6.63とわかるので,5.48<6.63より,この値は棄却域には入らず,帰無仮説を受容します。有意水準1%で独立ではない(関連がある)とは言えないという結論になります。
(解答終わり)
演習2 クラメールの連関係数
【問題】ある喫茶店では,A,B,Cの3種類のコーヒーを販売している。この喫茶店の客に「A,B,Cのうちの好きなコーヒーはどれか」というアンケートをとり,年代別にまとめたところ,次の分割表が得られた。
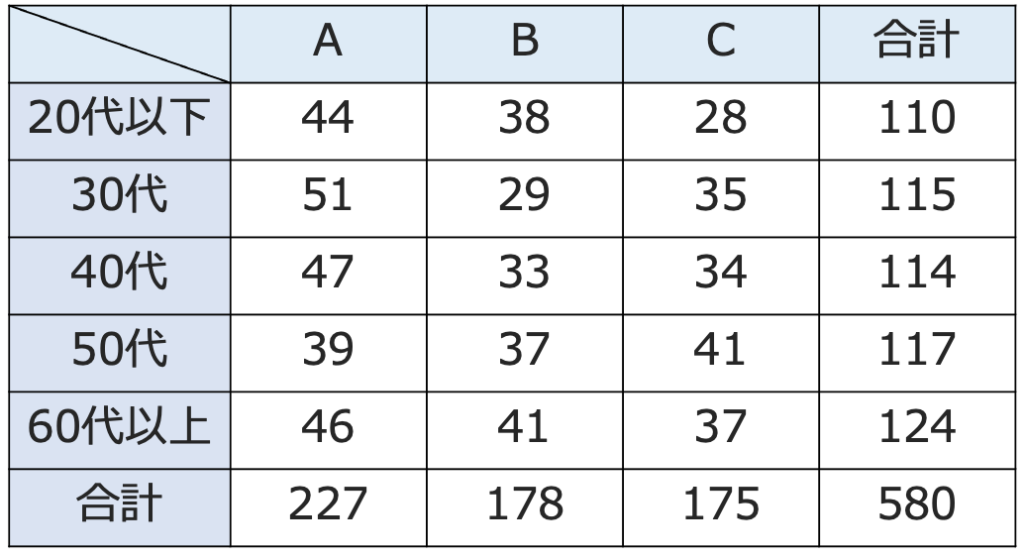
コーヒーの好みと年代に関連があるかどうかを調べるため,カイ2乗統計量を計算したところ,約24.25であった。次の問いに答えなさい。
(1)この分割表について,「コーヒーの好みと年代は無関係である」という帰無仮説を立て,独立性の検定を行うとき,30代でCのコーヒーを好む客の期待度数を,四捨五入して小数第1位まで求めなさい。
(2)クラメールの連関係数の値を,四捨五入して小数第2位まで求めなさい。
【解答】
(1)2行目・3列目の期待度数は,2行目の合計と3列目の合計の積を全度数でわって求めればよいので,次のように計算できます。
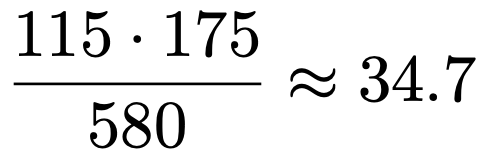
(2)5行3列の分割表なので,行数と列数のうちの大きくないほうの数は3です。よって,全度数が580,カイ2乗統計量が約24.25であることを用いて,クラメールの連関係数は次のように計算できます。
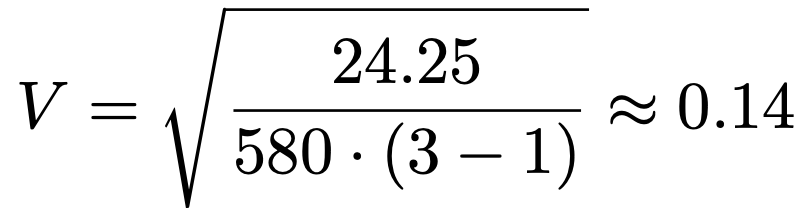
(解答終わり)
参考図書
本稿を執筆するにあたり,次の書籍を参考にしました。
①数理統計学の基礎(尾畑伸明著,共立出版)
2×2の分割表での独立性の検定と母比率の差の検定が等価であることが記載されています。
②まずはこの一冊から意味がわかる多変量解析(石井俊全著,ベレ出版)
クラメールの連関係数の最大値が1であることの一般的な証明を確認したい人はこちらを参照してください。
本稿は以上となります。最後までお付き合いいただき,ありがとうございました!






コメント