「2標本のt検定って,パターンが多くてわかりにくい」ですよね。また,「自由度m+n−2ってどこから出てきたの?」っていう疑問もよくありますね。この記事では,母平均の差の検定を「対応あり」と「対応なし」に分けて整理し,特に等分散を仮定できる場合の2標本のt検定についてカイ2乗分布との関係性を説明します。パターンを暗記してしまうのも1つのやり方ですが,この記事で紹介しているような導出ができるようになると,試験会場で忘れてしまったときにも動じることがなくなります。具体的な問題例を通して,わかりやすく説明していくので,ぜひついてきてほしいです。
2標本のt検定は論文を書くときなど,学問上の用途で使われるだけでなく,ビジネスでも使われます。例えば,企業がウェブサイトのデザインを決めるときに,パターンAとパターンBのどちらのほうがより大きな売上が見込めるかをテストすることがあります。これをABテストと言います。このABテストも,2つのパターンによる売上の差を比較していますので,母平均の差の検定と同じ考え方を使っています。
この記事で前提とする知識は,第7回の正規分布の内容,第8回のt分布の内容,第9回の区間推定で扱った中心極限定理の内容,第11回の仮説検定の内容,第13回のカイ2乗分布の内容になりますので,これらの内容に不安がある人は,先にそちらの記事を読んでください。では,はじめていきましょう!
母平均の差の検定
本題に入る前に,統計用語を確認しておきます。
標本の大きさ(サンプルサイズ)と標本数(サンプル数)という言葉は間違えやすいので注意しましょう。標本の大きさは,「1000人の有権者に聞いた」という場合の1000のことで,標本数というのは,標本のグループ(群)の数のことです。この記事では,2標本(標本数が2)の場合を考え,2つのグループ(群)の母平均に差があるかどうかを検定します。
さて,このような母平均の差の検定は,大きく分けて,次の2種類に分類できます。
- 対応のある2標本の検定
- 対応のない2標本の検定
さらに,対応のない2標本の検定は,次の3つに分類できます。
- 母分散が既知または大標本の場合
- 母分散が未知で等分散を仮定できる場合
- 母分散が未知で等分散でもない一般の場合(ウェルチのt検定)
以下では,これらを順に解説していきます。
対応のある2標本t検定
まず,2群のデータの間に1対1の対応(関連)がある場合を扱います。例えば,薬の効果を調べたりするときに有効なのは,同じ被験者に対して,薬を投与する前後で目的とする値(血圧など)を比較することです。同じ物や人を対象として,2回の測定値の平均に差があるかどうかを調べるのが,対応のある2標本t検定です。
対応するデータの差をとったとき,その差を表す確率変数Xが正規分布(期待値をμとする)に従うものとします。
大きさnの対応するデータに対して,差の標本平均をX,差の不偏分散をU2とすると,次の確率変数Tは自由度nー1のt分布に従います。
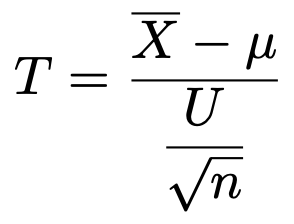
対応するデータの平均に差がない(μ=0)という帰無仮説を仮定し,次の式によって検定量を計算します。
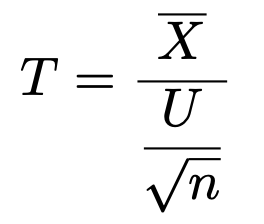
では,対応のある2標本t検定の問題を解いていきましょう。
【問題】ダイエット食品の効果を検証するため,無作為に選ばれた9人の被験者について,朝食をこのダイエット食品にかえて3か月過ごしてもらい,この3か月の直前と直後の体重を測定したところ,次の表のような結果が得られた。

このダイエット食品に体重を減少させる効果はあると言えるか,有意水準5%で検定しなさい。ただし,体重の差は同一の正規分布に従うものとし,必要ならば次のt分布表を用いなさい。
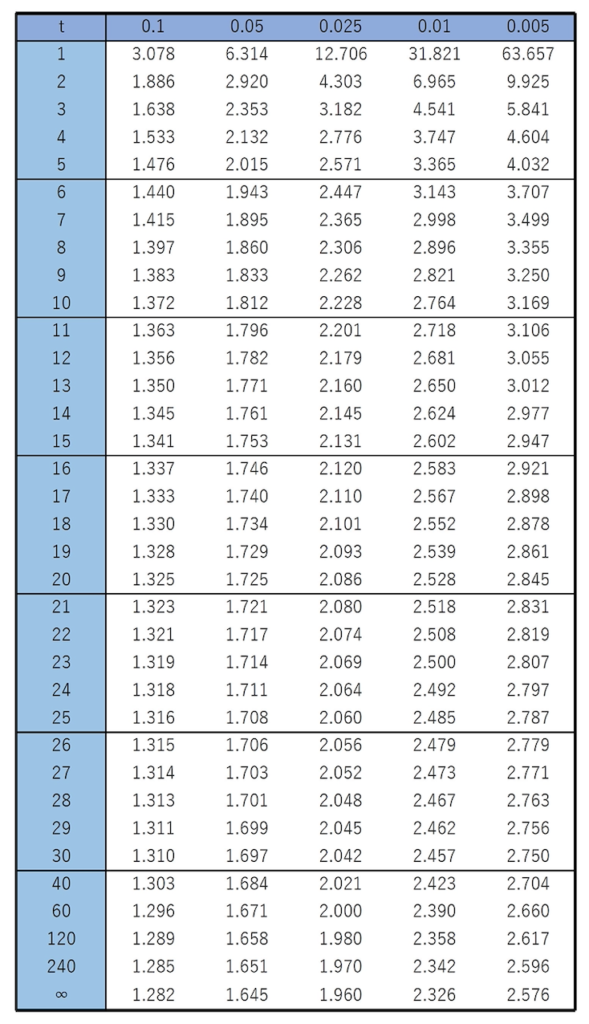
【解答】ダイエット食品を食べていた3か月間の直後の体重から直前の体重をひいた差をまとめると,次の表のようになります。
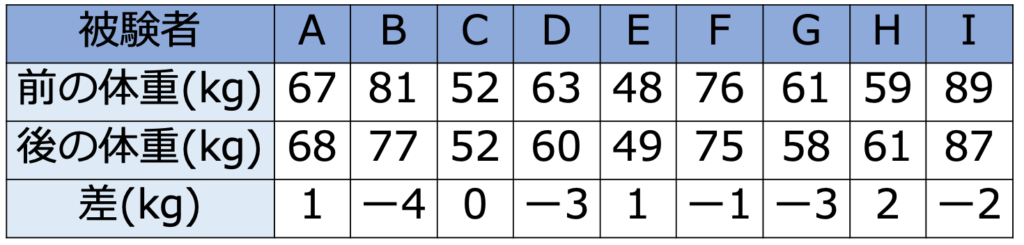
対応のある2標本t検定なので,体重の差を表す確率変数を考え,後の体重から前の体重をひいたものをXとします。Xが従う正規分布をN(μ,σ2)と表すと,帰無仮説はμ=0,対立仮説は,ダイエット食品に体重を減少させる効果があることを示したいので,μ<0となります。標本平均は次のように計算できます。
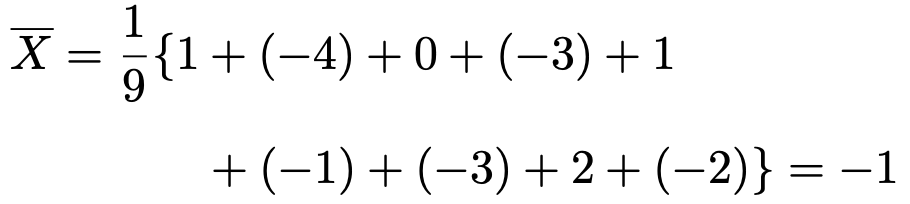
この値を使って,不偏分散は次のように計算できます。
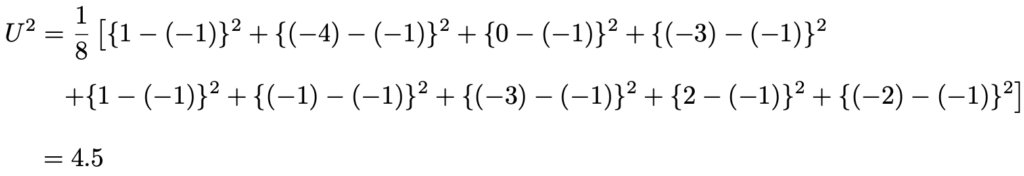
これらを使うと,検定量は次のように計算できます。
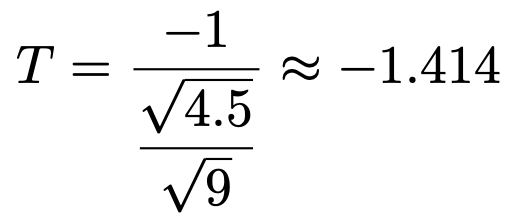
自由度8のt 分布の下側5%点はー1.86なので,この検定量の値は棄却域には入らないことになり,帰無仮説を受容します。このダイエット食品に体重を減少させる効果があるかどうか,どちらとも言えないという結論になります。
(解答終わり)
母分散既知または大標本の2標本z検定
対応がない場合というのは,確率変数が独立である場合と考えると良いです。
ここで,第7回の正規分布の記事や,第12回の母比率の差の記事でも紹介した「正規分布に従う独立な確率変数の差も正規分布に従う」という事実を振り返っておきます。
確率変数X,Yが独立で,それぞれ次の正規分布に従っているものとします。
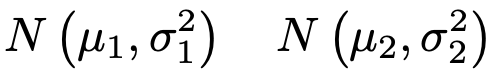
これらの母集団からそれぞれ大きさn1,n2の標本を無作為に抽出して得られる標本平均X,Yの従う確率分布は,次のようになります。
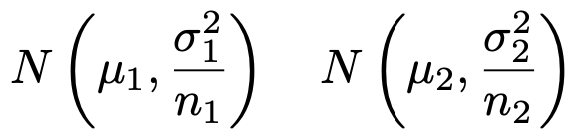
このとき,確率変数XーYは次の正規分布に従います。
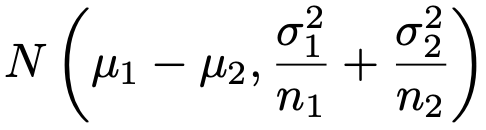
つまり,期待値は差に,分散は和になるんでしたね。ここまでは復習です。確率変数XーYを標準化すると次のようになります。
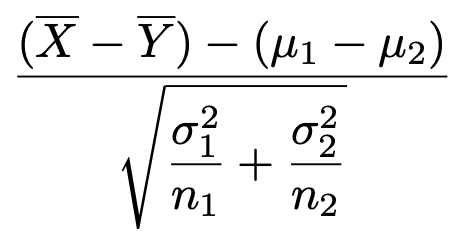
ここで,母平均の差の検定の帰無仮説μ1=μ2を適用すると,次の式が得られます。
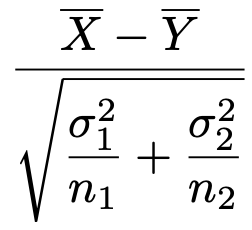
もし,母分散のσ12,σ22が既知であれば,この式を使って検定量を計算することができます。しかし,母平均に差があるかどうかを検定したいときに母分散が厳密にわかっているケースはあまりないと言えます。より現実的なのは,大標本で母分散がわからない場合です。標本の大きさが大きいとき,母集団が正規分布でなくとも,中心極限定理から標本平均は正規分布に従い,上の式が得られます。ただし,母分散はわからないという前提なので,上の式の母分散を標本から求められる不偏分散のU12,U22におきかえてしまうと,次のようになります。
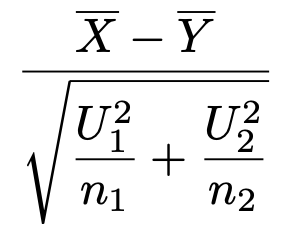
大標本のときには,この式から検定量を計算することができます。では,問題を解いてみましょう。
【問題】製品Aの組み立て工場で働く男性工員240人,女性工員250人を無作為に抽出し,製品Aを1個組み立てるのにかかる時間を調べたところ,男性工員について,標本平均は5.0分,標本の標準偏差は0.4分であり,女性工員について,標本平均は4.9分,標本の標準偏差は0.5分だった。男性工員と女性工員で,製品Aを1個組み立てるのにかかる時間に差があると言えるか,有意水準5%で検定しなさい。ただし,標本の標準偏差とは不偏分散の正の平方根のこととする。
【解答】男性工員の製品Aを1個組み立てるのにかかる時間の母平均をμ1,女性工員の製品Aを1個組み立てるのにかかる時間の母平均をμ2とすると,帰無仮説はμ1=μ2です。「差があるか,ないか」を問題にしたいときには,対立仮説はμ1≠μ2となり,両側検定になります。標本の大きさは十分に大きく,標本平均は正規分布に従うと考えられるので,検定量は次のように計算できます。
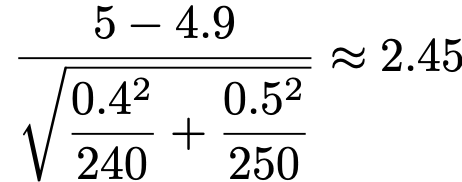
正規分布表から,標準正規分布の上側2.5%点は約1.96であるとわかるので,検定量の値は棄却域に落ちます。よって,有意水準5%で帰無仮説を棄却し,男性工員と女性工員の間で製品Aを1個組み立てるのにかかる時間の差があると言えます。
(解答終わり)
等分散仮定の2標本t検定(小標本)
このセクションでは,母分散σ12,σ22の値が未知であり,標本の大きさが小さい場合を考えます。前のセクションで導いた次の確率変数を思い出しましょう。
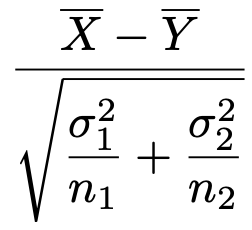
母集団が正規分布に従っているという仮定はそのままです。
さらに2つの母分散が等しいとすると,上の式で,σ12=σ22=σ2とおきかえて,次の式が得られます。
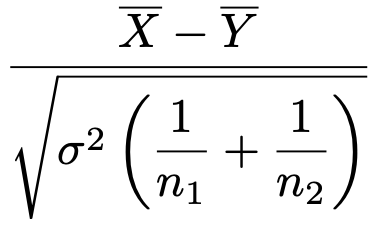
母分散の値がわからないので,分母のσ2を標本から求められる値におきかえたいですよね。ところが,標本平均X,Yは,別の母集団から抽出された標本から計算されているので,これまで学習してきた不偏分散ではうまくいきません。そこで,2つの母集団からそれぞれ抽出した大きさn1,n2の標本を次のように混ぜて計算したものを使います。
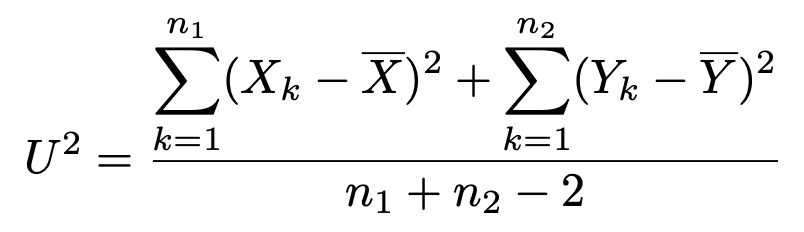
これまでの不偏分散から類推すれば,分母はn1+n2ー1になりそうですが,n1+n2ー2である点に注意が必要です。このU2をプールした分散と言います。ここでの「プールする」という言葉の意味は,「統合する」というようなものです。実際,プールした分散のことを,「統合分散」と呼ぶこともあります。さて,分母の母分散の代わりに,このプールした分散を使うと,次の確率変数が得られます。
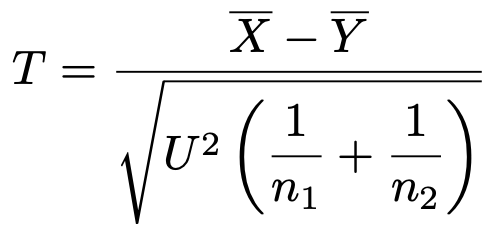
さて,ここで2つの疑問が残ります。1つ目は,プールした分散はなぜあの形をしているのか,ということです。2つ目は,プールした分散を使って表した確率変数Tが従う確率分布は何なのか,ということです。この疑問点を解決するために,正規分布とt分布,カイ2乗分布の間にある次のような関係を紹介しましょう。
2つの確率変数X,Yは互いに独立で,Xは標準正規分布に,Yは自由度nのカイ2乗分布に従うものとする。このとき,次の確率変数Tは自由度nのt分布に従う。
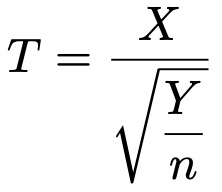
実は,この命題①から,第8回の記事で紹介した次のt分布の性質が導かれます。
次のようなN(μ,σ2)に従う大きさnの無作為標本を考える。
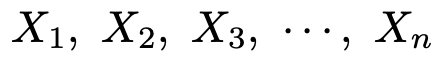
この標本から求められる標本平均をX,不偏分散をU2とするとき,次の確率変数Tは自由度nー1のt分布に従う。

第7回の正規分布の記事で説明したように,XがN(μ,σ2)に従うとすると,次の確率変数は標準正規分布に従います。
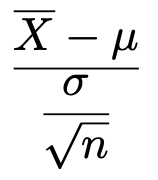
また,第13回のカイ2乗分布の記事で説明したように,同じ母集団から無作為抽出した大きさnの標本から得られる不偏分散をU2として,次の確率変数が自由度n−1のカイ2乗分布に従うんでしたね。
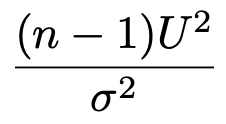
よって,上の命題①から,次のTは自由度nー1のt分布に従うことになるので,命題②が導けたことになります。
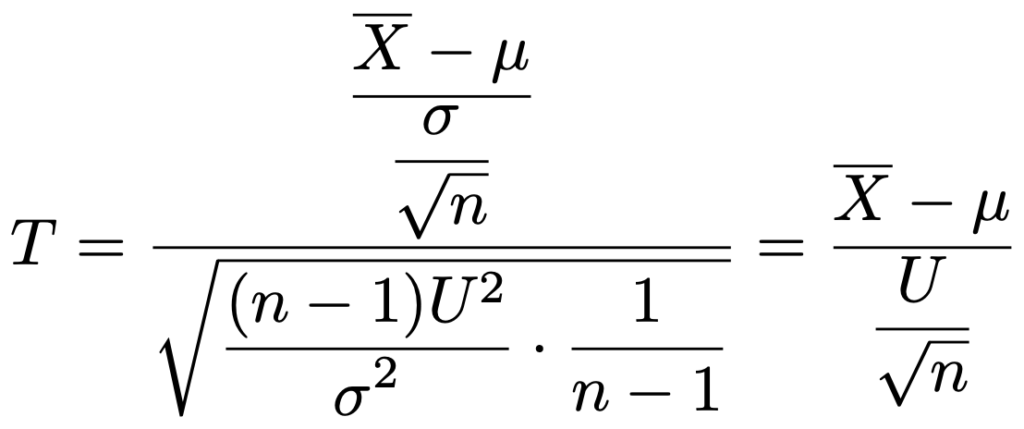
さて,プールした分散の話に戻ります。
母分散がともにσ2で等しい2つの正規母集団から無作為標本(標本の大きさはそれぞれn1,n2)を抽出し,不偏分散をそれぞれU12,U22(これらは独立であると仮定)とします。このとき,第13回の記事で説明したように,次の確率変数はそれぞれ自由度n1ー1,n2ー1のカイ2乗分布に従います。
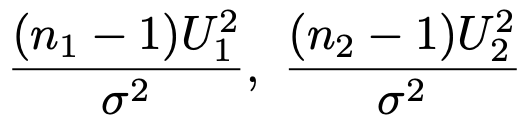
これらは独立なので,カイ2乗分布の性質から,次の確率変数は自由度n1+n2ー2のカイ2乗分布に従います。
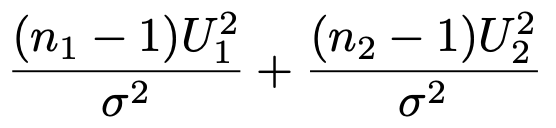
よって,次の確率変数Tは,右辺の分子が標準正規分布に従う確率変数で,右辺の分母のルートの中が自由度n1+n2ー2のカイ2乗分布に従う確率変数をその自由度でわったものなので,上の命題①から自由度n1+n2ー2のt分布に従います。
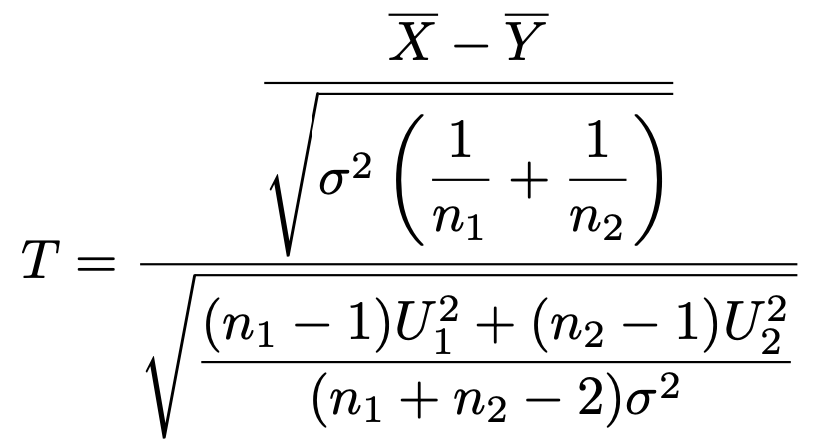
このTの式の右辺を整理すると,次のようになります。
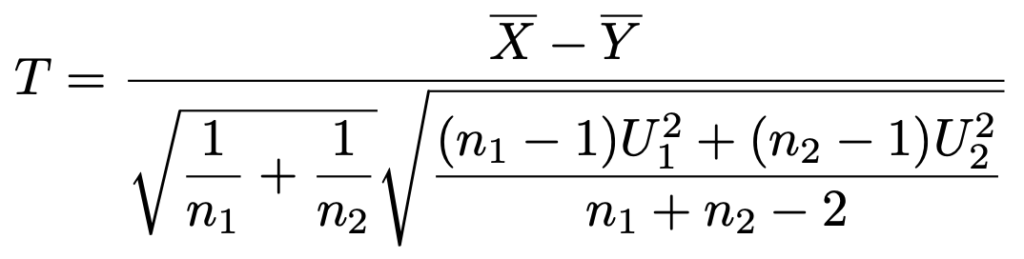
ここで,プールした分散をU2で表すと,次の式が得られます。
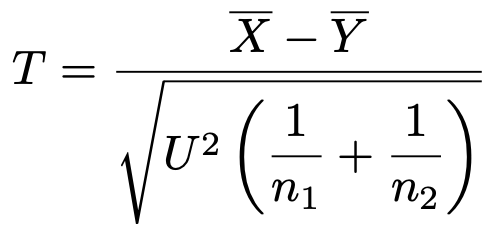
これでプールした分散の式の形の理由と,Tが自由度n1+n2ー2のt分布に従うことがわかりました。では,問題を解いてみましょう。
【問題】ある植物Aについて,2つの肥料P,Qを用いて,発芽してから植物Aの背丈が1mを超えるまでの日数を調べた。肥料Pを与えた植物Aのうち無作為に選んだ26本と肥料Qを与えた植物Aのうち無作為に選んだ36本について,標本の平均と偏差平方和は次の表(左が肥料P,右が肥料Q)の通りだった。

肥料P,Qについて,植物Aの背丈が1mを超えるまでの日数は分散の等しい独立な正規分布に従うものとして,母平均に差はあるか有意水準5%で検定しなさい。必要ならば上のt分布表を用いなさい。
【解答】肥料Pを与えた植物Aの背丈が1mを超えるまでの日数の母平均をμ1,肥料Qを与えた植物Aの背丈が1mを超えるまでの日数の母平均をμ2とすると,帰無仮説はμ1=μ2です。もし,肥料Qが肥料Pの改良版である場合ならば,その効果を検証するために片側検定を使いますが,ここでは,PとQに差があるかどうかを調べる目的の検定と捉えて,対立仮説をμ1≠μ2とし,両側検定を行います。まず,プールした分散は次のように計算できます。
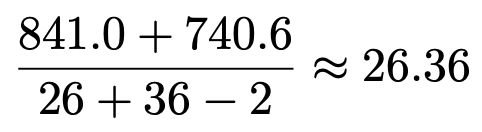
この値を使うと,検定量は次のように計算できます。
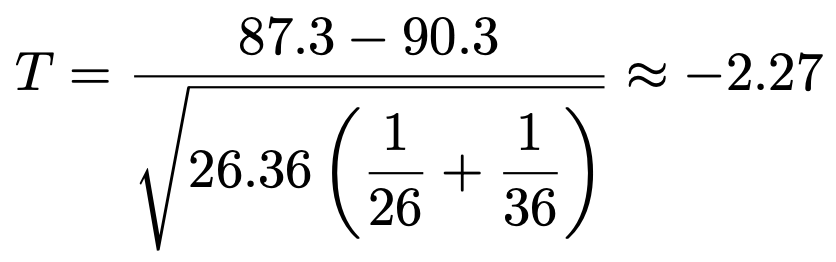
26+36ー2=60より,このTは自由度60のt分布に従います。t分布表から,自由度60のt分布の上側2.5%点は約2.0であるとわかるので,検定量の値は棄却域に落ちます。よって,有意水準5%で帰無仮説を棄却して,対立仮説を採択します。つまり,肥料PとQでは,植物Aの背丈が1mを超えるまでの日数の母平均に差があると言えます。
(解答終わり)
ウェルチのt検定
標本の大きさが小さいとき,等分散であるかどうかにかかわらず,より一般的な場合に使えるのが,ウェルチのt検定です。第14回で解説したF分布を使った等分散仮説の検定をはじめに行い,等分散仮説が受容されたら等分散仮定のt検定,等分散仮説が棄却されたらウェルチのt検定を行うと解説している本もありますが,二重に検定を行うことには問題点があり,現在では等分散が仮定できる場合もそうでない場合もウェルチのt検定を行うのがよいとされています。
大標本のときに検定量を計算するものとして紹介した次の確率変数を考えます。
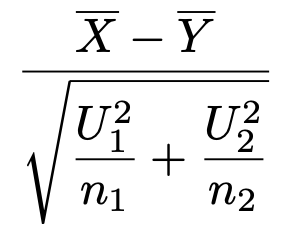
これが近似的に次の自由度のt分布に従うというのがウェルチのt検定です。
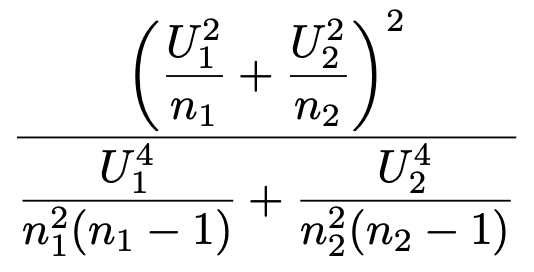
ちなみに,ウェルチというのは,この手法を発見した統計学者B.L.Welch(1911-1989)を指しています。ウェルチのt検定の場合,自由度は必ずしも整数にならないため,通常は統計ソフトを使って計算します。電卓で計算することも可能ですが,この自由度の式を覚えていなければならないことと,近似計算の扱いの難しさがあり,統計検定2級では出題されることはないと考えられますので,ここでは紹介だけにとどめておきます。
母平均の差の検定についての基本的な説明は以上になります。この後は,参考図書の紹介に続けて,さらに理解を深めるための演習問題を用意していますので,余力があればぜひチャレンジしてみてください。
参考図書
本稿を執筆するにあたり,参考にした図書を3つ挙げます。
①基本統計学[第5版](宮川公男,有斐閣)
母分散未知で大標本の場合と小標本で等分散を仮定できる場合が扱われています。特に,後者については2ページを割いて解説されています。
②入門統計解析(倉田博史・星野崇宏,新世社)
母分散既知の場合と小標本で等分散を仮定できる場合が扱われています。特に,後者の場合のプールした分散とカイ2乗分布との関係について参考にさせてもらいました。
③入門統計学,第2版(栗原伸一,オーム社)
対応のある場合とない場合に分けて,しっかりと解説されています。
演習1〜対応のある2標本t検定〜
【問題】無作為に選ばれた7人の被験者に,朝起きた直後の体温と起きてから3時間後の体温をそれぞれ測定してもらったところ,次の表のような結果が得られた。

起床直後の体温より起床3時間後の体温のほうが高いと言えるか,有意水準5%で検定しなさい。ただし,体温の差は同一の正規分布に従うものとし,必要ならば上のt分布表を用いなさい。
【解答】起床3時間後の体温から起床直後の体温をひいた差をまとめると,次の表のようになります。
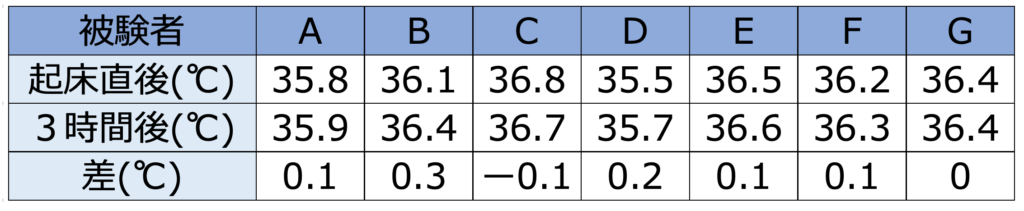
対応のある2標本t検定なので,この差を表す確率変数をXとします。Xが従う正規分布をN(μ,σ2)と表すと,帰無仮説はμ=0です。3時間後のほうが体温が高いことを示すのが目的であると考えられるので,対立仮説はμ>0となり,片側検定です。
まず,標本平均は次のように計算できます。
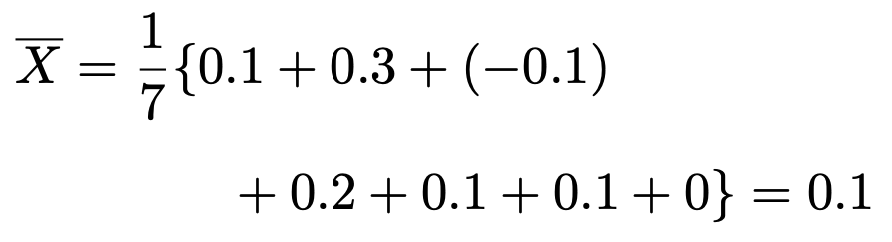
この値を使って,不偏分散は次のように計算できます。
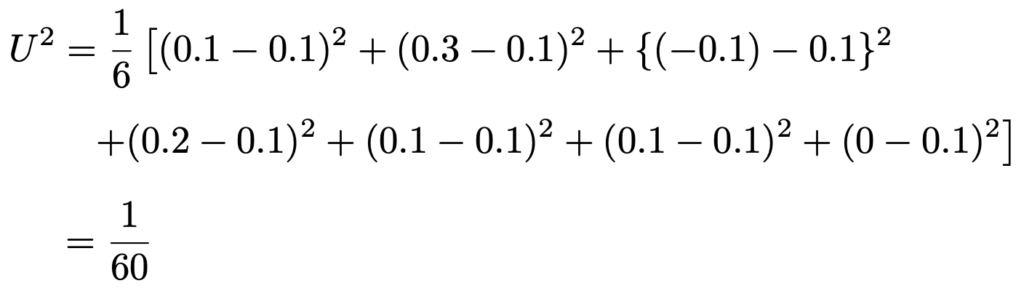
これらを使うと,検定量は次のように計算できます。
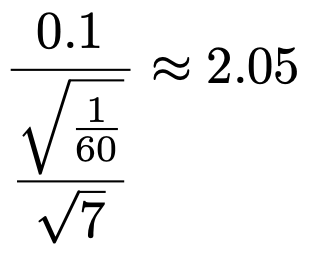
自由度6のt 分布の上側5%点は約1.943なので,この検定量の値は棄却域に落ちます。帰無仮説を棄却し,対立仮説を採択します。つまり,起床直後の体温より起床3時間後の体温のほうが高いと言えます。
(解答終わり)
演習2〜大標本の2標本z検定〜
【問題】A予備校が提供する数学のオンデマンド講座を受講した高校3年生360人と,B予備校が提供する数学のオンデマンド講座を受講した高校3年生450人を無作為に抽出し,受講終了時に同一の数学の試験を受けてもらったところ,A予備校の講座を受講した生徒の得点の標本平均は71.2点,標本の標準偏差は10.6点であった。また,B予備校の講座を受講した生徒の得点の標本平均は73.3点,標本の標準偏差は9.9点だった。A予備校の講座を受講した生徒とB予備校の講座を受講した生徒で,数学の得点力に差があると言えるか,有意水準1%で検定しなさい。ただし,標本の標準偏差とは不偏分散の正の平方根のこととする。
【解答】A予備校の講座を受講した高校生の得点の母平均をμ1,B予備校の講座を受講した高校生の得点の母平均をμ2とすると,帰無仮説はμ1=μ2,対立仮説はμ1≠μ2となり,両側検定になります。標本の大きさは十分に大きく,標本平均は正規分布に従うと考えられるので,検定量は次のように計算できます。
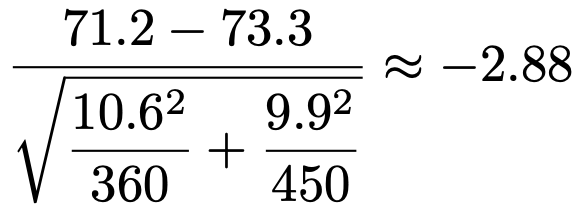
正規分布表から,標準正規分布の上側0.5%点はおよそ2.58であるとわかるので,下側0.5%点はおよそー2.58であり,検定量の値は棄却域に落ちます。よって,有意水準1%で帰無仮説を棄却し,A予備校の講座を受講した生徒とB予備校の講座を受講した生徒の数学の得点力に差があると言えます。
(解答終わり)
演習3〜等分散仮定の2標本t検定〜
【問題】湖Aと湖Bに共通して生息するある淡水魚の体長を調べる実験を行った。湖Aから釣り上げた20匹について,標本平均は35.7cm,標本の標準偏差は4.3cmであり,湖Bから釣り上げた22匹について,標本平均は34.2cm,標本の標準偏差は3.5cmだった。この淡水魚の体長は,湖Aと湖Bで差があると言えるか,有意水準5%で検定しなさい。ただし,湖Aと湖Bに生息するこの淡水魚の体長はそれぞれ正規分布に従うものとし,母分散は等しいものとする。また,標本の標準偏差とは不偏分散の正の平方根のこととする。必要ならば上のt分布表を用いなさい。
【解答】湖Aに生息するこの淡水魚の体長の母平均をμ1,湖Bに生息するこの淡水魚の体長の母平均をμ2とすると,帰無仮説はμ1=μ2,対立仮説はμ1≠μ2となり,両側検定になります。まず,プールした分散は次のように計算できます。
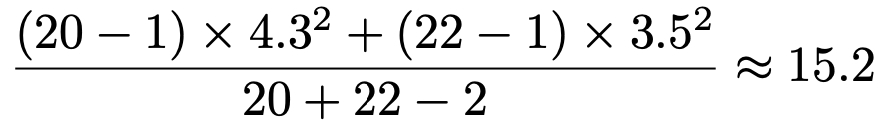
この値を使うと,検定量は次のように計算できます。
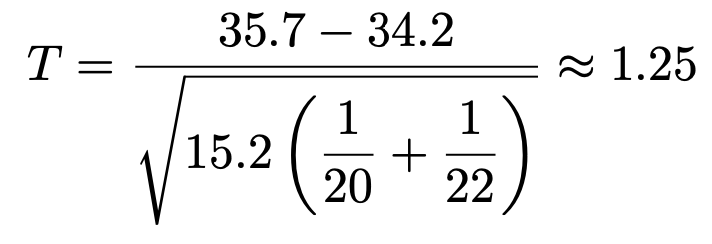
t分布表から,自由度40のt分布の上側2.5%点は約2.021であるとわかるので,検定量の値は棄却域には入りません。よって,有意水準5%で帰無仮説を受容し,湖Aと湖Bでこの淡水魚の体長に差があるとは言えないことになります。
(解答終わり)
第15回は以上となります。最後までお付き合いいただき,ありがとうございました!
引き続き,第16回以降の記事へ進んでいきましょう!
2023年1月に「統計検定2級公式問題集[CBT対応版](実務教育出版)」が発売されました!(CBTが何かわからない人はこちら)
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが,本書は分野ごとにその形式の問題を並べた構成になっていて,最後に模擬テストがついています。CBT対策の新たな心強い味方ですね!
さらに実戦に向けた演習を積みたい人は,「統計検定2級公式問題集2018〜2021年(実務教育出版)」を手に取ってみてください!
また,もっと別の問題を解いてみたい人は,さらにさかのぼって「統計検定2級公式問題集2016〜2017年(実務教育出版)」を解いて実力に磨きをかけましょう!





![統計検定2級公式問題集[CBT対応版]](https://m.media-amazon.com/images/I/51q3GfZId3L._SL500_.jpg)




コメント
とてもわかりやすいです。ありがとうございます。
統計webで手が届かない内容が書かれていて使いやすいです。