F分布【中学の数学からはじめる統計検定２級講座第14回】

「F分布の自由度２つもあるの？　どう違うの？　何の役に立つの？」なんて疑問ありますよね！　そんな人のために，「F分布とは何か」「F分布の２つの自由度を逆にするとどうなるのか」「どんなときにF分布を使うのか」についてわかりやすく説明していきます。

予備知識として，F分布とカイ二乗分布の関係を理解するため第13回の記事の内容と，不偏分散の比を利用した等分散仮説の検定を解説するため第11回の仮説検定の内容の理解を仮定します。これらの内容に不安がある人は，先にそちらの記事を読んでください。では，はじめていきましょう！

F分布【中学の数学からはじめる統計検定２級講座第14回】

F分布とは

唐突に難しい式をお見せしますが，この後の計算で使うことはありませんので，恐れなくても大丈夫です。では，F分布の定義です。

確率密度関数が次の式で表されるような確率分布を自由度(m，n)のF分布と言います。

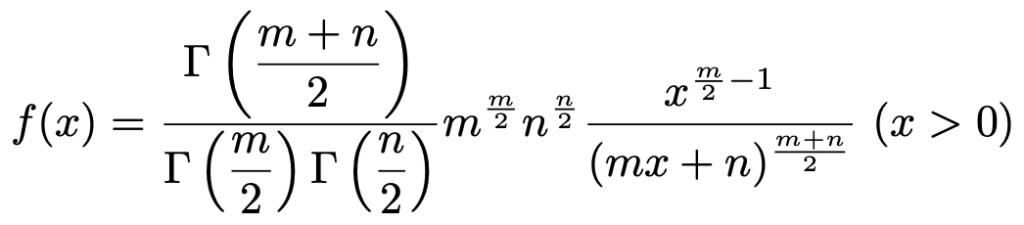
ただし，x≦０では，f(x)=0と定義します。

m，nは自然数で，Γ(s)はt分布やカイ２乗分布の確率密度関数にも登場したガンマ関数です。

ちなみに，F分布のFは，統計学者フィッシャー(1890〜1962)の頭文字をとったものです。

正規分布やt分布，カイ２乗分布の場合と同様に，F分布の確率は表にまとまっていますので，この式を覚える必要はありませんが，m，nを決めることでただ１つのxの関数が定まるんだな，ということを感じとってもらえればと思います。このm，nのことを自由度と呼びます。mを第１自由度，nを第２自由度と呼ぶことがあります。カイ２乗分布やt分布のときには自由度と呼ばれる文字は１つだけだったのに，F分布にはそれが２つもあるということで，複雑になったような気がしてしまいますが，大丈夫です。順を追って説明していきますので，慣れていきましょう。

自由度(m，n)のF分布のことを次のように表すことがあります。

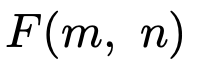
F分布は次の性質が特徴的です。

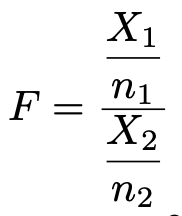
つまり，カイ２乗分布に従う２つの確率変数をその自由度でわったものの比がF分布に従うわけです。このFの確率密度関数がF分布のそれに一致することの証明は難しいので，ここでは省略しますが，どうしても知りたい人は，「確率・統計入門（小針晛宏著，岩波書店）」を参照してください。

このとき，Fの逆数として定められる次の確率変数は，自由度(n₂，n₁)のF分布に従います。

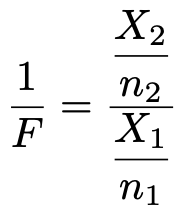
つまり，F分布に従う確率変数の逆数をとることは，２つの自由度を入れ替えることに相当します。

F分布のグラフ

F分布のグラフの形は，一見するとカイ２乗分布のグラフに似ています。左右非対称で，第１自由度が３以上ならば山が１つのグラフになるからです。

例えば，自由度(5，5)のF分布のグラフは次のようになります。

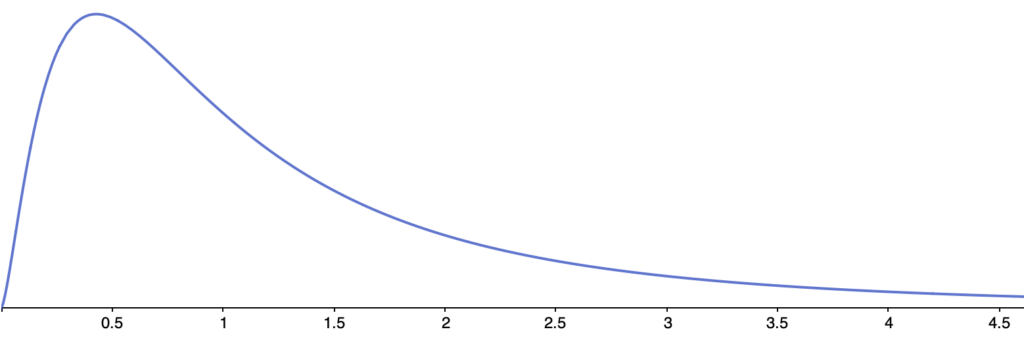
自由度(5，20)のF分布のグラフは次のようになります。

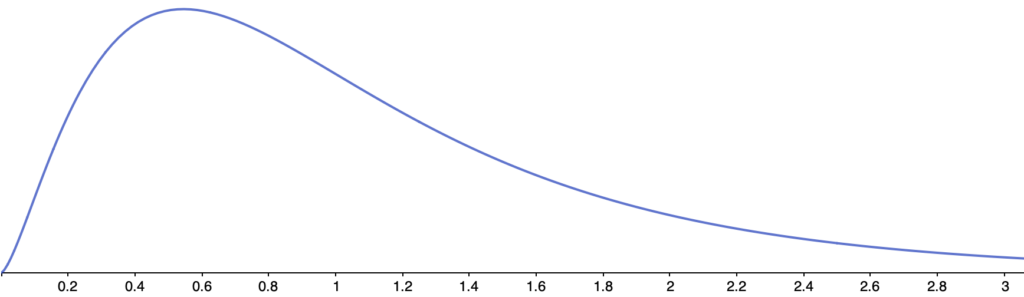
自由度(20，5)のF分布のグラフは次のようになります。上のグラフと比べると，自由度を入れ替えることで，グラフの形が変わっていることが確認できますね。

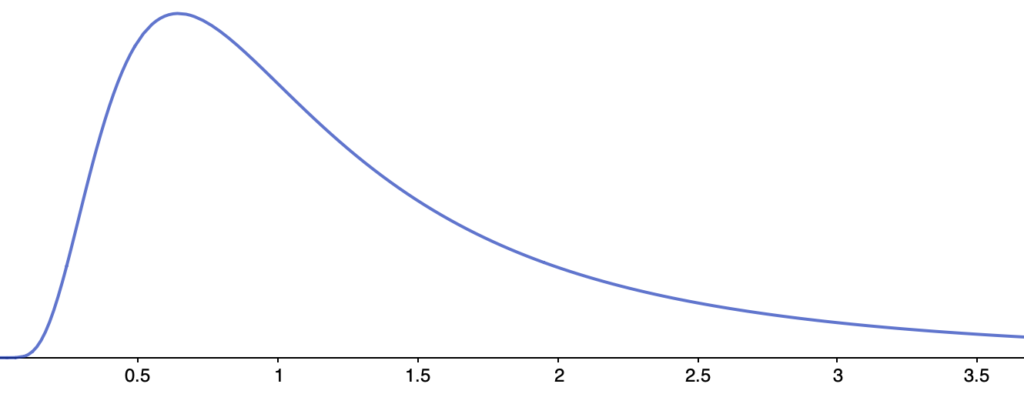
自由度(20，100)のF分布のグラフは次のようになります。

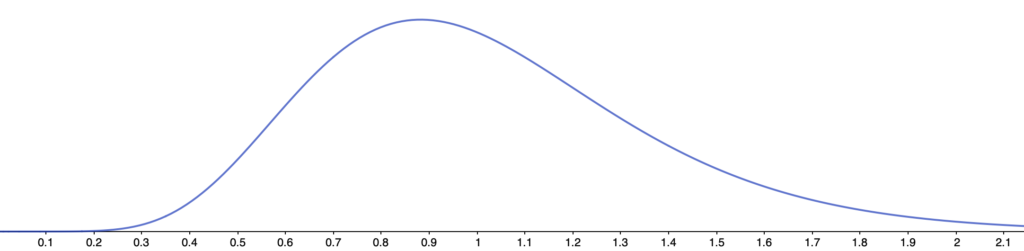
このように，F分布のグラフは横軸の目盛りで１の近くに山のピークがある点で，カイ２乗分布のグラフとは違いが見られます。これは，確率変数Xが自由度(m，n)のF分布に従うとき，その期待値が次のようになることに対応しています。

nが大きくなるにつれて，この期待値は１に近づいていきます。ただし，期待値と山のピークがある点が一致するわけではないので，ご注意ください。

F分布の確率

F分布に従う確率変数の確率は，正規分布やt分布，カイ２乗分布の場合と同じように，表を使って求めます。統計学のテキストには，次のようなF分布表が載っています。

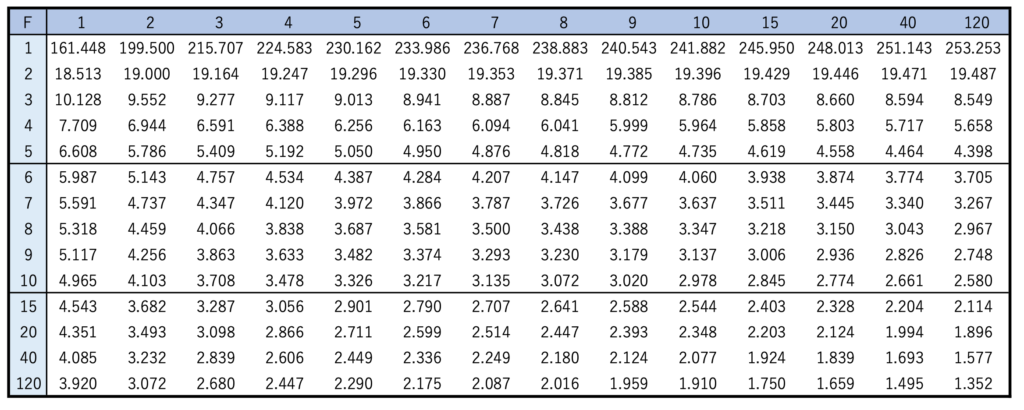
この表は，上側確率5％に特化したものです。いちばん上の行は第１自由度を，いちばん左の列は第２自由度を表しています。これらが交差したところに書かれている数が，上側5％点になります。上側確率5％だけでなく，上側確率2.5％や上側確率１％の表を掲載しているテキストもありますが，表の使い方は同じなので，この記事では上側確率5％の表のみを使って解説していきます。

なお，F分布表に記載されている自由度はとびとびの値になっています。記載されていない自由度については，前後の値から推定する必要がありますが，そのような問題が統計検定２級で出題されていないので，この記事では上記のF分布表から読み取れる値のみを使って解答できる問題のみを扱います。

では，実際に問題を解いていきましょう。

【問題】Xが自由度(7，5)のF分布に従うとき，次の式を満たすaの値をそれぞれ小数第２位まで求めなさい。

【解答】

（１）求めるものは，Xがa以上となる確率が５％となるようなaの値，つまり上側５％点です。これはF分布表を読み取れば，そのまま答えになります。次の図のように，上側5％点を示したF分布表において，いちばん上の行で７のところを縦に見ていき，いちばん左の列で５のところを横に見ていきます。

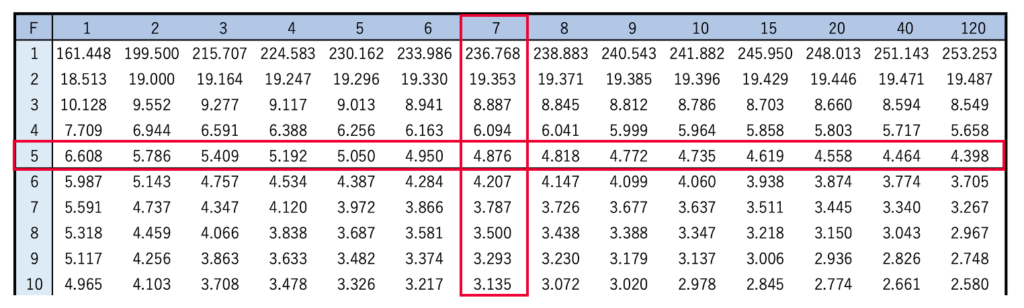
交わったところが求める上側５％点だから，小数第３位で四捨五入すると，a＝4.88

（２）求めるものは，Xがa以上となる確率が95％となるようなaの値ですが，言い換えると下側５％点を求めなさい，という問題です。式で表すと，次のようになります。

この式のかっこの中の不等式の両辺をaXでわると，次のようになります。

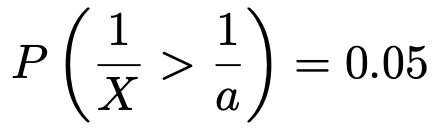
これで１/Xの上側５％点を求める問題に変わりました。そして，Xが自由度(7，5)のF分布に従うとき，すでに説明したF分布の性質から，１/Xは自由度(５，７)のF分布に従うんですよね。次の図のように，上側5％点を示したF分布表において，いちばん上の行で５のところを縦に見ていき，いちばん左の列で７のところを横に見ていきます。

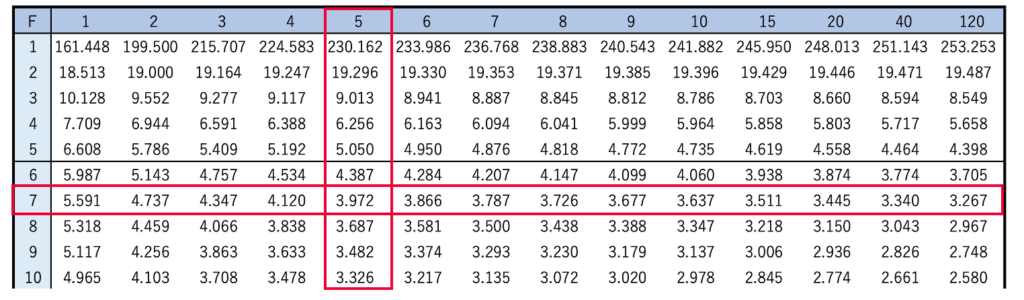
交わったところが上側５％点だから，3.972です。式で表すと，次のようになります。

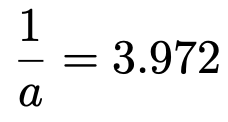
逆数をとって，小数第２位までで求めると，答えは次のようになります。

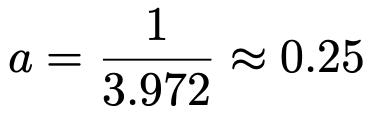
（解答終わり）

F分布表の上側５％点はすべて１より大きい値になっているので，上の問題の下側５％点の求め方を考えれば，下側５％点は逆に１より小さくなる点に注意しましょう。

等分散仮説の検定

２つの正規母集団を考え，それぞれの母標準偏差をσ₁，σ₂とします。これらの母分散の値がわからないとき，帰無仮説を「２つの母分散が等しい」とし，対立仮説を「一方の母分散が他方より大きい（または，等しくない）」とする検定を等分散仮説の検定と言います。

２つの正規母集団の無作為標本（標本の大きさはそれぞれn₁，n₂）から得られる不偏分散をU₁，U₂とし，これらが独立であるものとします。このとき，第13回の記事で説明したように，次の確率変数はそれぞれ自由度n₁ー１，n₂ー１のカイ２乗分布に従います。

したがって，これらを自由度でわって，比をとってできる次の確率変数Fは自由度(n₁ー１，n₂ー１)のF分布に従います。

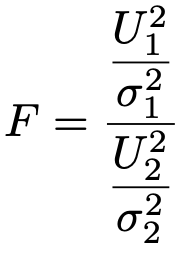
ここで，帰無仮説σ₁²＝σ₂²を仮定すると，不偏分散の比になりますね。ここに不偏分散の実現値を代入すれば，検定量が計算できます。

では，実戦的な問題を解いていきましょう。

【問題】A県について，無作為に抽出した７年間の年間快晴日数は，25，39，30，27，25，34，37（日）だった。また，B県について，無作為に抽出した６年間の年間快晴日数は，18，16，35，37，15，41（日）だった。A県，B県の年間快晴日数はそれぞれ独立に正規分布に従うものとし，母分散をそれぞれσ_A²，σ_B²とする。帰無仮説をσ_A²＝σ_B²，対立仮説をσ_A²＜σ_B²とし，有意水準５％で検定しなさい。

【解答】対立仮説が不等号を使って表されているので，片側検定です。不偏分散を求めるために，まずは標本平均を求めます。A県については次のようになります。

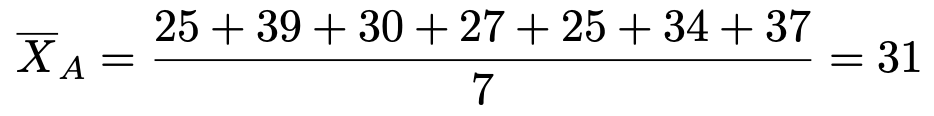
B県については次のようになります。

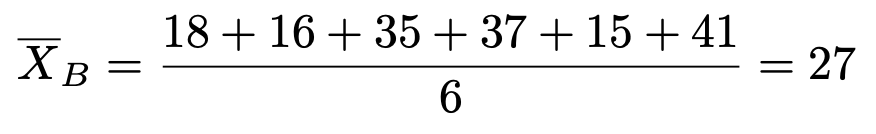
次に，A県の不偏分散は次のようになります。

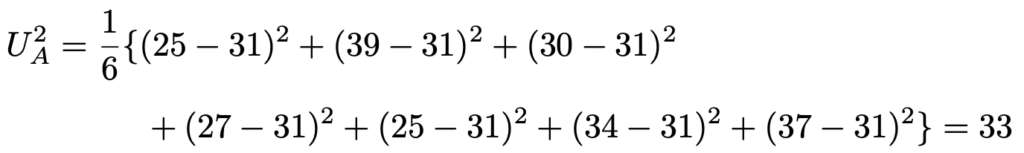
B県の不偏分散は次のようになります。

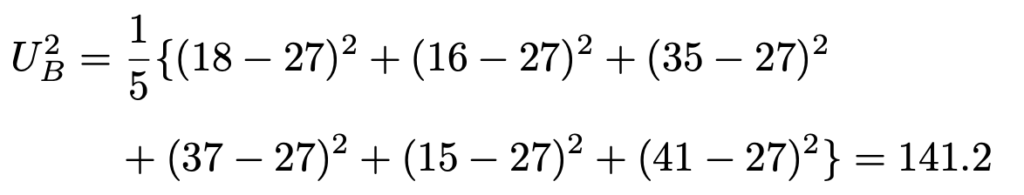
このとき，次の確率変数Fは自由度(５，６)のF分布に従います。

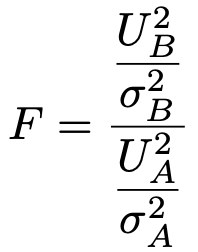
このFは，帰無仮説σ_A²＝σ_B²のもとで，次のように書き直すことができ，自由度(５，６)のF分布に従います。

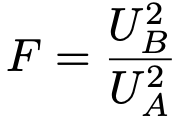
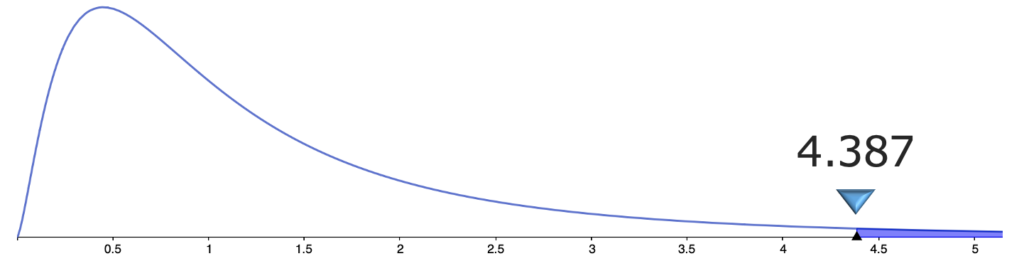
有意水準５％なので，自由度(５，６)のF分布の上側５％点をF分布表から調べると，4.387であることがわかり，棄却域を図に表すと，次の図の色のついた部分になります。

検定量を計算すると，次のようになります。

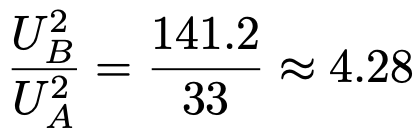
4.28＜4.387より，4.28は棄却域に入らず，有意水準５％で帰無仮説を受容します。年間快晴日数の母分散の大小について，結論は出せないことになります。

（解答終わり）

F分布についての基本的な説明は以上になります。この後は，参考図書の紹介に続けて，さらに理解を深めるための演習問題ですので，余力があればぜひチャレンジしてみてください。

参考図書

本稿を執筆するにあたり，次の書籍を参考にしました。

基本統計学　第５版（宮川公男，有斐閣）

等分散仮説の検定で，不偏分散の比が統計量になることがわかりやすく書かれており，下側５％点の求め方にも言及されています。

演習１〜F分布の確率〜

【問題】Xが自由度(8，6)のF分布に従うとき，次の式を満たすaの値を小数第２位まで求めなさい。

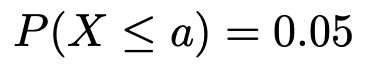
【解答】下側５％点を求めなさい，という問題です。この式のかっこの中の不等式の両辺をaXでわると，次のようになります。

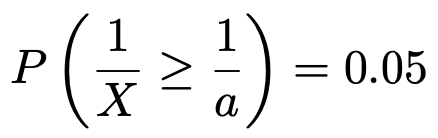
この式を言葉に直すと，1/Xの上側５％点が1/aだということです。そして，Xが自由度(８，６)のF分布に従うとき，１/Xは自由度(６，８)のF分布に従うんですよね。次のように，上側5％点を示したF分布表において，いちばん上の行で６のところを縦に見ていき，いちばん左の列で８のところを横に見ていきます。

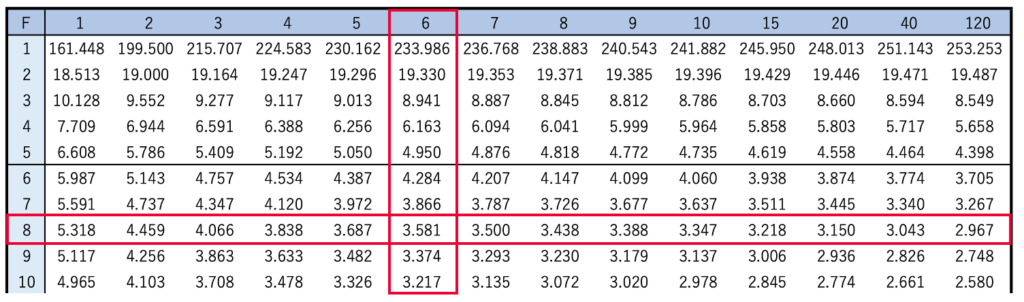
交わったところが上側５％点だから，3.581です。式で表すと，次のようになります。

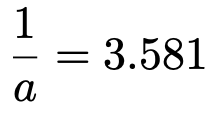
逆数をとって，小数第２位までで求めると，答えは次のようになります。

（解答終わり）

演習２〜カイ２乗分布とF分布の確率〜

【問題】次の確率変数が互いに独立に標準正規分布に従うものとします。

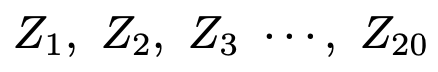
ここで，確率変数Xを次のように定めます。

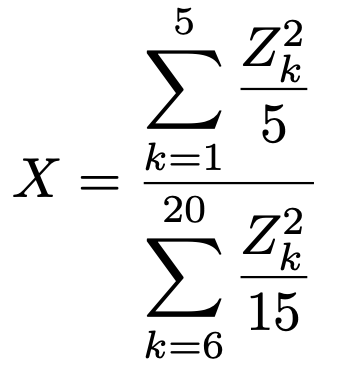
このとき，次の式を満たすaの値を小数第２位まで求めなさい。

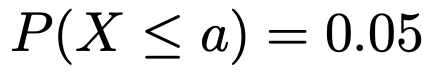
【解答】まず，Xの定義式を見て，「あ〜，あれね！」と思えるでしょうか。分子を書き直すと，次のようになります。

５つの標準正規分布に従う確率変数の２乗の和は自由度５のカイ２乗分布に従います。それを自由度の５でわっているんです。また，分母は15個の標準正規分布に従う確率変数の２乗の和（自由度15のカイ２乗分布）を自由度の15でわっています。すでに説明した命題から，XはF(5，15)に従うことがわかりますね。

次に求めるものを確認します。次の式のaを求めることは，「下側５％点を求めなさい」ということです。

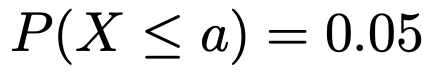
ところが，F分布表からは上側５％点しかわからないんでしたよね。そこで，上の式のかっこの中の不等式の両辺をaXでわると，次のようになります。

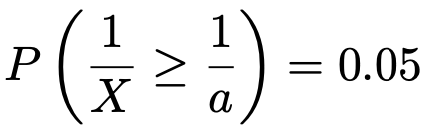
これで１/Xの上側５％点を求める問題に変わりました。XがF(5，15)に従うとき，1/XはF(15，5)に従うので，F分布表から自由度(15，5)のF分布の上側５％点は4.619とわかります。つまり，次の式が成り立ちます。

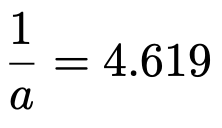
さらに逆数をとって，aの値を小数第２位まで求めると，次のようになります。

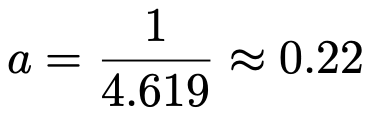
（解答終わり）

演習３〜等分散仮説の検定〜

【問題】あるメーカーが製造している商品Pについて，A工場で無作為に抽出した21日間の製造個数の不偏分散は322，B工場で無作為に抽出した11日間の製造個数の不偏分散は841だった。A，Bの工場での１日あたりの商品Pの製造個数はそれぞれ独立に正規分布に従うものとし，母分散をそれぞれσ_A²，σ_B²とする。帰無仮説をσ_A²＝σ_B²，対立仮説をσ_A²＜σ_B²とし，有意水準５％で検定しなさい。

【解答】対立仮説が不等号を使って表されているので，片側検定です。A工場，B工場について，標本から求められる不偏分散をそれぞれU_A²，U_B²とすると，次の確率変数Fは自由度(11ー１，21ー１)＝(10，20)のF分布に従います。

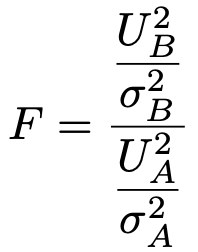
このFは，帰無仮説σ_A²＝σ_B²のもとで，次のように書き直すことができ，自由度(10，20)のF分布に従います。

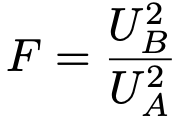
有意水準５％なので，自由度(10，20)のF分布の上側５％点をF分布表から調べると，2.348であることがわかり，棄却域を図に表すと，次の図の色のついた部分になります。

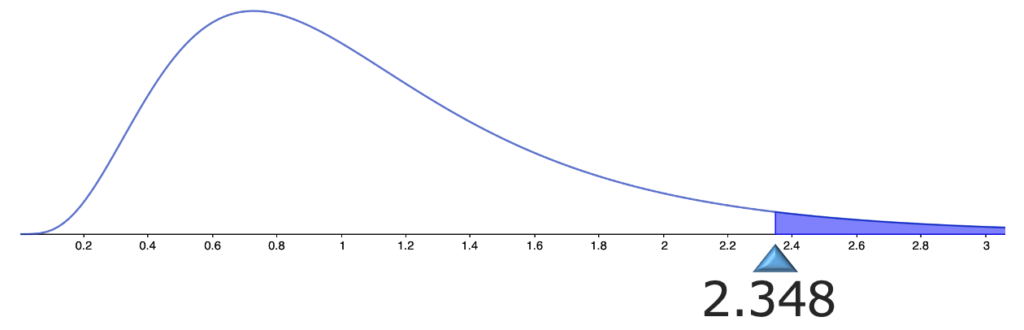
検定量を計算すると，次のようになります。

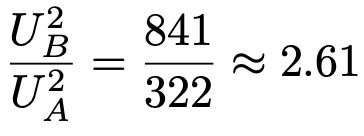
2.348＜2.61より，2.61は棄却域に落ちるので，有意水準５％で帰無仮説を棄却し，対立仮説を採択します。つまり，製造個数の母分散は，B工場のほうが大きいと言えます。

（解答終わり）

最後までお付き合いいただき，ありがとうございました！
引き続き，第15回以降の記事へ進んでいきましょう！

2023年1月に「統計検定２級公式問題集[CBT対応版]（実務教育出版）」が発売されました！（CBTが何かわからない人はこちら）
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが，本書は分野ごとにその形式の問題を並べた構成になっていて，最後に模擬テストがついています。CBT対策の新たな心強い味方ですね！

さらに実戦に向けた演習を積みたい人は，「統計検定２級公式問題集2018〜2021年（実務教育出版）」を手に取ってみてください。

また，もっと別の問題を解いてみたい人は，さらにさかのぼって「統計検定２級公式問題集2016〜2017年（実務教育出版）」を解いて実力に磨きをかけましょう！