カイ2乗分布は統計学の初心者にとっては難しいですよね。そもそも「カイ(χ)って何?」ってなりますから。そんな苦手意識を持つ人に向けて,「カイ2乗」という名前の由来からはじめて,確率の求め方,グラフの特徴,母分散の推定と検定への応用,適合度検定について例題を解きながらわかりやすく解説していきます。
この記事で前提とする知識は,第7回の正規分布の内容,第8回のt分布の内容,第9回の母平均の区間推定の内容,第11回の仮説検定の内容になります。これらの内容に不安がある人は,先にそちらの記事を読んでください。
なお,カイ2乗分布と,正規分布,t分布との間に成り立つ関係式については第15回の記事で扱います。また,独立性の検定については別の記事(リンクはこちら)で解説しています。
では,はじめていきましょう!
カイ2乗分布
確率密度関数が次の式で表されるような確率分布を自由度nのカイ2乗分布と言います。
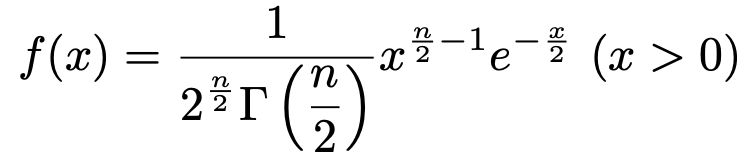
ただし,x≦0では,f(x)=0と定義します。
この式をはじめて見るとギョッとしてしまうかもしれませんが,大丈夫です。カイ2乗分布の確率は,正規分布やt分布の場合と同様に,表にまとまっていますので,この式を覚える必要はありません。
カイ2乗分布の確率密度関数は,t分布の確率密度関数と同様に,nを決めることでただ1つのxの関数が定まります。このnのことを,t分布のときと同様に,自由度と呼びます。Γ(s)はt分布の確率密度関数にも登場したガンマ関数です。
自由度nのカイ2乗分布のことを次のように表すことがあります。
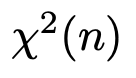
最初の文字がギリシア文字の「カイ」であり,アルファベットのxに対応します。「カイ2乗」という名称はひとまとまりで捉えるべきで,「カイ」が表す数学的な対象があるわけではないので,「カイ」の「2乗」と考えないほうがいいです。ギリシア文字のχを使って,はじめてχ2と表したのは統計学者のピアソンで,論文の中で確率変数の2乗の和を表すのに,Xを使うと他の文字と区別がつきにくいため,この文字を使用したのではないかと考えられます。それ以降,ピアソンにならって,χ2と表すことが定着したようです。
ただし,「カイ2乗分布」に「2乗」という言葉が入っていることには意味があります。実は,Xが標準正規分布に従うとき,X2は自由度1のカイ2乗分布に従います。
実際に,カイ2乗分布の確率密度関数にn=1を代入すると,自由度1のカイ2乗分布の確率密度関数は次の式になります。
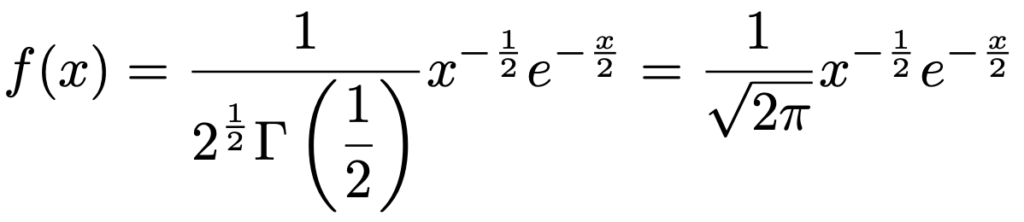
詳細は省略しますが,標準正規分布の確率密度関数を使ってy=x2と変数変換することで,この自由度1のカイ2乗分布との対応関係が確認できます。
次に,下のn個の確率変数が独立に標準正規分布に従っているとします。
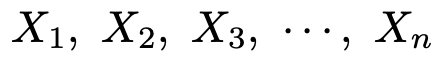
このとき,次の式で定まる確率変数Wnは自由度nのカイ2乗分布に従います。
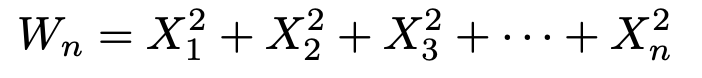
さらに,言い換えてみましょう。上のn個の確率変数が独立に次の正規分布に従っているとします。
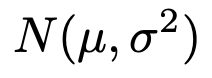
このとき,次の式で定まる確率変数は自由度nのカイ2乗分布に従います。なぜなら,X1からXnまでの1つずつの確率変数がすべて標準化されていて,上と同じようなn個の独立な標準正規分布に従う確率変数の2乗の和に等しいからです。
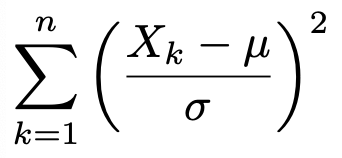
ということで,平たく言えば,カイ2乗分布というのは,標準正規分布の2乗の和であり,自由度はそれらがたし合わされている数に等しいのです。
このことから,次のカイ2乗分布の性質①も理解できるでしょう。
Xが自由度mのカイ2乗分布に,Yが自由度nのカイ2乗分布にそれぞれ従い,XとYが独立ならば,X+Yは自由度m+nのカイ2乗分布に従う。
m個の標準正規分布に従う確率変数の2乗の和とn個の標準正規分布に従う確率変数の2乗の和を加えれば,m+n個の標準正規分布に従う確率変数の2乗の和になるわけです。この性質を,正規分布のときと同じように,再生性と呼ぶことがあります。
このセクションの最後として,期待値と分散に触れておきます。Xが自由度nのカイ2乗分布に従うとき,その期待値,分散は次のようになります。
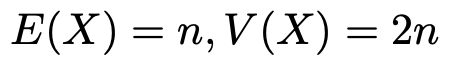
積分を計算することで,このことを確認することもできますが,ここでは省略します。
カイ2乗分布のグラフ
カイ2乗分布の確率密度関数のグラフは左右対称ではなく,確率密度が正の値をとるのはx≧0の範囲だけなので,正規分布やt分布の確率密度関数のグラフとは明らかに異なります。また,自由度によって,形が大きく変わります。自由度が3以上のときには1つの山があるので,これまでに学習した連続型の確率分布の確率密度関数のグラフと似ている面もありますが,自由度が1と2のときには,山がなく,単調に減少していくグラフなので,正規分布などとは全く異なります。以下では,自由度の違いによるグラフの形の違いを確認していきます。
自由度が1のときのグラフは次のようになります。
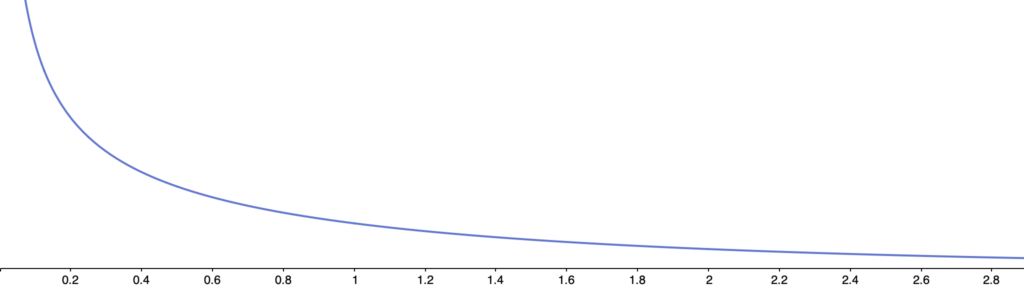
自由度nのカイ2乗分布の確率密度関数にn=1を代入すると,次のようになります。
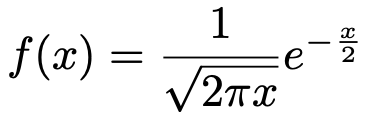
xが分母に入るので,x→0のとき,値は無限に大きくなります。
次に,自由度が2のときのグラフは次のようになります。
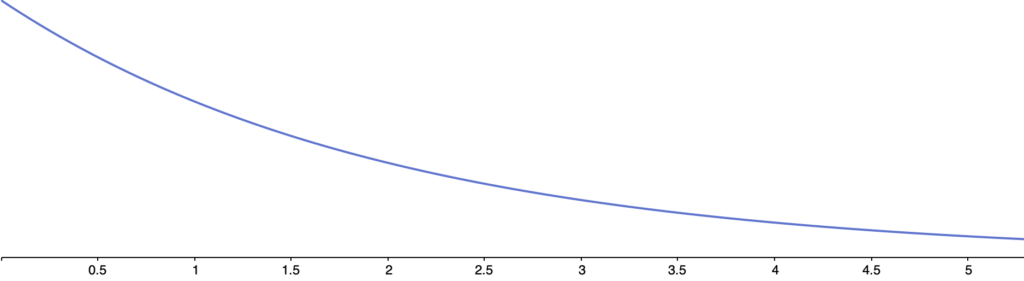
自由度nのカイ2乗分布の確率密度関数にn=2を代入すると,次のようになります。
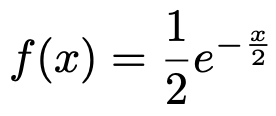
これは指数関数と呼ばれるもので,高校で学習したことのある人ならば,グラフが上の図のようになることは納得できるでしょう。
自由度が3のときのグラフは次のようになります。
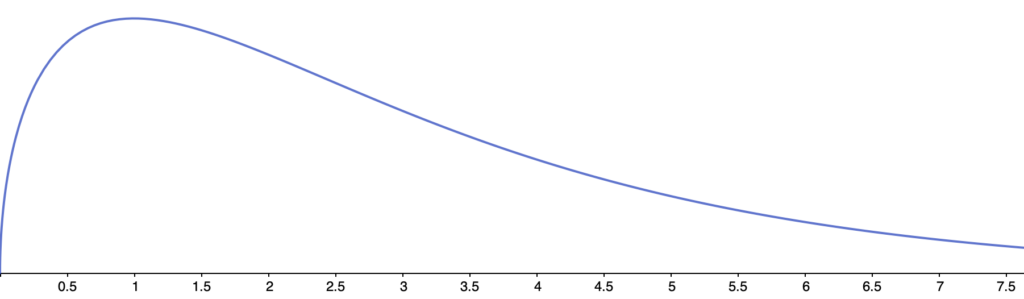
自由度が4のときのグラフは次のようになります。
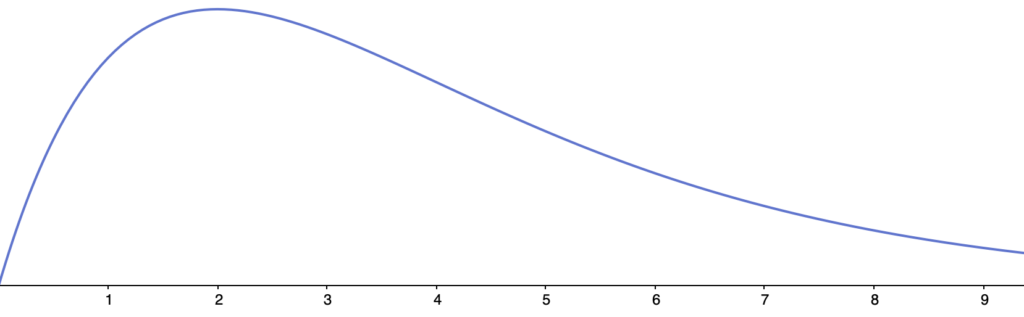
自由度が10のときのグラフは次のようになります。
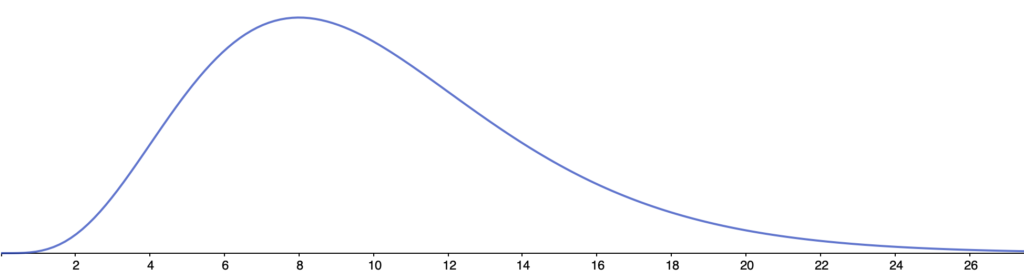
という感じで,目盛りを見ていくと,自由度が大きくなるにつれて山の位置が右にずれつつ,山の裾の幅も広がっています。カイ2乗分布の期待値が自由度に等しく,分散が自由度の2倍なので,期待値も分散も自由度とともに大きくなるからです。
カイ2乗分布の確率
カイ2乗分布に従う確率変数の確率は,正規分布やt分布の場合と同じように,表を使って求めます。統計学のテキストには,次のようなカイ2乗分布表が載っています。
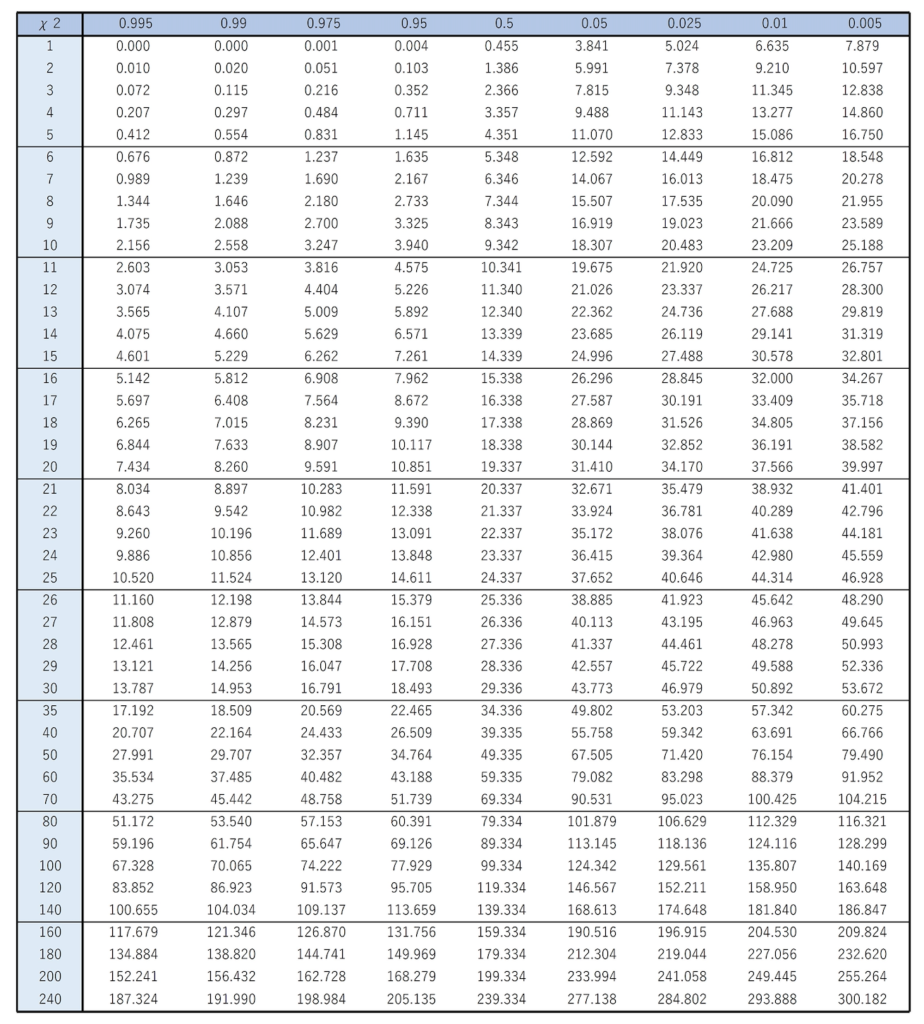
この表の見方は,はじめに,いちばん左の縦1列で自由度を指定して,その行を横に見ていきます。次に,いちばん上の行で上側確率αを指定して,その列を縦に見ていき,これらが交差したところに書かれている数が,上側100α%点になります。
では,実際にカイ2乗分布表を使って,問題を解いてみましょう。
【問題】確率変数X1,X2,X3は互いに独立に標準正規分布に従うものとし,次の式で確率変数Wを定める。
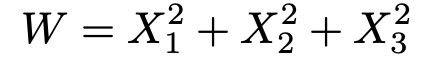
このとき,次の式を満たすaの値を,小数第2位まで求めなさい。

【解答】Wは標準正規分布に従う独立な3つの確率変数の2乗の和なので,自由度3のカイ2乗分布に従います。よって,次の図のように,カイ2乗分布表の自由度3の行を見ます。

求めるものは,a以上の値をとる確率が0.95となるa,つまり,上側95%点です。したがって,いちばん左の列で3の行を選び,いちばん上の行で0.95の列を選んで交わったところを見て,0.352とわかります。小数第3位を四捨五入して,答えは0.35です。
(解答終わり)
母分散の推定
母平均の推定は第9回の記事で解説しましたが,母分散の推定をするにはどうしたら良いでしょうか。第8回の記事で触れたように,母分散の推定量は不偏分散でしたね。そこで,不偏分散が従う確率分布がわかれば母分散の推定ができそうです。実は,そこで登場するのがカイ2乗分布であり,そこで使うのが次の性質です。
次のn個の確率変数を,正規母集団N(μ,σ2)からの無作為標本とする。
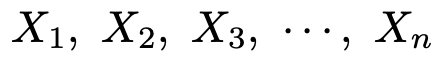
このとき,標本平均をXとして,次の確率変数は自由度n−1のカイ2乗分布に従う。
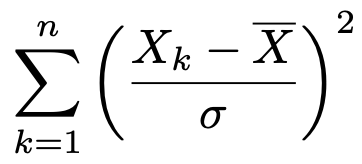
この性質②の最後の式で,標本平均Xを母平均μにおきかえた確率変数が自由度nのカイ2乗分布に従うことは,すでに述べた通りです。μの代わりに標本平均Xを使うと,カイ2乗分布に従うものの,自由度が1下がるというのが性質②の主張です。
この性質を証明することは難しいので,以下では直感的な説明をしていきます。もし,どうしても証明が知りたい方は,「データ解析のための数理統計入門(久保川達也著,共立出版)」を参照してください。
では,上の性質②で,自由度nー1のカイ2乗分布に従うことになる最後の式の分母のσ2をいったん忘れてしまい,分子の和を次のように変形します。
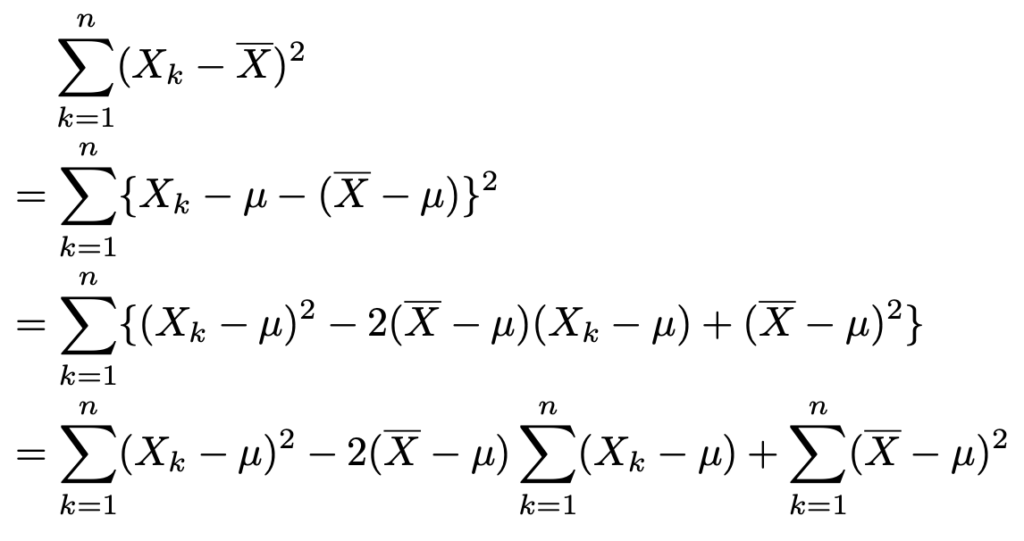
上の式の第2項だけを変形すると,次のようになります。
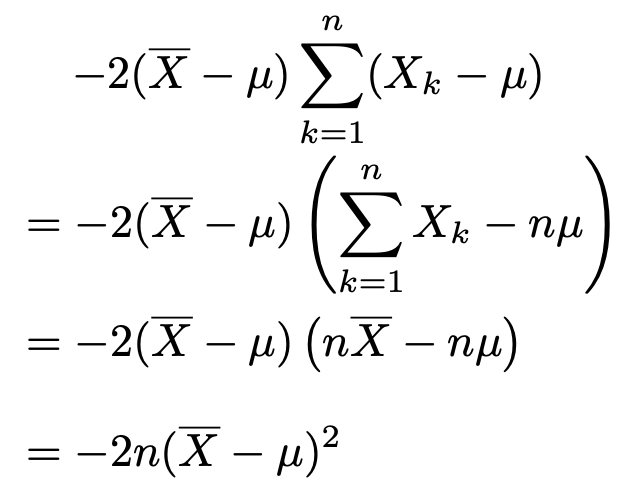
この結果を1つ前の式に代入すると,次の式が成り立ちます。
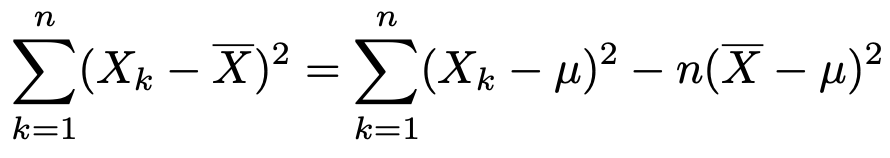
この式の両辺をσ2でわると,次のようになります。
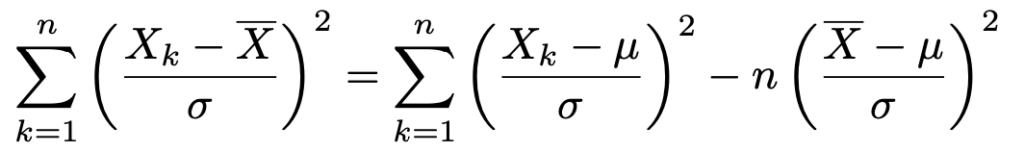
右辺第2項を左辺に移項して,nをかっこの中に入れると次のようになります。
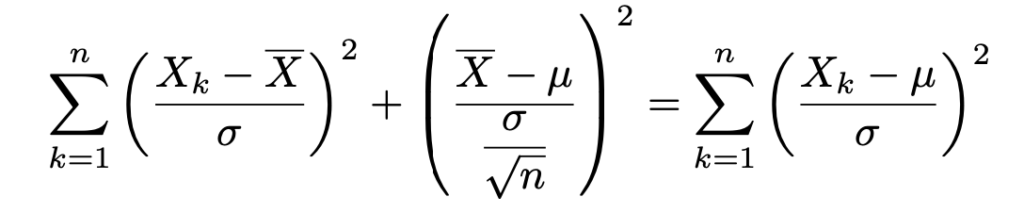
この式の左辺の第2項は標準正規分布に従う確率変数の2乗なので,自由度1のカイ2乗分布に従います。また,右辺は標準正規分布に従うn個の独立な確率変数の2乗の和なので,左辺の第1項は標準正規分布に従うnー1個の独立な確率変数の2乗の和に相当します。左辺の第1項が自由度nー1のカイ2乗分布に従うという性質②は,このように解釈できるわけです。
また,その項は,不偏分散をU2とすると次のようにも表せます。
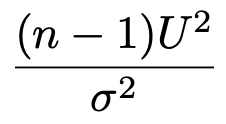
繰り返しになりますが,この確率変数が自由度nー1のカイ2乗分布に従うわけです。以下で,母分散の推定や検定の問題を解くときにはこの形で使うことが多いので,覚えておきましょう。では,これを踏まえて母分散の区間推定の問題を解いていきます。
【問題】あるメーカーが製造しているロープの破断荷重(ロープに物をつるしたときにロープが破損する重さ)を調べるために,6本のロープを無作為に抽出したところ,次のような結果になった。
5.1,4.7,5.3,5.2,5.5,4.8(トン)
このとき,母分散σ2の信頼度95%の信頼区間を求めなさい。ただし,メーカーが製造しているロープの破断荷重は正規分布に従うものとする。
【解答】標本の大きさが6なので,不偏分散をU2とすると,次の確率変数は自由度5のカイ2乗分布に従います。
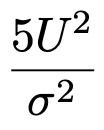
標本平均を計算すると,次のようになります。
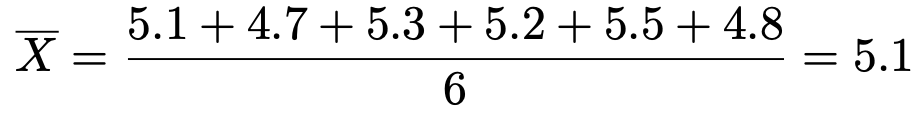
不偏分散の5倍を計算すると,次のようになります。
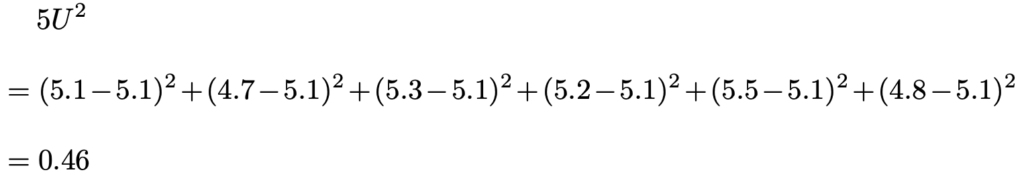
カイ2乗分布表から,自由度5のカイ2乗分布の下側2.5%点は0.831,上側2.5%点は12.833であるから,次の不等式が成り立ちます。
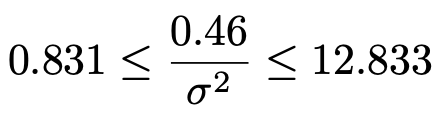
真ん中にσ2がくるように変形すると,次のようになります。
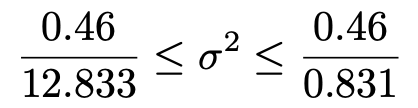
最左辺と最右辺を小数第4位を四捨五入して計算すると,母分散の信頼度95%の信頼区間は次のようになります。
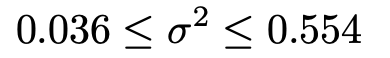
(解答終わり)
母分散の検定
推定のセクションで説明したように,正規母集団の母分散をσ2,無作為抽出した大きさnの標本から計算した不偏分散をU2として,次の確率変数が自由度n−1のカイ2乗分布に従うんでしたね。
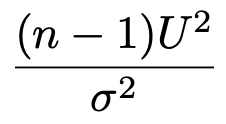
母分散がある値に等しいかどうかを検定するとき,これが検定量(検定統計量)になります。では,実際に問題を解いてみましょう。
【問題】あるフラワーパークのひまわりの背丈は,昨年まで標準偏差36cmの正規分布に従っていた。今年,このフラワーパークで20本のひまわりを標本として無作為に抽出して調べたところ,標本の標準偏差は54cmであった。今年のひまわりは,昨年までと比べて,背丈のばらつきが大きいと言えるか,有意水準1%で検定しなさい。ただし,標本の標準偏差とは不偏分散の正の平方根のこととする。
【解答】今年のひまわりの背丈の母標準偏差をσとすると,帰無仮説はσ=36,対立仮説はσ>36と表すことができ,片側検定です。帰無仮説のもとで検定量を計算すると,次のようになります。
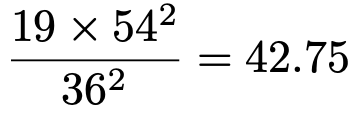
有意水準1%なので,この値を自由度19のカイ2乗分布の上側1%点と比べます。カイ2乗分布表より,この上側1%点は36.191なので,36.191<42.75より,有意水準1%で帰無仮説は棄却され,ひまわりの背丈のばらつきは,昨年までより大きくなったと言えます。
(解答終わり)
適合度検定
ある確率分布に,観測された度数が適合しないことを示すのが適合度検定です。この検定の帰無仮説と対立仮説は次の通りです。
帰無仮説:観測された度数は仮定した理論に適合する
対立仮説:観測された度数は仮定した理論に適合しない
適合度検定は,次の性質③によって成り立っています。
母集団がk個の排反な部分集団に分割されていて,これらのk個の部分集団に属する確率がそれぞれ次の通りであるとする。
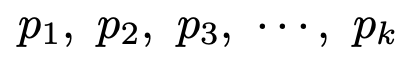
この母集団から無作為抽出された大きさnの標本のうち,これらのk個の部分集団に属する度数をそれぞれ次のようにおく。
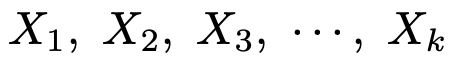
nが十分に大きいとき,帰無仮説のもとで次の確率変数は近似的に自由度kー1のカイ2乗分布に従う。
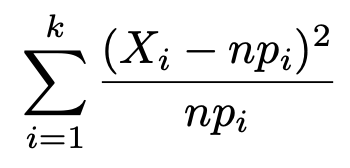
この性質③の最後のシグマの式をもとに検定量を計算することになります。この式のXiを観測度数,npiを理論度数または期待度数と言います。この証明もかなりの脱線になってしまうため,ここでは省略しますが,どうしても知りたい方は上で紹介済みの「確率・統計入門(小針晛宏著,岩波書店)」を参照してください。
性質③の最後のシグマの式の分子は,観測度数と理論度数のズレを計算しています。よって,理論度数からのズレが大きいという対立仮説が正しいとすると,カイ2乗統計量の値は大きくなり,カイ2乗分布の右裾付近の値を取ります。したがって,適合度検定は必ず右片側検定になります。
適合度検定のようにカイ2乗分布を使う検定のことをカイ2乗検定と呼ぶことがあります。カイ2乗検定のもう1つの例である独立性の検定については別の記事(リンクはこちら)で解説しています。
では,これを使って問題を解いていきましょう。
【問題】「一等が出る確率が10%,二等が出る確率が20%,三等が出る確率が30%」と言われているくじがある。ただし,一等,二等,三等以外はハズレである。このくじを80人がひいたところ,一等が2人,二等が13人,三等が30人,ハズレが35人だった。このくじで言われている「一等が出る確率が10%,二等が出る確率が20%,三等が出る確率が30%」は正しいと言えるか,有意水準5%で検定しなさい。
【解答】帰無仮説は「一等が出る確率が10%,二等が出る確率が20%,三等が出る確率が30%」です。帰無仮説のもとで期待度数を計算すると,一等は,80×0.1=8(人),二等は,80×0.2=16(人),三等は,80×0.3=24(人),ハズレは,80×0.4=32(人)となります。
この期待度数と問題で与えられた観測度数をもとに検定量を計算すると,次のようになります。
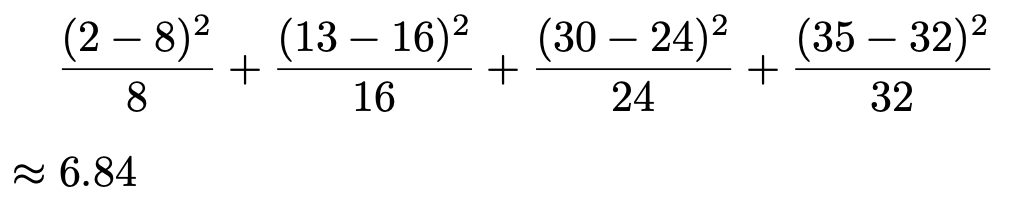
いま,4個の部分集団があるので,自由度3のカイ2乗分布の上側5%点を調べると,カイ2乗分布表から7.815とわかります。6.84<7.815より,帰無仮説は受容され,「一等が出る確率が10%,二等が出る確率が20%,三等が出る確率が30%」は正しくないとは言えないという結論になります。
(解答終わり)
カイ2乗分布についての基本的な説明は以上になります。ここからは,さらに理解を深めるための演習問題ですので,余力があればぜひチャレンジしてみてください。
演習1〜カイ2乗分布と正規分布〜
【問題】互いに独立な確率変数X,Yがそれぞれ次の正規分布に従うものとする。
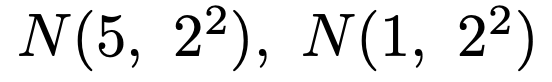
このとき,次の不等式が成り立つ確率を小数第2位まで求めなさい。
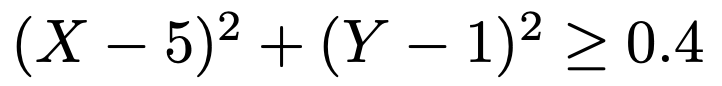
【解答】問題で与えられた不等式の両辺を,X,Yが従う正規分布の分散22=4でわると,次のようになります。
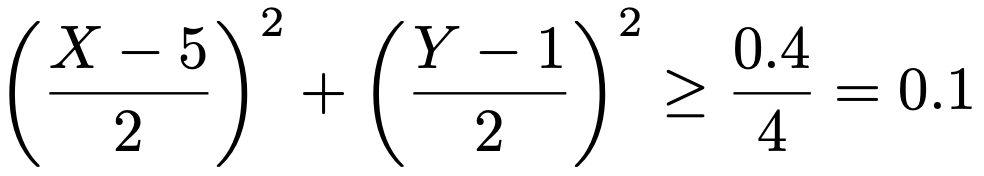
この不等式の最左辺の2つの項のかっこの中は,X,Yからそれぞれの期待値をひいて標準偏差でわった形をしているので,標準正規分布に従う確率変数になっています。互いに独立な標準正規分布に従う2つの確率変数の2乗の和は自由度2のカイ2乗分布に従うので,自由度2のカイ2乗分布に従う確率変数が0.1以上の値をとる確率を求めればいいことになります。
カイ2乗分布表で,自由度2の行を見ると,上側確率が0.95となるときの確率変数の値が0.1≒0.103であることがわかるので,答えは0.95です。
(解答終わり)
演習2〜カイ2乗分布の確率〜
【問題】次のn個の確率変数を考える。
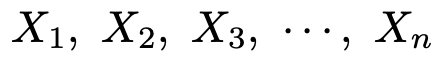
これらは互いに独立に標準正規分布に従うものとする。また,確率変数Wnを次の式で定める。
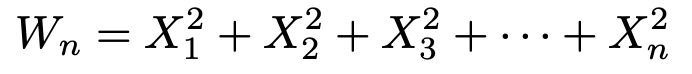
このとき,次の式を満たす自然数nのうち,最も小さい値を求めなさい。
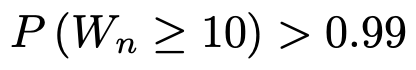
【解答】問題で与えられた不等式は,「10以上の値をとる確率が0.99を超える」という意味です。言い換えると,「上側99%点が10を超える」ということです。そこで,カイ2乗分布表で,上側99%点を調べます。自由度22の上側99%点は9.542だから,条件に合いませんが,自由度23の上側99%点は10.196だから,条件を満たします。よって,最も小さいnの値は23です。
(解答終わり)
演習3〜母分散の推定〜
【問題】ある自動車メーカー製の車種Aの新車を無作為に10台抽出して燃費を調べたところ,標本の標準偏差は0.4km/Lであった。このとき,母分散の信頼度99%の信頼区間を求めなさい。ただし,車種Aの燃費は正規分布に従うものとし,標本の標準偏差とは不偏分散の正の平方根のこととする。
【解答】標本の大きさが10なので,母分散をσ2,不偏分散をU2とすると,次の確率変数は自由度9のカイ2乗分布に従います。
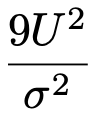
カイ2乗分布表から,自由度9のカイ2乗分布の下側0.5%点は1.735,上側0.5%点は23.589であるから,次の不等式が成り立ちます。
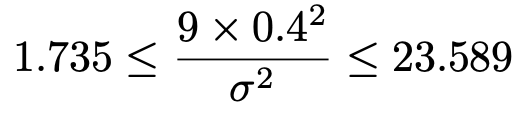
真ん中にσ2がくるように変形すると,次のようになります。
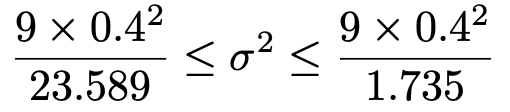
最左辺と最右辺を計算して小数第2位まで求めると,母分散の信頼度99%の信頼区間は次のようになります。
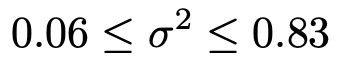
(解答終わり)
演習4〜母分散の検定〜
【問題】ある工場で製造されているペットボトル入りのジュースの内容量は,標準偏差7mLの正規分布に従っている。この工場の製造ラインのうちの1つで,15本の標本を無作為に抽出して調べたところ,標本の標準偏差は9mLであった。この製造ラインは,この工場の中で,内容量のばらつきが異常に大きいと言えるか,有意水準5%で検定しなさい。ただし,標本の標準偏差とは不偏分散の正の平方根のこととする。
【解答】この製造ラインで製造されているジュースの内容量の真の標準偏差をσとすると,帰無仮説はσ=7,対立仮説はσ>7と表せるので,片側検定になります。
帰無仮説のもとで,検定量は次のように計算できます。
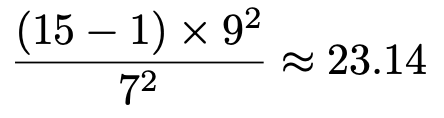
自由度14のカイ2乗分布の上側5%点は,カイ2乗分布表より23.685であるから,23.14<23.685より,この検定量の値は棄却域には入らず,帰無仮説は受容されます。
つまり,内容量のばらつきが異常に大きいとは言い切れない,という結論になります。
(解答終わり)
演習5〜適合度検定〜
【問題】次の表は,1個のサイコロを300回投げ,それぞれの目の数について,出た回数をまとめたものである。

このサイコロは正常であると言えるかを有意水準5%で検定しなさい。
【解答】サイコロを1回投げるとき,1〜6の目が出る確率をそれぞれ次のようにおきます。
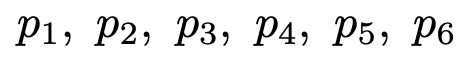
このとき,帰無仮説は次のように表せます。
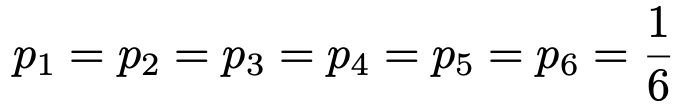
帰無仮説を仮定すると,i=1〜6について,理論度数は次のように求められます。
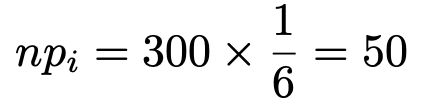
このとき,検定量は次のように求められます。
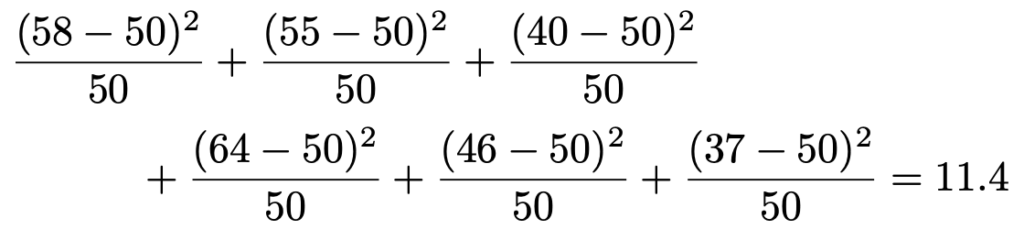
6ー1=5より,自由度5のカイ2乗分布の上側5%点をカイ2乗分布表から調べると,約11.07とわかります。
11.07<11.4であるから,検定量の値は棄却域に落ちます。有意水準5%で帰無仮説は棄却され,サイコロは正常ではないということになります。
(解答終わり)
最後までお付き合いいただき,ありがとうございました!
引き続き,第14回以降の記事へ進んでいきましょう!
2023年1月に「統計検定2級公式問題集[CBT対応版](実務教育出版)」が発売されました!(CBTが何かわからない人はこちら)
CBTは1つの画面で問題と選択肢が完結するシンプルな出題ですが,本書は分野ごとにその形式の問題を並べた構成になっていて,最後に模擬テストがついています。CBT対策の新たな心強い味方ですね!
さらに実戦に向けた演習を積みたい人は,「統計検定2級公式問題集2018〜2021年(実務教育出版)」を手に取ってみてください。
また,もっと別の問題を解いてみたい人は,さらにさかのぼって「統計検定2級公式問題集2016〜2017年(実務教育出版)」を解いて実力に磨きをかけましょう!



![統計検定2級公式問題集[CBT対応版]](https://m.media-amazon.com/images/I/51q3GfZId3L._SL500_.jpg)




コメント
適合度検定のくじの問題について質問があります。
なぜ両側ではなくどうして片側検定なのでしょうか。
「一等が出る確率が10%,二等が出る確率が20%,三等が出る確率が30%」が正しいかどうかを検定する問題である認識しており、対立仮説は不等号で表せないと思います。
この問題では両側検定をしても帰無仮説を受容するという結果は変わりませんが疑問に思いました。
この問題文の少し上で説明しているように,
カイ2乗統計量の実現値が大きいほど,
理論分布とのズレが大きいということになりますので,
カイ2乗統計量がある程度以上大きければ
帰無仮説を棄却する(片側検定)ということになります。
このように,適合度検定は必ず片側検定です。
「<or>」か「≠」かという判断基準は
片側と両側の両方が考えられる仮説検定の場合に用いてください。